Nanoscale radiofrequency impedance sensors with unconditionally stable tuning

Abstract

Impedance sensors perform an important role in a number of biosensing applications, including particle counting, sizing, and velocimetry. Detection of nanoparticles, or changes in, e.g., the interfacial Debye–Hückel layer, can also be performed using nanoscale impedance sensors. One method for monitoring changes in the local impedance is to use radiofrequency reflectometry, which when combined with an impedance-matched sensor can afford very high sensitivity with very large detection bandwidth. Maintaining sensitivity and dynamic range, however, requires continuous tuning of the impedance matching network. Here we demonstrate a dual feedback tuning circuit, which allows us to maintain near-perfect impedance matching, even in the presence of long-term drifts in sensor impedance. We apply this tuning technique to a nanoscale interdigitated impedance sensor, designed to allow the direct detection of nanoparticles or real-time monitoring of molecular surface binding. We demonstrate optimal performance of the nanoscale sensor and tuned impedance network both when modulating the concentration of saline to which the sensor is exposed and when electronically switching between sensors configured in a two-element differential array, achieving a stabilization response time of <20 ms.

INTRODUCTION

Biosensing using electronic methods holds great promise, both for the ease of constructing highly parallel sensor arrays and for simplified interfacing to semiconductor circuitry. Electronic sensing in biologically relevant saline solutions, however, presents challenges due to the relatively large electrical impedance exhibited by the saline solution and by the capacitive double layer formed between the solution and the sensor electrodes.^{1, 2, 3, 4} The use of radiofrequency (rf) signals above ∼1 MHz reduces the double-layer impedance compared to that at lower frequencies,^{5, 6, 7} allowing monitoring of the bulk solution impedance. We have used rf reflectometry to demonstrate a number of biometric sensing applications, including cell cytometry,⁸ particle and cell velocimetry, particle and cell volumetry,⁹ and the high-throughput detection and identification of micron-scale digital cell labels.¹⁰ The enumeration and measurement of particles or cells in the few-micron diameter size range, flowing at rates in excess of 10⁴–10⁵∕s through a microfluidic channel, is easily achieved, providing functionality comparable to fluorescence-activated cell sorters and Coulter counters,^{11, 12} but in a fully lithographed, compact system, that can easily be scaled to large array geometries.

We are extending these capabilities to enable nanoparticle detection (diameters <1 μm) and surface-bound molecules.^{13, 14} To this end, we have developed a novel nanoscale interdigitated transducer (nIDT) that should allow rf detection of individual target particles in ∼0.1–1M salt concentrations. Achieving and maintaining the desired sensitivity, however, requires that the reflectometry electronics be carefully tuned, and maintained at the optimal tuning point, over the entire measurement. For cell sorting, for example, this might require stable operation over ∼1 h, in the presence of slow temperature drifts, changes in saline concentration, and changes in the double layer, such as that due to adsorption of ionic species. Furthermore, if sensors are operated in an arrayed or multiplexed geometry, for multichannel or differential sensing, the readout electronics will need to be tuned each time a different sensor element is measured, requiring a rapid and unconditionally stable tuning protocol.

Here we demonstrate both the fabrication and operation of the nIDT sensors as well as the implementation and operation of an unconditionally stable reflectometer tuning circuit, which automatically adjusts the operating frequency and matching circuit parameters to maintain optimal nIDT tuning, achieved with better than 20 ms response time.

NANOSCALE IMPEDANCE SENSOR

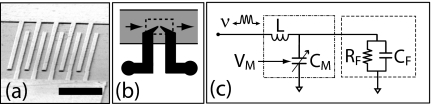
Our basic sensor design is shown in Fig. 1, with a device image shown in panel (a), the microfluidic embedding in (b), and the equivalent circuit in (c). The sensor has a very small active volume of ∼10 μm³=10⁻¹⁴ l, enclosed in a 0.1×1.5 mm² cross-section microfluidic channel. The sensor geometry consists of five pairs of 25 μm long, 200 nm wide interdigitated fingers separated by 200 nm gaps [see Fig. 1a]. Calculations indicate that for the relevant saline concentrations, the electric field between the interdigitated fingers is uniformly distributed along the finger length, so that the entire sensor participates in the response. The sensor can be accurately modeled over a small frequency range as a parallel combination of a resistor R_F and a capacitor C_F [see Fig. 1c]. Changes in the saline concentration, inclusion of nanoparticles in the flow volume, or binding of molecules to the sensor surface will all slightly change the sensor impedance. We have employed this sensor to perform detailed measurements of the voltage dependence of the Debye–Hückel double-layer capacitance,¹⁵ where changes in the saline electrostatic potential with respect to the electrode surface changes the ion shielding concentration and thus the double-layer capacitance.

Figure 1.

(a) Electron micrograph of nIDT; scale bar is 2 μm. (b) Sketch of nIDT large-scale electrodes (black) embedded in microfluidic channel (gray); nIDT is at the center of dashed box. (c) rf equivalent circuit of device and matching circuit, showing device (dashed box) modeled as parallel combination of fluid resistance R_F and capacitance C_F, and matching circuit (dashed-dot box), comprising a variable matching capacitor C_M controlled by external voltage V_M and inductor L. The measurement frequency ν is the other control variable in the circuit.

The circuit diagram in Fig. 1c shows two externally adjustable parameters: the operating frequency ν and the matching circuit varactor voltage V_M, the latter used to tune the matching circuit impedance. With these two adjustable parameters, our sensor can in principle always be perfectly impedance matched to 50 Ω, so that all power incident on the device would be absorbed. Monitoring this reflected power then effectively allows a differential measurement of the impedance of the device; using large incident rf power and a low-noise preamplifier for the reflected signal yields very high sensitivity to small changes in the device impedance;^{16, 17} we have achieved impedance matching to about 1 part in 10⁵. Large measurement bandwidths can also be achieved, typically 5%–10% of the measurement frequency.

The nIDT was fabricated on a polished glass substrate, using single-layer electron-beam lithography followed by lift-off of a thermally evaporated gold film (40 nm thick) with an underlying chromium adhesion layer (10 nm thick). We used gold and glass for their known biocompatibility, and for ease of integration with polydimethylsiloxane (PDMS)-based microfluidic structures¹⁸ (we note that the Cr adhesion layer was entirely covered in gold, and thus not exposed to fluid during measurements).

The nIDT was embedded in a PDMS microfluidic channel. The PDMS was cast on a mold made from photodefinable epoxy (SU-8, Microchem, Newton MA), consisting of a 0.5 μm thick base layer and 100 μm tall, 16 mm long ridge, patterned by photolithography on a silicon wafer. Brass tube fittings (1.52 mm outer diameter) were lightly adhered to the mold prior to casting the PDMS, to serve as fluid ports in the final structure. The PDMS was mixed from a ratio of 10 parts base to 1 part curing agent (RTV 615A∕B, GE Silicones, Waterford NY), thoroughly degassed in vacuum and poured onto the SU-8 mold. After partial fixing, the elastomer was baked for 1 h at 80 °C to complete curing. The molded elastomer was then released from the SU-8 mold.

The glass substrate with the patterned nIDT was cleaned in solvent (acetone and isopropanol, followed by a de-ionized water rinse). The glass was then soaked for 5 min in an 80 °C Piranha solution (3:1 parts by volume of bottle strength H₂SO₄:H₂O₂), and the PDMS surface treated in an ultaviolet-ozone reactor. When brought into contact and baked at 120 °C under moderate pressure for 5 min, the PDMS and glass are bonded, sealing the nIDTs within the elastomeric microchannel. A single PDMS microchannel accommodates 12 nIDTs with a pitch of 1 mm. The PDMS leaves a pair of wirebond pads exposed for each nIDT, to which wire bond connections were made with 25 μm (1 mil) diameter gold wire bonds, connecting each nIDT to a patterned copper stripline on an FR-8 single-sided circuit board [see Fig. 1b]. Fluidic connections were made by attaching 1.27 mm inner diameter Tygon tubing to the brass fittings embedded in the PDMS mold, supplying the channel with fluid analyte.

The equivalent parallel circuit parameters R_F and C_F for the nIDT are determined by the geometry of the nIDT and the electrical properties of the buffer in the microfluidic channel. For the measurements reported here, using tris-buffered saline [TBS: 1.5M NaCl, 0.1M tris(hydroxymethyl)aminomethane, 0.05M HCl, 0.05% w∕v polysorbate 20, pH 8.6], the equivalent parallel resistance is R_F≈500 Ω and capacitance C_F≈0.5 pF at 100 MHz.

The nIDT is embedded in the tuning circuit shown in Fig. 1. The electrical impedance presented by the matching circuit and the nIDT is approximately

$$Z\left(\omega \right)=i\omega L+\frac{1}{i\omega C+1∕R},$$ (1)

where C=C_M+C_F, with C_M the variable impedance matching capacitance, and 1∕R=1∕R_F+1∕R_S, with R_S∼10 kΩ the stray resistance associated with inductive and capacitive loss (not shown in Fig. 1); ω=2πν is the angular carrier frequency. The frequency and variable capacitance are adjusted to achieve impedance matching, so that Z(ω)=Z₀. This occurs when

$$Z_0=\frac{R}{1+{\omega }^2{R}^2{C}^2},$$ (2)

$${\omega }^2=\frac{1}{LC}-\frac{1}{R^2{C}^2}$$

two conditions that can be met simultaneously for the model circuit.

The voltage of the signal reflected from the nIDT and its impedance tuning circuit is given by

$$V_{\text{refl}}=\frac{Z-Z_0}{Z+Z_0}{V}_{\text{in}},$$ (3)

for an incident input voltage V_in. At the impedance matching point 2, the reflected power is in principle zero, and for small deviations from that point, the reflected power is quadratic in the impedance mismatch ΔZ=Z−Z₀. Operating at the impedance matching point therefore provides a “dark field” sensing technique, where changes in the device impedance yield increases in the reflected power from a nominally zero value, allowing very sensitive operation by using large amplification of the reflected signal. In a sense, the reflectometry can be viewed as an impedance bridge, balancing the device impedance against the 50 Ω system characteristic impedance. The bandwidth of the measurement, i.e., the speed the circuit can respond to changes in the device impedance, is determined by the width of the resonance between the inductor L and the parallel capacitances C_M and C_F; in most cases, the fluid resistance R_F is large compared to the implicit parallel 50 Ω impedance of the measurement cabling, so the bandwidth is determined by the latter and is approximately $\Delta \nu \approx \left(R∕\sqrt{L∕C}\right)\nu$, and is 5%–10% of the measurement frequency ν.

ACTIVE IMPEDANCE MATCHING

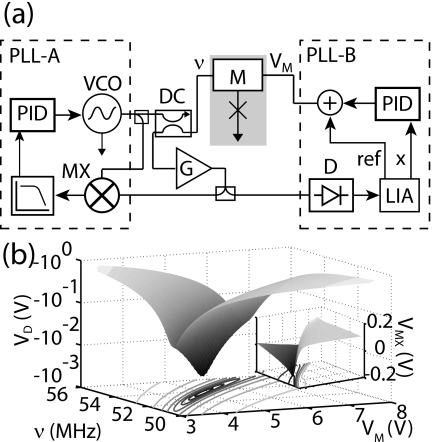
In order to achieve rapid and precise tuning, we have constructed a two-parameter closed-loop feedback circuit, shown in Fig. 2a, one loop of which tunes the frequency ν, while the second loop tunes the variable capacitance, to maintain operation at the optimal impedance-matched point.

Figure 2.

(a) Circuit diagram for dual feedback loops for frequency ν and varactor voltage V_M. Power detector (D) and mixer (MX) are heterodyne readouts of magnitude and phase of reflected signal. PIDs are feedback controllers, and LIA is a lock-in amplifier. (b) Main panel: Open-loop amplitude of reflected signal; the vertical scale is the detector output. Inset: Open-loop output of mixer; horizontal scales are the same as for main panel.

The first feedback phase-locked loop (PLL-A) measures the relative phase of the reflected signal by mixing it with the drive signal, generating a voltage proportional to the sine of the phase difference; this voltage is low-pass filtered below 2 kHz and passed to a proportional-integral-derivative (PID) controller, which in turn controls the voltage-controlled oscillator (VCO) frequency ν. The second phase-locked loop (PLL-B) measures the absolute reflected power P using a diode (D) and adjusts the varactor voltage V_M to minimize the derivative dP∕dV_M. This derivative is determined by modulating V_M using the reference signal of a lock-in amplifier (LIA), while monitoring the resulting modulation in the diode signal, yielding an output proportional to the derivative. The LIA output, filtered with a 3 ms time constant, is sent to a second PID controller, whose output together with the LIA reference signal control the dc set point and the modulation of the varactor voltage.

In Fig. 2b, we show the open-loop response of the diode detector (main panel) and the mixer (inset) as a function of VCO frequency ν and varactor voltage V_M. Note that the diode voltage scale is inverted and has an absolute minimum. This is as expected: for given fluid parameters R_F and C_F, ideal impedance matching will be achieved at a single measurement frequency ν=ω∕2π and total capacitance C=C_M+C_F, at which point the reflected power is in principle zero, yielding a single-point minimum in the diode detector response. As the frequency and varactor voltage are changed from this ideal point, the reflected power increases in proportion to the impedance mismatch (ΔZ)², convolved with the response of the diode.

By contrast, the mixer output has a monotonic, gradual steplike response as a function of frequency and voltage; this is again as expected, as the mixer output is proportional to sin(ϕ−ϕ₀), the sine of difference in the phase ϕ of the reflected signal from the reference phase ϕ₀. The reflected phase changes most rapidly near the impedance matching point, yielding the steplike response in the mixer output near that point. Choosing a set point for the feedback on the mixer output defines a line in the ν−V_M plane, which combined with the extremum in diode output defines a unique stable operating point. Note that we cannot easily use the diode output only, as one then has to find a minimum in two dimensions; combining the two measurements means that the optimal point is found by a one-dimensional tuning of the mixer output, which is done rapidly, combined with a slower adjustment to minimize the derivative in the diode output.

RESULTS AND DISCUSSION

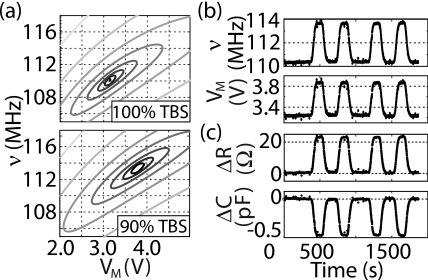
We tested the feedback control system by changing the electrolyte concentration, which changes the local nIDT electrical impedance. Using a constant buffer flow, we modulated between 100% and 90% TBS, a concentration modulation that should yield an approximately 10% change in the effective saline electrical resistance R_S and a 5% change in the double-layer capacitance C_DL of the saline solution. In Fig. 3a, we display the open-loop response of the diode detector, as a function of frequency and varactor voltage, for each saline concentration. In Fig. 3b, we show the time-domain response of the closed-loop feedback signals when the solution was modulated in time between the two buffer concentrations. The saline electrical resistance R_S and the double-layer capacitance C_DL are best physically modeled as a series-connected lumped circuit; the effective electrical circuit that is best suited to our reflectometer measurement, as shown in Fig. 1c, is, however, a parallel combination of the fluid resistance R_F and capacitance C_F. One can map from the series to the parallel circuit configuration using the impedance transformation equations

$$R_F=\frac{R_S^2+1∕{\left(\omega C_{\text{DL}}\right)}^2}{R_S},$$ (4)

$$\omega C_F=\frac{1}{\left[R_S^2+1∕{\left(\omega C_{\text{DL}}\right)}^2\right]}\frac{1}{\omega C_{\text{DL}}},$$

where ω is the measurement frequency; equivalent transformations allow extraction of C_DL and R_S from the parallel parameters R_F and C_F. The two circuits are completely equivalent for frequencies near the measurement frequency ω. As noted in the figure caption, the effective change in electrical resistance R_F is about 8% and that of the capacitance C_F is about 15%, close to that expected from the concentration change and the values of R_S and C_DL. Complete equilibration of the saline concentration between different concentration flow plugs took 10 s, a time much longer than the response time of the feedback circuit, which we show below to be less than 20 ms.

Figure 3.

(a) Contour map of open-loop reflected power as a function of frequency and varactor voltage, for 100% and 90% TBS; minima occur at slightly different operating points. (b) Feedback-controlled frequency ν and varactor voltage V_M signal, for saline concentration modulated in time. Data are for four 200 s pulses of 90% TBS solution separated by 150 or 300 s pulses of 100% TBS. (c) Calculated change in equivalent parallel resistance R and capacitance C corresponding to the modulation in (b). Reference values are R=424 Ω and C=9.3 pF, with the device in parallel to the varactor capacitance; other measurements indicate R_F≈450 Ω and C_F≈1.4 pF, changing by 8% and 15% due to the solution modulation.

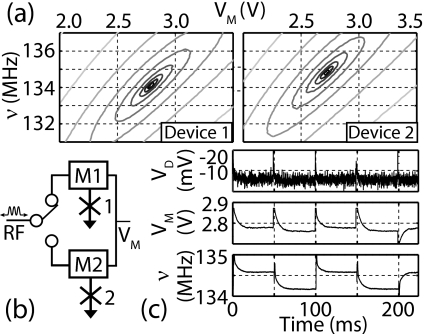
To test the circuit with arrayed sensors, we constructed a two-element sensor, as shown in Fig. 4, using a single two-parameter feedback system to alternately control each sensor. We show the open-loop response, with slightly different optimal operating points for each sensor. We then activated the dual feedback loop and electronically switched between the two sensors at 20 Hz. Stable operation was recovered after switching in a time shorter than 20 ms. This can easily be extended to larger arrays.

Figure 4.

(a) Open-loop reflected power as a function of frequency and varactor voltage for two nIDTs submerged in 100% TBS. Differences in electrical parameters yield different minima for the two sensors. (b) Schematic of multiplexed detectors. V_M is the varactor voltage, M1 and M2 are the matching networks. (c) Real-time feedback signals in closed-loop response when switching between devices at a rate of 20 Hz. V_D is the diode voltage, proportional to detected power.

In conclusion, we have demonstrated a novel nIDT for applications in microfluidic biosensing. Its design parameters permit sensing of extremely small volumes of saline solution, with large bandwidth. We have also developed a two-parameter feedback controller with which these sensors can be maintained ideally impedance-matched, yielding ultrasensitive operation in a reflectometer configuration. The basic sensor and reflectometer electronics used here are similar to recent demonstrations,^{8, 9} but the design and size of the nIDT are unique, greatly reducing the sensing volume and increasing the intrinsic speed of the sensor. In addition, our use of discrete components for detecting rf power and phase, coupled with the various PLL electronics, rather than employing a rf network analyzer, allows us to demonstrate the two-axis tuning that is key to maintaining optimal performance over time scales of hours rather than minutes.