Functional Heterogeneity of Inferior Parietal Cortex during Mathematical Cognition Assessed with Cytoarchitectonic Probability Maps

Abstract

Although the inferior parietal cortex (IPC) has been consistently implicated in mathematical cognition, the functional roles of its subdivisions are poorly understood. We address this problem using probabilistic cytoarchitectonic maps of IPC subdivisions intraparietal sulcus (IPS), angular gyrus (AG), and supramarginal gyrus. We quantified IPC responses relative to task difficulty and individual differences in task proficiency during mental arithmetic (MA) tasks performed with Arabic (MA-A) and Roman (MA-R) numerals. The 2 tasks showed similar levels of activation in 3 distinct IPS areas, hIP1, hIP2, and hIP3, suggesting their obligatory role in MA. Both AG areas, PGa and PGp, were strongly deactivated in both tasks, with stronger deactivations in posterior area PGp. Compared with the more difficult MA-R task, the MA-A task showed greater responses in both AG areas, but this effect was driven by less deactivation in the MA-A task. AG deactivations showed prominent overlap with lateral parietal nodes of the default mode network, suggesting a nonspecific role in MA. In both tasks, greater bilateral AG deactivation was associated with poorer performance. Our findings suggest a close link between IPC structure and function and they provide new evidence for behaviorally salient functional heterogeneity within the IPC during mathematical cognition.

Introduction

The neural basis of mathematical cognition has been intensely studied in recent years given its importance as a skill we use nearly every day. Brain imaging studies have consistently identified a distributed set of brain regions that includes, most prominently, the ventral visual areas, including the lingual and fusiform gyri, inferior parietal cortex (IPC), and the ventrolateral prefrontal cortex (PFC; Burbaud et al. 1995; Dehaene et al. 1999; Delazer et al. 2006; Menon, Rivera, White, Eliez, et al. 2000; Menon, Rivera, White, Glover, et al. 2000; Menon et al. 2002; Rickard et al. 2000; Zago et al. 2001). Within this distributed network, the IPC is thought to play a critical role in representing and manipulating quantitative information, whereas other brain regions, such as the ventrolateral and dorsolateral PFC, are engaged in supportive functions such as working memory, sequencing, controlled retrieval, and decision making (Rueckert et al. 1996; Dehaene et al. 1999; Kazui et al. 2000; Menon, Rivera, White, Glover, et al. 2000; Gruber et al. 2001; Delazer et al. 2003; Zago et al. 2008). The IPC comprises multiple heteromodal regions that play an important role in semantic, phonological, and visuospatial representation of numerical information (Caspers et al. 2008). IPC regions along the banks of the intraparietal sulcus (IPS) as well as the adjoining angular gyrus (AG) and supramarginal gyrus (SMG) have all been implicated in tasks involving mathematical problem solving. Little is known, however, about the differential contributions of these regions, an issue that has been particularly confounded by lack of knowledge about the precise anatomical boundaries of the IPC.

Current efforts in understanding the role of the IPC in mathematical cognition have focused on the IPS because of its role in basic number identification and number comparison tasks (Cohen et al. 2000; Duffau et al. 2002; Delazer et al. 2003; Cohen Kadosh et al. 2007; Piazza et al. 2007). To a lesser extent, the left AG has drawn interest, based on its purported role in rapid, verbally mediated fact retrieval. In a meta-analysis of their data, Dehaene et al. (2003) suggested that the number manipulation in the IPS is supplemented by the left AG when verbal manipulation of numbers is needed and that attention to visuospatial representations on the mental number line is supported by the bilateral posterior superior parietal lobule. Less attention has been paid to the SMG, a brain region important for phonological rehearsal and working memory functions that are evoked during mathematical problem-solving tasks.

Several brain imaging studies have investigated the role of the left and right IPC in mental arithmetic (MA) operations such as single- and double-digit addition, subtraction, and multiplication (Roland and Friberg 1985; Burbaud et al. 1995; Dehaene and Cohen 1997; Menon, Rivera, White, Eliez, et al. 2000; Gruber et al. 2001; Simon et al. 2002). IPC responses during the solution of more abstract and complex mathematical problems, such as calculus integrals, have also been investigated (Krueger et al. 2008). In both cases, the specific contribution of various subdivisions of the IPC in mathematical problem solving is still unclear. Findings to date have been contradictory with respect to task-related dissociations in the IPC during computationally demanding tasks compared with more automated tasks. Whereas some brain imaging studies have reported greater bilateral activation in the IPS during more computationally demanding MA tasks, others have reported greater responses in the left AG during more automated MA tasks (Grabner et al. 2007; Ischebeck et al. 2007). Importantly, at least one study has reported relative decreases, or deactivation, in the left and right AG and the SMG during a simple well-automated multiplication task, compared with a magnitude judgment task (Rickard et al. 2000). To our knowledge, the study by Rickard and colleagues was the first and only study that reported deactivation in both the left and right AG and SMG during MA. Interestingly, this study noted deactivation in every one of their participants, but the precise localization of this deactivation was ambiguously stated to be in a bilateral area centered between the SMG and the AG. Besides the lack of precise localization of IPC responses, another central issue here is that task-related differences can arise from greater activation in the more automated task or greater deactivation during the more computationally demanding task. We address both these issues here at length. Recent studies have highlighted prominent and consistent deactivations of IPC regions in and around the AG across a broad range of cognitive tasks (Greicius et al. 2003; Mechelli et al. 2003; Humphries et al. 2007; Schulman et al. 2003; Harrison et al. 2008; Sweet et al. 2008). Moreover, there is growing evidence to suggest that the level of deactivation decreases with increasing task difficulty (Greicius et al. 2003; Schulman et al. 2003). These deactivations have received less attention in the domain of MA problem solving, and several researchers have, on the contrary, highlighted the engagement, rather than disengagement of the AG in more automated fact retrieval. To address this issue, we systematically investigated both activation and deactivation in specific subdivisions of the IPC as a function of task difficulty.

A major reason for the contradictory findings in the literature has been the poor demarcation of the boundaries of regions that constitute the IPC. There are 2 fundamental problems here; first, the boundaries between the IPS and rest of the IPC are unknown. Second, demarcation of the AG from the SMG is ambiguous as far as macroanatomical features are concerned. Brodmann (1909) differentiated the IPC into 2 areas: the SMG (BA 40) on the rostral aspects of the IPC and AG (BA 39) on the caudal aspects of the IPC. According to Brodmann, the SMG and the AG are demarcated by the Jensen sulcus, but using this sulcus as a border between BA 40 and BA 39 is problematic because of its highly irregular and variable form. Even more problematic is the issue of demarcating the AG and the SMG from the IPS. Other more recently developed parcellation schemes (Tzourio-Mazoyer et al. 2002; Desikan et al. 2006) commonly used in brain imaging studies also suffer from similar deficiencies. Importantly, no existing methods offer a scheme to parcellate the IPS. The dorsal and ventral aspects of the IPS are often arbitrarily ascribed to the IPC or the superior parietal lobule. For example, some studies have treated the ventral bank of the IPS as a part of the AG, whereas others have referred to it as the IPS (Menon, Rivera, White, Glover, et al. 2000; Ischebeck et al. 2006). Thus, the boundaries segregating the IPS from the AG and the SMG are ill specified, leading to misrepresentation of observed functional brain responses in these regions.

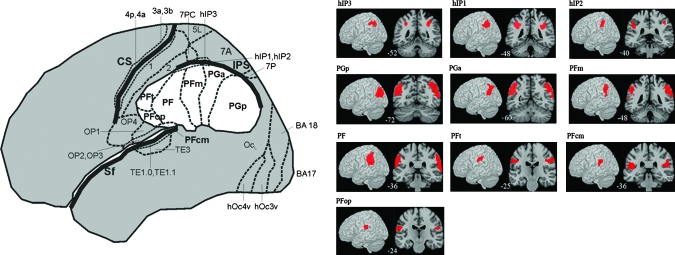
The recent availability of probabilistic cytoarchitectonic maps has the potential to inform and significantly enhance our understanding of the functional architecture of the IPC in mathematical cognition. Cytoarchitectonic maps obtained from postmortem brains suggest that the human IPC has a more finely grained parcellation than previously suggested by the classical Brodmann map. These maps provide objective a priori regions of interest (ROI) that can be used to test anatomically specific hypotheses about the localization of functional activations (Caspers et al. 2008). Recent studies have suggested that the borders of the IPS, SMG, and the AG cannot be reliably detected using macroanatomic or gross anatomical features on magnetic resonance images (MRIs) (Caspers et al. 2008). Detailed analysis of cell types suggests that the IPS can be subdivided into at least 3 regions, as shown in Figure 1. The human intraparietal area 2 (hIP2) occupies the anterior, lateral bank of the human IPS, and area hIP1 is located immediately posterior and medial to hIP2 (Choi et al. 2006). These regions correspond roughly to the monkey anterior intraparietal area, whereas area hIP3 that occupies the posterior human IPS corresponds approximately to monkey ventral intraparietal area (Scheperjans, Eickhoff, et al. 2008; Scheperjans, Hermann, et al. 2008). Ventral to these IPS regions are 2 areas that cover the AG and 5 that cover the SMG (Caspers et al. 2006). The AG consists of the anterior and posterior areas PGa and PGp, respectively, encompassing the caudal aspects of the IPC. In contrast, 3 larger, more dorsal regions— PFm, PF, PFt— and 2 smaller ventral regions— PFcm and PFop— encompass the rostral segments of the IPC along the rostral to caudal axis. Posteriorly, region PFm of the SMG borders the AG region PGa (Caspers et al. 2006, 2008). To account for variability in size and extent of these areas across individuals, cytoarchitectonic probabilistic maps have been calculated for each area in stereotaxic space (Caspers et al. 2008; Scheperjans, Eickhoff, et al. 2008). These probabilistic maps provide a robust anatomical reference for more accurately characterizing structure–function relations in the human IPC during mathematical problem solving.

Figure 1.

Cytoarchitectonic maps of the IPC. Cytoarchitectonic maps of 3 IPS—hIP3, hIP1, and hIP2, 2 AG—PGp and PGa, and 5 SMG—PFm, PF, PFt, PFcm, and PFop areas of the IPC used in the study, ordered along a posterior to anterior gradient (Caspers et al. 2006; Choi et al. 2006; Scheperjans, Hermann, et al. 2008). Surface renderings and coronal sections are shown with the numbers at the bottom of each panel indicating the location of the slices (y-axis in MNI coordinates).

In the present study, we compared brain responses to simple MA tasks involving familiar and well-rehearsed Arabic numerals to similar MA tasks performed with less familiar Roman numerals. Previous brain imaging studies of mathematical cognition have focused primarily on MA operations that are well rehearsed and automated in adults. An important question regarding the function of specific IPC regions relates to how they respond to different levels of task automaticity and individual differences in task proficiency. To address this question, we examined IPC responses during both automated and nonautomated MA tasks. We use the notion of automaticity here in the same sense as Logan (1988). In this view, automated processes are more dependent on memory-based solutions and retrieval, whereas nonautomated processes rely on algorithmic computations. It is currently not known exactly how IPS, AG, and SMG responses change with task automaticity, an issue we address here using cytoarchitectonically distinct maps of the IPC.

Behavioral studies have provided compelling evidence that changing the surface format of numerals is an effective way to alter the automaticity of mathematical information processing (Perry 1952; McCarthy and Dillon 1973; Gonzalez and Kolers 1982; Campbell and Fugelsang 2001; Hiscock et al. 2001; Venkatraman et al. 2006; Ansari 2007). For example, Campbell and Fugelsang (2001) found that participants were slower and less accurate at assessing 1-digit math problems that were presented in written English format (e.g. three + four = eight) than in a number format (e.g. 3 + 4 = 8). They proposed that the decrease in performance arose from the more complex written format using less efficient strategies and that participants relied more on explicit calculation than direct retrieval-based strategies (Schunn et al. 1997). Several studies have also compared processing of familiar Arabic numerals with the less familiar Roman numerals (Perry 1952; McCarthy and Dillon 1973; Gonzalez and Kolers 1982). These studies have consistently found that mental addition with Roman numerals takes significantly longer than with Arabic numerals. In a paced serial addition task, participants had significantly higher accuracy and shorter reaction times (RTs) when the stimuli were presented in Arabic, compared with Roman, format (Hiscock et al. 2001). Taken together, these studies suggest that automaticity of mathematical information processing can be manipulated in a controlled manner by merely altering the surface format of the numerals.

We used arithmetic verification tasks similar to those used in previous studies (Menon, Rivera, White, Eliez, et al. 2000; Menon, Rivera, White, Glover, et al. 2000), except that the participants performed 2 versions of the task—MA with Arabic (MA-A task) and MA with Roman numerals (MA-R task). Although the format of the Arabic and Roman equations (e.g. 2 + 3 − 1 = 4 and II + III − I = IV) was similar, the Roman numeral condition relied less on efficient and automatic memory retrieval than the Arabic numeral equations (Campbell and Fugelsang 2001; Hiscock et al. 2001). We used 3-operand, rather than 2-operand, equations in order to keep the tasks relatively simple while simultaneously providing sufficient variability in performance to facilitate examination of the relation between accuracy and brain response in the IPC (Menon, Rivera, White, Glover, et al. 2000). Lassaline and Logan (1993) have argued that transfer of memory-based automaticity is narrow because learning tends to be item specific. This suggests that participants typically cannot directly retrieve facts from memory when presented with MA problems in the Roman format. A key difference between the 2 tasks is that the MA-R requires more controlled and effortful retrieval, whereas the MA-A task involves more direct and effortless retrieval.

In summary, the main aims of our study were to 1) investigate the differential involvement of the IPS, AG, and SMG during MA using cytoarchitectonically defined subdivisions of the IPC, 2) examine activation and deactivation of the IPS, AG, and SMG as a function of task automaticity, 3) compare differential responses of the IPC and the PFC in relation to task automaticity, and 4) investigate the neural basis of individual differences in MA performance as a function of task automaticity. We predicted that participants would perform the MA-A task more accurately and faster than the MA-R task, reflecting the higher task automaticity with familiar mathematical symbols. In conjunction with these behavioral differences, we hypothesized that 1) the IPS would show activation in both tasks, with lesser activation during the more automated MA-A task, 2) the AG would show deactivation in both tasks, with greater deactivation in the MA-R task, 3) deactivations in the AG would overlap strongly with the default mode network (DMN), a set of brain regions that typically show domain general reductions in brain responses during difficult cognitive tasks (Greicius et al. 2003), 4) a dissociation between IPS and PFC responses would be observed, with the PFC showing greater between-task differences than the IPS, and 5) individual differences in MA task performance would be differentially related to activation in the IPS and deactivation in the AG.

Materials and Methods

Participants

Eighteen healthy adult participants (7 males and 11 females; ages 18–31.5, mean 22.28 years ± 3.95) participated in the study after giving written informed consent. All protocols were approved by the human participants Institutional Review Board at the Stanford University School of Medicine. All participants were volunteers and were treated in accordance with the APA “Ethical Principles of Psychologists and Code of Conduct.”

fMRI Experiments

This study consisted of 2 identical MA experiments, one using Arabic numerals and the other using Roman numerals. Arabic and Roman problems were presented in separate blocks in order to prevent subjects from switching across stimulus types and changing task strategy between conditions. The order of experiments was randomized across participants.

MA with Arabic numerals (MA-A)

Participants were presented with 16 alternating experimental and control epochs, each lasting 32 s. Each experimental (Calculation) epoch consisted of eight 3-operand equations of the form a + b − c = d (e.g. 5 + 4 − 2 = 7); only single-digit numerals from 1 to 9 were used. Each equation was presented for 3.5 s followed by a blank screen for 0.5 s. Participants were instructed to respond by pressing one of 2 keys, based on whether they thought the equation was correct (e.g. 4 + 5 − 2 = 7) or incorrect (e.g. 4 + 5 − 2 = 8). Half of the equations presented were correct, and the other half incorrect; the order of correct and incorrect equations was randomized. Each control (Identification) epoch consisted of eight 7-symbol strings (e.g. 4 @ 3 & 2 # 5). Each string was presented for 3.5 s followed by a blank screen for 0.5 s. Participants were instructed to respond by pressing one of 2 keys, based on whether they thought the string contained the numeral 5. Half of the strings presented contained the numeral 5, the other half did not; the order of presentation of these strings was randomized.

MA with Roman Numerals (MA-R)

This experiment was identical to the MA-A task, except that the equations consisted of Roman numerals (e.g. VI + II − I = VII). During the control epochs, participants were asked to determine whether the string contained the Roman numeral V (e.g. IX @ VI & I % V).

Stimulus presentation

The task was programmed using PsyScope (Cohen et al. 1993) on a Macintosh (Cupertino, CA) computer. Scan and task onsets were synchronized using a TTL pulse delivered to the scanner timing microprocessor board from a “CMU Button Box” microprocessor (http://poppy.psy.cmu.edu/psyscope) connected to the Macintosh. Stimuli were presented visually at the center of a screen using a custom-built magnet-compatible projection system (Resonance Technology, CA). An external timer maintained an accuracy of stimulus presentation to 1 ms.

Behavioral Data Analysis

RT and the number of correct responses for experimental and control epochs were computed. RT was analyzed using analysis of variance (ANOVA) with 2 repeated measures: numeral type (Roman vs. Arabic) and task condition (Calculation vs. Identification).

fMRI Data Acquisition

Images were acquired on a 3T GE Signa scanner using a standard GE whole head coil (software Lx 8.3). Head movement was minimized during scanning by a comfortable custom-built restraint. A total of 28 axial slices (4.5 mm thickness, 0.5 mm skip) parallel to the AC-PC line and covering the whole brain were imaged with a temporal resolution of 2 s using a T2*-weighted gradient echo spiral pulse sequence (Glover and Lai 1998) with the following parameters: TR = 2000 ms, TE = 30 ms, flip angle = 70°, 1 interleave. The field of view was 20 cm, and the matrix size was 64 × 64, providing an in-plane spatial resolution of 3.125 mm. To reduce blurring and signal loss arising from field inhomogeneities, an automated high-order shimming method based on spiral acquisitions was used before acquiring functional MRI scans (Kim et al. 2002). A high-resolution T1-weighted spoiled grass gradient recalled inversion recovery 3D MRI sequence was acquired to facilitate anatomical localization of functional activity. The following parameters were used: TI = 300 ms, TR = 8 ms; TE = 3.6 ms; flip angle = 15°; 22 cm field of view; 124 slices in coronal plane; 256 × 192 matrix; 2 NEX, acquired resolution = 1.5 × 0.9 × 1.1 mm. Structural and functional images were acquired in the same scan session.

fMRI Data Analysis

The first 5 volumes were not analyzed to allow for signal equilibration effects. Images were reconstructed, by inverse Fourier transform, for each of the time points into 64 × 64 × 28 image matrices (voxel size 3.125 × 3.125 × 4.5 mm). A linear shim correction was applied separately for each slice during reconstruction using a magnetic field map acquired automatically by the pulse sequence at the beginning of the scan (Glover and Lai 1998). Functional MRI data were preprocessed using SPM5 (http://www.fil.ion.ucl.ac.uk/spm). Images were realigned to correct for motion, corrected for errors in slice timing, spatially transformed to standard stereotaxic space (based on the Montreal Neurologic Institute coordinate system), resampled every 2 mm using sinc interpolation and smoothed with a 4-mm full-width half-maximum Gaussian kernel to decrease spatial noise prior to statistical analysis.

Statistical analysis was performed on individual and group data using the general linear model and the theory of Gaussian random fields as implemented in SPM5 (http://www.fil.ion.ucl.ac.uk/spm/software/spm5/). Individual subject analyses were first performed by modeling task-related and task-unrelated confounds. Low-frequency noise was removed with a high-pass filter (0.5 cycles/min) applied to the fMRI time series at each voxel. A temporal smoothing function (Gaussian kernel corresponding to half-width of 4 s) was applied to the fMRI time series to enhance the temporal signal-to-noise ratio. Regressors were modeled with a boxcar function corresponding to the epochs during which each condition was presented and convolved with a hemodynamic response function. We then defined the effects of interest for each participant with the relevant contrasts of the parameter estimates. Group analysis was performed using a random effects model that incorporated a 2-stage hierarchical procedure (Holmes and Friston 1998). For the first-level analysis, contrast images for each participant and each effect of interest were generated as described above. For the second-level analysis, these contrast images were analyzed using a general linear model to determine voxel-wise group t-statistics. One contrast image was generated per participant, for each effect of interest. Two-tailed t-tests were used to determine group-level activation for each effect. Finally, the t-statistics were normalized transformed to Z scores, and significant clusters of activation were determined using the joint expected probability distribution of height and extent of Z scores (Poline et al. 1997), with height (Z > 2.33; P < 0.01) and extent thresholds (P < 0.01).

The following between-task comparisons were then performed at the group level using paired t-tests: 1) MA-A: Arabic Calculation − Arabic Identification; (2) MA-R: Roman Calculation − Roman Identification; and the following between-numeral comparisons: (3) MA-A − MA-R: (Arabic Calculation − Arabic Identification) − (Roman Calculation − Roman Identification); (4) MA-R − MA-A: (Roman Calculation − Roman Identification) − (Arabic Calculation − Arabic Identification). In the latter 2 comparisons, which involve double subtractions, additional analyses were conducted to distinguish between differences arising from calculation task-related increases in activation, as opposed to identification task-related decreases in activation (or “deactivation”). For each significant cluster that was detected in these comparisons (i.e. comparisons 3 and 4), mean t-scores were first computed for the MA-A (comparison 1) and MA-R (comparison 2) tasks. Clusters in comparisons 3 and 4 were then categorized as arising from deactivation if 1) the mean t-score (averaged across all participants) was significantly negative in comparisons 2 and 1, respectively; and 2) the mean t-score was not significantly different from 0 in comparisons 1 and 2, respectively. A parallel analysis was conducted using percent signal change between the Calculation and Identification conditions. The results in each case were similar to those obtained using t-scores, so only the latter is reported here.

Regression analysis was used to examine the relation between MA experimental task accuracy and activation in the MA-A and MA-R tasks. Voxel-wise t-statistics maps were generated and significant clusters of activation were determined using a voxel-wise statistical height threshold of (Z > 2.33; P < 0.01), with corrections for multiple spatial comparisons at the cluster level (P < 0.05). Both the magnitude and the sign of the activations were examined in order to ascertain whether the observed brain–behavior relations were related to task-related activation or deactivation. Activation foci were superimposed on high-resolution T1-weighted images and their locations were interpreted using known neuroanatomical landmarks (Mai et al. 2007).

IPC ROI

ROI were based on the cytoarchitectonically distinct maps of 3 IPS (hIP3, hIP1, and hIP2), 2 AG (PGp and PGa), and 5 SMG (PFm, PF, PFt, PFcm, and PFop) regions, as described above (Fig. 1). In the order listed, these ROI run successively along the caudal to rostral axis of the IPC. Detailed information about the anatomical boundaries of these maps has been published elsewhere (Caspers et al. 2006; Choi et al. 2006; Scheperjans, Hermann, et al. 2008). Probability maps of each of these ROIs were evaluated using the SPM Anatomy Toolbox (Eickhoff et al. 2005).

The Anatomy Toolbox allowed us to characterize and label functional activations in relation to the probabilistic ROI. The spatial distribution of regional activations was characterized by 3 metrics— the percentage of an activation cluster that was in a specific ROI, the percentage of a specific ROI that belonged to an activated cluster, and probability that a peak in the cluster was assigned to an ROI (Eickhoff et al. 2005, 2007). Because of the spatial overlap in the 7 probabilistic IPC ROI, we used maximum probability maps, which yield nonoverlapping ROIs, to uniquely characterize the magnitude of regional responses. This approach yields regions that 1) reflect most adequately the underlying anatomy and 2) show a high degree of sensitivity in statistical analysis of functional activations (Eickhoff et al. 2007).

Results

Behavior

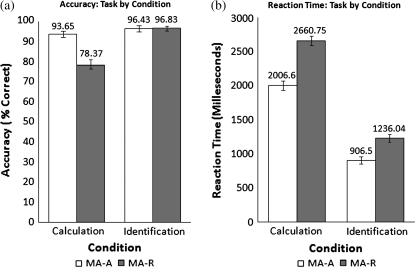
Accuracy and RTs for the MA-R and MA-A calculation and identification trials are summarized in Figure 2. For RT, ANOVAs revealed a significant 2-way interaction between condition (Calculation and Identification) and task (MA-A and MA-R); F (1,17) = 13.582, P < 0.005, partial η² = 0.444. RTs in both MA-A and MA-R conditions were significantly higher in Calculation than Identification conditions (F (1,17) = 481.423, P < 0.001, partial η² = 0.966). The mean RT for both conditions within the MA-A task were lower than the mean RT for MA-R (F (1,17) = 126.885, P < 0.001, partial η² = 0.882).

Figure 2.

Accuracy and RT during the MA-A and MA-R tasks. (a) Accuracy and (b) RT during Calculation and Identification conditions in the MA-A and MA-R tasks. Accuracy was significantly lower, and RTs were significantly greater, during the calculation condition of the MA-R task. A significant task by condition interaction was observed for both accuracy and RT. Mean and standard error are shown.

For accuracy, an ANOVA revealed a significant 2-way interaction between condition and task (F (1,17) = 33.437, P < 0.000, partial η² = 0.663). Average accuracy in both MA-A and MA-R tasks were significantly higher in Identification than Calculation (F (1,17) = 42.918, P < 0.001, partial η² = 0.716). The average accuracy for both conditions within the MA-A task was significantly greater than the average accuracy of the conditions in MA-R (F (1,17) = 20.631, P < 0.001, partial η² = 0.548).

IPC Activation during the MA-A and MA-R Tasks

MA-A (Arabic Calculation versus Number Identification)

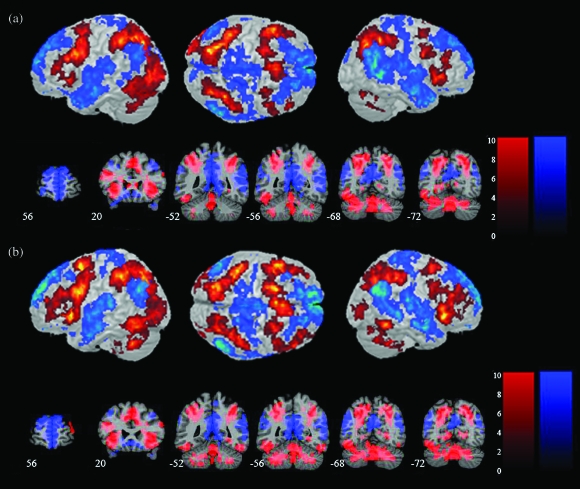
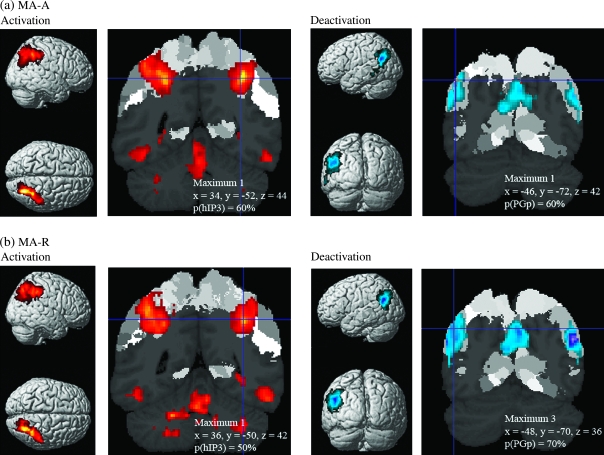
We detected significant activation (Calculation > Identification) as well as deactivation (Identification > Calculation) within the IPC, as shown in Figure 3a and Table 1. Note that deactivation here refers to greater activation during the low-level control (Identification) condition (see Discussion and Supplementary Fig. S3 for a consideration of deactivation with respect to a resting baseline). All 3 IPS areas (hIP1, hIP2, and hIP3) showed strong activation during the MA-A task, whereas the 2 AG areas (PGa and PGp) showed strong deactivation (Fig. 4). In contrast, the 5 SMG areas showed minimal activation. We then examined the spatial profile of activation using probabilistic labeling of IPC responses (Fig. 5a). The analysis showed that posterior IPS area hIP3 had the strongest and most spatially extensive activation, followed by area hIP1. In contrast, about 50% of PGp was deactivated, followed by 30% of PGa. The deactivations also extended anteriorly to cover 14% of SMG area PFm (Table 2).

Figure 3.

Brain activation and deactivation during the MA-A and MA-R calculation tasks. (a) Surface rendering and coronal sections of brain regions that showed significant activation (Calculation > Identification) and deactivation (Identification > Calculation) in the MA-A calculation task. Activations are shown in red and deactivations are shown in blue. (b) Activations and deactivations in the MA-R calculation task. Each cluster was significant after correction for height (p < 0.01) and spatial extent (p < 0.01).

Table 1.

Brain regions that showed significantly greater activation and deactivation during the MA-A and MA-R calculation, compared with number identification, tasks

Comparison	Brain region	BA	Corrected P value	No. of voxels	Peak Z score	Peak MNI coordinates (mm)
						x	y	z
MA-A
Calculation − Identification
	L inferior frontal gyrus, L insula	44, 47, 48	<0.001	12 210	5.12	−52	14	30
	L superior parietal lobule L middle occipital gyrus	7, 19	<0.001	10 206	6.03	−22	−70	42
	R inferior parietal lobule R middle occipital gyrus	40, 7	<0.001	2458	5.32	34	−52	44
Identification − Calculation
	L/R medial superior frontal gyrus	10, 30	<0.001	15 247	6.19	−2	54	8
	R middle temporal gyrus, R/L precuneus	37, 21, 23	<0.001	20 467	5.90	56	−58	12
	L angular gyrus	39	<0.001	1244	4.61	−46	−72	42
MA-R
Calculation − Identification
	R inferior parietal lobule, R middle occipital gyrus	40, 7	<0.001	2734	4.99	36	−50	42
	R inferior temporal gyrus	37	<0.01	361	5.18	54	−54	−18
	R cerebellum (vermis 8, crus 2)	47	<0.001	28 755	6.03	2	−64	−30
	R inferior/middle occipital gyrus	18, 19	<0.01	321	3.71	36	−88	4
Identification − Calculation
	L superior frontal gyrus, R middle cingulate, R precuneus	9, 23	<0.001	28 183	5.68	−14	52	34
	L angular gyrus	39	<0.001	1223	5.07	−54	−66	28
	R middle occipital gyrus, R superior/middle temporal gyrus	39, 22	<0.001	1813	5.38	48	−70	28

Note: For each significant cluster, region of activation, significance level, number of activated voxels, maximum Z score, and location of peak in MNI coordinates are shown. Each cluster was significant after correction for height (p < 0.01) and spatial extent (p < 0.01). BA, Brodmann area.

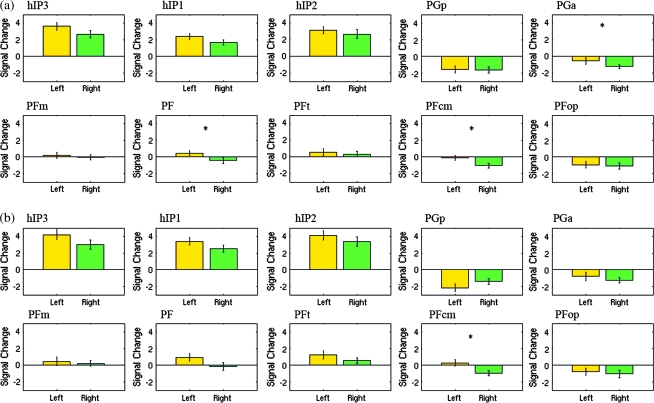
Figure 4.

Relative strength of activation and deactivation in each cytoarchitectonically defined IPC region during the MA-A and MA-R calculation tasks. (a) Activation and deactivation in each cytoarchitectonically defined IPC ROI during the MA-A task. All 3 IPS areas (hIP3, hIP1, and hIP2) were activated, whereas AG regions (PGp and PGa) were deactivated. SMG regions (PFm, PF, PFt, PFcm, and PFop) showed minimal activation. Hemispheric differences were observed in AG region PGa, and SMG regions PF and PFcm. (b) A similar pattern of activation and deactivation was observed during the MA-R task. In this case, hemispheric differences were observed only in the SMG region PFcm. *indicates regions that showed significant hemispheric differences, p < 0.05 after FDR correction for multiple comparisons. Mean and standard error are shown.

Figure 5.

Activation and deactivation in cytoarchitectonically defined IPC regions during the MA-A and MA-R calculation tasks. (a) Activations (Calculation > Identification) and deactivations (Calculation < Identification) during the MA-A task, overlaid on cytoarchitectonic probability maps of the IPC. Task-related activations had the highest probability of being localized to the posterior-most IPS region hIP3, whereas deactivations had the highest probability of being localized to posterior-most AG region PGp. (b) A similar profile was observed in the MA-R task, except that deactivations were more extensive and stronger within AG regions PGp and PGa. Each cluster was significant after correction for height (p < 0.01) and spatial extent (p < 0.01). Table 2 provides additional details of localization of activation and deactivation foci.

Table 2.

Probabilistic labeling of IPC regions that showed significant activation and deactivation during the MA-A and MA-R calculation, compared with number identification, tasks

Comparison	Assigned region	% of region activated	% of cluster in region	Probability of peak in assigned region (%)	Peak MNI coordinates (mm)
					x	y	z
MA-A
Calculation − Identification	R IPS (hIP3)	91.6	11.1	60	34	−52	44
	R IPS (hIP1)	62.1	5.8	20	44	−48	44
Identification − Calculation	L AG (PGp)	49.2	42.9	60	−46	−72	42
	L AG (PGa)	30.4	20.1
	L SMG (PFm)	13.6	5.5
	L SMG (PF)	1.6	1.2
MA-R
Calculation − Identification	R IPS (hIP3)	89.1	9.7	50	36	−50	42
	R IPS (hIP1)	80.3	6.7
Identification − Calculation	L AG (PGp)	54.1	48.0	70	−48	−70	36
	L AG (PGa)	33.6	22.6
	L SMG (PFm)	9.8	4.0
	L SMG (PF)	0.8	0.7

Note: IPC regions that showed significantly greater activation (Calculation > Identification) during the MA-A, compared with the MA-R, task (Identification > Calculation). For each significant cluster, the probabilistic region, percentage of activation in the region, percentage of cluster that was in the region, peak MNI coordinate, and the probability of the peak being in the region are shown. Each cluster was significant after correction for height (p < 0.01) and extent (p < 0.01). Cytoarchitectonically defined probability maps were used to interpret the locations of the cluster and peaks within subdivisions of the IPS, AG, and SMG.

MA-R (Roman Calculation versus Number Identification)

We detected significant activation as well as deactivation within the IPC, as shown in Figures 3b and 4b. As with the MA-A task, all 3 IPS ROI showed strong activation during the MA-A task, whereas the 2 AG ROI showed strong deactivation (Fig. 4b). Again, the SMG ROI showed minimal activation. Table 2 shows the spatial distribution of activations and deactivations in each of the IPC ROI. The relative pattern of activation and deactivation in these ROI is almost identical to that in the MA-A task, except that the deactivations were stronger and more spatially extensive in regions PGp and PGa of the AG (Table 2, Fig. 4b).

Activation Outside the IPC during the MA-A and MA-R Tasks

MA-A (Arabic Calculation versus Number Identification)

Significant activation was also observed in the left inferior PFC (BA 44, 47) and anterior insula (BA 48), left superior parietal lobule and midoccipital gyrus (BA 7, 19), and right midoccipital gyrus (BA 7, 40), right inferior temporal cortex (BA 37), the fusiform gyrus (BA 19), and cerebellum (vermis, bilateral crus 1 and 2, lobules VI, VIII, and right lobule 7b), as shown in Figure 3a (Schmahmann et al. 1999). Extensive deactivation was also observed in the right middle temporal gyrus and bilaterally in the superior frontal gyrus (Fig. 3a). A detailed listing of the brain areas that showed activations and deactivations is shown in Table 1.

MA-R (Roman Calculation versus Number Identification)

Outside the IPC, significant activation was observed in the right inferior and midoccipital gyri (BA 18, 19), the right inferior temporal gyrus (BA 37), the right insula and adjoining orbitofrontal cortex (BA 47/12), and cerebellum (vermis, bilateral crus 1 and 2, lobules IV, V, VI, and VIII). Extensive deactivation was also observed in the right superior and middle temporal gyri and in the left superior frontal gyrus (Fig. 3b, Table 1).

IPC Activation Differences between the MA-A and MA-R Tasks

MA-A − MA-R

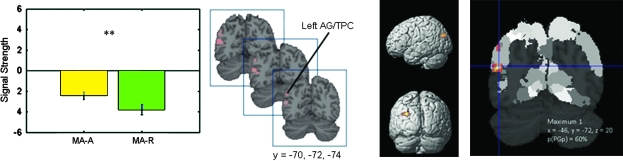
We examined brain regions that showed greater activation in the MA-A, compared with the MA-R, condition. As shown in Figure 6, a direct comparison between the 2 tasks revealed statistically significant differences in the left IPC and the adjoining temporoparietal cortex. More detailed analysis of the spatial distribution of the responses revealed that the differences were primarily localized to the AG − PGa and PGp together accounted for 73% of the activation and only 1.8% of the activation extended into SMG region PFm (Table 4). ROI analyses were conducted to further examine both the direction and magnitude of responses within the IPC cluster, in order to examine whether between-task differences above arose from increases during MA-A, or from decreases during the MA-R task (deactivation). This analysis revealed that activation in the AG cluster arose from greater deactivation during the MA-R condition (Fig. 6).

Figure 6.

Probabilistic labeling of IPC regions that showed significant differences in activation between the MA-A and MA-R calculation tasks. (Left) Task-related differences arose from activation, rather than deactivation, with the MA-R showing greater negative activations than the MA-A task. These differences were localized to the left AG and the posterior temporo-parietal cortex (TPC). **indicates that differences between the MA-A and MA-R task were significant at P < 0.01. (Right) Probabilistic labeling of IPC responses showing that deactivations had the highest probability of being localized to posterior-most angular gyrus region PGp. Each cluster was significant after correction for height (p < 0.01) and spatial extent (p < 0.01). Table 4 provides additional details of localization of task-related differences.

Table 4.

Probabilistic labeling of IPC regions that showed greater responses during the MA-A, compared with the MA-R, calculation task

Comparison	Assigned region	% of region activated	% of cluster in region	Probability of peak in assigned region (%)	Peak MNI coordinates (mm)
					x	y	z
MA-A − MA-R
	L AG (PGp)	17.5	50.8	60	−46	−72	20
	L AG (PGa)	10.0	22.0	30	−60	−60	22
	L SMG (PFm)	1.3	1.8

Note: IPC regions that showed significantly greater activations during the MA-A compared with MA-R task. Each cluster was significant after correction for height (p < 0.01) and spatial extent (p < 0.01). Other details as in Table 2. The MA-R task did not show significantly greater activations in any IPC region.

MA-R − MA-A

We then examined whether any brain regions showed greater activation in the MA-R, compared with the MA-A, tasks. No differences were observed in any of the IPC regions, even at a liberal threshold of P < 0.05, uncorrected.

Activation Differences Outside the IPC between the MA-A and MA-R Tasks

MA-A − MA-R

Compared with the MA-R task, the MA-A task showed greater responses bilaterally in the medial aspects of the superior frontal gyrus (BA 10). Further analysis revealed that in this cluster, between-task differences arose from greater deactivation during the MA-R task (Table 3).

Table 3.

Brain regions that showed significant differences between the MA-A and MA-R calculation tasks

Comparison	Brain region	BA	Corrected P value	No. of voxels	Peak Z Score	Peak MNI coordinates (mm)
						x	y	z
MA-A − MA-R
	L angular gyrus L temporoparietal cortex	39, 19	<0.001	373	3.87	−46	−72	20
	L/R superior frontal gyrus	10	<0.01	238	3.32	−4	56	24
MA-R – MA-A
	L inferior frontal gyrus, L anterior Insula	44, 48	<0.001	544	4.28	−54	10	8
	L inferior/middle frontal gyrus	47, 11	<0.01	331	3.59	−26	32	−4
	L middle/superior frontal gyrus	9, 8	<0.01	278	4.56	−22	8	58
	L/R presupplementary motor area	6	<0.01	286	3.44	−2	6	60
	R inferior frontal gyrus R anterior insula	47, 48	<0.01	227	4.19	38	20	−6
	L cerebellum (lobule VIII/vermis 8)		<0.001	947	4.54	−24	−58	−42

Note: Brain regions that showed significantly greater activations in the MA-A, compared with the MA-R task and the MA-R, compared with the MA-A task. For each cluster, region of activation, significance level, number of activated voxels, maximum Z score, and location of peak in MNI coordinates are shown. Each cluster was significant after correction for height (p < 0.01) and spatial extent (p < 0.01).

MA-R − MA-A

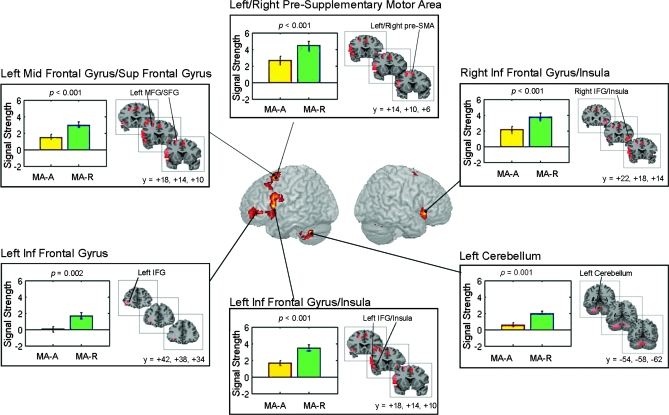
Compared with the MA-A task, the MA-R showed greater responses in 6 clusters within the PFC and the cerebellum (Fig. 7 and Table 3). PFC regions that showed differences included the left inferior frontal gyrus with adjoining anterior insula (BA 44, 48), left inferior and middle frontal gyrus (BA 47, 11), left middle and superior frontal gyri (BA 9, 8), and right inferior frontal gyrus and adjoining anterior insular (BA 47, 48) and the bilateral presupplementary motor area (pre-SMA; BA 6). Cerebellar regions that showed differences included the left cerebellum lobule VIII and vermis 8.

Figure 7.

Brain regions that showed significant differences in activation between the MA-R and MA-A calculation tasks. Six brain regions, all outside the IPC, showed significantly greater activation in the MA-R, compared with the MA-A, task: 1) left inferior frontal cortex and adjoining anterior insula (IFC; BA 44, 48), 2) left inferior frontal gyrus (BA 47), 3) middle and superior frontal gyri (BA 9, 8), 4) right inferior frontal cortex and adjoining insular cortex (BA 47, 48), 5) bilateral presupplementary motor area (pre-SMA; BA 6), and 6) left cerebellum (lobule VIII). In each of these regions, both the MA-R and the MA-A tasks showed positive activations (Calculation > Identification), and task-related differences arose from greater positive activations in the MA-R task. Each cluster was significant after correction for height (p < 0.01) and spatial extent (p < 0.01). Table 3 provides additional details of localization of activation foci.

We then examined whether the activation clusters noted in the MA-R − MA-A comparison above arose from task-related decreases during MA-A, or from task-related increases during MA-R (deactivation). This analysis showed that activation in all the 6 clusters arose from greater activation in the MA-R task (Fig. 7).

Relation of AG Deactivation to the DMN

The DMN (Greicius et al. 2003) consists of 2 bilateral nodes in the IPC as well as the medial PFC and posteromedial cortex (Greicius et al. 2003). These regions are typically deactivated during cognitive tasks in a domain general manner, and furthermore, the magnitude of deactivation normally increases in proportion to cognitive load. We first examined whether deactivations observed in the IPC during the 2 tasks overlapped with the DMN. We observed strong deactivation in the right AG area PGp in both tasks and more extensive bilateral overlap in the MA-R task (Supplementary Fig. S1). We then examined whether the left AG region that showed greater deactivation in the MA-R, compared with the MA-A, task overlapped anatomically with DMN. As shown in Supplementary Figure S2, there was significant overlap between AG regions deactivated during these tasks and the DMN.

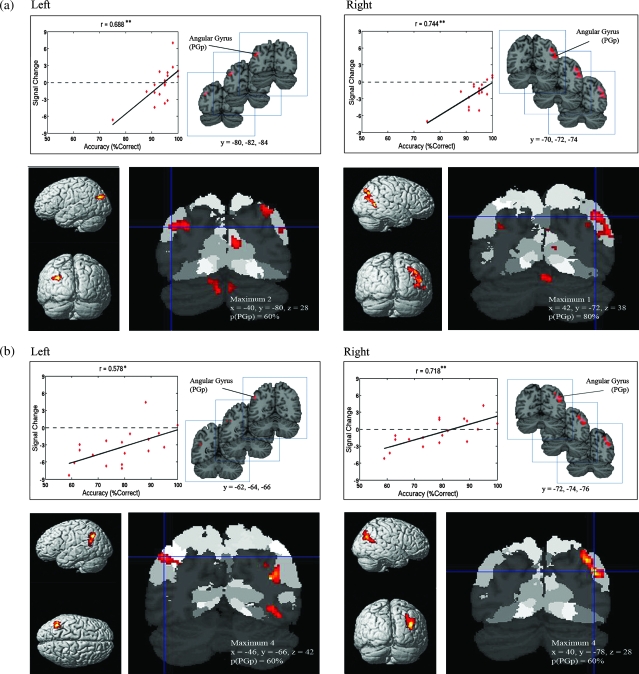
Relation between Performance and Brain Activation during the MA-A Task

We next examined the relationship between brain response and accuracy during the MA-A task. We found that accuracy during the MA-A task was associated with responses in the left (r = 0.69, P < 0.01) and right (r = 0.74, P < 0.01) IPC. Probabilistic labeling showed that both left and right IPC clusters overlapped most strongly with the posterior AG area PGp (Table 5 and Fig. 8). Furthermore, poorer accuracy was predominantly associated with deactivation in the AG region PGp (Fig. 8). No such relations were observed between brain activation and RT.

Table 5.

Probabilistic labeling of IPC regions where activation or deactivation was significantly correlated with accuracy during the MA-A and MA-R calculation tasks

Comparison	Assigned region	% of region activated	% of cluster in region	Probability of peak in assigned region (%)	Peak MNI coordinates (mm)
					x	y	z
MA-A
	L AG (PGp)	6.2	28.4	60	−40	−80	28
	R AG (PGp)	20.1	56.5	80	42	−72	38
MA-R
	L AG (PGa)	22.5	48.2	20	−40	−62	38
	L SMG (PFm)	4.7	6.1	20	−44	−60	30
	L IPS (hIP1)	3.4	4.1
	L AG (PGp)	1.3	3.7	60	−46	−66	42
	R AG (PGp)	18.3	44.0	60%	40	−78	28

Note: IPC regions that showed significant correlations between activation and performance accuracy during the MA-A and MA-R tasks. Each cluster was significant after correction for height (p < 0.01) and spatial extent (p < 0.05). Other details as in Table 2.

Figure 8.

Probabilistic labeling of IPC regions where brain responses were significantly correlated with accuracy on the MA-A and MA-R calculation tasks. (a) During the MA-A task, accuracy was significantly correlated with brain responses in the left and right posterior AG area PGp. The dashed line demarcates activation from deactivation and helps illustrate that performance was primarily related to deactivation, rather than activation. Furthermore, greater deactivation in focal clusters within the PGp was associated with poorer performance. As noted in the text, the outlier did not affect the statistical significance of these findings. The bottom panels show probabilistic labeling of responses overlaid on cytoarchitectonic maps of the IPC. (b) A similar pattern was observed in the MA-R task, except that responses were stronger in area PGp and accuracy was correlated with responses in the anterior AG region PGa (see Table 5). Each cluster was significant after correction for height (p < 0.01) and spatial extent (p < 0.01).

Relation between Performance and Brain Activation during the MA-R Task

Accuracy during the MA-R task was associated with reduced deactivation in the left (r = 0.578, P < 0.05) and right IPC (r = 0.718, P < 0.01). As shown in Figure 8 and Table 5, the clusters were localized to AG area PGa in the left hemisphere, extending anteriorly to SMG area PFm and dorsally to IPS region hIP1. The profile was somewhat different in the right hemisphere, with the cluster being localized more posteriorly to AG area PGp and the superior parietal lobule. No such relations were observed between brain activation and RT.

Discussion

Our findings provide new insights into the functional organization of the IPC during mathematical cognition. The newly developed cytoarchitectonically distinct maps of the IPC allowed us to localize brain responses to each task condition with an anatomical precision that was not possible heretofore. In particular, the demarcation of the IPS from the AG and the SMG allowed us to examine the extent, level, and distribution of brain responses in a reliable manner. This in turn allowed us to examine the effects of task automaticity in relation to individual subject differences in performance with a high level of precision and consistency. Our results point to important functional heterogeneities in the IPC, and they suggest that task automaticity modulates neural responses in the IPS, AG, and SMG differently. Our findings emphasize that the contributions of the IPC to mathematical cognition are not unitary. We discuss the implications of our findings for understanding the neural basis of mathematical cognition below.

Behavioral Differences

As predicted, we found that participants are less accurate and slower at processing the less familiar Roman numerals (Gonzalez and Kolers 1982; Hiscock et al. 2001). Accuracy and RTs were significantly different during the Calculation and Identification conditions in the MA-A and MA-R tasks. These results suggest that participants were equally adept at recognizing the 2 types of numerals, but were significantly slower in performing MA with Roman numerals. These results indicate that the MA-A task is performed in a significantly more automated manner than the MA-R task, consistent with the view that automatized processes are often marked by significant “speed-up” in response times due to more efficient memory retrieval (Logan 1988). Because the decision-making aspects of the MA-A and MA-R tasks did not differ, differences in RT likely reflect the effortful, directed, retrieval required during the MA-R task. RT differences in the identification condition suggest that Arabic numerals were recognized more efficiently than Roman numerals. Taken together with brain imaging results, the behavioral findings support the observation that cognitive operations are not independent of the symbols that initiate them (Gonzalez and Kolers 1982).

Differential IPC and PFC Responses in Relation to Task Automaticity

Before discussing regional differences within the IPC, we first focus on overall global differences in brain response in relation to task automaticity. Although there was extensive overlap in the IPC and PFC regions activated during the MA-A and MA-R tasks, activations in these regions could be dissociated: there was significantly greater activation of the PFC during the MA-R, compared with the MA-A, task, whereas there was greater “activation” of the IPC during the MA-A, compared with the MA-R, task. These results suggest that the IPC and PFC contribute differently to automated versus nonautomated MA tasks. Notably, activations of the right anterior insula in the PFC and the lobule VIII and vermis 8 regions of the cerebellum were observed only in the MA-R task.

During the MA-R task, greater activation was observed bilaterally in the ventrolateral PFC as well as the pre-SMA and the cerebellum. However, left hemisphere responses were stronger and more extensive and overlapped with language and syntactic processing regions in BA 44 and 47. These differences may arise from the need to transform numerals in the Roman format into phonological representations that facilitate fact retrieval and calculation. Lexical processing, translation of symbols, and the articulatory rehearsal needed prior to fact retrieval are also known to engage a frontocerebellar loop (Desmond et al. 1997; Fiez and Raichle 1997; Chen and Desmond 2005; Hayter et al. 2007), consistent with our finding of coactivation of the ventrolateral PFC and cerebellar lobule VIII. Interestingly, there were no differences in the mid-dorsolateral PFC, a finding that may reflect greater demands on retrieval and maintenance rather than active manipulation of numerical quantity in working memory (D'Esposito et al. 2000; Curtis and D'Esposito 2003; Derrfuss et al. 2004; Blumenfeld and Ranganath 2006). Importantly, our ventrolateral PFC foci overlap with prefrontal regions that have been implicated in effortful retrieval during a complex series of mental calculations (Anderson and Qin 2008).

Additionally, the MA-R task elicited greater responses in pre-SMA, a region that has been implicated in sequential planning of information in working memory. This may reflect preparation for motor output that accompanies multistage numerical computations during the more complex 3-operand condition. This region also showed greater responses in a previous study where we examined differences between processing of 3- and 2-operand MA trials (Menon, Rivera, White, Glover, et al. 2000). In that study, the increase in pre-SMA activation reflected the longer duration (about 850 ms) of the motor preparatory activity in a 3-operand, compared with a 2-operand, condition. Electrophysiological recordings have consistently implicated the SMA and pre-SMA during motor preparation (Tanji and Mushiake 1996) and delay-related fMRI responses have been reported during working memory tasks (Petit et al. 1998).

Dissociating IPS, AG and SMG Contributions to MA

During both the MA-A and MA-R tasks, the IPS showed increased activation during the Calculation compared with the Identification conditions (Figs 4 and 5). Increases were observed in the hIP3, hIP1, and hIP2, encompassing the posterior, middle, and anterior IPS segments shown in Figure 1. Activations were highest in the posterior-most area hIP3. In contrast, both the posterior AG area PGp and the anterior AG area PGa showed deactivation in both tasks, with stronger and more extensive deactivation in area PGp. Deactivation here refers to greater responses in the control number identification task compared with the calculation task. The MA-A task did not show activation above the control condition in either AG region, contrary to its predicted role in automated fact retrieval. Signal changes in the SMG were modest and nonsignificant in both tasks.

We then examined differences in activation of the IPS, AG, and the SMG between the automated and nonautomated tasks. We observed differences in the AG but not in the IPS or the SMG. It is particularly noteworthy that between-task differences arose from differences in deactivation rather than differences in activation (Figs 4 and 5). In the left AG, the MA-R task showed greater deactivation than the MA-A task, whereas the right AG showed equal levels of deactivation. Other regions of the IPC, including the left and right IPS areas hIP3, hIP1, and hIP2, showed similar levels of activation in both tasks; these IPC regions were not modulated by task automaticity.

One potential issue in interpreting these findings is that it leaves unclear whether the deactivations observed in our study may have arisen from greater activation of the AG during the number identification condition. In order to address this issue, we analyzed a different fMRI dataset, acquired in a separate group of 21 adult participants, with both number identification and passive fixation “rest” baseline conditions. We found no deactivations in the AG when we compared number identification to rest; in contrast, as expected, we observed significant activation in the left IPS, in the left and right striate, extrastriate, lingual, and fusiform gyri, and the left sensorimotor cortex (Supplementary Fig. S3). This analysis strongly suggest that the within-task deactivations and between-task differences in deactivation reported here arise from differences in deactivation during the MA Calculation task as opposed to activations during the Identification task.

Our findings help to clarify the functional distinction between key IPC regions that have been implicated in mathematical cognition. Delazer et al. (2003) suggested that with MA training, there is a shift from the bilateral IPS to the left AG, especially as individuals begin to rely less on computation and more heavily on retrieval. It is, however, not clear whether these changes are related to differences in activation or deactivation. Between-task comparisons indicated a positive difference in AG activation during the more automated task, compared with the less automated task, reflecting greater deactivation in the MA-R than in the MA-A task. In view of these findings, it is possible that the “shift” to the AG observed in the Delazer et al. study may have been due to decreased deactivation when the task became more automated after training. This notion was confirmed by the results of a subsequent study (Ischebeck et al. 2006), in which the AG showed less negative responses after training on multiplication problems. Similarly, Grabner et al. (2007) observed AG deactivation during mental calculation in individuals with poor mathematical abilities. However, to date, no study of mathematical cognition to our knowledge has examined whether task-related differences in specific IPS and AG regions arise primarily from activation or from deactivation, thus leaving unclear the precise functions subserved by the IPC. Importantly, many existing studies leave open the possibility that some of the IPC responses may reflect suppression from increased task difficulty rather than processing specificity for MA, an issue we address more directly in our study. Taken together, these findings highlight the need for careful analysis of the magnitude and sign of changes in activation in each specific MA task, particularly with respect to the AG but also to a lesser extent with the SMG whose various subdivisions showed a complex profile of low-level activation and deactivation. Most importantly, these findings point to functionally heterogeneous responses in cytoarchitectonically distinct areas of the IPC.

Obligatory Involvement of IPS in Automated and Nonautomated MA

All 3 segments of the IPS showed positive task-related activations during both the MA-R and MA-A tasks, but these activations did not differ between the 2 tasks. This suggests that the IPS is fully recruited in each condition, in contrast to the AG and the IFC. The invariant and obligatory nature of activation in the IPS further confirms its critical role in mathematical problem solving. The middle IPS area hIP1 overlaps with the horizontal IPS (hIPS), a region thought to be important for representing and manipulating quantity (Ansari 2008). This IPS region was activated strongly in both the MA-A and the MA-R tasks, even though the stimuli were visually well balanced in the MA and number identification tasks. However, no differences were observed between the MA-A and MA-R tasks. This suggests that although the hIPS region is sensitive to MA operations, it is not differentially modulated by task automaticity when basic number processing is controlled for. The same basic pattern was observed in each IPS region, even though the posterior-most area hIP3 had the strongest activation among the 3 subdivisions. All 3 IPS areas, hIP3, hIP1, and hIP2, therefore, appear to play an obligatory role in MA tasks, irrespective of the level of automaticity.

Task-Dependent AG Deactivation and Its Relation to the DMN

Our findings are inconsistent with simplistic notions of the left AG as being primarily involved in verbally mediated fact retrieval (Dehaene et al. 2003; Delazer et al. 2003). Although retrieval was more automated in the MA-A, very little positive activation was observed in this region in either task. Both the Rickard et al.’s (2000) study that involved simple 2-operand multiplication and our study, which involves 3-operand calculation, showed deactivation in the AG. Part of the reason for the divergence of these findings from studies such as those reviewed by Dehaene et al. (2003) is that sufficient attention has not been paid to deactivation when multiple task conditions were compared. For instance, the left AG was reported to show increased activation for multiplication relative to subtraction (Chochon et al. 1999; Lee 2000), for multiplication and division relative to a letter substitution control (Gruber et al. 2001), and for exact calculation than approximation (Dehaene et al. 1999). It is likely that these activations may have arisen from greater deactivation in the more difficult task. Our findings suggest that it is crucial to assess the precise, quantitative, profile of responses if we are to understand the nature of cognitive and brain mechanisms responsible for memory retrieval and algorithmic computation. It should also be noted that it was not just the left AG that showed significant deactivation in our study. The right AG also showed significant deactivation, but deactivation related differences between the MA-A and the MA-R tasks were more significant on the left than the right.

The AG regions that showed task-related deactivation differences in our study overlapped with IPC regions that have previously identified as being part of the DMN (Supplementary Fig. S1). More detailed analyses conducted to examine extent of the overlap showed that the parts of the AG that overlapped with the DMN were significantly more deactivated during the MA-R task than during the MA-A task. Other parts of the AG, which did not overlap with the DMN, showed positive activations in both the MA-A and MA-R tasks, but these activations did not differ between tasks (Supplementary Fig. S2).

AG areas outside of the DMN, most notably in the lateral temporal lobes, were also deactivated, but these deactivations did not differ between the MA-A and MA-R tasks. The DMN, and therefore the AG regions that overlap with it, are typically suppressed when the executive control network is recruited during demanding cognitive tasks (Seeley et al. 2007; Sridharan et al. 2008). In agreement with this observation, greater deactivation in the AG region was accompanied by greater activation in the bilateral PFC regions during the MA-R task. Our findings are also consistent with previous observations that suppression of the DMN increases with task difficulty (Schulman et al. 2003; Greicius and Menon 2004). The lateral IPC has been shown to be deactivated across a broad range of cognitive tasks, but its precise anatomical localization has not been adequately clarified. Whether these deactivations are primarily in the AG proper, rather than in more dorsal or rostral regions bordering the IPS and the SMG, has been unclear. Our analysis using the cytoarchitectonic maps described above strongly suggests that these deactivations are localized to the AG. One view of the deactivations observed in the IPC is that it helps to divert attentional resources to the PFC and more dorsal IPC regions for processing task-relevant visual information (Schulman et al. 2003; Greicius and Menon 2004; Todd et al. 2005). For example, Schulman et al. (2003) asked participants to search and detect stimulus targets embedded amongst nontarget stimuli and found that, whereas the IPS was activated both during search and target detection, the right AG was deactivated during search (Schulman et al. 2003). In addition, Todd et al. (2005) found that suppression of the AG increased with visual short-term memory load. These findings suggest that suppression of the right AG is necessary during demanding tasks, especially during tasks in which attention is voluntarily directed.

Importantly, the 2 other major nodes of the DMN— the posterior cingulate cortex and the ventromedial PFC—showed no differences between the tasks. These regions are also sensitive to task difficulty and typically are deactivated together during more difficult cognitive tasks (Schulman et al. 2003; Greicius and Menon 2004). Our findings therefore suggest that deactivation in the AG can be decoupled from most of the midline structures of the DMN. The reason for this functional dissociation is not entirely clear at this time, but our findings are consistent with the view that these nodes serve different cognitive and mental functions even though they are generally considered as operating within a “network”. Based on tasks that upregulate the DMN, it appears that posterior cingulate cortex and the ventromedial PFC are more related to self-related and autobiographical information processing (Greicius et al. 2003), whereas the AG is sensitive to integration of long-range semantic information (Humphries et al. 2007).

Task-Dependent Left AG Deactivation and Its Relation to Verbal Processing

How then are we to understand the role of the left AG in mathematical cognition? Although a role for the left AG in verbally mediated retrieval of MA facts has been suggested by several investigators, the nature of this involvement is unknown. In this context, recent findings in the literature on left AG involvement in verbal processing are quite revealing. The left AG shows deactivation to nonwords compared with a resting state baseline, with no difference observed between words and the resting state baseline (Mechelli et al. 2003; Rissman et al. 2003; Binder et al. 2005; Xiao et al. 2005). In an important study of the topic, Humphries et al. (2007) found that whereas the middle temporal gyrus and the inferior frontal gyrus showed greater activation during congruent, random, and pseudorandom sentences and word lists, the left AG showed activation only when semantic information had to be integrated over a 6–15 s time course. In all other conditions, the AG was either at baseline or significantly deactivated. Only very complex semantic processing elevates the AG above resting baseline, words, pseudowords, and even simple sentences suppress it. These findings led Humphries et al. (2007) to suggest that one important function of the AG is integration of semantic information into an ongoing context. The incoming stimulus interrupts processing of the internal narrative, but the level of semantic input to the AG is impoverished during low-level semantic processing, resulting in a reduction in AG activity compared with a low-level task or even the resting state baseline. In other words, during low-level tasks, the AG is engaged in internally generated cognitive processes that are suspended during more complex cognitive tasks (Greicius et al. 2003; Greicius and Menon 2004). Whether similar effects might be at play during demanding multistep problem solving, for example, in tasks involving word problems (Thevenot and Oakhill 2005) and elaborate verbal processes in calculation (Ansari 2008), remains to be investigated with more appropriate experimental designs.

An alternate view of the AG function centers on its role at the interface of memory and attention. Studies of memory retrieval in patients with lesions to the IPC suggest weakened retrieval effects in the absence of cues and paucity in the semantic contents of the retrieval (Cabeza et al. 2008). Clearly, further studies are needed to test these hypotheses and examine the precise conditions in which semantic content of individual stimuli modulate responses in the left and the right AG. Critically, for us here, these notions of AG function point to a domain-general, rather than a domain-specific, role in mathematical cognition.

AG and IPS Relation to Individual Differences in Performance

Analysis of brain–behavior relations provides further insights into the role of the IPS and AG in mathematical cognition. In the AG, deactivation was associated with reduced accuracy during both tasks. This effect was most strongly observed in the posterior AG area PGp in both hemispheres, although the effects were stronger in the right hemisphere. A similar pattern was observed in the MA-R task, except that responses were stronger in area PGp and accuracy was also correlated with responses in the anterior AG region PGa. These results converge on our findings of between-task differences in deactivation and further suggest that disengagement of the AG is necessary for accurate task performance. Our results are also consistent with the observation above that the AG is deactivated, or relatively suppressed, to a greater extent during performance of the less automated MA-R task. More importantly, these findings suggest that AG deactivation is related to individual differences in performance and the subjective difficulty of performing the MA tasks. These AG regions overlap with the DMN and provide new evidence that suppression of the lateral parietal lobe nodes, but not the midline structures of the DMN, such as the posterior cingulate cortex or the ventromedial PFC, is crucial for accurate MA task performance. In this regard, the observed brain–behavior relations differ in interesting ways from those in cognitive studies of other domains such as attention (Polli et al. 2005; Weissman et al. 2006).

Our findings are partly consistent with those of Grabner et al. (2007), who found that left AG responses during multiplication were correlated with measures of math competence acquired outside the scanner (Grabner et al. 2007). The AG cluster observed by Grabner and colleagues is in close proximity to the left PGa peak detected during the more demanding MA-R task. However, our findings of brain–behavior correlations were associated more with focal task-related deactivation, rather than activation. Furthermore, deactivations were observed in both hemispheres in our studies. There are 2 potential reasons for this discrepancy. One, our study used task-specific measures of performance, rather than general measures of math intelligence. Two, the use of just 2 fixation blocks, placed at the beginning and end of the task, may also have contributed to errors in estimating the profile of activation and deactivation during the multiplication task in the Grabner and colleagues’ study. Taken together, however, these findings suggest that performance, task automaticity as well as general domain competence—factors related to subjective difficulty—all contribute to modulation of AG responses during mathematical information processing tasks.

Beyond the AG, activations in the left mid-IPS area hIP1 and the adjoining SMG area PFm were also correlated with accuracy, but only in the more difficult MA-R task. These results suggest that modulation of responses in specific IPC regions depends on task automaticity and performance and that IPC contributions to increased performance and efficiency are heterogeneous not only between the 2 lateral IPC regions but also within each hemisphere.

Conclusions

Our study provides a unique understanding of the architecture of the IPC in mathematical cognition. More importantly, our findings also pinpoint the link between cytoarchitectonically defined regions of the IPC and the functionally heterogeneous contributions of the IPS and AG to mathematical cognition. The findings reported here point to close links between structure and function within the IPC and they provide new insights into the differential contributions of specific regions of the IPC in relation to automated and successful MA task performance. The functional heterogeneities we found are important for understanding the role of the IPS, AG, and the SMG of the IPC in mathematical cognition. Our study also suggest that failure to take into account the complex profile of activation and deactivation above baseline can lead to misleading conclusions about the role of the IPC in this domain. The systems neuroscience view advanced here suggests that the AG regions must be disengaged as part of a general cognitive mechanism involved during complex information processing tasks (Greicius and Menon 2004). In this context, we highlight further studies needed to investigate the precise cognitive operations subserved by both the activated and deactivated regions of the IPC and how they influence calculation, fact retrieval, learning, and development of domain proficiency.

Supplementary Material

Supplementary material can be found at: http://www.cercor.oxfordjournals.org/

Funding

National Institutes of Health (HD047520 and HD059205) and the National Science Foundation (BCS/DRL-0750340).