On the occurrence of linear groups in proteins

Abstract

Linear groups—polypeptide conformations based on a single repeating φ,ψ-pair—are a foundational concept in protein structure, yet how they are presented in textbooks is based largely on theoretical studies from the early days of protein structure analysis. Now, ultra-high resolution protein structures provide a resource for an accurate empirical and systematic assessment of the linear groups that truly exist in proteins. Here, a purely conformation-based survey of linear groups shows that only three distinct φ,ψ-regions occur: a diverse set of extended conformations mostly present as β-strands, a broad population of polyproline-II-like spirals, and a tight cluster that includes the highly populated α-helix and the conformationally-similar but much less populated 3₁₀-helix. Rare, short left-handed α-/3₁₀-helical turns with repeating φ,ψ-angles occur, but none are longer than three residues. Misperceptions dispelled by this study are the existence of 2.2₇- and π-helices as linear groups, the existence of specific ideal φ,ψ-angles for each linear group, and the existence of a substantive difference in the φ,ψ-preferences for parallel versus antiparallel β-strands. This study provides a concrete basis for updating and enhancing how we think about and teach the basics of protein structure.

Statement for Broader Audience

The fundamentals of protein conformation are currently presented in textbooks and taught based on out-of-date information that misses the true nature of the conformations that build proteins. This work asks one simple question that provides key information and insights needed for revising our understanding and teaching of these basics.

In 1950, based on crystal structures of five small-molecule peptides, Corey and Donohue¹ published the first set of standard bond lengths and angles for guiding polypeptide modeling. Pauling and coworkers then used this geometry to search for linear groups, defined as a series of residues all having identical conformations^†, that could enter regular hydrogen-bonded interactions: they predicted the γ- and α-helices² and the β-pleated sheet.³ Subsequently, additional linear groups were predicted including the π-helix,⁴ the 2.2₇-ribbon and the 3₁₀-helix.⁵ Later, structural studies led to the recognition of the poly-l-proline II (P_II)/polyglycine II/collagen-like helix as a linear group that does not undergo regular hydrogen bonding.^6–8 Although some predicted linear groups, such as Pauling's γ-helix,² were never seen in proteins and are no longer referred to, a subset of linear groups compiled in 1970,⁹ with a set of associated φ,ψ-angles, are often presented in contemporary biochemistry^10–13 and structural biology texts^14,15 as standard protein conformations (see Fig. 1).

Figure 1.

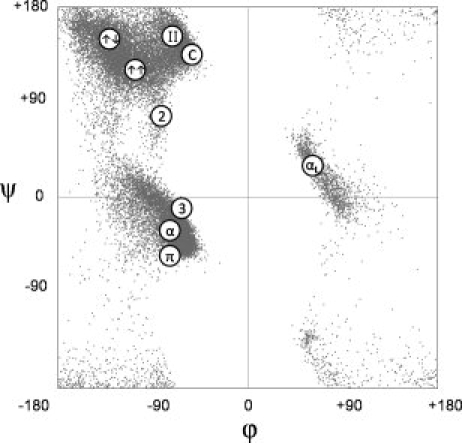
Linear groups as commonly cited in textbooks. Linear groups identified on the Ramachandran plot include the α-helix (α), 3₁₀-helix (3), π-helix (π), left-handed α-helix (α_L), 2.2₇-ribbon (2), polyproline-II (II), collagen (C), parallel β-sheet (↑↑), and anti-parallel β-sheet (↑↓). For reference, the background is a scatter plot of the 30,692 central residues used in this study. The figure is based on corresponding figures in textbooks cited in the text.^10–15

Although much has been learned about structural motifs in proteins,^16,17 we were surprised to find no single systematic survey in the literature directly addressing the occurrence of linear groups in proteins that updates the information summarized by IUPAC in 1970. What is needed is a simple, direct analysis that, independent of hydrogen bonding patterns, assesses which single conformations are seen to repeat in real proteins. Here, we present such an analysis.

The 1.2 Å Resolution Data Set

The primary data set was created by a search of a Protein Geometry Database (DSB, PAK, unpublished) for three-residue segments in protein structures determined at ≤1.2 Å resolution and which according to the PDBSelect March 2006 release¹⁸ had ≤25% sequence identity with any other included structure. Each residue furthermore was required to have an average backbone B-factor ≤25 Ų and a trans peptide bond (|ω| > 140°). The search resulted in 30,692 segments from 209 protein chains. Considering just the central residue of each segment, all amino acid types were well-represented (numbers of occurrences ranging from 2,710 for Ala to 472 for Trp) and the φ,ψ-angles [Fig. 2(A)] were distributed as expected based on previous analyses using strict selection criteria.^20–22 In terms of regular hydrogen-bonded secondary structures, 10,028 (33%), 8,756 (29%), 1,200 (4%), and 9 (0.03%) residues were classified by DSSP²³ as α-helix (α), β-sheet (β), 3₁₀-helix, and π-helix, respectively.

Figure 2.

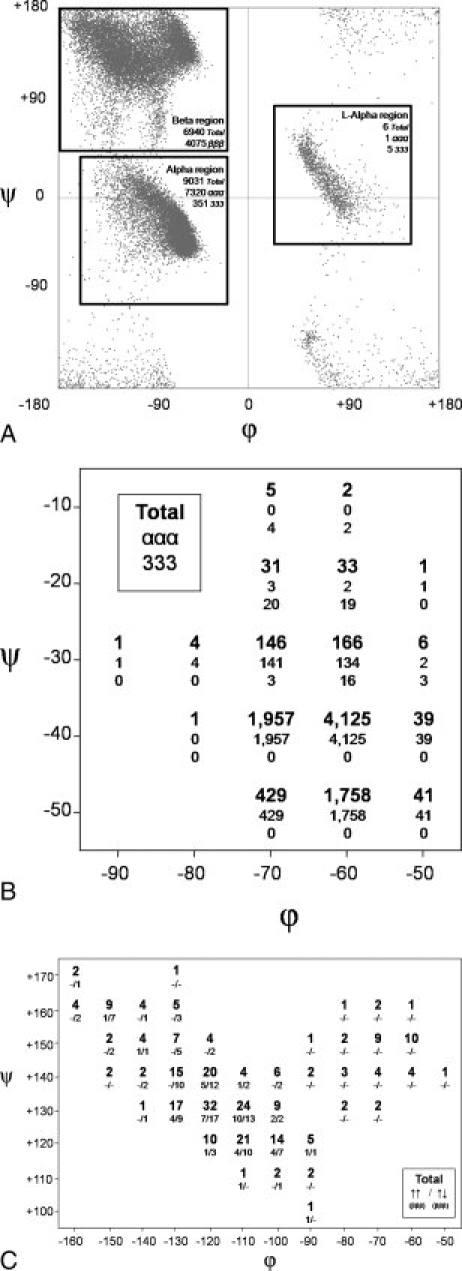
Linear groups in the 1.2 Å resolution dataset. (A) Ramachandran scatter plot of the 30,692 central residues qualifying for this study. Boxes outline the three major regions searched for occurrences of three contiguous residues all falling within the box. Each box is labeled (alpha, beta, and l-alpha) and the total number of qualifying segments in that box is given along with the subset of the results that fall completely within an α-helix (ααα), 3₁₀-helix (333), or β-strand (βββ) according to DSSP. Note that DSSP does not distinguish between left- and right-handed helices in its nomenclature. (B) Results for the fine search of the α-region. Each 20° × 20° box includes angles ±10° from its central value. As specified in the legend in the figure, within each box the top number reports the total number of segments having three consecutive residues in that box, and two numbers below this are how many of these are fully involved in purely α-helical (ααα) and purely 3₁₀-helical (333) H-bonding. Boxes outside of the displayed regions had zero observations. (C) Same as B but for the beta region. As noted in the legend in the figure given in each box are total occurrences (top), and the numbers of fully β-strand (βββ), residues involved in parallel and antiparallel strands. Mixed and outer strands are not included here, but can be seen in Supporting Information Figure S3. Assignments of β-strand orientation (parallel, anti-parallel, mixed or outer) were done using PDBsum.¹⁹ A parallel stand was defined as a strand that was H-bonded on both sides to parallel stands, an anti-parallel stand as H-bonded on both sides to anti-parallel strands, a mixed strand as H-bonded to both a parallel and an anti-parallel strand, and an outer strand as one that was H-bonded to only one strand. Supporting Information Figure S2 gives plots similar to Figures 2(B,C) but based on 30° × 30° boxes.

Identification of Linear Groups

Identifying linear groups requires selecting criteria for the minimal number of residues and the φ,ψ-variation allowed: the longer the minimal length and the narrower the allowed φ,ψ-variation, the fewer groups will be found but the more truly linear those groups will be. A minimal length of one is meaningless because it would simply define every observed conformation as a linear group. In addition, two φ,ψ-pairs are considered to define turn types rather than “regular” secondary structures.²⁴ While three residue segments also make up many turn structures,²⁵ we settled on three residues as the shortest (i.e. least stringent) reasonable length requirement, acknowledging that some of the groups satisfying these criteria will not actually represent true linear groups that occur at longer lengths.

In terms of φ,ψ-variation allowed, we first carried out a low-stringency study, considering each residue to simply belong to one of the three main well-populated regions of the Ramachandran plot often referred to as the alpha, beta, and l-alpha regions [Fig. 2(A)]. Segments with all three residues residing in the alpha, beta, or l-alpha regions accounted for approximately 30%, 23%, and 0.02% of all residues respectively, leaving over 45% of the segments adopting more conformationally diverse structures. Whereas no hydrogen-bonding criteria were used in the search, in all cases, the majority of qualifying segments were part of regularly hydrogen-bonded β-strands and right-handed α- or 3₁₀-helices [Fig. 2(A)]. The six segments qualifying in the L-alpha region included four 3-residue segments and one 4-residue segment, leading us to conclude that whereas they passed this minimal filter, they do not occur in segments long enough to be considered true linear groups (Supporting Information Fig. S1).

At a more discriminatory and informative level, we assessed linear groups as three consecutive residues all having the same φ,ψ-angles within ±10° by mapping φ,ψ-space in 20° × 20° boxes at 10° intervals. There were substantial numbers of observations in the alpha and beta regions [Figs. 2(B,C)]. Qualitatively equivalent results were obtained searching 30° × 30° boxes, showing that the results are not highly sensitive to the choice of box size (Supporting Information Fig. S2).

The alpha region shows a rather tight distribution of qualifying linear groups, with a single 20° × 20° box (centered at ϕ,ψ = −60, −40) having more than 4,000 observations [Fig. 2(B)]. In terms of hydrogen-bonding patterns, all occurrences at lower ψ-values were α-helical with 3₁₀- and mixed α-/3₁₀-helices occurring at the higher ψ-values.

For the beta region, this more stringent mapping reveals a natural division into two populations: a broad elliptical grouping with nearly all observations having β-sheet hydrogen-bonding patterns and a smaller but also well-dispersed grouping around the classical P_II conformation that is nearly devoid of regular β-sheet hydrogen bonding [Fig. 2(C)]. The narrow bridge between the two regions is centered near ϕ,ψ = −95,+140. Despite the standard depiction of distinct ideal values for antiparallel and parallel β-strands (see Fig. 1), both types of strands are seen to have their highest density of observations surrounding ϕ,ψ = −115, +130, and both occur throughout the elliptical β-sheet forming region. In agreement with Nagano,²⁶ it appears that the parallel strands are somewhat less diverse in conformation [Fig. 2(C), Supporting Information Figure S3].

Discussion

This survey shows that considering conformational properties alone, only three distinct linear groups comprise the protein-building toolkit. The most populated is a right-handed helical conformation dominated by the α-helix but also including the 3₁₀-helix and mixed α/3₁₀ forms. The second is a diverse group of extended conformations that are dominated by residues occurring in β-strands in both parallel and antiparallel β-sheets. The third is a set of left-handed spiral conformations in the P_II area that generally are not a part of β-sheets. Although these results may not surprise many structural biologists, they illustrate some basic features of protein structure that are not generally appreciated or incorporated into current curricula.

A first point worth emphasizing is that beyond these three clusters, no other true linear building blocks of proteins exist. Textbooks can now be clear that although isolated residues and rare short segments may exist with the 2.2₇-ribbon, the π-helical, and the left-handed α- or 3₁₀-helical conformations, those conformations do not occur in extended segments having repeating ϕ,ψ-angles. This conclusion is in apparent contradiction to reports describing π-helices in proteins as uncommon but real.^27,28 The resolution to this apparent contradiction is that the reported π-helices were defined not by conformation, but simply by the presence of two or more consecutive i+5,i hydrogen-bonds. They do not satisfy the definition of true linear groups as they are formed by a series of residues conformations varying by up to 60° in both ϕ and ψ (see Fig. 2 of Fodje and Al-Karadaghi²⁸); also, the large majority are short with only two hydrogen-bonds.

A related inference is that the 3₁₀-helices identified by hydrogen-bonding are mostly not built from a narrowly repeating conformation. Considering just the central residue of each three-residue segment (see above), there are 12% (1200/10,028) as many residues in 3₁₀-helices as in α-helices. In contrast, for the three-residue segments having consistent ϕ,ψ-angles, the ratio is only 0.8% [67/8,623 derived from the sums of the occurrences in Fig. 2(B)]. This means over 90% of residues identified as 3₁₀-helical in proteins are involved in turn-like conformations rather than true linear groups. This fits with the observation that 3₁₀-helices are mostly short and associated with the beginnings or ends of α-helices.²⁹

A second main point is that the β-strand and P_II represent fully distinct linear groups [Fig. 2(B)]. The P_II conformation was overlooked for many years in proteins because it is not defined by hydrogen bonding. It came to be recognized as an important element of folded proteins in the 1990s³⁰, occurring in lengths up to 12 residues,³¹ and since then has become recognized as a significant conformation in unfolded peptides and proteins.^32–34 It has been noted that P_II is a confusing and unfortunate designation, since the conformation is not just associated with Pro but can be adopted by all amino acids. In the study here, about one-third of the residues in the center of P_II tripeptides are Pro; the rest include all types of amino acids. Perhaps the common name could be changed to a more general “polypeptide-II” conformation. This would maintain the familiar P_II acronym, avoid the misleading association with only Pro, and be consistent with the observation that it is a prominent conformation in unfolded polypeptide chains. Similarly, we suggest that the region of the Ramachandran plot broadly referred to as the β-region [Fig. 2(A)], be renamed the β/P_II-region so the nomenclature used lays a foundation for proper recognition of both of the two main contributing conformations.

A third important point is that the β-strand and P_II populations are both very spread out and cannot be well-characterized by a single ϕ,ψ-conformation. In contrast, the α-/3₁₀-helix group is more tightly clustered. The tighter clustering of the ϕ,ψ-preferences for the α-/3₁₀-helices compared to the b-strand and P_II spirals is consistent with different hydrogen-bonding constraints: the α-/3₁₀-helices are constrained by the need to satisfy local hydrogen bonding, whereas both β-strands and P_II spirals exhibit variety as they access many relatively isoenergetic conformations to optimize tertiary hydrogen-bonding interactions with other parts of the protein and solvent. Given these spreads, it is misleading to give a single ϕ,ψ as the “ideal” β or P_II value. Also misleading is the assignment of distinct ideal values for parallel and anti-parallel β-strands (see Fig. 1) that are here shown to exhibit no large difference in preferred value [Fig. 2(C)]. Instead, we suggest a simple figure illustrating the full range of ideal values for each type of linear group would better convey the reality that a range of values can all be considered normal (Fig. 3, and Supporting Information Fig. S4).

Figure 3.

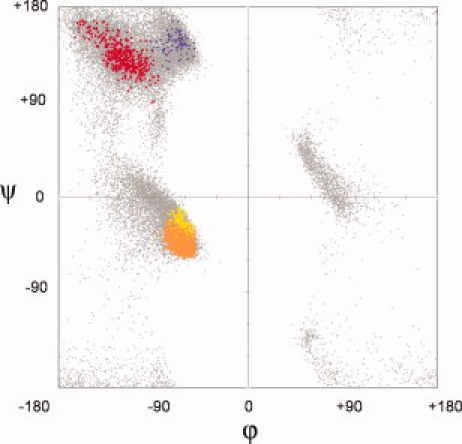
Locations and breadths of common linear groups in proteins. The composite scatter plot shows all triplets of residues found in the fine (20° × 20°) searches. Separate colors indicate the α (orange), 3₁₀ (yellow), β (red), and P_II (purple) residues. For reference, a background plot (gray) shows all the residues in the 1.2 Å data set. The α and 3₁₀ regions overlap. The most densely populated centers of each region are at α = (−63, −43), 3₁₀ = (−62, −22), β = (−116,129), P_II = (−65, 145). Supporting Information Figure S4 is similar, but based on 90,211 residues from diverse crystal structures at 1.75 Å resolution or better.