Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2009 Nov 9.
Published in final edited form as: Psychon Bull Rev. 2009 Jun;16(3):518–523. doi: 10.3758/PBR.16.3.518

Intrinsic Orientation and Study Viewpoint in Recognizing Spatial Structure of a Shape

Xiaoou Li 1, Weimin Mou 1,2, Timothy P McNamara 3
PMCID: PMC2774706  NIHMSID: NIHMS155442  PMID: 19451378

Abstract

Two experiments dissociated the roles of intrinsic orientation of a shape and participants’ study viewpoint in shape recognition. In Experiment 1, participants learned shapes with a rectangular background that was oriented differently from their viewpoint, and then recognized target shapes, which were created by splitting study shapes along different intrinsic axes, at different views. Results showed that recognition was quicker when the study shapes were split along the axis parallel to the orientation of the rectangular background than when they were split along the axis parallel to participants’ viewpoint. In Experiment 2, participants learned shapes without the rectangular background. The results showed that recognition was quicker when the study shape was split along the axis parallel to participants’ viewpoint. In both experiments, recognition was quicker at the study view than at a novel view. An intrinsic model of object representation and recognition was proposed to explain these findings.

People experience an object visually from a single viewpoint at any given time. In most situations, the viewpoint from which an object is first experienced is different from the viewpoint from which it is later recognized. Recognition must therefore rely on a representation and a process that can accommodate the change of the viewpoints from study to recognition. The models proposed to conceptualize the nature of such mental representation and process can be divided into two categories: structural description models and view-based models (Hayward, 2003).

Structural description models claim that an object is represented as a set of parts with a specific structural description of the spatial relations among the parts and recognition relies on matching the structure descriptions between the test object and the objects in memory (e.g. Biederman, 1987; Marr & Nishihara, 1978). For example, a hand can be represented as five fingers and one palm with specific spatial relations among them. The view-based models claim that snapshots of an object are represented at all learning viewpoints and recognition relies on the normalization between the recognition view and the closest snapshot in memory (e.g. Tarr & Pinker, 1989, 1990; Ullman, 1989).

The view-based models have found support in findings that object recognition performance is better at the familiar view than at the novel views and performance at a novel view decreases as the angular distance between the novel view and the closest study view increases (e.g., Cooper, 1975; Jolicoeur, 1988; Tarr & Pinker, 1989, 1990). In contrast the structural description models have found support in findings that object recognition can be viewpoint independent when object recognition relies on distinctive features that are viewpoint independent (e.g. the number of parts; e.g. Biederman & Gerhardstein, 1993). Recent studies have shown that object recognition can rely on both the structure information and the view information (e.g. Foster & Gilson, 2002).

In this project, we proposed and tested an intrinsic model of object representation and recognition. This model is derived from the intrinsic model of spatial memory (Mou, Fan, McNamara, & Owen, 2008; see also Mou & McNamara, 2002; Mou, McNamara, Valiquette, & Rump, 2004). The intrinsic model of spatial memory claims that interobject spatial relations in a layout of objects are represented with respect to the intrinsic orientation1 (intrinsic reference direction) of the layout. The study location of the observer is also represented with respect to the intrinsic orientation of the layout. Recognizing a previously learned configuration requires that the observer (a) identify the intrinsic orientation of the test scene, (b) align the intrinsic orientation of the test scene with the represented intrinsic orientation of the layout, and (c) compare the spatial relations in the test scene with the represented spatial relations of the layout.

Mou et al. (2008) demonstrated that scene recognition was both intrinsic-orientation dependent and viewpoint dependent. Participants were instructed to learn a layout of objects along an intrinsic axis that was different from their viewing direction. Participants were then given a scene recognition task in which they had to distinguish triplets of objects from the layout at different views from mirror images of those test scenes. The results showed that recognition latency increased with the distance between the test view and the study view. More important, participants were able to recognize intrinsic triplets of objects, which contained two objects parallel to the intrinsic axis that participants were instructed to use when they remembered the layout, faster than non-intrinsic triplets of objects, which did not contain two objects parallel to the instructed intrinsic axis. This pattern occurred for all test views. The intrinsic-orientation effect can be explained because participants were quicker in identifying the intrinsic orientation for the intrinsic triplets than for the non-intrinsic triplets. The view effect can be explained because participants had to align the intrinsic orientation in the test triplet with the represented intrinsic orientation of the layout in memory when the test view was different from the study view but did not need such alignment when the test view was the same as the study view.

We generalized the intrinsic model from scene recognition to object recognition because two observations suggested that these two visual processes share very similar mechanisms. First it has been shown that both object and scene recognition rely on the identification of intrinsic orientation. As described previously, identifying intrinsic orientation is important in scene recognition (e.g. Mou et al., 2008). Similarly it has been reported that identifying intrinsic orientation is important for shape (object) perception and recognition (e.g. Hinton, 1979; Hinton & Parsons, 1988; Palmer, 1989; Rock, 1973). For example, a square that is tilted 45° can be seen as either a tilted square or an upright diamond depending on whether an edge or a vertex is identified as the top. Second it has been shown that both object and scene recognition are viewpoint dependent. As reviewed previously, performance in object recognition is better at the familiar views and decreases as the angular distance between the novel view and the closest familiar view increases (e.g. Cooper, 1975; Jolicoeur, 1988; Tarr & Pinker, 1989, 1990). Similarly, it has been reported that performance in scene recognition is better at the familiar views and decreases as the angular disparity between the novel view and the closest study view increases (e.g. Burgess, Spiers, & Paleologou, 2004; Christou & Bülthoff, 1999; Diwadkar & McNamara, 1997).

In sum, the intrinsic model of object recognition claims that people represent the spatial structure of an object and their own study viewpoint with respect to the intrinsic orientation of the object. When they recognize an object, they first need to identify the intrinsic reference direction of the object and then align the intrinsic reference direction of the test object with the represented intrinsic reference direction established from the learned viewpoint (e.g. Ullman, 1989). According to this model, both intrinsic-orientation dependent and viewpoint dependent object recognition are expected. However to our knowledge, previous investigations of object and shape recognition have not dissociated viewpoint dependence from intrinsic-orientation dependence. Two experiments in this project were conducted to seek such dissociation in shape recognition.

Experiment 1

In Experiment 1, participants learned shapes of irregular hexagons surrounded by a rectangular background on a round table (Figure 1). The longer axis of the rectangular background was 60° different from the study viewpoint. The study viewpoint was arbitrarily labeled as 0° and all other directions were labeled counterclockwise from the study viewpoint. Target test shapes were created by splitting study shapes along a 0° –180° axis or along a 60°–240° axis and presenting them at the study view (view of 0°) or at a novel view (view of 30°) by rotating shapes 30° clockwise (Figure 2). The purpose of this experiment was to examine both the intrinsic-orientation effect (split along 0°–180° vs. 60°–240°) and the view effect (familiar view vs. novel view) on participants’ recognition of the target test shapes. We assumed that the intrinsic orientation of a shape was determined by the external rectangular background (e.g. Palmer, 1999; Pani & Dupree, 1994). Hence we expected that shape recognition should be better when the shape was split along the axis of 60°–240° than along the axis of 0°–180°.

Figure 1.

Figure 1

Open in a new tab

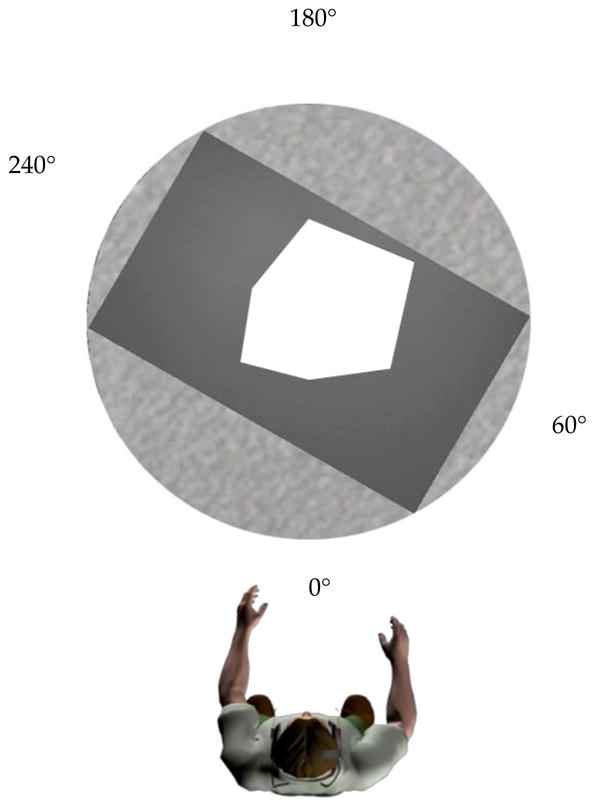
One sample of the study shapes.

Figure 2.

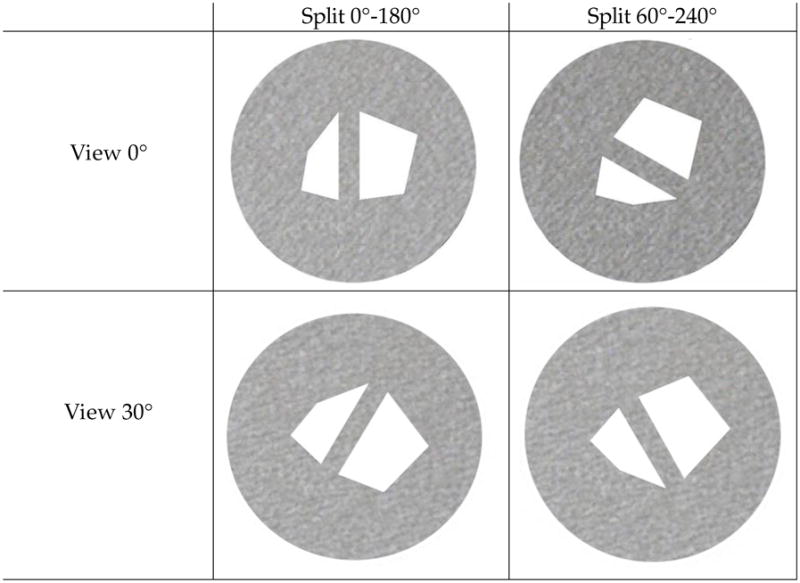
Figure 2

Open in a new tab

Sample of the target test shapes in combination of splitting axis (0°–180°, 60°–240°) and test view (0°, 30°).

Method

Participants

Twelve university students (6 women, 6 men) participated in return for monetary compensation.

Materials and design

The experiment was conducted in a room (6.0 by 6.0 m) with walls covered in black curtains. The virtual environment with shapes, rectangular backgrounds and round tables were displayed on the room floor in stereo with an I-glasses PC/SVGA Pro 3D head-mounted display (HMD, I-O Display Systems, Inc. California). Participants sat in a chair (51 cm high) 180 cm from the table center. Participants’ head motion was tracked with an InterSense 900 motion tracking system (InterSense Inc., Massachusetts). As illustrated in Figure 1, the study hexagon was presented with a rectangular background (60.6 cm by 100 cm) that was fit inside the round table (diameter of 117cm) and tilted 60° from participants’ viewpoint.

Twelve study hexagons were created with the following constraints: the six vertices of the hexagons were located in the directions of 0°, 60°, 180°, 120°, 240°and 300° from the center of the table; the distances between the vertices and the center of the table were randomized within the range from 15 cm to 35 cm and different from each other such that the hexagons were not symmetric along any axis. As shown in Figure 2, four target test shapes were created from each study hexagon by splitting the study hexagon into two quadrilaterals (4 cm apart from each other) along the axis of 0°–180° or the axis of 60°–240° and presenting the quadrilaterals from the view of 0° or from the view of 30° (by rotating the quadrilaterals 30° clockwise). Four distracter test shapes were created for each study hexagon by mirror reflecting the target test shapes about the viewing axis at test. The test shapes were presented only on the round table with the removal of the rectangular background.

Each study hexagon was followed by 8 test shapes (4 targets and 4 distracters). Participants were required to judge whether each test shape was the same as the study shape regardless of the view change. Participants were told to imagine that there was no gap between the quadrilaterals. In this way, there were 12 blocks of trials corresponding to 12 study hexagons and for each block there were 8 recognition trials. The 12 study hexagons and the 8 test shapes for each study hexagon were presented in a random order.

The two independent variables were splitting axis (0–180° vs. 60–240°) and test view (0° vs. 30°). The dependent variables were response accuracy and latency. Response latency was measured as the time from the presentation of the test shapes to the response of the participant.

Procedure

Before entering the experiment room, each participant was instructed to be familiar with the experiment procedure and requirements. Then the participant was blindfolded and led to be seated in the chair at the viewing position in the room. All the lights in the room were turned off. The blindfold was removed and the participant wore the head mounted display. The participant held a mouse in the right hand.

Each study hexagon was displayed with the rectangular background on the round table for 60 s. Participants were required to remember the shape. Then eight test shapes were presented sequentially. Prior to the presentation of each test shape, only a red cross was presented at the center of the table for 4 s and participants were required to fixate at the cross. Each test shape was displayed on the round table until participants pressed the mouse buttons (left button for targets and right button for distracters). Participants were required to respond as quickly and accurately as possible. There were four extra shapes for practice.

Results and Discussion

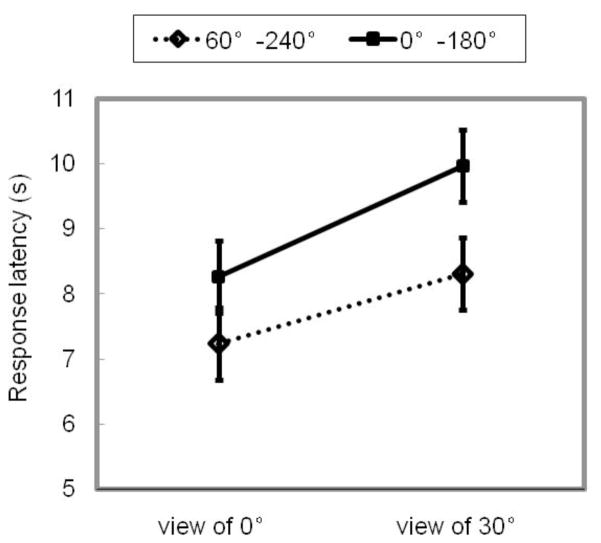
Mean response latency for correct responses to targets is plotted in Figure 3 as a function of splitting axis and test view. As shown in Figure 3, participants recognized shapes quicker when the shapes were split along the axis of 60°–240° than when the shapes were split along the axis of 0°–180°. Participants recognized shapes quicker at the study view than at the view of 30°. Mean response latencies per participant per condition were analyzed in repeated measures ANOVAs with terms for splitting axes and test view. The main effect of splitting axis was significant, F(1,11) = 4.92, p <.05, MSE = 4.43. The main effect of test view was significant, F(1,11) = 9.46, p <.05, MSE = 2.44. The interaction between splitting axis and test view was not significant, F(1,11) = 0.29, p >.05, MSE = 4.12.

Figure 3.

Figure 3

Open in a new tab

Mean response latency in correctly recognizing target shapes as a function of splitting axis and test view in experiment 1. (Error bars are confidence intervals corresponding to ±1 standard errors, as estimated from the analysis of variance.)

Mean accuracy for targets is listed in Table 1 as a function of splitting axis and test view. Mean response accuracies per participant per condition were analyzed in repeated measures ANOVAs with terms for splitting axis and test view. The test view was the only significant effect, F(1,11) = 12.0, p <. 01, MSE = .028. Participants recognized shapes more accurately at the study view than at the view of 30°. Mean accuracy of responses to distracters is listed in Table 2 as a function of splitting axis and test view. The ANOVA revealed no significant effects, indicating that effects in accuracy for targets were not caused by response biases2.

Table 1.

Mean (and Standard Deviation) accuracy (in percent) in recognizing target shapes as a function of splitting axis and test view in the Experiments.

0°–180° 60°–240°
EXP. View 0° View 30° View 0° View 30°
1 0.64 (0.21) 0.50 (0.13) 0.72 (0.13) 0.53 (0.25)
2 0.75 (0.17) 0.55 (0.23) 0.72 (0.21) 0.59 (0.21)
Open in a new tab

Table 2.

Mean (and Standard Deviation) accuracy (in percent) in recognizing distracter shapes as a function of splitting axis and test view in the Experiments.

0°–180° 60°–240°
EXP. View 0° View 30° View 0° View 30°
1 0.57 (0.21) 0.59 (0.21) 0.48 (0.19) 0.56 (0.23)
2 0.53 (0.19) 0.57 (0.17) 0.47 (0.22) 0.51 (0.24)
Open in a new tab

This experiment successfully dissociated the intrinsic-orientation effect and the view effect. Participants determined the intrinsic orientation of the shape using the longer axis of the rectangular background.

Experiment 2

The purpose of Experiment 2 was to investigate whether the intrinsic-orientation effect could be dissociated from the view effect when no rectangular background was presented with the study shapes. We hypothesized that under such conditions the intrinsic orientation of the study shape would be determined by particpants’ study viewpoint (e.g. Rock, 1973; Shelton & McNamara, 1997). Hence we predicted that shape recognition should be better when the shape was split along the axis of 0°–180° than along the axis of 60° –240°.

Method

Participants

Twelve university students (6 women, 6 men) participated in return for monetary compensation.

Materials, design, and procedure

The Materials, design, and procedure were identical to those of Experiment 1 except during learning, no rectangular background was presented.

Results and Discussion

As shown in Figure 4, participants were quicker in recognizing target test shapes when the study hexagons were split along the axis of 0°–180° than along the axis of 0° –240°, F(1,11) = 5.01, p <.05, MSE = 5.03. Participants were quicker in recognition at the view of 0° than at the view of 30°, F(1,11) = 15.02, p <.01, MSE = 1.81. The interaction between splitting axis and test view was not significant, F(1,11) = 0.18, p >.05, MSE = 3.71. As shown in Table 1, participants were more accurate in recognizing the target shapes at the view of 0° than at the view of 30°, F(1,11) = 8.06, p <.05, MSE = 0.04. No other effects were significant. As shown in Table 2, no effects were significant in recognizing the distracter shapes. Hence without the influence of the rectangular background, we still dissociated the intrinsic-orientation effect and the view effect, and the intrinsic orientation of the hexagons was determined by the study viewpoint of the participants.

Figure 4.

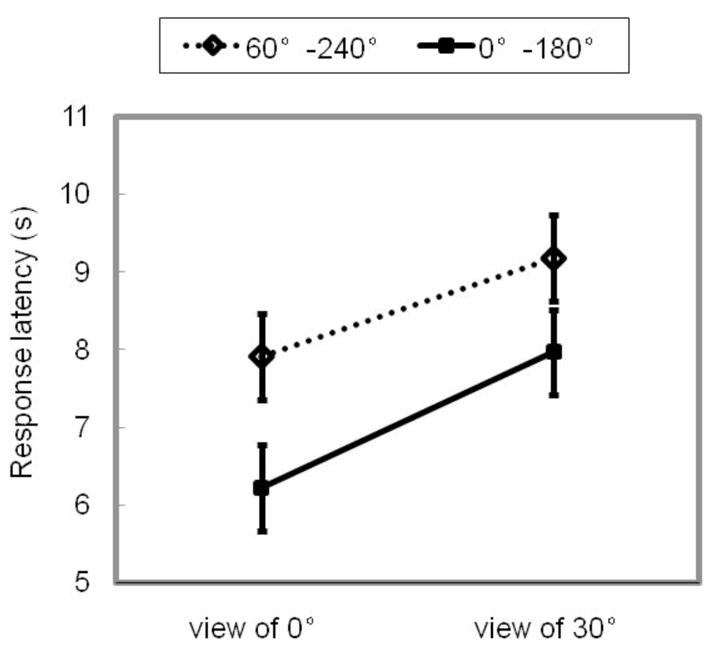
Figure 4

Open in a new tab

Mean response latency in correctly recognizing target shapes as a function of splitting axis and test view in experiment 2.

General Discussion

This project successfully dissociated the intrinsic-orientation effect from the view effect in shape recognition. In Experiment 1, the hexagons were presented with one intrinsic axis parallel to the study viewpoint and another intrinsic axis parallel to the orientation of an external rectangular background. The results showed that participants were quicker in recognizing the target shapes when the study hexagons were split along the intrinsic axis parallel to the orientation of the rectangular background than when the study hexagon was split along the intrinsic axis parallel to the study viewpoint and were quicker at the same view than at the novel view. The intrinsic-orientation effect and the view effect were independent. In Experiment 2, the external rectangular background was removed during learning. The results showed that participants were quicker in recognizing the target shapes when the study hexagons were split along the intrinsic axis parallel to the study viewpoint than when the study hexagons were split along the intrinsic axis not parallel to the study viewpoint and were quicker at the same view than at the novel view. The intrinsic-orientation effect and the view effect were independent.

Although view-based models of object recognition (e.g. Tarr & Pinker, 1989, 1990; Ullman, 1989) can readily explain the view effect, they have difficulty explaining the intrinsic-orientation effect. The view-based models predict that the shapes presented from the same test view (both the study view and the novel view) should be equivalent regardless of the intrinsic axis along which the shape was split.

These findings, however, can be explained by the intrinsic model proposed in the Introduction. According to the model, participants needed to identify the intrinsic orientation of the test shape in shape recognition. We assume that the intrinsic orientation of a test shape was more salient when the study shape was split along the intrinsic orientation than when the shape was split along another intrinsic axis. Hence identifying the intrinsic orientation was easier in the former condition than in the latter condition leading to the intrinsic-orientation effect. Because participants represented their study viewpoint with respect to the intrinsic orientation of the shape, when they were tested at the study position and the test view was different from the study view, the test shape was oriented differently from the mental representation of the study shape. Participants needed to align these two intrinsic orientations leading to the view effect. We acknowledge that the intrinsic model is similar to the structural description models (e.g. Biederman, 1987; Marr & Nishihara, 1978) in that it claims that object representation is object-centered but different from structure description models it that can also explain the view effect.

The dissociation of the intrinsic-orientation effect and the view effect in object recognition in this project echoes the dissociation of the intrinsic-orientation effect and the view effect in scene recognition reported by Mou et al. (2008, see also Schmidt & Lee, 2006). We acknowledge that in both studies, participants’ recognition decisions were primarily based on spatial structure rather than unique features (e.g. number of parts) because the distracters were the mirror images of the shape or the scene. Hence at least recognition of spatial structures of shapes and scenes seem to share similar mechanisms. Such similarity implies that a unified model of visual representation and recognition may be possible to accommodate both object and scene recognitions (e.g. Christou & Bülthoff, 1999; Diwadkar & McNamara, 1997).

Acknowledgments

Preparation of this paper and the research reported in it were supported in part by the 973 Program of Chinese Ministry of Science and Technology (2006CB303101) and by a grant from the Natural Sciences and Engineering Research Council of Canada to WM and National Institute of Mental Health Grant 2-R01-MH57868 to TPM. We are grateful to Dr. Michael Brown, Dr. Thomas Schmidt, and two anonymous reviewers for their helpful comments on a previous version of this manuscript.

Footnotes

1

Intrinsic orientation is used here to indicate an orientation that is perceived or identified by a viewer for a specific scene, rather than to imply an orientation that is determined by the intrinsic property of the scene e.g. symmetric axis. An intrinsic orientation can be perceived or identified with different kinds of cues including viewpoints, intrinsic properties of the scene, local or global contexts etc.

2

The results when d-prime is used as dependent variable are the same to those when accuracy of the response to the target shapes is used as dependent variable in both Experiments 1 and 2.

References

  1. Biederman I. Recognition-by-components: A theory of human image understanding. Psychological Review. 1987;94:115–147. doi: 10.1037/0033-295X.94.2.115. http://dx.doi.org/10.1037/0033-295X.94.2.115. [DOI] [PubMed]
  2. Biederman I, Gerhardstein PC. Recognizing depth-rotated objects: Evidence and conditions for three-dimensional viewpoint invariance. Journal of Experimental Psychology: Human Perception and Performance. 1993;19:1162–1182. doi: 10.1037//0096-1523.19.6.1162. http://dx.doi.org/10.1037/0096-1523.19.6.1162. [DOI] [PubMed]
  3. Burgess N, Spiers HJ, Paleologou E. Orientational manoeuvres in the dark: Dissociating allocentric and egocentric influences on spatial memory. Cognition. 2004;94:149–166. doi: 10.1016/j.cognition.2004.01.001. http://dx.doi.org/10.1016/j.cognition.2004.01.001. [DOI] [PubMed]
  4. Christou CG, Bülthoff HH. View dependence in scene recognition after active learning. Memory & Cognition. 1999;27:996–1007. doi: 10.3758/bf03201230. [DOI] [PubMed] [Google Scholar]
  5. Cooper LA. Mental rotation of random two-dimensional shapes. Cognitive Psychology. 1975;7:20–43. http://dx.doi.org/10.1016/0010-0285%2875%2990003-1.
  6. Diwadkar VA, McNamara TP. Viewpoint dependence in scene recognition. Psychological Science. 1997;8:302–307. http://dx.doi.org/10.1111/j.1467-9280.1997.tb00442.x.
  7. Foster DH, Gilson SJ. Recognizing novel three-dimensional objects by summing signals from parts and views. Proceedings of the Royal Society of London Series B-Biological Sciences. 2002;269:1939–1947. doi: 10.1098/rspb.2002.2119. http://dx.doi.org/10.1098/rspb.2002.2119. [DOI] [PMC free article] [PubMed]
  8. Hayward WG. After the viewpoint debate: Where next in object recognition. Trends in Cognitive Sciences. 2003;7:425–427. doi: 10.1016/j.tics.2003.08.004. http://dx.doi.org/10.1016/j.tics.2003.08.004. [DOI] [PubMed]
  9. Hinton GE. Some demonstrations of the effects of structural descriptions in mental imagery. Cognitive Science. 1979;3:231–250. http://dx.doi.org/10.1016/S0364-0213(79)80008-7.
  10. Hinton GE, Parsons LM. Scene-based and viewer-centered representations for comparing shapes. Cognition. 1988;30:1–35. doi: 10.1016/0010-0277(88)90002-9. http://dx.doi.org/10.1016/0010-0277%2888%2990002-9. [DOI] [PubMed]
  11. Jolicoeur P. Mental rotation and the identification of disoriented objects. Canadian Journal of Psychology. 1988;42:461–478. doi: 10.1037/h0084200. [DOI] [PubMed] [Google Scholar]
  12. Marr D, Nishihara HK. Representation and recognition of spatial-organization of three-dimensional shapes. Proceedings of the Royal Society of London Series B-Biological Sciences. 1978;200:269–294. doi: 10.1098/rspb.1978.0020. [DOI] [PubMed] [Google Scholar]
  13. Mou W, Fan Y, McNamara TP, Owen CB. Intrinsic frames of reference and egocentric viewpoints in scene recognition. Cognition. 2008;106:750–769. doi: 10.1016/j.cognition.2007.04.009. http://dx.doi.org/10.1016/j.cognition.2007.04.009. [DOI] [PubMed]
  14. Mou W, McNamara TP. Intrinsic frames of reference in spatial memory. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2002;28:162–170. doi: 10.1037/0278-7393.28.1.162. http://dx.doi.org/10.1037/0278-7393.28.1.162. [DOI] [PubMed]
  15. Mou W, McNamara TP, Valiquiette CM, Rump B. Allocentric and egocentric updating of spatial memories. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2004;30:142–157. doi: 10.1037/0278-7393.30.1.142. http://dx.doi.org/10.1037/0278-7393.30.1.142. [DOI] [PubMed]
  16. Palmer SE. Reference frames in the perception of shape and orientation. In: Shepp BE, Ballesteros S, editors. Object perception: Structure and process. Hillsdale, NJ: Lawrence Erlbaum Associates; 1989. [Google Scholar]
  17. Pani JR, Dupree D. Spatial reference systems in the comprehension of rotational motion. Perception. 1994;23:929–946. doi: 10.1068/p230929. http://dx.doi.org/10.1068/p230929. [DOI] [PubMed]
  18. Rock I. Orientation and form. New York: Academic Press; 1973. [Google Scholar]
  19. Schmidt T, Lee EY. Spatial memory organized by environmental geometry. Spatial Cognition & Computation. 2006;6:347–369. http://dx.doi.org/10.1207/s15427633scc0604_4.
  20. Shelton AL, McNamara TP. Multiple views of spatial memory. Psychonomic Bulletin & Review. 1997;4:102–106. [Google Scholar]
  21. Tarr MJ, Pinker S. Mental rotation and orientation-dependence in shape recognition. Cognitive Psychology. 1989;21:233–282. doi: 10.1016/0010-0285(89)90009-1. http://dx.doi.org/10.1016/0010-0285%2889%2990009-1. [DOI] [PubMed]
  22. Tarr MJ, Pinker S. When does human object recognition use a viewer-centered reference frame? Psychological Science. 1990;1:253–256. http://dx.doi.org/10.1111/j.1467-9280.1990.tb00209.x.
  23. Ullman S. Aligning pictorial descriptions: An approach to object recognition. Cognition. 1989;32:193–254. doi: 10.1016/0010-0277(89)90036-x. http://dx.doi.org/10.1016/0010-0277%2889%2990036-X. [DOI] [PubMed]

RESOURCES