Abstract
Eight experiments examined the use of representations of self-to-object or object-to-object spatial relations during locomotion. Participants learned geometrically regular or irregular layouts of objects while standing at the edge or in the middle, and then pointed to objects while blindfolded in three conditions: before turning (baseline), after rotating 240 degrees (updating), and after disorientation (disorientation). The internal consistency of pointing in the disorientation condition was equivalent to that in the updating condition when participants learned the regular layout. The internal consistency of pointing was disrupted by disorientation when participants learned the irregular layout. However when participants who learned the regular layout were instructed to use self-to-object spatial relations, the effect of disorientation on pointing consistency appeared. When participants who learned the irregular layout at the periphery of the layout were instructed to use object-to-object spatial relations, the effect of disorientation disappeared. These results suggest that people represent both self-to-object and object-to-object spatial relations, and primarily use object-to-object spatial representation in a regular layout and self-to-object spatial representation in an irregular layout.
Keywords: self-to-object spatial relations, object-to-object spatial relations, spatial updating, disorientation
An object’s location is usually perceived in the context of other objects. When a person locomotes in an environment, he or she may encounter many different arrays of objects. On some occasions, an array of objects forms a more regular structure. For example, tables in a classroom are aligned column by column, row by row. But on other occasions, an array of objects forms a less regular structure. For example, objects in an office (e.g., phone, mug, pen, stapler) may appear to be arranged haphazardly. Research has shown that human spatial memory tends to regularize the structure of an array of objects so as to line up objects relative to each other (e.g., Tversky, 1981). The aim of this project was to investigate whether the regularity of array structure1 also affects the nature of spatial memory, in particular the selection of reference object (egocentric or allocentric) in spatial memory.
One key question of research on spatial memory is to determine the extent to which spatial memory depends on egocentric or allocentric frames of reference (e.g. Burgess, 2006; Easton & Sholl, 1995; Klatzky, 1998; McNamara, Rump, & Werner, 2003; Shelton & McNamara, 2001; Sholl, 2001; Wang & Spelke, 2000; 2002). Egocentric means that the spatial reference system depends on the observers’ body; allocentric means that the spatial reference system is independent of the observers’ body. Mou, Xiao, and McNamara (2008) proposed that spatial reference systems should be examined by dissociating reference directions and reference objects separately because reference directions and reference objects can both be egocentric or allocentric. For example, a viewer may represent in memory the location of an object relative to his or her own body but use an allocentric reference direction (e.g. the car is east of him or her); alternatively, a viewer may represent the location of an object relative to other objects but use an egocentric reference direction determined by his or her own body axes (e.g. the car is on the left side of the garage).
Mou, McNamara, Rump, and Xiao (2006) reported evidence that the regularity of array structure may affect the selection of reference object egocentrically or allocentrically. In their experiments, participants learned an array of objects and then pointed to each object while blindfolded before and after they were disoriented. Following Wang and Spelke (2000), Mou et al. used the comparison of configuration error, which is defined as the standard deviation across target objects of the mean signed pointing errors, before and after disorientation to determine whether participants represented and updated self-to-object spatial relations or object-to-object spatial relations. Wang and Spelke (2000) hypothesized that self-to-object spatial relations are updated independently during locomotion, and therefore, disorientation introduces independent, uncorrelated error into those representations. In contrast, object-to-object spatial relations are not changed during locomotion. The fidelity of the mental representation is therefore not compromised after disorientation. Hence the configuration error increases after disorientation if one primarily represents and updates self-to-object spatial relations and the configuration error does not increase after disorientation if one primarily represents and updates object-to-object spatial relations.
Mou et al. (2006, Experiment 4) observed an increase in configuration error after disorientation (disorientation effect) when participants learned a layout of four objects that were randomly scattered around their bodies. Strikingly they reported that there was no effect of disorientation after participants learned a layout with a good geometric structure in the same test room (the layout of nine objects formed a column by column, row by row structure). These results indicate that self-to-object spatial relations may be represented and updated when the layout is not readily organized perceptually into a regular pattern but object-to-object spatial relations may be represented and updated when the layout has a good regularity.
However there are factors other than the structural regularity of an array that may lead to discrepancies in the disorientation effect when people point to recently learned objects. The potential factors were discussed below in the context of the experiments of Mou et al. (2006) and other studies examining the disorientation effect on configuration error in the literature (Holmes & Sholl, 2005; Waller & Hodgson, 2006; Wang & Spelke, 2000). As illustrated in Table 1, there are four potential factors that may lead to the discrepancies (Mou et al. 2006): (a) Learning position: In all experiments in which the disorientation was observed, participants learned the objects’ locations while standing in the midst of the array. In contrast, in two of the experiments in which the disorientation was not observed, participants learned the objects’ locations from outside of the array (Mou et al, 2006, Experiments 1 & 2). (b) Geometry of the array: In all experiments in which the disorientation was observed, the layout did not have a regular structure (column by column, row by row) whereas in those experiments in which the disorientation was not observed the array had a regular structure. (c) The number of objects: In the experiments showing a disorientation effect, people learned locations of a relatively small number of objects (4 to 6) whereas in the experiments showing no disorientation effect, people learned locations of a relatively large number of objects (6 to 9). (d) The testing location: in all experiments showing a disorientation effect, the testing location of the participants was not occupied by an object during the learning phase whereas in two of the experiments showing no disorientation effect, the testing location of the participants was occupied by an object during the learning phase (Mou et al, 2006, Experiments 1 & 2). The first specific aim of this study was to systematically examine which of these factors caused the appearance or disappearance of the disorientation effect in pointing to recently learned objects.
Table 1.
Presence or absence of disorientation effect as function of participants’ learning position, layout geometry, number of objects in the layout and whether the testing location was occupied by an object in the previous studies
| Study/Experiment | Learning position | Layout geometry | Number of objects | Testing location | |
|---|---|---|---|---|---|
| Showing a disorientation effect | Wang & Spelke (2000) | Midst | Irregular | 4 or 6 | No object |
| Waller & Hodgson (2006) | Midst | Irregular | 6 | No object | |
| Mou et al. (2006)/Exp 4 | Midst | Irregular | 4 | No object | |
| Showing no disorientation effect | Holmes & Sholl (2005) | Midst | Regular | 6 | No object |
| Mou et al. (2006)/Exps 1, 2 | Outside | Regular | 9 | Occupied | |
The second specific aim of this study was to investigate whether the appearance or disappearance of the disorientation effect is the consequence of representing different spatial relations (self-to-object or object-to-object) during learning or updating different spatial relations during locomotion. It has been assumed that people update the spatial relations that they have represented (e.g. Wang & Spelke, 2000). If people represent self-to-object spatial relations, then they update self-to-object spatial relations during locomotion. The disorientation effect on configuration error is expected because disorientation disrupts self-to-object spatial relations independently. If people represent object-to-object spatial relations, then they update object-to-object spatial relations during locomotion. The disorientation effect on configuration effect is not expected because disorientation does not disrupt object-to-object spatial relations. Hence the appearance or disappearance of the disorientation effect is the consequence of representing self-to-object spatial relations or object-to-object spatial relations during learning. Alternatively it is possible that the form of spatial relations that is updated can be different from the form of spatial relations that has been represented. People might represent both self-to-object and object-to-object spatial relations during learning (e.g. Sargent, Dopkins, Philbeck, & Modarres, 2008; Waller & Hodgson, 2006) but update only one form during locomotion, with the form modulated by the layout regularity. For instance, people may update object-to-object spatial relations in a regular layout and update self-to-object spatial relations in an irregular layout although both forms of spatial relations are represented during learning. The form of spatial relations that is updated is maintained whereas the form that is not updated decays without rehearsal. If object-to-object spatial relations are updated, then self-to-object spatial relations decay and disorientation has no effect on the configuration error. If self-to-object spatial relations are updated, then object-to-object spatial relations decay and disorientation has an effect on the configuration error. Hence the appearance or disappearance of the disorientation effect is the consequence of updating self-to-object spatial relations or object-to-object spatial relations during locomotion rather than representing self-to-object spatial relations or object-to-object spatial relations during learning.
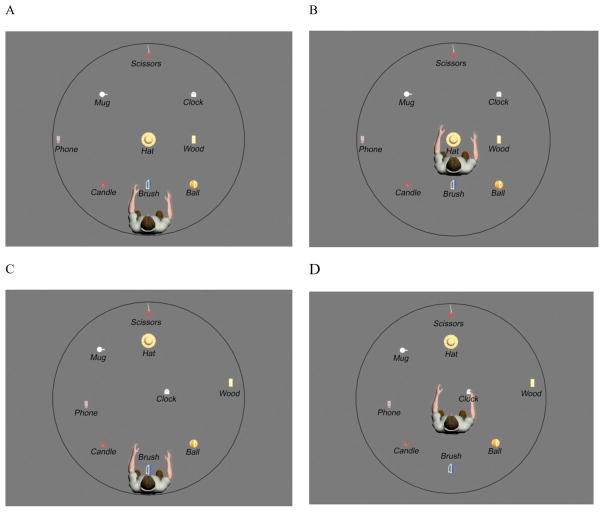
There were 8 experiments in this study (see Table 2 for a summary of the manipulations). Experiments 1–4 addressed the first aim of this study, systematically investigating which factor caused the appearance or disappearance of the disorientation effect on the configuration error. In these experiments, participants learned a layout with 9 objects and the testing location of the participants was not occupied by an object during the learning phase, removing the inconsistency of object number and testing location. In Experiments 1 and 2, participants learned a layout with a good regularity as illustrated in Figures 1A and 1B whereas in Experiments 3 and 4, participants learned a layout with a poor regularity as illustrated in Figures 1C and 1D. In Experiments 1 and 3, participants stood outside of the layout, as illustrated in Figures 1A and 1C, during the learning phase, whereas in Experiments 2 and 4, participants stood in the midst of the layout, as illustrated in Figures 1B and 1D, during the learning phase. In all experiments, participants were tested in the location illustrated in Figures 1B and 1D. To preview, the results showed that the disorientation effect was modulated by layout geometry and not by participants’ learning position. In particular, the disorientation effect was found in Experiments 3 and 4 but not in Experiments 1 and 2.
Table 2.
Manipulations in terms of the instructed spatial relations to update, participants’ learning position, layout geometry and the resulting disorientation effect in each experiment
| Instructed spatial relations | Learning position | Layout geometry | Disorientation effect | |
|---|---|---|---|---|
| Exp 1 | No | Outside | Regular | No |
| Exp 2 | No | Midst | Regular | No |
| Exp 3 | No | Outside | Irregular | Yes |
| Exp 4 | No | Midst | Irregular | Yes |
| Exp 5 | self-to-object | Outside | Regular | Yes |
| Exp 6 | self-to-object | Midst | Regular | Yes |
| Exp 7 | object-to-object | Outside | Irregular | No |
| Exp 8 | object-to-object | Midst | Irregular | Yes |
Figure 1.
Layouts of objects and participants’ learning positions. 1A for Experiments 1 and 5,1B for Experiments 2 and 6, 1C for Experiments 3 and 7, 1D for Experiments 4 and 8.
In Experiments 5–8, the updating of self-to-object or object-to-object spatial relations was directly manipulated by instruction. These experiments corresponded to Experiments 1–4 in terms of participants’ learning position and layout geometry (see Table 2). In Experiments 5 and 6, participants learned a layout with a good regularity as illustrated in Figures 1A and 1B and were instructed to use self-to-object spatial relations during locomotion. In Experiments 7 and 8, participants learned a layout with a poor regularity as illustrated in Figures 1C and 1D and were instructed to use object-to-object spatial relations during locomotion. We wanted to see whether the appearance or disappearance of the disorientation effect in configuration error could be altered by instructions to update one type of spatial relation vs. the other. In particular, we wanted to see whether the disorientation effect would appear in a regular layout in Experiments 5 and 6 and disappear in an irregular layout in Experiments 7 and 8. A finding that the appearance or disappearance of the disorientation effect in configuration error could be altered by updating instructions would indicate that the form of spatial relations that is updated can be different from the form of spatial relations that has been represented and that the appearance or disappearance of the disorientation effect is the consequence of updating mental representations of self-to-object spatial relations or of object-to-object spatial relations during locomotion. On the other hand, a finding that updating instructions have no influence on the disorientation effect would indicate that people only update spatial relations that they have represented and that the appearance or disappearance of the disorientation effect is the consequence of representing self-to-object spatial relations or object-to-object spatial relations during learning.
Experiment 1
Participants learned the locations of objects while standing at the periphery of a regular object array, and then were blindfolded and tested under baseline, updating, and disorientation conditions. The same regular layout as in Mou et al. (2006) was used, but the testing location was changed. Instead of being tested at the location of the hat, participants were tested at a location 30 cm behind the hat. In this way, the testing locations were not occupied by any object during the learning phase.
Method
Participants
Twenty-four university students (12 men and 12 women) participated in this study in return for monetary compensation.
Materials and Design
The regular layout of Mou et al. (2006) was used in this experiment. As illustrated in Figure 1A, nine objects were presented in a cylinder that was located in an experiment room. The cylinder was 3.0 m in diameter, made by black fabric and reinforced cloth. Objects were chosen with the restrictions that they were visually distinct, fit with approximately 0.3 m on each side, were familiar to people, and shared no obvious semantic association. The hat was placed in the middle of the cylinder, the distance from the hat to the wood and the brush was 0.7 m, and the distance from the hat to the scissors and the phone was 1.4 m. A light was placed on the ceiling near the middle of the cylinder to illuminate the area. The floor was covered with gray carpet. The testing location was between the hat and the brush, and 0.3 m away from the hat (the testing location is illustrated in Figure 1B).
Each test trial was composed of a warning indication (“start”) and a target object (e.g. “please point to the candle”). Trials were presented by a computer outside the cylinder via wireless earphone. A joystick was used as the pointing apparatus.
The primary independent variable was the locomotion of participants just before testing. In the baseline condition, participants stood at the testing location and maintained their learning orientation. In the updating condition, participants turned to face a new heading. In the disorientation condition, participants kept on rotating until they were disorientated. In each locomotion condition, 8 blocks of trials were included, each block involving pointing to all 9 objects once in a random order.
As in Mou et al (2006), the actual direction of a target object was defined with respect to the learning heading (baseline) or the 120° headings (updating and disorientation). The judged direction was defined with respect to the participant’s egocentric heading. The same variables were measured as in Mou et al.: Signed pointing error, defined as the signed angular difference between the judged direction of the target object and the actual direction of the target object (see Mou et al. (2006), Table 1); configuration error, defined as the standard deviation of the means per target object of the signed pointing errors; heading error, defined as the mean of the means per target object of the signed pointing errors; pointing variability, defined as the square root of the mean of the variances per target object of the signed pointing errors; and pointing latency, measured as the latency from presentation of the target object to the onset of joystick deflection.
Procedure
After learning how to use the joystick in the preparation room, participants were blindfolded outside of the study room and then led to the learning position (close to the Brush, see Figure 1A) by the experimenter. The blindfold was removed and the names of objects were given by the experimenter. Participants viewed the layout for 30 seconds and then closed their eyes and named and pointed to each object with one of their fingers. Each participant received 10 such learning-pointing sessions. Then they put on the wireless earphone and held a joystick, and received 5 more learning-pointing sessions. But in these sessions, they pointed to objects with the joystick instead of fingers. Participants held the joystick against their front waist. They were instructed to click the trigger on the joystick when they heard the warning (“start”). Then the name of the target object was presented (e.g. “please point to the mug”) and they were instructed to point to the direction of the target object as accurately as possible. Feedback and corrections were given if any absolute pointing error was more than 20 degrees.
After that, the experimenter indicated the testing position to participants and asked them walk to that location blindfolded. All participants were tested in the order of baseline, updating, and disorientation conditions. In the baseline condition, participants maintained their heading to scissors. In the updating condition, participants rotated 240 degrees by themselves (e.g. “please turn right until you are facing the candle”). Half of the participants turned right to face the candle and half of the participants turned left to face the ball. In the disorientation condition, participants rotated in place until stopped by the experimenter. After every minute, they pointed to the location of an object named by the experimenter (e.g. “please point to the ball”). Participants kept on rotating until the absolute pointing error was larger than 90 degrees. Then they were instructed to turn to face the ball (or candle) if they faced the candle (or ball) in the updating condition (“please turn left until you believe you are facing the ball”). They were allowed to adjust their position by themselves if they thought they had drifted off of the testing location while rotating. A recovery period was given before the final pointing test. At each testing orientation, participants had 8 blocks of trials, each of which included pointing to all 9 objects once in a random order. Participants were instructed to point to the direction of the target object as accurately as possible and were discouraged from pointing too quickly. No feedback was given at test.
Results and Discussion
The dependent variables were analyzed in repeated measures analyses of variance (ANOVAs) with one term for locomotion condition (baseline, updating, and disorientation). As discussed in the Introduction and consistent with previous studies (Holmes & Sholl, 2005; Mou, McNamara, Rump, & Xiao, 2006; Waller & Hodgson, 2006; Wang & Spelke, 2000), in this experiment and all following experiments, configuration error was used to determine the disorientation effect. Configuration error was more sensitive than pointing variability or pointing latency to the effects of disorientation and no reversed pattern (less variability or shorter latency in the disorientation condition than in the updating condition) was evident in any other variables in any experiments. The effects of disorientation on heading error followed the exactly same pattern as on the configuration error.
For the interest of brevity, only the analyses on configuration error were reported in detail. Means and standard deviations of pointing variability, absolute heading error, and pointing latency are provided in Tables 3–5.
Table 3.
Means (and Standard Deviations) of pointing variability as a function of locomotion condition for each experiment
| Exp | Locomotion condition | Comparison | ||
|---|---|---|---|---|
| B | U | D | ||
| 1 | 9.94 (2.36) | 13.57 (2.88) | 14.47 (4.12) | B < U; B < D; U = D |
| 2 | 8.78 (1.73) | 15.63 (11.01) | 18.62 (13.40) | B < U; B < D; U = D |
| 3 | 10.45 (2.46) | 14.37 (4.35) | 13.21 (3.03) | B < U; B < D; U = D |
| 4 | 9.55 (2.05) | 14.32 (3.65) | 18.33 (11.99) | B < U; B < D; U = D |
| 5 | 9.40 (2.35) | 13.91 (3.33) | 14.01 (5.49) | B < U; B < D; U = D |
| 6 | 8.84 (1.95) | 15.30 (3.65) | 17.14 (5.94) | B < U; B < D; U = D |
| 7 | 10.11 (1.90) | 14.71 (4.14) | 13.74 (2.68) | B < U; B < D; U = D |
| 8 | 9.43 (2.00) | 15.20 (3.39) | 15.45 (3.75) | B < U; B < D; U = D |
Note: n = 24 in all experiments. B = Baseline; U = Updating; D = Disorientation. In comparison “<” refers to significantly smaller at .05 level; “=” refers to no significantly difference at .05 level.
Table 5.
Means (and Standard Deviations) of response latency as a function of locomotion condition for each experiment
| Exp | Locomotion condition | Comparison | ||
|---|---|---|---|---|
| B | U | D | ||
| 1 | 1.383 (0.406) | 1.803 (0.604) | 1.920 (0.595) | B < U; B < D; U = D |
| 2 | 1.082 (0.341) | 2.071 (1.221) | 2.062 (1.178) | B < U; B < D; U = D |
| 3 | 1.199 (0.458) | 1.600 (0.747) | 1.606 (0.630) | B < U; B < D; U = D |
| 4 | 1.125 (0.425) | 1.887 (1.105) | 2.382 (1.818) | B < U; B < D; U = D |
| 5 | 1.389 (0.474) | 2.066 (1.119) | 2.269 (1.758) | B < U; B < D; U = D |
| 6 | 1.121 (0.368) | 2.023 (0.896) | 2.072 (0.776) | B < U; B < D; U = D |
| 7 | 1.182 (0.446) | 1.482 (0.527) | 1.592 (0.601) | B < U; B < D; U = D |
| 8 | 0.916 (0.367) | 1.380 (0.593) | 1.463 (0.620) | B < U; B < D; U = D |
Note: All latencies are measured in seconds. n = 24 in all experiments. B = Baseline; U = Updating; D = Disorientation. In comparison “<” refers to significantly smaller at .05 level; “=” refers to no significantly difference at .05 level.
Configuration error is plotted in Figure 2A as a function of locomotion condition. As shown in the figure, the main effect of locomotion condition was significant, F (2, 46) = 13.60, p < 0.01, MSE = 26.10. Pairwise comparisons showed that configuration error was smaller in the baseline condition than in the updating and disorientation conditions, ts (46) ≥ 4.08. The difference between the latter two conditions was not evident, t (46) = 0.78.
Figure 2.
Configuration errors as a function of locomotion condition in Experiments 1 to 4. 2A for Experiment 1, 2B for Experiment 2, 2C for Experiment 3, 2D for Experiment 4. (Error bars are confidence intervals corresponding to ±1 standard error, as estimated from the analysis of variance.)
The results of Experiment 1 replicated the results of Experiment 2 of Mou et al. (2006), even though the testing location was not occupied by an object in the present experiment, whereas it was so occupied in Mou et al.’s Experiment 2. These results indicated that participants represented and updated object-to-object spatial representations when participants learned a regular layout at the periphery of it. In Experiment 2, participants learned the same regular layout as in Experiment 1 while standing in its center.
Experiment 2
Method
Participants
Twenty-four university students (12 male and 12 female) participated in return for monetary compensation.
Material, Design and Procedure
Participants learned the same regular layout as in Experiment 1 (Figure 1B). They studied and were tested at the location 30 cm behind the hat, which was the testing location in Experiment 1. The procedure was otherwise the same as in Experiment 1.
Results and Discussion
Configuration error is plotted in Figure 2B as a function of locomotion condition. As shown in the figure, the main effect of locomotion condition was significant, F (2, 46) = 19.55, p < 0.01, MSE = 90.11. Pairwise comparisons showed that people pointed with smaller configuration error in the baseline condition than in the updating and disorientation conditions, ts (46) ≥ 5.34. The difference between the latter two conditions was not evident, t (46) = 0.14.
The results of Experiment 2 replicated those of Experiment 1. Configuration error was not affected by disorientation, relative to the updating condition. Hence, there appears to be no effect of the learning location on the selection of reference objects when participants learned a regular layout. In Experiments 3 and 4, participants learned either at the periphery of or in the middle of an irregular object array. We predicted that configuration error would increase after disorientation in both experiments if the layout geometry determined the appearance or disappearance of the configuration error.
Experiment 3
Method
Participants
Twenty-four university students (12 male and 12 female) participated in return for monetary compensation.
Material, design and procedure
The configuration of 9 objects was constructed as illustrated in Figure 1C. The locations of scissors, ball, and candle were the same as those in the regular layout, but the other 6 objects’ locations were changed by randomizing their distances to the testing location while keeping their angular bearing. In this way, an irregular object array (Figure 1C, for all participants) was constructed without changing pointing angles, which made the irregular layout and the regular layout comparable. The method was otherwise the same as in Experiment 1. Participants learned at the periphery of the irregular layout and then were tested in the middle (testing location is illustrated in Figure 1D).
Results and Discussion
Configuration error is plotted in Figure 2C as a function of locomotion condition. As shown in the figure, the main effect of locomotion condition was significant, F (2, 46) = 13.22, p < 0.01, MSE = 42.53. Pairwise comparisons showed that participants pointed with larger configuration error in the disorientation condition than in the baseline and updating conditions, and also pointed with larger configuration error in the updating condition than in the baseline condition, ts (46) ≥ 2.24.
These results indicated that participants represented and updated self-to-object spatial representations when participants learned an irregular nine-object array from its periphery.
Experiment 4
Method
Participants
Twenty-four university students (12 male and 12 female) participated in return for monetary compensation.
Material, design and procedure
The irregular layout in Experiment 3 was used. Participants learned it while standing in the middle and were tested in the same location (Figure 1D). The procedure was otherwise the same as in Experiment 3.
Results and Discussion
Configuration error is plotted in Figure 2D as a function of locomotion condition. As shown in the figure, the main effect of locomotion condition was significant, F (2, 46) = 18.40, p < 0.01, MSE = 53.80. Pairwise comparisons showed that people pointed with larger configuration error in the disorientation condition than in the baseline and updating conditions, and also pointed with larger configuration error in the updating condition than in the baseline condition, ts (46) ≥ 2.63.
Learning amidst the irregular layout, participants pointed with larger configuration error in the disorientation condition than in the updating condition. This replicated the result of Experiment 3, and indicated that participants represented and updated self-to-object spatial representations when they learned an irregular object array no matter where they stood during learning.
In sum, the results of Experiments 1–4 indicated that the effect of disorientation on configuration error was modulated by the layout geometry structure rather than by participants’ learning position. These findings indicated that participants represented and updated object-to-object spatial relations when they learned a regular layout whereas they represented and updated self-to-object spatial relations when they learned an irregular layout.
In Experiments 5 and 6, participants learned a regular layout and were instructed to update self-to-object spatial relations during locomotion. In Experiments 7 and 8, participants learned an irregular layout and were instructed to update object-to-object spatial relations during locomotion. We wanted to see whether the appearance or disappearance of the disorientation effect in the previous experiments could be altered by instructions. If so, we can conclude that the appearance or disappearance of the disorientation effect depends on whether self-to-object spatial relations or object-to-object spatial relations are primarily updated during locomotion regardless of which forms of spatial relations are represented during learning. Otherwise the appearance or disappearance of the disorientation effect may be determined by the spatial relations that are represented during learning and then updated during locomotion.
Experiment 5
Method
Participants
Twenty-four university students (12 male and 12 female) participated in return for monetary compensation.
Material, design and procedure
Participants learned at the periphery and were tested in the middle of the regular layout (learning location is illustrated in Figure 1A; testing location illustrated in Figure 1B). This experiment was the same as Experiment 1 except for the instruction immediately before locomotion. After the baseline condition and before locomotion, participants were explicitly instructed to use self-to-object spatial relations (e.g. “please keep track of all of the locations of the objects relative to yourself while you are turning to face the ball.”).
Results and Discussion
Configuration error is plotted in Figure 3A as a function of locomotion condition. As shown in the figure, the main effect of locomotion condition was significant, F (2, 46) = 10.38, p < 0.01, MSE = 80.42. Pairwise comparisons showed that people pointed with larger configuration error in the disorientation condition than in the baseline and updating conditions, and also pointed with larger configuration error in the updating condition than in the baseline condition, ts (46) > 2.25.
Figure 3.
Configuration errors as a function of locomotion condition in Experiments 5 to 8. 3A for Experiment 5, 3B for Experiment 6, 3C for Experiment 7, 3D for Experiment 8.
The results of Experiment 5 indicated that participants could follow the instructions to use self-to-object spatial relations after they learned at the periphery of an array with a good geometric structure. In Experiment 6, participants were instructed to use self-to-object spatial relations after they learned the layout while standing in the middle.
Experiment 6
Method
Participants
Twenty-four university students (12 male and 12 female) participated in return for monetary compensation.
Material, design and procedure
Participants learned and were tested amidst the regular layout (Figure 1B). This experiment is identical to Experiment 2 except for the instruction of using self-to-object spatial relations in locomotion as in Experiment 5.
Results and Discussion
Configuration error is plotted in Figure 3B as a function of locomotion condition. As shown in the figure, the main effect of locomotion condition was significant, F (2, 46) = 26.50, p < 0.01, MSE = 32.77. Pairwise comparisons showed that people pointed with larger configuration error in the disorientation condition than in the baseline and updating conditions, and also pointed with larger configuration error in the updating condition than in the baseline condition, ts (46) ≥ 3.24.
The results of Experiment 6 indicated that participants could follow the instruction to update self-to-object spatial relations during locomotion when they learned an array with good geometric structure while standing in the middle of the array.
Experiment 7
Method
Participants
Twenty-four university students (12 male and 12 female) participated in return for monetary compensation.
Material, design and procedure
Participants learned at the periphery and then were tested in the middle of the irregular layout (Figures 1C and 1D respectively). This experiment was the same as Experiment 3 except for the instruction before locomotion. Before locomotion, participants were explicitly instructed to use object-to-object spatial relations during locomotion (“please keep track of all of the locations of the objects relative to other objects while you are turning to face the ball.”).
Results and Discussion
Configuration error is plotted in Figure 3C as a function of locomotion condition. As shown in the figure, the main effect of locomotion condition was significant, F (2, 46) = 16.29, p < 0.01, MSE = 19.91. Pairwise comparisons showed that people pointed with smaller configuration error in the baseline condition than in the updating and disorientation conditions, ts (46) ≥ 4.57. The difference between the latter two conditions was not evident, t (46) = 0.67.
The results of Experiment 7 indicated that participants could follow the instruction to use object-to-object spatial relations after they learned an array without a good geometry structure while standing at the periphery.
Experiment 8
Method
Participants
Twenty-four university students (12 male and 12 female) participated in return for monetary compensation.
Material, design and procedure
Participants learned and then were tested amidst the irregular layout as in Experiment 4 (Figure 1D). This experiment was the same as Experiment 4 except for the instruction to use object-to-object spatial relations.
Results and Discussion
Configuration error is plotted in Figure 3D as a function of locomotion condition. As shown in the figure, the main effect of locomotion condition was significant, F (2, 46) = 59.45, p < 0.01, MSE = 22.10. Pairwise comparisons showed that people pointed with larger configuration error in the disorientation condition than in the baseline and updating conditions, and also pointed with larger configuration error in the updating condition than in the baseline condition, ts (46) ≥ 4.88. The results of Experiment 8 indicated that participants could not follow the instruction to use object-to-object spatial relations after they learned amidst an irregular layout. This result contrasts with those obtained in Experiments 5–7, all of which showed that the updating of spatial relations was altered by instruction. An explanation of this finding is discussed in the General Discussion.
General Discussion
This study provided evidence that layout geometry modulates the effect of disorientation on pointing consistency. The disorientation effect was not present when participants pointed to objects in a regular layout no matter whether they learned at the periphery or in the middle of the layout (Experiments 1, 2). The disorientation effect was present when participants pointed to objects in an irregular layout regardless of participants’ learning position (Experiments 3, 4). However the influence of layout geometry can be overridden by instructions, with one apparent exception. The disorientation effect was present if participants who learned a regular layout were instructed to keep track of self-to-object spatial relations (Experiments 5, 6). The disorientation effect disappeared if participants who learned an irregular layout from its periphery were instructed to use object-to-object spatial relations (Experiment 7). The only exception is that the disorientation effect was not eliminated by instruction if participants learned an irregular layout from the middle (Experiment 8).
These findings indicated that participants who learned a regular layout at both learning positions might represent both self-to-object and object-to-object spatial relations. The disorientation effect was not observed without instruction indicating that the default process is to primarily update the representation of object-to-object spatial relations during locomotion, e.g. only rehearsing object-to-object spatial relations. The disorientation effect was observed when participants were instructed to monitor and update self-to-object spatial relations indicating that self-to-object spatial relations may also be represented during learning because the instruction was presented after participants learned the layout and finished the baseline condition.
These findings also indicated that participants who learned an irregular layout while standing at its edge represented both self-to-object and object-to-object spatial relations. However, the default process seems to be to update self-to-object spatial relations during locomotion, as the disorientation effect appeared in the absence of instructions. The disorientation effect was eliminated when participants were instructed to monitor and update object-to-object spatial relations indicating that object-to-object spatial relations may also be represented during learning because the instruction was presented after participants learned the layout and finished the baseline condition. Participants who learned an irregular layout while standing in its center, however, appeared to represent self-to-object spatial relations only, as the disorientation effect was not sensitive to instructions in this condition.
The conclusion that representations of self-to-object and object-to-object spatial relations coexisted is consistent with the findings in previous studies (Sargent et al., 2008; Waller & Hodgson, 2006). The interaction between layout geometry and learning position on the selection of reference objects (egocentrically or allocentrically) has not been reported before. In the regular layout, object-to-object spatial relations were salient (Figures 1A and 1B). Even participants who learned inside could perceive object-to-object spatial relations easily (Figure 1B). In the irregular layout, object-to-object spatial relations were not salient (Figures 1C and 1D). Participants who learned the layout from its periphery may represent object-to-object spatial relations because they could view the whole layout from a single viewpoint. However participants who learned an irregular object in the middle could not easily perceive object-to-object spatial relations. Hence, object-to-object spatial relations were represented minimally, if at all.
This interaction between layout geometry and learning position on the appearance or disappearance of the disorientation effect creates difficulties for an alternative explanation of the findings, which is that only one type of spatial relation was encoded and then converted into the other form (e.g. Klatzky, 1998) when participants were instructed to do so. According to this explanation, in Experiments 5 and 6, participants represented object-to-object spatial relations during learning and converted object-to-object spatial relations to self-to-object spatial relations when they were instructed to use self-to-object spatial relations. This explanation, however, has difficulty accounting for the findings of Experiments 7 and 8. As the explanation goes, in Experiments 7 and 8, participants represented self-to-object spatial relations during learning but converted self-to-object spatial relations to object-to-object spatial relations when they were instructed to use object-to-object spatial relations. Hence, no disorientation effect would be expected in either experiment. However the results showed that the disorientation effect was found in Experiment 8 but not in Experiment 7. According to this explanation, then, participants converted self-to-object spatial relations to object-to-object spatial relations in Experiment 7 but not in Experiment 8. It is difficult to understand why participants could convert self-to-object spatial relations to object-to-object spatial relations when they learned outside of the layout in Experiment 7 but could not when they learned inside of the layout in Experiment 8. In contrast, as discussed above, it is more likely that the encoding of object-to-object spatial relations in an irregular layout depends on whether participants learned the layout from the periphery or middle.
Importantly these findings also suggested that only a single representation—either self-to-object or object-to-object—is primarily maintained and updated during locomotion, even though both are represented. Why are object-to-object spatial relations maintained and updated when people locomote in a regular layout and self-to-object spatial relations maintained and updated when people locomote in an irregular layout? We assume that maintaining representations of spatial relations during locomotion requires mental resources. People can compute object-to-object spatial relations using self-to-object spatial relations and vice versa (e.g. Klatzky, 1998). Hence, only one representation needs to be maintained, and doing so preserves mental resources for other tasks. Selecting which spatial representation to maintain during locomotion may depend on the fidelity of spatial representations as conjectured by Mou et al. (2006). In a regular layout, the fidelity of the object-to-object spatial representation may be higher than that of the self-to-object spatial representation, whereas in an irregular layout, the reverse may be true. Participants may maintain the representation with higher fidelity during locomotion. Another possibility is that people are able to form object-to-object and self-to-object representations of equal fidelity, regardless of the nature of the layout, but the process of maintaining each type of representation during locomotion depends on the geometric regularity of the layout. These two possibilities are not exclusive.
This project showed that layout geometry and instructions were two cues leading to an apparent reliance during locomotion on one type of spatial representation versus another. Another cue that may be used is physical connections between objects. For instance, in Wang and Spelke’s (2000) study, the disorientation effect was not observed when participants pointed to corners of an irregular room. We speculate that corner-to-corner spatial relations were highlighted because these corners were connected by the walls, leading to maintenance of an object-to-object representation and absence of the disorientation effect. The disorientation effect was also not observed when people pointed to objects in a familiar environment in the studies of Holmes and Sholl (2005) and Waller and Hodgson (2006). It is possible that object-to-object spatial relations are better represented as navigators experience an environment more frequently; this of course is predicted by classical theories of the microgenesis of spatial knowledge (Siegel & White, 1975; but see Montello, 1998, Ishikawa & Montello, 2006). These speculations deserve a systematic empirical investigation in future.
This project examined reference objects in spatial memory and showed that reference objects could be the observer or other objects. Although the reference directions are not primarily examined, this project still showed that spatial memory has a reference direction. Even when people learned a layout from its periphery, configuration error was significantly smaller in the baseline condition than in the updating condition (Experiments 1, 3, 5, and 7). This orientation dependent result cannot be attributed to the practice during learning because participants’ testing location was different from their learning position. Is the reference direction egocentric or allocentric? It really depends on the definitions of egocentric and allocentric. In the experiments of this study the reference direction is established by the learning orientation of the participant but is not fixed to the body front of the participant when the participant locomote in the environment (Mou et al. 2004). Otherwise no orientation dependent results should be observed.
In sum, this project demonstrated that on most occasions, people represent both self-to-object and object-to-object spatial relations during learning but during locomotion, they primarily maintain and update one of the spatial relations. In particular they primarily maintain and update self-to-object spatial relations in an irregular layout and maintain and update object-to-object spatial relations in a regular layout.
Table 4.
Means (and Standard Deviations) of heading error as a function of locomotion condition for each experiment
| Exp | Locomotion condition | Comparison | ||
|---|---|---|---|---|
| B | U | D | ||
| 1 | 3.68 (3.07) | 16.98 (11.82) | 17.29 (13.28) | B < U; B < D; U = D |
| 2 | 4.50 (2.87) | 21.60 (13.70) | 25.55 (13.57) | B < U; B < D; U = D |
| 3 | 4.11 (3.98) | 15.81 (13.29) | 26.30 (13.13) | B < U; B < D; U < D |
| 4 | 4.85 (4.69) | 16.48 (10.39) | 27.73 (19.46) | B < U; B < D; U < D |
| 5 | 4.14 (3.07) | 12.83 (9.90) | 29.05 (24.09) | B < U; B < D; U < D |
| 6 | 4.19 (3.35) | 15.48 (12.30) | 25.19 (20.63) | B < U; B < D; U < D |
| 7 | 5.19 (3.79) | 16.82 (10.51) | 19.48 (17.03) | B < U; B < D; U = D |
| 8 | 4.10 (2.64) | 14.40 (9.94) | 26.12 (18.22) | B < U; B < D; U < D |
Note: n = 24 in all experiments. B = Baseline; U = Updating; D = Disorientation. In comparison “<” refers to significantly smaller at .05 level; “=” refers to no significantly difference at .05 level.
Acknowledgments
Preparation of this paper and the research reported in it were supported in part by a grant from the Natural Sciences and Engineering Research Council of Canada and a grant from the National Natural Science Foundation of China (30770709) to WM and National Institute of Mental Health Grant 2-R01-MH57868 to TPM. We are grateful to Dr. Laura Carlson and three anonymous reviewers for their helpful comments on previous versions of this manuscript.
Footnotes
The regularity of array structure is determined by whether objects in the array line up row by row and column by column.
References
- Burgess N. Spatial memory: how egocentric and allocentric combine. Trends in Cognitive Sciences. 2006;10:551–557. doi: 10.1016/j.tics.2006.10.005. [DOI] [PubMed] [Google Scholar]
- Easton RD, Sholl MJ. Object-array structure, frames of reference, and retrieval of spatial knowledge. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1995;21:483–500. doi: 10.1037//0278-7393.21.2.483. [DOI] [PubMed] [Google Scholar]
- Holmes MC, Sholl MJ. Allocentric coding of object-to-object relations in overlearned and novel environments. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2005;31:1069–1087. doi: 10.1037/0278-7393.31.5.1069. [DOI] [PubMed] [Google Scholar]
- Ishikawa T, Montello DR. Spatial knowledge acquisition from direct experience in the environment: Individual differences in the development of metric knowledge and the integration of separately learned places. Cognitive Psychology. 2006;52:93–129. doi: 10.1016/j.cogpsych.2005.08.003. [DOI] [PubMed] [Google Scholar]
- Klatzky RL. Allocentric and egocentric spatial representations: Definitions, distinctions, and interconnections. In: Freksa C, Habel C, Wender KF, editors. Spatial cognition: An interdisciplinary approach to representing and processing spatial knowledge LNAI. Vol. 1404. Berlin: Springer-Verlag; 1998. pp. 1–17. [Google Scholar]
- McNamara TP, Rump B, Werner S. Egocentric and geocentric frames of reference in memory of large-scale space. Psychonomic Bulletin & Review. 2003;10:589–595. doi: 10.3758/bf03196519. [DOI] [PubMed] [Google Scholar]
- Montello DR. A new framework for understanding the acquisition of spatial knowledge in large-scale environments. In: Egenhofer MJ, Golledge RG, editors. Spatial and temporal reasoning in geographic information systems. New York: Oxford University Press; 1998. pp. 143–154. [Google Scholar]
- Mou W, McNamara TP, Rump B, Xiao C. Roles of egocentric and allocentric spatial representations in locomotion and reorientation. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2006;32:1274–1290. doi: 10.1037/0278-7393.32.6.1274. [DOI] [PubMed] [Google Scholar]
- Mou W, McNamara TP, Valiquette CM, Rump B. Allocentric and egocentric updating of spatial memories. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2004;30:142–157. doi: 10.1037/0278-7393.30.1.142. [DOI] [PubMed] [Google Scholar]
- Mou W, Xiao C, McNamara TP. Reference directions and reference objects in spatial memory of a briefly viewed layout. Cognition. 2008;108:136–154. doi: 10.1016/j.cognition.2008.02.004. [DOI] [PubMed] [Google Scholar]
- Sargent J, Dopkins S, Philbeck J, Modarres R. Spatial memory during progressive disorientation. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2008;34:602–615. doi: 10.1037/0278-7393.34.3.602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shelton A, McNamara TP. Systems of spatial reference in human memory. Cognitive Psychology. 2001;43:274–310. doi: 10.1006/cogp.2001.0758. [DOI] [PubMed] [Google Scholar]
- Sholl MJ. The role of a self-reference system in spatial navigation. In: Montello D, editor. Spatial information theory: Foundations of geographical information science. Berlin: Springer-Verlag; 2001. pp. 217–232. [Google Scholar]
- Siegel AW, White SH. The development of spatial representations of large-scale environments. In: Reese HW, editor. Advances in child development and behavior. Vol. 10. Academic Press; 1975. pp. 9–55. [DOI] [PubMed] [Google Scholar]
- Tversky B. Distortions in memory for maps. Cognitive Psychology. 1981;13:407–433. [Google Scholar]
- Waller D, Hodgson E. Transient and enduring spatial representations under disorientation and self-rotation. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2006;32:867–882. doi: 10.1037/0278-7393.32.4.867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang RF, Spelke ES. Updating egocentric representations in human navigation. Cognition. 2000;77:215–250. doi: 10.1016/s0010-0277(00)00105-0. [DOI] [PubMed] [Google Scholar]
- Wang RF, Spelke ES. Human spatial representation: insights from animals. Trends in Cognitive Sciences. 2002;6:376–382. doi: 10.1016/s1364-6613(02)01961-7. [DOI] [PubMed] [Google Scholar]