Abstract
This paper proposes a methodology to segment near-tubular fiber bundles from diffusion weighted magnetic resonance images (DW-MRI). Segmentation is simplified by locally reorienting diffusion information based on large-scale fiber bundle geometry. Segmentation is achieved through simple global statistical modeling of diffusion orientation. Utilizing a modification of a recent segmentation approach by Bresson et al. allows for a convex optimization formulation of the segmentation problem, combining orientation statistics and spatial regularization. The approach compares favorably with segmentation by full-brain streamline tractography.
1 Introduction
Diffusion weighted (DW) magnetic resonance imaging (MRI) allows for in-vivo measurements of water diffusion in tissues such as the human brain. While brain white matter appears uniform in structural MRI, DW-MRI measurements can provide estimates of macroscopic fiber bundle direction as well as indicate changes in tissue properties. However, the relation between DW-MRI signal and white matter ultra-structure is only known partially. For example, the manner in which axonal organization and geometry relate to a measured diffusion profile in general remains an open question. Axonal organization is likely a major factor for diffusion anisotropy [Beaulieu (2002)], with axonal myelinization having a modulating (though not dominant) effect on water diffusion. Fiber bundle direction correlates with the major diffusion direction in fiber bundle areas comprised of large numbers of approximately unidirectional axons [Bihan (2003)]. This allows for the estimation of distinct fiber bundles from DW-MRI measurements.
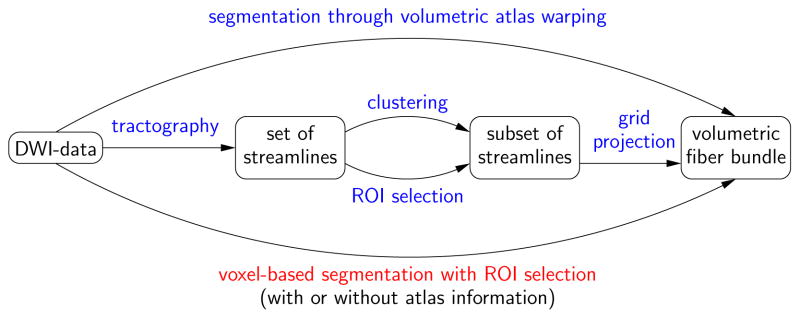
A variety of approaches to extract white matter bundles from diffusion weighted images exist. They may be classified into streamline-based approaches and voxel-based approaches (see Figure 1 for an overview of the approaches). The streamline-based approaches utilize streamline tractography to come up with bundle segmentations. For example, this can be direct voxelization of the streamlines, voxelization preceded by streamline clustering [O’Donnell and Westin (2007)], or stochastic tractography [Behrens et al. (2003); Friman et al. (2006)]. Voxel-based approaches aim at extracting white matter bundles directly from the voxel data without using streamline tractography. Approaches include voxel-based clustering [Wiegell et al. (2003)], surface-evolution using global statistics [Lenglet et al. (2006); Wang and Vemuri (2005)] or local similarity terms [Jonasson et al. (2005)], optimal connectivity methods [Jeong et al. (2007); Fletcher et al. (2007)], region-growing [Melonakos et al. (2007)], hidden Markov measure fields [McGraw et al. (2006)] and fuzzy segmentation [Awate et al. (2007)].
Fig. 1.
Approaches for fiber bundle segmentation. Fiber bundle segmentation may be performed directly on voxel data or through streamline tractography with subsequent selection of the fibers of interest (either through region of interest specification or automatic clustering). Atlas information may be used to incorporate prior information into the segmentation process or to facilitate segmentation through atlas registration itself.
Though a large number of segmentation approaches exist, none of them can claim truly universal applicability. The use of one method over another is typically based on some of the following considerations:
Usability: How difficult is it to obtain robust, reliable results for large population studies? How much user intervention is required?
Focus of analysis: Should all major fiber bundles in the brain be investigated, or only a specific one?
Measure of interest: Are global measurements of interest or does locality play a role? Is it important to obtain an accurate segmentation of the bundle or does a consistent segmentation of a bundle core suffice?
Data quality: What is the resolution of the data and how noisy is it?
This paper proposes a segmentation approach based on reorienting the diffusion measurements. Reorientation information is derived from large-scale fiber bundle geometry. This facilitates region-based bundle segmentation with global statistics. However, it also presupposes a robust method to compute an estimation of the geometry information. We propose in this work a method for the segmentation of near-tubular fiber bundles only (whose large-scale geometry can be approximated by a one-dimensional space curve with locally varying, approximately circular, cross-sections) and can thus utilize optimal path methods or simple streamlining to obtain the geometry information. Extensions to sheet-like fiber bundles are conceivable. While the proposed approach is restricted to segmentations that conform to the imposed geometry information, it is computationally efficient, is simple, allows for reliable optimization, is robust to local noise effects, and relies only on a small number of parameters.
Briefly summarizing the remainder of this paper, in Section 2, we give an overview of the system. Section 3 introduces the local coordinate system used for the reorientation of diffusion information. Section 4 describes how to extend the local coordinate system to the complete image volume. The reorientation of diffusion data is described in Section 5. Sections 6 and 7 describe the statistical modeling of fiber bundle direction and its use for bundle segmentation respectively. Results are given in Section 8. Section 9 concludes the paper with a discussion of the approach, and an outlook on possible future work.
2 System Overview
This section summarizes the key steps of the proposed segmentation approach. The overall goal of the method is to be able to segment near-tubular fiber bundles from diffusion weighted images. Segmentation requires a suitable similarity measure for voxel grouping into object foreground and object background. While a multitude of segmentation methods for diffusion weighted images exists (see Section 1) arguably the methods used in practice are based on streamlining: direct voxelization of streamlining results, clustering of streamlines, or stochastic tractography (see Figure 2 for a depiction of the principle of segmentation through streamline tractography). This is surprising, because (i) streamlining approaches are sensitive to noise and (ii) volumetric segmentation algorithms (resulting in grid-based voxel classifications) developed outside the area of diffusion weighted imaging have either not been applied to DW-MRI or only with limited success. Edge-based and region-based surface evolutions, graph cuts, and region growing are examples of such volumetric segmentation approaches. A major impediment to their adoption for DWI segmentation is the nature of DWI data. DWI data is (i) vector-valued (tensor-valued if diffusion tensors are computed), is (ii) axial (identifying antipodal directions), typically has (iii) low signal to noise ratio and is of relatively low resolution, and is (iv) spatially non-stationary (i.e., large scale orientation changes are expected to occur within individual fiber bundles).
Fig. 2.
Principle of a simple segmentation by streamline tractography. Streamlines are seeded either in a region of interest or globally. Only streamlines passing through one or multiple regions of interest are kept. The voxels traversed by streamlines constitute the volumetric fiber bundle segmentation.
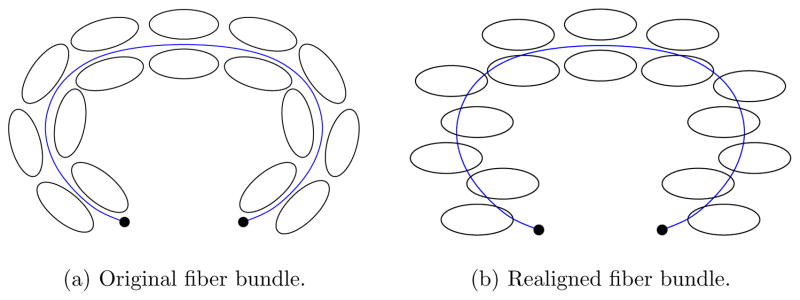
Figure 3 illustrates diffusion tensors changing direction along a fiber bundle and the same set of diffusion tensors when realigned relative to a representative fiber tract. This realignment process is at the core of the approach proposed in this paper. Realignment simplifies the original problem by making it spatially stationary. Segmentation methods for vector-valued images can then be employed for fiber bundle segmentation. Note that standard streamline tractography usually incorporates a weak, implicit form of spatial realignment by disallowing orientation changes considered too drastic.
Fig. 3.
Tensor reorientation concept. The spatially varying tensor orientation can largely be removed by reorientation with respect to a representative fiber tract (blue).
The proposed approach is:
Find a representative fiber tract (e.g., by streamlining, by an optimal path approach, or through atlas warping of a predefined representative fiber tract).
For every candidate point in the image volume, find the closest point on the representative fiber tract.
Regard the candidate point as part of the fiber bundle if its diffusion information is similar to the diffusion information at the closest point.
Create a spatially consistent segmentation based on the similarities of 3).
The key questions are, what is meant by “closest,” “similar,” and “spatially consistent.” The direct approach to measure closeness is to look at Euclidean distance. Euclidean distance typically does not yield unique point to point correspondences. Section 4 thus proposes a method based on frame diffusion. Since the focus of this paper is the segmentation of near-tubular fiber bundles, the overall fiber bundle geometry can be approximately described by the space curve given by a representative fiber tract. The (regularized) Frenet frame of the space curve can then be used as a local coordinate frame and as the basis for frame diffusion; see Section 3.
Many probabilistic and deterministic similarity measures have been proposed for diffusion weighted imaging (in particular, for diffusion tensor imaging; see for example [Lenglet et al. (2006); Jonasson et al. (2005)]). One of the simplest measures of diffusion similarity is to measure angular deviations of the major directions of diffusion. This is in line with streamline tractography which typically uses only the principal diffusion direction for streamline propagation 1 and will be used in a probabilistic formulation in this paper as discussed in Section 6. To obtain spatial consistency, which cannot be achieved by local segmentation decisions based on directional statistics and reorientation of diffusion measurements alone, regularization is necessary. Section 7 describes the proposed segmentation approach based on a slight modification of the convex optimization formulation by [Bresson et al. (2007)].
3 The Regularized Axial Frenet Frame
To parameterize near-tubular fiber bundles, a suitable coordinate system is necessary. For space-curves, the Frenet frame can be used. Given a parameterized curve 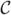 (p): [0, 1] ↦ ℝ3, such that
(p): [0, 1] ↦ ℝ3, such that 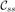 ≠ 0,
≠ 0, 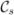 ≠ 0 (i.e., without singular points of order 0 and 1 [do Carmo (1976)]) the Frenet frame is given by
≠ 0 (i.e., without singular points of order 0 and 1 [do Carmo (1976)]) the Frenet frame is given by
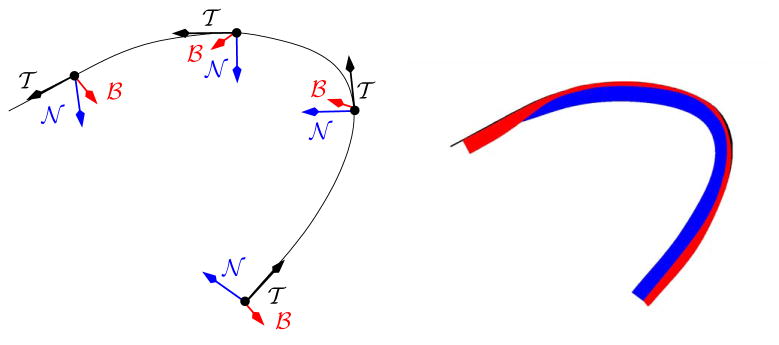
is the unit tangent vector, 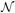 and ℬ are the normal and the binormal, κ and τ denote curvature and torsion respectively, and s denotes arc-length. See Figure 4 for a depiction of the Frenet frame. Computing
and ℬ are the normal and the binormal, κ and τ denote curvature and torsion respectively, and s denotes arc-length. See Figure 4 for a depiction of the Frenet frame. Computing 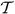 from
from 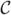 is immediate. Computing
is immediate. Computing 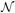 yields ℬ =
yields ℬ = 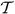 ×
× 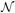 and thus the desired local coordinate frame.
and thus the desired local coordinate frame.
Fig. 4.
The Frenet frame. A frame {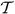 ,
, 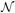 , ℬ} consisting of the tangent, the normal, and the binormal to
, ℬ} consisting of the tangent, the normal, and the binormal to 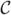 can uniquely be assigned to every point for a non-singular space curve through the Frenet equations.
can uniquely be assigned to every point for a non-singular space curve through the Frenet equations.
In this paper the space curve is given by a representative fiber tract. For the experiments of Section 8 streamline tractography was used to compute the representative fiber. For a more robust approach, streamlining should be replaced by an optimal path method [Pichon et al. (2005)]. In what follows, a known representative fiber tract is assumed.
Since the Frenet frame is based on differential properties of the space curve it is sensitive to noise. Instead of using the Frenet frame directly, the frame diffusion is instead based on a regularized version of the Frenet frame as discussed in Appendix A.1. Figure 5 shows a progressively more regularized Frenet frame. Note that for the reorientation of diffusion information (see Section 5) the Frenet axes can be flipped. All computations in this paper identify antipodal directions; derivatives are computed by prealigning all vector-valued quantities locally before derivative computation.
Fig. 5.
Regularization of the Frenet frame with tangential direction fixed helps obtaining smoothly varying frames from noisy data on a space curve.
4 Frame Diffusion
Instead of declaring a point in space to correspond to its closest point (measured by Euclidean distance) on the representative tract, here, correspondence is established implicitly through a diffusion process. This allows for smoother correspondences avoiding orientation jumps which occur at shock points for the Euclidean distance map. Since orientation is the quantity of interest, the orientation information is diffused away from the representative tract. Tschumperle and Deriche [Tschumperle et al. (2001)] regularize diffusion tensor fields by evolutions on frame fields. This can be used to define the diffusion of the frame field off the reference tract. Formally,
| (1) |
where 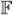 = {
= {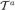 ,
, 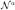 , ℬa} is the set of the axes implied by the regularized Frenet frame,
, ℬa} is the set of the axes implied by the regularized Frenet frame, 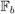 denotes the boundary condition given by the Frenet-frame-implied axes on the tract, x ∈ ℝ3 denotes spatial position, θ artificial evolution time, and
the spatial Laplacian operator. The frame diffusion problem (1) can be solved [Tschumperle et al. (2001)] by evolving a set of three coupled vector diffusions:
denotes the boundary condition given by the Frenet-frame-implied axes on the tract, x ∈ ℝ3 denotes spatial position, θ artificial evolution time, and
the spatial Laplacian operator. The frame diffusion problem (1) can be solved [Tschumperle et al. (2001)] by evolving a set of three coupled vector diffusions:
which may be rewritten [Tschumperle et al. (2001)] as the rotations
where R = 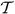 × Δ
× Δ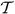 +
+ 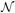 × Δ
× Δ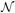 + ℬ × Δℬ and
+ ℬ × Δℬ and 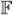 = {
= {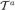 ,
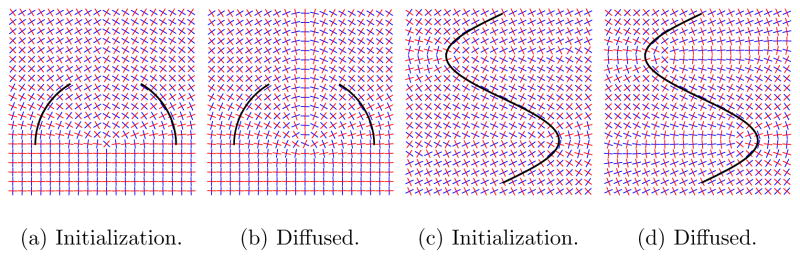
, 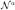 , ℬa} is given by identifying antipodal directions. While the statistics used for the segmentation in Section 7 only use directional information, diffusing the complete frame information specifies a local rotation. This allows for easy extension of the methodology to formulations using for example the full tensor information or orientation distribution functions. Figure 6 shows two 2D examples of frame diffusion. The resulting diffused frame field is smoother. Interestingly, the partial half-circle example shows that, to a limited extent, frame diffusion can be used to fill in missing information. This is a useful feature in case it is not possible to obtain one connected representative fiber tract.
, ℬa} is given by identifying antipodal directions. While the statistics used for the segmentation in Section 7 only use directional information, diffusing the complete frame information specifies a local rotation. This allows for easy extension of the methodology to formulations using for example the full tensor information or orientation distribution functions. Figure 6 shows two 2D examples of frame diffusion. The resulting diffused frame field is smoother. Interestingly, the partial half-circle example shows that, to a limited extent, frame diffusion can be used to fill in missing information. This is a useful feature in case it is not possible to obtain one connected representative fiber tract.
Fig. 6.
Frame diffusion results in smooth frame fields and consequentially in smooth reorientations. Initializations show frames based on closest Euclidean distance point correspondences, resulting in frame discontinuities. The diffused results are obtained through frame diffusion from the initializations.
5 Frame Reorientation
The diffused frames can be used to reorient diffusion measurements locally to a canonical frame M2. This reorientation can be applied to any representation of diffusion information, e.g., the diffusion tensor, orientation distribution functions, etc. For clarity, reorientation is explained here for the case of diffusion tensors T. Given the diffused frame {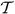 ,
, 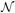 , ℬ} and the associated rotation matrix F = [
, ℬ} and the associated rotation matrix F = [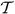 ,
, 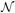 , ℬ] a tensor T is reoriented by applying the relative rotation MFT, i.e., by
, ℬ] a tensor T is reoriented by applying the relative rotation MFT, i.e., by
The tensor reorientation yields tight tensor statistics while allowing a segmentation algorithm to apply spatial regularizations in the original space. It greatly simplifies computations by avoiding an explicit warping to straighten a curved fiber bundle.
6 Orientation Statistics
To segment fiber bundles of interest requires a connection between the diffusion weighted images and the macroscopic geometric orientation of the underlying axon bundles. How diffusion measurements relate to fiber structure and geometry is not completely clear. However, a common assumption is that the major direction of diffusion aligns with the main fiber direction 3. We now describe the probabilistic modeling of fiber bundle orientations.
6.1 Watson Distribution
The Watson distribution is one of the simplest distributions for directional random variables [Watson (1965); Bingham (1974); Mardia (1975)]. It is radially symmetric around a mean direction μ, with a spread controlled by the concentration parameter k.
The Watson distribution on the unit sphere S2 has probability density
where μ is the mean direction vector, k the concentration parameter 4, q ∈ S2 is a direction represented as a column vector, and 1F1(·; ··) denotes the confluent hypergeometric function. The Watson distribution is bipolar for k > 0, with maxima at ±μ and uniform for k = 0. To model the interior of a fiber bundle, μ is set to the tangential direction of the canonical frame M. Reorienting diffusion information results in a tight Watson distribution with large concentration parameter k. The statistics outside the fiber bundle are modeled using the uniform distribution, since no preferred direction can be assumed in general in the fiber exterior.
Noting that cos θ = μTd, for fixed μ and k, the critical angle (pw(d|μ, k) = pw(d|·, 0) where the voxel probability for the interior and the exterior of the fiber bundle are equal) is the solution of the following equation:
The critical angle has the following limiting cases
illustrating the fact that larger values for the concentration parameter k enforce stricter classification for interior voxels. The critical angle for k → 0 corresponds to the maximal angle dispersion [Schwartzman et al. (2008)]. It shows that voxels with directions deviating by more than 54.74° from the mean direction μ cannot be classified as belonging to the interior using the probabilistic modeling proposed 5. This is not a practical limitation for reoriented diffusion data which is expected to have (and has in practice; see Section 8) a large concentration k by design.
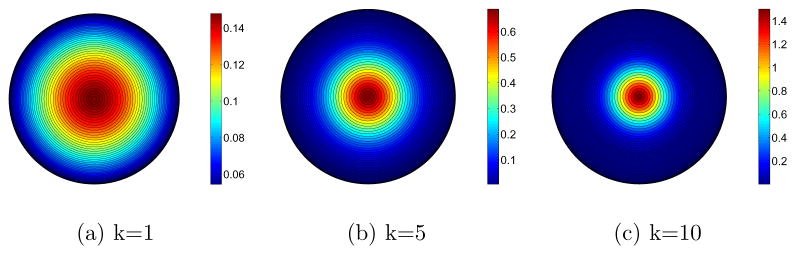
Figure 7 illustrates the relation between concentration parameter k and the critical angle θ. Figure 8 shows some sample Watson distributions. While it is possible to use more complicated probability distributions (e.g., the Bingham distribution, or distributions on the diffusion tensor directly) to model a fiber tract orientation distribution, the Watson distributions chosen (in conjunction with the reorientation scheme) have the advantage of modeling the interior and the exterior of the fiber bundle with only one free parameter, the concentration k, greatly simplifying the estimation task and allowing for an easy interpretation of the estimated probability distribution.
Fig. 7.
Critical angle θ vs. concentration k.
Fig. 8.
Watson distributions projected along direction μ onto the unit disk for a sample of concentration parameters k.
6.2 Parameter estimation for the Watson distribution
The distribution parameters k and μ are easy to estimate. Given a set of N points qi ∈ S2 (written as column vectors and representing spatial directions), the maximum likelihood estimate of μ is the major eigenvector of the sample covariance [Schwartzman et al. (2008)]
and 1 − λ1 (with λ1 the largest eigenvalue of C) is the maximum likelihood estimate of . Estimation of μ is performed only as a means of estimating the canonical frame direction and computed only on the representative tract. It is assumed fixed throughout the segmentation process described in Section 7. Only the concentration parameter k is estimated during bundle segmentation. For increased estimation robustness, robust estimators for the concentration parameter k may be used [Fisher (1982); Kimber (1985)] to account for cases where orientation measurements are either incorrect or cannot be reliably determined (as for example for isotropic tensors).
Estimating μ and k allows for
parameter-adaptive segmentations and
the estimation of a preferred reoriented coordinate-system direction, assuring that the main direction of diffusion is preserved on average after reorientation.
7 Segmentation
We now integrate the diffusion data reorientation method and the statistical modeling described in Section 6 within a probabilistic version of the Chan-Vese [Chan and Vese (2001)] segmentation framework [Cremers et al. (2007)] using the probability distributions of Section 6.
7.1 Optimization Problem
The Chan-Vese segmentation approach [Chan and Vese (2001)] is a piecewise-constant approximation formulation, minimizing the energy
| (2) |
where f(·) denotes image intensities, c1 and c2 are the intensity estimates for the interior and the exterior of the segmentation respectively, Ω is the computational domain, Ωi is the interior domain, and s indicates arc-length. The Chan-Vese energy has the probabilistic formulation
| (3) |
which reduces to Equation 2 (with a rescaling of λ) for with . Thus the Chan-Vese optimization problem 2 can be interpreted as finding the best two-phase segmentation assuming Gaussian probability distributions of equal variance interior and exterior to the sought for segmentation.
In the probabilistic formulation f(·) denotes an image feature (here, direction), p1 and p2 are the likelihoods for the interior and the exterior of the segmentation respectively. Choosing
constitutes the segmentation approach. See Section 6.1 for a discussion of this choice.
7.2 Numerical Solution
According to a slight modification of the solution approach in [Bresson et al. (2007)], the probabilistic Chan-Vese energy minimization problem 3 (on log-likelihood functions instead of image intensities) can be recast as the minimization of
| (4) |
where
The boundary is recovered as Ωi = {x: u(x) > ξ}, ξ ∈ [0, 1]. Equation 4 can be solved efficiently through a dual formulation of the total-variation norm [Bresson et al. (2007)]:
-
Solve for u keeping v fixed:
(5) -
Solve for v keeping u fixed:
(6) Repeat until convergence.
Equation 6 has the solution v = min{max{u(x) − θλr1(x, p1, p2), 0}, 1} and Equation 5 can be solved using a fixed-point iteration
To enforce segmenting a bundle containing the representative tract set
The segmented fiber bundle is defined as the set of voxels with which are contained in the connected component containing the voxels of the representative tract. This is also the volume which is used throughout the evolution to update the estimation of the concentration k of the fiber bundle’s Watson distribution.
8 Results
This section gives results for the proposed segmentation approach. Synthetic examples are discussed in Section 8.1. Section 8.2 presents results for a real DW-MRI of the brain and compares them to segmentation results obtained through streamline tractography based on the major eigenvectors of the diffusion tensors and Runge-Kutta numerical integration.
8.1 Synthetic example
A synthetic tensor example was generated. Tensors are assumed of uniform shape with eigenvalues (1.5, 0.5, 0.5)e − 3 oriented along a circular path to model a fiber bundle. Tensors oriented orthogonally to the circular path model the outside. Diffusion weighted images were generated using the Stejskal Tanner equation , where Sk denotes the diffusion weighted image acquired by applying a gradient direction gk with b-value b, and T the diffusion tensor. Parameters were S0 = 1000, b = 1000 with 46 gradient directions distributed on the unit sphere using an electric repulsion model and enforcing icosahedral symmetry. Rician noise of σ = 70 was introduced to the baseline image S0 (non-diffusion weighted) and the diffusion weighted images Sk. Figure 9 shows the original data and the resulting segmentation on the top row (with the streamline indicating the computed representative tract) and the reoriented data with associated segmentation on the bottom row. For this synthetic example, reorientation results in an almost perfectly uniform tensor distribution on the inside and the outside of the simulated fiber bundle. Consequently, while the proposed approach fails at segmenting the original data, it segments the reoriented data well. Note, that the failure to segment the original data is not merely a result of the segmentation method employed. Any segmentation relying purely on region-based statistics will either have to include some of the background in its bundle segmentation or will severely under-segment the bundle itself, since background and foreground are not clearly separable based on global statistics. While including edge-based terms may improve the segmentation of the original data, regional terms will be of limited use and will locally counteract the edge influence requiring a delicate balance between region-based and edge-based energies to faithfully segment the simulated fiber bundle.
Fig. 9.
Segmentation of a synthetic example. Reorienting diffusion information based on the representative streamline (top left) result in almost uniform tensor distributions interior and exterior to the fiber bundle. While segmentation for the original data is difficult and leads to unsatisfactory results, segmentation of the reoriented data is much easier leading to a faithful segmentation with the proposed approach. For both segmentations, k = 10, θ = 0.01, λ = 0.7.
8.2 Real example
The real example was computed for the cingulum bundle using a 3T DW-MRI upsampled to isotropic resolution (0.93 mm3) with 8 baseline images and 51 gradient directions distributed on the sphere by electric repulsion (b=586). The representative tract was computed using streamline tractography.
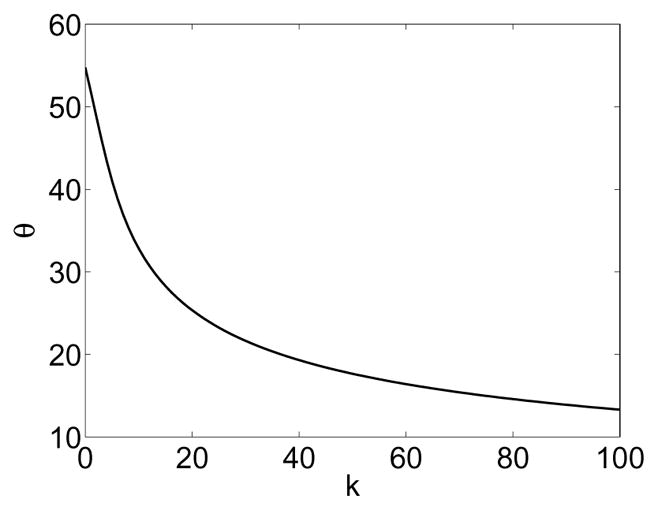
Figure 10 shows color by orientation representations for a sagittal slice through the brain with the cingulum bundle (mainly in green) before and after reorientation. The reoriented image shows a consistently green cingulum bundle, whereas in the original image the cingulum bundle is colored blue when wrapping posteriorly around the corpus callosum, indicating a change of orientation from anterior-posterior to superior-inferior. This result demonstrates the beneficial effect of reorientation on the real data set (effectively removing large-scale geometry effects), which allows for fiber bundle segmentation with a global statistical model. Example segmentation results of the proposed approach are shown for the reoriented and the original data. Algorithm parameters were set to θ = 0.01, λ = 0.5, dmax = 10 mm. The concentration parameter was set to k = 100 and converged to k = 19.5 throughout the evolution for the reoriented dataset. The surface models generated from the computed segmentations show that the segmentation for the reoriented data approximates the cingulum bundle more faithfully.
Fig. 10.
Sagittal slice of the cingulum bundle, before and after tensor reorientation. The cingulum bundle appears more uniform in direction (green) after reorientation. Reorientation greatly improves the segmentation result of the proposed approach.
Finally, to demonstrate the strength of the reorientation approach, Figure 11 gives an example for the cingulum bundle segmentation at a posterior slice of the cingulum bundle where the cingulum bundle wraps around the corpus callosum. While in the reoriented case the segmentation is successful and the direction of the cingulum bundle is uniform (green), the segmentation on the original data fails in this part of the fiber bundle.
Fig. 11.
Effect of reorientation on orientation and segmentation, depicted for a posterior coronal slice. Reorientation results in a consistent orientation of the cingulum bundle changing from blue to green, indicating a directional change from inferior-superior to posterior-anterior. While segmentation using the proposed approach fails for the original data it succeeds after reorientation.
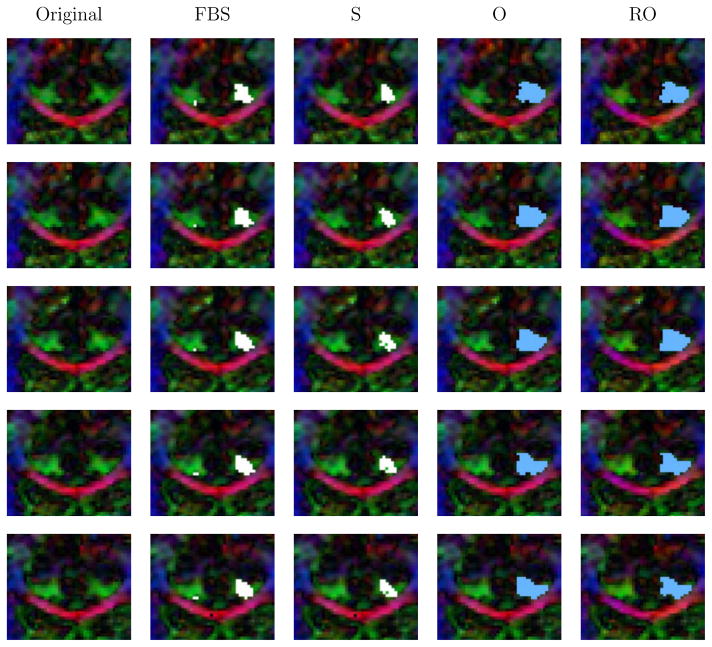
To compare the proposed methods to alternative segmentation approaches, the cingulum bundle was segmented using a region of interest based approach (the same regions of interest used to generate the representative fiber tract for reorientation). Two small axial regions of interest were defined for the cingulum bundle (superiorly to the corpus callosum). Streamline tractography with voxelization, full brain streamline tractography with voxelization, as well as segmentation on the original and reoriented data using the proposed approach was performed. Figure 12 illustrates segmentation results for these methods for coronal slices in the superior part of the cingulum bundle (where the cingulum bundle is not strongly curved). As expected streamline tractography and full brain streamline tractography mainly capture the interior of the fiber bundle, with full brain tractography performing qualitatively better than standard region of interest based streamline tractography (streamlines were seeded one per voxel in the regions of interest). The proposed segmentation approach captures the cingulum bundle well for the reoriented and for the original data, showing the utility of segmenting in orientation space. However, the reoriented segmentation results are better where the cingulum bundle curves strongly, as shown in Figure 11.
Fig. 12.
Superior coronal slices: Original data; results for streamline (S) and full brain streamline (FBS) tractography, for the proposed segmentation on original data (O) and on reoriented data (RO). Only the proposed approach segments up to the perceived bundle boundary in orientation space.
9 Conclusion and Discussion
This paper proposed a new segmentation method for near-tubular fiber bundles. It is based on reorientation of diffusion measurements resulting in more uniform data distributions inside the fiber bundle of interest. Segmentation is performed by an efficient convex approximation of the probabilistic Chan-Vese energy using region-based directional statistics. The approach compares favorably to streamline approaches for bundle segmentation.
Extensions to sheet-like structures are conceivable, where the representative tract would be replaced by a representative sheet [Yushkevich et al. (2007); Smith et al. (2006)] (using the major diffusion direction combined with the normal to the medial sheet to define a frame for reorientation). Population studies could be performed by either performing segmentation in atlas space, or by using an atlas defined representative tract and subject-specific bundle segmentations. Integrating the segmentation scheme into an approach such as tract based spatial statistics (TBSS) [Smith et al. (2006)] would be an interesting future research direction.
Since resolving individual axons fibers is beyond today’s measurement technology, brain connectivity cannot be measured directly. However, the macroscopic effect of large collections of axons can at least give estimations of major fiber pathways in the brain. Consequentially, fiber bundle segmentation algorithms need to strike a balance between data fidelity and segmentation consistency across a number of subjects. While the proposed algorithm imposes geometric constraints on the segmentation by adhering (in a probabilistic sense) to a given large-scale model of fiber geometry, the geometry constraints allow it to be relatively insensitive to local measurement noise.
Acknowledgments
This work was supported in part by grants from NSF, AFOSR, ARO, MURI, as well as by a grant from NIH (NAC P41 RR-13218) through Brigham and Women’s Hospital. Allen Tannenbaum is also with the Department of Electrical Engineering, Technion, Israel Institute of Technology where he is supported by a Marie Curie Grant through the EU. This work is part of the National Alliance for Medical Image Computing (NAMIC), funded by the National Institutes of Health through the NIH Roadmap for Medical Research, Grant U54 EB005149. Information on the National Centers for Biomedical Computing can be obtained from
http://nihroadmap.nih.gov/bioinformatics.
Role of the Funding Source
The sponsors of this research had no part in the conduct of this research and/or preparation of the article. In particular they had no part in the study design; in the collection, analysis and interpretation of data; in the writing of the report; and in the decision to submit the paper for publication.
A Derivations
A.1 Regularized Frenet Frame
One needs to require that the curvature κ be non-vanishing, in order for the normal vector  to be uniquely defined through
to be uniquely defined through 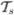 = κ
= κ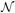 for a space curve without singular points of order 0. Intuitively, this means that for straight line segments (and inflection points) the normal and the binormal vectors are not uniquely defined. While for practical purposes the curvature is not expected to vanish frequently, it cannot be guaranteed. To be able to define a suitable frame at locations where κ = 0 the solution to the Frenet equations can be replaced by the following (regularized) minimization problem
for a space curve without singular points of order 0. Intuitively, this means that for straight line segments (and inflection points) the normal and the binormal vectors are not uniquely defined. While for practical purposes the curvature is not expected to vanish frequently, it cannot be guaranteed. To be able to define a suitable frame at locations where κ = 0 the solution to the Frenet equations can be replaced by the following (regularized) minimization problem
| (A.1) |
A solution can be obtained using calculus of variations following Tschumperle [Tschumperle and Deriche (2002)]. Problem A.1 can be reformulated as the unconstrained minimization of
where λ is the Lagrangian multiplier. The first Gateaux variation is then
evaluating to
Assuming Neumann boundary conditions for Q and using the constraint QTQ − 1 = 0 simplifies the variation to
which needs to vanish for a candidate minimizer and any perturbation. Thus
But then [Tschumperle and Deriche (2002)]
and the resulting gradient descent flow is
Solving the minimization problem requires the computation of derivatives with respect to arc-length. The tangential vector is
. The quantities Qss, κ, and 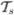 can all be expressed in terms of the parametrization p. First note that
can all be expressed in terms of the parametrization p. First note that
Thus
and
In practice a cubic smoothing spline is used to represent the parametric form of the space curve 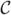 .
.
Footnotes
Tensor derived measures other than principal diffusion direction are typically only used as tract termination criteria.
See Section 6 for a way to determine the canonical frame automatically
For complicated fiber arrangements, such as fiber crossings, multiple “main” directions may emerge. This paper concentrates on one main fiber direction as derived for example from the diffusion tensor model.
To avoid ambiguities the concentration is denoted as k; κ denotes curvature in this paper.
More expressive distributions, for example the Bingham distribution, can get around this limitation for non-radially symmetric fiber direction distributions, if radial symmetry is not enforced. The price to pay is more parameters to estimate.
Disclosure Statement
The authors report no conflicts of interest.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Contributor Information
Marc Niethammer, Email: mn@cs.unc.edu.
Christopher Zach, Email: cmzach@cs.unc.edu.
John Melonakos, Email: jmelonak@ece.gatech.edu.
Allen Tannenbaum, Email: tannenba@ece.gatech.edu.
References
- Awate S, Zhang H, Gee J. A Fuzzy, Nonparametric Segmentation Framework for DTI and MRI Analysis: With Applications to DTI-Tract Extraction. IEEE Transactions on Medical Imaging. 2007;26 (11):1525–1536. doi: 10.1109/TMI.2007.907301. [DOI] [PubMed] [Google Scholar]
- Beaulieu C. The basis of anisotropic water diffusion in the nervous system- a technical review. NMR in Biomedicine. 2002;15 (7–8):435–455. doi: 10.1002/nbm.782. [DOI] [PubMed] [Google Scholar]
- Behrens T, Woolrich M, Jenkinson M, Johansen-Berg H, Nunes R, Clare S, Matthews P, Brady J, Smith S. Characterization and propagation of uncertainty in diffusion-weighted MR imaging. Magnetic Resonance in Medicine. 2003;50 (5):1077–1088. doi: 10.1002/mrm.10609. [DOI] [PubMed] [Google Scholar]
- Bihan DL. Looking into the functional architecture of the brain with diffusion MRI. Nature Neuroscience. 2003;4 (6):469–480. doi: 10.1038/nrn1119. [DOI] [PubMed] [Google Scholar]
- Bingham C. An antipodally symmetric distribution on the sphere. The Annals of Statistics. 1974;2 (6):1201–1225. [Google Scholar]
- Bresson X, Esedoglu S, Vandergheynst P, Thiran JP, Osher S. Fast global minimization of the active contour/snake model. Journal of Mathematical Imaging and Vision. 2007;28 (2):151–167. [Google Scholar]
- Chan T, Vese L. Active contours without edges. Image Processing, IEEE Transactions on. 2001;10 (2):266–277. doi: 10.1109/83.902291. [DOI] [PubMed] [Google Scholar]
- Cremers D, Rousson M, Deriche R. A review of statistical approaches to level set segmentation: Integrating color, texture, motion and shape. International Journal of Computer Visio. 2007;72 (2):195–215. [Google Scholar]
- do Carmo MP. Differential Geometry of Curves and Surfaces. Prentice Hall; 1976. [Google Scholar]
- Fisher NI. Robust estimation of the concentration parameter of Fisher’s distribution on the sphere. Applied Statistics. 1982;31 (2):152–154. [Google Scholar]
- Fletcher PT, Tao R, Jeong W-K, Whitaker RT. A volumetric approach to quantifying region-to-region white matter connectivity in diffusion tensor MRI. Information Processing in Medical Imaging (IPMI). Lecture Notes in Computer Science. 2007:346–358. doi: 10.1007/978-3-540-73273-0_29. [DOI] [PubMed] [Google Scholar]
- Friman O, Farneback G, Westin C. A Bayesian approach for stochastic white matter tractography. IEEE Transactions in Medical Imaging. 2006;25(8) doi: 10.1109/tmi.2006.877093. [DOI] [PubMed] [Google Scholar]
- Jeong W, Fletcher P, Tao R, Whitaker R. Interactive Visualization of Volumetric White Matter Connectivity in DT-MRI Using a Parallel-Hardware Hamilton-Jacobi Solver. IEEE Transactions on Visualization and Computer Graphics. 2007:1480–1487. doi: 10.1109/TVCG.2007.70571. [DOI] [PubMed] [Google Scholar]
- Jonasson L, Bresson X, Hagmann P, Cuisenaire O, Meuli R, Thiran J. White matter fiber tract segmentation in DT-MRI using geometric flows. Medical Image Analysis. 2005;9 (3):223–236. doi: 10.1016/j.media.2004.07.004. [DOI] [PubMed] [Google Scholar]
- Kimber AC. A note on the detection and accomodation of outliers relative to Fisher’s distribution on the sphere. Applied Statistics. 1985;34 (2):169–172. [Google Scholar]
- Lenglet C, Rousson M, Deriche R. DTI segmentation by statistical surface evolution. IEEE Transactions on Medical Imaging. 2006;25 (6):685–700. doi: 10.1109/tmi.2006.873299. [DOI] [PubMed] [Google Scholar]
- Mardia KV. Statistics of directional data. Journal of the Royal Statistical Society. 1975;37(3):349–393. Series B. [Google Scholar]
- McGraw T, Vemuri B, Yezierski R, Mareci T. Segmentation of High Angular Resolution Diffusion MRI Modeled as a Field of von Mises-Fisher Mixtures. ECCV. 2006:463–475. [Google Scholar]
- Melonakos J, Niethammer M, Mohan V, Kubicki M, Miller J, Tannenbaum A. Locally-Constrained Region-Based Methods for DW-MRI Segmentation. Computer Vision, 2007. ICCV 2007; IEEE 11th International Conference; 1–8; 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Donnell L, Westin C. Automatic Tractography Segmentation Using a High-Dimensional White Matter Atlas. IEEE Transactions on Medical Imaging. 2007;26 (11):1562–1575. doi: 10.1109/TMI.2007.906785. [DOI] [PubMed] [Google Scholar]
- Pichon E, Westin C-F, Tannenbaum A. A Hamilton-Jacobi-Bellman approach to high angular resolution diffusion tractography. Proceedings of the Conference on Medical Image Computing and Computer Assisted Intervention (MICCAI); 2005. pp. 180–187. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwartzman A, Dougherty RF, Taylor JE. False discovery rate analysis of brain diffusion direction maps. Annals of Applied Statistics. 2008;2 (1):153–175. doi: 10.1214/07-AOAS133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith SM, Jenkinson M, Johansen-Berg H, Rueckert D, Nichols TE, Mackay CE, Watkins KE, Ciccarelli O, Cader MZ, Matthews PM, Behrens TEJ. Tract-based spatial statistics: Voxelwise analysis of multi-subject diffusion data. Neuroimage. 2006;31:1487–1505. doi: 10.1016/j.neuroimage.2006.02.024. [DOI] [PubMed] [Google Scholar]
- Tschumperle D, Deriche R. Diffusion tensor regularization with constraints preservation. Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition; 2001. pp. 948–953. [Google Scholar]
- Tschumperle D, Deriche R. Orthonormal vector sets regularization with PDE’s and applications. International Journal of Computer Vision. 2002;50 (3):237–252. [Google Scholar]
- Wang Z, Vemuri B. DTI segmentation using an information theoretic tensor dissimilarity measure. IEEE Transactions on Medical Imaging. 2005;24 (10):1267–1277. doi: 10.1109/TMI.2005.854516. [DOI] [PubMed] [Google Scholar]
- Watson GS. Equatorial distributions on a sphere. Biometrika. 1965;52 (12):193–201. [Google Scholar]
- Wiegell M, Tuch D, Larsson H, Wedeen V. Automatic segmentation of thalamic nuclei from diffusion tensor magnetic resonance imaging. Neuroimage. 2003;19 (2):391–401. doi: 10.1016/s1053-8119(03)00044-2. [DOI] [PubMed] [Google Scholar]
- Yushkevich PA, Zhang H, Simon TJ, Gee J. Structure-specific statistical mapping of white matter tracts using the continuous medial representation. Proceedings of the International Conference on Computer Vision (ICCV); 2007. pp. 1–8. [Google Scholar]