Abstract
Human carbonic anhydrase II (HCA II) is one of the fastest known enzymes, which utilizes a rate-limiting proton transport (PT) step in its enzymatic reaction. To evaluate the PT event at an atomistic level, the multistate empirical valence bond (MS-EVB) method has been utilized in this work. It is observed that the PT event in HCA II exploits a transient active site water cluster to transport the excess proton between the catalytic zinc-bound water/hydroxide and the proton shuttling residue, His64. This PT event is found to be dependent on the enzyme's ability to form and stabilize the active site water cluster in addition to its ability to orient His64 in a favorable conformation. Evaluation of the PT free energy barrier for different orientations of His64 reveals this residue's vital role as a proton transporter and elucidates its direct effect on the barrier to PT through the active site water. It is suggested that the rate-limiting step oscillates between the active site water PT event to His64 and the de/protonation of His64 depending on the exogenous buffer concentration and the orientation of His64. In the absence of a PT acceptor/donor at position 64, it is found that the excess proton will utilize one of three distinct paths to enter/leave the active site. This latter result not only allows for an increased understanding of how enzymes capitalize on the protein/solvent interface to guide excess protons to/from areas of interest, it also provides valuable insight into the chemical rescue experiments on HCA II mutants.
1. Introduction
Carbonic anhydrases (CAs) are mostly zinc–metalloenzymes that catalyze the reversible hydration of carbon dioxide to form bicarbonate and the release of a proton:
| (1) |
CAs are ubiquitous and well-studied enzymes found in microbial organisms, plants, and animals. There are currently five known CA families, comprised of the structurally characterized α-, β-, and γ- classes and the more recently discovered δ- and ε- classes. The ability of CA to carry out the CO2 hydration/dehydration reaction near the diffusion controlled limit has made CA central to respiration and cellular pH maintenance.1–6 The mammalian α-class CAs have become one of the most extensively characterized enzymes that utilize a proton transport (PT) event in their catalysis. They have also become a cornerstone of PT research because they are unique in occupying the boundary between proton transport and transfer (i.e., proton exchange through several intervening waters versus proton exchange directly between donor and acceptor groups, respectively).1,7–23 Research on the catalytic event in CA has provided invaluable insight into how an enzyme can stabilize and transport protons.
Human carbonic anhydrase II (HCA II) is the fastest of the known expressed and catalytically active α-CA isozymes with a turnover number approaching 0.8 μs−1. Its catalytic mechanism can be described by two distinctly separate reactions (the “ping-pong” mechanism). The first, which is not rate limiting, is the conversion of carbon dioxide into bicarbonate by the nucleophilic attack of a zinc-bound hydroxide and the subsequent dissociation of the bicarbonate that results in a water molecule bound at the zinc:
| (2) |
The second part of the reaction, the PT step, is the transfer of a proton to solution to regenerate the zinc-bound hydroxide. This step, which is rate limiting, has been shown to be dependent on the exogenous buffer concentration.1,24 At physiological conditions where the exogenous buffer concentration is in excess, the PT from the zinc-bound water through an active site water cluster to a proton shuttling residue, His64, is believed to be the rate-limiting step:9,25,26
| (3) |
During this process, the proton is transferred 8 to 10 Å across the active site by utilizing an active site water cluster (see Figure 1).3,11,27 When the exogenous buffer concentration is limited, the PT event from His64 to the exogenous buffer becomes the rate-limiting step:
Figure 1.
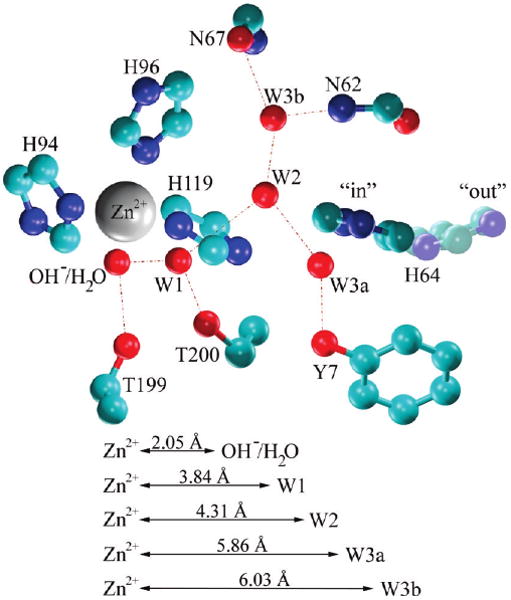
Schematic representation of the WT HCA II active site showing the active site water cluster. Coordinates were taken from the X-ray crystallographic structure PDB accession # 2CBA.14 Red dotted lines indicate hydrogen bonding.
| (4) |
Previous studies have shown residue His64 to be the major contributor to the proton acceptor/donor shuttling in the catalytic mechanism, as the mutation of His64 to Ala (H64A HCA II) had the effect of reducing the PT step by ∼20-fold and therefore significantly reducing the catalytic turnover number.28,29 It has also been shown that the addition of an exogenous buffer, 4-methyl-imidazole (4MI), can almost fully recover the catalytic activity of H64A HCA II to wild-type (WT) levels. In addition to the kinetic studies, the X-ray crystal structures of H64A HCA II in complex with 4MI have been determined, and two possible binding sites for 4MI have been identified.18 One of the binding sites is near Ala64 (the site of the mutation), at the rim of the active site cavity, where 4MI π-stacks with the indole ring of Trp5, while the other is in a cleft within the active site, located in close proximity to residues Asn67, Glu69, Asp72 and Ile91. Kinetic analysis reveals that both of these binding sites may be nonproductive thereby indicating that the chemical rescue PT event utilizes a yet unknown pathway.30,31
In addition to the proton donor/acceptor mediator, the other critical aspect of the PT event is the nature of the active site water cluster. Ab initio studies have indicated that smaller water clusters are more conducive to PT, thereby implying that the HCA II reaction will utilize relatively small water clusters.32 Computational and experimental studies indicate that the active site water cluster consists of between two and four water molecules that are involved in the rate-limiting PT event.10,11,14,32–36
Recent simulations of the rate-limiting step in HCA II conducted with the semiempirical self-consistent charge-density functional tight-binding (SCC-DFTB) method have raised questions about the importance of the active site water cluster, the orientation of His64, and the role of proton vs proton-hole transport.33,37–39 These SCC-DFTB simulations, which suggest the proton-hole hypothesis, indicate that the position of His64, and therefore the size of the active site water cluster, has a negligible impact on the overall free energy pathway (potential of mean force or PMF) describing the rate-limiting step.39 The use of the semiempirical SCC-DFTB method also indicates that PT in the H64A HCA II mutant provides a PMF with a free energy barrier of ΔF‡ ≈ 21.4 kcal/mol, which is significantly different from the experimentally determined barrier in the H64A mutant of ΔF‡ ≈ 11 kcal/mol. (For comparison, the autoionization of water yields a ΔF‡ ≈ 21.6 kcal/mol.) While the SCC-DFTB simulations predict that the orientation of His64 and the size of the active site water cluster are not important in the rate-limiting reaction of HCA II, it should be noted that the SCC-DFTB method has received limited validation for the hydrated proton and hydroxide in aqueous environments.
The multistate empirical valence bond (MS-EVB) method23,40–43 used on the present work yields significantly different results from those generated by the SCC-DFTB method for the PT event in HCA II. As described below, the MS-EVB simulations reported here reproduce experimental PT values for the WT HCA II system and, because the simulations allow for extensive sampling and analysis, provide clear atomistic insight into the reaction mechanism. The MS-EVB description of the PT event indicates that the orientation of His64, the size of the active site water cluster, and the concentration of the exogenous buffer are crucial for the rate-limiting PT event in HCA II.
The MS-EVB model has been shown to accurately model the delocalized nature of the excess proton in bulk water,41–44 weak acids,45–47 and biomolecules.23 MS-EVB differs significantly from the standard EVB approach of Warshel and co-workers48–50 as discussed in ref 23. The most important difference is that MS-EVB fully describes the dynamical charge defect delocalization and Grotthuss shuttling involving the hydrated proton and multiple water molecules. The present work expands on the MS-EVB description of the ionizable moieties47 previously incorporated into the MS-EVB model by including the zinc-bound water/hydroxide of HCA II. During the parametrization of the zinc-bound solvent moiety, a more efficient way of incorporating environmental effects into the underlying ab initio potential energy surface has been implemented, which increases the accuracy of the resulting model while reducing the time needed for parametrization. The resulting MS-EVB model, which includes the zinc-bound solvent, active site water cluster and the proton acceptor/donor (His64) was then used to evaluate how the HCA II enzyme stabilizes the excess proton, active site water cluster, and the orientation of His64 to produce a fast and efficient enzymatic PT behavior.
2. Methodology
MS-EVB Potential
The MS-EVB methodology, which has been described in detail elsewhere, will only be briefly described here.23,40–43,47 Given a set of nuclear coordinates, r⃗, the MS-EVB algorithm determines a set of classical valence states that depict the different possible bonding arrangements (Figure 2). The valence bond states, |i〉, which are defined by a classical force field, in this case the AMBER parm9951 force field, are used as the diagonal portion of the MS-EVB Hamiltonian:
Figure 2.
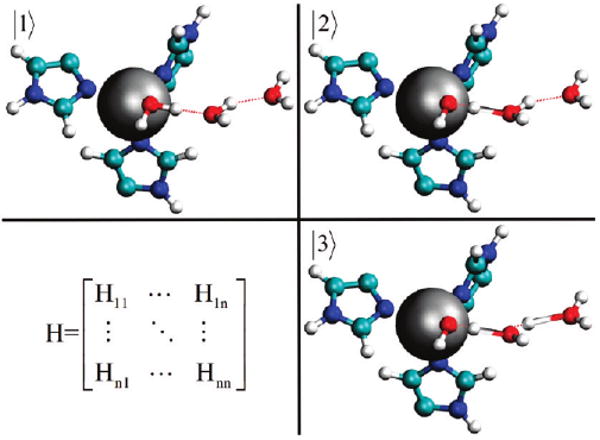
Schematic picture of the ZnH2O2+–(H2O)2 (|1〉) and ZnOH+–H2O–H3O+ (|2〉 and |3〉) EVB states used in the MS-EVB model and the corresponding Hamiltonian matrix. Several additional states are used to represent the excess proton shuttling through active site water.
| (5) |
where the vector r⃗ represents the complete set of nuclear degrees of freedom. The off-diagonal elements of the MS-EVB Hamiltonian describe the coupling between the EVB states |i〉 and |j〉. The functional form of the off-diagonal elements are represented by
| (6) |
where q is the PT coordinate, RDA is the distance between the donor (D) and acceptor (A) atoms, and is an adjustable parameter as described previously.47 The functional form of f(RDA) and g(q) are given, respectively, by
| (7) |
| (8) |
where C, α, β, γ, ε, aDA, bDA, and cDA are adjustable parameters determined during the parametrization process (described below). The PT coordinate q is a geometric reaction coordinate based on the distance between the excess proton and the donor molecule projected on the line connecting the donor and acceptor molecule, as described by
| (9) |
where
| (10) |
and , λ, and are additional adjustable parameters determined during the parametrization process. It is often beneficial to modify the bond between the donating molecule and the excess proton from the standard harmonic approximation to a Morse potential:
| (11) |
where a0, a1, and a2 are parameters. The is done, for example, in the next subsection. The MS-EVB2 model,43,47 which currently simulates an excess hydrated proton but not a hydroxide, was used as the baseline parameter set in this work.
The most common method of tracking the charge defect associated with the excess proton in MS-EVB simulations is the use of the center of excess charge (CEC).43 The CEC is the preferred method of following the protonic defect because it eliminates the discontinuity of following an arbitrarily defined excess proton, which changes identity during a simulation due to Grotthuss shuttling. The CEC is given by
| (12) |
The CEC is the summation of the MS-EVB coefficient weighted center of charge (COC), where the COC is described by
| (13) |
and the summations are over all the atoms (with partial charge qk) composing the ith EVB state.
Parametrization of the (His)3–Zn–H2O2+/OH+ Moiety
The MS-EVB2 parametrization of the zinc-bound solvent in the active site of HCA II is based on the original parametrization scheme published previously for the histidine and glutamic acid systems.47 In this parametrization, the underlying ab initio potential energy surface (PES) was generated using a two-layered ONIOM model52–60 as defined in the Gaussian03 software package.61 The use of a hybrid QM/MM method allows for the environmental effects of the enzyme to be incorporated into the ionization PES. As previously described,16 the ONIOM (B3LYP/6-31G(d):AMBER) system was used to determine the classical point charge representation, using a restrained electrostatic potential fitting procedure (RESP).62 The QM/MM system was also utilized to determine the parameters for the Morse potential, which were used to describe the labile protons on the zinc-bound water. The fitting of the Morse function to the QM/MM deprotonation potential energy profile yielded the following parameters: a0 = 90.97 kcal/mol, a1 = 2.33 Å−1, and a2 = 0.97 Å. In addition to the classical point charges and Morse potential, the ONIOM system was also utilized to create a PES describing the deprotonation event of the zinc-bound water in the HCA II system by conducting relaxed optimization scans of the system while constraining the RDA and RDH+ bond lengths (Supporting Information Figure S1). The ONIOM (B3LYP/6-31G(d):AMBER) PES surface was then used as the reference surface to which the MS-EVB2 parameters were fit. The fitting procedure was conducted by using a variant of the Simplex algorithm63 to generate a nonunique set of MS-EVB2 parameters that minimize the sum of square deviations between the MS-EVB PT PES and the ONIOM (B3LYP/6-31G(d):AMBER) PT PES. With the newly determined MS-EVB parameters, RESP charges and Morse potential for the labile hydrogen, the MS-EVB2 model for the HCA II active site was complete.
The parameters for the His64 ionizable moiety in this study are a variant of the histidine parameters previously published.47 The variation was made to the Vii term, which was modified to be −101.4229 kcal/mol. These modified parameters yield a pKa in the bulk water environment of 5.9 ± 0.3, which is in good agreement with experimental results (6.04–6.07). The method used to determine the pKa has been outlined in a previous publication47 and is in agreement with a recent publication stressing the importance of the standard state correction.64
MS-EVB Simulation Setup
The MS-EVB2 systems for the WT HCA II simulations were taken from the X-ray crystal structure (PDB accession # 2CBA) with its original 220 placed waters.14 The system was then solvated in a cubic simulation box (L = 60 Å) of modified TIP3P43 water molecules. The AMBER parm9951 force field was used to describe the enzyme while the parameters for the catalytic zinc active site were taken from previously published work.16 Two independent HCA II systems were created to study the rate-limiting PT event. These two systems consisted of the zinc-bound water and an unprotonated His64 (EZnH2O2+-His) with either the His64 oriented toward the active site, the “in” orientation, or away from the active site, the “out” orientation. These two conformers of the WT HCA II are observed in X-ray crystal structure (PDB accession #s 2CBA and 2ILI).14,65 The two systems were pre-equilibrated for 200 ps of molecular dynamics (MD) in the constant NPT ensemble followed by 2.5 ns in the constant NVT ensemble.66 The pre-equilibration was conducted in the AMBER 8 software package at 300 K using periodic boundary conditions with long-range Coulombic interactions calculated by the Ewald summation.67,68 The short-ranged nonbonded interactions and forces were subject to a 9 Å cutoff. The MD integration time step within the leapfrog Verlet integrator was 1 fs in all simulations. Within the constant NPT ensemble, simulations were run at 1 atm and with Langevin dynamics utilized for the thermostat. The pre-equilibrated systems were then transferred to a modified DL-POLY 2.15 software69 package incorporating the MS-EVB2 algorithm. In the MS-EVB2 simulations the excess proton charge defect is delocalized due to explicit Grotthuss shuttling behavior, which requires additional equilibration for the system to accommodate the newly delocalized charge. Therefore, the two systems were equilibrated in the constant NVT ensemble for an additional 500 ps using the MS-EVB2 code.
Three separate deprotonation free energy profiles (PMFs) were generated to evaluate different aspects of the PT in the HCA II enzyme. The first PMF entailed the deprotonation of the zinc-bound water through the active site water cluster and out to the bulk environment. In this system His64 was in the “out” orientation and was not explicitly involved in the MS-EVB state space. Eliminating His64 from the MS-EVB state space ensured that in this particular PMF the excess proton would explore alternate water cluster paths that the excess proton may take to reach the bulk environment, such as in the case of the H64A HCA II mutant. The simulation consisted of 72 umbrella sampling windows spanning the range of , where is defined as the distance between the zinc ion and the excess proton CEC. An umbrella force constant, kn, was used with values between 40 and 160 kcal mol−1 Å−2 to ensure adequate sampling along the reaction coordinate. Each window was equilibrated in the constant NVT ensemble for 200 ps followed by a data collection period of 500 ps to 1 ns depending on convergence of the window.
The second simulation entailed calculating the PMF for the deprotonation of the zinc-bound solvent, the subsequent transport through the active site water, the deposition of the excess proton onto His64 while in the “out” orientation and the final release of the excess proton from His64 to the surrounding bulk environment. This calculation required the use of 66 adaptive umbrella sampling70 windows and spanned . The initial guess for the adaptive potential was taken from the zinc-bound water deprotonation simulation. The geometries for the adaptive windows were taken from the final configuration of a representative window from the 72 windows used in the zinc-bound water deprotonation simulation. The windows were then equilibrated for 25 ps in the constant NVT ensemble followed by up to 1 ns of data collection in the constant NVT ensemble.
The third and final PMF evaluated the mechanism involving the deprotonation of the zinc-bound water, PT transfer through the active site water, the deposition of the excess proton on His64 while in the “in” orientation, the rotation of the His64 amino acid from the “in” to the “out” orientation and the release of the proton into the bulk environment. This computation required 72 adaptive windows spanning . The initial guess for the adaptive potential was taken from the zinc-bound water to His64 “out” simulation. The geometries were taken from the zinc-bound water to His64 “out” when applicable. When geometries from the previous MS-EVB simulations were not available appropriate configurations from the AMBER simulations were used. If configurations from the AMBER simulations were used, additional pre-equilibration and equilibration runs were conducted as stated earlier. Each of the 72 windows was equilibrated for 25 ps in the constant NVT ensemble followed by up to 1 ns of data collection in the constant NVT ensemble. For the MS-EVB simulations the number of waters included in the EVB state set varied dynamically from 5 to ∼20, with ∼20 representing a bulk water environment. All simulation were run at 300 K, used the Nosé-Hoover thermostat, periodic boundary conditions with long-range Columbic interactions calculated by the Ewald summation, a 9 Å cutoff for the short-range nonbonded interactions and a Verlet integrator step of 1 fs. In all cases, the weighted histogram analysis method (WHAM)71,72 was used to match the umbrella sampling windows together to form a continuous free energy profile. The error for all PMF calculations was evaluated by calculating PMFs for subsets of the total data and then directly calculating the standard deviation using these PMFs.
Differences in the Helmholtz free energy (ΔF) calculated from the current simulations are used throughout the manuscript interchangeable with the differences in the Gibbs free energy (ΔG). In the limit of constant volume and small fluctuations around the average pressure as in the present studies, the differences in the Helmholtz free energy may be directly compared to the differences in the Gibbs free energy.
Occupancy and Correlation Analysis
The stabilization of the active site water cluster and the CEC were analyzed by utilizing the correlation analysis of the active site water cluster and the surrounding amino acids. To determine the position of the water molecules in the active site that are stable throughout the trajectory, occupancy plots of the water oxygens were created. To create the occupancy plots the trajectories were first centered and root-mean-square (rms) fitted to the average configuration and then the volmap tool in VMD73 was used to generate the average occupancy of the water oxygens in the active site. The water positions that were stable for over 50% of the trajectory were then used to determine the identity of the waters that would subsequently be used for the correlation analysis.74 The identity of the water was chosen by selecting the water in each frame that was closest to the conserved water position (50% occupancy). The residues in the protein were then mapped to one site, at the center of mass for the residue, and the mass-weighted correlation of the movement for these points with the movement of the water oxygens was evaluated to yield a mass weighted correlation matrix. The analysis of the occupancy and correlation analysis was conducted using the utility ptraj with the AMBER 7 suite.68
3. Results and Discussion
Throughout the remainder of the paper the reader is reminded that the acronym “CEC” refers to the center of excess charge (center of the charge defect) associated with the excess proton as mathematically defined in eqs 12 and 13 for the MS-EVB model.
Zinc-Bound Water
The results for the MS-EVB2 parametrization of the zinc-bound water in HCA II are given in Table 1. Bond lengths and angle values for the active site residues and the active site water cluster from the biased sampling simulations were compared to the X-ray crystal structures (PDB accession #s 2CBA and 2ILI)14,65 and were in good agreement (Table 2). In addition to geometrical properties, the pKa of the zinc-bound water was determined from the PMF using methods previously discussed in the literature.47,64,75 The value for the pKa derived from the PMF was determined to be 7.1 ± 0.3, which is in good agreement with the experimental value of 6.9 ± 0.1.13 Given the structural and pKa value agreement of the newly parametrized MS-EVB model with the X-ray structure and kinetic experiments, and the ability of the model to transfer a proton based on a surface that was fit to a QM/MM PES, the model was then used in the study of the PT event in HCA II.
Table 1.
MS-EVB2 Parameters for the Zn-Bound Water of HCA II
| parameter | Zn |
|---|---|
| Vii0 | −88.99 |
| Vijconstant | −42.48 |
| rsc0 | 1.09 Å |
| λ | 0.073 |
| RDA0 | 1.00 Å |
| C | 0.53 |
| α | 1.24 Å−2 |
| aDA | 3.29 Å |
| β | 5.16 Å−2 |
| bDA | 1.83 Å |
| ε | 42.38 Å−1 |
| cDA | 2.45 Å |
| γ | 1.72 Å−2 |
Table 2.
Structural Comparisons between Experiment and Simulation
| 2CBAa | 2ILIb | MS-EVBc Zn–H2O2+ | MS-EVBd Zn-OH+ | |
|---|---|---|---|---|
| RZn–O | 2.1 Å | 1.9 Å | 2.02 ± 0.03 Å | 1.79 ± 0.06 Å |
| RN119–Zn | 2.1 Å | 2.0 Å | 2.04 ± 0.09 Å | 2.05 ± 0.08 Å |
| RN96–Zn | 2.1 Å | 2.0 Å | 2.03 ± 0.08 Å | 2.03 ± 0.08 Å |
| RN94–Zn | 2.1 Å | 2.0 Å | 2.03 ± 0.08 Å | 1.98 ± 0.08 Å |
| AN119–Zn–O | 111° | 115° | 112 ± 4° | 107 ± 6° |
| AN96–Zn–O | 113° | 117° | 110 ± 4° | 116 ± 6° |
| AN94–Zn–O | 113° | 105° | 112 ± 4° | 112 ± 6° |
| AN96–Zn–N119 | 99° | 99° | 104 ± 5° | 103 ± 4° |
| AN94–Zn–N119 | 115° | 115° | 113 ± 4° | 112 ± 4° |
| AZn–O–O106 | 72° | 67° | 81 ± 7° | 78 ± 7° |
| AZn–O–O199 | 106° | 103° | 130 ± 11° | 118 ± 9° |
The results for the deprotonation of the zinc-bound water with His64 in the “out” orientation and not as an explicit acceptor state in the MS-EVB state space is shown in Figure 3. The choice to exclude the contribution of the His64 residue from the PT process in this case was made in order to study the PT event without any bonding of the excess proton with His64. This not only allowed for a more direct analysis of the pKa of the zinc-bound water, but it also explores alternate paths that the excess proton can utilize to enter/leave the active site other than transferring to/from His64.
Figure 3.
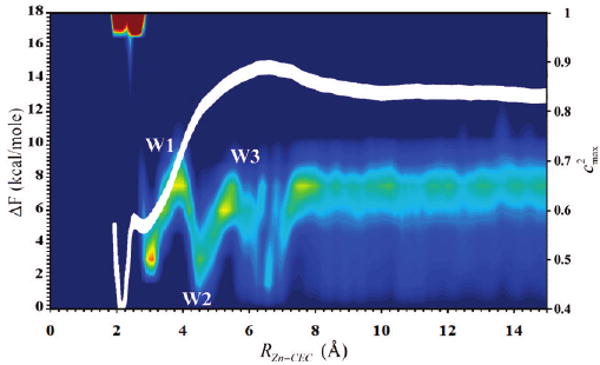
Free energy profile (PMF) for the zinc-bound water deprotonation reaction when His64 is not included as a proton acceptor in the MS-EVB model. The PMF is plotted as a function of the radial distance of the CEC to the catalytic zinc, RZn–CEC. The thickness of the line denotes the standard deviation, which was evaluated to be 0.4 kcal/mol. Also shown is the largest EVB state population (colored contours) as a function of the center of excess charge coordinate RZn-CEC. Red indicates high probability while blue indicates low probability. A Zundel cation has a , whereas the Eigen cation has a .
Inspection of Figure 3 reveals a weakly stabilized contact ion pair between the zinc-bound hydroxide and the hydronium cation at ∼2.8 Å. Examination of the largest MS-EVB amplitude indicates that the contact ion prefers the Zundel cation form , which is formed from the zinc-bound water and W1. It is apparent from the MS-EVB simulations that the zinc-bound water is the primary (lowest free energy) species, which is in agreement with previous analysis based on standard MD and the atomic resolution crystal structure of the WT HCA II (PDB accession # 2ILI).16,65
The rate-limiting step of a reaction generally corresponds to the highest free energy barrier in the PMF. In the ionization process of the zinc-bound solvent this barrier corresponds to the transport of the excess proton through the active site water. When evaluating the character of the CEC as described by the square of the maximum MS-EVB coefficient, Figure 3 indicates that at the barrier of the PMF the CEC corresponds to a high free energy Eigen cation, H9O4+. This structure supports the hypothesis22,32 that a split or branching in the active site water cluster, which may reflect the transient formation of an Eigen cation, is responsible for the barrier. It is evident that near the third water, W3, is the location of the barrier and not the second water, W2, as previously thought.32 Inspection of the CEC character reveals that the W1 corresponds to an Eigen cation, W2 corresponds to a Zundel cation, and the barrier corresponds to an Eigen cation more in line with waters near W3b. These results modify the previous hypothesis that an Eigen cation at W2 is the location of the barrier and shifts the origin of the barrier to a high free energy Eigen cation on W3b or other nearby waters.
The barrier for the PT event that does not utilize His64 as a proton acceptor is ΔF‡ = 14.6 ± 0.4 kcal/mol, indicating the free energy cost of the excess proton leaving the active site by one or more of the alternate paths and bypassing His64. This barrier converts to a rate of ∼0.0004 μs−1 using
| (14) |
where krxn is the transition state theory rate constant, kB is the Boltzmann constant, T represents the standard temperature, ω0 is the fundamental frequency of the reactant state around its minimum, and ΔF‡ is the free energy barrier height. The fundamental frequency was calculated to be ω0 = 3336 cm−1, where ω0 = √−(∂2PMF(r)/∂r2)/meff. This expression was determined using the equipartition theorem, meff〈 ν2〉/2 = kBT/2, to obtain the effective mass, meff, of the reaction coordinate from the value of 〈 ν2〉 calculated from the MD trajectory. The second derivative of the reactant well PMF at its minimum was obtained from the umbrella sampling data. Kinetic experiments on the WT HCA II enzyme13 and H64A mutant17 yielded rate constants of 0.8 and ∼0.02 μs−1, respectively. It is evident that this particular calculated PMF gives a significantly lower overall rate when compared to the WT enzyme and a rate suggesting an inactivated enzyme, thus illuminating the importance of a functioning proton donor/acceptor group at position 64 for the overall PT event.
To evaluate the alternate pathways accessible to the excess proton as it enter/leaves the HCA II active site, spatial occupancy plots of the CEC were created and are shown in Figure 4. It is seen that the CEC utilizes three distinct paths to enter/leave the active site as revealed by the occupancy isosurface data. The most densely populated path takes the excess proton along the top of the active site cavity tracking near the hydrophobic residue of Phe130 and Val134. The preference of the excess proton to associate near these hydrophobic residues is interesting given the recent discovery of the excess proton's affinity for the liquid/vapor and liquid/hydrophobic interfaces.76–82
Figure 4.
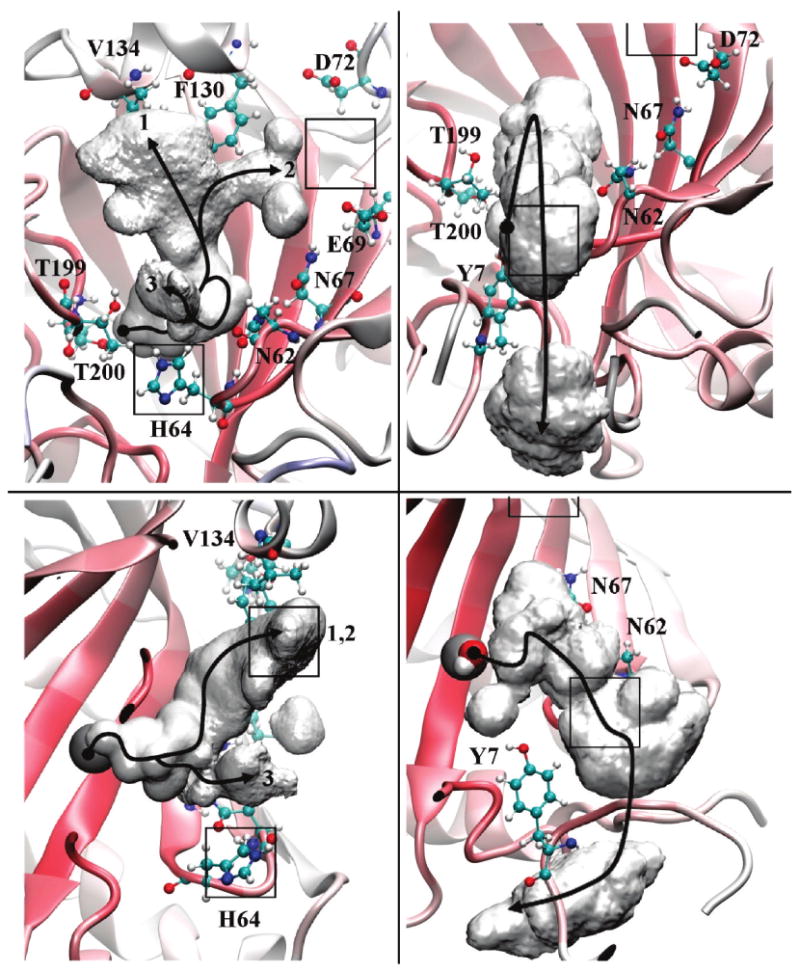
Spatial occupancy plot of the CEC for the excess proton in the HCA II enzyme active site. The left panels (top and bottom) are determined from simulations of the HCA II enzyme when His64 is not included as an explicit acceptor group of the excess proton. The right panels (top and bottom) are determined from simulations of the HCA II enzyme with His64 included as an explicit acceptor group for the excess proton. The gray volume represents the isosurface wherein the excess proton CEC resides 98% of the time. The numbers indicate the respective paths for the CEC (i.e., 1, 2, or 3). (Top) Representation looking down the active site cavity with H64 near the bottom, T200 and T199 on the left, N62, N67, and E69 on the right, and D72, F130, and V134 on top. (Bottom) Representation looking from the side with H64 on bottom and the zinc at the base of the isosurface on the left. The black boxes represent binding sites for the chemical rescue agent 4MI from 1MOO.pdb. The black line depicts the most probable path the CEC may take inside the CEC density. The black circle at the beginning of each path resides on the catalytic zinc.
Another path that the excess proton may take brings it within the vicinity of Glu69 and Asp72, a known binding site for the chemical rescue agent 4MI.18 While these residues are not hydrophobic they stabilize water molecules in the active site, via hydrogen bonding, that are in turn favorable for the excess proton. When evaluating the actual distance of the CEC density from the residues it is again apparent that the excess proton resides closer to the hydrophobic residues than it does the hydrophilic ones. In fact, the distance of the CEC density from Glu69 and Asp72 would indicate a bridging water between the residues and the excess proton; this is not the case with Phe130 and Val134. The third and least densely populated path is for the CEC to travel out of the active site passing near Trp5 and position 64. This path also intersects a known binding site of 4MI, in this case Trp5.18 While the CEC density and the binding sites of 4MI indicate possible chemical rescue paths, recent kinetic studies indicate that there may exist a third pathway not yet detected by X-ray.13,31 From the present CEC density analysis it is proposed that the third path resides around Phe130 and Val134. Further work into binding of 4MI to the H64A mutant and the explicit simulation of the proton defect using the MS-EVB methodology is currently underway. In addition to the implications for chemical rescue another important feature of Figure 4 is how the excess proton moves along the interface between the solvent and the enzyme. The overall density appears as a “catcher's mitt” as the proton avoids the bulk solvent and utilizes the protein/water interface to be channeled in/out of the active site. This ability of the enzyme to direct the proton to and from the active site opens new avenues for mutation experiments. These mutation experiments could probe the enzymes ability to utilize the protein/water interface to direct proton movements by mutating residues far from the active site that are in the path of the CEC density.
Proton Transfer Event in the WT HCA II
With the parametrized MS-EVB2 model for the zinc-bound moiety in hand it is now possible along with the modified MS-EVB2 histidine model to simulate the rate-limiting PT event in the WT HCA II enzyme. To evaluate the effect of the orientation of His64 on the PT event, two PMFs were generated. Figure 5A shows the PT PMF for His64 in the “out” orientation while Figure 5B depicts the PT PMF for His64 in the “in” orientation and the subsequent rearrangement of His64 to the “out” orientation. These PMFs reveal the role of His64 as the proton acceptor/donor in the PT event in HCA II. When His64 is in the “in” orientation the free energy barrier, ΔF‡, for PT through the active site water is lowered from the 14.6 ± 0.4 kcal/mol (i.e., the pathway not utilizing His64 as the proton donor/acceptor described in the previous subsection) to 10.0 ± 0.4 kcal/mol. The relatively low free energy barrier for PT through the active site water cluster when His64 is in the “in” orientation is due to smaller water clusters and the stabilizing force that the His64 in the “in” orientation has on the active site water cluster, as well as the delocalized charge defect of the hydrated excess proton. As the proton moves from the Eigen cation on W1 through a Zundel cation containing W2, to an Eigen cation on W3a, and finally to His64 it is clear that indeed an Eigen cation resides at the barrier as previously hypothesized. At the barrier the active site water cluster is dominated by a high free energy Eigen cation represented by the excess proton residing on W3a with a small amplitude contribution from W2 and His64. Similar to the PMF without His64 as the proton donor/acceptor, the Eigen does not reside on W2 but on W3, in this case on W3a and not W3b (see Figure 1). The MS-EVB amplitude analysis reveals that W2 is primarily populated by a Zundel cation changing the previous notion that it would be an Eigen cation and therefore the cause of the barrier.32
Figure 5.
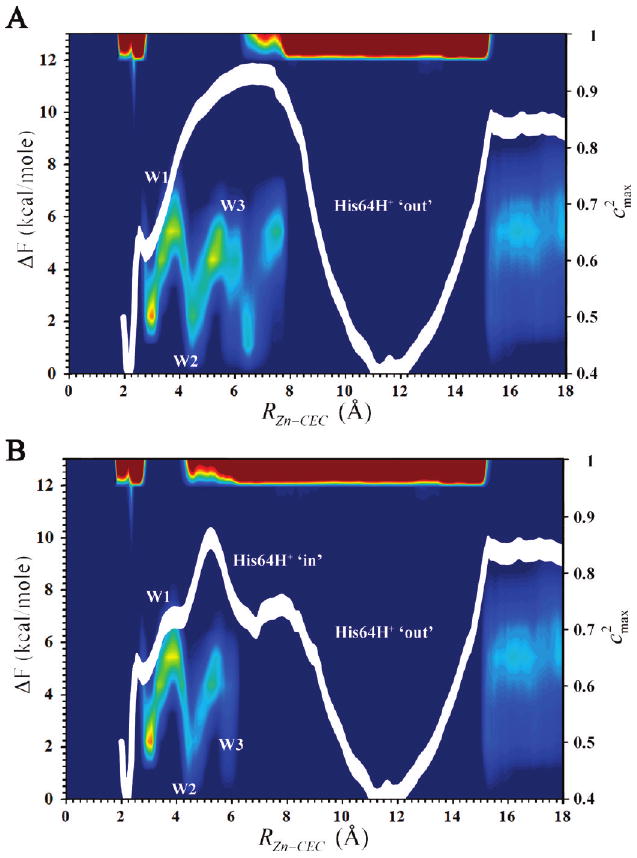
Free energy curve for the zinc-bound water deprotonation reaction as a function of the radial distance of the CEC to the catalytic zinc, RZn–CEC. The thickness of the line denotes the standard deviation, which was evaluated to be 0.4 kcal/mol. Also shown is the largest EVB state population (colored contours) as a function of the center of excess charge coordinate RZn-CEC. Red indicates high probability while blue indicates low probability. (A) His64 in the “out” orientation. (B) His64 in the “in” orientation.
When the excess proton has moved to His64, the orientational rearrangement of His64 can now easily be accomplished after passing through a relatively small free energy barrier. The “out” orientation of protonated His64 appears to be more favorable than the “in” orientation (as seen in Figure 5B and ref 16), which facilitates the transport of the excess proton from inside the active site to a more bulk like region outside the active site. The direction of the free energy shift between the “in” and “out” orientations indicates a lower pKa (acidification) for His64 in the “in” orientation when compared to the “out” orientation. This acidification of His64 has been confirmed by experimental studies of mutant HCA II systems.7 The acidification of His64 when in the “in” orientation ensures that the His64 is either donating its excess proton to the zinc-bound hydroxide (dehydration reaction) or unprotonated and waiting to accept the proton from the zinc-bound water (hydration reaction).
Evaluation of the CEC probability density during this PT event (utilizing His64 as the proton donor/acceptor) is significantly different from the density found for the PT transfer to solution utilizing alternate pathways (Figure 4), with almost all of the density residing in the bottom pathway (i.e., toward His64). This illustrates the important role of His64 as the transporter of the excess proton into and out of the active site. After the deprotonation of His64 the CEC density plot indicates that the excess proton does not proceed directly to the bulk environment. Instead it moves between the cleft at the bottom of the active site and tracks along the protein/solvent interface. This behavior of the excess proton to prefer the interface region raises important questions as to how enzymes may funnel protons to areas of interest.
To better understand the behavior of the active site water during the proton transfer event, correlation analysis was conducted on the active site water and surrounding amino acids, shown in Figure 6. Correlation analysis as used in this context generally indicates long-range interactions and hydrogen bonding patterns. When analyzing the ZnH2O2+-His system with His64 in the “in” orientation and the CEC residing between the zinc-bound solvent and W1, the CEC correlates with the zinc-bound solvent and W1 as one would expect, due to direct hydrogen bonding. Yet, when the CEC resides on the His64 while in the “in” orientation a significantly different correlation pattern emerges. In this system there appears to be two main overlapping correlated groups. The first group consists of the ZnOH+, Wd, W1, W2, and the CEC while the second group consists of the CEC, Wd, W1, and W3a. The correlation analysis from MD simulation of the WT HCA II enzyme reveals that for the ZnH2O2+–His system there are three uncorrelated groups.83 The analysis of the ZnOH+–HisH+ system with protonated His64 in the “in” orientation was not conducted in the previous study83 due to the short lifetime of the ‘in’ orientation before reorienting to the ‘out’ orientation for this protonation state. The “in” orientation for the ZnOH+–HisH+ system, at least for the hydration pathway, is thus assumed to be primarily there to accept the proton and then carry it out of the active site. Therefore, the active site water correlation is not of great importance after the PT event in the hydration direction. In the dehydration pathway the correlation of the active site water is crucial due to the short lifetime of the “in” orientation. During the dehydration pathway the presence of two overlapping correlated groups indicates that in order to capitalize on the “in” orientation the HCA II enzyme has created an environment that is more favorable for hydrogen bonded active site water. This implies that even though the “in” orientation for the ZnOH+–HisH+ system is rare, when it happens the active site waters are favored to form a complete water cluster that will carry the excess proton to the zinc-bound hydroxide.
Figure 6.
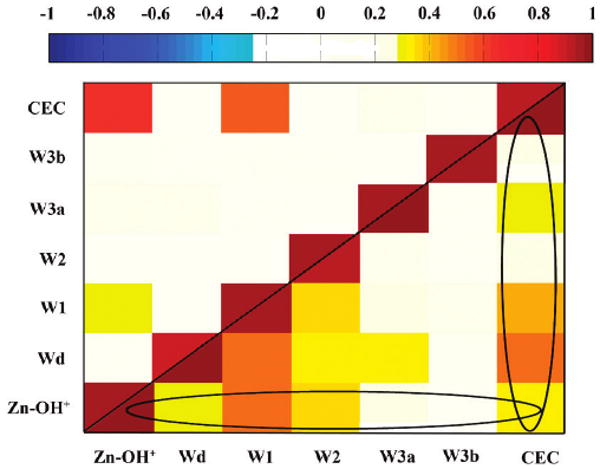
Correlation analysis of the active site residues and the active site water cluster. (Top left) Correlation analysis for the ZnH2O2+–His system with the excess proton CEC residing on the zinc-bound solvent (i.e., zinc-bound water). (Bottom right) Correlation analysis for the ZnOH+–HisH+ system with His64 residing in the “in” orientation. The black circles encompass the two separate correlated groups.
Looking at the PT free energy barrier when His64 is always in the “out” orientation (Figure 5A) reveals the ΔF‡ for PT through the active site water to be 11.4 ± 0.4 kcal/mol. The coupling of the His64 accepting group with the active site water has the effect of lowering the barrier to a value closer to that measured by WT kinetic experiments (krxn = 0.8 μs−1), compared to the alternate pathway PT not involving His64. It is clear from the “in” and “out” PMFs in Figure 5 that the orientation of His64 and therefore the active site water cluster size is intimately coupled to the active site PT barrier. Analysis of the character of the CEC reveals that the barrier is dominated by an Eigen cation and the position of the barrier precludes W2 from carrying an appreciable amount of the protonation probability. Instead, the barrier region corresponds to W3b or other waters in that region. The CEC occupancy for the His64 “out” system is very similar to the His64 “in” to “out” system (data not shown). The only noticeable difference is an increased sampling of the CEC on other waters in the active site before transferring to His64. The deprotonation of His64 and the subsequent CEC density moving between the cleft at the bottom of the active site are similar between the His64 “in” systems and the His64 “in” to “out” system. It is apparent that the free energy change between the zinc-bound water and the protonated His64 (Figure 5A and B) is near zero. This would indicate similar pKa values for both species and an overall thermoneutral reaction for this PT event, both in agreement with experiment.3,13
Exogenous Buffer Concentration and the Rate-Limiting Step
It should be noted that for all the simulations reported here the exogenous buffer concentration is nonexistent. Kinetic studies that vary the exogenous buffer concentration find that at high buffer concentrations the reaction proceeds optimally, yet when the buffer concentration is reduced the overall rate of the reaction is also reduced.1,24 This has generally been interpreted as shifting the rate-limiting step from the active site water to the de/protonation of His64. Due to the large number of pathways that an excess proton may take between His64 and an exogenous buffer, explicit simulation of such a reaction is currently computationally intractable. Therefore, defining a range of values for the PT barrier is presently more useful for understanding the rate-limiting step than attempting to calculate the PT barrier for every exogenous buffer type, concentration, environment, and separation distance. To this end, computational and experimental data are used here to determine upper and lower bounds for the PT barrier between His64 and an exogenous buffer.
Examination of the PT event with His64 in the “in” orientation reveals that the rate-limiting step may not reside in the active site water cluster as suggested by kinetic studies at high buffer concentration. It is clear from the PT PMF for the His64 in the “in” orientation that the active site water cluster PT transfer barrier to the His64 acceptor is ∼10.0 kcal/mol (see Figure 5B), while the deprotonation of His64, in the absence of exogenous buffer, is 12.0 ± 0.4 kcal/mol. It is noted that at RZn-CEC > 18 Å, when the excess proton CEC leaves the protein/water interface for the bulk environment, the tail of the PMF converges to ∼12.0 kcal/mol, for both Figure 5A and B, in agreement with the PMF in Figure 3 (data not shown). This reveals that the deprotonation of His64 consists of ∼9.7 kcal/mol free energy barrier for the deprotonation of His64 to the protein/water interface and another ∼2.3 kcal/mol barrier for the PT between the protein/water interface and the surrounding bulk solvent, for a total barrier of ∼12.0 kcal/mol in the absence of exogenous buffer. This suggests the rate-limiting step is on the de/protonation of His64 with a ΔF‡ = 12.0 ± 0.4 kcal/mol and would result in a rate of krxn ≈ 0.03 μs−1, which is in line with experimental data in the limit of no/low exogenous buffer.28 As exogenous buffer concentrations are increased the probability of the excess proton transferring from the His64 to an exogenous buffer or from the protein/water interface to an exogenous buffer, instead of transferring directly to the bulk solution, greatly increases. Therefore, at adequate/high exogenous buffer concentration the ∼2.3 kcal/mol barrier for the PT from the protein/water interface to the bulk solvent would be replaced by a more probable protein/water interface to exogenous buffer PT reaction, which is predicted to be almost barrierless based on the current PMF's and His64 deprotonation PMF's in mutant.84 Therefore, at adequate/high exogenous buffer concentrations the rate-limiting step is a combination of the PT through the active site water and the de/protonation of His64, both due to processes having the same barrier within statistical error. For the active site water PT the ΔF‡ = 10.0 ± 0.4 kcal/mol with a krxn ≈ 1.0 μs−1 and the de/protonation of His64 PT has a ΔF‡ = 9.7 ± 0.4 kcal/mol with a krxn ≈ 1.5 μs−1.
With the His64 in the “out” orientation, due to the higher PT barrier through the active site water cluster to His64, it is more difficult to decipher the possible position of the rate-limiting step when there is no/low exogenous buffer. The overall free energy barrier for PT (when His64 is in the “out” orientation) is between ∼11.4 kcal/mol and ∼12.0 kcal/mol, depending on the concentration of the exogenous buffer. Like in the His64 “in” PMF as the exogenous buffer concentration is lowered the free energy barrier to PT will approach ∼12.0 kcal/mol. Therefore, the rate-limiting step in the absence of exogenous buffer will be a combination of the de/protonation of His64, as predicted by experiment, and the PT through the active site water. Again, within the uncertainty of the measurement these two paths are equivalent. As the exogenous buffer concentration is increased the rate limiting step becomes the PT event involving the active site water, in line with the hypothesis determined from exogenous buffer concentration experiments.
Taking these limits on the PT barrier into account it is concluded that the rate-limiting step shifts between the PT in the active site water cluster to His64 and the de/protonation of His64 to the bulk solvent depending on His64's orientation and the exogenous buffer concentration. As to the importance of His64's orientation to the overall observed rate, the results here are different than those proposed by Riccardi et al. (ref 39). By invoking the proton-hole mechanism, the semiempirical SCC-DFTB methodology utilized in ref 39 suggests that the reaction would be insensitive to the orientation of His64 and the size/stability of the intramolecular water cluster. As a result, the “out” orientation was hypothesized to be as productive as the “in” orientation. This is in contrast to the present MS-EVB simulations, which predict that the His64 “in” orientation is more productive (lower barrier) than the “out” orientation. In addition to indicating the importance of the orientation of His64 the MS-EVB results also suggest an important role for the intramolecular water cluster. Due to the shorter water cluster being more conducive to PT the rate-limiting step may be shifted to the deprotonation of His64 to the bulk and may not reside within the intramolecular water cluster as seen in Figure 5B. However, this does not mean there is no functional advantage for the enzyme to maintain small water clusters. If there were no small water clusters the barrier to PT through the intramolecular water cluster would increase, possibly making it the rate-limiting step and thereby decreasing the observed rate. Therefore, it seems important to have facile PT through smaller water clusters because this, in addition to the pKa of donor and acceptor, places the barrier at ∼10.0 kcal/mol, as seen in Figure 5B.
To summarize, when His64 is “in” and there exists adequate/high exogenous buffer the rate-limiting free energy barrier corresponds to a combination of the de/protonation of His64 and the PT through the active site water with a value of ∼10.0 kcal/mol and a krxn ≈ 1.0 μs−1. When there is low/no exogenous buffer the rate-limiting free energy barrier, which also corresponds to the de/protonation of His64, converges to ∼12.0 kcal/mol and a krxn ≈ 0.03 μs−1. When His64 is “out” and there exists adequate/high exogenous buffer the rate-limiting free energy barrier corresponds to the PT through the active site water to His64 with a value of ∼11.4 kcal/mol and a krxn ≈ 0.09 μs−1, but when there exists no/low exogenous buffer concentration the rate-limiting free energy barrier shifts to a combination of the de/protonation of His64 and the PT through the active site water with a free energy barrier of ∼12.0 kcal/mol and a krxn ≈ 0.03 μs−1. Therefore, the overall reaction at adequate/high exogenous buffer concentrations is a combination of the PT through the active site waters and the de/protonation of His64, depending on the orientation of His64. For the hydration of CO2, ZnH2O2+–His system, previous simulation work has indicated a 86% “in” orientational preference of His64 while for the dehydration of CO2, ZnOH+–HisH+ system, His64 is 97% “out”.16 This would result in an overall hydration rate of ∼0.9 μs−1 and an overall dehydration rate of ∼0.1 μs−1. At the low/no exogenous buffer concentrations the overall free energy barrier, for both hydration and dehydration, converges to 12.0 ± 0.4 kcal/mol and a krxn ≈ 0.03 μs−1 corresponding to a greatly reduced overall rate when compared to adequate/high exogenous buffer concentrations, again in agreement with experiment.28
4. Conclusions
In this paper, an in depth analysis of the rate-limiting PT event in HCA II has been presented within the MS-EVB2 model framework. The PT free energy pathway for His64 in both the “in” and “out” orientations reveals that the “in” orientation has a reduced free energy barrier for the PT through the active site water. The transition state (free energy barrier) in the PT through the active site water is identified as a high free energy Eigen cation, and the identity of the most probable protonated water is predicted to be W3a instead of W2 (cf. Figure 1). Taking into account the effects of the exogenous buffer concentration on the deprotonation of His64, it is also possible to identify where the rate-limiting step occurs. It was found that the rate-limiting PT step shifts from the PT through the active site water to His64 to the de/protonation of His64, depending on the orientation of His64 and the exogenous buffer concentration. Correlation analysis of the ZnOH+–HisH+ with His64 in the “in” orientation suggests that the dehydration direction of the reaction capitalizes on the short-lived “in” orientation by reducing the number of uncorrelated active site water groups needed to form the active site water cluster.
When elucidating alternate PT paths for the excess proton CEC in the absence of direct participation by His64, three distinct paths that may be utilized to enter/leave the active site were found. Two of the three paths were shown to intersect known binding sites of the chemical rescue agent 4MI, thereby indicating possible chemical rescue pathways. These results suggest new avenues for future mutagenesis experiments to enhance or inhibit these pathways in an effort to better understand how HCA stabilizes and transports excess protons and its implications for the chemical rescue pathway. A modest preference of the excess proton to follow water pathways near hydrophobic residues was also found from the MS-EVB2 simulations. These latter results may therefore suggest that enzymes may use hydrophobic interfaces76,79 to facilitate the transport of an excess proton toward/away from the active site.
Supplementary Material
Acknowledgments
This work was supported by the National Institutes of Health (R01-GM53148 and R01-GM25154). The computational resources for this project have been provided in part by the National Institutes of Health (Grant # NCRR 1 S10 RR17214-01) on the Arches Metacluster, administered by the University of Utah Center for High Performance Computing. We thank Dr. Vinod Krishna for helpful discussions.
Footnotes
Supporting Information Available: Figure S1. Complete refs 61 and 68. This material is available free of charge via the Internet at http://pubs.acs.org.
References
- 1.Lindskog S, Behravan G, Engstrand C, Forsman C, Jonsson B, Liang Z, Ren X, Xue Y. In: Carbonic Anhydrase--From Biochemistry and Genetics to Physiology and Clinical Medicine. Botre F, Gros G, Storey BT, editors. VCH; Weinheim, Germany: 1991. pp. 1–13. [Google Scholar]
- 2.Fersht A. Enzyme Structure and Mechanism. W H Freeman and Sons; New York: 1985. [Google Scholar]
- 3.Silverman DN, Lindskog S. Acc Chem Res. 1988;21:30–36. [Google Scholar]
- 4.Davies DR. Annu Rev Biophys Biophys Chem. 1990;19:189–215. doi: 10.1146/annurev.bb.19.060190.001201. [DOI] [PubMed] [Google Scholar]
- 5.Maren TH. Physiol Rev. 1967;47:595–781. doi: 10.1152/physrev.1967.47.4.595. [DOI] [PubMed] [Google Scholar]
- 6.Tashian RE. BioEssays. 1989;10:186–192. doi: 10.1002/bies.950100603. [DOI] [PubMed] [Google Scholar]
- 7.Fisher SZ, Tu C, Bhatt D, Govindasamy L, Agbandje-McKenna M, McKenna R, Silverman DN. Biochemistry. 2007;46:3803–3813. doi: 10.1021/bi602620k. [DOI] [PubMed] [Google Scholar]
- 8.Nair SK, Christianson DW. J Am Chem Soc. 1991;113:9455–9458. [Google Scholar]
- 9.Christianson DW. Adv Protein Chem. 1991;42:281–335. doi: 10.1016/s0065-3233(08)60538-0. [DOI] [PubMed] [Google Scholar]
- 10.Lesburg CA, Christianson DW. J Am Chem Soc. 1995;117:6838–6844. [Google Scholar]
- 11.Erikson AE, Jones AT, Liljas A. Proteins. 1988;4:274–282. doi: 10.1002/prot.340040406. [DOI] [PubMed] [Google Scholar]
- 12.Liljas A, Kannan KK, Bergsten PC, Waara I. Nature. 1972;235:131–137. doi: 10.1038/newbio235131a0. [DOI] [PubMed] [Google Scholar]
- 13.Duda D, Tu C, Qian M, Laipis P, Agvandje-McKenna A, Silverman DN, McKenna R. Biochemistry. 2001;40:1741–1748. doi: 10.1021/bi002295z. [DOI] [PubMed] [Google Scholar]
- 14.Håkansson K, Carlsson M, Svensson LA, Liljas A. J Mol Biol. 1992;227:1192–1204. doi: 10.1016/0022-2836(92)90531-n. [DOI] [PubMed] [Google Scholar]
- 15.Kannan KK, Ramanadham M, Jones TA. Ann NY Acad Sci. 1984;429:49–60. doi: 10.1111/j.1749-6632.1984.tb12314.x. [DOI] [PubMed] [Google Scholar]
- 16.Maupin CM, Voth GA. Biochemistry. 2007;46:2938–2947. doi: 10.1021/bi062170f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Fisher Z, Hernandez Prada JA, Tu C, Duda D, Yoshioka C, An H, Govindasamy L, Silverman DN, McKenna R. Biochemistry. 2005;44:1097–1105. doi: 10.1021/bi0480279. [DOI] [PubMed] [Google Scholar]
- 18.Duda D, Govindasamy L, Agbandje-McKenna, Tu C, Silverman DN, McKenna R. Acta Crystallogr, Sect D. 2003;59:93–104. doi: 10.1107/s0907444902019455. [DOI] [PubMed] [Google Scholar]
- 19.Schimara H, Yoshida T, Shibata Y, Shimizu M, Kyogoku Y, Sakiyama F, Nakazawa T, Tate S, Ohki S, Kato T, Moriyama H, Kishida K, Tano Y, Ohkubo T, Kobayashi Y. J Biol Chem. 2007;282:9646–9656. doi: 10.1074/jbc.M609679200. [DOI] [PubMed] [Google Scholar]
- 20.Marino S, Hayakawa K, Hatada K, Benfatto M, Rizzello A, Maffia M, Bubacco L. Biophys J. 2007;93:2781–2790. doi: 10.1529/biophysj.107.107540. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Roy A, Taraphder S. J Phys Chem B. 2007;111:10563–10576. doi: 10.1021/jp073499t. [DOI] [PubMed] [Google Scholar]
- 22.Silverman DN, McKenna R. Acc Chem Res. 2007:40. doi: 10.1021/ar7000588. [DOI] [PubMed] [Google Scholar]
- 23.Swanson JMJ, Maupin CM, Chen H, Petersen MK, Xu J, Wu Y, Voth GA. J Phys Chem B. 2007;111:4300–4314. doi: 10.1021/jp070104x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Silverman DN, Vincent SH. CRC Crit Rev Biochem. 1983;14:207–255. doi: 10.3109/10409238309102794. [DOI] [PubMed] [Google Scholar]
- 25.Lindskog S, Coleman JE. Proc Natl Acad Sci USA. 1973;70:2505–2508. doi: 10.1073/pnas.70.9.2505. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Lindskog S. In: Zinc enzymes. Spiro TG, editor. John Wiley & Sons; New York: 1983. pp. 78–121. [Google Scholar]
- 27.Erikson AE, Kylsten PM, Jones TA, Liljas A. Proteins: Struct, Funct, Genet. 1988;4:283–293. doi: 10.1002/prot.340040407. [DOI] [PubMed] [Google Scholar]
- 28.Tu C, Silverman DN, Forsman C, Jonsson BH, Lindskog S. Biochemistry. 1989;28:7913–7918. doi: 10.1021/bi00445a054. [DOI] [PubMed] [Google Scholar]
- 29.Qian M, Tu C, Earnhardt N, Laipis PJ, Silverman DN. Biochemistry. 1997;36:15758–15764. doi: 10.1021/bi972081q. [DOI] [PubMed] [Google Scholar]
- 30.Haiqian A, Tu C, Duda D, Montanez-Clemente I, Math K, Laipis PJ, McKenna R, Silverman DN. Biochemistry. 2002;41:3235–3242. doi: 10.1021/bi0120695. [DOI] [PubMed] [Google Scholar]
- 31.Bhatt D, Fisher SZ, Tu C, McKenna R, Silverman DN. Biophys J. 2007;92:562–570. doi: 10.1529/biophysj.106.093203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Cui Q, Karplus K. J Phys Chem B. 2003;107:1071–1078. [Google Scholar]
- 33.Riccardi D, Schaefer P, Yang Y, Yu H, Ghosh N, Prat-Resina X, Konig P, Li G, Xu D, Guo H, Elstner M, Cui Q. J Phys Chem B. 2006;110:6458–6469. doi: 10.1021/jp056361o. [DOI] [PubMed] [Google Scholar]
- 34.Toba S, Colombo G, Merz KM., Jr J Am Chem Soc. 1999;121:2290–2302. [Google Scholar]
- 35.Lu D, Voth GA. Proteins. 1998;33:119–134. [PubMed] [Google Scholar]
- 36.Lu D, Voth GA. J Am Chem Soc. 1998;120:4006–4014. [Google Scholar]
- 37.König PH, Ghosh N, Hoffmann M, Elstner M, Tajkhorshid E, Frauenheim Th, Cui Q. J Phys Chem A. 2006;110:548–563. doi: 10.1021/jp052328q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Riccardi D, Konig P, Prat-Resina X, Yu H, Elstner M, Frauehneim T, Cui Q. J Am Chem Soc. 2006;128:16302–16311. doi: 10.1021/ja065451j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Riccardi D, Konig P, Guo H, Cui Q. Biochemistry. 2008;47:2369–2378. doi: 10.1021/bi701950j. [DOI] [PubMed] [Google Scholar]
- 40.Voth GA. Acc Chem Res. 2006;39:143–150. doi: 10.1021/ar0402098. [DOI] [PubMed] [Google Scholar]
- 41.Schmitt UW, Voth GA. J Phys Chem B. 1998;102:5547–5551. [Google Scholar]
- 42.Schmitt UW, Voth GA. J Chem Phys. 1999;111:9361–9381. [Google Scholar]
- 43.Day TJ, Soudackov AV, Cuma M, Schmitt UW, Voth GA. J Chem Phys. 2002;117:5839–5849. [Google Scholar]
- 44.Kim J, Schmitt UW, Gruetzmacher JA, Voth GA. J Chem Phys. 2002;116:737–746. [Google Scholar]
- 45.Cuma M, Schmitt UW, Voth GA. J Phys Chem A. 2001;105:2814–2823. [Google Scholar]
- 46.Cuma M, Schmitt UW, Voth GA. Chem Phys. 2000;258:187–199. [Google Scholar]
- 47.Maupin CM, Wong KF, Soudackov AV, Kim S, Voth GA. J Phys Chem A. 2006;110:631–639. doi: 10.1021/jp053596r. [DOI] [PubMed] [Google Scholar]
- 48.Warshel A. Annu Rev Biophys Biomol Struct. 2003;32:425–443. doi: 10.1146/annurev.biophys.32.110601.141807. [DOI] [PubMed] [Google Scholar]
- 49.Warshel A. Computer Modeling of Chemical Reactions in Enzymes and Solutions. John Wiley and Sons; New York: 1991. [Google Scholar]
- 50.Warshel A, Weiss RM. J Am Chem Soc. 1980;102:6218. [Google Scholar]
- 51.Wang J, Cieplak P, Kollman PA. J Comput Chem. 2000;21:1049–1074. [Google Scholar]
- 52.Vreven T, Morkuma K, Farakas O, Schlegel HB, Frish MJ. J Comput Chem. 2003;24:760–769. doi: 10.1002/jcc.10156. [DOI] [PubMed] [Google Scholar]
- 53.Dapprich S, Komaromi I, Byun KS, Morokuma K, Frisch MJ. J Mol Struct Theochem. 1999;462:1–21. [Google Scholar]
- 54.Humbel S, Sieber S, Morokuma K. J Chem Phys. 1996;105:1959–1967. [Google Scholar]
- 55.Kuno M, Hannongbua S, Morokuma K. Chem Phys Lett. 2003;380:456–463. [Google Scholar]
- 56.Maseras F, Morokuma K. J Comput Chem. 1995;16:1170–1179. [Google Scholar]
- 57.Svensson M, Humbel S, Morokuma K. J Chem Phys. 1996;105:3654–3661. [Google Scholar]
- 58.Svensson M, Humbel S, Froese RDJ, Matsubara T, Sieber S, Morokuma K. J Phys Chem. 1996;100(50):19357–19363. [Google Scholar]
- 59.Vreven T, Morokuma K. J Comput Chem. 2000;21:1419–1432. [Google Scholar]
- 60.Vreven T, Mennucci B, da Silva CO, Morokuma K, Tomasi J. J Chem Phys. 2001;115:62–72. [Google Scholar]
- 61.Frish MJ, et al. Gaussian03. Gaussian Inc.; Pittsburgh, PA: 2003. [Google Scholar]
- 62.Cieplak P, Cornell WD, Bayly C, Kollman PA. J Comput Chem. 1995;16:1357–1376. [Google Scholar]
- 63.Rowan T. PhD thesis. Department of Computer Science, University of Texas at Austin; 1990. Functional Stability Analysis of Numerical Algorithms. [Google Scholar]
- 64.Chen J, Brooks CL, Scheraga HA. J Phys Chem B. 2008;112:242–249. doi: 10.1021/jp074355h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Fisher SZ, Maupin CM, Govindasamy L, Budayova-Spano M, Govindasamy L, Tu C, Agbandje-McKenna M, Silverman DN, Voth GA, McKenna R. Biochemistry. 2007;46:2930–2937. doi: 10.1021/bi062066y. [DOI] [PubMed] [Google Scholar]
- 66.Kast SM, Nicklas K, Bär HJ, Brickmann J. J Chem Phys. 1994;100:566–576. [Google Scholar]
- 67.Hummer G, Pratt LR, Garcia AE. J Phys Chem. 1996;100:1206–1215. [Google Scholar]
- 68.Case DA, et al. AMBER. 7th. University of California; San Francisco: 2002. [Google Scholar]
- 69.Smith W, Forester TR. CCLRC. Daresbury Laboratory; Daresbury, Warrington, England: 1999. [Google Scholar]
- 70.Mezei M. J Comput Phys. 1987;68:237–248. [Google Scholar]
- 71.Kumar S, Bouzida D, Swendsen RH, Kollman PA, Rosenberg JM. J Comput Chem. 1992;13:1011–1021. [Google Scholar]
- 72.Roux B. Comput Phys Commun. 1995;91:275–282. [Google Scholar]
- 73.Humphrey W, Dalke A, Schulten K. J Mol Graphics. 1996;14:33–38. doi: 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
- 74.Reinhard F, Grubmüller H. J Chem Phys. 2007;126:014102. doi: 10.1063/1.2400220. [DOI] [PubMed] [Google Scholar]
- 75.Gilson MK, Given JA, Bush BL, McCammon JA. Biophys J. 1997;72:1047–1069. doi: 10.1016/S0006-3495(97)78756-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Petersen MK, Iyengar SS, Day TJF, Voth GA. J Phys Chem B. 2004;108:14804–14806. [Google Scholar]
- 77.Petersen PB, Saykally RJ. J Phys Chem B. 2005;109:7976–7980. doi: 10.1021/jp044479j. [DOI] [PubMed] [Google Scholar]
- 78.Petersen MK, Voth GA. J Phys Chem B. 2006;110:7085–7089. doi: 10.1021/jp060698o. [DOI] [PubMed] [Google Scholar]
- 79.Iuchi S, Chen H, Paesani F, Voth GA. J Phys Chem. 2008 doi: 10.1021/jp805304j. in press. [DOI] [PubMed] [Google Scholar]
- 80.Tian C, Ji N, Waychunas GA, Shen YR. J Am Chem Soc. 2008;130:13033–13039. doi: 10.1021/ja8021297. [DOI] [PubMed] [Google Scholar]
- 81.Levering LM, Sierra-Hernanadez MR, Allen HC. J Phys Chem C. 2007;111:8814–8826. [Google Scholar]
- 82.Tarbuck TL, Ota ST, Richmond GL. J Am Chem Soc. 2006;128:14519–14527. doi: 10.1021/ja063184b. [DOI] [PubMed] [Google Scholar]
- 83.Maupin CM, Saunders MG, Thorpe IF, McKenna R, Silverman DN, Voth GA. J Am Chem Soc. 2008;130:11399–11408. doi: 10.1021/ja802264j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Roy A, Taraphder S. J Phys Chem B. 2008;112:13597–13607. doi: 10.1021/jp0757309. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


