Longitudinal Formulas to Estimate GFR in Children with CKD

Abstract

Background and objectives: Whereas current GFR estimating equations approximate direct GFR measurement at a single time point, formulas that capitalize on changes in easily measured biologic parameters could improve the accuracy and precision of GFR estimation.

Design, setting, participants, & measurements: In the Chronic Kidney Disease in Children Cohort (aged 1 to 16 yr), we measured GFR by plasma disappearance of iohexol (iGFR) and biomarkers in the first two annual visits. Models took the form GFR₂ = a[GFR₁/40]^b[X₂/X₁]^c, where GFR₂ and GFR₁ represented the current and previous years' iGFR, 40 ml/min per 1.73 m² was the cohort mean, and X₂/X₁ was the change in predictors over time. Using data from 360 participants with a median age of 12.1 yr, we evaluated the predictive performance of a past GFR measurement and 20 other variables using a two-thirds random sample of the data. A one-third sample was reserved for validation.

Results: Previous iGFR measurements were strongly predictive of subsequent iGFR and adding change in height/serum creatinine significantly improved the explanatory power to 78%. In the validation set, the correlation between estimated and measured GFR was 0.88, and 48 and 88% of estimated GFRs were within 10 and 30% of observed iGFRs. When the past GFR measurement was not used, addition of change in markers to a cross-sectional model did not improve prediction.

Conclusions: Longitudinal formulas to estimate iGFR capitalize on the high predictive power of previous iGFR measurements and in this study yielded a parsimonious prediction model with the potential for assessing progression in the clinical setting.

GFR, the gold standard for assessing kidney function, is a measure of the volume of plasma filtered each minute through the glomeruli of the kidneys. Direct measurement of GFR requires timed blood draws or urine collection to estimate clearance of an endogenous or exogenous marker that is ideally freely filtered and neither reabsorbed nor secreted. These methods can be challenging and time-consuming for both study personnel and participants. Investigators, therefore, often turn to estimation of GFR using current measurements of biomarkers, such as serum creatinine (SCr). A valid and precise estimate of GFR that is based on easily measured variables could greatly simplify studies of kidney disease. Although available formulas provide reasonable approximation to clearance-based direct GFR measurements, the variability can be large (1,2), yielding the potential for attenuation of risk estimates for risk factors under study.

A recently published GFR-estimating equation by Schwartz et al. (3) achieved improved prediction by adding cystatin C and blood urea nitrogen (BUN) to SCr. Another approach, however, is to recover more information from known predictors by taking advantage of a longitudinal study design. The predictive value of current biomarkers and bioeffects (hereafter called simply biomarkers) could be augmented with past biomarker data by using the change over time of a given biomarker as the predictive quantity in an estimating equation. More important, one powerful predictor that could be incorporated using a longitudinal context for estimation would be past GFR measurements. This idea forms the basis for transition models that regress current outcomes on past values of the outcome and on current and past values of predictors. Such models provide one tool for the analysis of longitudinal data and have been used in etiologic investigations of personal cigarette smoking on changes in pulmonary function in children (4); however, these models have not been extended to the arena of prediction, although they have much to offer.

Using a method that incorporates past measured GFR into the estimation of current values has a number of advantages. Grounding the estimation in past GFR levels smoothes the GFR function over time and lends continuity to the GFR data. Within the context of a longitudinal study, a more natural estimation vehicle is a longitudinal prediction model that capitalizes on past kidney function assessment and borrows strength from biomarker information at both a previous and a current visit. In research settings, participants could undergo direct GFR measurement at fewer time points, reducing the stress of study involvement while maintaining the integrity of GFR information over designs with pure estimation strategies. There are also clinical benefits given that patients often have a previous GFR measurement, and clinicians could capitalize on that information to predict current GFR and, potentially, future decline.

Here, we describe the development of a longitudinal estimating equation for GFR within the context of the Chronic Kidney Disease in Children Cohort Study (CKiD). The CKiD uses iohexol plasma clearance data to measure GFR (iGFR) in each member of the cohort. This method has been shown to be a robust direct measurement of GFR (5–7). We evaluated the predictive benefit of capitalizing on these direct GFR measurements taken in a previous annual study visit for estimation of a current GFR. The strength of past measurements in predicting current GFR, we hypothesized, would yield a parsimonious estimating equation with good predictive credentials. Given that direct GFR measurements are not available in many study settings, we also explored the predictive gain of incorporating information on past biomarker levels into a cross-sectional biomarker-only estimating equation.

Materials and Methods

Study Participants and Design

The CKiD has been described previously (8). Briefly, children with mild to moderate CKD (30 to 90 ml/min per 1.73 m²) were recruited on the basis of the original Schwartz formula (1,9,10) from 43 participating pediatric nephrology centers. Eligible children were 1 to 16 yr of age and had never undergone dialysis or organ transplant. GFR was determined from plasma iohexol disappearance curves at baseline, 1 yr later, and every other year thereafter. Data from participants with attainable iGFR measurements in visit 1 (baseline) and in visit 2 (1 yr later) were used to build and validate GFR estimating equations.

GFR Measurement and Biomarker Assays

At the study visit, an intravenous line or butterfly needle was used to administer 5 ml of iohexol. A second intravenous line was saline locked and used for obtaining blood samples for measurement of SCr and BUN; an aliquot was also obtained for HPLC determination of an iohexol blank. SCr (enzymatic) and BUN were analyzed centrally at the CKiD's laboratory at the University of Rochester (G.J.S.) on an Advia 2400 (Siemens Diagnostics, Tarrytown, NY). Blood samples were collected at four time points (10, 30, 120, and 300 min) after infusion, and serum iohexol concentrations were used to calculate iGFR. The method of GFR determination using the plasma disappearance of iohexol in a two-compartment system has been previously reported (2). GFR values were scaled to body surface area (BSA), which was determined using the formula of Haycock et al. (11). Chemistry panels (sodium, potassium, chloride, BUN, SCr, calcium, and phosphorus) and iohexol concentrations were entered by the Central Biochemistry Laboratory into a web-based data management system (Nephron) developed by the Data Coordinating Center.

Statistical Analysis

Twenty variables (age, height, weight, BSA, glomerulonephritis diagnosis, male, white race, height/SCr [ht/SCr], BUN, albumin, phosphate, calcium, glucose, proteinuria, hemoglobin, potassium, systolic BP, hematocrit, carbon dioxide, and sodium) were available in the data set for inclusion in a predictive model of GFR previously demonstrated to be associated (either cause or effect) with kidney function (12–15). Because cystatin C had been processed in only 59% of the participants, it was not used in the primary equation development but was used for sensitivity analysis (16). Parameter estimates from bivariable regressions adjusting for the variability in iGFR₂ explained by iGFR₁ were evaluated for predictive strength in the full data set. Factors that were significantly associated with iGFR₂ in the adjusted models (P < 0.05) were further evaluated in multivariate models using a two-thirds random sample of the data, which formed a training set for development of a prediction model. Demographic and morphologic variables were included to explain remaining variability after all of the biomarkers were assessed. A one-third random sample was reserved as an independent data set for validating the model fit.

The longitudinal GFR estimating equation was of the form log(iGFR₂) = α + γlog(iGFR₁/40) + βlog(X₂/X₁) + ε, where iGFR₂ and iGFR₁ represented the current and previous year's iGFR and X₂/X₁ was the series of current year divided by the previous year's biomarker values. The estimate of the cohort mean (40 ml/min per 1.73 m²) was used to standardize iGFR and make estimated effects interpretable. Specifically, exponentiating the intercept, α, yields the GFR in visit 2 for a child whose GFR in visit 1 was 40 ml/min per 1.73 m² and whose biomarker values remained unchanged between visits (X₂ = X₁). The parameter γ is the power that describes the impact on GFR₂ of the GFR at visit 1 because it deviates from the mean in individuals with the same changes in the Xs. Likewise, the parameter vector β is the power that quantifies the impact of the ratio of visit 2 to visit 1 biomarker values in individuals with the same GFR₁. In particular, for two children who have the same GFR₁ but one has twice the change in a biomarker relative to the other, the one with the higher change is expected to have 2^β the GFR₂ of the other. The quantity, ε, represents the error between estimated GFR₂ and the observed value.

Similarly, a complementary biomarker-only longitudinal formula that added the change in biomarker levels to a cross-sectional model was developed. The equation was of the form log(iGFR₂) = α + δlog(X₂) + βlog(X₂/X₁) + ε, where log(X₂) was the log of the visit 2 values centered at their means and X₂/X₁ was defined as previously. The parameter interpretations are similar to those already described with the parameter vector δ now representing the power that describes the impact on GFR₂ of the biomarker values in visit 2. The log normality assumption for these models was validated by fitting a generalized γ distribution and assessing whether the shape parameter estimate was statistically different from a value of 0 (3,17).

Results

A total of 362 study participants had available iGFR measurements that were based on iohexol plasma disappearance curves from the first and second annual study visits. Two individuals with extreme changes in iGFR from visit 1 (62.7 and 40.0 ml/min per 1.73 m²) to visit 2 (8.1 and 7.5 ml/min per 1.73 m², respectively) were removed, leaving data from 360 children for analysis. The median age was 12.1 yr (visit 2), the baseline (visit 1) median iGFR was 42.7 ml/min per 1.73 m², and the median iGFR at visit 2 was 42.2 ml/min per 1.73 m². Descriptive statistics of the visit 2 characteristics and the ratios of visit 2 to visit 1 values are provided in Table 1. The median ratio for iGFR is <1.0, indicating declining values, although the decline was minimal during the first year of the study.

Table 1.

Descriptive statistics at first annual follow-up visit (visit 2) and ratios from baseline visit (visit 1) to visit 2 (n = 360)

Variable	Visit 2	Visit 2/Visit 1
Age (yr; median [IQR])	12.10 (8.80 to 15.70)	1.10 (1.07 to 1.15)a
Height (m; median [IQR])	1.50 (1.20 to 1.60)	1.04 (1.02 to 1.06)a
Weight (kg; median [IQR])	40.00 (26.00 to 56.70)	1.10 (1.05 to 1.17)a
BSA (m2; median [IQR])	1.30 (0.90 to 1.60)	1.07 (1.04 to 1.11)a
Glomerulonephritis diagnosis (%)	20	–
Male gender (%)	61	–
White race (%)	72	–
Ht/SCr (m/mg per dl; median [IQR])	1.00 (0.70 to 1.30)	0.96 (0.85 to 1.08)
BUN (mg/dl; median [IQR])	30.0 (22.0 to 41.0)	1.05 (0.86 to 1.29)
Albumin (g/dl; median [IQR])	4.30 (4.10 to 4.50)	1.00 (0.95 to 1.04)
Phosphate (mg/dl; median [IQR])	4.70 (4.20 to 5.10)	1.02 (0.95 to 1.14)
Calcium (mg/dl; median [IQR])	9.70 (9.30 to 10.00)	1.00 (0.97 to 1.03)
Glucose (mg/dl; median [IQR])	89.00 (83.00 to 95.00)	0.99 (0.88 to 1.06)
Urine protein/urine creatinine (median [IQR])	0.50 (0.20 to 1.10)	1.00 (0.72 to 1.55)
Hemoglobin (g/dl; median [IQR])	12.70 (11.70 to 13.70)	1.01 (0.95 to 1.06)
Potassium (mmol/L; median [IQR])	4.50 (4.20 to 4.90)	1.00 (0.94 to 1.08)
Systolic BP (mmHg; median [IQR])	107.00 (99.00 to 116.00)	1.01 (0.93 to 1.09)
Hem to rit (%; median [IQR])	37.10 (34.20 to 40.00)	1.00 (0.95 to 1.06)
Carbon dioxide (mmol/L; median [IQR])	21.00 (19.00 to 23.00)	1.00 (0.91 to 1.11)
Sodium (mmol/L; median [IQR])	140.00 (138.00 to 141.00)	1.00 (0.99 to 1.01)
Cystatin C (mg/L; median [IQR] ;n = 213)	2.00 (1.60 to 2.50)	1.08 (0.95 to 1.27)
iGFR (ml/min per 1.73 m2; median [IQR])	42.20 (31.60 to 53.40)	0.98 (0.87 to 1.11)

IQR, interquartile range.

^aIQRs that do not contain 1.0.

Table 2 shows the results of univariate linear regression models for iGFR₂ (in the log scale) on each one of the variables in Table 2. In addition, it provides the adjusted regression coefficient arising from a regression of the bivariable model including iGFR₁. The explained variability is the percentage of the variability in iGFR₂ accounted for by the independent variable after removing the effects of other variables in the model. From the unadjusted estimates, we found the strongest predictors of the log(iGFR₂) to be log(iGFR₁) (R² = 68%), the change in log(ht/SCr) (R² = 20%), the change in log(BUN) (R² = 3%), log(age) (R² = 3%), the change in log(phosphate) (R² = 2%), log(height) (R² = 2%), and the change in log(albumin) (R² = 1%). These factors remained strongly associated with current iGFR after removing the effect of previous iGFR by adding it to the model. Weight and BSA were also significant in the adjusted models but were strongly correlated with height, which had the highest R² estimate. Glomerular diagnosis and the change in log(calcium) were also significant factors independent of the previous iGFR.

Table 2.

Univariate and iGFR₁-adjusted (bivariate) linear regression parameter estimates for various putative predictors of log(GFR₂) (n = 360) that were evaluated for inclusion in a GFR estimation model

Predictor	Miss	Unadjusted		iGFR1 Adjusted
		Estimate (SE)	Explained Variability (%)	Estimate (SE)	Explained Variability (%)
log(iGFR1)	0	0.95 (0.03)a	68	–	–
Δ log(ht/SCr)	0	0.71 (0.08)a	20	0.52 (0.04)a	30
Δ log(BUN)	0	−0.23 (0.07)a	3	−0.18 (0.04)a	6
Δ log(albumin)	21	−0.64 (0.29)b	1	−0.77 (0.16)a	6
log(age2)	1	−0.15 (0.05)b	3	−0.11 (0.03)a	5
log(ht2)	0	−0.27 (0.11)b	2	−0.29 (0.06)a	5
log(BSA2)	0	−0.08 (0.06)	1	−0.15 (0.03)a	5
log(weight2)	0	−0.05 (0.04)	<1	−0.10 (0.02)a	5
Δ log(phosphate)	29	−0.38 (0.14)b	2	−0.25 (0.08)b	3
Δ log(calcium)	21	−0.72 (0.39)	1	−0.66 (0.22)b	3
Glomerular diagnosis	3	−0.02 (0.05)	<1	−0.09 (0.03)b	2
Male gender	0	−0.01 (0.04)	<1	−0.03 (0.03)	1
Δ log(glucose)	21	0.03 (0.11)	<1	0.08 (0.06)	1
Δ log(proteinuria)	42	−0.01 (0.03)	<1	0.00 (0.02)	1
White race	0	−0.10 (0.05)	1	0.03 (0.03)	<1
Δ log(hemoglobin)	32	0.19 (0.22)	<1	0.00 (0.12)	<1
Δ log(potassium)	28	−0.01 (0.17)	<1	−0.09 (0.10)	<1
Δ log(systolic BP)	35	0.22 (0.20)	<1	−0.02 (0.12)	<1
Δ log(hematocrit)	32	0.11 (0.21)	<1	0.06 (0.12)	<1
Δ log(CO2)	23	0.60 (0.12)	<1	0.03 (0.07)	<1
Δ log(sodium)	21	−0.83 (1.11)	<1	0.04 (0.63)	<1

Δ = log(X₂) − log(X₁) = log(X₂/X₁); GFR given in ml/min per 1.73 m².

^aP < 0.001.

^bP ≥0.001 and < 0.05.

In the training set of 220 randomly selected children from the 329 who had complete data for all of the variables of interest (iGFR₁, ht/SCr, BUN, albumin, age, height, phosphate, calcium, and glomerular diagnosis), we evaluated significant predictive factors (P < 0.05) from the adjusted regressions shown in Table 2. Table 3 shows the parameter estimates and predictive properties of the models, which contained various combinations of the predictors log(iGFR₁), change in log(ht/SCr), the change in log(BUN), the change in log(albumin) and log(height at visit 2). Other factors were NS predictors in adjusted multivariable models. Including all of the significant biomarkers resulted in model III with an R² of 79%, a root mean squared error (RMSE) of 0.190, and 84% of the predicted GFR₂ values within 30% of the observed iGFRs. Adding log(height₂) to the model yielded a small increase in R² to 80% (model IV); however, an estimating equation using only GFR₁ and the change in log(ht/SCr) (model IIa) resulted in a model with similar performance.

Table 3.

Estimating formulas for longitudinal prediction of visit 2 GFR using a visit 1 iGFR measurement and changes in biomarker values between the two visits

$eGF{R}_2=a{\left[\frac{iGF{R}_1}{40}\right]}^b{\left[\frac{ht/SC{r}_2}{ht/SC{r}_1}\right]}^c{\left[\frac{BU{N}_2}{BU{N}_1}\right]}^d{\left[\frac{AL{B}_2}{AL{B}_1}\right]}^e{\left[h{t}_2\right]}^f$

Model	a	b	c	d	e	f	R2 (%)	% within 30%	% within 10%	$\sqrt{\text{MSE}}$a
None	40.78 ± 1.14	0	0	0	0	0	–	48	17	0.414
I	39.68 ± 0.61	0.996 ± 0.044	0	0	0	0	70	80	43	0.229
IIa	40.48 ± 0.55	0.912 ± 0.039	0.514 ± 0.058	0	0	0	78	85	41	0.197
IIb	39.88 ± 0.59	0.978 ± 0.043	0	−0.206 ± 0.046	0	0	73	80	43	0.219
IIc	39.56 ± 0.58	0.999 ± 0.042	0	0	−0.947 ± 0.197	0	73	81	44	0.218
III	40.37 ± 0.53	0.919 ± 0.038	0.431 ± 0.061	−0.089 ± 0.042	−0.579 ± 0.178	0	79	84	47	0.190
IV	40.20 ± 0.53	0.921 ± 0.038	0.405 ± 0.061	−0.100 ± 0.042	−0.543 ± 0.177	−0.172 ± 0.071	80	86	45	0.188

Formulas have parameters estimated in a training set of 220 children.

^aOf the log-transformed iGFR₂.

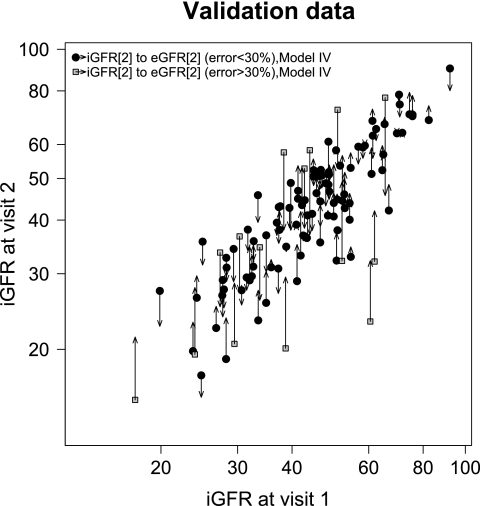
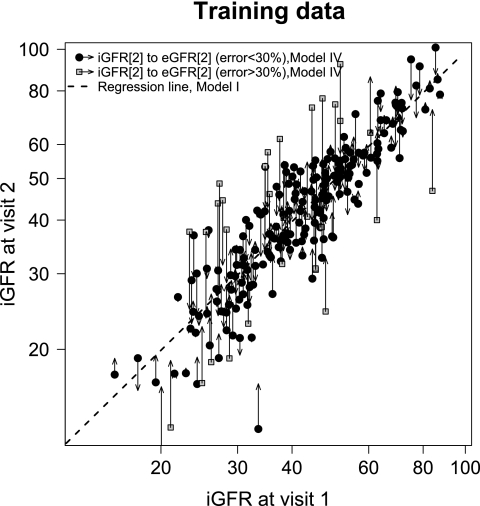
The models from Table 3 were evaluated in an independent set of data (not used for model development) that consisted of 109 participants with results shown in Table 4. Because the estimated GFR originates from data on the log scale, both the bias and the 95% limits of agreement are presented as percentages. The model with only the previous GFR and the change in log(ht/SCr) (model IIa) yielded the best performance in the validation set with a correlation of 0.88, errors within 10 and 30% of 88 and 48%, respectively, and a small bias of 0.5%. The predictive performance of the estimation using all of the predictors (model IV) is graphically illustrated in Figures 1 and 2 for the training and validation set, respectively. The departure of the predicted GFR estimates from the regression line through the data, which represents model I, highlights the degree to which the additional biomarker terms contribute information to the estimation.

Table 4.

Predictive performance in the validation set of 109 individuals of a longitudinal estimating equation for GFR incorporating a previous direct GFR measurement

Model	eGFR	Bias (%)	95% Limits of Agreement (%)	Correlation	% within 30%	% within 10%
I	45.19 ± 14.45	4.6	−32.5, 62.0	0.81	81	38
IIa	43.60 ± 14.55	0.5	−28.6, 41.6	0.88	88	48
IIb	44.24 ± 14.16	2.4	−32.9, 56.2	0.83	80	41
IIc	45.39 ± 14.80	4.9	−32.3, 62.4	0.80	81	34
III	43.53 ± 14.45	0.4	−28.9, 41.8	0.88	86	47
IV	43.22 ± 14.42	−0.3	−29.5, 41.0	0.88	86	39

Validation set has 109 individuals with mean iGFR = 43.72 ± 15.31 ml/min per 1.73 m². eGFR, estimated GFR.

Figure 1.

Distribution of iGFR visit 2 measurements by iGFR at visit 1 within the training data (n = 220). The regression line fit for regressing iGFR at visit 2 on iGFR at visit 1 is shown (Table 3, model I). The magnitude of the error between iGFR and estimated GFR (eGFR) is illustrated by the length of the arrows with the origin at the observed data (iGFR₁, iGFR₂) and the arrowhead at the estimated value (iGFR₁, eGFR₂ using model IV, Table 3; data point at iGFR₂ = 9.5 ml/min per 1.73 m²; not shown).

Figure 2.

Distribution of iGFR visit 2 measurements by iGFR at visit 1 within the validation data (n = 109). The magnitude of the error between iGFR and eGFR is illustrated by the length of the arrows with the origin at the observed data (iGFR₁, iGFR₂) and the arrowhead at the estimated value (iGFR₁, eGFR₂ using model IV, Table 3).

Table 5 contains the results from replacing iGFR₁ in the model with the log of the cross-sectional measurements of visit 2 predictive biomarkers from Table 3 (ht/SCr, BUN, and albumin). Model V, the purely cross-sectional model, results in an R² of 76%, an RMSE of 0.204, and percentages of errors within 10 and 30% of 35 and 82%, respectively. When terms for the change in those biomarkers from visit 1 to visit 2 were added to the model, only the change in the log of ht/SCr was significant (Table 5, model VI). The R² increased slightly to 77%, the RMSE became 0.202, and the percentages of errors within 10 and 30% remained similar (36 and 81%, respectively). Hence, current levels of ht/SCr and BUN were important for predicting current GFR, whereas the speed at which the current level of ht/SCr is achieved was statistically significant but added little to the predictive performance of the model.

Table 5.

Estimating formulas for longitudinal prediction of visit 2 GFR using the visit 2 cross-sectional measures and change of biomarker values from the two visits $eGF{R}_2=a{\left[\left(ht/SC{r}_2\right)\right]}^b{\left[\left(30/BU{N}_2\right)\right]}^c{\left[\frac{ht/SC{r}_2}{ht/SC{r}_1}\right]}^d$

Model	a	b	c	d	R2 (%)	% within 30%	% within 10%	$\sqrt{\text{MSE}}$a
None	40.78 ± 1.14	0	0	0	–	48	17	0.414
V	41.91 ± 0.58	0.671 ± 0.042	0.169 ± 0.041	0	76	82	35	0.204
VI	41.75 ± 0.58	0.732 ± 0.048	0.170 ± 0.041	−0.188 ± 0.075	77	81	36	0.202

Parameters were estimated in a training set of 220 children.

^aOf the log transformed iGFR₂

Evaluating the predictive performance of model VI in the validation set (Table 6), the change of ht/SCr did not affect the predictive value or fit of the estimating equation. The bias decreased to −2.1 from −3.2%, but the 95% limits of agreement remained approximately the same width.

Table 6.

Predictive performance in validation data set of 109 children of a biomarker-only GFR estimating formula using both cross-sectional markers and the change in biomarkers from visit 1 to visit 2

Model	eGFR	Bias (%)	95% Limits of Agreement (%)	Correlation	% within 30%	% within 10%
V	41.82 ± 13.26	−3.2	−36.1, 46.6	0.82	78	46
VI	42.29 ± 13.48	−2.1	−35.3, 48.1	0.82	78	49

Validation set has 109 individuals with mean iGFR = 43.72 ± 15.31 ml/min per 1.73 m².

The distribution of iGFR₂ was found to be consistent with a log-normal distribution in the models presented (e.g., 95% confidence interval for shape parameter of model IV: −0.4242 to 0.0496). Although we presented the results from only one data split (two thirds training and one third validation), 10 repetitions of the analysis with resampling of the training and validation set produced consistent results.

Discussion

Cohort studies offer inferential advantages over cross-sectional studies in their ability to provide information on individual changes in biomarkers and factors of interest over time. Evaluating cohort data cross-sectionally ignores the additional information on disease natural history that is captured in longitudinal measurement. Prediction models should similarly benefit from capitalizing on the longitudinal data collection by using past and present biomarker data to predict the measure of interest. In this study, we evaluated whether this supposition would hold true for the estimation of GFR. We found that a direct iGFR measurement taken in the first year of the CKiD study was highly predictive of the GFR value measured in the second year of the study. Variability in the prediction was reduced by adding the change in ht/SCr to the model. The change in log BUN and the change in log albumin added slightly to the predictive performance in the training set of data but had a detrimental effect on the error percentages in the validation data set, although BUN has been found valuable in cross-sectional GFR estimating formulas (3). Performance in an independent data set indicated that an estimating equation based on the previous iGFR measurement and the change in ht/SCr resulted in the fewest errors and a bias of 0.5%.

The predictive power of the change in cystatin C, when evaluated in a subanalysis of the 60% (n = 122) with turbidimetric (DAKO SD, Copenhagen, Denmark) cystatin C measurements, did not contribute significantly (P = 0.08) to the prediction of the longitudinal model III in Table 3. Because cystatin C has been shown to contribute substantially to cross-sectional equations (3,18,19), it is possible that a larger availability of measurements and/or alternative methods, such as nephelometry (20) (Siemens Dade-Behring), for measuring cystatin C will result in improvements of the prediction of the proposed longitudinal equations.

Although the change in ht/SCr was informative when complementing the previous GFR measurement, the change in this biomarker was not as informative when added to a cross-sectional equation. The performance in both the training and validation data sets indicates that visit 1 biomarker levels do not contain much information regarding GFR 1 yr later after taking into account the attained levels observed at visit 2; however, the decline in GFR during a single year was minimal in a majority of the participants. The benefit to prediction from previous biomarker measurements may be realized only with greater degrees of progression after more follow-up time has accrued.

These results indicate that the use of immediate biomarker values provides an adequate GFR estimate, but future investigations will be needed to evaluate the potential for using past biomarker data and direct GFR measurement to anticipate GFR decline. Current results suggest that when GFR measurements are available, using that past GFR information and the change in ht/SCr during the follow-up period improves the estimation compared with cross-sectional prediction with equivalent biomarkers. Model IIa in Table 3, which relies primarily on the previous year's GFR measurement, yielded an RMSE of 0.197 compared with 0.204 for the purely cross-sectional biomarker-only equation, model V in Table 5.

The limitations to drawing broad conclusions from these results include the selectivity of participants in CKiD, who primarily represent children who have urologic disease, are under the care of pediatric nephrologists, and are mostly at Tanner stage I. In addition, the analyses used the logarithm of the predictors, which may prove, with the accumulation of more follow-up time, to be a suboptimal transformation for some biomarkers; however, the assumptions that accompanied the form of our equation were evaluated and not found to be violated to an extent that would invalidate our conclusions.

Conclusions

We have shown that during a 1-year follow-up period, longitudinal direct measurement of GFR can be complemented with consistent estimates of GFR using transition models and biomarker data. The marriage of direct and estimated GFR provides a continuity of GFR data that befits the longitudinal study platform. Additional follow-up time and the availability of new biomarker data hold the promise for realizing the full potential of longitudinal estimating equations.

Disclosures

None.