World Color Survey color naming reveals universal motifs and their within-language diversity

Abstract

We analyzed the color terms in the World Color Survey (WCS) (www.icsi.berkeley.edu/wcs/), a large color-naming database obtained from informants of mostly unwritten languages spoken in preindustrialized cultures that have had limited contact with modern, industrialized society. The color naming idiolects of 2,367 WCS informants fall into three to six “motifs,” where each motif is a different color-naming system based on a subset of a universal glossary of 11 color terms. These motifs are universal in that they occur worldwide, with some individual variation, in completely unrelated languages. Strikingly, these few motifs are distributed across the WCS informants in such a way that multiple motifs occur in most languages. Thus, the culture a speaker comes from does not completely determine how he or she will use color terms. An analysis of the modern patterns of motif usage in the WCS languages, based on the assumption that they reflect historical patterns of color term evolution, suggests that color lexicons have changed over time in a complex but orderly way. The worldwide distribution of the motifs and the cooccurrence of multiple motifs within languages suggest that universal processes control the naming of colors.

English and many other languages spoken in industrialized societies include 11–12 basic color terms. In contrast, there is great diversity in color terminology across languages spoken in preindustrialized cultures, with some languages using as few as two or three color terms, and other languages using more. To account for this diversity, Berlin and Kay (1) proposed two conjectures: (i) there exists a limited set of “universal” categories from which all languages draw their color lexicons, and (ii) languages “evolve” by adding color names in a relatively fixed sequence. There is now overwhelming empirical support for the first conjecture (1–4). The second conjecture has been more difficult to evaluate, in part because it has proven difficult to compare color naming across languages, and in part because it is difficult to test an inherently time-dependent process with synchronic data.

In this paper, we explore an important idea that links these two conjectures: that color lexicons occur in only a modest number of distinct, universal color-naming systems, which can be placed in an ordered hierarchy from simple to complex based on the number of categories into which color space is lexically partitioned. We evaluated this idea by analyzing the data of the World Color Survey (WCS) (www.icsi.berkeley.edu/wcs/), a corpus of color-naming data from 110 world languages. The results of our analysis indicate that color-naming lexicons tend to cluster statistically into just a few systems, which we call motifs, which occur, with some individual variation, in the lexicons of informants living in all parts of the world. In this sense, motifs are universal. Analysis further revealed a striking cooccurrence of multiple distinct motifs within most of the WCS languages.

We then examined Berlin and Kay's second conjecture, on the hypothesis that within-language lexical diversity is a marker for lexical change in synchronic data. In broad agreement with Berlin and Kay and their collaborators (5–7), our analysis suggested that color terms change over time in a principled way.

Results

Cluster Analysis.

Traditionally, linguists and anthropologists interested in color naming across cultures have supposed that each language has a particular set of color terms in its vocabulary, so they have started their analysis at the level of the language (1, 8). To avoid that assumption, we carried out a cluster analysis of the WCS at the level of the idiolect (the personal language variety of the individual speaker), without regard to language of origin.

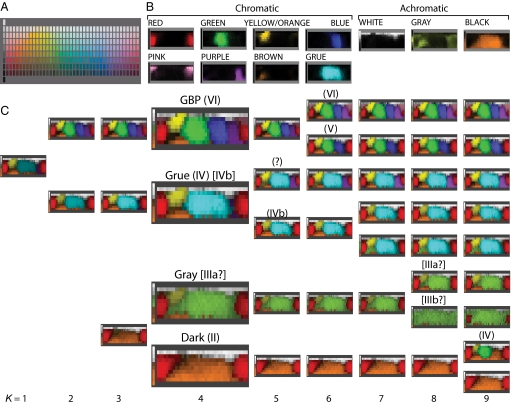
The WCS dataset consists of the color terms provided by 2,616 informants, each speaking one of 110 languages, in response to a standard set of 330 Munsell color samples (Fig. 1A), which were presented one at a time in a fixed pseudorandom order. To compare color naming across WCS languages, we used K-means cluster analysis of native color terms to derive a universal lexicon to which all color terms could be glossed (4). Our analysis of chromatic color-naming patterns revealed eight statistically significant clusters (Fig. 1B). These clusters glossed easily to English basic color terms or their composites: namely, RED, GREEN, BLUE, GRUE (“green-or-blue”), YELLOW-OR-ORANGE, BROWN, PINK, and PURPLE. For the present study, we added three achromatic color categories, glossed as BLACK (for color-naming patterns that included the darkest achromatic color sample in the WCS chart), GRAY (for patterns that included one or more achromatic samples but excluded the black and white samples), and WHITE (for color-naming patterns that included the lightest achromatic color sample). The diversity within color categories is illustrated by the concordance maps in Fig. 1B, where each sample within the WCS array (Fig. 1A) is false-colored with a hue corresponding to its gloss and a lightness corresponding to the concordance with which the gloss was used. Thus, we arrived at an objective mapping of all of the color words used by all of the WCS informants into 11 universal glossed color terms.

Fig. 1.

Glossary and motifs in the WCS. (A) The WCS color chart, arranged according to Munsell hue (horizontal) and value (vertical), with 10 neutral samples (leftmost column). (B) Concordance maps of the 11 color terms, in false color, with the color terms used in this paper. (C) Concordance maps of the color-naming systems (motifs). Columns indicate solutions for K clusters (K = 1 is the whole dataset). Titles are motif names. Roman numerals indicate corresponding stages from Berlin and Kay (parentheses) or Kay and Maffi (brackets). At K = 4 (concordance maps enlarged for clarity), 614 informants used the Green/Blue motif, 1,063 used the Grue motif, 313 used the Gray motif, and 377 informants used the Dark motif.

In the present analyses, we reassembled each informant's color-naming data into his or her own objectively glossed color-naming system. Then, we used K-means analysis to cluster the individual color-naming systems of the 2,367 informants who provided color terms for 320 or more of the 330 color samples in the WCS chart [90.5% of WCS informants, representing 109 of 110 languages, excluding language 31 (Eastern Cree), because only one informant provided names for 320 or more color samples (see Methods)].

Fig. 1C shows our results for assumed numbers of clusters ranging from K = 1 to K = 9. Each multicolored rectangle is the concordance map obtained from all of the informants included in one of the K clusters. Each graphic element within each map represents the proportion of informants (the lightness of the element) assigned to that cluster who used the most prevalent gloss (the false-color hue of the element) to name the corresponding color sample in the WCS chart. A striking feature of these concordance maps is the distinct (light) regions of high concordance (near 1.0), separated by well-defined boundary regions (dark) of low concordance (<50%). The main types of concordance map are evident by K = 3–6 clusters, and these types persist with systematic but incremental variation out to at least K = 15 clusters (maps for K = 1–15 shown in Fig. S1). All of the maps display a dominant RED region, and most display a clear YELLOW-OR-ORANGE region, but they vary notably in the partition of the cool region of the WCS chart (corresponding to the English terms “green,” “blue,” and “purple”).

We use the term “motif” to denote the patterns of color term vocabulary and usage illustrated by these concordance maps. We chose this term to convey the notion that our analysis revealed recurring patterns of color naming that repeated, with individual variation, throughout the WCS dataset, much as an element might be repeated, perhaps with variation, throughout a musical, literary, or artistic work.

The structure of these motifs is clearly reminiscent of the “stages” of color term evolution proposed by Kay and colleagues (1, 6, 7), although several motifs have no perfect counterpart in those stages. For example, at K = 4, {BLACK/WHITE/RED} (hereafter, the Dark motif) is similar to Stage II in both Berlin and Kay (1) and Kay and Maffi (7). However, also at K = 4, the {BLACK/WHITE/RED/YELLOW/GRAY} motif (the Gray motif) does not correspond exactly to any of the stages but is a candidate for Kay and Maffi's (7) Stage IIIa, if we are willing to allow GRAY to correspond to their BLACK. The K = 4 {BLACK/WHITE/RED/YELLOW/GRUE} motif (the Grue motif) corresponds closely to Stage IV of Berlin and Kay (1) and Stage IVb of Kay and Maffi (7). However, that motif bifurcates at K = 5, adding a {BLACK/WHITE/RED/YELLOW/GRUE/PURPLE} motif that does not correspond to any of the stages of Kay and colleagues, as far as we know. At K = 4, the {BLACK/WHITE/RED/YELLOW/GREEN/BLUE/PURPLE} (the “GBP” motif) corresponds reasonably well to Berlin and Kay's (1) Stage VI. Other correspondences and differences between our motifs and the stages from Kay and colleagues are marked in Fig. 1C. It is important to note that the layout within which the various motifs appear in Fig. 1C is a purely statistical hierarchy of associations, and it should not be construed as a temporal hierarchy of color term evolution.

How Many Motifs?

It is clear from inspection of Fig. 1C that most of the variation in color naming among WCS informants is captured in the motifs obtained for K = 3–6, which suggests that there are only about three to six motifs in the WCS. Three lines of quantitative analysis support this conclusion (see Methods). First, we used Gap Statistic analysis (9), which compared the degree of clustering in the WCS dataset to that in a representative sample of simulated uniform reference datasets. The Gap Statistic indicated that K = 3 is the optimal number of clusters. Second, we calculated the degree of clustering within our motifs by using the C-index, which was derived from a comparison of within- vs. between-cluster similarities as K was varied. The C-index suggested that K = 4 is optimal. Finally, we compared within-cluster pairwise agreement among WCS informants. For K ≥ 6, there was, on average, greater agreement among informants within K-means clusters (concordance = 0.55) than there was within the natural languages of the WCS (concordance = 0.53).

Although our three analyses suggested slightly different optimum values of K, they all indicated that most of the variance in the WCS could be accounted for by only a few canonical color-naming motifs. Our analysis does not refute the existence of other distinct but minority motifs. Indeed, the concordance maps at higher values of K (Fig. 1C) reveal higher-order motifs that are reminiscent of other stages proposed by Kay and collaborators (1, 6, 7). However, these motifs are relatively rare and require a value of K that is larger than our analyses suggest.

Universality Across, Diversity Within Languages.

Our K-means analysis reveals only three to six motifs, many fewer motifs than there are languages in the WCS. Therefore, each motif is widespread and is observed in many linguistically unrelated languages (Fig. 2B). In this sense, the motifs are universal, and they challenge us to understand what universal processes underlie their structure. The small number of statistically significant motifs, which occur in unrelated languages, leads us to seek an explanation for their structures that stresses universal neurobiological, cognitive, or linguistic processes. Although there has been notable progress on this issue recently (10, 11), there is currently no full consensus view on the details of such an explanation (10, 12–16).

Fig. 2.

Within-language diversity in color naming. (A) Diversity in 110 WCS languages. Each pie chart represents one WCS language (numbers at the top). The wedges within pie charts are the proportion of informants assigned to each motif at K = 4 (color codes on the top correspond to the enlarged clusters in Fig. 1C). Excluded informants named fewer than 320 of the 330 color samples. (B) Examples of WCS data from four languages; language numbers from A. The top two rows are the two K = 6 branches of the GBP (Green|Blue|Purple) motif; the second two rows are the two K = 5 branches of the Grue motif, both of which are united as single motifs at K = 4. False colors indicate glossed color terms (Fig. 1B). Notice the similarity among speakers from different continents (rows) and the diversity among speakers of each language (columns).

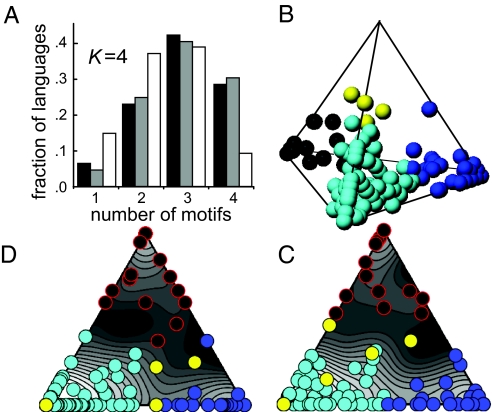
Next, we determined the prevalence of each of the motifs at K = 4 (Dark, Gray, Grue, and GBP) among the informants speaking each of the WCS languages. The results of this analysis (Fig. 2 A and B) reveal remarkable within-language diversity. Examples of individual languages containing multiple motifs appear in Fig. 2B. The modal number of motifs per language was three (Fig. 3A), the median number was also three, and only seven languages (6.4%) had single motifs. Most languages (70.6%) contained three or four motifs defined at K = 4.

Fig. 3.

Languages with multiple motifs. (A) Histogram of the number of languages with one to four motifs at K = 4. Full dataset (black bars indicate K-means; gray bars, spectral clustering). White bars indicate aggressively culled data (hierarchical clustering). (B) Full dataset of languages (spheres) in tetrahedral coordinates based on the prevalence of the motifs within languages obtained by K-means analysis. False colors indicate the most frequent motif: Dark (black), Gray (yellow), Grue (cyan), and GBP (blue). Full dataset (C) and culled dataset (D) projected onto the Dark–Grue–GBP facet, with contour plots of language density based on a Gaussian sampling kernel (σ = 0.01). Languages on the rising facets of the tetrahedron project to the edges of the triangles in C and D.

We tested the robustness of this unexpected result in three ways. First, we repeated the analysis for other values of K (2 ≤ K ≤ 15). The modal number of motifs per language was always greater than one. Second, we obtained substantially the same results (Fig. 3A, gray bars) when we reanalyzed the entire dataset by using spectral clustering (17), a modern clustering method that has certain advantages over traditional techniques like K-means or hierarchical clustering. Third, we asked whether this diversity was due to noisy data, or to informants who did not understand the task. We used hierarchical clustering to create a four-cluster solution, while culling those informants whose color-naming systems fell outside a threshold dissimilarity range for each cluster. This aggressive culling method eliminated the data from 688 informants (29% of the 2,367 who named at least 320 colors). The average concordance among informants within these new clusters was 0.7, which falls at the 90th percentile of all individual WCS languages. The resulting motifs were indistinguishable from the K = 4 K-means solution. When we recalculated the number of clusters per language, three was still the modal number of motifs per language (Fig. 3A, white bars). Therefore, we are confident that the results shown in Figs. 2 and 3A are robust: most languages are diverse in the color-naming behavior of their informants. Webster and Kay (18) have also noted significant within-language diversity in the focal colors of informants who share color lexicons.

These analyses allow us to reject two extreme statistical hypotheses. One is that individuals within languages conformed perfectly in their color-naming behavior. The other is that individuals chose their motifs strictly at random from among the four motifs, without regard to conformity with the other members of their community. If that were the case, about 0.95 of WCS languages should contain all four motifs defined at K = 4. This is far more than the observed fraction, which is 0.28 (the rightmost black bar in Fig. 3A).

Why don't all speakers of a given language use the same motif? One might think that a typical WCS “language” might be made up of several distinct languages or dialects, but this is unlikely to explain the within-language diversity, because informants from each language were dialectically uniform so far as the field workers were aware and were almost always recruited from a single locality. However, there remain three other plausible explanations. (i) Maybe some of the color terms are loanwords, which might have entered a language from migration, trade, or intermarriage. (ii) Maybe subgroups within a culture developed a specialized color vocabulary because they need one. (iii) Maybe the motif diversity is an artifact of the method of data collection, and the receptive vocabulary of understood terms might vary less across individuals than the (productive) color-naming data of the WCS suggest. Any of these three reasons, alone or in combination, could be invoked to explain the existence of multiple color-naming systems within a language.

Whatever its proximal causes, diversity in color term usage is a ubiquitous feature of color naming in WCS languages. Although it may seem reasonable to characterize the color lexicon of a language by its predominant motif, our analysis reveals a richness of color cognition within preindustrial languages that is not well captured by such a strategy.

Trajectories of Color Term Change.

Now we turn to Berlin and Kay's second conjecture, namely that color lexicons change over time, starting with fewer color terms, and adding color terms a few at a time, in a relatively fixed order, to arrive finally at about 11 basic color terms. The languages presently spoken in the world are taken to instantiate the various “stages” along these trajectories of color term change. Are the data of the WCS consistent with this conjecture?

For our analysis, we considered the fraction of speakers (x_i) who used each of the four main motifs. This dataset forms a simplex (0 ≤ x_i ≤ 1; i ∈ {Grue, GBP, Dark, Gray}; Σ_i x_i = 1), and each language can be plotted in barycentric coordinates within a regular tetrahedron (Fig. 3B). Languages with one motif map onto the four vertices of the tetrahedron, languages with two motifs map onto the edges, languages with three motifs map onto the facets, and languages with four motifs map into the interior of the tetrahedron.

The simplex representation of WCS diversity revealed that most languages fall near the lower facet of the tetrahedron (x_Gray = 0; Fig. 3B). Consistent with this observation, a principal components analysis on the log ratio-transformed data (17) yielded two principal components, which accounted for 88.5% of the dispersion in the transformed whole dataset (89.4% in the culled dataset) and defined a surface near the Dark–Grue–GBP facet of the tetrahedron. This result suggested that the Gray component is relatively minor, in agreement with the Gap Statistic result that K = 3 is the optimal number of WCS motifs. Therefore, we collapsed the tetrahedral simplex onto a reduced-dimension triangular simplex defined by the Dark, Grue, and GBP vertices (Fig. 3 C and D).

We then used the simplex to examine Berlin and Kay's (1) second conjecture by using Kay's principle that “diachronic change implies synchronic variation” (ref. 5, p. 262). According to this principle, languages that are undergoing change from one stage of color term evolution to another (e.g., between Dark and GBP, via Grue) will have multiple motifs represented among their speakers. This suggests that an analysis of the current spatial distribution of languages within the simplex (synchronic variation) can be used to make inferences regarding temporal variations in lexicon (diachronic change). If we analyze a large and diverse enough sample of languages (the WCS), the distribution of languages in the simplex will reveal the trajectories the languages followed as the modern lexicons emerged.

A plausible mapping of Berlin and Kay's (1) stages of color term evolution onto our motifs framework (Fig. 1C) suggests that languages may progress along a Dark → Grue → GBP trajectory. In its purest form, this hypothesis predicts that lexically stable languages should map to the simplex vertices, whereas languages “in transition” (6, 7) should map to the two edges joining the Dark and Grue, and the Grue and GBP vertices, respectively. Examining the 2D simplex (Fig. 3 C and D), there is a prominent string of languages stretching from the Grue vertex to the GBP vertex, along the Grue–GBP edge, and the density plot shows contours running alongside that edge [note: all languages on the Gray–Grue–GBP facet project onto the Grue–GBP edge when we reduce to 2D, in both the full and the culled datasets (Fig. 3 C and D)]. A similar, although less compelling, distribution of languages runs between the Dark and Grue vertices. The relative weakness of the Dark–Grue trajectory might be due to the particular languages in the WCS sample. However, it is also plausible that the Dark-motif “stage” was the ancestral state, but that it was prevalent long before the WCS sample was collected. According to this view, the Dark-to-Grue trajectory in the synchronic WCS dataset is weakly represented because it is ancient, not because it was unlikely to occur.

Less consistent with the Dark → Grue → GBP hypothesis are two other features of the simplex data, which appear in both the full WCS dataset (Fig. 3C) and in the heavily culled subset (Fig. 3D): a few languages map to the Dark–GBP edge of the simplex, and many languages contain more than two motifs, and therefore plot well into the interior of the simplex. Given the limitations of synchronic data, we can do little more here than point out that these features suggest that color terms changed along more reticulate pathways, rather than the relatively linear trajectory required by the Dark → Grue → GBP motif model. Kay and his colleagues (6, 7) have also suggested more complex trajectories.

Discussion

Our analyses indicate that the color terms used by the WCS informants are drawn on a universal glossary of 11 color terms, and that the particular suite of color terms used by each informant is drawn on a set of about three to six universal color-naming systems, which we call motifs. Each motif is characterized by distinct regularities in the patterns of color naming among the idiolects of a subset of WCS speakers.

A striking and unexpected result of this analysis is the diversity of motifs within most WCS languages, and yet the remarkable similarity among the color-naming systems of individuals speaking completely unrelated, internally diverse, languages. This counterintuitive result is all the more remarkable when we consider that within-culture communication often promotes within-language standardization of the color lexicon, instead of the diversity that we observe. Likewise, a lack of contact between cultures that are widely separated geographically is expected to facilitate diversity across languages. Instead, patterns of color naming worldwide coalesce around a small number of distinctive motifs. Thus, whatever its proximal causes, an individual's choice of a color lexicon is highly constrained.

Variations in within-language diversity across the WCS provide a way to examine color term evolution by using synchronic data. Our simplex analysis of these variations indicates that color lexicons change over time and do so in a reasonably orderly fashion. Taken as a whole, the results of our motif analyses are broadly in agreement with the work of Berlin and Kay and their coworkers (1, 6, 7), and add to the growing body of evidence in support of the universality in color naming and color term evolution.

What is universal across cultures that leads to universal motifs, and what is specific to the individual speaker that leads to diversity among informants? As we discussed above, different individuals within a culture may experience different features in the environment to be more or less salient, depending on their needs, habits, or roles in society. This could easily lead to diversity among speakers in their color term usage. It is also possible that some of these needs and salient features might be universal across environments and cultures, contributing to the establishment of universal motifs. However, it is hard to imagine that the motifs, and the color terms that they contain, would be so similar across cultures in the absence of some universal neurobiological or cognitive factors, which show individual variation but which are common to all people and constrain the development of individual speakers' color lexicons.

Methods

Derivation of the Universal Glossary of Color Terms.

In previous work (4), we used K-means cluster analysis to obtain glosses for the chromatic color terms used by all 2,616 WCS informants to name one or more of the 320 chromatic samples, but none of 10 achromatic samples, in the WCS color chart. We encoded the terms as 320-element binary vectors (v), indicating whether that term labeled the ith color sample in the WCS chart. Distance (dissimilarity) between two color term vectors was defined to be one minus the Pearson correlation coefficient calculated for the two vectors. We compared the total within-cluster dissimilarity in the K-means partition of the data to that obtained by identical analysis of a sample of synthetic uniform reference distributions. The Gap Statistic (9) showed that the optimal number of clusters in the dataset was eight.

Derivation of the Motifs.

Here, we analyzed the glossed color-naming systems of 2,367 WCS informants by using K-means analysis. The color-naming datasets were represented as 11 × 330 element binary matrices L⁽ⁿ⁾ (n = 1, …, 2,367). L⁽ⁿ⁾ coded the association between the informant's color terms, reduced by translation to the 11 universal glosses and the 330 color samples in the WCS color chart. The entries l_ij⁽ⁿ⁾ were either 0 or 1. If the jth color sample was assigned gloss i, l_ij⁽ⁿ⁾ = 1, and all other entries in the jth column of L⁽ⁿ⁾ were 0.

The centroids of the K-means clusters, C^(k) (k = 1, …, K), were 11 × 330 real-valued matrices. Each element c_ij^(k) was the prevalence of the ith gloss (out of 11) applied to the jth color sample (out of 330) by all of the informants assigned by K-means to the kth cluster. Hence, Σ_i=1¹¹ c_ij^(k) = 1.

As a test of consistency in our K-means analysis, we ran the analysis for each value of K twice, each based on the minimum obtained from 100 iterations. The agreement in the clusters obtained from these two runs always exceeded 0.99.

Dissimilarity Metric.

We used D₁₂ = 1 − J(S⁽¹⁾, S⁽²⁾) as a dissimilarity metric to express the distance between two speakers' color-naming systems, S⁽¹⁾ and S⁽²⁾, or between an informant's color-naming system and a K-means cluster centroid (i.e., S⁽²⁾ = C^(k)). J(.) represents the similarity between S⁽¹⁾ and S⁽²⁾ (0 ≤ J(.) ≤ 1). When we computed J(.) between two speakers' color-naming systems, we were interested in the proportion of cases where their glossed color terms matched; i.e., when the corresponding elements of both S⁽¹⁾ and S⁽²⁾ were 1. Hence,

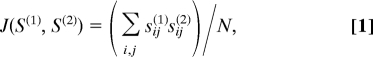where N is the number of samples named by both informants. Thus, when comparing color-naming systems, J(.) is the Jaccard coefficient. We also used J(.) to compute the dissimilarity between each informant's color-naming system (S⁽¹⁾ = L⁽ⁿ⁾) and a cluster centroid (S⁽²⁾ = C^(k)) in our K-means analysis. Recall that the entries of each column of C^(k) are real-valued, and represent the prevalences of the 11 glosses in the current cluster k for a particular color sample. In this case, Eq. 1 represents the weighted Jaccard coefficient, and similarity was based on an informant's glossed terms for the samples, each weighted by their prevalence among current members of a particular cluster, rather than on the binary matches.

Optimal Numbers of Motifs.

To use the Gap Statistic method (9) to determine the optimal number of clusters, we created synthetic reference distributions of color-naming systems by using a competitive process among N color-naming mechanisms. These mechanisms had 2D Gaussian-distributed response functions, which were mapped into the 2D coordinate frame of the WCS color chart so that a particular color sample, located in the chart at location (θ, y), activated mechanism n by amount:

The gloss assigned to a given color sample was the mechanism yielding the largest response at the location (θ, y). Each synthetic color-naming system was created by random assignment of parameters in Eq. 2. N was drawn from a normal distribution whose parameters (μ = 6.75, σ = 1.86) closely matched that of the glossed WCS. Coordinates θ_n and y_n were uniformly distributed across the WCS chart, and log(σ_θ,n) and log(σ_y,n) were uniformly distributed between 0.3 and 0.6. The resulting reference distributions closely approximated the WCS in the numbers of glossed terms deployed per “informant” and in the sizes of the regions of the WCS chart assigned a particular term (except that WCS informants had significantly more one- and two-sample color categories than predicted from our model). In this way, we created 20 “populations” of 2,367 simulated color-naming systems. Then, we partitioned each into different numbers of clusters by using K-means analysis, we calculated the total within-cluster, pairwise dissimilarities for each such partition, and we compared them to those obtained for the WCS dataset by using Gap Statistic analysis.

We calculated the C-index (19, 20) as a function of the number of clusters, K: CI(K) = (Sum − Min)/(Max − Min), where Sum is the sum of the total within-cluster pairwise dissimilarities for all K clusters. Let N_wc be the number of these pairwise dissimilarity calculations. Then, Max is the sum of the N_wc largest dissimilarities among all dissimilarities, calculated without regard for cluster membership, and Min is the sum of the N_wc smallest dissimilarities among all dissimilarities. Sum − Min approaches 0 when the clusters are well separated from one another; hence, a small C-index is better. An optimal value of K corresponds to a minimum or knee in CI(K).

Spectral Clustering.

In our implementation of the algorithm of Ng et al. (21), the ijth entry in the affinity matrix was A_ij = e^{−D_ij2/2(0.35)2}, where D_ij is the dissimilarity in color naming between the ith and jth informants (as described above). Subsequent clustering was based on the six largest eigenvectors of the normalized affinity matrix A. This resulted in a Gray category, a GBP category, a Dark category, and three Grue categories; we combined the three Grues into a single Grue category.