Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2010 Jan 1.
Published in final edited form as: Magn Reson Med. 2009 Jan;61(1):16–21. doi: 10.1002/mrm.21831

Orientation of Lipid Strands in the Extracellular Compartment of Muscle: Effect on Quantitation of Intramyocellular Lipids

Anthony Khuu 1, Jimin Ren 1, Ivan Dimitrov 1,6, Donald Woessner 1, James Murdoch 6, A Dean Sherry 1,2,5, Craig R Malloy 1,2,3,4
PMCID: PMC2775057  NIHMSID: NIHMS73842  PMID: 19097207

Abstract

Single voxel 1H NMR spectra from gastrocnemius and soleus muscle were acquired in healthy volunteers at 7 Tesla with the objective of measuring the concentration of intramyocellular lipid [IMCL]. However, significant asymmetry in the resonance assigned to the methylene protons (-CH2-)n in extramyocellular lipids (EMCL) interfered with fitting the spectra. Since muscle fibers in these tissues are generally not parallel to Bo, the influence of variable orientation in strands of extracellular fat was examined using a mathematical model. Modest variation in orientation produced asymmetric lineshapes qualitatively similar to typical observations at 7T. Analysis of simulated spectra by fitting with a Voigt function overestimated [IMCL]/[EMCL] except when EMCL fibers were nearly parallel to Bo. Estimates of [IMCL]/[EMCL] were improved by including variations in fiber orientation in lineshape analysis (fiber orientation modeling, FOM). Calculated [IMCL] using FOM, 4.8 ± 2.2 mmol/kg wet weight, was lower compared to most previous reports in soleus.

Keywords: fatty acids, triglycerides, spectroscopy, metabolism, musculoskeletal, lipid composition, 7 Tesla

Introduction

Analysis of the lipid content in skeletal muscle by 1H NMR spectroscopy has attracted widespread interest (1 – 4). In these spectra, chemical shift resolution of the 1H signal from intra- vs. extracellular fat occurs because the magnetic field inside a diamagnetic structure depends on its shape, orientation, and magnetic susceptibility (5 – 8). It is often assumed that intramyocellular lipids (IMCL) are approximately spherical droplets and that extramyocellular lipids (EMCL) may be modeled as strands of fat (2, 9). This model has been confirmed in phantoms (10), animals (11) and human subjects (2, 12), and, as predicted, optimal chemical shift resolution is observed in the anterior tibialis where EMCL strands are thought to be parallel to one another and to Bo (2, 4, 12 – 14).

The dominant methylene proton signal from (-CH2-)n is used to assess the IMCL content, but both the IMCL and EMCL signals must be fit because they tend to overlap (1, 4, 14 – 23). These resonances are generally fit with symmetrical lineshapes such as Gaussian, Lorentzian or Voigt functions. Notwithstanding widespread acceptance, investigators have remarked on the difficulty of fitting spectra from muscle other than the anterior tibialis (2, 24) due to asymmetry of the signal from EMCL (2). An asymmetrical EMCL with a large upfield component may actually be more prevalent rather than an exceptional finding (2, 4, 24). In fact, since muscle and fat fibers are generally not parallel to Bo or to one another (25), an asymmetric lineshape of EMCL should be expected.

Higher magnetic fields promise improved chemical shift dispersion and sensitivity, but in principle line broadening due to susceptibility-induced static field inhomogeneities may offset these benefits (2). Consistent with this prediction, in our initial studies of skeletal muscle at 7T conventional line fitting was unsatisfactory because of marked asymmetry in the methylene resonance from EMCL. Therefore, the effect of orientation of extracellular fat on the 1H NMR spectrum of the EMCL methyl and methylene resonances was evaluated using an approach termed fiber orientation modeling (FOM). In this study, simulated spectra and data from human subjects at 7T were both analyzed by fitting with a Voigt lineshape and by FOM. The estimated [IMCL] in the gastrocnemius and soleus was significantly lower when the EMCL signal was assume to originate from multiple strands of fat with variable orientations relative to Bo.

Methods

Human MR Spectroscopy and Imaging

The protocol was approved by the Institutional Review Board of UT Southwestern Medical Center. Healthy sedentary adults (2 females and 7 males) age 21 – 68 years (average 44 years, without known vascular disease or diabetes, body mass index: 26.6 ± 2.4 kg m−2) were studied supine in a 7T system (Achieva, Philips Medical Systems, Cleveland, OH). Spectra and images were acquired with a partial-volume quadrature transmit/ receive coil. Axial, coronal and sagittal T2 weighted turbo spin echo images were acquired from the left calf muscle with field-of-view FOV 180 × 180mm, TR 1500 ms, TE 75 ms, turbo factor 16, and number of acquisitions 1. The T2 weighted planar image data were used to reconstruct 3D images using maximum intensity projection (MIP). Parameters for the single-voxel STEAM spectra were: voxel size 1.0 mL, TR 2000 ms, TE 13 ms, spectral bandwidth 4000 Hz, number of points 4096, number of acquisitions 192, with water suppression. The volume of interest was chosen to minimize obvious extramyocellular fat signal (2, 3).

Subjects were instructed to move slowly to avoid physiological effects associated with rapid changes in the static magnetic field. The scanning session was 60 min or less and it was well-tolerated by all subjects. All subjects were interviewed after the exam and again at 24 hours after the exam. All subjects specifically denied dizziness, nausea, vertigo, headaches or visual changes.

Model of the 1H NMR Spectrum from Extramyocellular Lipids

The lipids detected in typical 1H NMR spectra of skeletal muscle are located either in an intracellular compartment or an extracellular compartment. Lipids in the intracellular compartment are generally considered as nearly spherical droplets (1 – 4). Consequently, the field experienced by intracellular lipids is independent of orientation of the myocyte relative to Bo (5, 6, 8). Lipids in the extracellular environment, in contrast, are located in interstitial adipocytes clustered in relatively long strands between muscle fibers. It was assumed that these strands of lipid can be represented as cylinders with the long axis at an angle θ relative to Bo. The influence of orientation on the field inside a cylinder was modeled as 3cos2 θ− 1 (26). This relationship predicts that signal from the intracellular and extracellular compartments will overlap at an orientation of about 55 degrees, an approximation that has been confirmed experimentally (10).

It was assumed that the 1H NMR signal from lipid protons is the sum of signal from two sources: intracellular droplets and extracellular strands. In a spherical coordinate system, two variables describe the orientation of a fatty strand: an angle θ which varies from 0° to 90° and describes the orientation relative to Bo, and an angle φ which varies from 0° to 360° and describes the orientation around the axis of Bo. In the current model, the number of protons (N) in a lipid strand at an angle (θ) relative to Bo represents the sum of all strands for that value of θ and every value of φ It has been suggested that orientation of EMCL strands can be described as a Gaussian distribution (27). For the current model, N(θ) is described as a Gaussian distribution with a dominant angle (α) and a width of the distribution (β) with a range from 0 to 90°, as N(θ) = exp(−((θ− α)/β)2). The width of the distribution (β) characterizes the dispersion in orientations of fatty strands within the voxel relative to Bo. Each source was assumed to produce a single resonance with a Gaussian lineshape and relative chemical shift obtained from the relationship 3cos2 θ −1. The amplitude of each resonance was determined by the relative amount of lipid at that angle θ The model, illustrated schematically in Figure 1, is termed fiber orientation modeling (FOM). By incrementing θ and summing the results, it is a simple matter to simulate 1H NMR EMCL spectra.

Figure 1.

Figure 1

Open in a new tab

Schematic Description of Fiber Orientation Modeling. In this example, the Gaussian distribution of extracellular fat (panel A) was α = 15° and β = 30°. The chemical shift for each angle was calculated and represented as a Gaussian line with the appropriate amplitude. Panel A also shows a schematic of fiber orientation. Panel B illustrates conversion of orientation, θ, to ppm. Panel C shows a linear axis in ppm plus a subset of the amplitude-scaled individual signals of equal linewidth. These resonances are not equally spaced on the chemical shift axis. The final simulated spectrum, D, is the sum of 91 such resonances.

To explore the effect of orientation and dispersion on the observed spectrum, simulations were performed assuming [IMCL]/ [EMCL] = 0.5. The chemical shift was scaled so the maximum range of chemical shift was 0.36 ppm corresponding to a change in orientation, θ, from 0° to 90°. The concentration of the seven predominant fatty acids (28) was used to calculate the relative area of the methyl resonance, the (-CH2-)n resonance, and the resonance from the protons on the carbon β to the carbonyl, 1.0 : 6.6 : 0.67. The EMCL signal was generated as the sum of signals of equal linewidth from 91 sources with equal increments in θ from 0° to 90°. Different combinations of central angles (α) and dispersions (β) were generated using orientations ranging from 0°, approximately representative of anterior tibialis, to 45° approximately representative of the muscle fiber angles in soleus (25).

Fitting 1H NMR Spectra

A least-squares fitting algorithm written in MATLAB (The MathWorks, Natick, MA) and based on fiber orientation modeling was used to simultaneously fit six overlapping components of the simulated spectra. Three resonances from IMCL were fit as Gaussian lineshapes and assigned to the protons β to the COO, protons in (-CH2-)n, and protons in CH3. Three other resonances from EMCL were shifted downfield by approximately 0.2 ppm. These resonances were also fit simultaneously using FOM. The signal from the protons βto COO in IMCL (“buried β”) overlaps with the (-CH2-)n methylene signal from EMCL. Because there are two β protons compared to the methyl group with three protons, a 2/3 scaling factor was used. Since a larger number of increments in the possible angles of extracellular fibers did not improve the fitting and increased computation time significantly, the two EMCL methylene resonance and the methyl resonances were each represented as the sum of 11 resonances of equal linewidths originating from lipid strands oriented at equal increments from 0 to 90°. The amplitude of each resonance was determined from the center angle, α, and the width, β, of the Gaussian distribution of orientations of EMCL fibers. The center angle and width were included as separate parameters in the fitting. The chemical shift of the IMCL resonance was assumed to be located at the same chemical shift as an EMCL oriented at 54.7°.

Three sets of simulated spectra for each combination of α and β were fit assuming that each resonance could be represented as the sum of a Lorentzian and Gaussian line (the Voigt lineshape, ACD/Specmanager, Advanced Chemistry Development, Inc.). The following resonances were estimated between 0.5 – 1.9 ppm: the IMCL and EMCL signals from protons in the -CH3 groups, (-CH2-)n groups, and the -CH2- group βto the carbonyl (-CH2-CH2-COO-). The same dataset was fit using the FOM least-squares algorithm.

Spectra from the gastrocnemius and soleus from healthy subjects were also analyzed by FOM and Voigt fitting in the region of interest from 0.5 to 1.9 ppm and also in the region around the CH2 resonance of creatine (2). Prior knowledge of the resonances’ chemical shift assignments was used, and it was assumed that the IMCL signal could be represented by a Voigt lineshape. Otherwise, no prior knowledge was used to constrain linewidth, lineshape or amplitude. The creatine signal was fit as two Voigt lines to accommodate various shapes of the signal. The concentration of IMCL triglycerides was then calculated using the creatine signal as a concentration standard and assuming [creatine] = 30 mmoles/kg wet weight muscle (2). Resonance areas were corrected for differential relaxation losses as described (29) assuming a T1 and T2 for creatine of 1050 and 74 msec, respectively, and measured T1 and T2 at 7T for (-CH2-)n in human marrow or subcutaneous fat, 540 and 65 msec (unpublished observations).

Results

The complex three-dimensional structure of extracellular fat in skeletal muscle is shown in Figure 2, a conventional cross sectional image (A) and two MIP images for fat volumetric distribution (B and C). The bright regions in the MIP images, reconstructed from T2-weighted images, represent subcutaneous fat (the large curved plate in B), bone marrow of the fibula (the thickest cylinder in C) or strands of extracellular fat between muscle fibers (the finer strips in C). If the lower leg is positioned approximately parallel to Bo, most strands of extracellular fat are not parallel to Bo and are not parallel to one another.

Figure 2.

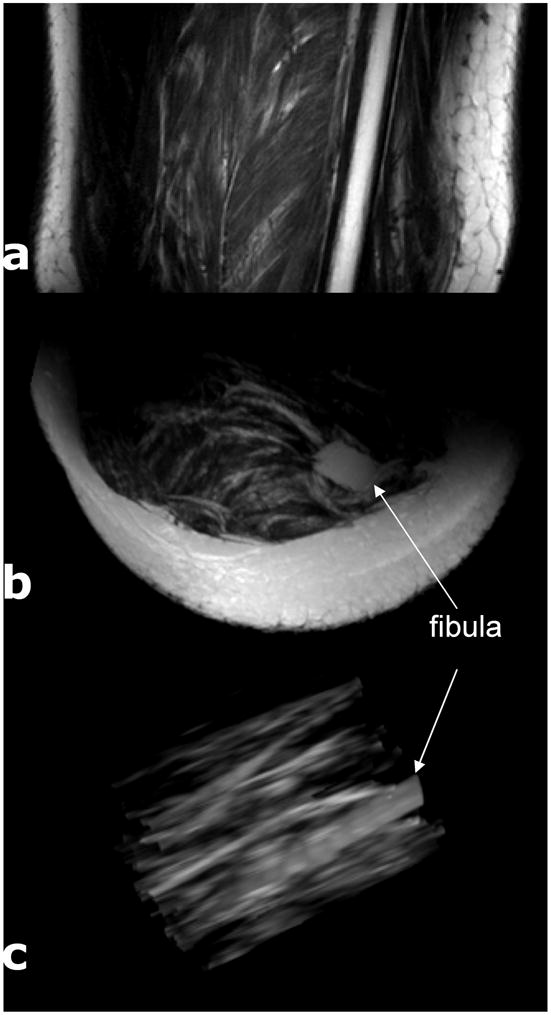
Figure 2

Open in a new tab

Coronal, Axial and Maximal Intensity Projection Images of the Calf. Panel A shows a T2 weighted coronal image with substantial subcutaneous fat, fat strands throughout, and marrow fat in the fibula. The axial MIP is Panel B. After removal of subcutaneous fat, C, the variability in orientation of the extracellular fat relative to fibula marrow is evident.

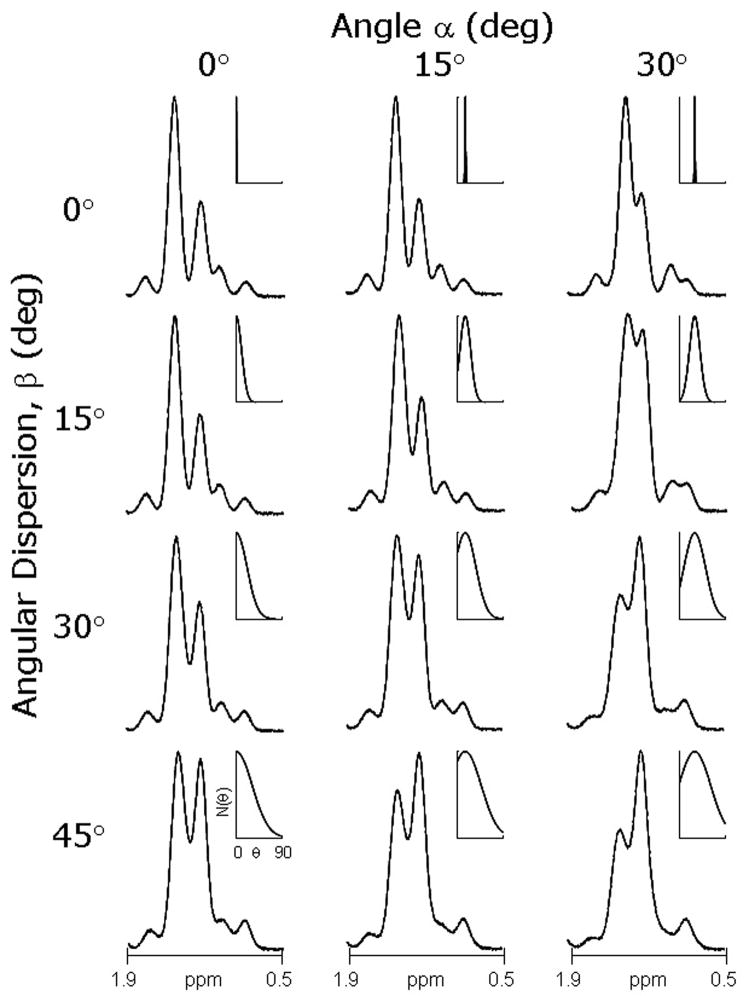
The effect of variable orientation on the simulated 1H NMR spectrum of muscle with preset [IMCL]/ [EMCL] = 0.5 is illustrated in Figure 3. The spectrum in the upper left panel demonstrates optimal resolution because the dominant angle of extracellular fibers, α, is 0° relative to Bo and the dispersion in orientation, β, is minimal. Consequently the [IMCL]/ [EMCL] is ~ 0.5 by visual inspection. With increasing dispersion (β), moving down the column, the extracellular signal becomes asymmetric and the apparent amplitude of the IMCL increases. Since the asymmetry caused by variable orientation occurs upfield to the EMCL signal and is superimposed on the IMCL signal, it may not be obvious that the spectrum in the lower left panel was also generated with [IMCL]/ [EMCL] = 0.5. The effects of changing the dominant angle, α, from 0° to 15° to 30° relative to Bo is illustrated by moving horizontally across Figure 3. Increasing the dominant angle relative to Bo is equivalent to reducing resolution and as a result the spectrum in the upper right shows poorer resolution but the apparent [IMCL]/ [EMCL] remains ~ 0.5. Because of the combined effects of reduced chemical shift resolution and variable orientation, [IMCL]/ [EMCL] appears much greater than 0.5 in the lower right panel.

Figure 3.

Figure 3

Open in a new tab

Influence of Orientation on 1H NMR Spectra for [IMCL]/ [EMCL] = 0.5. As the dominant angle α relative to Bo changes from 0°− 30°, the chemical shift resolution is reduced. With increasing dispersion β, the EMCL signal broadens asymmetrically. The inset shows N(θ) as a function of the dominant angle (α) and dispersion (β) used to calculate each spectrum using the same format as Figure 1A.

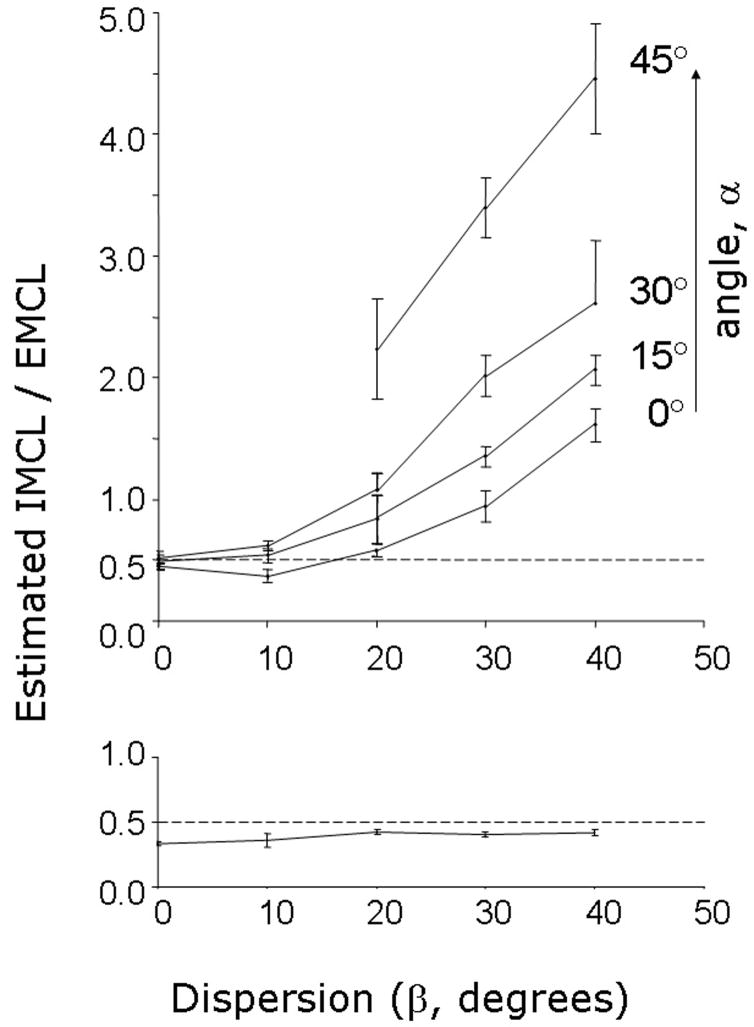
Fitting results with Voigt lineshape are shown in the upper panel of Figure 4, demonstrating the effects of variable orientation on estimated [IMCL]/[EMCL]. If dispersion is minimal, less than ~ 15°, fitting with the Voigt lineshape returned [IMCL]/ [EMCL] accurately. However, [IMCL]/ [EMCL] was significantly overestimated at higher dispersion using Voigt lineshape. The same data set was analyzed by FOM and the results are shown in the lower panel of Figure 4. Unlike fitting with the Voigt lineshape, there was little effect of variation in the central angle on the estimated [IMCL]/[EMCL]. Therefore, all results for each orientation angle were aggregated (lower panel, Figure 4). More importantly, there was no effect of dispersion on the estimated [IMCL]/ [EMCL]. FOM underestimated [IMCL]/ [EMCL] by 10 – 20%.

Figure 4.

Figure 4

Open in a new tab

Comparison of Voigt Fit and Fiber Orientation Modeling. Simulated spectra with [IMCL]/ [EMCL] = 0.5 were generated using different central angles and dispersions. Typical spectra are shown in Figure 3. When the spectra were analyzed using Voigt lineshape, [IMCL]/ [EMCL] was overestimated except when angular dispersion was small (upper panel). There was no effect of dispersion on the accuracy of estimated [IMCL]/ [EMCL] using the FOM algorithm (lower panel).

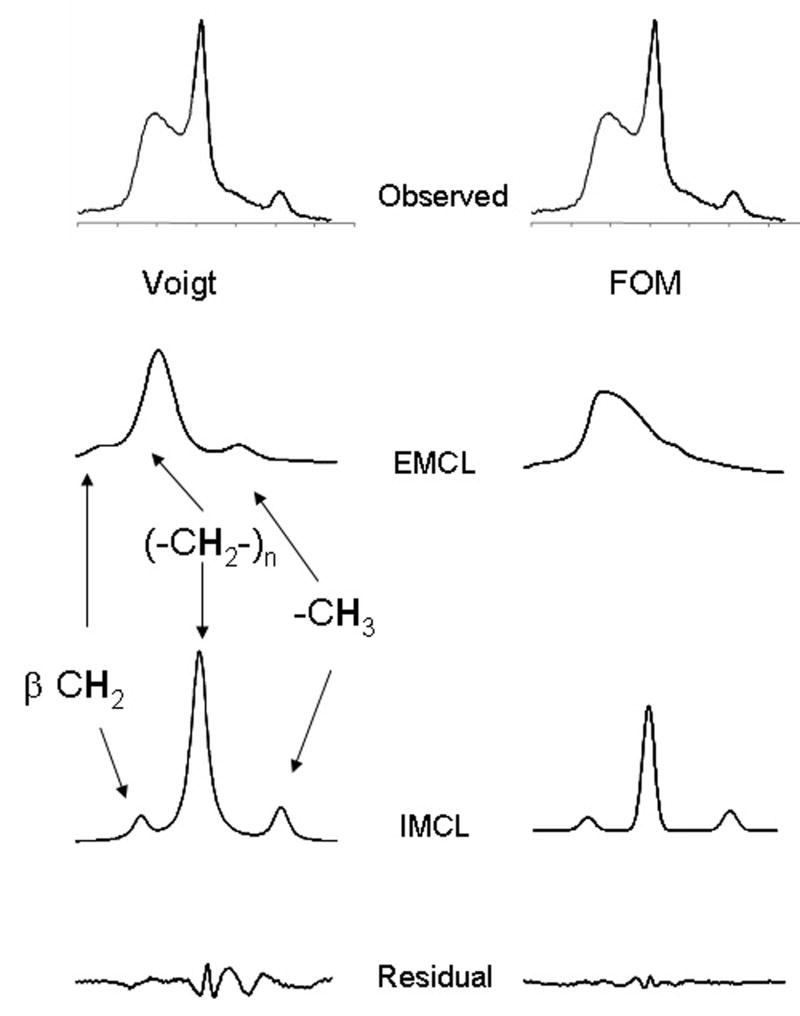
The difference in curve fitting by FOM compared to Voigt fit is illustrated in Figure 5, a spectrum from the soleus of a healthy volunteer. The observed spectrum from 0.5 – 1.9 ppm is shown in the upper panel. The estimated EMCL and IMCL signals from methyl, bulk methylene (-CH2-)n and CH2 β to COO, as well as the residual, are shown assuming Voigt lineshape. There were two effects of FOM. The residual was reduced, but more significantly the estimated [IMCL]/ [EMCL] was reduced from 0.91 to 0.25, a rather dramatic difference. In this example the dominant orientation (α) of extracellular triglycerides was 23° relative to Bo with a dispersion width (β) of 38°.

Figure 5.

Figure 5

Open in a new tab

Analysis of a 1H NMR Spectrum Using a Voigt Function vs. Fiber Orientation Modeling. The 1H NMR spectrum between 0.6 and 1.9 ppm from the gastrocnemius was fit using a Voigt function (left panel) and FOM (right panel).

[IMCL]/ [EMCL] was measured by Voigt fitting and by FOM in all subjects in both gastrocnemius and soleus. The average [IMCL]/ [EMCL] was 0.41 ± 0.31 (mean ± s.d.) in the gastrocnemius and 0.67 ± 0.26 in the soleus when spectra were analyzed by Voigt fitting. However, the average value for [IMCL]/ [EMCL] was significantly lower in both gastrocnemius (0.18 ± 0.11) and in soleus (0.29 ± 0.06) when fit with FOM. In both muscle groups, FOM returned a value for [IMCL]/[EMCL] that was about 44% of the results from conventional fitting and the variance was smaller. Presumably the amount of extracellular fat in each voxel was roughly similar since we followed the standard practice of selecting “lean” voxels for data acquisition. The fact that [IMCL]/ [EMCL] was significantly lower when estimated by FOM compared to a symmetric function suggests that the overestimation of [IMCL] when fit with a symmetric function was due to selection of regions with variable fiber orientations.

The ratio [IMCL]/[EMCL] was determined because signal from lipids in both compartments generally overlap and must be fitted. However, the most interesting biological information is probably not this ratio but rather the concentration of intracellular lipids. Using the creatine signal as an internal concentration standard and assuming [creatine] is 30 mmol/kg wet weight in healthy subjects (2), the concentration of IMCL was 8.9 ± 8.4 mmol/kg wet weight in the gastrocnemius and 10.5 ± 3.4 mmol/kg wet weight in the soleus from analysis with the Voigt lineshape. Using FOM, the concentration of IMCL was significantly lower in both muscle groups, 3.9 ± 2.1 mmol/kg wet weight in the gastrocnemius and 4.8 ± 2.2 mmol/kg wet weight in the soleus.

Discussion

The current work was motivated by large residuals evident when fitting 1H NMR spectra of gastrocnemius or soleus at 7T using a Voigt lineshape. Other investigators previously have observed asymmetry in the EMCL methylene resonance. Steidle et al. suggested a method of separating IMCL from an overlapping EMCL signal by estimating magnetic field distribution with a reference spectrum obtained from bone marrow and assuming that the IMCL signal had the same linewidth as an aqueous metabolite, creatine (24). Weis et al. obtained a reference EMCL spectrum by fitting a series of pure EMCL spectra from bone marrow and subcutaneous fat (15). This approach again required a reference spectrum from a different anatomical region. Fiber orientation modeling (FOM) is an alternative that does not require a reference spectrum or prior knowledge of the linewidth of the IMCL signal.

FOM is founded on a standard theoretical model (26) demonstrating that the interior field in a cylinder is sensitive to orientation relative to Bo. Using this approximation it is practical to estimate the orientation of EMCL lipids in single-voxel spectra and to remove the effects of overlap when calculating [IMCL]. The results with FOM confirm the general consensus that spectra from the anterior tibialis (where the muscle fibers are predominantly parallel to Bo) may be analyzed confidently with symmetrical lineshapes (13). In simulations, with a dominant angle of ~ 10° or less relative to the applied field and little dispersion, Voigt lineshape accurately determined IMCL/EMCL ratio. Even at a dispersion of 20° with a dominant angle parallel to Bo, Voigt lineshape analysis was accurate. In additional simulations (data not shown) the linewidth and lineshape (Gaussian vs. Lorentzian) of the EMCL and IMCL signals had little effect on the accuracy of IMCL estimates with a dominant angle less than 10° and little dispersion.

The calculated [IMCL] in human subjects using FOM was less than half the value calculated using a Voigt lineshape in our study. The [IMCL] in soleus observed using FOM, about 4.8 mmol/kg wet weight, is also somewhat less than the values reported at lower fields where [IMCL] was 10.7 mmol/kg wet weight (at 1.5 T, ref. 11), 10.3 mmol/kg wet weight (at 1.5 T, ref. 20), or 7.6 mmol/kg wet weight (at 4.0 T, ref. 19). Hwang et al., working at 4.0 T utilizing Gaussian lineshapes, reported [IMCL] of 4.8 mmol/kg wet weight, identical to our finding (21). However, the linewidth of the IMCL signal was not determined by fitting but rather was fixed at the linewidth of the methyl resonance of creatine, a process that conceivably reduces the estimated area of the IMCL signal.

Multiple laboratories have shown that the amplitude of the resonance assigned to IMCL methylene protons is increased in subjects with insulin resistance, and high concentrations of IMCL may predispose a person to type 2 diabetes (22, 23, 30). Somewhat paradoxically, the amplitude of the signal assigned to IMCL methylene protons is also increased among highly-trained endurance athletes who are exquisitely sensitive to insulin (30). The relevance of the current results at 7T to studies at lower field is unknown, but these data stress that the three-dimensional structure of fat in the extracellular compartment strongly influence the apparent quantity of IMCL if the spectra are fit using conventional symmetric lineshapes.

Acknowledgments

This study was supported by the National Institutes of Health (NIH-RR02584) and the Department of Defense (W81XWH-06-2-0046). Jeannie Davis provided outstanding support for the studies with human subjects.

References

  • 1.Schick F, Eismann B, Jung WI, Bongers H, Bunse M, Lutz O. Comparison of localized proton NMR signals of skeletal muscle and fat tissue in vivo: two lipid compartments in muscle tissue. Magn Reson Med. 1993;29:158–67. doi: 10.1002/mrm.1910290203. [DOI] [PubMed] [Google Scholar]
  • 2.Boesch C, Machann J, Vermathen P, Schick F. Role of proton MR for the study of muscle lipid metabolism. NMR Biomed. 2006;19:968–88. doi: 10.1002/nbm.1096. [DOI] [PubMed] [Google Scholar]
  • 3.Boesch C. Musculoskeletal spectroscopy. J Magn Reson Imaging. 2007;25:321–38. doi: 10.1002/jmri.20806. [DOI] [PubMed] [Google Scholar]
  • 4.Boesch C, Slotboom H, Hoppeler H, Kreis R. In vivo determination of intra-myocellular lipids in human muscle by means of localized 1H-MR-spectroscopy. Magn Reson Med. 1997;37:484–493. doi: 10.1002/mrm.1910370403. [DOI] [PubMed] [Google Scholar]
  • 5.Klein MP, Phelps DE. Evidence against orientation of water in rat phrenic nerve. Nature. 1969;224:70–1. doi: 10.1038/224070a0. [DOI] [PubMed] [Google Scholar]
  • 6.Barbara TM. Cylindrical demagnetization fields and microprobe design in high-resolution NMR. J Magn Reson Series A. 1994;109:265–269. [Google Scholar]
  • 7.Chu SC, Xu Y, Balschi JA, Springer CS., Jr Bulk magnetic susceptibility shifts in NMR studies of compartmentalized samples: use of paramagnetic reagents. Magn Reson Med. 1990;13:239–62. doi: 10.1002/mrm.1910130207. [DOI] [PubMed] [Google Scholar]
  • 8.Ulrich R, Glaser RW, Ulrich AS. Susceptibility corrections in solid state NMR experiments with oriented membrane samples. Part II:theory. J Magn Reson. 2003;164:115–27. doi: 10.1016/s1090-7807(03)00208-8. [DOI] [PubMed] [Google Scholar]
  • 9.Boesch C, Decombaz J, Slotboom J, Kreis R. Observation of intramyocellular lipids by means of 1H magnetic resonance spectroscopy. Proc Nutr Soc. 1999;58:841–50. doi: 10.1017/s0029665199001147. [DOI] [PubMed] [Google Scholar]
  • 10.Szczepaniak LS, Dobbins RL, Stein DT, McGarry JD. Bulk magnetic susceptibility effects on the assessment of intra- and extramyocellular lipids in vivo. Magn Reson Med. 2002;47:607–10. doi: 10.1002/mrm.10086. [DOI] [PubMed] [Google Scholar]
  • 11.Szczepaniak LS, Babcock EE, Schick F, Dobbins RL, Garg A, Burns DK, McGarry JD, Stein DT. Measurement of intracellular triglyceride stores by 1H spectroscopy: validation in vivo. Am J Physiol. 1999;276:E977–89. doi: 10.1152/ajpendo.1999.276.5.E977. [DOI] [PubMed] [Google Scholar]
  • 12.Kreis R, Boesch C. Spatially localized, one- and two-dimensional NMR spectroscopy and in vivo application to human muscle. J Magn Reson B. 1996;113:103–18. doi: 10.1006/jmrb.1996.0163. [DOI] [PubMed] [Google Scholar]
  • 13.Machann J, Haring H, Schick F, Stumvoll M. Intramyocellular lipids and insulin resistance. Diabetes Obes Metab. 2004;6:239–48. doi: 10.1111/j.1462-8902.2004.00339.x. [DOI] [PubMed] [Google Scholar]
  • 14.Howald H, Boesch C, Kreis R, Matter S, Billeter R, Essen-Gustavsson B, Hoppeler H. Content of intramyocellular lipids derived by electron microscopy, biochemical assays, and (1)H-MR spectroscopy. J Appl Physiol. 2002;92:2264–72. doi: 10.1152/japplphysiol.01174.2001. [DOI] [PubMed] [Google Scholar]
  • 15.Weis J, Courivaud F, Hansen MS, Johansson L, Ribe LR, Ahlstrom H. Lipid content in the musculature of the lower leg: evaluation with high-resolution spectroscopic imaging. Magn Reson Med. 2005;54:152–8. doi: 10.1002/mrm.20518. [DOI] [PubMed] [Google Scholar]
  • 16.Larson-Meyer DE, Newcomer BR, Hunter GR. Influence of endurance running and recovery diet on intramyocellular lipid content in women: a 1H NMR study. Am J Physiol Endocrinol Metab. 2002;282:E95–E106. doi: 10.1152/ajpendo.2002.282.1.E95. [DOI] [PubMed] [Google Scholar]
  • 17.Befroy DE, Petersen KF, Dufour S, Mason GF, de Graaf RA, Rothman DL, Shulman GI. Impaired mitochondrial substrate oxidation in muscle of insulin-resistant offspring of type 2 diabetic patients. Diabetes. 2007;56:1376–81. doi: 10.2337/db06-0783. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Petersen KF, Dufour S, Befroy D, Garcia R, Shulman GI. Impaired mitochondrial activity in the insulin-resistant offspring of patients with type 2 diabetes. N Engl J Med. 2004;350:664–71. doi: 10.1056/NEJMoa031314. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19.Cui MH, Hwang JH, Tomuta V, Dong Z, Stein DT. Cross contamination of intramyocellular lipid signals through loss of bulk magnetic susceptibility effect differences in human muscle using (1)H-MRSI at 4 T. J Appl Physiol. 2007;103:1290–8. doi: 10.1152/japplphysiol.01088.2006. [DOI] [PubMed] [Google Scholar]
  • 20.Rico-Sanz J, Thomas EL, Jenkinson G, Mierisová S, Iles R, Bell JD. Diversity in levels of intracellular total creatine and triglycerides in human skeletal muscles observed by (1)H-MRS. J Appl Physiol. 1999;87:2068–72. doi: 10.1152/jappl.1999.87.6.2068. [DOI] [PubMed] [Google Scholar]
  • 21.Hwang JH, Pan JW, Heydari S, Hetherington HP, Stein DT. Regional differences in intramyocellular lipids in humans observed by in vivo 1H-MR spectroscopic imaging. J Appl Physiol. 2001;90:1267–74. doi: 10.1152/jappl.2001.90.4.1267. [DOI] [PubMed] [Google Scholar]
  • 22.Krssak M, Falk Petersen K, Dresner A, DiPietro L, Vogel SM, Rothman DL, Roden M, Shulman GI. Intramyocellular lipid concentrations are correlated with insulin sensitivity in humans: a 1H NMR spectroscopy study. Diabetologia. 1999;42:113–6. doi: 10.1007/s001250051123. [DOI] [PubMed] [Google Scholar]
  • 23.Jacob S, Machann J, Rett K, Brechtel K, Volk A, Renn W, Maerker E, Matthaei S, Schick F, Claussen CD, Haring HU. Association of increased intramyocellular lipid content with insulin resistance in lean nondiabetic offspring of type 2 diabetic subjects. Diabetes. 1999;48:1113–9. doi: 10.2337/diabetes.48.5.1113. [DOI] [PubMed] [Google Scholar]
  • 24.Steidle G, Machann J, Claussen CD, Schick F. Separation of intra- and extramyocellular lipid signals in proton MR spectra by determination of their magnetic field distribution. J Magn Reson. 2002;154:228–35. doi: 10.1006/jmre.2001.2481. [DOI] [PubMed] [Google Scholar]
  • 25.Vermathen P, Boesch C, Kreis R. Mapping fiber orientation in human muscle by proton MR spectroscopic imaging. Magn Reson Med. 2003;49:424–32. doi: 10.1002/mrm.10396. [DOI] [PubMed] [Google Scholar]
  • 26.Haacke EM, Brown RW, Thompson MR, Venkatesan R. Magnetic Resonance Imaging: Physical Principles and Sequence Design. Wiley-Liss; New York: 1999. pp. 749–757. [Google Scholar]
  • 27.Vermathen P, Kreis R, Boesch C. Distribution of intramyocellular lipids in human calf muscles as determined by MR spectroscopic imaging. Magn Reson Med. 2004;51:253–62. doi: 10.1002/mrm.10721. [DOI] [PubMed] [Google Scholar]
  • 28.Field CJ, Angel A, Clandinin MT. Relationship of diet to the fatty acid composition of human adipose tissue structural and stored lipids. Am J Clin Nutr. 1985;42:1206–20. doi: 10.1093/ajcn/42.6.1206. [DOI] [PubMed] [Google Scholar]
  • 29.Soher BJ, Hurd RE, Sailasuta N, Barker PB. Quantitation of automated single-voxel proton MRS using cerebral water as an internal reference. Magn Reson Med. 1996;36:335–9. doi: 10.1002/mrm.1910360302. [DOI] [PubMed] [Google Scholar]
  • 30.van Loon LJ, Goodpaster BH. Increased intramuscular lipid storage in the insulin-resistant and endurance-trained state. Pflugers Arch. 2006;451:606–16. doi: 10.1007/s00424-005-1509-0. [DOI] [PubMed] [Google Scholar]

RESOURCES