A Simple and Accurate Equation for Peak Capacity Estimation in Two Dimensional Liquid Chromatography

Abstract

Two dimensional liquid chromatography (2DLC) is a very powerful way to greatly increase the resolving power and overall peak capacity of liquid chromatography. The traditional “product rule” for peak capacity usually overestimates the true resolving power due to neglect of the often quite severe under-sampling effect and thus provides poor guidance for optimizing the separation and biases comparisons to optimized one dimensional gradient liquid chromatography. Here we derive a simple yet accurate equation for the effective two dimensional peak capacity that incorporates a correction for under-sampling of the first dimension. The results show that not only is the speed of the second dimension separation important for reducing the overall analysis time, but it plays a vital role in determining the overall peak capacity when the first dimension is under-sampled. A surprising subsidiary finding is that for relatively short 2DLC separations (much less than a couple of hours), the first dimension peak capacity is far less important than is commonly believed and need not be highly optimized, for example through use of long columns or very small particles.

Introduction

High-resolution analytical techniques are essential when dealing with complex samples^{1, 2}. No single technique has the ability to fully handle samples such as those encountered in proteomic³ and metabolomic research⁴; however, two dimensional liquid chromatography (2DLC) is attracting increasing attention due to its very high resolving power. In principle, 2DLC can greatly increase the peak capacity of HPLC over highly optimized one dimensional HPLC. This improvement results predominantly from the multiplicative relationship between the peak capacities of the first and second dimension separations and the total 2DLC peak capacity which leads to the so-called “peak capacity product rule” discussed by Karger, Snyder and Horvath⁵, and later elaborated by Giddings⁶. Under ideal conditions, the total peak capacity of a two dimensional liquid chromatography (n_c,2D) is the product of the peak capacities of the first (¹n_c) and the second dimensions (²n_c)⁶.

$$n_{c,2D}={}^{1}n_c\times {}^{2}n_c$$ (1)

However, the 2DLC peak capacity given by eq 1 will not be fully realized whenever the first dimension separation is under-sampled as is the case in a majority of experimental work². To understand under-sampling effects it is perhaps best to think of a two dimensional separation as a three step process. The first step is the first dimension separation, the second is the “sampling” of the first dimension separation, and the third is the second dimension separation of the sample of first dimension effluent collected and transferred to the second dimension during the sampling step. Clearly the consequences of the sampling step are not reflected in eq 1. Each of these three operations has an impact on the overall 2DLC peak capacity, and in computing realistic estimates of the 2DLC peak capacity we need to correct for the loss in peak capacity due to the sampling step.

Choosing the proper sampling time is very important in practical 2DLC work. Murphy, Schure and Foley (M-S-F)⁷ developed a quantitative approach to estimating a sampling correction factor which has become the basis for a widely accepted sampling criterion^8-10; it states that the effluent must be sampled at least three times over the 8σ base width of a first dimension peak to avoid serious loss of resolution between a pair of peaks when the first dimension separation contributes heavily to the overall resolution. The work of Murphy et al. was extended by Seeley¹⁰, whose results for the 100% duty cycle case fully corroborate the findings of Murphy et al. Horie et al.⁹ also investigated the under-sampling problem and concluded that a favorable sampling time would be around 2.2 to 4σ of a first dimension peak to realize a 2D peak capacity given by eq 1. It is important to understand that all of this work^{7, 9, 10} is based on the impact of under-sampling on a single pair of equal size peaks. Recently, Davis et al. significantly refined the M-S-F work⁸ by taking quite a different approach to estimating the effect of sampling. In essence their results are based on the simulation of entire multi-constituent 2DLC chromatograms, and include the effect of random retention time coordinates, random peak heights and the effect of under-sampling on the number of observed peaks. Thus their results are based on the effect of under-sampling on the overall chromatogram and not just a single pair of peaks. Their quantitative results differed only slightly from those of Murphy in the region of fast sampling but significant differences were seen in the severely under-sampled region. Since it is the first dimension that is under-sampled, although the effect propagates through both dimensions, the correction factor is applied when calculating the first dimension peak capacity. The equation of Davis is best written for present purposes as:

$${}^{1}n_c^{\prime }=\frac{{}^{1}n_c}{\beta }=\frac{{}^{1}n_c}{\sqrt{1+3.35\ast ({}^{t}s∕{}^{1}W{)}^2}}$$ (2)

Here ¹n_c represents the first dimension peak capacity and ${}^{1}n_c^{\prime }$ is the corrected peak capacity at the actual sampling rate and should be used in eq 1. The under-sampling correction factor (β) is defined implicitly. The numerical factor in the denominator results from rearranging an equation given by Davis et al. The terms t_s and ¹w are the sampling time and first dimension peak width taken as 4*¹σ such that the resolution of adjacent peaks will be unity.

Eq 2 is central to this work wherein the goal is to investigate the effective 2DLC peak capacity of the entire system, realizing that there is a strong interaction between the sampling time and other system parameters, such as the first dimension gradient time (¹t_g) and first dimension peak width, and thus with the first dimension peak capacity. Here we introduce a simple yet accurate model for estimating the total 2DLC peak capacity that reveals seemingly counterintuitive insights into the process of optimizing 2DLC separations.

Theory

We assume that gradient elution is used in both dimensions, as is typically the case when dealing with complex samples. In eq 2 we take the first dimension sampling time (t_s) to be equal to the second dimension separation cycle time (²t_c), which is the sum of the second dimension gradient time (²t_g) and system re-equilibration time (²t_reeq)

$$t_s={}^{2}t_c={}^{2}t_g+{}^{2}t_{reeq}$$ (3)

According to Snyder¹¹, the peak capacity of a gradient separation can be estimated by eq 4:

$${}^{1}n_c=1+\frac{{}^{1}t_g}{W}\cong \frac{{}^{1}t_g}{W}$$ (4)

where the time window for the separation is made a maximum by taking it as t_g Substitution of eqs 3 and 4 in our implicit eq for β gives the following:

$$\beta =\sqrt{1+3.35{\left[\frac{{}^{2}t_c{}^{1}n_c}{{}^{1}t_g}\right]}^2}$$ (5)

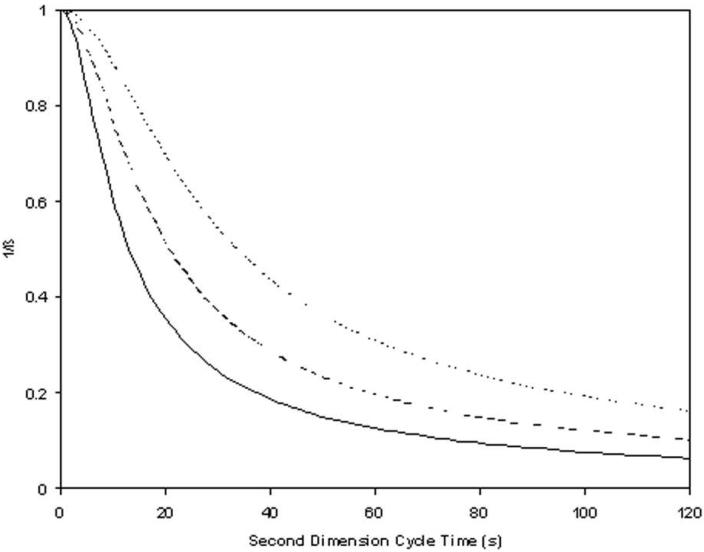
A plot of 1/β vs. ²t_c is shown in Figure 1. It is evident that at very short second dimension cycle times the correction factor approaches unity but becomes quite large at long second dimension cycle times. It is convenient to note here that when sampling is quite slow, that is, when the second term under the root is dominant, the sampling correction factor reaches the limiting form:

$$\beta \approx 1.83\frac{{}^{2}t_c{}^{1}n_c}{{}^{1}t_g}$$ (6)

We now combine eqs 1, 2 and 5, and an important result for the effective 2D peak capacity (defined as $n_{c,2D}^{\prime }$) is obtained:

$$n_{c,2D}^{\prime }=\frac{{}^{1}n_c\times {}^{2}n_c}{\sqrt{1+3.35{\left(\frac{{}^{2}t_c{}^{1}n_c}{{}^{1}t_g}\right)}^2}}$$ (7)

This equation clearly shows that the dependence of the total 2DLC peak capacity on the first dimension peak capacity (¹n_c) is weakened when under-sampling occurs and the denominator in eq 7 becomes bigger than unity. As the degree of under-sampling worsens the dependence of $n_{c,2D}^{\prime }$ on ¹n_c becomes less than first power. When we take the limit as under-sampling becomes very severe (and combine eqs 1, 2 and 6) we see that the dependence of the total 2DLC peak capacity on the first dimension peak capacity drops out entirely.

$$n_{c,2D}^{\prime }\cong \frac{{}^{1}t_g{}^{2}n_c}{1.83{}^{2}t_c}$$ (8)

Figure 1.

1/β versus second dimension cycle time (s) based on eq 5. The first dimension gradient times are 15 min (−−−−), 30 min (− − −) or 60 min (.......). The corresponding first dimension peak capacity at each first dimension gradient time is the corresponding real peak capacity from Table 1.

We refer to eq 8 as the approximate model. Its accuracy and implications are discussed below. In the derivation of eq 8 we have assumed that the retention mechanisms of the first and second dimension separations are not correlated. While we are certainly aware that this is rarely strictly the case in practice¹², we expect no qualitative differences when the two separation mechanisms are not totally orthogonal (uncorrelated) and only small quantitative differences when the model is applied to somewhat correlated data.

Experimental

Materials and Reagents

All solutes were of reagent grade or better and were used without further purification. Alkylphenones (acetophenone, butyrophenone, valerophenone, hexanophenone and heptanophenone) were purchased from Aldrich (Milwaukee, WI, USA). Acetonitrile was obtained from Burdick and Jackson (Muskegon, MI). HPLC grade water was obtained in-house from a Barnstead Nanopure deionizing system (Dubuque, IA). This water was boiled to remove carbon dioxide and cooled to room temperature before use. All pure solvents were filtered through a 0.45-μm nylon filtration apparatus (Lida Manufacturing Inc., Kenosha, WI) before use. All eluent mixtures were prepared gravimetrically.

Measurement of Second Dimension Peak Capacity

In the work reported here the peak capacities of the second dimension column were measured with a Halo C₁₈ type phase (MacMod Analytical, Chadds Ford. PA, 2.7 μm particle size, 90 Å pore size, 33 mm × 2.1 mm i.d.). Absorbance spectra were collected at a rate of 80 Hz. Each second dimension separation in the 2DLC separations consisted of a reversed-phase gradient from 20 to various final percentages of B solvent, where the A solvent was 0.1% trifluoroacetic acid in water and the B solvent was pure acetonitrile. The column was held at 100°C by use of the heater described in ref. 13. The final %B was varied with the gradient time to maximize the retention window. The total gradient cycle times used were 12, 21, 42, 63, 105, 147 and 189 s, with the corresponding gradient times (t_g) of 9, 18, 39, 60, 102, 144 and 186 s; and the re-equilibration time for the second dimension HPLC column was fixed at 3 s. The corresponding final %B values were 66.5, 55, 45, 37, 30 26 and 23 %, respectively. The 3-s re-equilibration time corresponds to roughly two column volumes of solvent; one column volume is required to flush strong (ACN-rich) solvent out of the tubing, and the second column volume is required to actually re-equilibrate the HPLC column to the extent that the repeatability of retention time in the second dimension is satisfactory (0.002 min standard deviation)^{13, 14}. A flow rate of 3.0 mL/min. was used throughout the experiment. LabVIEW 6.0 software and a 6024E data acquisition board (National Instruments Inc., Austin, TX) were used to control the coordination of the first dimension system, the 10-port valve, second dimension pumping system, and photodiode array detector using simple programs written in-house.

Results and Discussion

Experimental Peak Capacity Data

In the following section we use experimental data obtained under conditions typical of 1D and 2DLC separations for low molecular weight compounds to compare the various ways of calculating the 2DLC peak capacity. For both the first and second dimensions of the 2DLC system we use a set of compounds that spans the range in retention typically observed in 2DLC separations of complex natural materials (e.g., urine, aqueous plant extracts).

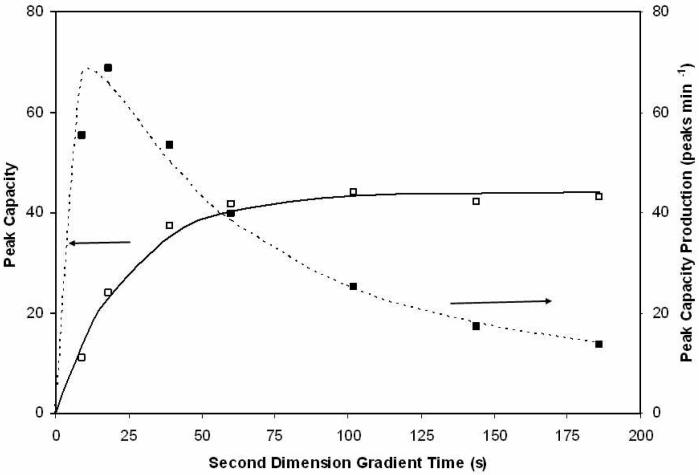
A homologous series of alkylphenones was used for measuring the second dimension peak capacity as a function of the second dimension cycle time, using the method of Wang and coworkers¹⁵. Figure 2 shows the observed peak capacities and the peak capacity production rates (units of peak capacity per min of gradient time). Inspection shows that the peak capacity measurements are reasonably well fit (solid line) by eq 9 which was chosen purely for convenience because it looked like it would fit the data; it has no theoretical significance.

$${}^{2}n_c=44.05\times (1-\exp (-0.04\ast {}^{2}t_g)$$ (9)

The absolute peak capacity increases quite rapidly at first, but reaches a plateau after about 1 min. The peak capacity production rate reaches a maximum at a gradient time of about 15 to 20 s. The peak capacity computed using eq 9 is used as the second dimension peak capacity for the calculation of the 2DLC peak capacity shown below.

Figure 2.

Second dimension peak capacity and second dimension peak capacity production rate versus the second dimension gradient time. Points are the measured values and the curves are the least squares fit based on eq 9. Solid line (−−−−) is the peak capacity (fit to eq 9), dashed line (.......) is the peak capacity production (fit to eq 9/²t_g).

The two different types of first dimension peak capacities used here (see Table 1) were reported previously in a comparative study of fully optimized 1D and of experimentally feasible 2D liquid chromatography¹⁶. We believe these peak capacities are reasonably representative of the range of what can be achieved in practice for current HPLC systems. We have used two different measured values of the first dimension peak capacity: 1) the peak capacity of the first dimension found when a 2DLC system was really implemented (from ref. 16, Table 3, row 9 referred to herein as the real peak capacity), and 2) the peak capacity of a highly optimized (column length, flow rate, and final eluent composition) 1DLC gradient separation for the same mixture of compounds as separated in the same gradient time (from ref. 16, Table 1, row 8) as in the 2DLC separation as actually performed. We refer to these two first dimension peak capacities as `real' and `optimized', respectively. The substantial difference between the `optimized' and `real' values reflects the fact that there are far more constraints which must be met when dealing with the first dimension separation of a 2DLC system as compared to a 1DLC separation by itself. For example, the flow rate through the first dimension column is tightly coupled to the volume of sample injected into the second dimension, and this tradeoff can essentially force the use of a sub-optimum flow rate, at least from the perspective of optimizing the first dimension peak capacity under gradient elution conditions.

Table 1.

First dimension peak capacities for low molecular weight compounds^a

Analysis time (min)b	Gradient time (min)c	Optimized Peak Capacity	Real Peak Capacity
15	12	136	52
30	24	148	66
60	52	157	88

^aData are from ref. 16

^bTotal analysis time which is the sum of the first dimension gradient time and reequilibration time

^cReal gradient time

Comparison of methods of computing 2DLC peak capacity and accuracy of the approximate model

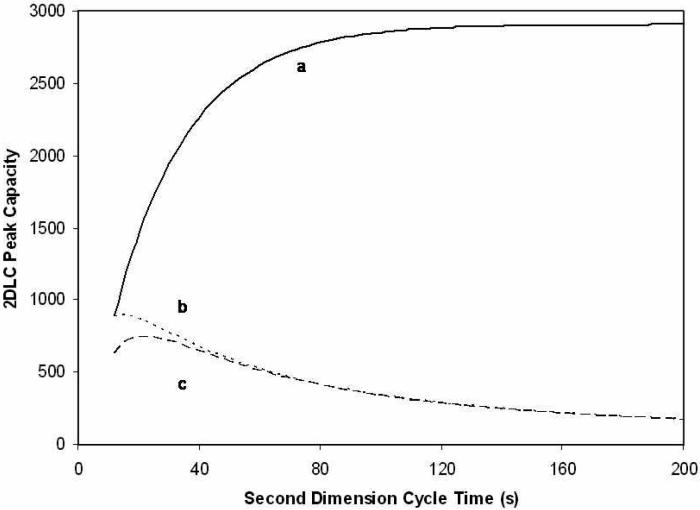
Inspection of Figure 3 shows that the uncorrected product rule (eq 1) grossly overestimates the effective 2DLC peak capacity (see eq 7) while the approximate model (eq 8), although simple, agrees quite well with the eq 7 over a wide range in second dimension cycle times. Clearly the product rule is only accurate when rather fast sampling rates are employed. The general shape of curves b-c (see Figure 3) results from the initial increase in second dimension peak capacity with second dimension cycle time followed by a decline in the effective first dimension peak capacity due to under-sampling which is accounted for by the first dimension sampling correction (see Figure 1). As the second dimension gradient time increases beyond a certain point the first dimension becomes seriously under-sampled, thus, the product rule becomes progressively less accurate and eq 8 becomes more accurate. Unfortunately many workers appear to use the uncorrected product rule quite frequently even when it is grossly wrong¹⁷.

Figure 3.

2DLC peak capacity versus second dimension cycle time (s) at a first dimension cycle time of 30 min.

(a) Computed using the uncorrected product rule and the actual first dimension peak capacity values from Table 1.

(b) Computed using eq 8 and the real first dimension peak capacity.

(c) Computed using eq 7 and the real first dimension peak capacity.

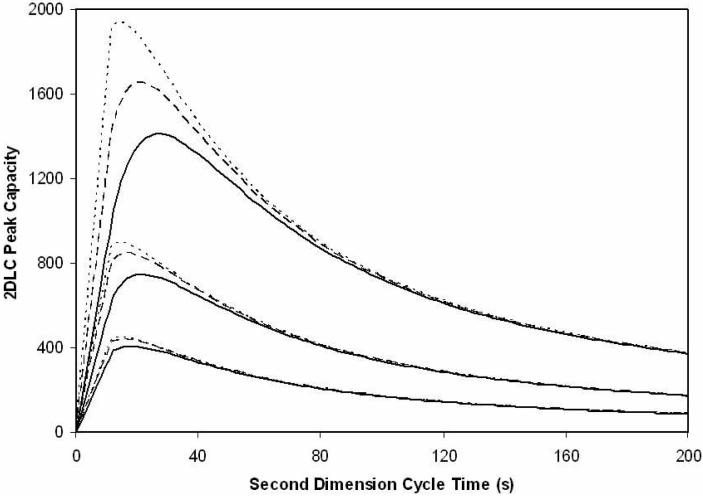
Inspection of Figure 4 shows that the curves computed from eq 8 are quite close to those based on eq 7. Comparing the two equations in question it is evident that the approximate model will be more accurate when 3.35${\left(\frac{{}^{2}t_c{}^{1}n_c}{{}^{1}t_g}\right)}^2$ is much greater than unity. Thus, the extent to which the approximate model overestimates the real results will increase as the second dimension cycle time becomes shorter or as the first dimension gradient time becomes longer. This is why the larger differences between the eqs 7 and 8 are seen at the shorter second dimension gradient times and at the longer first dimension gradient times. However, even the largest discrepancy over the range of conditions examined in this work is only about 30%. At the relatively long second dimension cycle time and the shortest first dimensions gradient time, the approximation model is surprisingly accurate.

Figure 4.

Plot of 2DLC peak capacity versus the second dimension cycle time (s). The curves denoted optimized (− − −) and real (−−−−) are based on the optimized and real first dimension peak capacities given in Table I in conjunction with eq 7. The curves denoted approximate (.......) are based on the real first dimension peak capacity and eq 8. The bottom set of three curves correspond to a first dimension cycle time of 15 min, the central three curves correspond to a first dimension cycle time of 30 min, and the top three curves correspond to a first dimension cycle time of 60 min.

Dependence of 2DLC peak capacity on optimization of the first dimension separation

The true importance of Figure 4 is the surprising fact that the value of the first dimension peak capacity which is the cause of the difference between what we have called the “real” and “optimized” curves has such a small effect on the total 2D peak capacity. This can be seen by comparing the optimized curve to the real curve. For example, if we look at the 30 min analysis time comparisons, there is little difference whether one uses the optimized (¹n_c = 148) or the real, actually achievable peak capacity (¹n_c = 66). That is, a more than two-fold increase in the first dimension peak capacity has almost no impact on the effective 2D peak capacity despite the very high speed of the second dimension separation. Especially when we look at a second dimension cycle time of 60 s or longer, there is virtually no difference. This difference increases as we shorten the second dimension cycle time; however, even at the shortest second dimension cycle time (12 s), the total 2D peak capacity only increases from 563 to 745, a 30% increase. At 21 s, where the maximum total 2D peak capacity is achieved, the total 2D peak capacity increase from 750 to 850, a mere 13% increase.

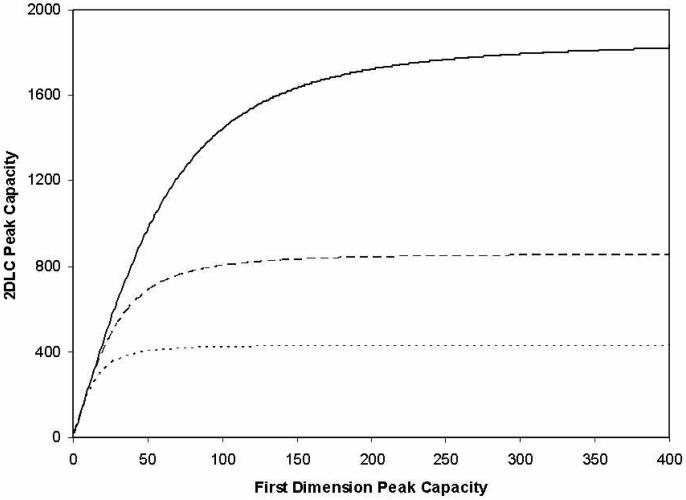
Figure 5 demonstrates the minor influence of the first dimension peak capacity on the overall 2DLC peak capacity. The 2DLC peak capacity increases linearly with the first dimension peak capacity only when it is small, and after a certain point, the overall 2DLC peak capacity becomes independent of the first dimension peak capacity. What this clearly says is that for relatively fast 2DLC separations (much less than a couple of hours) the first dimension separation does not need to be rigorously optimized, because the values of ¹n_c that correspond to the transition regions in Figure 5 are easily achieved using ordinary HPLC materials and equipment, and less than fully optimized separations. It will be a waste of effort to use a super high resolution system to provide excellent peak capacity in the first dimension when the second dimension cycle time is slow. Inspection of the literature makes it clear that often more effort is put into the first dimension than is required^18-21.

Figure 5.

Contribution of first dimension peak capacity to the overall 2DLC peak capacity for first dimension cycle times of 60 (−−−−), 30 (− − −) and 15 (.......) min.

Implications of the simplified approximation

Eq 8 implies several important ideas related to maximizing the total 2D peak capacity. First, the overall 2D peak capacity is approximately independent of the first dimension peak capacity provided that it is above a certain `critical' level such that the quantity 3.35${\left(\frac{{}^{2}t_c{}^{1}n_c}{{}^{1}t_g}\right)}^2$ is substantially larger than unity; this `critical' value varies with the values of ¹t_g and ²t_c. Second, above this critical value, at fixed values of ²t_c and ²n_c, the 2DLC peak capacity increases linearly with first dimension gradient time. Lastly, at fixed values of ¹t_g the total 2DLC peak capacity increases in proportion to the second dimension peak capacity production rate (²n_c/²t_c). Since ²n_c/²t_c increases in proportion to ²n_c, we should try to optimize ²n_c by optimizing the particle size and type (e.g., pellicular vs. fully porous) and operating conditions (e.g., pressure, temperature) and by use gradient elution instead of isocratic elution.

Finally, the practical consequences of the curves in Figures 2 and 4 are striking. In Figure 2 we see that there is a maximum in ²n_c/²t_c at a gradient time of around 15 to 20 s, which also corresponds roughly to the maxima in the curves of Figure 4. This result implies that even though the deleterious effect of under-sampling the first dimension separation can be mitigated by decreasing ²t_c relative to ¹w, from the perspective of maximizing $n_{c,2D}^{\prime }$ this is not always the best idea. The tradeoff brought about by the sharp decrease in ²n_c/²t_c at small values of ²t_c (< 15 s) ultimately results in the sharp decrease in $n_{c,2D}^{\prime }$ at small values of ²t_c (see Figure 4). The optimum in ²n_c/²t_c at 15 to 20 s (see Figure 2) is fortuitously close to the gradient cycle time used in our own initial work on fast 2DLC^{22, 23}; this suggests that existing instrumentation (for the second dimension) will be quite adequate for a great deal of practical fast 2DLC, and that significant changes to pump design to make significantly faster second dimension separations (e.g., ²t_c < 10 s) possible are not warranted until the fundamental factors that control the position of the maximum in ²n_c/²t_c in Figure 2 are better understood and can be controlled. We point out that at these very short second dimension gradient cycle times, careful optimization of the gradient elution hardware is critical to avoid wasting a large portion of the cycle time in flushing out the gradient system and column re-equilibration. In this and much of our other work this system/column re-equilibration time has been 3 s, which we believe is close to the practical limit with the pumps used. The optimization of 2DLC separations involving isocratic separations will be treated in a separate, more extensive manuscript which is in preparation.

Conclusions

In this work a simple yet accurate equation is introduced for the a priori estimation of the overall peak capacity in dual gradient elution 2DLC. The model is robust and accurate especially with longer second dimension gradient time (> 1 min) and shorter first dimension gradient time (< 30 min). Compared to the uncorrected `product rule' usually used to estimate the 2DLC peak capacity, the new approach is more accurate under conditions of fast but practical (ca. 15-60 min) 2DLC. Although the accuracy of the simplified equation is tested with data based low molecular weight analytes we believe that qualitatively similar results will be found for separations of peptides.

The first rather surprising and quite important conclusion resulting from the approximate model is that the total 2DLC peak capacity is, over a fairly wide range in conditions, only weakly dependent on the first dimension peak capacity. With current technology it makes almost no sense when first dimension gradient times are 30 min or less to use very small particles or take other steps to improve the first dimension peak capacity above a value of about 50 to 100. Only in very slow (> 2 hour) 2DLC separations does it make sense to improve the first dimension peak capacity beyond what can currently be achieved under practical 2DLC conditions. Second, we conclude that the dependence of the productivity of the second dimension separation (peak capacity per unit of gradient cycle time) absolutely dictates the choice of the rate at which the first dimension separation should be sampled to maximize the total 2DLC peak capacity. Of greater practical consequence is the finding that the optimum values of the second dimension productivity occur at second dimension gradient cycle times on the order of 20 s which are within reach of existing instrumentation.

The new approximate model developed here provides a simple yet accurate means of accounting for the trade-offs encountered in the complex process of optimizing dual gradient 2DLC. It is now clear that the second dimension separation time must be properly optimized and thus be made quite fast, not only to improve the overall 2DLC analysis time, but also to maximize the overall 2DLC peak capacity.