Ants in rectangular arenas

Abstract

Although spatial cognition is studied by neuroscientists, psychologists, biologists and computer scientists, it suffers from a lack of integrative studies. The topic of geometry of space for instance, has been studied since twenty years only in vertebrates and only in artificial and visually poor environments. But recently, similar results have been obtained with ants, supporting the recent idea of global matching. Contrary to the other theories about geometry, global matching is parsimonious, testable in natural conditions and makes sense in an ecological context. Here, further investigations into the data obtained in ants describe and support a new concept for the global matching theory: the Mismatch Tolerance Threshold (MTT). This new idea can be tested in other species and we stress the importance of considering the whole paths displayed by the animals in future experiments.

How animals encode the visual shape of their environment has drawn an increasing interest since the seminal work of Cheng.¹ This topic is now studied across many vertebrate species² and several theories on how the geometry of space is extracted and encoded are debated.³ However, most of those studies were conducted in artificial rectangular arenas and little attention has been paid to the relevance of such spatial information in nature.⁴

Recently, Wystrach and Beugnon⁵ used Cheng's paradigm¹ to test a visual ant species (Gigantiops destructor) in the typical rectangular arena, a première among invertebrates. The results obtained with ants are similar to those of vertebrates but, without summoning theories about geometry, can be parsimoniously explained by a global matching hypothesis.⁵ The concept of global matching is simple and requires no feature extraction: the agent relies on a panoramic view previously stored at the goal location, and moves in order to minimize the mismatch between its current view and the memorized view. When the two views match, the goal is reached. Global matching can not only explain the results obtained in rectangular arenas⁶ but can also be applied in natural conditions⁷ (Wystrach et al., in preparation).

In nature, once a forager ant has caught a prey, it immediately runs back to its nest. In our laboratory experiments,⁵ the loaded ant was released at the centre of a rectangular arena and had to reach one of the four corners to get back to its nest. All four corners led to the nest.

When the rectangular arena was simply put on a table, all the tested ants spontaneously chose a particular corner and systematically returned to it, trial after trial (Fig. 1A). They could do so by using the extra-arena cues from the experimental room (above the walls of the arena). These results support a global matching hypothesis. The homing ant matches its current view with the one memorized during the previous trials (when it succeeded in reaching its nest), and thus always returns home via the same corner.

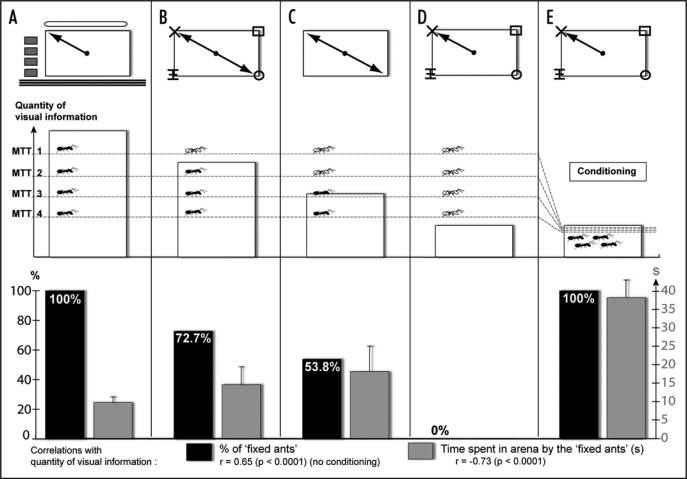
Figure 1.

This figure is divided horizontally in three different parts. The top part illustrates the different experimental conditions: (A) presence of conspicuous extra-arena cues; the ants systematically return to a preferred corner. (B) No extra-arena cues but black features (10 × 10 cm) emphasize the corners and the ants display a preference for two diagonally opposite corners. (C) Only the cue given by the shape of the rectangular arena is present and the ants display a preference for two diagonally opposite corners. (D and E) Same visual condition than in (B) but the ants use the subtle difference between the features to select a unique preferred corner. In (A–D) the four corners lead to the nest (spontaneous) whereas in (E), only one corner leads to the nest (conditioning). The middle part illustrates the concept of Mismatch Tolerance Threshold (MTT). The graph shows the assumed amount of visual information given by the global view in order to display the corner preferences illustrated in the top part. Four hypothetical MTTs are represented: depending on their MTT, the figured ants are black (fixed ants, display corner preferences) or white (random ants, display random corner choices). The bottom part presents the actual data. In black, the proportion of fixed ants (display the corner preference). In grey, the time spent by the fixed ants in the arena before reaching a corner. Both “time” and “% of fixed ants” are correlated to the amount of visual information (p < 0.0001).

When the plain white walls arena was covered by an opaque plastic dome, however, the ants could not see the extra-arena cues and had to rely on the shape of the arena only. Because it is a rectangle, each corner is indistinguishable from its diagonally opposite one. In this condition, only 53.8% of the ants managed to solve the task (i.e., displayed a preference for two diagonally opposite corners) (Fig. 1C). The others ants displayed random choices. This significant decrease of the number of ‘fixed ants’ is not surprising: the presence of the dome, in hiding the extra-arena cues, removes a lot of visual information. Here, most of the panoramic scene is just white, and the mismatch in the global view between pairs of corners from different diagonals becomes low. It is likely that all the ants matched their view from one trial to another. The 53.8% ‘fixed ants’ were subtle enough to detect that mismatch and thus returned systematically to two diagonally opposite corners; the other ants tolerated it and therefore displayed random choices.

A third group of ants was also tested within the dome, but in the presence of featural cues: one distinct black shape in each corner (Fig. 1B and D). Although they could discriminate the different features, no ant used them to systematically return in the same corner (Fig. 1D). This makes sense: as all the features together cover only 7% of the arena, therefore the mismatch in the global view between facing one corner and its diagonally opposite one is minor, and the ants paid no heed to it. However, the percentage of ants displaying a preference for one diagonal increased to 72.7% (Fig. 1B). This makes sense insofar as the presence of the black features in the corners outlined the rectangular shape of the arena better, and thus increased the mismatch between two corners from different diagonals.

Overall, in those three experiments, because all the corners led to the nest, the ants only needed to store and use views that were precise enough to lead them towards any corner. Yet individual differences appeared. Some ants spontaneously used more precise views than required, and returned systematically to the same corners. Interestingly, the relative frequencies of those ‘fixed ants’ across the different conditions reflect the quantity of information given by the global view (correlation r= 0.65411, p < 0.0001). It seems like each ant possesses a spontaneous “mismatch tolerance threshold”, which vary between individuals. Individuals with a high threshold tolerate high mismatch and thus, if the visual information is not obvious enough, display random choice. Individuals with a lower threshold, however, tolerate lesser mismatch and consequently, use more details of the visual information and systematically return to the same corners.

The question then arises as to whether that MTT is fixed by individual physiological factors, or is flexible and can be adapted to the situation. The next experiment gives the answer. The visual conditions were the same as in the experiment with the black features in the corner, but in this case, only one particular corner led to the nest (Fig. 1D). The ants were thus forced to use the subtle information given by the differences between the features in order to succeed. In the previous experiment, no ant chose a single corner spontaneously (Fig. 1D). But in the present case, they all did (Fig. 1E). Ants can therefore lower this “matching tolerance threshold” if required for reaching the nest. Why would the ants not always apply a low threshold? Probably because a low threshold costs in storing visual details, and the process of matching detailed views may be computationally intensive. Indeed, the subtler the visual information was (the harder the process of matching), the slower the ‘fixed ants’ were in choosing a corner (correlation inf/time = −0.7323, p < 0.0001).

The global matching hypothesis fits the present results remarkably well, and can explain most of the data in insect navigation.^8–10 It can also parsimoniously explain results obtained with vertebrates in rectangular arena¹¹ that other models cannot.³ Our concept of an adaptable “mismatch tolerance threshold” explains the use of featural details in a conditioning procedure, consistent with associative principles applied to spatial learning.¹² Furthermore, global matching can be applied as well in outdoor scenes⁷ and describes paths in addition to corner choices. In reality, an animal integrates information and makes decisions before even starting; it continues to do so while moving, until eventually reaching its goal. The “corner choice” is just the tip of the iceberg. Future models and experiments should take into account the paths, so much rich in information (Fig. 2).

Figure 2.

The red lines represent 16 successive paths of a same ant released at the centre of a rectangular arena. The black arrows and grey areas illustrate a global matching model based on panoramic pictures (after Stürzl et al. model⁶ Fig. 2E). The model's reference picture is taken at one corner (black square) and a picture of each position in the arena is compared to the reference picture. Each arrow points to the neighbour that is the most similar to the reference picture. Catchment areas appear (grey and white areas). The ant's paths are matching the model's prediction remarkably well.

Abbreviation

MTT

mismatch tolerance threshold

Addendum to: Wystrach A, Beugnon G. Ants learn geometry and features. Curr Biol. 2009;19:61–66. doi: 10.1016/j.cub.2008.11.054.