Single-cell response to stiffness exhibits muscle-like behavior

Abstract

Living cells sense the rigidity of their environment and adapt their activity to it. In particular, cells cultured on elastic substrates align their shape and their traction forces along the direction of highest stiffness and preferably migrate towards stiffer regions. Although numerous studies investigated the role of adhesion complexes in rigidity sensing, less is known about the specific contribution of acto-myosin based contractility. Here we used a custom-made single-cell technique to measure the traction force as well as the speed of shortening of isolated myoblasts deflecting microplates of variable stiffness. The rate of force generation increased with increasing stiffness and followed a Hill force–velocity relationship. Hence, cell response to stiffness was similar to muscle adaptation to load, reflecting the force-dependent kinetics of myosin binding to actin. These results reveal an unexpected mechanism of rigidity sensing, whereby the contractile acto-myosin units themselves can act as sensors. This mechanism may translate anisotropy in substrate rigidity into anisotropy in cytoskeletal tension, and could thus coordinate local activity of adhesion complexes and guide cell migration along rigidity gradients.

As part of their normal physiological functions, most cells in the organism need to respond to mechanical stimuli such as deformations, forces, and the geometry and stiffness of the extracellular matrix (1, 2). Aberrant mechanical responsiveness is often associated with severe diseases, including cardiovascular disorders, asthma, fibrotic diseases, or cancer metastasis.

Since the early 1980s, several techniques have been developed to characterize the forces generated by living cells (3–5) and to investigate the effect of the mechanical properties of two-dimensional (2D) substrates (6–8). It was shown that cells are able to sense and respond to the rigidity of their surroundings. For instance, cells cultured on elastic substrates with a rigidity gradient preferably locomote towards stiffer regions and align their shape, their cytoskeletal structures, and their traction forces along the direction of highest stiffness (9–11). Moreover, it has been demonstrated that matrix rigidity could direct stem cells' lineage specification (12).

It is generally assumed that rigidity sensing is based on mechanochemical signal-transduction pathways. The search for the mechanosensing element has generated numerous plausible candidates (reviewed in ref. 2). The most prominent of them is the focal adhesion complex (13, 14). These molecular assemblies consist of numerous proteins that are associated with integrin adhesion receptors (15) and provide the pathway of force transmission from the cytoskeleton to the extracellular matrix (16). Adhesion of integrins to extracellular matrix proteins triggers the formation of focal adhesions, their connection to actin, and the contraction of the cytoskeleton by myosin II (17–19). On a soft substrate, the acto-myosin contraction force predominantly results in substrate deformation, whereas on a rigid substrate, it results in the deformation of the adhesion complex and conformational changes of its proteins (9, 20–22). Such conformational changes may then lead to the growth of focal contacts and, in conjunction with Ca²⁺ influx from cytoskeleton-coupled stress-activated channels, to a subsequent increase in acto-myosin contraction.

Here we focus on the role of myosin II-based contractility in cell response to rigidity. By using a parallel microplates technique (23), we measured the force generated by single myoblasts pulling on springs of variable stiffness. The rate of force generation increased with increasing stiffness and followed a Hill force-velocity relationship. Hence, cell response to stiffness was similar to muscle adaptation to load. Thus, we argue below that contractile acto-myosin units themselves can act as rigidity sensors, providing a synergistic mechanism to mechanosensing through adhesion complexes and their associated signal-transduction pathways.

Results

We let single, isolated C2.7 myoblast cells spread between two parallel glass plates of a custom-made microrheometer (23). One plate was rigid, the other was flexible and could be used as a nano-Newton force sensor. The glass microplates were coated with fibronectin to trigger cell adhesion, spreading, and contraction. During spreading, cells developed traction forces that caused deflection of the flexible microplate towards the rigid plate. By using flexible microplates of different stiffness values, we were able to characterize the effect of rigidity on force generation.

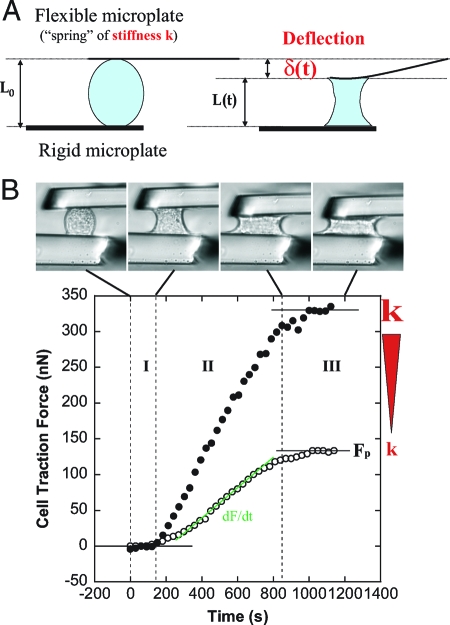
Force generation and cell shape evolution were closely correlated and could be divided into three regimes (Fig. 1 B): First, cells started to spread and changed from a convex to a concave curvature at zero force. Second, cells continued to spread while the force increased during the following ≈10 min. Third, cell spreading slowed down, and the force saturated.

Fig. 1.

Traction force measurements. (A) Principle of force measurements and specific geometrical relations. A single cell spreading between two parallel glass microplates generates traction forces. One plate is rigid and maintained at a fixed position, the other is flexible, calibrated in stiffness, and used as a nano-Newton force sensor. Thus, force, stiffness, and deflection are related: F = kδ. Moreover, the flexible plate deflection δ is equal to the cell shortening (L ₀ − L). Hence, the rate of force increase dF/dt is proportional to the speed V of cell shortening. (B) A single C2.7 cell spreading between the two parallel microplates. The upper plate is flexible, the other rigid. Cell-shape evolution during spreading and traction force generation were related (See also supplementary movies M1 and M2 in the SI Appendix). The plateau force F _p as well as the rate of force increase $\frac{dF}{dt}$ were increasing functions of the stiffness k of the flexible plate. The two sets of data are representative of force evolution at low (open circles, k = 21 nN/μm) and high stiffness values (filled circles, infinite k).

The plateau force F _p was proportional to the stiffness of the flexible plate as long as the stiffness was less than 60 nN/μm. At higher plate stiffness values of 60 and 176 nN/μm, the plateau force was in both cases ≈300 nN (Fig. 2 A), suggesting that this was the maximum traction force that C2.7 cells could generate in a parallel plate arrangement. To measure forces at higher stiffness values, we could not simply use flexible plates of higher stiffness because the plate deflections would have been too small for accurate force measurement. To overcome this difficulty, we controlled the position of a ≈10 nN/μm flexible plate such that the plate-to-plate distance was constant regardless of cell force and plate deflection (23), which was equivalent to an infinite plate stiffness. Under these conditions, we observed shape evolutions and force curves very similar to those obtained at stiffness of 60 and 176 nN/μm, confirming that 300 nN was the maximum force generated by these cells (Fig. 2 A).

Fig. 2.

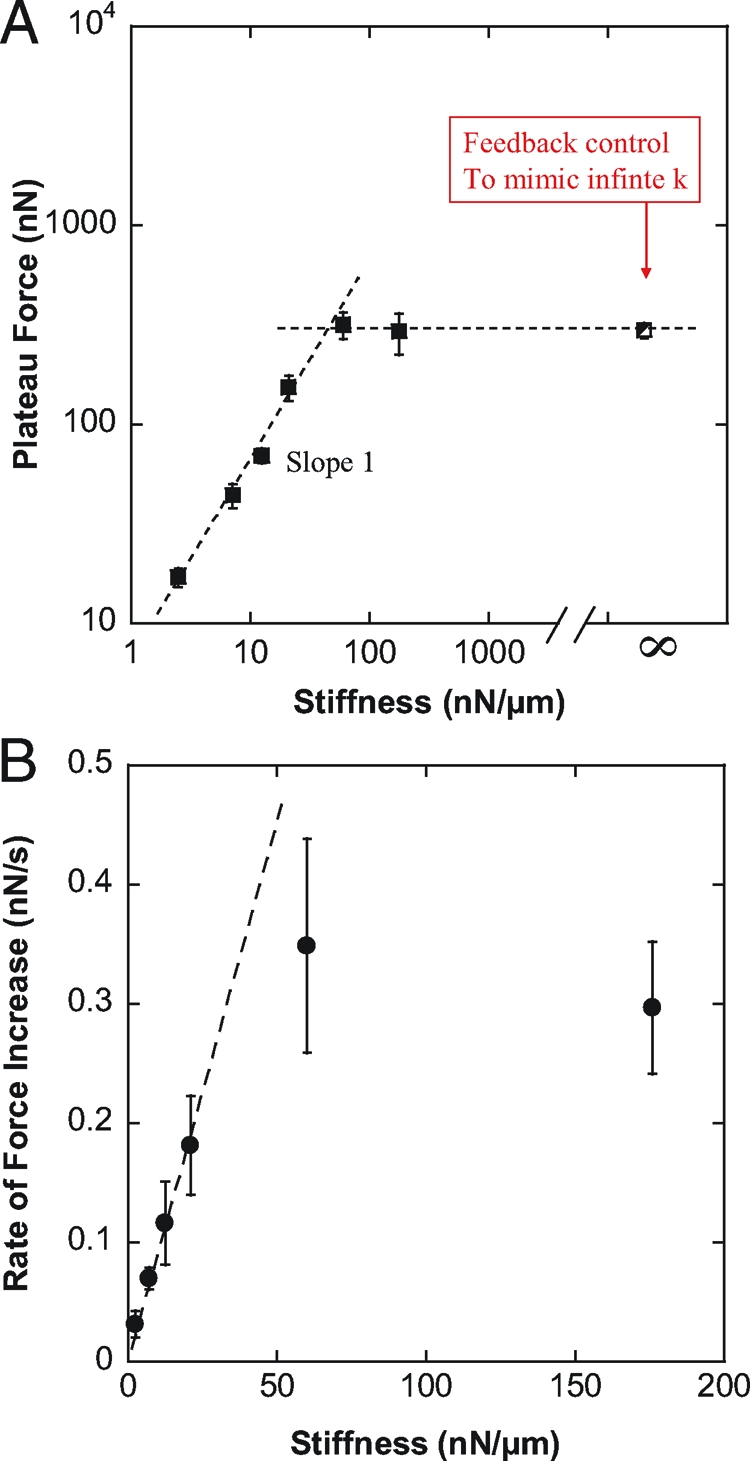
Effect of the stiffness on force generation. (A) Plateau force F _p (filled squares) vs. flexible plate stiffness k in log–log coordinates. The partially filled square corresponds to relaxation experiments allowing us to mimic the effect of infinite stiffness (see Results for details). F _p was proportional to k for stiffness values lower than 60 nN/μm, and saturated at ≈300 nN, which appeared to be the maximum traction force the C2.7 myoblasts could generate in a parallel plates arrangement. (B) Rate of force increase $\frac{dF}{dt}$ (filled circles) measured at a plate deflection δ₀ = 1 μm. The force generated by the cell increased faster when pulling on a stiffer plate. In particular, $\frac{dF}{dt}$ was proportional to k for stiffness values lower than 60 nN/μm, in excellent agreement with F _p behavior.

To quantify the contribution of myosin motor activity for force generation, we studied the effect of various concentrations of the myosin inhibitor blebbistatin. Force values with blebbistatin F([Blebb]) relative to maximum force under control conditions (F _max = 297 nN) were reported as function of blebbistatin concentration (Fig. 3). Contractile forces in single C2.7 cells were inhibited by increasing doses of blebbistatin with an inhibitory constant Ki ∼ 2.8 μM, similar to that of mouse cardiac muscles (Ki = 1.3 − 2.8 μM) (24), and in excellent agreement with the inhibition of the ATPase activity of nonmuscle myosin II measured in chemical assays (Ki ∼ 1.4 μM) (25). Thus, force generation in single C2.7 cells required the ATPase activity of nonmuscle myosin II.

Fig. 3.

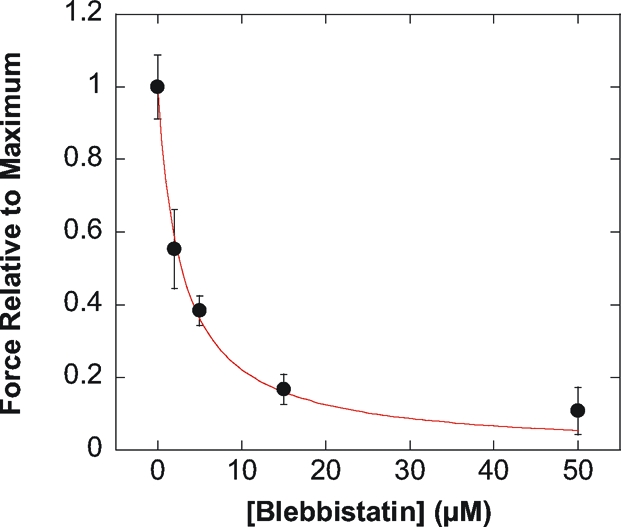
Contractile activity of single C2.7 cells in response to the myosin inhibitor blebbistatin. Contractile activity was expressed as the ratio of the maximal traction force after addition of blebbistatin F([Blebb]) and the maximal force without blebbistatin (F _max = 297 nN). F([Blebb])/F _max decreased with blebbistatin concentration. The inhibitory constant (Ki ∼ 2.8 μM) was in excellent agreement with the Ki values found for mouse cardiac muscles as well as for the ATPase activity of nonmuscle myosin II (24, 25).

Proportionality between equilibrium traction forces and stiffness as shown in Fig. 2 A has been reported previously for cells cultured on 2D arrays of pillars (26). It was suggested that cell response to rigidity could be controlled by deformation rather than force. However, the force curves of Fig. 1 B indicate that increase of F _p with stiffness could be correlated to increase of $\frac{dF}{dt}$ (i.e. the slope of the F(t) curve) with plate rigidity. Thus, we decided to focus on the rate of force increase $\frac{dF}{dt}$ as a function of the plate stiffness k (Fig. 2 B).

For each cell, $\frac{dF}{dt}$ was measured at a flexible plate deflection δ₀ = 1 μM. Measuring dF/dt at a given deflection value ensured a similar cell geometry for all k values tested, thus decoupling the effects of spreading and plate stiffness (see Appendix 1 and Fig. S4 of the SI Appendix). Below 60 nN/ μ m, $\frac{dF}{dt}$ was proportional to k (Fig. 2 B), in excellent agreement with the stiffness-dependence of the plateau force (Fig. 2 A). Indeed, increase of $\frac{dF}{dt}$ with stiffness leads, at any given time t, to higher traction forces on the stiffer plates (Fig. 1 B). This is conceptually one strategy that allows cells to align and migrate along the direction of highest stiffness (27) (see also discussion and illustrations in the SI Appendix).

To understand how cells could adapt their rate of force generation to stiffness, we analyzed further the $\frac{dF}{dt}$ data by taking into account some simple geometrical relations (see Appendix 1). For a fixed plate deflection δ₀, $\frac{dF}{dt}$ is proportional to the mechanical power P generated by the cell to bend the flexible plate: $\frac{dF}{dt}=\frac{P}{{\delta }_0}$ (Appendix 1, Eq. 7). Thus, the increase of $\frac{dF}{dt}$ with the stiffness k (Fig. 2 B) is equivalent to an increase of the generated mechanical power with increasing rigidity. Moreover, the speed V of cell shortening (which is also the speed of plate deflection) can be derived easily from $\frac{dF}{dt}$ measurements: $V=\frac{d\delta }{dt}=\frac{1}{k}\frac{dF}{dt}$ (Appendix 1, Eq. 6). Thus, $\frac{dF}{dt}(k)$ data can be converted to a more familiar force-velocity (F-V) relationship.

The speed of shortening V decreased with increasing load F (Fig. 4 A). In particular, velocity and load were related by a hyperbolic function, the so-called Hill equation of muscle contraction. Superimposed over the force–velocity data in Fig. 4 A is the fit of the Hill equation (F + a)(V + b) = c, where a, b, and c are positive constants. As a consequence, mechanical power P = FV data (Fig. 4 A), as well as rate of force increase $\frac{dF}{dt}=\frac{P}{{\delta }_0}$ data (Appendix 1, Eq. 11), could be fitted with the same Hill parameters a, b, and c. Thus, cell response to stiffness ($\frac{dF}{dt}$ increasing with k) is identical to a Hill force–velocity relationship. This Hill-like behavior is not specific to the myogenic C2.7 line; preliminary results on 3T3 fibroblasts revealed a similar force–velocity relationship (see Fig. S1 in the SI Appendix).

Fig. 4.

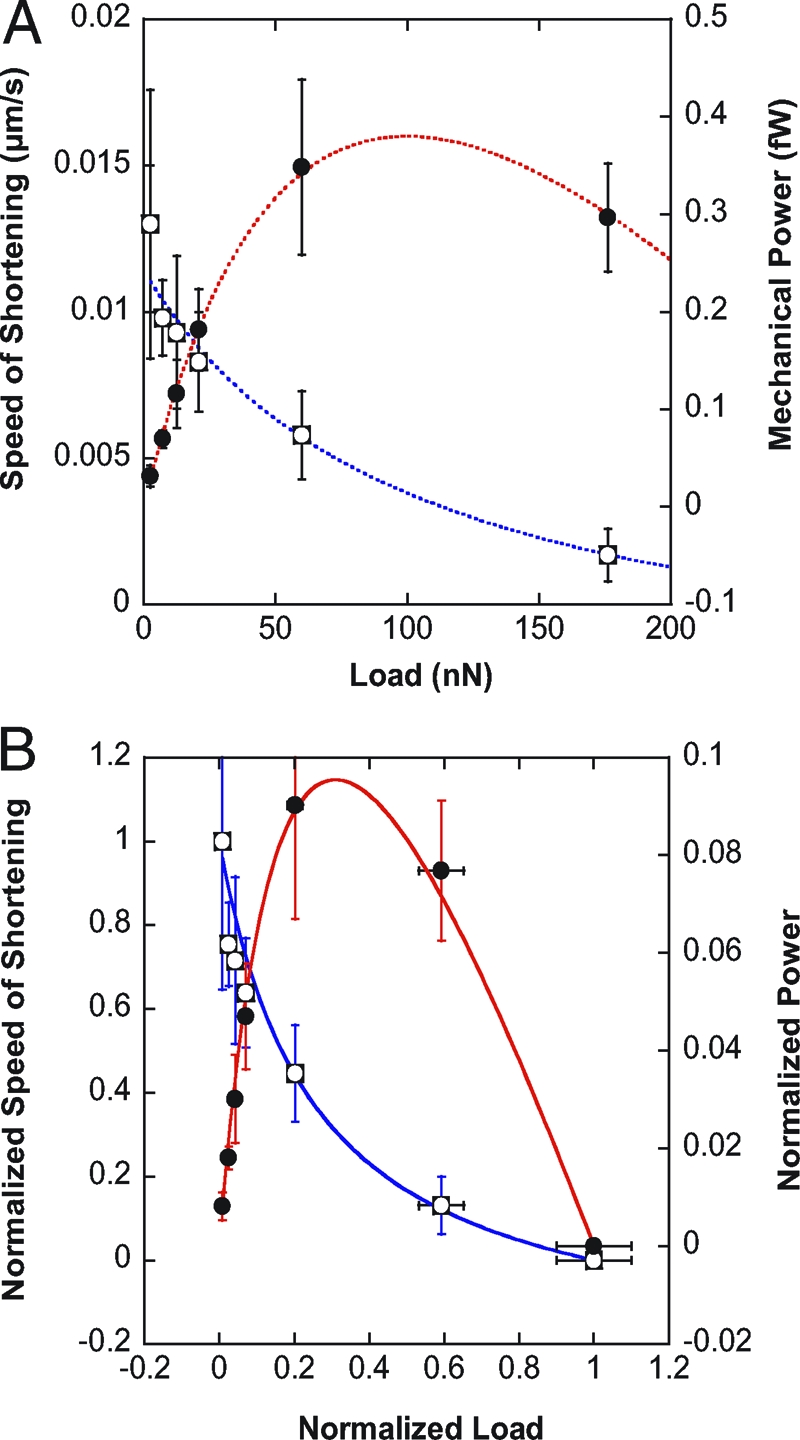
Hill equation of muscle contraction fits single cell data. (A) Cell speed of shortening V (open squares) and mechanical power P = FV (filled circles) as functions of the load F. V and P data were fitted following the Hill equation of muscle (acto-myosin) contraction: $V=\frac{c}{F+a}-b$, where a, b, and c are characteristic constants. V and P data were fitted using the same set of constants {a,b,c}. (B) Normalized speed of cell shortening $v=\frac{V}{V_{\max }}$ (open squares) and normalized power $p=\frac{P}{F_{\max }{V}_{\max }}$ as a function of the normalized load $f=\frac{F}{F_{\max }}$. The solid curves correspond to the reduced Hill equation accounting for muscle adaptation to load ((f + r)(v + r) = (1 + r)r, r = 0.25). Note that the normalized data conform to the Hill curve without any fitting. p is maximum at ≈0.31F _max as observed in muscles, which corresponds to a maximum efficiency of the C2.7 myoblasts when deforming substrates of ≈ 8 kPa Young modulus, and can be compared to optimum striation of myotubes around 12 kPa (34) (see Discussion and Appendix 2 for details).

It may appear surprising that the force–velocity relationship of single cells conforms to an empirical equation established initially for frog skeletal muscles (28). In fact, the Hill-type F-V relationship is not specific to frog muscles. Skeletal muscle from other species, cardiac muscle, and even smooth muscle—with less organized and malleable contractile units—all conform to the Hill equation (29). Each muscle is characterized by a specific set of constants {a,b,c}, a specific maximum speed of shortening V _max at zero load, as well as a specific maximum force F _max that it can generate in isometric tetanus (V = 0). However, it was found that the data corresponding to different muscle types could be normalized to conform to a common reduced (dimensionless) Hill equation (f + r)(v + r) = (1 + r)r, with $f=\frac{F}{F_{\max }}$, $v=\frac{V}{V_{\max }}$, and $r=\frac{b}{V_{\max }}=\frac{a}{F_{\max }}$ which is a shape factor ≈0.25 for all muscle types (29).

The fact that the same Hill behavior was observed over a wide range of structurally and functionally distinct muscle types suggested a common cause. A molecular explanation was found by A.F. Huxley who attributed this behavior to force-dependent kinetics of myosin binding to actin (30). Indeed, recent measurements of the speed of an actin filament sliding on a mini-ensemble (≈8 heads) of myosin motors revealed that the F-V relationship at the molecular level also obeys the Hill equation (31).

After normalizing the F-V data in Fig. 4 A, we found that the dimensionless force–velocity relationship of our isolated C2.7 cells also conforms to the reduced Hill equation, with the same factor r = 0.25 as found in muscles (Fig. 4 B). Force was normalized to F _max = 297 nN (the maximum force measured for an infinite plate stiffness, averaged over 20 cells), and velocity was normalized to V _max = 0.013 μm/s (the maximum speed measured at the smallest plate stiffness of 2.5 nN/μm, averaged over seven cells). It is noteworthy that the reduced Hill equation matched the C2.7 normalized data (speed of shortening V as well as mechanical power P) with no need of any fitting.

Discussion

The observation that the response of C2.7 cells to the myosin inhibitor blebbistatin was similar to the dose-dependent response of mouse cardiac muscle, as well as to the relative ATPase activity of myosin II, underscores the fundamental role of acto-myosin contraction for establishing mechanical responsiveness. In the case of C2.7 cells and fibroblasts, the contractile proteins may be spatially disordered and evanescent, unlike the almost crystalline arrangement of actin and myosin in skeletal muscle sarcomeres. But sliding between actin and myosin filaments is still the fundamental molecular event responsible for contractile force generation and shortening. Thus, the increase of $\frac{dF}{dt}$ with stiffness (Fig. 2 B) is equivalent to a Hill-like F-V relationship (Fig. 4), and can be explained by mechanisms specific to sliding filaments-based contractility.

Efficient acto-myosin sliding not only requires the buildup of tension, but also requires the detachment of the acto-myosin connections that limit the velocity of contractile shortening. According to Huxley's sliding filaments theory (30), the coefficient “a” in the Hill equation corresponds to the internal load imposed by the not-yet-detached myosin heads past their power stroke. This internal load is equivalent to “friction” between actin and myosin filaments. The “ aV ” term thus represents the part of the mechanical power dissipated into heat [“Fenn effect” (32)]. Decreasing the external load applied to a muscle leads to higher speed of shortening and hence to more energy converted to heat. In particular, at zero external load, the mechanical power is entirely dissipated into heat, and the whole energy produced in the muscle (ATP hydrolysis) is used to overcome the internal friction.

In contractile cells other than striated muscle, numerous molecules other than myosin can form cross-links between sliding filaments and can thereby dominate the internal load that is faced by the contractile motor proteins during shortening. Regardless of which molecules form those cross-links, however, contractile shortening is always associated with an additional energy expenditure that is needed to overcome the internal friction. It follows that cells contracting against softer microplates will experience larger energy dissipation, and hence the rise in force will be slower (Fig. 2 B).

Thus, Huxley-type, force-dependent binding kinetics of acto-myosin bridges may provide a plausible mechanism for cell durotaxis (9) or cell alignment in the direction of highest substrate stiffness (11). Contractile units pulling in the direction of high rigidity will automatically pull harder than contractile units aligned with the axis of low stiffness because during contractile filament sliding on soft substrates, more of the energy derived from myosin ATPase activity is needed to overcome the internal load imposed by filament crosslinkers (including the attached myosin heads), and hence less force can be transmitted to the substrate. Thus, force-dependent binding kinetics can translate the anisotropy in substrate rigidity into anisotropy in cytoskeletal tension.

This mechanism may act synergistically with the mechanosensitivity of focal contacts. For instance, myosin-dependent sensitivity may adapt cytoskeletal tension to substrate rigidity at the scale of the whole cell, this tension being then transduced locally—through focal contacts sensitivity—into adhesion complexes of adapted size and stability (detailed discussion on protein recruitment in SI Appendix). Such a synergistic scenario may explain how local activity at the focal contacts can be coordinated at the cell scale (33).

Beyond its role in cell alignment and migration, myosin-dependent rigidity sensing may also be involved in more sophisticated biochemical processes, such as cell differentiation. It was, for instance, shown that the striation of myotubes was maximum for substrate rigidities around 12 kPa, which corresponds to the Young's modulus of striated mucles (34). The question then arose of what chemical regulations could lead to such a nonlinear response to substrate elasticity. In this context, it is noteworthy that the mechanical power generated by acto-myosin fibers is, by itself, a nonmonotonous function of the load. Indeed, C2.7 myoblasts generated maximum mechanical power at a stiffness of ≈100 nN/μm (Fig. 4). This value corresponds to an elastic substrate with a ≈8 kPa Young's modulus (see Appendix 2), in good agreement with the ≈12 kPa found for maximal myotube striation. The early biochemical processes leading to cell differentiation may thus be sensitive not only to force but also to the mechanical power P = FV, i.e. to a combination of force and rate of strain.

The effects of external forces have been extensively studied in skeletal and smooth muscle tissue for many decades, and the data have been traditionally interpreted as arising from force-dependent binding interactions between actin and myosin. The idea that force and length adaptation of muscle may also be actively regulated by mechanochemical signalling processes has only quite recently gained widespread acceptance (35). The situation appears reversed when it comes to the mechanical responses in nonmuscle cells that have been almost exclusively attributed to mechanochemical signalling pathways. Our data suggest that mechanochemical regulation may not be the only mechanism of cell adaptation to their mechanical environment. In some sense, cells can feel with their muscles.

The challenge is now to understand how the muscle-like behavior analyzed here is coordinated with cell-specific processes like spreading and cytoskeletal remodeling. For instance, it is well documented that contractile stress fibers are mechanochemical sensors that reorient, remodel, and regulate focal contact complexes in response to mechanical cues (36 –38). In this context, it is noteworthy that the characteristic time needed to reach the plateau force was independent of plate stiffness (Fig. 1 B). Force saturation may thus be controlled by mechanochemical signalling through stress fibers remodeling and/or regulation of cell-substrate interaction at the focal contacts. This issue should be addressed in future investigations by combining traction force measurements and visualization of cytoskeletal remodeling by fluorescence techniques. Nonetheless, even without considering more complex and cell-specific regulatory and signalling processes, the intrinsic mechanosensitivity of acto-myosin interactions provides a simple, fundamental, and universal mechanism for durotaxis and rigidity sensing.

Materials and Methods

Cell Culture.

The C2-7 myogenic cell line is a subclone of the C2 line derived from the skeletal muscle of adult CH3 mice (39). C2-7 cells used in this study were generously provided by Denise Paulin and Zhigang Xue (Biologie Moléculaire de la Différentiation, Université Paris 7). They were grown in 25-cm² culture flasks using DMEM medium supplemented with 10% heat-inactivated fetal calf serum, 2 mM glutamin, 50 units/mL penicillin, and 50 μg/mL streptomycin and until confluence reached 50%. All cultures were maintained at 37° C under humidified 5% CO₂ atmosphere.

Cell Preparation.

Cells at 50% confluence were trypsinized, centrifuged at 140 × g for 3 minutes, resuspended in DMEM supplemented with 15 mM HEPES, and maintained under smooth agitation for 2 hours at 37° C. If used immediately after trypsination, cells showed weak adhesion to the microplates. The delay of 2 hours was necessary for the trypsinated cells to regenerate adhesion proteins expressed at the cell surface.

Fibronectin Coating.

Glass microplates were cleaned ten minutes in “piranha” mixture (67% sulfuric acid + 33% hydrogenperoxyde), rinsed in water, dipped in a (90% ethanol + 8% water + 2% 3-aminopropyltriethoxysilane) bath for 2 hours and then rinsed in ethanol and water. Finally, microplates were coated with 5 g/ML Fibronectin F1141 from Sigma.

Experimental Procedure.

First, the rigid and flexible microplates were placed near the bottom of the manipulation chamber. Then, the chamber was filled with cells suspended in 10 mL of DMEM buffered with 15 mM HEPES, and we waited until cells deposition on the chamber's bottom. During cells sedimentation, we added 10 mL of liquid GPR paraffin (BDH Laboratory Supplies Pool) at the DMEM surface to avoid O ₂ exchange between medium and air (ensuring, thus, long-time pH stability). All manual micrometers were then mechanically locked to avoid any drift during the experiment. Finally, by using piezoelectric stages, the microplates were lowered toward the chamber's bottom and placed in contact with a cell. After a few seconds, the two microplates were simultaneously and smoothly lifted to 60 μm from the chamber's bottom to get the desired configuration of one cell adherent between two parallel plates.

Cells spreading between the microplates were visualized under bright-light illumination with a Plan Fluotar L 63x/0.70 objective and a Micromax digital CCD camera (Princeton Instruments). The setup, enclosed in a Plexiglas box, was maintained at 37 +/− 0.2°C by an Air-Therm heater controller (World Precision Instruments). Vibration isolation was achieved by a TS-150 active antivibration table (HWL Scientific Instruments Gmbh).

Blebbistatin Specific Procedure.

To avoid phototoxicity and photoinactivation of blebbistatin, cells were illuminated through a high-pass colored glass filter (Melles Griot, 03FCG089) transmitting only wavelengths higher than 575 nm.

Appendix 1: dF/dt as a Function of K and Hill V-F Relationship

dF/dt, V, and P Are Geometrically Related.

The uniaxial geometry of our setup leads to a simple relation between the rate of force increase dF/dt and the speed of cell shortening.

The traction force F(t) applied by the cell at a given time t is equal to the flexible plate deflection δ(t) times the plate stiffness k (Fig. 1 A):

Thus, the rate of force increase dF/dt is proportional to the rate of deflection dδ/dt of the flexible plate:

At any given time t, the cell length L(t) is directly related to the initial cell length L ₀ and the flexible plate deflection δ(t) (Fig. 1 A):

The speed of cell shortening V is then equal to the rate of flexible plate deflection dδ/dt:

Combining Eqs. 2 and 4, we find that the rate of force increase dF/dt is equal to the speed of cell shortening V times the plate stiffness k:

The mechanical power P generated by the cell to bend the flexible plate is then given by

In particular, for a given deflection δ₀, $\frac{dF}{dt}$ is proportional to the mechanical power

For a Given Deflection δ₀, the Force–Velocity Relationship V(F) Determines Cell Response to Stiffness $\frac{dF}{dt}(k)$.

The force–velocity relationship expresses the speed of contraction V as a function of the force F:

where f is a mathematical function defining how V varies when changing the load F. Eq. 8 implies that, as the cell is deflecting an elastic plate, V is a function of the plate stiffness k as well as of the plate deflection δ. Eq. 5 then implies that $\frac{dF}{dt}(k)$ is also a function of the two parameters k and δ:

Thus, the force–velocity relationship (i.e. f(kδ)) determines the way the cell will pull on its substrate (g(k,δ)). One must then distinguish the effect of the stiffness k on cell traction force (rigidity sensing) from that of the plate deflection δ (Fig. S4 of the SI Appendix). By analyzing the time evolution of F(t) and V(t) for a given cell pulling on a plate of given stiffness k, one can determine the influence of δ which is related to changes in cell shape and remodeling (see discussion on protein recruitment in the SI Appendix). Conversely, to define the specific effect of the stiffness k on the cell mechanical activity (rigidity sensing), one must measure the force and speed values (F(δ₀) and V(δ₀)) observed at a given plate deflection δ₀ for different cells pulling on plates of different stiffness (Fig. S4 of the SI Appendix). We used the latter analysis to obtain the data shown in Fig. 2 B and Fig. 4.

Specific Expressions Obtained for a Hill F-V Relationship.

The force–velocity data reported in Fig. 4 A conformed to the Hill equation of muscle contraction:

where a, b, and c are Hill-fitting constants and δ₀ = 1 μm is the deflection value at which V and F data were measured. By combining Eq. 10 with Eqs. 5, 8, and 9, one finds:

This equation describes the rate of force increase dF/dt for different plate stiffnesses k and accounts for the data shown in Fig. 2 B. In particular, for low stiffness values, $[\frac{c}{k+a}-b]$ is nearly constant, and $\frac{dF}{dt}$ is proportional to k as observed experimentally. Thus, rigidity sensing (increase of $\frac{dF}{dt}$ with increasing k) and F-V Hill behavior can be understood as two different manifestations of the same phenomenon. As a consequence, to explain stiffness-sensing by the cells ($\frac{dF}{dt}(k)$) we suggest a well-known molecular process namely, load-dependent acto-myosin binding and sliding that was proposed historically to account for Hill F-V behavior of contracting muscles.

Appendix 2: Stiffness k and Young Modulus E

A flexible glass microplate of stiffness k, and a 2D substrate of Young's modulus E are mechanically equivalent if they lead to the same cell force–contraction relationship. In other words, a cell pulling with a force F on both substrates should shorten the same distance δ. In the case of a flexible glass plate, the relationship between F and δ is given by

and for a 2D substrate by (40):

where D is the diameter of the cell-substrate contact area, and ν is the Poisson's ratio of the substrate. Mechanical equivalence between the two substrates then implies

The mechanical power generated by isolated myoblasts to bend the flexible glass microplates was maximum for plate stiffness k _m ≈ 100 nN/μm (Fig. 4). The typical values of D and ν being respectively ≈10 μm and ≈0.5, k _m is equivalent to a Young's modulus E _m ≈ 8 kPa.