Mechanochemical model for myosin V

Abstract

A rigorous numerical test of a hypothetical mechanism of a molecular motor should model explicitly the diffusive motion of the motor's degrees of freedom as well as the transition rates between the motor's chemical states. We present such a Brownian dynamics, mechanochemcial model of the coarse-grain structure of the dimeric, linear motor myosin V. Compared with run-length data, our model provides strong support for a proposed strain-controlled gating mechanism that enhances processivity. We demonstrate that the diffusion rate of a detached motor head during motor stepping is self-consistent with known kinetic rate constants and can explain the motor's key performance features, such as speed and stall force. We present illustrative and realistic animations of motor stepping in the presence of thermal noise. The quantitative success and illustrative power of this type of model suggest that it will be useful in testing our understanding of a range of biological and synthetic motors.

Myosin V moves cargo through eukaryotic cells by walking in a hand-over-hand fashion along actin filaments (1, 2). Recent high-resolution, single-molecule experiments have provided an unprecedented level of insight into the physical mechanism underlying the coordinated steps of this biological motor. A growing level of support is beginning to form around a hypothetical stepping mechanism in which a step takes place through biased tethered diffusion of a detached head (3–5), and detachment of the two heads is coordinated through intramolecular strain, facilitating hand-over-hand forward stepping and avoiding motor detachment (6–9).

One can expect that the realization of such a stepping mechanism should require delicate mutual fine-tuning of the involved chemical rates, the motor's structural and mechanical properties, and the diffusive motion of the motor's degrees of freedom. For example, the rate of tethered diffusion (a function of motor size and stiffness) must be matched to the binding and unbinding rates of the motor head. Furthermore, the effectiveness of a strain-controlled gating mechanism depends on the detailed diffusive motion of the motor's internal degrees of freedom, because intramolecular strain is a quickly varying function of the instantaneous motor conformation.

To test the feasibility of a given stepping mechanism of dimeric molecular motors, it is therefore necessary to model the random thermal motion of the molecule's degrees of freedom as well as its mechanical and the kinetic properties. Most suited for this task are so-called “mechanochemical” models, which include a discrete set of chemical states and some coarse-grained mechanical features. Their advantage is that they are more detailed than discrete kinetic models that treat the motor as one or two “points” that discretely hop along a track and yet allow full simulation of hand-over-hand stepping, in contrast to computationally expensive full atomistic models that also require large numbers of parameters (10).

Two recent studies have applied mechanochemical approaches to myosin V (11, 12). Both of these models treat the neck domains as elastic filaments and predict transition rates between quasiequilibrium mechanical and chemical states based on the elastic potential energy of the dimer in each state. They correctly predict the predominant mechanochemical cycles as well as some characteristics of the load dependence of myosin V. However, neither of these models reports sensitivity to the choice of mechanical parameters, and each requires five or more free parameters. More importantly, these previous models either do not include conformation-dependent transition rates (12) or do not allow motor dissociation from actin (11) and, thus, do not test the role of strain-dependent gating in achieving motor processivity.

Here we present a mechanochemical model of myosin V that takes the key step forward to explicitly model the thermally activated motion and conformational changes of the molecule throughout all chemical and mechanical transitions. This approach enables us to make several contributions: First, we are able to test a hypothesized strain-dependent coordination mechanism in which head detachment is gated by neck conformation, which depends on molecular fluctuations and intramolecular strain (6–8). We confirm the feasibility of such a mechanism and explore how its effectiveness depends on the motor's mechanical properties. Second, the present model produces computational data amenable to direct comparison with recent single-molecule experimental data on myosin-V walking with unprecedented spatial and temporal resolution, including during the fleeting one-head-bound portion of the step (3, 5). Prior models have not been able to produce such data because they modeled reattachment by a discrete rate constant rather than simulating the motion of the detached head. Finally, but not least important, by modeling the motor's realistic thermal motion we are able to produce unique, highly illustrative animations [see supporting information (SI) Movies S1–S3] of motor stepping, which we believe will be very useful in raising the level of intuitive understanding of the physical conditions under which molecular motors operate.

An additional strength of our model is that its mechanical assumptions (detailed in the next section) are well-supported by the most recent experiments. Most input parameters of our model are taken directly from measurements, and we vary the small number of parameters that are not experimentally constrained to explore how they affect the performance of the motor. Our minimal model reproduces key performance features of myosin V, including the run length, the velocity, the relaxation (“working stroke”) distance, and the stall force. We are able to make predictions of parameters that are yet to be measured, including details of the molecule's flexibility, and to establish experimentally accessible performance characteristics (such as the relative probability for trailing head to leading head detachment) that can be used to test these predictions. We propose specific experiments that could test and fully constrain our model.

Model

Model Assumptions.

To construct a minimal model, we use the following assumptions:

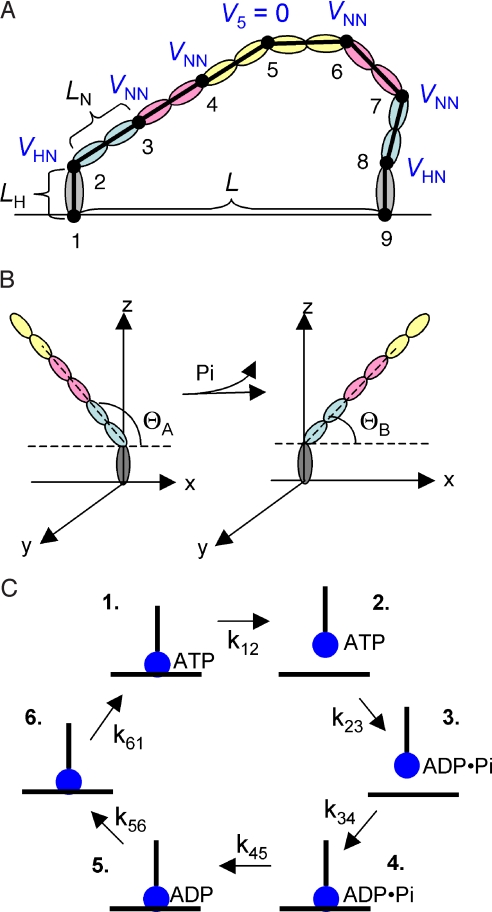
1. Semiflexible neck domains with three rigid segments. The neck domain of myosin V incorporates six tandem elements called IQ motifs (13, 14). A model of the neck domain based on the crystal structure, combined with FRET measurements of distances between IQ complexes, suggests that the neck domain can be thought of as three pairs of strongly interacting IQ motifs, with minimal interaction between adjacent pairs, allowing bending primarily at these junctures (Fig. 1A) (14).

2. State-dependent equilibrium angles of neck domains. We treat the juncture between each head and the adjacent neck domain (points 2 and 8 in Fig. 1A) as a semiflexible joint with an equilibrium angle that depends on the chemical state of the head [an assumption that is supported by EM images (15, 16)]. We define the equilibrium angle with respect to the direction of motility along the filament, which we denote as the +x direction. We assume that a forward rotation in the equilibrium angle (from θ_A to θ_B) between head and neck is tightly coupled to phosphate release from the head (Fig. 1B).

3. Free rotation about neck domain juncture. EM images (15) and observations of the motion of the detached neck domain by tracking an attached gold nanoparticle (3) or a microtubule filament (4) support a model in which a detached head and its adjacent neck domain undergo tethered diffusion about the juncture between neck domains, with free rotation about this joint (point 5 in Fig. 1A).

4. Binding to track. We assume that if a detached head has undergone ATP hydrolysis and diffuses close enough to a binding site to interact with it electrostatically (R < R_screen; see Table 2), it will attach to this site. We make the simplification of treating the actin filament as a one-dimensional array of evenly spaced binding sites with separation L = 36 nm. We do not include nonspecific binding to actin or other electrostatic interactions with the filament away from the binding sites.

Fig. 1.

Mechanochemical model for myosin V. (A) The neck domains are modeled as chains of three rigid segments, each representing a pair of IQ motifs. Semiflexible joints between segments are characterized by a neck–neck potential V_NN (see text), and the semiflexible joints to the head domains (gray) are characterized by V_HN (points 2 and 8). The juncture between neck domains (point 5) is treated as a freely rotating joint (V₅ = 0). (B) The equilibrium angle of the neck–head junctures (points 2 and 8 in A) is assumed to rotate forward (from θ_A to θ_B) upon phosphate release from the head. (C) In our simulations, each head cycles stochastically through the relatively long-lasting states in the observed monomer cycle (see Table 1 for transition rates).

Table 2.

Mechanical input parameters, as defined in Fig. 1

Parameter	Value	Source
VNN	Tunable	Estimated range: see SI Text
VHN	Tunable
θB	Tunable
θA	0.72π	Ref. 32
V5	0 kT	Refs. 3 and 4
LH	5 nm	Ref. 33
LN	10 nm	Refs. 6 and 34
L	36 nm	Refs. 1, 16, 20, and 22
γH	6.2 × 10−8 pN/nm	Calculated estimate
γN	4.1 × 10−8 pN/nm	Calculated estimate
Rscreen	0.6 nm	Calculated estimate

The drag coefficient of a head domain, γ_H, is calculated using Stoke's Law, and that of a neck domain segment, γ_N, is approximated by the transverse drag coefficient of a cylinder with length L_N = 10 nm and diameter 2 nm. A detached head attaches to an actin binding site if the distance between the head and the site is less than R_screen = 0.6 nm, equal to the Debye length for electrostatic screening in a fluid under physiological conditions. See SI Text for an estimated range of experimentally supported values of V_NN.

Brownian Dynamics (BD) Simulations.

In our model, the myosin-V molecule is represented by a chain of eight rigid segments (two head domains and three segments in each of the two neck domains) (Fig. 1A). Each segment endpoint (i = 1–9) is a mathematical point with a spatial coordinate and an associated drag coefficient, corresponding to the estimated size and shape of each segment of the molecule (see Table 2). To simulate the motion of this semiflexible filament model, we use BD methods based on the overdamped Langevin equation:

where −γ_iṙ_i represents the viscous drag force on point i, −∇U(r_i) represents the internal forces on point i due to bending or stretching the semielastic filament, and ξ_i(t) is a Gaussian-distributed white noise term that represents the thermal noise of the environment. The total potential energy of the semiflexible filament is given by

where the first term represents the elastic energy associated with bending at the joints and the second term is a harmonic potential energy included to impose a fixed separation distance between adjacent points. This phenomenological expression for the bending energy, where φ_i is the angle between filament segments that meet at point i and φ_i⁰ is the equilibrium angle, reduces in the limit of small δ = φ_i − φ_i⁰ to an expression that is quadratic in δ, consistent with the form used in Allen and Tildsley (17). The equilibrium angle between adjacent neck domain segments is φ_i⁰ = 0, such that the elastic energy of a neck domain is minimized when the neck domain is straight. The stiffness parameter V_i characterizes the elastic stiffness of a joint (for example, if V_i = 100 kT, an elastic energy of U = V_i/2 = 50 kT is required to bend the joint 90° away from its preferred angle). The input parameters V_NN and V_HN represent the elastic stiffness of the neck domain joints and the head–neck junctures, respectively (Fig. 1A). In the second term of Eq. 2, K is the harmonic stiffness, r₀ is the rest length, and r_ij is the separation distance between adjacent particles i and j, where j = i + 1. We used K = 10⁵ kT and program time step dt = 1.175 × 10⁻¹⁰ s, which keeps fluctuations in interparticle distance small (〈∣r_ij − r₀∣〉 < 0.01r₀).

In each time step, we evaluate the positional change of each point in response to internal forces and external stochastic thermal forces. We allow each head to cycle stochastically through the relatively long-lasting states in the predominant observed cycle of a monomer (18, 19), as summarized in Fig. 1C. To limit the number of parameters in our minimal model, we include forward chemical transitions with experimentally measured transition rates (Table 1) and do not allow backward chemical transitions.

Table 1.

Chemical transition rates of a myosin-V monomer

Rate	Value	Source
k12	dt−1	Ref. 18
k23	700 s−1	Ref. 18
k34	Diffusion limited	Model output
k45	200 s−1	Refs. 19 and 21
k56	15 s−1	Refs. 8 and 21
k61	1.6 μM−1·s−1, [ATP] = 1 mM	Refs. 18 and 31

These transition rates were used to determine the probability for a transition to occur in each simulation time step (dt = 1.175 × 10⁻⁴ s). For example, the probability for a transition from chemical state I to state II in a given time step is equal to k₁₂dt.

Based on measurements and hypotheses in Veigel et al. (6) and Purcell et al. (8), we test a coordination mechanism in which the ADP release rate from a head is reduced if the adjacent neck domain has a rearward rotation with respect to the equilibrium angle, θ_B. Such a mechanism could enhance processivity, because intramolecular strain after phosphate release from the leading head would make the leading head unlikely to detach prematurely. We incorporate this gating mechanism by using the following expression for the ADP release rate, k₅₆ (Fig. 1C):

where θ_i is the instantaneous angle with respect to the filament of the neck domain at point “i”, where i = 2 or 8 (Fig. 1A). Here, the parameter ξ (in units of kT) quantifies the sensitivity of k₅₆ to angular displacement from the preferred head-neck juncture angle, θ_B. Using a procedure described in SI Text, we calibrate the parameter ξ to match experimental measurements (Fig. S1). To adjust to the physical properties of the molecule, a different value for ξ is used for each set of values of V_NN and V_HN.

We use measured values for almost all of the mechanical and chemical input parameters (see Tables 1 and 2). Three mechanical parameters, namely θ_B, V_NN, and V_HN, are not well-known. Estimates of the persistence length, l_p, of myosin-V neck domains in the literature varies over a wide range (l_p = 100–400 nm) (12). Within the framework of our computational model, this range suggests that V_NN is on the order of 10 kT < V_NN < 100 kT [using V_NN ∼ 2l_p kT/L_N, where L_N is the length of a rigid segment in the neck domain (17)]. To further constrain these remaining three free parameters and to evaluate the validity of our model, we have at our disposal as many as five measured performance features of myosin V (Table 3).

Table 3.

Experimentally measured performance features against which we test our model

Feature	Value	Source
Velocity	550 (± 40) nm/s	Ref. 21
Run length	20–60 steps	Ref. 6
Stall force	2–3 pN	Refs. 22 and 23
Relaxation distance, Rx	≈25 (± 2) nm	Refs. 3 and 5–7
Relaxation distance, Rz	≈6 (± 4) nm	Ref. 5

The experiments cited used saturating ATP concentrations of at least 1 mM.

Results and Discussion

Dominant Dimeric Cycle.

We find that the model reproduces hand-over-hand transport of myosin V at a speed consistent with experimental measurements (for an illustration, see Movie S1) without the need for any fine-tuning of the mechanical parameters, as long as the neck domains have a forward-leaning preferred angle after phosphate release (0 < θ_B < 0.5π). Using the chemical cycle of the monomer as an input (Fig. 1C), we obtain as a model output that the dimer typically undergoes a mechanochemical cycle consistent with the kinetic model proposed in Rief et al. (20) (Fig. 2A). The mechanochemical states in this cycle can be represented, within the framework of our model, in terms of the three distinct mechanical states that are characterized by the equilibrium angles (θ_A or θ_B) of the leading and trailing heads (labeled I–III and illustrated in Fig. 2B). In Fig. 2C, we show a sample of the time-dependent motion of each head and of the neck domain juncture (point 5 in Fig. 1A) during hand-over-hand stepping. It is important to note that the model allows the possibility of backward steps, which can occur through leading head detachment followed by reattachment at a binding site in the −x direction.

Fig. 2.

The typical mechanochemical cycle resulting from our model is consistent with the kinetic model proposed in Rief et al. (20). (A and B) As each head undergoes kinetic state transitions (A), the myosin V dimer typically cycles through three distinct mechanical states, I–III (B). Color-coded boxes indicate the correspondence between mechanical states and kinetic states. (C) Data representative of hand-over-hand stepping as the motor undergoes the mechanochemical transitions illustrated in A and B, showing the time-dependent motion of each head domain (red and blue) and the neck domain juncture (black).

Relaxation Distance.

Several recent experiments demonstrate that the step average of myosin V (i.e., the center-of-mass motion averaged over a large number of synchronized steps) has two characteristic phases in the direction of transport (x direction): a fast 25-nm phase followed by a slower, 11-nm motion to complete the step (3, 5–7). The first phase can be interpreted as the average x motion corresponding to the relaxation of the attached neck domain, suggesting a relaxation distance R_x ≈ 25 nm (sometimes referred to as the “working stroke”). Also, Cappello et al. (5) measure an average motion (R_z ≈ 6 nm) away from the filament aligned in their step averages with the onset of the R_x ≈ 25 nm motion. In our model, these distances correspond to the change in the average position of the neck domain juncture (point 5 in Fig. 1A) that takes place after the motor transitions from mechanical state II to state III upon trailing head detachment (Fig. 3A).

Fig. 3.

Relaxation distance calculations. (A) Schematic of the x and z components of the relaxation distance, R_x and R_z. (B) Simulated values of R_x as a function of V_NN/V_HN, with the following values of θ_B from top to bottom: 0.2π, 0.3π, 0.4π, and 0.5π. (C) R_z from the same simulations as in B, with the same symbols to denote the value of θ_B.

For comparison between our simulations and the above experimental measurements, we assume a stiff coupling between cargo and motor, such that the motion of the juncture between neck domains (point 5 in Fig. 1A) corresponds approximately to the motion of the cargo measured experimentally. This approximation is reasonable for comparison to Cappello et al. (5), because they report that the relaxation time of this linkage in their experiment is very fast compared with the time scale of the step phases. By simulating the average conformation of the motor in mechanical states II and III, we find that the model approximately reproduces R_x = 25 nm as long as θ_B ≈ 0.4π for all tested values of V_NN and V_HN, although the optimal value of θ_B depends somewhat on the stiffness parameters (Fig. 3B). We also obtain R_z > 0, in agreement with experiment, when θ_B = 0.4π for all tested values of V_NN and V_HN (Fig. 3C). For the remainder of this study, we use θ_B = 0.4π unless otherwise noted.

Tethered Diffusion and Stall Force.

To characterize the tethered diffusional search during mechanical state III, we simulate the average time, τ, between when the trailing head detaches and when it reaches the next binding site through tethered diffusion. For a broad range of stiffness parameters, the tethered diffusion rate, 1/τ, under zero load is about an order of magnitude higher than the rate of ATP hydrolysis (k₂₃ = 700 s⁻¹) (Fig. 4A). This computational result provides a consistency test by showing that reattachment is limited by ATP hydrolysis rather than tethered diffusion, consistent with experiment. Our result also suggests that the effectiveness of the tethered diffusion stepping mechanism is not highly dependent on mechanical parameters, such as the stiffness, and that the processivity of the motor is not hampered by the “search” process. Because the tethered diffusion rate is fast compared to the relevant chemical transitions, the simulated motor speed is relatively independent of the mechanical input parameters and depends primarily on the chemical transition rates. For this reason, the speed of the motor is consistent with experimental measurements at saturating ATP concentrations (v ≈ 500–600 nm/s) (21) over the range of mechanical parameters tested.

Fig. 4.

Tethered diffusion and stall force. (A) Simulated values of the tethered diffusion rate, 1/τ, as a function of load force applied to the neck domain juncture (point 5 in Fig. 1A), for V_NN = V_HN = 100 kT (red triangles); and V_NN = 100 kT, V_HN = 10⁵ kT (black squares). (B) Stall force, f_stall, as a function of V_NN for V_HN = 100 kT (circles) and V_HN = 10,000 kT (squares). Values are based on an exponential fit to the tethered diffusion rate versus load data exemplified in A. (C) f_stall as a function of V_HN for V_NN = 100 kT.

For load forces applied to the cargo domain, several single-molecule experiments find stall forces in the range f_stall = 2–3 pN, based on the distance from the center of a stationary optical trap at which the motor stalls and dissociates from actin (5, 22, 23). To enable comparison of our model to these data, we define f_stall in a consistent way, namely as the detachment force at which the tethered diffusion rate is equal to the ADP release rate (on the order of k₅₆⁰ = 15 s⁻¹, represented by the dashed line in Fig. 4A), because for large load forces, when 1/τ < k₅₆, the motor is more likely to dissociate than to complete a step. (Note that this approach is likely to yield a conservative estimate of the stall force; if rearward load decreases the ADP release rate, the motor has a better chance to complete a step without premature dissociation and could thus take consecutive steps under higher loads than we estimate in Fig. 4.)

We find that f_stall increases with stiffness parameters V_NN and V_HN, leveling off for high values of either parameter, as shown in Fig. 4 B and C. A range of V_NN and V_HN combinations can produce stall forces in the experimentally observed range f_stall = 2–3 pN. However, if we assume that V_NN is in the range 10–100 kT (based on estimated persistence lengths; see SI Text), then we need V_NN in the upper end of this range, with V_HN ≫ V_NN, to produce a stall force of at least 2 pN (Fig. 4C).

Processivity and Gating.

In Fig. 5A we show data on the motor's dynamics with and without the stepping coordination introduced in Eq. 3 (for illustrative animations, see Movies S2 and S3). When ADP release is taken independent of conformation (no gating, k₅₆ = k₅₆⁰), the leading head and trailing head detach with equal likelihood. Trailing head detachments are often followed by forward steps, whereas leading head detachments often result in futile cycles with no net progress (Fig. 5A). The mean number of steps the motor takes along actin before detaching is ≈11 steps (Fig. 5B), which falls short of the experimentally observed run lengths of 20–60 steps (7). When conformation-dependent gating of ADP release is included (Eq. 3), the mean run length increases significantly (Fig. 5C) and is within the margin of error of experimental estimates over the range of V_HN and V_NN we tested.

Fig. 5.

Run length and processivity simulations (θ_B = 0.4π, and V_NN = V_HN = 100 kT, unless noted). (A) Sample data of the x position (along the filament) of the neck domain juncture (point 5 in Fig. 1A), with (black) and without (red) conformation-dependent coordination between heads (Eq. 3). The small “spikes” apparent in the simulations without head–head coordination correspond to futile cycles of the motor in which a head detaches from actin and reattaches in its original location. (B) Histogram of run length (number of steps before detachment) for ≈250 individual walking simulations with uncoordinated steps (ξ = 0, Eq. 3). (C) Run length histogram with coordinated stepping (ξ = 4.0 kT, based on calibration to experiment for the mechanical parameters used here). (D) Mean run length as a function of V_HN, averaged over ≈250 individual runs with conformation-dependent, head–head coordination (data points), and without head–head coordination (dashed line). (E) Average kinetic asymmetry, 〈λ〉, as a function of V_NN, with the following values of V_HN from bottom to top: 10², 10³, 10⁴, and 10⁵ kT.

To continue to quantitatively assess the effectiveness of this angle-dependent gating mechanism (Eq. 3), we define kinetic asymmetry, λ, as the probability for ADP dissociation from the trailing head, relative to the total probability of ADP dissociation from either head:

The kinetic asymmetry, λ(t), must be modeled numerically, because it depends on the instantaneous conformation of the motor (λ is highest when the leading neck domain is rotated in the rearward direction with respect to the preferred angle, θ_B). Because ADP release is the rate-limiting process for detachment of a myosin head from actin, λ is an approximate measure of the likelihood for trailing head detachment, relative to the overall probability for either head to detach.

BD simulations of the motor in mechanical state II demonstrate that the average kinetic asymmetry, 〈λ〉, increases with increasing V_NN, because the rearward rotation of the leading neck domain increases as the neck domains become stiffer (Fig. 5E), making the gating mechanism more effective. In the limit of large V_HN (which produces the best stall force performance in our model), the value of 〈λ〉 depends very little on V_HN and is primarily a function of V_NN. If future experiments show that the head–neck juncture can be treated as a very stiff joint (V_HN > 10³ kT), then comparing a measurement of the ratio of leading to trailing head detachment with the theoretical prediction of 〈λ〉 could indicate whether the neck domains of myosin V are relatively flexible (V_NN ≈ 10 kT) or relatively stiff (V_NN ≈ 100 kT).

Concluding Remarks.

In conclusion, the known kinetic, mechanical, and structural parameters of myosin V (Tables 1 and 2) interplay with thermal noise in such a way that the feasibility of the hypothetical stepping mechanism for myosin V was demonstrated: Individual hand-over-hand steps occur through a process of biased tethered diffusion of a detached head, and processive hand-over-hand stepping is facilitated by a conformation-dependent intramolecular coordination mechanism that reduces the likelihood of leading head detachment. Furthermore, we find that our model reproduces the measured relaxation distance and stall force of myosin V particularly well if we choose the values θ_B = 0.4π, V_NN ≈ 100 kT, and V_HN ≫ V_NN.

By varying the few unfixed parameters, we explore the sensitivity to these parameters and gain a fuller understanding of the range of possible motor performance. For example, a previous model assumes completely rigid state-dependent attachment angles and concludes as a result of this assumption that energetic constraints prevent the leading-head working stroke from occurring before trailing head detachment (12). In contrast, our model treats the head–neck junctures as elastic joints of variable stiffness and thus allows the motor to transition into a mechanochemical state characterized by a “telemark” configuration, similar to those that have been observed in some EM images (16).

The following set of experiments could completely constrain this model: (i) If the average run length and the relevant transition rates under consistent solution conditions were measured more precisely, it would be possible to further constrain the head–neck stiffness, V_HN (see Fig. 5D). (ii) In our model, if the head–neck juncture is very stiff, the trailing/leading head detachment ratio depends only on V_NN (Fig. 5E), which means that a measurement of this performance feature would amount to a measurement of V_NN. To experimentally determine the trailing/leading head detachment ratio, high temporal resolution is needed to detect the fleeting events in which the leading head detaches and reattaches in its original place. Recent high-resolution experimental studies such as Cappello et al. (5) show evidence of such events and provide a promising route toward more stringent performance tests of this model. Detailed comparison between our computational data and the experimental data of Cappello et al. (5) is necessary.

The model developed here is particularly powerful because it combines a limited set of kinetic and mechanical parameters and explicitly models diffusion and conformational changes due to thermal noise. The quantitative conclusions enabled by such a well-constrained model and the illustrative nature of resulting animations (see Movies S1–S3 and Table S1) will be useful for many other motor systems. For example, a similar approach could be taken to study the strain-dependent gating of kinesin-1 (24) and to help interpret recent high-resolution observations of the unbound head of kinesin-1 during steps (25). The model could be extended to include reverse chemical rate transitions to study the physical mechanism of the recently observed processive backward stepping of myosin V under superstall load forces (26). This type of model could also be used to model the dynamics of molecular motors at filament intersections (27, 28), to study the more complex cooperative gating of multiple motors attached to a single cargo (29), or in the design of synthetic molecular motors (30).