Evidence for adaptive radiation from a phylogenetic study of plant defenses

Abstract

One signature of adaptive radiation is a high level of trait change early during the diversification process and a plateau toward the end of the radiation. Although the study of the tempo of evolution has historically been the domain of paleontologists, recently developed phylogenetic tools allow for the rigorous examination of trait evolution in a tremendous diversity of organisms. Enemy-driven adaptive radiation was a key prediction of Ehrlich and Raven's coevolutionary hypothesis [Ehrlich PR, Raven PH (1964) Evolution 18:586–608], yet has remained largely untested. Here we examine patterns of trait evolution in 51 North American milkweed species (Asclepias), using maximum likelihood methods. We study 7 traits of the milkweeds, ranging from seed size and foliar physiological traits to defense traits (cardenolides, latex, and trichomes) previously shown to impact herbivores, including the monarch butterfly. We compare the fit of simple random-walk models of trait evolution to models that incorporate stabilizing selection (Ornstein-Ulenbeck process), as well as time-varying rates of trait evolution. Early bursts of trait evolution were implicated for 2 traits, while stabilizing selection was implicated for several others. We further modeled the relationship between trait change and species diversification while allowing rates of trait evolution to vary during the radiation. Species-rich lineages underwent a proportionately greater decline in latex and cardenolides relative to species-poor lineages, and the rate of trait change was most rapid early in the radiation. An interpretation of this result is that reduced investment in defensive traits accelerated diversification, and disproportionately so, early in the adaptive radiation of milkweeds.

The tempo of evolution is a key parameter in describing the diversification of life and is fundamental to the concept of adaptive radiation (1). It has been argued that an initially high rate of trait evolution followed by the slowing of trait change is a signature of adaptive radiation (1–3), because this pattern is concordant with niche-filling models where high rates of phenotypic change occur during ecological diversification. However, comparatively few studies have investigated the rate of trait evolution through time (4), with the notable exception of paleontological approaches (5). Now, the rapidly expanding palette of phylogenetic tools supports the rigorous test of historical hypotheses, such as rate change and directionality in character evolution, even for those taxonomic groups completely lacking a fossil record (4, 6–8). Recently developed models of adaptive radiation predict that trait change should be concentrated at early speciation events during clade diversification, followed by a decline in rate as the number of species increases (9, 10).

In this study, we assess the tempo of trait evolution in American milkweeds (Apocynaceae, Asclepias), a speciose clade (≈130 species) of toxic plants (11, 12). Enemy-driven adaptive radiation via the evolution of plant defenses was a key prediction of Ehrlich and Raven's coevolutionary theory (13), and milkweeds have played a prominent role in understanding the evolutionary ecology of plant-herbivore interactions (14–16). We thus focus on 7 traits, including seed size, foliar structural traits (leaf size, specific leaf area, and water content), and defenses (latex, trichomes, cardenolide content), and model their evolution on a molecular phylogeny. In particular, the defensive traits have been strongly implicated in providing milkweed protection against herbivores. Each trait can affect behavior (17), performance (14, 18, 19), and abundance of herbivores in the field (20). Given the potent defenses of the plant and the intimate evolutionary relationship with a highly specialized insect fauna (e.g., ref. 21), we propose that milkweeds are an excellent model system to test for the relationship between defense and adaptive radiation.

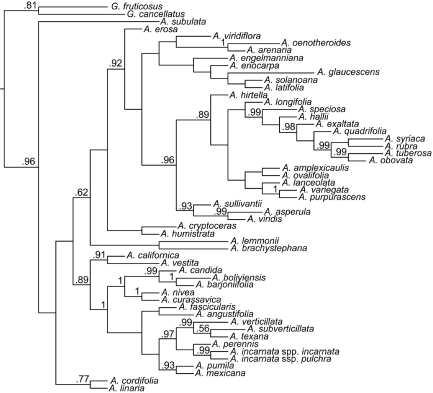
Here we test 1 prediction of the adaptive radiation hypothesis by modeling the tempo of phenotypic evolution through time using maximum likelihood techniques (2, 22). Our phylogenetic framework is a nearly complete species-level phylogeny of Asclepias (117 of ≈130 spp.) estimated from noncoding organellar DNA sequences (12), from which phenotypic data were obtained from 53 species (Fig. 1). Analyses were conducted assuming gradual and speciational modes of phenotypic evolution. Gradual evolution was modeled as occurring in proportion to branch lengths in a time-calibrated phylogeny; alternatively, speciational evolution was modeled as occurring in proportion to the number of intervening nodes (i.e., speciation events) from root to tips. For both gradual and speciational modes, we first fit 3 alternative models of how trait evolution depends on gradual or speciational distance on the underlying phylogeny: a simple random walk or Brownian motion; “varying rates,” in which a scaling parameter (δ) specifies whether the rate of trait evolution accelerates or decelerates through time; and “static optimum,” which proposes that trait evolution follows a constrained random walk through time with a single, global optimal trait value. The third model is an example of an Ornstein-Uhlenbeck (O-U) process (23). This static-optimum model is expected to fit the data best when traits are under stabilizing selection or, alternatively, when constraints impose bounds on possible phenotypic trajectories (23). The parameter δ scales the influence of shared phylogenetic path lengths: δ<1 indicates that shorter paths (i.e., those from the root to older nodes) have contributed disproportionately to trait evolution, indicative of adaptive radiation (1, 2).

Fig. 1.

Phylogeny of milkweed species sampled for phenotypic traits. The phylogeny is the all-compatible consensus of trees sampled in a Bayesian analysis of the complete dataset of 155 samples, pruned to the 53 taxa investigated here. Branch lengths are drawn in proportion to the number of speciation events between nodes; they are not equivalent in length because multiple speciation events in the complete phylogeny may occur on a single branch of the pruned phylogeny. Bayesian posterior probabilities >0.50 are indicated.

During evolutionary radiations, changes in diversification rate (i.e., speciation minus extinction), may be associated with directional trait evolution, thus leading to a phylogenetic trend. To test for this relationship, we evaluated the fit of an additional parameter (β) specifying a proportional relationship between the number of intervening nodes between the root and tips on the speciational phylogeny and the magnitude of trait values (2, 7, 24, 25). With a speciational mode of evolution, species with greater root-to-tip distances are members of lineages that have undergone greater net diversification; thus, a significant trend reflects an association between diversification rates and directional trait change. Using a smaller and independently collected dataset on 34 milkweeds (a subset of the species investigated here), we previously reported on directional trends in the expression of defense traits associated with resistance (mostly declining trends) and tolerance (increasing trends) (7, 24). However, these analyses assumed a constant rate of trait evolution; as developed here, changes in tempo and directional trends represent distinct aspects of trait evolution (Fig. 2).

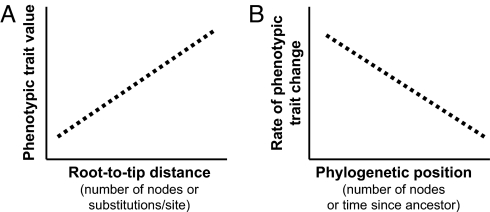
Fig. 2.

Two possible relationships between trait values and amount of phylogenetic divergence. (A) Directional evolutionary trend: root-to-tip phylogenetic distance is proportional to phenotypic trait value (e.g., body size, defense). When the x-axis is scaled as the number of nodes, this signifies a correlation between speciation events and trait evolution, possibly implicating the trait as a driver of diversification. When the x-axis is scaled as substitutions/site, this suggests a correlation between molecular divergence and phenotypic evolution. Such directional trends can be estimated with Pagel's scaling parameter β (2). (B) Shifting tempo of phenotypic evolution: scaled phylogenetic distances are proportional to phenotypic trait value. An exponent scales the relationship between phylogenetic distance and trait value; thus, the tempo of phenotypic change varies over time. In this study we used Pagel's δ as the scaling exponent (2). The commonly assumed constant rate of trait change would be represented by a flat line. Here, we assume that the rate of trait change decelerates, as is predicted during adaptive radiation, with early diverging lineages predicted to exhibit higher rates of trait change (and greater variance) as compared to later diverging lineages.

Thus, we take a rarely attempted integrated approach to address whether directional trait change is a component of adaptive radiation. A signature of traits influencing diversification rate that is consistent with adaptive radiation is directional phenotypic change, with early speciation events showing greater trait change than later speciation events (25).

Results and Discussion

Four of 7 traits (cardenolides, latex, trichomes, and seed mass) showed substantial phylogenetic signal, indicating that patterns of variation were predicted by evolutionary relationships (Tables 1 and 2); the 3 traits that lacked discernable phylogenetic signal (leaf water content, specific leaf area, and leaf size), also showed no evidence for a shifting tempo of trait evolution. These traits were best fit by a static-optimum (O-U process), suggesting bounds on phenotypic evolution that are often interpreted as indicating stabilizing selection or constraint. Both functional constraints and stabilizing selection have been shown to erode phylogenetic signal in trait variation (26). However, these same model comparisons (see Table 1) indicated evidence for an early burst of trait evolution (δ<1) for latex (speciational mode) and seed mass (gradual mode). Latex has been strongly implicated in adaptive radiation across angiosperm lineages as a key defensive innovation that spurred species diversification (27), and seed mass has similarly been suggested to be a key innovation through effects on habitat colonization (28).

Table 1.

Modeling the macroevolution of seven 7 milkweed traits using GEIGER

Evolutionary model	Gradual mode				Speciational mode				Interpretation
	P-value	Model parameter MLE	LL	AIC	P-value	Model parameter MLE	LL	AIC
Cardenolides
Phylogenetic signal	P = 0.007				P = 0.019				Phylogenetic signal in both models.
Brownian motion			−120.8	245.6			−124.2	252.4	O-U (stable optimum) is favored under both branch- length models.
Shifting tempo		δ = 3.810	−117.6	241.1		δ = 0.638	−123.8	253.6
O-U		α = 0.021	−117.4	240.9		α = 0.364	−119.4	244.9
Latex exudation
Phylogenetic signal	P = 0.012				P = 0.002				Phylogenetic signal in both models.
Brownian motion			−58.1	120.1			−68.1	140.2	Constant rate Brownian motion favored under gradual evolution.
Shifting tempo		δ = 0.504	−57.6	121.2		δ = 0.348	−65.8	137.6
O-U		α ≈ 0	−58.1	122.1		α = 0.129	−66.6	139.1	Shifting tempo evolution favored under speciational evolution (early burst, δ<1).
Trichome density
Phylogenetic signal	P = 0.040				P = 0.053				Phylogenetic signal in both models.
Brownian motion			−219.2	442.5			−224.5	453.0	Constant rate Brownian motion favored under both branch-length models.
Shifting tempo		δ = 0.564	−218.8	443.7		δ = 0.729	−224.2	454.5
O-U		α ≈ 0	−219.2	444.5		α ≈ 0.080	−224.3	454.6
Seed mass
Phylogenetic signal	P = 0.003				P = 0.384				Phylogenetic signal only in gradual model.
Brownian motion			−193.4	390.7			−219.9	443.8	Shifting tempo evolution favored under gradual evolution (early burst, δ < 1).
Shifting tempo		δ = 0.198	−190.8	387.6		δ = 0.096	−211.9	429.8
O-U		α ≈ 0	−193.4	392.7		α ≈ 0.422	−208.7	423.5	Stable optimum (O-U process) favored under speciational evolution.
Leaf water content
Phylogenetic signal	P = 0.336				P = 0.2756				No phylogenetic signal in either model.
Brownian motion			−167.4	338.8			−167.0	338.0	O-U (stable optimum) is favored under both branch-length models.
Shifting tempo		δ = 11.365	−157.7	321.4		δ = 1.964	−162.5	331.0
O-U		α ≈ 0.065	−157.7	321.4		α ≈ 0.735	−157.5	321.1
Specific leaf area
Phylogenetic signal	P = 0.079				P = 0.103				No phylogenetic signal in either model.
Brownian motion			−173.3	350.6			−174.5	353.0	O-U (stable optimum) is favored under both branch-length models.
Shifting tempo		δ = 8.329	−167.5	340.9		δ = 1.725	−173.1	352.3
O-U		α ≈ 0.047	−167.4	340.9		α ≈ 0.660	−167.2	340.5
Leaf size
Phylogenetic signal	P = 0.268				P = 0.4898				No phylogenetic signal in either model.
Brownian motion			−200.5	405.1			−204.7	413.4	O-U (stable optimum) is favored under both branch-length models.
Shifting tempo		δ = 8.243	−192.2	390.3		δ = 2.779	−196.8	399.5
O-U		α ≈ 0.048	−192.2	390.4		α ≈ 0.920	−192.8	391.5

Models were fit under 2 modes of evolution: gradual, in which phylogenetic distance is scaled as time, and speciational, in which phylogenetic distance is scaled as number of nodes (speciation events). The presence of phylogenetic signal was assessed using PHYSIG.M; P values reflect the probability of the data under the null hypothesis of no signal. Log Likelihood (LL) and Akaike's Information Criterion (AIC) values signify model fit (higher LL and lower AIC values indicate a better fit). A difference of 2 units is the cutoff for significance for tests of superior fit of one model over another using a likelihood ratio test (with df = 1). Fitted models include Brownian motion, shifting tempo, and stable optimum (O-U, modeled by an Ornstein-Uhlenbeck process). The shifting-tempo model assumes underlying Brownian motion evolution with an additional parameter (δ) that scales the relationship between branch length and character evolution. The O-U model includes a parameter (α) specifying the character's optimum. These analyses do not model directional trait evolution.

Table 2.

Maximum likelihood estimates (MLE) of phylogenetic signal (λ), path-length scaling parameter of varying rates model (δ), ancestral state, and slope of directional trend (β) on an equal branch-length phylogeny corresponding to speciational evolution (Figure 1) using Bayes Traits

	λ	δ	LL1	Ancestral state	β	LL2
Cardenolides	0.60* (0–0.69)	0.33* (0.22–0.48)	−119.9	13.94 (7.72–15.43)	−4.53* (−6.02 to −1.83)	−117.05
Latex exudation	1.03 (0.99–1.08)	0.36* (0.25– 0.77)	−65.9	5.33 (1.57–6.18)	−1.95* (−2.19 to −0.14)	−63.7
Trichome density	1 (0.99–1.07)	0.65 (0.31–1.65)	−225.1	7.09 (1.04–16.02)	−0.31 (−1.22 to 1.10)	−225.1
Sum of Z scores	1.03 (1–1.07)	0.44* (0.30–0.97)	−103.79	7.72 (1.60–933)	−2.64* (3.13 to −0.24)	−101.71
Seed mass	1 (0–1.09)	0.09* (0.05–0.37)	−211.94	360.22 (155.58–379.51)	−292.16* (−293.43 to −124.22)	−207.17
Leaf water content	0* (0–0.40)	1.28 (0.23–2.12)	−155.5	81.16 (81.00–81.75)	−0.13 (−0.41 to −0.01)	−155.1
Specific leaf area	0.36* (0–0.80)	0.26 (0.01–0.42)	−169.5	20.33 (20.17–21.67)	0.4 (−0.07 to 0.52)	−168.6
Leaf size	0.05* (0–0.25)	1.05 (0.38–1.42)	−191.62	12.35 (11.35–12.76)	0.45 (0.23 to 0.81)	−191

Seven milkweed traits and a composite defense index (sum of the Z-scores for cardenolides, trichomes, and latex) were analyzed. Sets that are 95% credible are reported for parameters by excluding the lowest and highest 2.5% of estimates across the 1,000 tree samples from the Bayesian stationary distribution. Starred values (*) are significantly different from a value of 1 for λ and δ, or from 0 (the null expectation of no trend) for β. λ and δ were estimated sequentially (simultaneous estimation gave very similar values) and fixed prior to estimating β (when the maximum likelihood values were not significantly different than 1, the parameters were set to 1). Log likelihood values are provided for a model without (LL1) and with (LL2) a directional trend, β (λ and δ were held constant) and the difference in LL values was tested using a likelihood ratio test with df = 1.

In previous studies we demonstrated directional trends in the evolution of milkweed defense traits (7). In particular, cardenolides (24) and latex (29) showed declining expression during the diversification of Asclepias, trichomes showed no trend (30), and phenolics and plant tolerance to damage showed evidence for escalation (7, 24). In this new, larger dataset we have evaluated not only the presence of directional trends in these and other traits, but importantly have evaluated the tempo of evolutionary changes. Here, because we focus on the relationship between traits and diversification, we only fit models of evolution to a speciational phylogeny (see Fig. 1). We found that seed mass shows a decelerating declining trend (see Table 2), possibly indicating that reduced investment in seed resources contributed to adaptive radiation of Asclepias. Additionally, we confirm declining directional trends for cardenolides and latex, and now show that the evolutionary models are best fit by accounting for a change in tempo (δ<1) (see Table 2, Fig. 3). As an index of overall defense investment, we also assess trait evolution of the sum of the Z-scores (standard normal scores) for cardenolides, latex, and trichomes (29, 31). Although this approach certainly omits some potentially important defensive traits of milkweeds (e.g., phenolics, cysteine proteases, waxes), given our previous demonstration of covarying evolution of milkweed defense traits (14), it is a better assessment of directional trends in overall defense expression than singleton measures. Indeed, here we also find a decelerating decline of defense investment (see Table 2). We thus interpret this result as consistent with an association between reduced investment in defense and species diversification that is disproportionately strong early in the history of Asclepias, as expected for adaptive radiation.

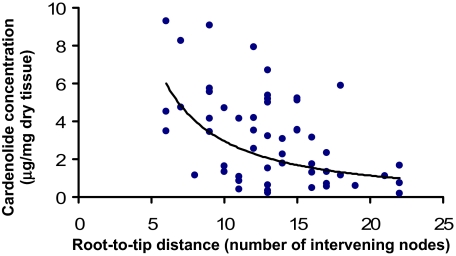
Fig. 3.

Phylogenetic deceleration of declining investment in cardenolides across 53 milkweeds. The x-axis shows the number of intervening nodes between the root and each taxon, calculated from the comprehensive phylogeny. Note that the decline is not linear, but is best fit by an exponential decrease (δ) in the rate of trait evolution during the radiation (see Table 2). The reduction of investment in cardenolides occurred disproportionately early in the diversification process.

In addition to the tempo of trait evolution shown here, Asclepias conforms to the general prediction of adaptive radiation in that early diversification appears to have been quite rapid. Although Apocynaceae fossils are too few to permit precise estimation of the clade's age, the preponderance of species in grasslands suggests a post-Miocene diversification (<25 MY) and the exceedingly short branches along the backbone of the phylogeny suggest that the initial diversification was especially rapid (12).

These decelerating declines in trait expression at macroevolutionary scales are somewhat nonintuitive, especially given the classic scenario proposed by Ehrlich and Raven (13) that increasing investment in defense would open adaptive zones during species radiation. We have speculated that paradoxical declines in investment may be the result of the dominance of the milkweed herbivore fauna by specialist insects (7). Despite the fact that cardenolides and latex reduce herbivory in extant communities, each of the specialized herbivores employs several mechanisms to circumvent or attenuate the negative effects of these defensive traits (17, 32). Thus, costs of investment in poorly functioning defenses may present limitations on diversification, and investment in alternative strategies may be favored (7, 14, 33). Recent theory has begun to address countervailing trends at micro- and macroevolutionary scales, which are apparently common (34). How and why particular traits (and their impact on herbivory) may affect diversification is mechanistically unclear (35). Nonetheless, we have shown here that some traits show patterns of evolution consistent with an impact on adaptive radiation.

Modeling Trait Evolution in Adaptive Radiation.

Because most models of trait evolution posit that closely related species will be more phenotypically similar than distantly related species, it is critical to address whether Brownian motion models are sufficient to explain patterns of trait evolution, or data are better fit by alternative models of processes, such as stabilizing selection, adaptive radiation, or directional trends (9, 10). Statistical models for the evolution of phenotypic characters on phylogenies are increasing in complexity and power (8, 26, 36, 37). Even so, available approaches can be limited when it comes to simultaneously evaluating diverse evolutionary processes. Here, we have considered stable optima, shifting tempos, and directional trends in trait evolution, but with the limitation that the generalized least-squares approaches we favor do not accommodate simultaneous evaluation of all these processes. In particular, we cannot evaluate directional trends on a phylogeny in which branch lengths are scaled to time (8). Thus, we compared 3 evolutionary models on both gradual and speciational phylogenies, but without assessing directional trends (see Table 1). We evaluated evolutionary trends in comparison to 2 other models, but only under the assumption of a speciational mode of evolution (see Table 2). We consider the latter comparisons important because of the apparently strong directional trends observed in this system (7, 24) and because some traits (e.g., seed mass and defense traits) exhibit strong patterns of both shifting tempo and directional trends. Our results highlight the need for further analytical development of unified approaches to the macroevolution of phenotype.

Thus far, most studies of directional trends and early bursts of evolution indicative of adaptive radiation have focused on single traits (6, 38, 39). In this study, we consider several defense traits, seed mass, and leaf structure. We are in need of more general predictions for the types of traits we expect to show particular macroevolutionary patterns. Indeed, we have shown that divergent traits show radically different patterns of trait evolution, although the causes of such variation are poorly understood.

Future Directions.

We conclude with a set of questions, speculation, and suggested avenues for future work. Although we find that some traits exhibit changes in evolutionary tempo and direction consistent with adaptive radiation, we lack a mechanistic understanding that would predict the relationship between population processes and macroevolutionary patterns. Further theoretical and empirical work is needed to answer several key questions:

• (i) Why do some traits show evidence for static optima (O-U model) and others not? Does this truly reflect stabilizing selection across the vast range of ecological and physiological conditions tolerated by milkweeds? Or might this reflect developmental constraints, pleiotropy, or other factors that impose limits on phenotypic evolution? Can the O-U process be incorporated into models with directional trends or time-varying optima (40) to take a more holistic approach to bridging population and clade-level processes in a statistical modeling framework? Additional phylogenetic methods are needed, and multiple traits should be considered in future studies.

• (ii) Are milkweeds a special case, where resistance strategies have not only declined during the radiation, but the declining investment shows a pattern of early burst trait change? It may be that alternative defensive strategies are evolving in response to the specialized herbivore community of milkweeds, and the pattern of early deceleration observed here corresponds with escalation of other traits (7, 14, 24). Patterns in other systems need to be identified, and greater phylogenetic depth should be included in future studies, so as to address the impact of traits on diversification at broader scales.

• (iii) Although our data are somewhat consistent with the basic tenets of Ehrlich and Raven's coevolutionary model, a more mechanistic theory is needed to address why specific traits may influence diversification rates (both increases and decreases). How might costs of defense, plant allocation patterns, and differential investment in alternative defenses interact with the speciational process? Are there alternative interpretations of the association between directional trends and early burst trait evolution? Is a revision of the classic model of Ehrlich and Raven (13) required to accommodate potentially conflicting effects of traits, some of which covary in syndromes, as well as the potential for various guilds of herbivores that may differ dramatically in degree of host specialization?

• (iv) Does adaptive evolution spur speciation or does speciation spur character change? Correlational analyses, such as those used here, may find associations between tempo, direction of character change, and the diversification of clades. Certain classes of traits might drive evolutionary trends through their effects on rates of speciation and extinction (41). However, it is also true that trends might arise as a consequence of speciation itself, if either speciation events tend to preserve character change within lineages (42), or if postspecational character displacement is common (1).

Materials and Methods

Plants and Traits.

Plants from the 53 species were grown from seed in a controlled-environment growth room and traits were assessed following the protocols outlined in ref. 14, with modifications listed below (mean of 8 replicate plants per species). After 1 month of growth, we assayed latex exudation, sampled a 6-mm diameter punch (for percent-water and specific leaf area), and harvested all above-ground tissues directly above the soil with scissors. Trichome density was assessed using a dissection microscope and was specifically aimed at determining the number of trichomes encountered by small chewing herbivores, such as monarch caterpillars. Thus, in a transect perpendicular to the mid-vein, we counted the number of hairs on the abaxial side that intersected a 3-mm line (0.25 mm wide) segment using an ocular micrometer. All above-ground plant tissues were freeze-dried, weighed to assess dry mass, ground to a fine powder, and analyzed for cardenolides. Cardenolides were assessed on 2 replicates of each species by high-performance liquid chromatography using methods modified from ref. 43, with digitoxin as the internal standard.

Phylogenetic Analysis.

We estimated the phylogeny of the 51 Asclepias and 2 Gomphocarpus species using DNA sequences obtained for a comprehensive phylogeny of the genus (125 Asclepias and 20 Gomphocarpus) (12). The 53 species were selected primarily because of seed availability; however, the sample includes representatives of 10 of the 13 major clades identified in analyses of the complete dataset (12), minimizing the potential for bias because of nonrandom sampling. Analyses of trait evolution used the “all compatible” consensus of trees sampled from the stationary distribution of the Bayesian analysis, from which all taxa for which we did not obtain trait data were pruned. Branch lengths under the gradual mode were estimated by expected rates of nucleotide substitution in the noncoding plastid DNA sequences. To preserve true path lengths in the speciational tree, we set all branch lengths in the full (n = 145) taxon tree equal to unity, then pruned the tree to the set of taxa for which trait data were collected (n = 53). Hence, all branch lengths in the speciational tree were integer values that reflected the true number of speciation events inferred to have occurred, and path lengths in the speciational tree are not biased by incomplete taxon sampling.

For analyses under the gradual mode, trait change was modeled as a function of time. We generated an ultrametric phylogeny of Asclepias from the Bayesian consensus tree using penalized likelihood in the program r8s (44), with a smoothing parameter selected via cross-validation. Because of the absence of a fossil record for the milkweed subfamily Asclepiadoideae, we lack adequate calibration points for dating nodes and use a relative time-scale for lineage divergence. Because some partitions of the all-compatible consensus had low Bayesian posterior probabilities, we accounted for phylogenetic uncertainty where possible by estimating parameters across a sample of 1,000 trees from the posterior distribution of the Bayesian analysis.

Trait Evolution.

We modeled trait evolution with maximum likelihood methods using GEIGER (22) and Continuous implemented in Bayes Traits (2). We first tested whether the 7 traits showed phylogenetic signal using PHYSIG.M (45). Phylogenetic signal was assessed under both gradual and speciational evolutionary modes. We next fitted and compared 3 models of trait evolution in GEIGER, including Brownian motion, shifting tempo modeled with Pagel's parameter δ (2), and stable optimum modeled by an O-U process with a single optimum (23).

We assessed the presence of phylogenetic trends in each trait using model comparisons in Continuous (2). We sequentially estimated phylogenetic signal modeled by the parameter λ (46) and shifting tempo modeled by δ (2). The significance of each parameter is assessed by comparison to a model lacking that parameter. Departures of the maximum likelihood estimates of λ and δ from 1 were made with likelihood ratio tests (2). After fixing the values of λ and δ to 1 (if not significantly different) or their maximum likelihood estimates, we estimated directional trends modeled by the parameter β (2, 8). The β parameter is the regression slope of trait value on root-to-tip branch length.