Encoding and Decoding of Learned Smooth-Pursuit Eye Movements in the Floccular Complex of the Monkey Cerebellum

Javier F Medina; Stephen G Lisberger

doi:10.1152/jn.00075.2009

. 2009 Jul 22;102(4):2039–2054. doi: 10.1152/jn.00075.2009

Encoding and Decoding of Learned Smooth-Pursuit Eye Movements in the Floccular Complex of the Monkey Cerebellum

Javier F Medina ¹, Stephen G Lisberger ^2,^✉

PMCID: PMC2775373 PMID: 19625543

Abstract

We recorded the simple-spike (SS) firing of Purkinje cells (PCs) in the floccular complex both during normal pursuit caused by step-ramp target motions and after learning induced by a consistently timed change in the direction of target motion. The encoding of eye movement by the SS firing rate of individual PCs was described by a linear regression model, in which the firing rate is a sum of weighted components related to eye acceleration, velocity, and position. Although the model fit the data well for individual conditions, the regression coefficients for the learned component of firing often differed substantially from those for normal pursuit of step-ramp target motion. We suggest that the different encoding of learned versus normal pursuit responses in individual PCs reflects different amounts of learning in their inputs. The decoded output from the floccular complex, estimated by averaging responses across the population of PCs, also was fitted by the regression model. Regression coefficients were equal for the two conditions for on-direction pursuit, but differed for off-direction target motion. We conclude that the average output from the population of floccular PCs provides some, but not all, of the neural signals that drive the learned component of pursuit and that plasticity outside of the flocculus makes an important contribution.

INTRODUCTION

The floccular complex of the cerebellum plays a critical role for the initiation and steady state of smooth-pursuit eye movements. Lesions of the floccular complex cause deficits in pursuit (Rambold et al. 2002; Zee et al. 1981), whereas stimulation evokes smooth eye movements with latencies of about 10 ms (Lisberger 1994), as expected, given the disynaptic pathway from floccular Purkinje cells (PCs) to extraocular motoneurons (e.g., Highstein 1973). Recordings have revealed strong modulation of the simple-spike (SS) firing of floccular PCs during pursuit of sinusoidal and step-ramp target motion (Highstein and Hirata 2000; Lisberger and Fuchs 1978; Miles and Fuller 1975; Stone and Lisberger 1990a). The SS response is driven by a combination of inputs related to visual image motion and eye motion and can be described in terms of the kinematics of the eye movement: eye position, velocity, and acceleration (Shidara et al. 1993).

Several lines of evidence suggest that the floccular complex also plays a key role in motor learning in pursuit, and even could be a site of plasticity. Recordings from floccular PCs during learning have revealed changes in SS responses (Kahlon and Lisberger 2000; Medina and Lisberger 2008), as also has been found across the cerebellar cortex in several other motor systems (Blazquez et al. 2003; Catz et al. 2008; Dufossé et al. 1978; Gilbert and Thach 1977; Green and Steinmetz 2005; Lisberger et al. 1994b; Ojakangas and Ebner 1992). Analysis of the smooth eye movement region of the frontal eye fields suggested that learning occurs downstream from the cerebral cortex, perhaps in the cerebellum (Chou and Lisberger 2004). Finally, there is evidence of climbing-fiber–driven plasticity in the floccular complex during learning in pursuit (Medina and Lisberger 2008).

To better understand the operation of the floccular complex during pursuit learning, we have studied two separate but related issues regarding the effects of learning on the SS responses of floccular PCs. The first issue is about encoding: how are learned eye movements represented in the SS firing of individual floccular PCs? Does each PC undergo changes in its SS response that can be predicted from its individual response during normal pursuit? An affirmative answer would suggest that the learned component of the SS response simply reflects the kinematics of the learned movement itself. Alternatively, if we found that the learned component of the SS responses was larger or smaller than predicted, given each PC's responsiveness during normal pursuit, then we might conclude that each PC undergoes local plasticity in proportion to some feature of the inputs it receives during learning. Our data support the latter conclusion: the encoding of eye-movement kinematics by individual PCs can be quite different for normal versus the learned component of pursuit. We suggest that the encoding of learned eye movements results from local plasticity in each individual PC based on its private blend of inputs from parallel fibers and climbing fibers during learning.

The second issue is about decoding: how are the output signals from the population of PCs converted into smooth eye movement? Does the pooled output from floccular PCs have the same relationship to eye movement for the normal and the learned components of pursuit? If so, we could conclude that the output from the floccular complex is appropriate to drive smooth eye movements under all conditions. If not, we would have to propose that other structures make differential contributions that depend on the behavioral condition. For example, it is possible that the learned change in floccular output is small compared with its output during the same size eye movements in normal pursuit. In that case, another structure would have to contain the majority of the neural plasticity responsible for pursuit learning. Our data show that the relationship between the population average of SS firing rate and eye movement is somewhat different for normal initiation versus the learned component of pursuit, at least in the off-directions of PCs. We suggest that there are other sites of plasticity that contribute—along with the floccular complex—to pursuit learning.

METHODS

We recorded eye movements and the activity of single Purkinje cells in the floccular complex of the cerebellum during normal and learned pursuit eye movements in two awake monkeys who had been trained to fixate and track visual stimuli in exchange for fluid reinforcements. All procedures were approved in advance by the Institutional Animal Care and Use Committee at University of California, San Francisco (UCSF) and were in compliance with the National Institutes of Health Guide for the Care and Use of Laboratory Animals.

Surgical procedures, monkey training, recording methods, and visual stimuli

After the monkeys had undergone initial behavioral conditioning to move voluntarily from their home cage to the primate chair and to take water from a spout, we performed three surgeries to instrument them for experiments (see Ramachandran and Lisberger 2005). Monkeys were anesthetized with isoflurane during surgery and received nonsteroidal antiinflammatory drugs (Meloxicam) and opiate analgesics (Buprenex) for several days after each surgery. First, we used dental acrylic and orthopedic-grade titanium screws (6–8 mm) and straps to secure a socket on the skull that served as a receptacle for restraining the monkey's head during experiments. After allowing 4 wk for the bone to heal around the screws and straps, we performed a second surgery to suture a 16-mm-diameter coil to the sclera so that we could use the magnetic search coil system to measure horizontal and vertical eye positions with high spatial and temporal resolution. We then took several weeks to train the monkey to fixate and track visual stimuli in exchange for fluid reinforcements. Once fully trained, monkeys received most of their fluid during daily experiments, plus supplements to bring them up to a level of fluid intake sufficient to maintain their weight and health as judged by UCSF veterinarians. Finally, we performed a third surgery to make a circular opening in the bone and cement a cylinder to the skull to provide access to the floccular complex with metal microelectrodes. The cylinder was cleaned regularly and maintained with topical antibiotics.

During experiments, we used an analog circuit to create signals proportional to horizontal and vertical eye velocities. The circuit differentiated the eye-movement signals from the eye coil electronics for frequencies ≤25 Hz and rejected higher frequencies. We then digitized signals proportional to horizontal and vertical eye position, eye velocity, and target position at 1 kHz per channel during experiments. Neural recordings were amplified and filtered using conventional electronics (band-pass 100 Hz to 8 kHz) and viewed on oscilloscopes. We rewarded the monkey for tracking sinusoidal target motion at 0.5 Hz along the horizontal and vertical axes while searching for PCs. Each PC we encountered was characterized as primarily horizontal or vertical by listening to its discharge on the audio monitor. Characterization was confirmed by quantitative analysis after the experiment. During single-unit recording, we used a time and amplitude window discriminator to trigger the action potentials from a single PC and the computer recorded the time of spikes to the nearest 10 μs. We also digitized the raw spike records at 25 kHz and saved the entire record to allow the option of software window discrimination after the experiment. Inspection of the records from all PCs verified that we had recorded the activity of single PCs and that each exhibited a complex spike during at least part of the recording session.

Visual stimuli consisted of bright spots, 0.5° in diameter, presented on the face of an analog oscilloscope. The inputs to the oscilloscope were provided by a digital signal processing board in our experimental control computer, allowing nominal spatial resolution up to the 16 bits of the D/A converters (2¹⁶ pixels across the screen) and temporal resolution of 4 ms. The oscilloscope screen measured 12 in. along the diagonal and was positioned 30 cm in front of the monkey to cover 48 × 38° of visual field in the horizontal and vertical directions.

Experimental design

Tracking stimuli were presented in discrete trials. Each trial began with the appearance of a stationary spot that the monkey was required to fixate for a random period that varied from 600 to 1,000 ms. Then, the target underwent step-ramp motion (Rashbass 1961) and continued in one of the four possible trajectories shown in Fig. 1. In a prelearning block of trials, we studied the normal initiation and steady state of pursuit by presenting targets that moved at 20°/s in the on- and off-directions for the SS firing of the PC under study; some prelearning blocks also included target motion in the on-direction at 10 and 30°/s. Figure 1A shows the eye movements and average SS firing rate for a typical PC during step-ramp target motion at 20°/s in its on-direction (rightward). In the prelearning block, we also collected a baseline for evaluating the effects of learning by presenting “probe” trials in which the target moved at 20°/s in a direction that was orthogonal to the preferred axis of the PC under study. In Fig. 1B, the direction of the prelearning probe target was downward and there was no clear SS response before learning (black traces). The prelearning control block also contained trials that we called “mimic” trials (Fig. 1C) because they caused eye motion in the direction of the learned eye movement we expected to see after learning. Mimic trials provided data to compare PC responses to smooth eye movements of approximately the same direction and speed, but measured either for normal pursuit initiation or as a consequence of learning. In Fig. 1C, the target moved downward at 20°/s and to the right at 4°/s.

Finally, we proceeded to a learning block that was designed to cause directional learning in pursuit (Medina et al. 2005). Learning trials (Fig. 1D) started with target motion in the same direction as the probe trials, orthogonal to the preferred-null axis of the PC under study. After 250 ms of motion, the target changed direction and provided an instructive signal for learning by adding a component of motion at 30°/s in either the on- or off-direction of the PC. In any given learning block, the instructive signal was always in the same direction. In addition, each learning block contained a low density of randomly interspersed probe trials, with the density increased to 10% after 100 learning trials, when the learned behavior was clearly established; data from those postlearning probe trials appear as gray traces in Fig. 1B. For most PCs, we were able to run a full learning block in each direction with nearly 100 probe trials interspersed between blocks to extinguish the prior learning.

Data analysis

Data were analyzed after the experiments in two steps. In the first step, we inspected every trial, verified that the individual action potentials were triggered reliably, and used a cursor to point out the start and end of all saccades. In the second step, we grouped all the responses to the same type of trial and calculated the average eye movement and firing rate. Firing rate was estimated using the algorithm developed by Lisberger and Pavelko (1986) to calculate the reciprocal of interspike intervals at each time in the analysis. Intervals in which saccades had occurred were treated as missing data, by completely leaving those intervals out of the analysis. As a result, averages were based on fewer trials in the intervals in which the structure of the target motions cause a high probability of saccades.

Analysis was performed using Matlab (The MathWorks, Natick, MA). Regression analysis used the function “regress,” which returns statistics as well as confidence intervals on each regression coefficient. In some analyses, we performed regression using the firing rate and eye movement that had been averaged across multiple repetitions of the same target motions. Before performing regression, we computed average eye acceleration as the difference of successive time points in the averages of eye velocity, divided by the temporal interval of 2 ms. We then smoothed the averaged eye velocity, eye acceleration, and firing rate traces with a 16-point filter implemented by the function “filter.” Averages of eye position did not require smoothing. In other analyses, we performed regression using the firing rate from individual trials and either the average eye movement or the eye movements from individual trials. To do this, we extracted the relevant segments of firing rate from each trial and concatenated them to create a long array of firing rates. We created equal-length arrays that either comprised sequential repetitions of identical averages of eye velocity, acceleration, and position the requisite number of times or the eye movements from the individual trials. For example, for an analysis based on 550 samples of data (at 2-ms intervals) from each of 40 trials, each array was 22,000 points long (550 points × 40 repetitions). We will show that we obtained the same results when we constructed the arrays with either the average eye movements or the data from each individual trial. We chose to emphasize the results based on average eye movements because differentiation of the individual eye velocity traces yielded eye acceleration records that were quite noisy. Further analyses are described at the relevant locations in the results.

RESULTS

The simple-spike (SS) firing of floccular Purkinje cells (PCs) is modified in association with learning in pursuit eye movements (Kahlon and Lisberger 2000; Medina and Lisberger 2008). One of the goals in the present study was to evaluate whether the size of the learned changes in a given PC is predicted by the response of the same PC during the initiation of pursuit or whether the learned component of PC firing rate shows a markedly different relationship to the learned component of eye movement. To do so, we went through a series of analyses. First, we expanded others' use of linear regression to describe the SS firing rate of PCs as a linear combination of eye-movement parameters (Krauzlis and Lisberger 1994; Shidara et al. 1993), testing which components of eye movement should be included in the most appropriate regression model. Second, we used the most appropriate regression models to show that the sensitivity to eye velocity can be very different for the learned component versus the initiation of pursuit and that the differences are statistically significant. Third, we verified that our conclusions did not depend on the direction of the eye movements evoked during the initiation of pursuit. Fourth, we showed that the differences do not depend on the details of the regression model. We concluded with two analyses designed to inform questions of how learning in SS firing is controlled by climbing fiber and parallel fiber inputs in individual floccular PCs and of the overall contribution of the population of floccular PCs to the learned response.

Linear regression analysis of floccular SS firing rate

We analyzed data from 48 PCs studied before and after learning in both the on- and off-directions and from 8 additional PCs for learning in the off-direction only. The same PCs comprised much of the database for a prior study (Medina and Lisberger 2008). During pursuit of step-ramp target motion, the encoding of eye movement by the SS firing rate [fr(t)] of individual floccular PCs can be described as a linear function of eye acceleration, velocity, and position (Krauzlis and Lisberger 1994; Shidara et al. 1993). Herein, we start by addressing the question of the most appropriate regression model by testing four different models

f r (t) = a Ë (t + Δ t) + b Ė (t + Δ t) + r r

(1)

f r (t) = a Ë (t + Δ t) + b Ė (t + Δ t) + c E (t + Δ t) + r r

(2)

f r (t) = a_{p} Ë_{p} (t + Δ t) + a_{n} Ë_{n} (t + Δ t) + b Ė (t + Δ t) + r r

(3)

∥ f r (t) = a_{p} Ë_{p} (t + Δ t) + a_{n} Ë_{n} (t + Δ t) + b Ė (t + Δ t) + c E (t + Δ t) + r r ∥

(4)

where Ë(t), Ė(t), and E(t) indicate, respectively, eye acceleration, velocity, and position as functions of time. Ë_p(t) and Ë_n(t) indicate the positive and negative going parts of eye acceleration, respectively, with values of the opposite sign replaced by zeros. The various coefficients, a, a_p, a_n, b, and c are scaling factors that can be thought of as the sensitivity of the PC to each of these kinematic parameters and rr is the resting rate during fixation at straight-ahead gaze.

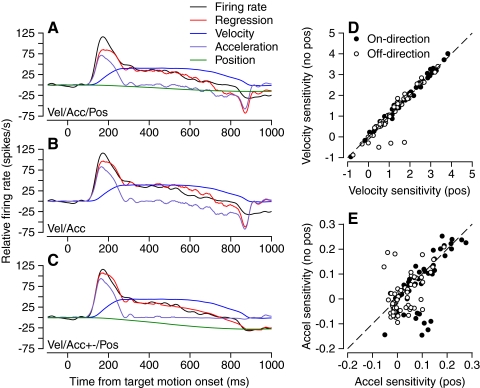
Figure 2 compares the results of regression analysis with Eqs. 1, 2, and 4 for normal pursuit of step-ramp target motion in a representative PC. For all three equations (Fig. 2, A–C), the average firing rate (black trace) was reproduced quite well by the linear regression model (red trace). However, there are subtle differences that are related to the temporal structure of eye velocity and firing rate. The fit is best for Eq. 4 (Fig. 2C), which includes separate coefficients for positive and negative values of eye acceleration and a coefficient for eye position. Comparison with the fit obtained from Eq. 2 (Fig. 2A), with a single eye acceleration coefficient, reveals that splitting the eye acceleration into positive and negative parts allows the model to better reproduce the firing rate at the onset and offset of pursuit, when there were large positive and negative eye accelerations. A single eye acceleration coefficient yields poorer fits because it forces a compromise between a high sensitivity to eye acceleration at the start of pursuit and a lower sensitivity to deceleration at the offset, leading to a decrement in the accuracy of the linear regression model at those times. Comparison with the fit obtained from Eq. 1 (Fig. 2B), without a position coefficient, reveals that the presence of a position coefficient allows the model to fit the change in steady firing rate between the two fixation intervals, before and after pursuit. The fit for Eq. 3 is not shown, but had the advantages of the split acceleration sensitivity in Fig. 2C and the disadvantages of the absence of a position coefficient in Fig. 2B. Even without statistical analysis of the quality of the fits, Fig. 2, A–C illustrates that the best account of PC firing during the initiation of pursuit will come from Eq. 4 because it is best suited to account for the temporal structure of PC responses.

Fig. 2. — Linear regression analysis of the initiation of pursuit for a representative PC. In A–C, the *black*, *red*, *purple*, *blue*, and *green traces* show, respectively, the actual firing rate, the prediction of the linear regression model, the eye acceleration component [aË(t) or *a_p*Ë(t) + *a_nË_n*(t)], the eye velocity component [bË(t)], and the eye position component [cE(t)]. Regression models are *Eq. 2* in A, *Eq. 1* in B, and *Eq. 4* in C. D: scatterplot showing near identity of eye velocity regression coefficients based on regression with *Eq. 3* on the y-axis vs. *Eq. 4* on the x-axis. E: scatterplot showing similarity of positive eye acceleration regression coefficients based on regression with *Eq. 3* on the y-axis vs. *Eq. 4* on the x-axis. In D and E, filled and open symbols show data for on-direction and off-direction of pursuit.

Figure 2D shows that the eye velocity coefficient of the regression did not depend materially on whether the regression model was Eq. 3 or 4, with or without the eye position coefficient. Only a few PCs fell far from the line of slope 1 (dashed line) and only for off-direction pursuit initiation. The positive acceleration sensitivity (a_p) depended somewhat more on whether the regression model included a position coefficient, but most PCs still fell close to the line of slope 1 (Fig. 2E, dashed line). Given the similarity of the velocity and acceleration regression coefficients across regression models, it is not surprising that the conclusions of the study are insensitive to the choice of regression model, as we will show in the following text.

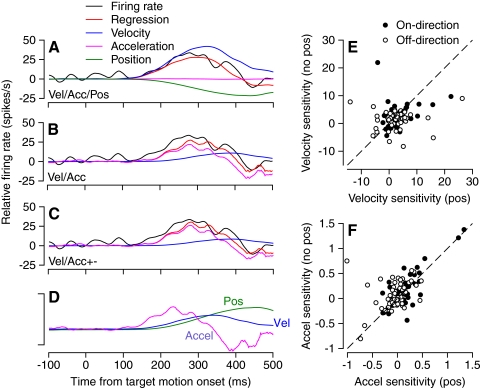
Figure 3 compares the results of using the regression model in Eqs. 1, 2, and 3 to fit the learned component of a representative PC's responses. To isolate the learned component of the response, we subtracted the average eye velocity and firing rate for prelearning probe trials from the average responses for probe trials that were presented late in the learning block. The subtraction procedure allowed us to separate the learned response from the initiation of pursuit and made it possible to ask the question of whether the regression coefficients for the learned component were different from those for the initiation of pursuit. Attempts to perform regression analysis without isolating the learned component would have led to a compromise between the correct coefficients for pursuit initiation in the direction of the probe trials and for the learned component and would have prohibited a clear answer to our main question. As illustrated in Fig. 1B, the SS firing rates in prelearning and postlearning probe trials superimposed during the initiation of pursuit and separated transiently only in relationship to the learned component of the eye movement. The similarity of the pre- and postlearning firing rates during the first part of the probe trial is an important prerequisite for the success of the subtraction analysis and was confirmed by inspection of the averaged responses from each PC in our sample.

For the PC illustrated in Fig. 3, all three regression models provided quite good accounts of the learned component of firing rate. However, the model that included a position coefficient (Fig. 3A) overfitted the response by playing the velocity (blue curve), acceleration (purple curve), and position (green curve) components against each other, leading to a much larger eye velocity coefficient than that found with models that did not include the position coefficient (Fig. 3, B and C). Finally, comparison of Fig. 3, B and C shows that it did not make much difference whether the regression model for the learned component included positive and negative components of eye acceleration. The fit for Eq. 4 is not shown because it had the same disadvantages provided by the position coefficient in Eq. 2 (Fig. 3A).

For the population of PCs, the presence or absence of a position component in the regression equation had a substantial impact on the values of regression coefficients for eye velocity (Fig. 3E) and positive eye acceleration (Fig. 3F). By comparison with the same analysis for the initiation of pursuit (Fig. 2, D and E), the values of each coefficient varied over a much wider range and the points for the individual cells did not cluster effectively around the lines of slope one (dashed lines).

Does the best regression model for the learned component of pursuit include a position component or not? We think that the position component allows overfitting for the learned component of firing rate and risks giving incorrect velocity and acceleration coefficients. For the learned component of pursuit, eye position is the same at the start and end of the response and does not constrain the eye position coefficient in the way it does for pursuit of step-ramp target motion. For the learned component, the regression model can play position against velocity or acceleration. Further, the maximum excursion of eye position in the learned component of eye movement averaged just 1° and should not be an important factor in determining the SS firing of PCs that are normally much more sensitive to eye velocity and eye acceleration. For the initiation of on-direction of pursuit, the position coefficient using regression Eq. 4 averaged 0.13 with SD of 1.96. For the on-direction learned component of pursuit, the position coefficient for the same regression equation averaged −6.75 with SD of 36.5. Only 11 of 48 of the position coefficients for the learned component fell within the full range of position coefficients for the initiation of pursuit. The situation was just as extreme for the off-direction data. We find it hard to imagine that such an enormous difference between the initiation of pursuit and the learned component is anything but an artifact of overfitting. We conclude that Eq. 3 is best suited to account for the temporal structure of PC responses when the position coefficient is unconstrained by the data and that it provides the most appropriate regression model for the learned component of pursuit.

Figure 4 compares cumulative probabilities of the “Variance Accounted For” or “VAF,” for each of the different regression models

V A F = 1 - \frac{var [f r {(t)}_{p r e d} - f r (t)]}{var [f r (t)]}

(5)

where the variances are computed across the full time course of the fitted response and fr(t) and fr(t)_pred are the actual firing rate and the prediction from the best fitting regression model as functions of time. For the initiation of pursuit (Fig. 4, A and B), VAF was generally quite high, with all regression models accounting for >75% of the variance of firing rate in about 70% of PCs. There were subtle differences between models. For both on-direction and off-direction pursuit initiation, the models that included position components (solid red and blue curves) provided the best account of firing rate, although the other models were little worse. It made little difference in VAF to split the eye acceleration traces into positive and negative components, but we chose to do so because it provided esthetically more pleasing regression fits, as illustrated in Fig. 2C. For the learned components of pursuit (Fig. 4, C and D), all the regression models accounted for less of the variance than they did for the initiation of pursuit. We attribute this difference to the fact that the noise levels were comparable for the initiation of pursuit and the learned component, but the response amplitudes were much larger during pursuit initiation. Thus the difference in VAF between conditions reflects the signal-to-noise properties of the data rather than a differential success of the regression models. Finally, although adding parameters to the regression model always improved the fit according to the coefficient of determination (r²), there were some minor deviations from this expectation for VAF computed by Eq. 5, leading to some crossed curves in Fig. 4.

Fig. 4. — Analysis of the fraction of variance of average firing rate accounted for by different regression models. Each graph shows a collection of cumulative distributions of variance accounted for (VAF) when different regression models were applied to the same data. A: on-direction pursuit initiation. B: off-direction pursuit initiation. C: on-direction learned component of pursuit. D: off-direction learned component of pursuit. Key is: *Eq. 1*, acc/vel; *Eq. 2*, acc/vel/pos; *Eq. 3*, acc+−/vel; *Eq. 4*, acc+−/vel/pos.

During data analysis, we ran the regression models for values of Δt ranging from firing rate lagging to leading the regression model by ≤80 ms. We then used the regression fit for the value of Δt that provided the highest value of r². For Eqs. 1–4, the median values of Δt for the initiation of pursuit in the on-direction were 2, 12, 12, and 14 ms, indicating that the firing rate led the regression prediction for eye movement. For the initiation of pursuit in the off-direction, the values were: −10, 2, 14, and 16 ms. For Eq. 3, the median value of Δt for the learned component of firing rate was 8 ms leading the regression prediction in the on-direction and 0 ms in the off-direction. These values established the plausibility that PC firing is timed appropriately to drive both the initiation of pursuit and the learned component of eye movement (see also Medina and Lisberger 2008).

Encoding of eye movement during different tracking conditions in individual PCs

The encoding of eye movement varied quite considerably within individual PCs when comparing normal versus learned pursuit responses. In making this comparison, it is important to emphasize that we are testing for a difference in the regression coefficients for the initiation of pursuit versus the learned component that has been isolated from the response to the initiation of pursuit. Our analysis is not intended to test for a change in the regression coefficients during the initiation of pursuit as a function of learning. Indeed, we would not expect to find changes in sensitivity or response amplitude outside the brief window when the learned response is expressed (Fig. 1B), around the time of the instructional change in target direction in the learning trials (Fig. 1D).

Figure 5 shows traces of average firing rate and eye velocity as a function of time for a PC that had a much larger eye velocity coefficient for the learned component versus the response for pursuit initiation. The averages of eye velocity show a large difference between the two conditions, with a steady eye velocity of 20°/s during the initiation of pursuit (Fig. 5B, black arrow) and a peak of just under 5°/s in the learned component of pursuit (Fig. 5B, dashed arrow). However, the part of the firing rate response that was related to eye velocity was disproportionately large for the learned component. The sustained firing rate in the interval from 300 to 500 ms after the onset of target motion for pursuit initiation averaged around 30 spikes/s above the resting rate (Fig. 5A, black trace and arrow), whereas the learned component of SS firing rate was a satisfactory model of eye velocity and reached a peak of 40 spikes/s (Fig. 5A, dashed trace and arrow). Because the firing rate was quite large and the eye velocity small during the learned component, the regression coefficient for eye velocity was much larger for the learned component than that during the initiation and steady state of pursuit. In interpreting Fig. 5, note that the early, large peak of firing rate during pursuit initiation (Fig. 5A, black trace) occurs during the initial eye acceleration of pursuit and would be reflected in the regression coefficient for positive eye acceleration rather than that for eye velocity.

Fig. 5. — Comparison of learned component of responses and initiation of pursuit for a PC with a large difference in eye velocity regression coefficients. *Black* and dashed *traces* show responses to step-ramp target motion and the learned component of pursuit. Arrows show the values of each curve during the appropriate measurement interval. Note that the data for the initiation of pursuit have a large transient response during the rapid eye acceleration, but a lower steady firing related to steady eye velocity. The latter is responsible for the value of the eye velocity regression coefficient for the responses to step-ramp target motion.

To compare the coefficients for the initiation of pursuit statistically with those for the learned component in each PC, we performed regression analysis on the full set of individual firing rate responses for each condition, using an approach that provided confidence intervals for each regression coefficient. For the initiation of pursuit we collected all trials in either the on- or off-direction of the PC and used Eq. 4 as a regression model. For the learned component, we started from the fifth probe trial after the onset of the learning conditions, to ensure that some learning had occurred. For each probe trial, we isolated the learned component by subtracting the average response to prelearning probe trials. We then used Eq. 3 to compute the regression coefficients. In each case, we assembled all the data for each PC into long arrays containing the firing rates and the eye kinematics for all individual trials (see methods) and then performed the regression analysis once over the entire length of the arrays. For this regression, we used the value of Δt that provided the largest VAF for the average SS firing rate in each condition.

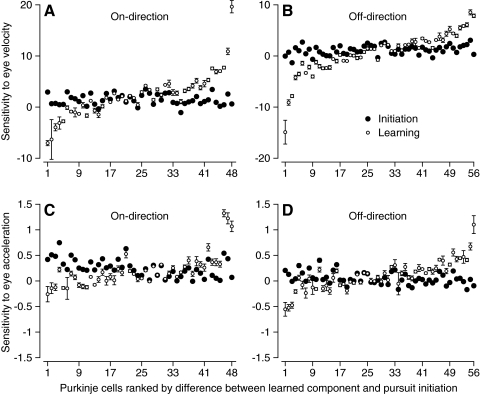
In Fig. 6, we directly compare the regression coefficients that provided the best accounts of the learned component of SS firing rate (open symbols) and the responses during the normal initiation of pursuit (filled symbols). In each graph, there is a pair of symbols for each PC and PCs are ranked from left to right according to the magnitude of the difference between the regression coefficients for the learned component of SS firing versus those for the responses during pursuit initiation. Thus in Fig. 6A, a rank of 1 was assigned to a PC in which the sensitivity to eye velocity for the learned component of pursuit was a large negative value, even though the sensitivity during pursuit initiation was positive; a rank of 48 was assigned to a PC in which the sensitivity was positive and much larger for learned eye movements than that for the initiation of pursuit. Many PCs showed quite different values of sensitivity to eye velocity during the two conditions and, as shown by the error bars, the 95% confidence intervals on the regression coefficients did not overlap in about 29 of the 48 PCs. The data were similar for pursuit in the off-direction (Fig. 6B), where the 95% confidence intervals did not overlap in nearly 40 of 56 PCs. The same kind of graphs indicated that the sensitivity to eye acceleration also differed for the learned component versus the pursuit evoked by step-ramp target motion (Fig. 6, C and D).

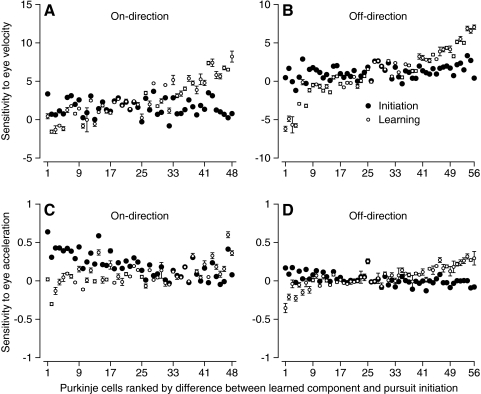
In the regression analysis in Fig. 6, we used the data from single trials for firing rate, but repeated the averages of eye movement for eye velocity, acceleration, and position for all trials. We preferred to use the averages for eye movements because they contained less noise than the single traces and therefore were more amenable to differentiation to obtain eye acceleration signals. However, Fig. 7 shows that we obtained the same basic result when we performed the regression analysis using both the eye movement and firing rate from single trials. The differences in regression coefficients during the learned component and normal pursuit were smaller than those for the prior analysis (note that the y-axes have half the scale in Fig. 7 compared with Fig. 6), but differences in both eye acceleration sensitivity and eye velocity sensitivity for the initiation of pursuit versus the learned component still exceed the confidence intervals in more than half of PCs. We have greater confidence in the regression analysis that used the averages of eye movement across trials, but the results in Fig. 7 add to our confidence that the sensitivity to eye velocity and acceleration differs, frequently substantially, between the learned component of SS firing rate and the responses to step-ramp target motion.

Fig. 7. — Statistical analysis of the difference between the eye velocity and acceleration sensitivities for the learned component of SS firing vs. the response during the initiation of pursuit. A: eye velocity sensitivity in the on-direction. B: eye velocity sensitivity in the off-direction. C: eye acceleration sensitivity in the on-direction. D: eye acceleration sensitivity in the off-direction. Filled and open symbols summarize the regression analysis for the responses to step-ramp target motion along the preferred axis, and for the learned component of SS firing. Error bars indicate confidence intervals for the regression coefficients. Regression was performed using both the firing rate and the eye movements from individual trials.

Comparison of learned component of SS firing with initiation of pursuit in a similar direction

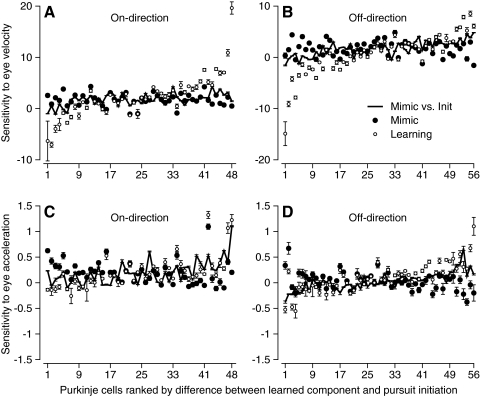
Figures 6 and 7 compared the regression coefficients for the initiation of pursuit along the preferred axis of the PC under study with those for a learned component that is part of the pursuit in an oblique direction, with a large component orthogonal to the preferred axis. We ensured that we were comparing two eye movements in the same direction by subtracting prelearning probe responses to isolate the learned component of pursuit, which was in the on- or off-direction of the PC under study. As a further control, however, it makes sense to compare the learned component of SS firing rate with responses during the initiation of pursuit in a similar direction.

For each PC, the prelearning control block included some trials with step-ramp target motion that took the eyes in approximately the same direction as did the learned eye movements in the postlearning probe trials. Because these prelearning trials were designed to mimic the learned eye movement without causing learning, we call them “mimic” trials. For an experiment that used downward probe trials in a PC that preferred ipsiversive smooth eye motion, the direction of the mimic trials was down and ipsiversive or contraversive for on-direction or off-direction learning (Fig. 1C). Figure 8, A and B illustrates the average eye velocity (A) and firing rate (B) for a typical PC during on-direction mimic trials (black traces) and prelearning probe trials (red traces). Even though the prelearning probe trials in this example were purely downward, there was a small positive deflection of both eye velocity and firing rate, reflecting a small deviation from the cosine tuning that characterizes the direction tuning of most PCs (Krauzlis and Lisberger 1996). To allow us to perform comparable analyses, we subtracted the prelearning probe responses from the mimic responses, just as we had done to isolate the learned component of the eye velocity and firing rate responses.

Regression analysis of the mimic responses with Eq. 4 again yielded excellent fits, as shown in the example of Fig. 8C. Here, eye velocity (blue trace), eye acceleration (purple trace), and eye position (green trace) all contributed to the model of SS firing rate. Across the full sample of 49 PCs, regression accounted for more of the variance during on-direction pursuit initiation (Fig. 8D, black curve) than that during mimic direction pursuit initiation (red curve), presumably because the responses in the on-direction were larger and thus more effectively diluted the inherent noise in firing rate. In contrast, the amplitudes of the firing rate responses were comparable for the learned component and the mimic responses, yielding similar values of VAF across the sample population (Fig. 8D, red vs. blue curves). Figure 8E plots the peak eye velocity along the preferred axis for the learned versus the mimic responses, showing excellent agreement for movements in both the on-direction (filled symbols) and off-direction (open symbols). For both the learned component and the mimic response, there also was eye velocity at 20°/s in the direction of the prelearning probe trials (Fig. 1, B and C). Thus the direction and speed of the overall eye motion were similar for the learned component and the mimic responses. The dynamics of the on-direction components of the two responses were somewhat different, however, with a briefer response and somewhat larger eye acceleration and decelerations for the learned component of eye velocity (Fig. 8F). Regression analysis should be insensitive to the differences in the dynamics of the two responses.

The eye velocity coefficients for the learned component of SS firing rate were different from those for the initiation of pursuit in the mimic direction for many PCs (Fig. 9, A and B). Importantly, 95% confidence intervals were small, indicating that the differences in regression coefficients between the two conditions were statistically significant in many PCs. Eye acceleration regression coefficients also differed for the learned component of PC firing rate versus the initiation of pursuit in the mimic direction (Fig. 9, C and D). In an important control shown by the solid traces in all panels of Fig. 9, we plotted the regression coefficients along the mimicry axis in rank order according to the difference between the coefficients for the mimicry versus the preferred axis. Thus the points used to create the solid traces have the same values as those used to plot the solid points, but now in a different order. For the eye velocity coefficients in Fig. 9, A and B, the solid curves are similar to the filled symbols, indicating that the change in direction from the preferred to the mimicry axis did not have a great effect on the eye velocity coefficients of the fits. Therefore the different eye velocity sensitivities seem to be related to learning and not to the direction of the eye movement that contained the learned component of pursuit. For the eye acceleration coefficients in Fig. 9, C and D, however, the solid traces were more similar to the open symbols. Therefore the change in direction to the mimicry axis did alter the eye acceleration coefficients and may be sufficient to cause much of the difference in sensitivities to eye acceleration we observed in the learned component.

Fig. 9. — Statistical analysis of the difference between the eye velocity and acceleration sensitivities for the learned component of SS firing vs. the response during the initiation of pursuit along the mimic axis. A: eye velocity sensitivity in the on-direction. B: eye velocity sensitivity in the off-direction. C: eye acceleration sensitivity in the on-direction. D: eye acceleration sensitivity in the off-direction. Filled and open symbols summarize the regression analysis for the responses to step-ramp target motion along the mimic axis, and for the learned component of SS firing. Error bars indicate confidence intervals for the regression coefficients. Solid traces show the results of the same analysis for the responses to step-ramp target motion along the mimicry axis, compared with that along the preferred axis. Regression was performed using the firing rate from individual trials and the averages of eye movement across trials.

To test our confidence in the reliability of the regression coefficients for the initiation of pursuit, we next asked how repeatable they are across target speeds. For a sample of 49 PCs used mainly for a different experimental question (Medina and Lisberger 2007), we performed regression analysis using Eq. 4 for average SS responses to step-ramp target motion at 10, 20, and 30°/s. Figure 10A shows the cumulative probabilities of VAF for the three different target speeds, revealing that Eq. 4 accounted for >75% of the variance of average firing rate in the overwhelming majority of PCs at all three target speeds. The remaining panels of Fig. 10 illustrate that the regression coefficients for responses to target motion at 10 and 30°/s agreed well with those for target motion at 20°/s, for eye velocity (B), eye acceleration (C), and eye position (D). Although there are some systematic differences, in particular a tendency for larger eye velocity regression coefficients for lower target speeds, these differences are tiny compared with those we saw when comparing the regression coefficients for the learned component of SS firing rate versus the responses during the initiation of pursuit. We conclude the regression analysis of the average SS responses to step-ramp target motion yields reliable estimates of the regression coefficients in Eq. 4.

Fig. 10. — Similarity of regression coefficients for initiation of pursuit at different target speeds. A: cumulative distribution of VAF for target motion at 10, 20, and 30°/s. B–D: scatterplots showing similarity of velocity sensitivity (B), positive acceleration sensitivity (C), and position sensitivity (D) of PC firing rate during target motion at 10 or 30 vs. 20°/s. Each symbol shows data for an individual PC.

Choice of regression model does not alter differences between encoding of learned component and initiation of pursuit

So far, we have presented the sensitivities to eye acceleration and eye velocity using the regression models that we deemed to be the most appropriate for the data. In fact, the choice of regression models had minimal impact on the differences in the eye velocity regression coefficients between the learned component of SS firing and the responses during the initiation of pursuit. Figure 11 shows for on-direction target motion that it did not matter whether the data for the initiation of pursuit were fitted with (A) or without (B) a position coefficient and with one (A) or two (C) eye acceleration coefficients. Further, the distributions showed the same vertical elongation whether the learned component of firing rate was fitted with one eye acceleration coefficient (A–C), or with separate coefficients for positive and negative eye accelerations (D and E). It also did not change the result to allow an eye position coefficient in the regression model used to fit the learned component of pursuit (F). The average sensitivity to eye velocity (large open symbols) was very similar in all six graphs, with values of 1.67 and 2.78 for the responses to step-ramp target motion and the learned component of pursuit in Fig. 11D, which plots the data using the regression models that we deemed to be the most appropriate. For off-direction pursuit (Fig. 12), the same kind of plots of eye velocity coefficients for the learned component of pursuit versus those for the initiation of pursuit showed the same strong vertical elongation irrespective of which regression model we used. Again the average sensitivities to eye velocity were similar in all six graphs, now with values of 1.24 and 1.45 for the responses to step-ramp target motion and the learned component of pursuit in Fig. 12D.

Fig. 11. — Comparison of regression coefficients for eye velocity for the learned component of pursuit vs. the initiation of pursuit in the on-direction of each PC. Each symbol in the scatter responses shows data from an individual PC. Each point shows data from a single PC and different graphs summarize the results obtained with different regression models. A: *Equation 2* for initiation, *Eq. 1* for learning. B: *Equation 1* for both initiation and learning. C: *Equation 4* for initiation, *Eq. 1* for learning. D: *Equation 4* for initiation, *Eq. 3* for learning. E: *Equation 3* for both initiation and learning. F: *Equation 4* for initiation, *Eq. 2* for learning. The large open symbol in each graph shows the averages across the full sample of PCs.

Fig. 12. — Comparison of regression coefficients for eye velocity for the learned component of pursuit vs. the initiation of pursuit in the off-direction of each PC. Each symbol in the scatter responses shows data from an individual PC. Each point shows data from a single PC and different graphs summarize the results obtained with different regression models. A: *Equation 2* for initiation, *Eq. 1* for learning. B: *Equation 1* for both initiation and learning. C: *Equation 4* for initiation, *Eq. 1* for learning. D: *Equation 4* for initiation, *Eq. 3* for learning. E: *Equation 3* for both initiation and learning. F: *Equation 4* for initiation, *Eq. 2* for learning. The large open symbol in each graph shows the averages across the full sample of PCs.

Response features of PCs correlated with learning magnitude

Figures 6, 7, 9, 11, and 12 show that the eye velocity regression coefficient for the learned component of smooth eye movement can be very different from that for the normal initiation of pursuit in many PCs. Figures 6, 7, and 9 indicate that the differences are statistically significant in many PCs and Figs. 11 and 12 show that the differences do not depend on the choice of regression model. Given the evidence that the differences are real, we next asked what might drive the wide range of learned changes in SS responses across PCs. To do so, we defined the “learning-related difference in eye velocity sensitivity” as the difference between the eye velocity sensitivities for the learned component of pursuit and the normal initiation of pursuit. Then, we analyzed the relationship between the “learning-related difference in eye velocity sensitivity” and other response parameters of floccular PCs. We chose this awkward terminology to be mindful that we have isolated the learned components of SS firing and eye velocity from the responses of PCs during the initiation of pursuit. Our data do not imply any changes in PC responses during the initiation of pursuit as a consequence of learning. Instead, we suggest that the SS response of each PC during the learned eye movement contains an additional component that can have a different relationship to the kinematics of eye velocity, compared with the responses during pursuit initiation.

For each PC in our sample, we plotted the learning-related difference in eye velocity sensitivity as a function of the prelearning sensitivities to eye acceleration and eye velocity, the latter quantities measured from regression fits with Eq. 4 to responses during the initiation of normal pursuit along the preferred axis of the PC under study. For on-direction data (filled symbols), the learning-related difference in eye velocity sensitivity showed a statistically significant positive correlation with the normal sensitivity to eye acceleration (Fig. 13 A, r = 0.37, P < 0.01), but not with the sensitivity to eye velocity (Fig. 13B, r = 0.14, P > 0.3). The off-direction data (open symbols) showed the opposite pattern: a significant correlation with the sensitivity to eye velocity (r = 0.28, P < 0.05) but not with sensitivity to eye acceleration (r = 0.12, P > 0.3).

Fig. 13. — Relationship between learned change in sensitivity to eye velocity and other parameters of PC responses. In all graphs, the y-axis plots the sensitivity to eye velocity of the learned component of firing rate, measured during probe trials, minus the sensitivity to eye velocity during the normal initiation of pursuit. A and B: data for all PCs in our sample, plotting the learning-related difference in eye velocity sensitivity vs. the sensitivity to eye acceleration (A) or eye velocity (B) during the normal initiation of pursuit along the preferred axis of the PC under study. C: data for a small sample of PCs for which the complex spike response remained isolated during a full set of learning trials. The graph plots the learning-related difference in eye velocity sensitivity vs. the size of the complex response, measured during the first 50 learning trials and expressed as a multiple of the baseline complex spike firing. In all 3 panels, filled and open symbols show data for on- vs. off-direction pursuit.

For a smaller sample of PCs, we were able to measure the magnitude of the complex-spike (CS) response evoked by the instructive change in target direction during learning trials. For each PC, we accumulated poststimulus time histograms of the probability of CS responses in 50-ms-wide bins and estimated the size of the CS instructive signal from the probability in the bin centered 125 ms after the instructive change in target direction (see Medina and Lisberger 2008). The correlation between the learning-related change in sensitivity to eye velocity and the log of the size of the instructive CS responses was not significant for on-direction learning (Fig. 13C, filled symbols, r = 0.3, P > 0.4), but was significant for off-direction learning (open symbols, r = 0.63, P < 0.05). There was also a strong correlation between the size of the instructive CS signal for off-direction learning and the eye acceleration sensitivity during normal on-direction pursuit (data not shown; r = 0.85), implying that the strengths of the CS and SS responses to visual motion (Stone and Lisberger 1990a,b) are well correlated within individual PCs.

Decoding of the population SS response to drive eye movement

We have shown so far that any given PC can encode the eye velocity for the learned component of pursuit in a way that is quite different from its encoding of normal pursuit of step-ramp target motion. Given that the encoding by individual PCs can be different depending on the behavioral condition, it is important to assess whether the signals averaged across the population provide a consistent drive for eye movement across conditions. In other words, we need to ask whether the relationship between the PC population activity and the eye movement is the same for the normal initiation of pursuit and the learned component of smooth eye movement.

We evaluated decoding of the floccular population response by averaging the responses across all PCs in our sample and performing linear regression analysis using Eq. 4 for the data from the initiation of pursuit and Eq. 3 for the learned component. For normal pursuit of step-ramp target motion in the on- or off-direction along the preferred axis (Fig. 14A) or mimic axis (Fig. 14C) regression analysis provided a prediction (red traces) that was an excellent fit to the average SS firing across all PCs (black traces). A separate fit to the data for the learned component provided a similar result (Fig. 14, B or D, “self” regression fit): for both on- and off-direction learning, the prediction from the regression (red traces) provided an excellent fit to the average SS firing across all PCs (black traces).

Fig. 14. — Inverse model analysis based on the average responses across the population of floccular PCs. Each panel shows actual and predicted firing rate as a function of time. In all 4 panels, *black traces* show actual firing rate and *red traces* show the prediction of the linear regression model for the actual firing rate. Responses for on-direction and off-direction pursuit shown as positive and negative going traces, respectively. In B and D, blue traces show the predicted learned component of firing rate based on the regression coefficients obtained for normal pursuit of step-ramp target motion. A and B show data for pursuit along the preferred axes of the PCs under study, whereas C and D show analysis for pursuit along the axis that mimicked the speed and direction of the learned component of pursuit.

The eye velocity sensitivity of the population average firing rate (Table 1) showed good agreement with the average of the coefficients calculated separately for each cell (Figs. 11 and 12), for both on- and off-direction responses to step-ramp target motion and for the on-direction learned component of pursuit. We cannot explain the discrepancy between the two estimates of sensitivity to eye velocity for the off-direction learned component of pursuit. Table 1 also provides some interesting comparisons among conditions. First, different regression coefficients were needed to provide good fits to the population data for the on- and off-directions of target motion. Second, the eye velocity sensitivity for the on-direction was similar for pursuit initiation along the preferred axis, the mimic axis, and the learned component. However, the eye velocity coefficient for the learned component in the off-direction was quite different from that for the initiation of pursuit along the preferred or the mimic axis (Table 1). The discrepancy appears graphically in attempts to predict the firing rate related to the learned component of pursuit using regression coefficients obtained from responses to step-ramp target motion. For pursuit initiation along either the preferred axis (Fig. 14B) or the mimic axis (Fig. 14D), the prediction of the learned component of SS firing based on initiation regression coefficients (blue traces) was excellent for the on-direction, but discrepant for the off-direction.

Table 1.

Regression coefficients for population averages of different pursuit conditions

Tracking Condition	Velocity Sensitivity	Positive Acceleration Sensitivity	Negative Acceleration Sensitivity
Tracking Condition	Velocity Sensitivity	Positive Acceleration Sensitivity	Negative Acceleration Sensitivity
Preferred, on-direction, normal pursuit	1.72	0.27	0.08
Mimic, on-direction, normal pursuit	1.96	0.25	0.07
Learned component, on-direction	2.28	0.26	0.22
Preferred, off-direction, normal pursuit	1.12	0.06	0.08
Mimic, off-direction, normal pursuit	1.62	0.11	0.19
Learned component, off-direction	0.25	0.06	0.15

Open in a new tab

Regression coefficients are not given for eye position because they were small on average (≈0.25) during the initiation of pursuit and eye position was not included in the regression equation for the learned component.

DISCUSSION

We have examined the encoding and decoding of learned eye movements by Purkinje cells in the floccular complex of awake-behaving monkeys. Our results have a number of important implications regarding 1) the locus of neuronal plasticity and the nature of the cerebellar inputs that are modified in association with learning, 2) the instructive signals that guide learning, and 3) the relative importance of floccular PCs and other components of the pursuit circuit in driving learned changes in pursuit behavior. We elaborate all three of these issues in the following text.

Locus of neuronal plasticity

There have been numerous demonstrations that the SS responses of PCs change in association with learning of different movements. Our laboratory has focused on changes in the floccular complex during learning in smooth-pursuit eye movement (Kahlon and Lisberger 2000; Medina and Lisberger 2008), whereas others have explored similar issues in arm-movement adaptation (Gilbert and Thach 1977; Ojakangas and Ebner 1992), eyelid conditioning (Green and Steinmetz 2005), vestibuloocular reflex adaptation (Blazquez et al. 2003; Dufossé et al. 1978; Lisberger et al. 1994b; Miles et al. 1980), and saccade adaptation (Catz et al. 2008).

We have used directional learning in smooth-pursuit eye movements in an attempt to go one step further by asking not whether the responses of PCs are modified in association with learning, but rather by asking whether the sensitivity of PCs to specific movement parameters is different between baseline and learned responses. This is an important distinction. If the learned component of each PC's SS response showed the same sensitivity to the kinematics of eye motion as that during the initiation of pursuit, it could mean that the site of learning is outside the cerebellar cortex and that all PCs inherit changed inputs in exact proportion to their individual responses during normal pursuit. In contrast, if learning occurs through modification of synaptic strengths in the cerebellar cortex, then we might expect the sensitivity of individual PCs to particular movement parameters to be quite different for the learned component versus the normal initiation of pursuit. Further, those differences could be quite variable across PCs if the instructive signals available during learning also varied in efficacy or size across PCs. Our findings are compatible with the latter situation and are in good agreement with the results of a similar analysis of PC responses in the cerebellar vermis during adaptation of saccadic eye movements (Catz et al. 2008). We find that the sensitivity of PCs to their eye velocity inputs can be very different for the learned component of pursuit compared with that during normal pursuit. Further, the size of the difference in sensitivity varies widely across PCs.

As part of our analysis, we showed that our conclusion about the regression coefficients for the learned component of pursuit and the normal initiation of pursuit did not depend strongly on the regression models we used. We explained why a regression model with coefficients for eye velocity, positive and negative eye acceleration, and eye position was correct to account for the functional response properties of PCs during the initiation of pursuit and why it was not practical to include the eye position coefficient when fitting the learned component of PC firing. Finally, we provided evidence that the differences in eye velocity regression coefficients between the learned component of SS firing rate and the response during the initiation of pursuit are statistically significant in many PCs. Together, these controls indicate that the differences between the regression coefficients for the learned component and normal initiation of pursuit are neither the result of an analysis artifact based on averaging small numbers of noisy responses nor a consequence of the choice of regression model. Finally, the use of the mimic trials indicates that our results cannot be attributed to differences in the direction or magnitude of the learned eye movement versus the normal initiation of pursuit.

We suggest that the large range of eye velocity sensitivities for the learned component of SS firing, compared with the coefficients during normal pursuit, reflects differences in the amount of local plasticity that occurs in different individual PCs. Thus our data are consistent with the hypothesis that learning occurs locally in the cerebellar cortex (Albus 1971; Ito 1972; Marr 1969). Because the eye velocity coefficients in the regression model for learned eye movements show the largest differences relative to the coefficients for normal pursuit, our results imply that learning is associated with selective adjustment of the weight of eye velocity inputs to PCs. At the same time the excellent timing of the learned eye movement (Medina et al. 2005) and its neural correlates implies that the modified input must be activated transiently and only around the time of the instructive stimulus (see Buonomano and Mauk 1994). The modified signal cannot be a tonic eye velocity input that is present whenever the eyes are moving because learning would then be expressed throughout steady-state pursuit rather than specifically around the time of the instructive change in target direction. We cannot exclude the alternative idea that learned changes in floccular SS firing are inherited from upstream sources, although our data then imply that changed inputs are inherited differentially across the PC population, with some PCs inheriting learned changes out of proportion with their responsiveness during the normal initiation of pursuit.

Differences in the stimulus conditions provide an alternative explanation for the difference in regression coefficients between the normal initiation of pursuit and the learned component. During the normal initiation of pursuit, target motion provides a large retinal image motion that causes rapid eye acceleration followed by sustained eye velocity. During the probe trials used to evaluate the learned component of pursuit, the learned component of eye movement occurs without any visual motion input to drive it and actually creates retinal image motion in the direction opposite to the learned eye movement. Therefore the difference in the visual input in the two conditions is a possible explanation for the difference in the regression coefficients. However, the current understanding of the signal processing of floccular PCs does not support this alternative explanation. PCs in the floccular complex encode eye movements in motor coordinates in the sense that firing rate can be modeled as a linear combination of eye acceleration, velocity, and position (Shidara et al. 1993). Visual inputs are thought to drive the eye acceleration sensitivity of floccular PCs (Stone and Lisberger 1990a), which showed smaller differences between the learned component and the initiation of pursuit. An eye movement corollary discharge appears to drive the eye velocity sensitivity of floccular PCs (Stone and Lisberger 1990a), the component of the linear regression that is strikingly different when comparing normal pursuit initiation and the learned component. Thus the modification is expressed in a component of PC firing that is not driven by visual inputs, making it unlikely that differences in the visual conditions can account for our findings. Unfortunately, it is difficult to see how to circumvent this issue with a change in experimental design: visual inputs are needed to drive the initiation of pursuit, but are absent, by definition, when probing pursuit learning.

Possible instructive signals for learning

Our analysis of the correlation between the size of the learned change in eye velocity sensitivity and other parameters of PC responses offers some insight into possible signals that might instruct learning in the floccular cortex. We interpret these data under the assumption that the induction of plasticity depends on the conjunction of 1) instructive signals that guide plasticity and 2) a preexisting state of neural electrical activity that determines the eligibility of a neuron to be modified. In our data, differences in the results for on- versus off-direction learning imply that the two conditions should be considered separately.

For target motions in the on-direction, only a PC's sensitivity to eye acceleration during normal pursuit is related to the difference between the eye velocity sensitivities for the learned component versus normal pursuit. Prior recordings suggest that the acceleration sensitivity of SS firing results from mossy fibers that convey visual motion inputs to PCs (Miles and Fuller 1975; Stone and Lisberger 1990a). The presence of these visual motion inputs in high strengths could create a membrane state that is particularly conducive to the induction of cellular plasticity underlying motor learning in the PC's on-direction. We noted in prior studies, and confirmed here, that the traditional complex-spike mediation of learning probably is not a large contributor to on-direction learning because the probability of complex spikes does not deviate far from control values during on-direction learning trials (Kahlon and Lisberger 2000; Medina and Lisberger 2008).

For off-direction learning, the positive correlation between the magnitude of the learning-related difference in eye velocity sensitivity and the size of the instructive CS response is in line with prior hypotheses suggesting that CS responses guide one form of plasticity at the synapse from parallel fibers to PCs (Albus 1971; Ito 1972; Marr 1969). However, the significant correlation between the learned change in eye velocity sensitivity and the normal sensitivity to eye velocity prevents us from making conclusions about whether any one signal, or potentially both, drive plasticity in the off-direction.

The full picture of possible instructive signals for learning agrees with our prior suggestions (Medina and Lisberger 2008) and those of others (Boyden and Raymond 2006; Hansel et al. 2001; Hirata and Highstein 2001; Jörntell and Ekerot 2002; Medina et al. 2000; Miles and Lisberger 1981; Perrett et al. 1993) that the cerebellar component of motor learning results from multiple signals, sites, and cellular mechanisms of plasticity. Our data suggest that multiple input signals to the floccular complex could provide instruction for learning and that different signals might control learning in the on- versus off-direction of PCs. Even though we tend to think of PCs as the locus of plasticity, our results do not provide any evidence against the possibility that some or all of the plasticity occurs in cerebellar interneurons (Jörntell and Ekerot 2002).

Contribution of the floccular complex to learned eye movements

Floccular PCs project via a disynaptic pathway to extraocular motoneurons (e.g., Highstein 1973), implying that floccular output plays an important role in driving smooth eye movement. We found that the velocity sensitivity of the population response in the on-direction was similar for normal pursuit of step-ramp target motion and for learned eye movements, implying that the floccular complex drives eye movement equally under these different conditions. In contrast, the velocity sensitivity of the population response in the off-direction for learned eye movements was smaller than that for normal pursuit. Given the directness of the synaptic connection from PCs to motoneurons, we expect that the processing of floccular output in brain stem circuits would be the same for the learned component of pursuit as that for the pursuit evoked by step-ramp target motion. Thus the finding of equal population sensitivity to on-direction eye movements under different conditions implies that floccular output drives eye movement equally for the initiation of pursuit and for the learned component of pursuit. Because each floccular complex mainly drives ipsiversive eye motion (Lisberger 1994; Ron and Robinson 1973), our findings imply that for rightward smooth eye movements, the signal emanating from the right floccular complex provides the same drive for eye movements, regardless of the condition. However, for the same rightward smooth eye movements, the left floccular complex would make less of a contribution to learned eye movements than to normal pursuit of target motion.

Our results suggest that for learned eye movements in a particular direction, floccular output in the contralateral hemisphere is shirking, and that other structures must shoulder more than their normal share of the burden for driving the eye. Given that the two floccular complexes work together to generate horizontal eye movements, it was possible that the discrepancy would disappear when we used an opponent signal computed as on-direction minus off-direction data to estimate the average output of one floccular complex minus that of the other floccular complex (Krauzlis and Lisberger 1994)—but it did not. For the learned component, the opponent floccular output changes less than does the opponent eye velocity. We conclude that another structure must contribute to the signals that drive the learned component of pursuit in an amount that is out of proportion to its contribution to normal pursuit of step-ramp target motion. One strong candidate for another structure is the smooth-pursuit region of the oculomotor vermis (Shinmei et al. 2002; Takagi et al. 2000). Of course, alternative scenarios might be possible if we abandoned the simplifying assumptions behind this explanation, such as using the average activity of the PC population as the decoding algorithm. However, the situation was not improved by weighting each PC's contribution to the population response according to its sensitivity to eye velocity during pursuit initiation.

In broad strokes, our analysis of the decoding of floccular PC signals for learning is similar to that of Catz et al. (2008) for vermal outputs during saccade adaptation. However, we have been able to go farther because the inverse model framework (Krauzlis and Lisberger 1994; Shidara et al. 1993) provides a single relationship that describes fairly well the transformation of the opponent population average of PC firing into eye movement for both the learned component and the normal initiation of pursuit. Taken as a whole, our data on single PCs and population averages imply that local plasticity in the floccular cortex causes diverse expressions of learning in different PCs. The population output from the floccular complex might contribute equally during the generation of normal and learned pursuit eye movements in the on-direction. At least for off-direction target motion, however, floccular PCs drive the learned component of smooth-pursuit eye movement less strongly than they drive the normal initiation of pursuit, implying that other structures make a somewhat larger contribution to the learned component of pursuit.

GRANTS

This research was supported by the Howard Hughes Medical Institute and National Eye Institute Grant EY-017210.

ACKNOWLEDGMENTS

We thank P. Sabes, W. Bialek, and J. A. Movshon for helpful discussions; H. Heuer for comments on the manuscript; and K. MacLeod, E. Montgomery, S. Tokiyama, S. Ruffner, D. Kleinhesselink, D. Wolfgang-Kimball, L. Bosckai, K. McGary, and D. Frank for technical assistance.

REFERENCES

Albus JS. A theory of cerebellar function. Math Biosci 10: 25–61, 1971 [Google Scholar]
Blazquez PM, Hirata Y, Heiney SA, Green AM, Highstein SM. Cerebellar signatures of vestibulo-ocular reflex motor learning. J Neurosci 23: 9742–9751, 2003 [DOI] [PMC free article] [PubMed] [Google Scholar]
Buonomano DV, Mauk MD. Neural network model of the cerebellumml: temporal discrimination and the timing of motor responses. Neural Comput 6: 38–55, 1994 [Google Scholar]
Catz N, Dicke PW, Their P. Cerebellar-dependent motor learning is based on pruning a Purkinje cell population response. Proc Natl Acad Sci USA 105: 7309–7314, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
Chou I, Lisberger SG. Role of the frontal pursuit area in motor learning in smooth pursuit eye movements in monkeys. J Neurosci 24: 4124–4133, 2004 [DOI] [PMC free article] [PubMed] [Google Scholar]
Dufossé M, Ito M, Jastreboff PJ, Miyashita Y. A neuronal correlate in rabbit's cerebellum to adaptive modification of the vestibulo-ocular reflex. Brain Res 150: 611–616, 1978 [DOI] [PubMed] [Google Scholar]
Fuchs AF, Luschei ES. Firing patterns of abducens neurons of alert monkeys in relationship to horizontal eye movement. J Neurophysiol 33: 382–392, 1970 [DOI] [PubMed] [Google Scholar]
Gilbert PF, Thach WT. Purkinje cell activity during motor learning. Brain Res 128: 309–328, 1977 [DOI] [PubMed] [Google Scholar]
Green JT, Steinmetz JE. Purkinje cell activity in the cerebellar anterior lobe after rabbit eyeblink conditioning. Learn Mem 12: 260–269, 2005 [DOI] [PMC free article] [PubMed] [Google Scholar]
Hansel C, Linden DJ, D'Angelo E. Beyond parallel fiber LTD: the diversity of synaptic and non-synaptic plasticity in the cerebellum. Nat Neurosci 4: 467–475, 2001 [DOI] [PubMed] [Google Scholar]
Highstein SM. Synaptic linkage in the vestibulo-ocular and cerebello-vestibular pathways to the VIth nucleus in the rabbit. Exp Brain Res 17: 301–314, 1973 [DOI] [PubMed] [Google Scholar]
Highstein SM, Hirata Y. Analysis of the discharge pattern of floccular Purkinje cells in relation to vertical head and eye movement in the squirrel monkey. Prog Brain Res 124: 221–232, 2000 [DOI] [PubMed] [Google Scholar]
Hirata Y, Highstein SM. Acute adaptation of the vestibuloocular reflex: signal processing by floccular and ventral parafloccular Purkinje cells. J Neurophysiol 85: 2267–2288, 2001 [DOI] [PubMed] [Google Scholar]
Ito M. Neural design of the cerebellar motor control system. Brain Res 40: 81–84, 1972 [DOI] [PubMed] [Google Scholar]
Jörntell H, Ekerot CF. Reciprocal bidirectional plasticity of parallel fiber receptive fields in cerebellar Purkinje cells and their afferent interneurons. Neuron 34: 797–806, 2002 [DOI] [PubMed] [Google Scholar]
Kahlon M, Lisberger SG. Changes in the responses of Purkinje cells in the floccular complex of monkeys after motor learning in smooth pursuit eye movements. J Neurophysiol 84: 2945–2960, 2000 [DOI] [PMC free article] [PubMed] [Google Scholar]
Krauzlis RJ, Lisberger SG. Simple spike responses of gaze velocity Purkinje cells in the floccular lobe of the monkey during the onset and offset of pursuit eye movements. J Neurophysiol 72: 2045–2050, 1994 [DOI] [PubMed] [Google Scholar]
Krauzlis RJ, Lisberger SG. Directional organization of eye movement and visual signals in the floccular lobe of the monkey cerebellum. Exp Brain Res 109: 289–302, 1996 [DOI] [PubMed] [Google Scholar]
Lisberger SG. Neural basis for motor learning in the vestibuloocular reflex of primates. III. Computational and behavioral analysis of the sites of learning. J Neurophysiol 72: 974–997, 1994 [DOI] [PubMed] [Google Scholar]
Lisberger SG, Fuchs AF. Role of primate flocculus during rapid behavioral modification of vestibuloocular reflex. I. Purkinje cell activity during visually guided horizontal smooth-pursuit eye movements and passive head rotation. J Neurophysiol 41: 733–763, 1978 [DOI] [PubMed] [Google Scholar]
Lisberger SG, Pavelko TA, Brontë-Stewart HM, Stone LS. Neural basis for motor learning in the vestibuloocular reflex of primates. II. Changes in the responses of horizontal gaze velocity Purkinje cells in the cerebellar flocculus and ventral paraflocculus. J Neurophysiol 72: 954–973, 1994b [DOI] [PubMed] [Google Scholar]
Lisberger SG, Pavelko TA, Broussard DM. Neural basis for motor learning in the vestibuloocular reflex of primates. I. Changes in the responses of brain stem neurons. J Neurophysiol 72: 928–953, 1994a [DOI] [PubMed] [Google Scholar]
Marr D. A theory of cerebellar cortex. J Physiol 202: 437–740, 1969 [DOI] [PMC free article] [PubMed] [Google Scholar]
Medina JF, Carey MR, Lisberger SG. The representation of time for motor learning. Neuron 45: 157–167, 2005 [DOI] [PubMed] [Google Scholar]
Medina JF, Lisberger SG. Variation, signal, and noise in cerebellar sensory-motor processing for smooth pursuit eye movements. J Neurosci 27: 6832–6842, 2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
Medina JF, Lisberger SG. Links from complex spikes to local plasticity and motor learning in the cerebellum of awake-behaving monkeys. Nat Neurosci 11: 1185–1192, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
Medina JF, Nores WL, Ohyama T, Mauk MD. Mechanisms of cerebellar learning suggested by eyelid conditioning. Curr Open Neurobiol 10: 717–724, 2000 [DOI] [PubMed] [Google Scholar]
Miles FA, Braitman DJ, Dow BM. Long-term adaptive changes in primate vestibuloocular reflex. IV. Electrophysiological observations in floccular of adapted monkeys. J Neurophysiol 43: 1477–1493, 1980 [DOI] [PubMed] [Google Scholar]
Miles FA, Fuller JH. Visual tracking and the primate flocculus. Science 189: 1000–1002, 1975 [DOI] [PubMed] [Google Scholar]
Miles FA, Lisberger SG. Plasticity in the vestibulo-ocular reflex: a new hypothesis. Annu Rev Neurosci 4: 273–299, 1981 [DOI] [PubMed] [Google Scholar]
Ojakangas CL, Ebner TJ. Purkinje cell complex and simple spike changes during a voluntary arm movement learning task in the monkey. J Neurophysiol 68: 2222–2236, 1992 [DOI] [PubMed] [Google Scholar]
Perrett SP, Ruiz BP, Mauk MD. Cerebellar cortex lesions disrupt learning-dependent timing of conditioned eyelid responses. J Neurosci 13: 1708–1718, 1993 [DOI] [PMC free article] [PubMed] [Google Scholar]
Ramachandran R, Lisberger SG. Normal performance and expression of learning in the vestibulo-ocular reflex (VOR) at high frequencies. J Neurophysiol 93: 2028–2038, 2005 [DOI] [PMC free article] [PubMed] [Google Scholar]
Rambold H, Churchland AK, Selig Y, Jasmin L, Lisberger SG. Partial ablations of the flocculus and ventral paraflocculus in monkeys cause linked deficits in smooth pursuit eye movements and adaptive modification of the VOR. J Neurophysiol 87: 912–924, 2002 [DOI] [PMC free article] [PubMed] [Google Scholar]
Rashbass C. The relationship between saccadic and smooth tracking eye movements. J Physiol 159: 326–338, 1961 [DOI] [PMC free article] [PubMed] [Google Scholar]
Ron S, Robinson DA. Eye movements evoked by cerebellar stimulation in the alert monkey. J Neurophysiol 36: 1004–1022, 1973 [DOI] [PubMed] [Google Scholar]
Shidara M, Kawano K, Gomi H, Kawato M. Inverse dynamics model eye movement control by Purkinje cells in the cerebellum. Nature 365: 50–52, 1993 [DOI] [PubMed] [Google Scholar]
Shinmei Y, Yamanobe T, Fukushima J, Fukushima K. Purkinje cells of the cerebellar dorsal vermis: simple-spike activity during pursuit and passive whole-body rotation. J Neurophysiol 87: 1836–1849, 2002 [DOI] [PubMed] [Google Scholar]
Skavenski AA, Robinson DA. Role of abducens neurons in vestibuloocular reflex. J Neurophysiol 36: 724–738, 1973 [DOI] [PubMed] [Google Scholar]
Stone LS, Lisberger SG. Visual responses of Purkinje cells in the cerebellar flocculus during smooth-pursuit eye movements in monkeys. I. Simple spikes. J Neurophysiol 63: 1241–1261, 1990a [DOI] [PubMed] [Google Scholar]
Stone LS, Lisberger SG. Visual responses of Purkinje cells in the cerebellar flocculus during smooth-pursuit eye movements in monkeys. II. Complex spikes. J Neurophysiol 63: 1262–1275, 1990b [DOI] [PubMed] [Google Scholar]
Takagi M, Zee DS, Tamargo RJ. Effects of lesions of the oculomotor vermis on eye movements in primate: smooth pursuit. J Neurophysiol 83: 2047–2062, 2000 [DOI] [PubMed] [Google Scholar]
Zee DS, Yamazaki A, Butler PH, Gücer G. Effects of ablation of floccular and paraflocculus on eye movements in primate. J Neurophysiol 46: 878–899, 1981 [DOI] [PubMed] [Google Scholar]

[B1] Albus JS. A theory of cerebellar function. Math Biosci 10: 25–61, 1971 [Google Scholar]

[B2] Blazquez PM, Hirata Y, Heiney SA, Green AM, Highstein SM. Cerebellar signatures of vestibulo-ocular reflex motor learning. J Neurosci 23: 9742–9751, 2003 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B3] Buonomano DV, Mauk MD. Neural network model of the cerebellumml: temporal discrimination and the timing of motor responses. Neural Comput 6: 38–55, 1994 [Google Scholar]

[B4] Catz N, Dicke PW, Their P. Cerebellar-dependent motor learning is based on pruning a Purkinje cell population response. Proc Natl Acad Sci USA 105: 7309–7314, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B5] Chou I, Lisberger SG. Role of the frontal pursuit area in motor learning in smooth pursuit eye movements in monkeys. J Neurosci 24: 4124–4133, 2004 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B6] Dufossé M, Ito M, Jastreboff PJ, Miyashita Y. A neuronal correlate in rabbit's cerebellum to adaptive modification of the vestibulo-ocular reflex. Brain Res 150: 611–616, 1978 [DOI] [PubMed] [Google Scholar]

[B7] Fuchs AF, Luschei ES. Firing patterns of abducens neurons of alert monkeys in relationship to horizontal eye movement. J Neurophysiol 33: 382–392, 1970 [DOI] [PubMed] [Google Scholar]

[B8] Gilbert PF, Thach WT. Purkinje cell activity during motor learning. Brain Res 128: 309–328, 1977 [DOI] [PubMed] [Google Scholar]

[B9] Green JT, Steinmetz JE. Purkinje cell activity in the cerebellar anterior lobe after rabbit eyeblink conditioning. Learn Mem 12: 260–269, 2005 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B10] Hansel C, Linden DJ, D'Angelo E. Beyond parallel fiber LTD: the diversity of synaptic and non-synaptic plasticity in the cerebellum. Nat Neurosci 4: 467–475, 2001 [DOI] [PubMed] [Google Scholar]

[B11] Highstein SM. Synaptic linkage in the vestibulo-ocular and cerebello-vestibular pathways to the VIth nucleus in the rabbit. Exp Brain Res 17: 301–314, 1973 [DOI] [PubMed] [Google Scholar]

[B12] Highstein SM, Hirata Y. Analysis of the discharge pattern of floccular Purkinje cells in relation to vertical head and eye movement in the squirrel monkey. Prog Brain Res 124: 221–232, 2000 [DOI] [PubMed] [Google Scholar]

[B13] Hirata Y, Highstein SM. Acute adaptation of the vestibuloocular reflex: signal processing by floccular and ventral parafloccular Purkinje cells. J Neurophysiol 85: 2267–2288, 2001 [DOI] [PubMed] [Google Scholar]

[B14] Ito M. Neural design of the cerebellar motor control system. Brain Res 40: 81–84, 1972 [DOI] [PubMed] [Google Scholar]

[B15] Jörntell H, Ekerot CF. Reciprocal bidirectional plasticity of parallel fiber receptive fields in cerebellar Purkinje cells and their afferent interneurons. Neuron 34: 797–806, 2002 [DOI] [PubMed] [Google Scholar]

[B16] Kahlon M, Lisberger SG. Changes in the responses of Purkinje cells in the floccular complex of monkeys after motor learning in smooth pursuit eye movements. J Neurophysiol 84: 2945–2960, 2000 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B17] Krauzlis RJ, Lisberger SG. Simple spike responses of gaze velocity Purkinje cells in the floccular lobe of the monkey during the onset and offset of pursuit eye movements. J Neurophysiol 72: 2045–2050, 1994 [DOI] [PubMed] [Google Scholar]

[B18] Krauzlis RJ, Lisberger SG. Directional organization of eye movement and visual signals in the floccular lobe of the monkey cerebellum. Exp Brain Res 109: 289–302, 1996 [DOI] [PubMed] [Google Scholar]

[B19] Lisberger SG. Neural basis for motor learning in the vestibuloocular reflex of primates. III. Computational and behavioral analysis of the sites of learning. J Neurophysiol 72: 974–997, 1994 [DOI] [PubMed] [Google Scholar]

[B20] Lisberger SG, Fuchs AF. Role of primate flocculus during rapid behavioral modification of vestibuloocular reflex. I. Purkinje cell activity during visually guided horizontal smooth-pursuit eye movements and passive head rotation. J Neurophysiol 41: 733–763, 1978 [DOI] [PubMed] [Google Scholar]

[B21] Lisberger SG, Pavelko TA, Brontë-Stewart HM, Stone LS. Neural basis for motor learning in the vestibuloocular reflex of primates. II. Changes in the responses of horizontal gaze velocity Purkinje cells in the cerebellar flocculus and ventral paraflocculus. J Neurophysiol 72: 954–973, 1994b [DOI] [PubMed] [Google Scholar]

[B22] Lisberger SG, Pavelko TA, Broussard DM. Neural basis for motor learning in the vestibuloocular reflex of primates. I. Changes in the responses of brain stem neurons. J Neurophysiol 72: 928–953, 1994a [DOI] [PubMed] [Google Scholar]

[B23] Marr D. A theory of cerebellar cortex. J Physiol 202: 437–740, 1969 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B24] Medina JF, Carey MR, Lisberger SG. The representation of time for motor learning. Neuron 45: 157–167, 2005 [DOI] [PubMed] [Google Scholar]

[B25] Medina JF, Lisberger SG. Variation, signal, and noise in cerebellar sensory-motor processing for smooth pursuit eye movements. J Neurosci 27: 6832–6842, 2007 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B26] Medina JF, Lisberger SG. Links from complex spikes to local plasticity and motor learning in the cerebellum of awake-behaving monkeys. Nat Neurosci 11: 1185–1192, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B27] Medina JF, Nores WL, Ohyama T, Mauk MD. Mechanisms of cerebellar learning suggested by eyelid conditioning. Curr Open Neurobiol 10: 717–724, 2000 [DOI] [PubMed] [Google Scholar]

[B28] Miles FA, Braitman DJ, Dow BM. Long-term adaptive changes in primate vestibuloocular reflex. IV. Electrophysiological observations in floccular of adapted monkeys. J Neurophysiol 43: 1477–1493, 1980 [DOI] [PubMed] [Google Scholar]

[B29] Miles FA, Fuller JH. Visual tracking and the primate flocculus. Science 189: 1000–1002, 1975 [DOI] [PubMed] [Google Scholar]

[B30] Miles FA, Lisberger SG. Plasticity in the vestibulo-ocular reflex: a new hypothesis. Annu Rev Neurosci 4: 273–299, 1981 [DOI] [PubMed] [Google Scholar]

[B31] Ojakangas CL, Ebner TJ. Purkinje cell complex and simple spike changes during a voluntary arm movement learning task in the monkey. J Neurophysiol 68: 2222–2236, 1992 [DOI] [PubMed] [Google Scholar]

[B32] Perrett SP, Ruiz BP, Mauk MD. Cerebellar cortex lesions disrupt learning-dependent timing of conditioned eyelid responses. J Neurosci 13: 1708–1718, 1993 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B33] Ramachandran R, Lisberger SG. Normal performance and expression of learning in the vestibulo-ocular reflex (VOR) at high frequencies. J Neurophysiol 93: 2028–2038, 2005 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B34] Rambold H, Churchland AK, Selig Y, Jasmin L, Lisberger SG. Partial ablations of the flocculus and ventral paraflocculus in monkeys cause linked deficits in smooth pursuit eye movements and adaptive modification of the VOR. J Neurophysiol 87: 912–924, 2002 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B35] Rashbass C. The relationship between saccadic and smooth tracking eye movements. J Physiol 159: 326–338, 1961 [DOI] [PMC free article] [PubMed] [Google Scholar]

[B36] Ron S, Robinson DA. Eye movements evoked by cerebellar stimulation in the alert monkey. J Neurophysiol 36: 1004–1022, 1973 [DOI] [PubMed] [Google Scholar]

[B37] Shidara M, Kawano K, Gomi H, Kawato M. Inverse dynamics model eye movement control by Purkinje cells in the cerebellum. Nature 365: 50–52, 1993 [DOI] [PubMed] [Google Scholar]

[B38] Shinmei Y, Yamanobe T, Fukushima J, Fukushima K. Purkinje cells of the cerebellar dorsal vermis: simple-spike activity during pursuit and passive whole-body rotation. J Neurophysiol 87: 1836–1849, 2002 [DOI] [PubMed] [Google Scholar]

[B39] Skavenski AA, Robinson DA. Role of abducens neurons in vestibuloocular reflex. J Neurophysiol 36: 724–738, 1973 [DOI] [PubMed] [Google Scholar]

[B40] Stone LS, Lisberger SG. Visual responses of Purkinje cells in the cerebellar flocculus during smooth-pursuit eye movements in monkeys. I. Simple spikes. J Neurophysiol 63: 1241–1261, 1990a [DOI] [PubMed] [Google Scholar]

[B41] Stone LS, Lisberger SG. Visual responses of Purkinje cells in the cerebellar flocculus during smooth-pursuit eye movements in monkeys. II. Complex spikes. J Neurophysiol 63: 1262–1275, 1990b [DOI] [PubMed] [Google Scholar]

[B42] Takagi M, Zee DS, Tamargo RJ. Effects of lesions of the oculomotor vermis on eye movements in primate: smooth pursuit. J Neurophysiol 83: 2047–2062, 2000 [DOI] [PubMed] [Google Scholar]

[B43] Zee DS, Yamazaki A, Butler PH, Gücer G. Effects of ablation of floccular and paraflocculus on eye movements in primate. J Neurophysiol 46: 878–899, 1981 [DOI] [PubMed] [Google Scholar]

PERMALINK

Encoding and Decoding of Learned Smooth-Pursuit Eye Movements in the Floccular Complex of the Monkey Cerebellum

Javier F Medina

Stephen G Lisberger

Abstract

INTRODUCTION

METHODS

Surgical procedures, monkey training, recording methods, and visual stimuli

Experimental design

Fig. 1.

Data analysis

RESULTS

Linear regression analysis of floccular SS firing rate

Fig. 2.

Fig. 3.

Fig. 4.

Encoding of eye movement during different tracking conditions in individual PCs

Fig. 5.

Fig. 6.

Fig. 7.

Comparison of learned component of SS firing with initiation of pursuit in a similar direction

Fig. 8.

Fig. 9.

Fig. 10.

Choice of regression model does not alter differences between encoding of learned component and initiation of pursuit

Fig. 11.

Fig. 12.

Response features of PCs correlated with learning magnitude

Fig. 13.

Decoding of the population SS response to drive eye movement

Fig. 14.

Table 1.

DISCUSSION

Locus of neuronal plasticity

Possible instructive signals for learning

Contribution of the floccular complex to learned eye movements

GRANTS

ACKNOWLEDGMENTS

REFERENCES

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases