Abstract
During growth or degeneration neuronal surface area can change dramatically. Measurements of membrane protein concentration, as in ion channel or ionic conductance density, are often normalized by membrane capacitance, which is proportional to the surface area, to express changes independently from cell surface variations. Several electrophysiological protocols are used to measure cell capacitance, all based on the assumption of membrane isopotentiality. Yet, most neurons violate this assumption because of their complex anatomical structure, raising the question of which protocol yields measurements that are closest to the actual total membrane capacitance. We measured the capacitance of identified neurons from crab stomatogastric ganglia using three different protocols: the current-clamp step, the voltage-clamp step, and the voltage-clamp ramp protocols. We observed that the current-clamp protocol produced significantly higher capacitance values than those of either voltage-clamp protocol. Computational models of various anatomical complexities suggest that the current-clamp protocol can yield accurate capacitance estimates. In contrast, the voltage-clamp protocol estimates rapidly deteriorate as isopotentiality is reduced. We provide a mathematical description of these results by analyzing a simple two-compartment model neuron to facilitate an intuitive understanding of these methods. Together, the experiments, modeling, and mathematical analysis indicate that accurate total membrane capacitance measurements cannot be obtained with voltage-clamp protocols in nonisopotential neurons. Furthermore, although current-clamp steps can theoretically yield accurate measurements, experimentalists should be aware of limitations imposed by step duration and numerical errors during fitting procedures to obtain the membrane time constant.
INTRODUCTION
During development, growth, or neuronal degeneration, cell size can change dramatically and neuronal plasticity may involve changes in the cell surface area (Chklovskii et al. 2004). Because total membrane capacitance is directly proportional to the membrane surface area, it is an important cellular feature to measure to express changes in cellular properties after taking size differences and changes into account. Changes in ionic conductance during plasticity or developmental changes, for example, are often expressed as conductance densities to remove potential effects of changes in neuronal size during these processes (Haedo and Golowasch 2006; Iwasaki et al. 2008; Khorkova and Golowasch 2007; Pineda et al. 2008; Royeck et al. 2008).
Several experimental methods exist for determining total membrane surface area which rely on membranes having a specific membrane capacitance that is similar in most cells and generally agreed to be 0.5–1.0 μF/cm2 (Koch 1999; Solsona et al. 1998). Capacitance can be calculated from the rate and amplitude changes in the voltage or current responses under current- and voltage clamp, respectively. These methods are used extensively to determine the total membrane capacitance of neurons of various sizes and architectures. However, these methods were derived for, and can correctly be applied only to, isopotential cells. Biological neurons rarely conform to this constraint. Consequently, these methods are likely to yield incorrect estimates of cell capacitance and consequently cell surface area. Nevertheless, a cursory look at current editions of major neuroscience journals indicates that capacitance measurements are made without regard to the validity of the assumptions underlying the method used. Assessing the accuracy of these methods to estimate total membrane capacitance in neurons with complex architectures is essential if capacitance measurements are to be used to make correct inferences about changes in cell surface area as a measure of neuronal conductance density changes.
We compared the capacitance values of identified neurons in the crab stomatogastric nervous system using three of the most commonly used methods for capacitance measurement. We show that these different protocols yield significantly different values for the measured total membrane capacitance in the same neuron. We then evaluate the accuracy of these methods using simple computer models of nonisopotential cells. Our results confirm that appropriate exponential fits to voltage profiles in response to DC current step injection can provide an accurate measure of total membrane capacitance values over a wide range of cell sizes and architectures (for a theoretical analysis, see Major et al. 1993a). In contrast, measurements of the charge accumulated in the membrane capacitor using voltage-clamp steps, among the most commonly used methods in electrophysiology (cf. Haedo and Golowasch 2006; Iwasaki et al. 2008; Khorkova and Golowasch 2007; Pineda et al. 2008; Royeck et al. 2008), is shown to yield the least accurate capacitance estimates. To provide insight into the discrepancy observed in these methods, we use a simple two-compartment model to derive mathematical expressions that show the source of the different total membrane capacitance measurements with the current- and voltage-clamp protocols. Equivalent equations can also be derived in more general form, for an arbitrary treelike neuronal structure, from the theoretical work of Major et al. (1993a,b). Our results suggest that, although current-clamp steps should be the preferred method to reduce the inaccuracies in capacitance determination, the difference in capacitance values measured with the different methods can be used to make approximate inferences about cell surface distribution among different neuronal compartments. Finally, simple two-compartment theoretical analysis can be used to obtain an intuitive understanding of the source of errors in total capacitance measurement with these different methods.
METHODS
Electrophysiology
The lateral pyloric (LP) and pyloric dilator (PD) neurons from the pyloric network of the crab Cancer borealis, localized in the stomatogastric ganglion (STG), were identified using standard procedures previously described (Harris-Warrick 1992; Selverston et al. 1976). Individual neurons were then impaled with two microelectrodes pulled using a Flaming-Brown micropipette puller (P87, Sutter Instruments, Novato, CA) and filled with a 0.6 M K2SO4 + 20 mM KCl solution (electrode resistance was 20–25 MΩ). One of the electrodes was used to pass current and the other to record voltage. Neurons were recorded in either two-electrode current-clamp or two-electrode voltage-clamp mode using an Axoclamp 2B amplifier (Molecular Devices, Union City, CA). In voltage-clamp mode, the amplifier gain was set to a value around 3–8. We did not attempt to increase the gain to its maximum possible even if stability could be ensured using appropriate phase lag settings (see following text). The preparations were bathed in 10 μM picrotoxin (Sigma–Aldrich, St. Louis, MO) to block glutamatergic synaptic input, 0.1 μM tetrodotoxin (TTX; Biotium, Hayward, CA) to block fast Na+ current-dependent action potentials and consequently all oscillatory activity, and 5 mM CsCl to block the hyperpolarization-activated inward current. Capacitance was measured at voltages between −50 and −60 mV to avoid activation of voltage-gated currents (Golowasch and Marder 1992; Haedo and Golowasch 2006). Data were acquired with the Digidata 1322A board and pClamp 9.2 software (Molecular Devices).
Capacitance measurements
1) Current-clamp protocol (CC_step).
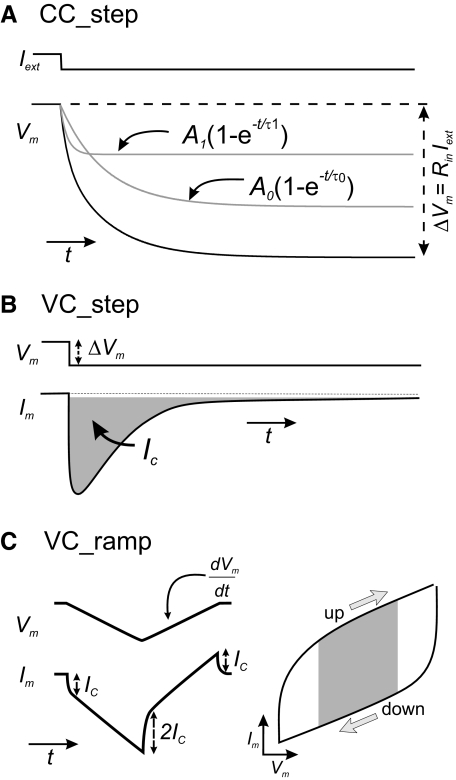
DC current steps (−0.5 to −2 nA, 500- to 1,000-ms duration) were injected in the soma and the membrane potential (Vm) change was recorded with a sampling rate of 50 kHz. Thirty consecutive traces were averaged to remove noise. In an isopotential cell this results in a membrane potential change characterized by a single exponential (Eq. 1) with time constant τm= rmcm, where rm is the cell membrane resistance and cm is the total membrane capacitance. In such an isopotential cell, rm is equal to the cell's input resistance Rin. The maximal membrane potential change is given by ΔVm= Vm −Vrest= RinIext, where Iext is the injected current step. When a cell is nonisopotential, an equalizing process related to current flow between electrical compartments of the cell takes place (Major et al. 1993a; Rall 1977); the membrane potential change ΔVm(t) is now determined by a series of exponential terms (Eq. 1) and Rin is no longer equal to rm. Typically only two or three terms adequately describe Vm(t) (Fig. 1 A), given by the equation
| (1) |
By dividing through by Iext, one obtains a series of resistive terms Ri= Vi/Iext. At steady state, the sum of these resistive terms is Rin = ΔVm/Iext. The time constant of the slowest exponential term τ0 corresponds to the membrane time constant τm= rmcm (Holmes et al. 1992; Major et al. 1993a; Rall 1977). To determine the values of Vi and τi we fit the Vm(t) curve obtained in response to the current step using two or three exponential terms using the Levenberg–Marquardt (LM) algorithm of the Clampfit analysis software in the pClamp package, with a precision of 10−6. To obtain the best fits to both fast and slow components, we fit the trace between t = 0 and a time at which the voltage had reached steady state, usually the end of the 500- to 1,000-ms step.
Fig. 1.
Total membrane capacitance measurement protocols. Schematic diagrams representing the protocols used. A: current-clamp step. The membrane potential change (black trace) elicited by a 1-s-long current step (Iext) was fitted with 2 exponentials (gray traces). The slowest component corresponds to the charging of the membrane capacitor. B: voltage-clamp step. The area under the capacitive current transient (gray) is the charge deposited on the membrane for a given ΔVm. The duration of this pulse is typically shorter than that of the current-clamp steps. C: voltage-clamp ramp. Membrane potential ramps elicit a capacitive current step Ic. The sign of Ic depends on the slope of the voltage ramp. If a symmetric voltage ramp is used, the difference between the values of Im measured at the same membrane potential during the up and down ramps is equal to 2Ic. This value was calculated by measuring the average current value of the upper and the lower branches over the grayed area in the current–voltage (I–V) curve and dividing by 2(dV/dt) (see methods; arrows correspond to the slope of the voltage ramp).
2) Voltage-clamp step protocol (VC_step).
Steps 1,000 ms long between −50 and −60 mV were applied in voltage clamp and 20–30 sweeps were averaged to remove noise. The membrane current and membrane potential were sampled at 50 kHz. This method relies on the measurement of the total charge Q accumulated on the membrane capacitor during the initial (capacitive) current transient (Fig. 1B, gray area) and can be calculated by the following equations
| (2) |
| (3) |
where tp is the step duration.
Determination of the capacitive transient's integral is sensitive to the rate of current change during the transient. This sensitivity is attributed to aliasing if the sampling frequencies are lower than the Nyquist frequency (Harris 2006). In turn, the rate of current change increases with the gain setting of the voltage clamp. Thus the voltage-clamp gain was set high enough to ensure that the voltage settled at the test voltage within the duration of the step, but not necessarily at the highest possible value, to avoid aliasing.
3) Voltage-clamp ramp protocol (VC_ramp).
Ramps of voltage were applied from a holding membrane potential of −50 mV. A 10-mV hyperpolarizing ramp was immediately followed by a 10-mV depolarizing ramp of the same duration (Fig. 1C, left, top trace). The protocol was repeated 30 times and the current traces were averaged to remove noise (Fig. 1C, left, bottom trace). Two different ramp slopes were used: 0.02 and 0.5 mV/ms. The sampling rate was set to 50 kHz and the same gain setting as in the voltage-clamp step protocol was used. The current was plotted versus the voltage (Fig. 1C, right) and the capacitive current was obtained by measuring the resulting capacitive current difference (2ic) between the two ramps at a given voltage. We used the average current values around the middle 50% of the current–voltage (I–V) curve to measure 2ic, avoiding the beginning and end of the ramps to elude spurious effects (Fig. 1C, right, gray area). cm was calculated according to
| (4) |
where dVm/dt corresponds to the slope of the voltage ramp (Fig. 1C, top left trace).
Modeling
We used model anatomical structures of varying complexity, with the simplest consisting of two spheres attached to the respective ends of a cable, which represents a neurite, and has length len and diameter dc. One sphere represents the soma (with diameter ds) and current and voltage are measured and manipulated only in this compartment. The second sphere represents the combined area of all dendrites and has diameter dd. We modeled variations in neuronal size by changing dd (see inset in Fig. 3A). More complex models are treelike structures with a sphere (the soma) attached to a cable (the primary neurite) and additional branched cables, representing dendrites of various orders, attached to the opposite end. In the “asymmetric tree” structure, the second-, third-, and fourth-order neurites are connected to only one branch of the primary or (n − 1)-order neurites (see inset in Fig. 5A). The number of primary dendrites was limited to two, secondary dendrites to four, and tertiary dendrites to eight, and each higher-order dendrite had a diameter of half of the previous order dendrite diameter. A “concentric” tree was built by attaching all these higher-order dendrites directly to the soma (see inset in Fig. 5B) and a “symmetric tree” was built by distributing the same number of dendrites symmetrically—i.e., instead of all secondary and tertiary branches always originating respectively in the same primary and secondary dendrite, they are distributed evenly among all the (n − 1)-order dendrites (see inset in Fig. 5C).
Fig. 3.
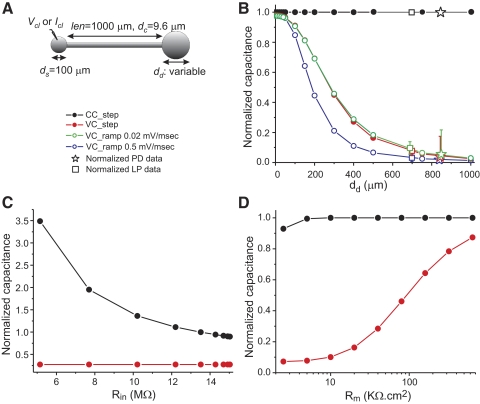
Effect of measurement protocol on total membrane capacitance estimates in a simple neuronal model. A: diagram of the model cell. The length of the neurite is 0.25λ. B: the capacitance in the model was determined with the three protocols described in methods and with two ramp slopes. Values were normalized against the actual total capacitance of the cell and are plotted against the diameter of the dendritic compartment. Normalized capacitance values measured in PD neurons (n = 29) and LP neurons (n = 19) using the same protocols as in the model. Capacitance values of each PD and LP neuron recorded were normalized to the neuron's own current-clamp–measured capacitance (Table 1). C: dependence of the measurements on soma and input resistance. The model cell shown in A with a dendrite diameter of 400 μm was used and the conductance of the soma compartment was varied (0.5 to 125 nS). The capacitance was measured with the CC_step and VC_step methods in response to 1-s-long current and voltage pulses, respectively, and normalized by the actual cell capacitance. The input resistance Rin was measured using Ohm's law. D: dependence of the measurements on specific membrane resistivity. The model cell shown in A with a dendrite diameter of 400 μm was used and current-clamp and voltage-clamp pulses of 1-s duration were used. As in B, measured capacitance values were normalized against the actual total capacitance of the cell and are plotted against the specific membrane resistivity Rm.
Fig. 5.
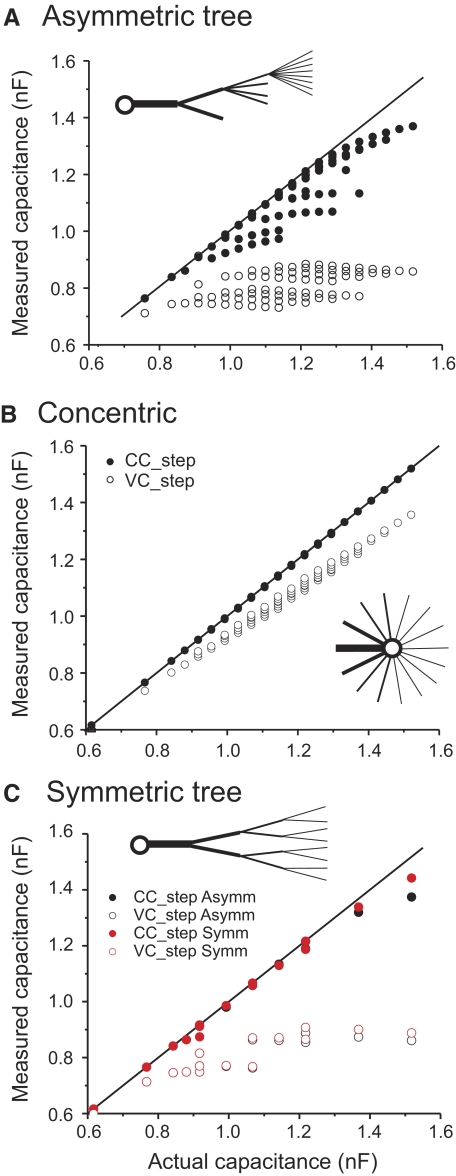
Effect of cell architecture on total membrane capacitance estimates. Capacitance was measured using either the current-clamp (CC_step; filled symbols) or voltage-clamp step protocols (VC_step; open symbols) and is graphed without normalization. The actual capacitance was determined from the surface area of the cell and the specific membrane capacitance. A: asymmetric tree. The inset illustrates the architecture of this model: each subsequent dendritic level has a maximum of double the number of dendrites of the preceding level and all branches at any given level emerge from a single dendrite. B: concentric tree. The same dendrites as in A all emerge directly from the soma. C: comparison of the data from the asymmetric tree (from A) and data from a “symmetric tree” in which the same branches as in A emerge symmetrically from the previous level (see text).
Passive cables and spheres were used for these models and the passive parameters were chosen as Cm = 1 μF/cm2, Rm = 40,000 Ω·cm2, and Ra = 60 Ω·cm (Rabbah et al. 2005). For simulations, each cable was compartmentalized into segments with length of at most λ/20, and each compartment j obeyed the current balance equation
| (5) |
where Ileak,j is the linear leak current of compartment j and Iaxial,j is the axial current flowing from adjacent compartment(s) into compartment j.
The membrane and cable equations were numerically integrated using the software Network (http://stg.rutgers.edu/software/network.htm) using a fourth-order Runge–Kutta integration method and a time step of 10 μs. Simulation data were sampled at 10 kHz for the CC_step and VC_ramp protocols and at 100 kHz for the VC_step protocol.
Data are expressed as average ± SD.
RESULTS
Measurement protocol determines capacitance measurement discrepancies
We explored how the measured capacitance of a neuron depends on the particular protocol used by examining measured values, with distinct protocols in the crab pyloric dilator (PD) and lateral pyloric (LP) neurons, which are readily identified in the STG. Three measurement protocols were used, one using current steps and the other two in voltage-clamp mode (see methods).
Measurements of capacitance using DC current steps depend on accurate measurement of the membrane time constant and resistance. Frequently, when this method is used to estimate the total membrane capacitance of a neuron, cm is derived by dividing τm by the input resistance Rin (e.g., Dougherty et al. 2005; Golowasch and Marder 1992). Although this is correct for an isopotential cell, in which case Vm(t) can be fit with a single-exponential term, it is not correct for a nonisopotential cell. In the case of a finite tree with sealed ends, Vm(t) can be fit as a sum of exponentially decaying terms given by Eq. 1, where τ0 > τ1 > τ2 >… is a sequence of time constants (Major et al. 1993a; Rall 1977). The slowest component corresponds to the charging of the membrane capacitor and therefore the exponential fit to the slowest component provides the membrane time constant τm. The correct measurement of cm is obtained by dividing τm (= τ0) by the resistance coefficient R0= V0/Iext (and not the input resistance of the cell) (Major et al. 1993a). In practice, the passive response of a neuron to DC current injection can be adequately fit with only two or three exponential terms. The diagram in Fig. 1A shows the membrane potential response (Vm, dark trace) to a current step (Iext). In the case shown, Vm can be decomposed into two exponentially decaying components whose sum adequately fits this voltage trace (gray traces). Once again, the correct measurement of cm in this case is obtained as τ0/R0. To demonstrate the difference in the measured values when using Rin or R0, we compared these measurements in recordings of PD neurons. The time constant is 151.10 ± 89.52 ms (n = 29). The calculated cm using Rin was 12.43 ± 7.44 nF, whereas, using R0, the value was 65.61 ± 68.23 nF (Student's t-test, P < 0.0001, n = 29). It is these latter values that we use as our measurements for CC_step in both the experimental protocols and in the computational models described in the following text.
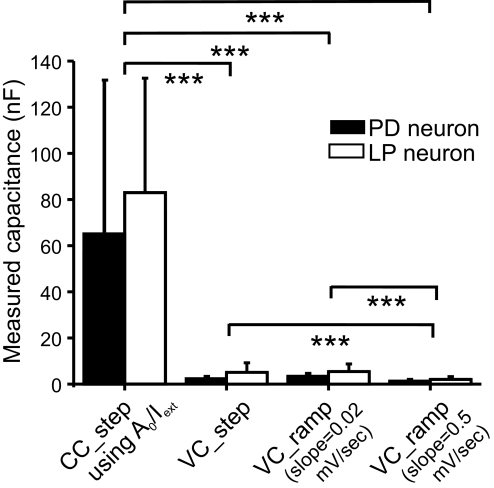
We compared the CC_step measurements with measurements done using the voltage-clamp step (VC_step) protocol and the voltage-clamp ramp (VC_ramp) protocol using two different slopes of 0.02 and 0.5 mV/ms (Fig. 2). In measurements from either the PD neuron or the LP neuron, these values were significantly different (Kruskal–Wallis one-way ANOVA on ranks, P < 0.0001, for both PD and LP neurons; see Table 1 and Fig. 2). A post hoc analysis using Dunn's method showed that the current-clamp estimate of capacitance is significantly higher than that of either of the two voltage-clamp methods, and that the fast voltage-clamp ramp method is significantly different from that of either VC_step or slow (0.02 mV/ms) voltage-clamp ramp method.
Fig. 2.
Effect of experimental protocol on total membrane capacitance measurements. Pyloric dilator (PD) and lateral pyloric (LP) neurons were impaled with 2 electrodes and capacitance was measured in either current clamp (CC_step) or voltage clamp (VC_step or VC_ramp) in the presence of tetrodotoxin (TTX) and Cs+ in the bath, as described in methods. The capacitance values were compared with a Kruskal–Wallis one-way ANOVA on ranks with post hoc Dunn's test comparisons. ***P < 0.001. More details in Table 1.
TABLE 1.
Capacitance values of PD and LP neurons obtained with different protocols
| Protocol | PD Neuron Capacitance, nF |
LP Neuron Capacitance, nF |
||||
|---|---|---|---|---|---|---|
| Average | SD | n | Average | SD | n | |
| CC_step | 65.61 | 68.23 | 29 | 83.82 | 50.71 | 18 |
| VC_step | 2.61 | 0.23 | 30 | 5.23 | 4.23 | 18 |
| VC_ramp (dV/dt = 0.02 mV/ms) | 3.61 | 1.23 | 29 | 5.48 | 3.41 | 18 |
| VC_ramp (dV/dt = 0.5 mV/ms) | 1.61 | 0.23 | 32 | 2.03 | 1.18 | 18 |
The average values of τm, τ1, R0, and Rin for the PD neuron were 158.7 ± 96.4 ms, 33.9 ± 17.0 ms, 2.3 ± 1.7 MΩ, and 11.4 ± 6.0 MΩ, respectively (n = 29). The average values of τm, τ1, R0, and Rin for the LP neuron were 215.2 ± 67.1 ms, 29.0 ± 10.3 ms, 2.1 ± 0.9 MΩ, and 9.7 ± 6.8 MΩ, respectively (n = 18). A post hoc analysis with Dunn's method showed that the CC_step estimate is significantly higher (P < 0.001) than that of either of the two voltage-clamp methods, and that the capacitance estimate with the fast voltage-clamp ramp method (0.5 mV/ms) is significantly (P < 0.001) different from that with either VC_step or slow (0.02 mV/ms) voltage-clamp ramp method. The capacitance estimates with VC_step and slow (0.02 mV/ms) voltage-clamp ramp protocols are not significantly different.
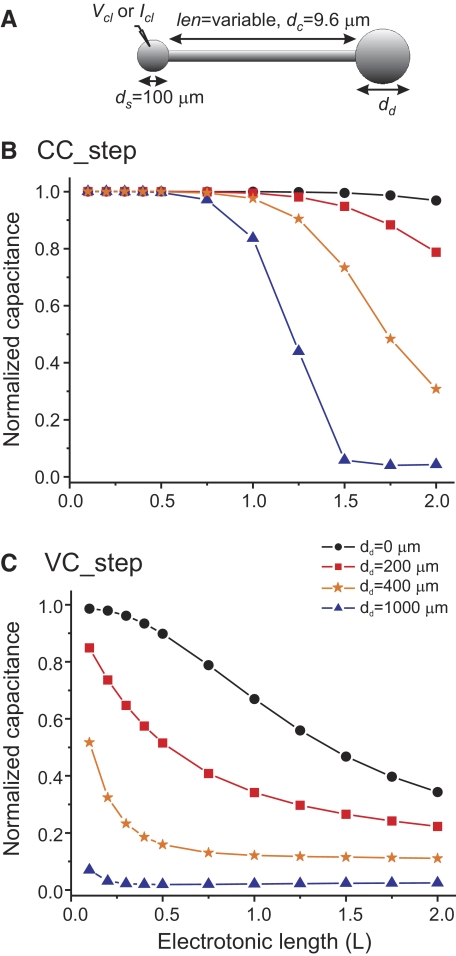
To explore the source of this large difference in total membrane capacitance estimates obtained using the current-clamp and voltage-clamp protocols, we built a simple passive model and measured its total membrane capacitance using these three protocols. The model consisted of a spherical soma of fixed diameter connected to a cable representing a primary neurite connecting the soma to more distal compartments (see methods for parameters). The distal end of the cable was connected to a second sphere representing the equivalent area of distant dendritic compartments (Fig. 3A). With the exception of the length of the neurite, the passive membrane parameters used are approximations to values assumed to be typical of PD neurons until now (Hartline and Castelfranco 2003; Nadim and Golowasch 2006; Rabbah et al. 2005). With these parameters, the dendritic compartment is at an electrotonic distance of L = len/λ = 0.25 away from the soma. Figure 3B shows the results of applying the current-clamp and voltage-clamp protocols by recording the voltage and injecting current into the soma compartment and varying the diameter of the dendritic “sphere.”
The capacitance values measured in the model cell were normalized to their actual capacitance (determined from the total cell surface and the specific membrane capacitance Cm) and are shown in Fig. 3B as colored circles. The current-clamp protocol yielded capacitance estimates (using the τm/R0 measurement described earlier) that were indistinguishable from the actual capacitance of the cell for all values of dendritic compartment size tested (black symbols). However, capacitance value measurements obtained with the voltage-clamp protocols underestimated actual capacitance values for all dendritic compartment sizes, with errors increasing rapidly as the dendritic compartment diameter exceeded 100 μm. Estimates obtained with the ramp protocol depended on the slope of the voltage ramp (dV/dt), with better results obtained with the slow ramps (dV/dt = 0.02 mV/ms, green circles). Faster ramps (blue circles) led to increasingly worse capacitance estimates than those obtained with the voltage-clamp step protocol (red circles). Voltage ramps with slopes <0.02 mV/ms did not significantly improve the capacitance estimates and are not shown. Reducing the pulse duration in the VC_step protocol further reduced the capacitance estimates. Adding noise to the voltage traces obtained with the current-clamp protocol had a minimal impact on the capacitance estimates (<1% error with 5-kHz white noise current injection of 5% amplitude as the current step; not shown).
To determine whether such a simple model could represent the surface area distribution of a biological neuron, we compared the capacitance values of the biological PD and LP neurons measured with the three protocols (and two different voltage ramp slope values) with the values obtained in the model. The biological capacitance values obtained are listed in Table 1 and the normalized values (normalized to each neuron's capacitance value measured with the CC_step protocol) are plotted in Fig. 3B (LP neuron: squares; PD neuron: stars). When these data were compared with the data obtained with the same protocols on the ball-stick-ball model we found that the PD neuron could reasonably be fit by a model with an approximate dendritic “sphere” diameter dd of 820 μm and the LP neuron with an approximate diameter dd of 700 μm. The comparison derived from Fig. 3B is meaningful in only two general ways: it indicates that the “dendritic compartment” is much larger than the “somatic compartment” in both neuron types and it suggests that PD neurons appear to have a larger dendritic surface area than that of LP neurons.
Because the voltage-clamp step and ramp protocols (with dV/dt = 0.02 mV/ms) yielded similar results henceforth we show only the VC_step data.
Effect of membrane leak, resistivity, and electrotonic length on capacitance measurement
Using our simple ball-stick-ball model we examined the effect of three important factors that are commonly thought to affect current- and voltage-clamp measurements: soma leak (such as is induced by the damage to the membrane due to microelectrode penetration), overall membrane resistivity, and the electrotonic distance of the distal dendritic compartment from the soma. Changes in the conductance of the soma compartment alone (range: 0.5–125 nS) had no effect at all on the total membrane capacitance when measured with either voltage-clamp protocol, but greatly affected the measurement using the current-clamp protocol. In Fig. 3C, the effect of changing the soma conductance on capacitance measurement is plotted as a function of the resulting input resistance Rin in each case. High values of soma resistance tended to lead to slight underestimates of the total membrane capacitance with the CC_step protocol, whereas low soma resistance led to marked overestimates (Fig. 3C). In contrast, reducing the specific membrane resistivity Rm uniformly over the entire surface of the cell substantially reduced the estimates obtained with both voltage-clamp protocols (Fig. 3D), but had little impact on the estimates obtained with the CC_step protocol.
The membrane voltage attenuates with the distance from the point of current injection. Therefore the electrotonic distance of the dendritic compartment from the point of measurement (i.e., the soma) is likely to affect the accuracy of the capacitance measurements. To determine how the cm value obtained by different measurement protocols may be affected by the electrotonic size of the neuron, we used the same model and varied the length of the neurite while keeping the dendrite diameter fixed (Fig. 4 A). Capacitance estimates using the current-clamp protocol yielded almost perfect estimates for up to about one length constant away from the soma even for the largest dendritic compartment (i.e., dd = 1,000 μm, Fig. 4B). For electrotonic lengths L > 1, the capacitance measurement deteriorated in a manner that depended on the dendrite compartment size. The capacitance measurement error is nevertheless remarkably small even with a dendrite diameter of dd = 200 μm and almost nonexistent when no dendrite compartment is added, i.e., dd = 0 μm (Fig. 4B). When the voltage-clamp step protocol is used, these estimates drop much more abruptly. In this case, error values of <20% are obtained for L < 0.75 when no dendritic compartment is present or L < 0.15 with a dendrite with diameter 200 μm (Fig. 4C). For all other conditions the errors are much larger and, for L > 1.4, the voltage-clamp protocol results in errors of >50% even when no dendritic compartment exists.
Fig. 4.
Effect of distance of the dendritic compartment from the point of recording. A model identical to that used in Fig. 3 was used (A) but the dendritic diameter was fixed at four different values and the length of the neurite was varied and plotted as the electrotonic length (B, C). Measured capacitance was normalized by the actual total cell capacitance.
Effect of neuronal architecture on capacitance measurements
Since both the size of the dendritic compartment and its distance from the site of measurement affect all of the capacitance estimates, we built more complex and realistic neuronal models to better understand the role of neuronal architecture on capacitance measurements. Figure 5 shows capacitance measurements in three different neuronal models. The first of these models (“asymmetric tree”; see diagram in Fig. 5A) consists of a soma connected to a tree of branching dendrites, all with equal length (len = 1,000 μm; see methods for additional parameters). Each dendritic “level” has one half the diameter and at most double the number of branches of the previous level. All branches in a given level emerge from only one of the branches from the previous level (see diagram in Fig. 5A, inset). The first (primary) dendritic level consisted of a single cable with diameter dc1 = 9.6 μm, which was connected to either one or two secondary dendrites with diameter dc2 = 4.8 μm, and so on.
To examine the effect of the complexity of the tree architecture we added one branch at a time and measured capacitance of the cell with the three methods described earlier. With this architecture, when all branches are present (i.e., each dendritic level has exactly double the number of branches of the preceding branch), the total capacitance of each dendritic level is the same. Again, as with the simpler model, we observed that the current-clamp protocol (Fig. 5A, filled symbols) yields capacitance values that are much closer to the actual total capacitance (identity line) than the voltage-clamp protocols (Fig. 5A, open symbols). The two clusters that can be observed with the VC_step data are due to the presence of either one (lower cluster) or two (higher cluster) secondary-level branches because an additional secondary branch adds a large amount of capacitance at a short electrotonic distance from the soma. The same phenomenon occurs when the CC_step method is used, except that the data are closer to the identity line, making it more difficult to distinguish the clusters. The apparent “branches” emerging from the identity line for the CC_step protocol data correspond to changes in tertiary branch numbers, with the values along each branch corresponding to variation in quaternary branch numbers. The abrupt decreases in capacitance when new branches are added are probably due to increasingly large numerical errors in the multiexponential fitting procedure, since it has been shown that the slow exponential term correctly represents the charging of the membrane in neurons of any arbitrarily complex architecture (Major et al. 1993a). The same phenomenon is also observed with the VC_step data but here the data corresponding to tertiary branch numbers are less clearly separated. As in the simpler model, voltage-clamp ramp protocol results (with dV/dt = 0.02 mV/ms) were very similar to those obtained with the voltage-clamp step protocol and are not shown.
To examine the effect of the tree structure on these measurements, we applied the same measurements to a model neuron in which the same branches were all connected directly to the soma (“concentric tree”; see diagram in Fig. 5B). In this case all current-clamp data fell almost perfectly on the identity line and the voltage-clamp data deviated from this line only modestly (Fig. 5B). Thus not surprisingly, a more compact neuronal structure yields far better capacitance estimates regardless of the number of branches, with the current-clamp step method always producing values that are more accurate than those of either voltage-clamp method (ramp data not shown).
We also explored the effect of asymmetry in the neuronal tree structure on our measurements in a symmetric model. The “symmetric tree” model was built by having the branches emerge symmetrically from the previous level dendrite, rather than having all emerge from a single dendrite (see diagram in Fig. 5C). The resulting capacitance measurements of the symmetric tree structures are plotted together with the corresponding asymmetric tree data (with the same branch numbers at each level) in Fig. 5C. The number of points in this plot is lower than that in Fig. 5B because there are fewer possible symmetric than asymmetric structures and we plotted only those points of the asymmetric tree for which a distinct capacitance value was measured. We observe that evenly distributing the dendritic load among branches (as in the symmetric structure) improves the capacitance estimates, although the differences are slight and are noticeable for only the largest tree structures.
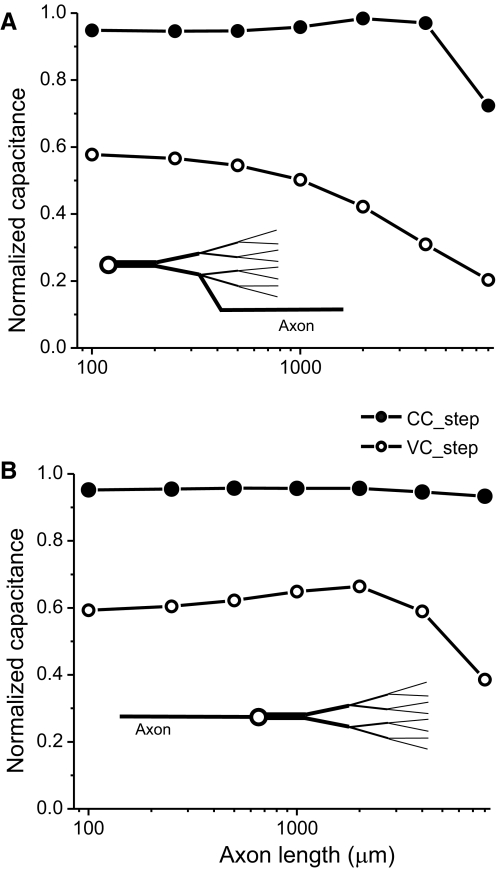
The symmetric tree model was used to examine the effect of an axon emerging at different locations in a neuron. Figure 6 A shows the effects of attaching axons of different lengths to the end of the secondary dendrite, approximately corresponding to what is observed in STG neurons (Bucher 2007). Capacitance measurements obtained with the CC_step protocol produced accurate estimates for axon lengths of several millimeters, beyond which estimates began to deteriorate. In contrast to the CC_step measurements, VC_step estimates rapidly deteriorated for all axon lengths. In contrast, when the axon emerges directly from the cell body, as is commonly seen in vertebrate CNS neurons, CC_step total capacitance estimates are accurate for much longer axons than in the previous case (Fig. 6B).
Fig. 6.
Effect of the presence of an axon on total membrane capacitance estimates. Capacitance was measured using the current-clamp (CC_step; filled symbols) and voltage-clamp step protocols (VC_step; open symbols) as described in methods using 1-s-long pulses in both cases. The model used was identical to that described in Fig. 5C except that axons of different lengths and 10-μm diameter were added at the end of one of the two secondary dendrites (A) or to the soma (B).
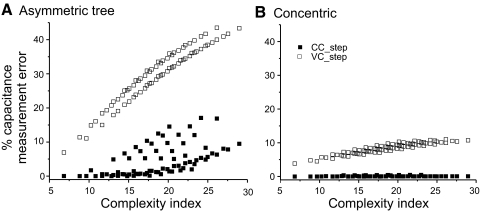
Finally, to evaluate the degree to which neuronal complexity affects the determination of cell capacitance, we calculated a complexity index for the tree structures based on the electrotonic length of each dendrite. The complexity index was defined simply as the sum of the electrotonic lengths of all dendrites of the cell. Figure 7 shows the same data as those in Fig. 5, A and B, indicating again that the current-clamp method provides a good estimate of cell capacitance for the neurons with fewer branches, i.e., lowest complexity index (Fig. 7A, filled symbols). However, some estimates have large errors even when the complexity index is low. Closer inspection of the data reveals that in all such cases the cells had a high number of quaternary dendrites (>5), but low number of lower-level dendrites. This generated low complexity index values but a widely distributed capacitance, in turn leading to large capacitance estimate errors. In general, however, there is a relatively good correlation of the measurement error level and neuronal complexity (i.e., branch number and total electrotonic length). The voltage-clamp protocol produces much larger estimate errors (Fig. 7A, open symbols), with two distinct clusters due to the presence of either two (high error level cluster) or only one (low error level cluster) secondary level branch (also seen in Fig. 5A). The concentric cell in which all branches emerge directly from the soma predictably produces much lower estimate errors with both current- and voltage-clamp methods, as would be expected from an electrotonically more compact neuron, with voltage-clamp protocols again generating manyfold larger errors than those of the current-clamp protocol (Fig. 7B).
Fig. 7.
Effect of cell complexity on capacitance estimates. A measurement error was calculated as (Cm actual −Cm measured)/Cm actual and plotted against a complexity index that corresponds to the sum of the dendritic electrotonic lengths of all the branches in the model. The asymmetric (A) and concentric (B) models described in Fig. 5 are compared.
Discrepancy between the voltage-clamp and the current-clamp measurements can be elucidated using a two-compartment model
The responses to current- and voltage-clamp pulses have been previously derived for an arbitrarily complex neuronal architecture (Major et al. 1993a,b). Although the derivations of Major and collaborators can be used to estimate the effect of the methods of capacitance measurements for complex structures (particularly for the current-clamp case; see Eq. 36 in Major et al. 1993a), we present a comparison using a two-compartment model to help gain a simpler and more intuitive understanding of the factors that affect total membrane capacitance measurements in electrophysiological experiments. For brevity, we will compare only the CC_step and VC_step methods here, but the VC_ramp method can be dealt with in a similar fashion, as shown in the appendix (Eqs. A27–A31).
It can be shown that this circuit responds to a current-clamp step of size Iext with a double-exponential voltage trace described by
| (6) |
where R0, τ0, R1, and τ1 (τ0 > τ1) are constants determined by the values of Ra (the axial resistance) and Cn, Rn, Cf, and Rf, denoting, respectively, the membrane capacitance and resistance of the “near” and “far” compartments. If we assume that RnCn = RfCf, as would be the case for a cell with uniform specific membrane resistance and capacitance, then it can be shown that
| (7) |
Thus in this simplified model, it can be proven mathematically that the current-clamp step method described earlier always gives the correct answer for the total capacitance (see appendix).
The response of this simple model to a voltage-clamp step of size ΔVm can also be derived and is given by
| (8) |
where Cpulse, Gin, Gdecay, and τvc are constants determined by the values of Ra, Cn, Rn, Cf, and Rf (see Eqs. A18–A21 in the appendix). δ(t) is the Dirac delta function, here representing the mathematical idealization of a large brief pulse of current corresponding to the capacitive transient and u(t) is the unit step function denoting the current pulse. If we subtract off the steady-state current and integrate, we find that the charge delivered by the capacitive transient and the subsequent exponential decay is given by Q = ΔVm(Cpulse + Gdecayτvc). Since the voltage-clamp step estimate of capacitance is given by Q/ΔVm (Eq. 2), this yields an estimate of Cpulse + Gdecayτvc. It can be shown that this expression is equal to
| (9) |
(see appendix). The factor 1/[1 + (Ra/Rf)]2 is <1 for nonzero Ra, indicating that the voltage-clamp method provides an underestimate of the total capacitance for all nonisopotential cells and that this estimate approaches the capacitance of the near compartment as the axial resistance increases.
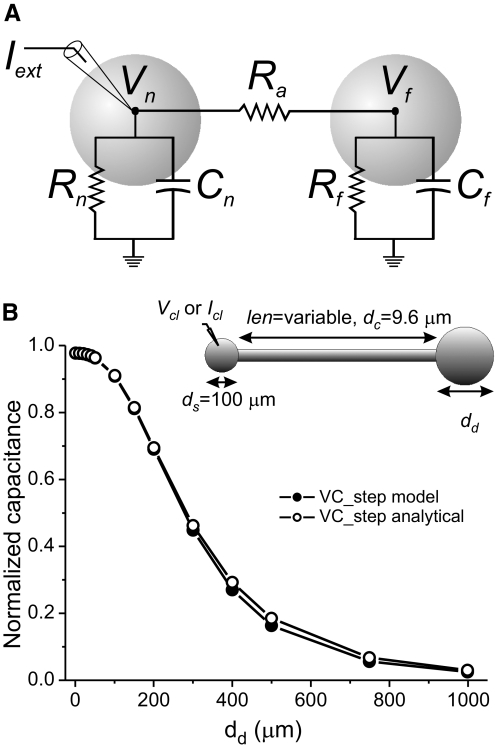
The ratio of the VC_step estimate of capacitance to the CC_step estimate can be predicted from the parameters R0, R1, τ0, and τ1 obtained from exponential fits to voltage traces obtained with the CC_step protocol (Eq. A26 in the appendix). This is demonstrated in Fig. 8 B, in which the normalized total membrane capacitance is plotted as a function of the dendritic compartment diameter in our simple ball-stick-ball model neuron, for capacitance values determined with the VC_step protocol (same data as those in Fig. 3B) and applying Eq. A26 to parameters measured with the CC_step protocol. The same is not true when the neuronal anatomy is more complex and is better approximated with three or more compartments (and thus the data from CC_step experiments are better fitted with three or more exponential terms), such as in the case of our treelike neuron models (Fig. 5) or the biological STG neurons. In these cases estimates obtained with Eq. A26 do not provide a good match to the VC_step measurements (not shown).
Fig. 8.
Analytical estimates of capacitance in a two-compartment equivalent circuit of the ball-stick-ball neuron model. A: diagram and equivalent circuit representation of a two-compartment ball-stick-ball neuron. Vn denotes the membrane potential in the soma (near) compartment and Vf the membrane potential in the distal (far) compartment (both are offset by the resting potential, e.g., Vn = Vmn − Vrest), coupled with resistance Ra. The electrode in the soma represents the site of current injection (Iext) in current- or voltage-clamp recording mode. B: capacitance measurements normalized by the actual total capacitance of the cell are plotted against the diameter of the distal compartment dd of the ball-stick-ball model neuron used before (inset). Measurements labeled “VC_step model” were obtained with the voltage-clamp step protocol applied to the ball-stick-ball model and are identical to those shown in Fig. 3B. Measurements labeled “VC_step analytical” were calculated using Eq. A26 and parameters R0, R1, τ0, and τ1 determined from two-exponential fits to CC_step data using the same ball-stick-ball model.
DISCUSSION
Total membrane capacitance is a common measure of cell surface area and is used in electrophysiology recordings as a means for measuring ionic conductance, or ion channel density or to normalize for changes in cell size (Haedo and Golowasch 2006; Iwasaki 2008; Khorkova and Golowasch 2007; Pineda et al. 2008; Royeck et al. 2008). A common protocol used to measure total membrane capacitance is to integrate the transient capacitive current produced during voltage-clamp steps (Haedo and Golowasch 2006; Iwasaki et al. 2008; Khorkova and Golowasch 2007; Pineda et al. 2008; Royeck et al. 2008). This method is fast and simple to use and some electrophysiological data acquisition software includes an automatic capacitance calculation based on this method (e.g., pClamp, Molecular Devices). The application of this protocol is based on the crucial assumption that the cell is isopotential. Occasionally, this assumption is satisfied, such as with small cells with few and or short processes. Another common method for measuring total membrane capacitance is to calculate the ratio of the membrane time constant, measured using current steps, to the cell input resistance. This method applies to an isopotential cell as well as a finite cable (or, using a correction factor, to a cable connected to a spherical soma) if the correct resistive term is used rather than the input resistance (Rall 1977). Other methods, such as applying a voltage ramp under voltage-clamp conditions (Nadim et al. 1995) or phase-shift measurements in response to sine-wave current inputs (Johnson et al. 2002; Joshi and Fernandez 1988; Neher and Marty 1982), can also be used to measure total membrane capacitance. A voltage ramp, for example, uses the fact that the capacitive current is proportional to the rate of change of the membrane potential with the constant of proportionality equal to the membrane capacitance (Eq. 4). All these methods are based on the theoretical assumption of isopotentiality or, alternatively, having a finite uniform cable structure. However, most biological neurons violate these assumptions and thus these methods can produce erroneous total membrane capacitance values.
In this study we use identified neurons of the crab STG to demonstrate that three different protocols—the voltage-clamp step, the current-clamp step, and voltage-clamp ramps—yield significantly different capacitance values. We then use neuronal models of varying architectures to examine which method produces a more accurate estimate of total membrane capacitance. The modeling results show that both voltage-clamp methods produce significantly lower capacitance values than those of the current-clamp method and that, for more complex neurons, all methods underestimate the actual total membrane capacitance values. Using mathematical derivations of the transient solution to a current-clamp pulse it can be shown that the slowest exponential term should provide an accurate estimate of total capacitance for any neuron independent of the anatomical complexity (Major et al. 1993a). Thus it appears that the deviations from the actual capacitance observed using the current-clamp method (Figs. 5, A,C, and 7A) stem from an increasingly large numerical error in the multiexponential fits with increasingly complex architectures. However, the current-clamp method produces extremely accurate estimates of a cell's total membrane capacitance even for highly complex architectures and a very large range of specific membrane resistivity values. For instance, high accuracy is obtained in a ball-cable-ball model (with the two balls representing the soma and the dendrite surfaces; e.g., Fig. 3A) for cable lengths ≤1.25λ and a dendritic compartment of diameter 200 μm. The model shows that there is a trade-off in accuracy between the dendritic compartment size and cable length. With smaller dendritic compartments, accuracy is maintained even for longer cables (Fig. 4), whereas for shorter cables, accuracy is maintained for much larger dendritic compartments (Fig. 3B).
Similar accuracy levels can be obtained for neuron models with dendritic surface distributed over a tree of connected dendrites, even for neurons with several branching levels (Figs. 5–7). The maximum total capacitance of our most complex model is similar to that of our ball-cable-ball model with a dendrite compartment diameter of 200 μm and a cable of only 0.25λ. However, in contrast to the ball-cable-ball model, the capacitance estimates in this tree model are not as accurate, even with the current-clamp step method, indicating that the distributed capacitance over large electrotonic distances is partly responsible for the inaccuracy. At the same time, the capacitance load at the dendritic terminal also plays a role since different dendritic terminal sizes lumped into a simple sphere at the end of a fixed-length cable also yield different levels of accuracy.
Increasing the leakiness of the soma, such as produced by impalement damage, leads to an overestimate of the total membrane capacitance measurements with the current-clamp step method. This suggests that an independent knowledge of the input resistance of an undamaged cell (such as can be obtained in the whole cell patch-clamp mode) can help set acceptable minimum input resistance levels to minimize capacitance estimate errors. In contrast, voltage-clamp capacitance measurement methods are independent of soma damage because with high enough gain the voltage clamp can inject sufficient current into the soma to overcome the increased membrane leak. The charging of the membrane capacitance can then proceed at the clamped voltage and thus the capacitive current remains unaffected. A different effect occurs when the overall membrane resistivity Rm is modified. The current-clamp protocol estimate is negatively affected only at Rm values that are very low (≲3,000 Ω·cm2), which are seldom encountered in neurons (but see Hodgkin and Huxley 1952), whereas the voltage-clamp protocol estimates deteriorate steeply with reduced Rm. Changing Rm also results in changing Rin, yet in contrast to the effect of soma leak conductance on Rin, there is little change in the measured total membrane capacitance with the current-clamp method (Fig. 3, C and D). The difference between these two effects is likely explained by the fact that changing the soma leak conductance leads to different τm values between the soma and the dendritic structure, whereas changing Rm does not.
The distinct estimates of capacitance values provide information about the approximate distribution of surface area over the neuron's structure. In particular, although the current-clamp estimate gives a total capacitance that is remarkably close to the actual capacitance of the cell (especially if the electrotonic length of the cell is relatively short, e.g., L < 2), the voltage-clamp protocols yield estimates of the capacitance of the compartments only near the site of current injection. The capacitance difference between these estimates corresponds to the capacitance of membrane located in distal compartments of the cell. However, the assumption that the current-clamp step protocol always gives a correct estimate of the total neuronal capacitance is likely erroneous. Anatomical studies have shown that the LP and PD neurons have many long, fine dendrites (Bucher et al. 2007). The extremely large capacitance values we obtain in our current-clamp protocols are likely a reflection of the many thin and long dendrites these cells possess (cf. Figs. 4 and 7 in Bucher et al. 2007). Such dendrites may have large electrotonic lengths and thus current-clamp measurements likely underestimate the total capacitance of these neurons, albeit by a lower degree than the voltage-clamp measurements, as our modeling experiments with complex neuron models that include multiple dendrites demonstrate. The role played by the presence of a long axon on these measurements depends on the location where the axon emerges, with more accurate estimates obtained in neurons resembling typical vertebrate CNS neurons, in which an axon often emerges directly from the soma.
The estimates from the three measurement protocols can be used to determine the approximate surface area distribution in a model that accounts for the neuron's spatial structure. As a result, even the simple ball-cable-ball model used in this study may provide a good approximation for the distribution of ion channel conductances over functionally distinct neuronal structures representing those of a biological neuron (e.g., soma and dendrites). We used the estimates of the total membrane capacitance of the PD and LP neurons obtained with the different measurement protocols to predict the relative distribution of surface areas over functionally relevant compartments of these cells (Fig. 3B). Our results suggest that the compartment distal from the recording site has a surface area ≥15 to 25 times larger than that of the near compartment. We emphasize that this result does not imply that the near compartment corresponds to the soma and the distal compartment to the rest of the neuron's membrane. Indeed, exact inferences of total dendritic surface distribution cannot be made from such a simple comparison but would require a combination of accurate anatomical and physiological measurements. Yet, the ratio of the CC-measured capacitance to the VC-measured capacitance in different cells can provide an estimate of the relative sizes of the dendritic surface area in different neurons (Fig. 3B). From such measurements we can conclude that PD neurons appear to have a larger “dendritic” surface area than that of LP neurons. This may be a reflection of an extended surface area due to strong gap junctions between the PD neuron and other neurons to which it is strongly coupled (see Rabbah et al. 2005); this additional surface area would be absent in the LP neuron, which has much weaker gap junctional connections.
Another difficulty with capacitance estimation is deciding the part of the cell surface to use for estimating the capacitance. If studying changes in membrane surface area as a result of growth or degeneration, total capacitance would likely be the appropriate choice. If seeking to normalize measurements of voltage-gated conductances, the choice is less clear. In this case, one would like to measure a capacitance that reflects the portion of membrane that contributes to the measured voltage-clamp current. However, it is not clear that such a specialized portion of the membrane is a well-defined notion because a voltage-clamp step applied to the soma affects the voltage of a patch of membrane to a greater or lesser extent depending on the electrotonic distance from the soma to that patch. Here we have focused on measuring the total capacitance of the membrane and our results imply that voltage-clamp measurements provide a poor estimate of the total capacitance.
Because the membrane time constant is a property of the membrane and not of geometric factors, it is equal to the product of the actual capacitance and resistance of the membrane or of the specific membrane capacitance and resistivity, τm= rmcm = RmCm. The specific membrane capacitance of most neurons falls in the range of 0.5–1.0 μF/cm2 (Koch 1999; Solsona et al. 1998). Table 1 shows that the time constants of PD and LP neurons are about 155 and 220 ms, respectively. Thus even with the more conservative value of Cm = 1.0 μF/cm2, the specific membrane resistivity of these cells is ≥155 and 220 kΩ·cm2, respectively, which is more than threefold higher than previously thought (Nadim and Golowasch 2006; Rabbah et al. 2005). It remains to be determined how this difference may influence the behavior of existing models of LP and PD neurons (Golowasch and Marder 1992; Soto-Trevino et al. 2005).
Although our study is restricted to the three methods described earlier, alternative methods for measuring total membrane capacitance exist based on the frequency-dependent impedance measured in response to sinusoidal current inputs. This dependency is applied, for example, by lock-in amplifiers for capacitance measurements and has been used to measure membrane surface changes during exocytosis (Johnson et al. 2002; Joshi and Fernandez 1988; Neher and Marty 1982). This method also assumes a compact cell structure and suffers from similar limitations as those found with the current-clamp step method. The current-clamp step method allows for a straightforward decomposition of the voltage response in the form of multiple exponential terms, with one of these terms (the slowest) corresponding to the charging of the membrane capacitance. The two parameters (amplitude and time constant) of this slow exponential term can then be used to calculate the total membrane capacitance. A different current-clamp protocol that uses a continuously varying frequency sinusoidal current injection (ZAP function) also allows the determination of the slow membrane time constant and thus membrane capacitance using a similar decomposition into multiple terms (Puil et al. 1986).
Capacitance measurements are often used to determine the conductance density of ionic currents. Although the electrotonic structure of the neuron affects the accuracy of the measured total membrane capacitance, these effects are probably not the same as space-clamp errors produced when measuring voltage-gated ionic conductances. Capacitance measurements are ideally conducted in the linear range of membrane potential near the resting potential and thus membrane conductance changes do not play any role. In contrast, when voltage-gated channels are activated, the membrane potential is affected both by the electrotonic structure, which can be significantly different from the resting electrotonic structure due to conductance activation, and by additional loss of voltage control due to the nonlinear conductance changes. In fact, the loss of voltage control due to space-clamp errors leads to the underestimation of outward currents, but leads to under- or overestimates of inward currents that depend on the membrane potential, the overestimates being due to the regenerative effects of inward currents on the membrane potential at distant regions (e.g., Hartline and Castelfranco 2003). As a consequence of the well-known anisotropy of ion channel distribution, most salient for synaptic contacts, normalizing conductance measurements to total membrane capacitance measurements needs to be performed with caution, even if the total cell surface area is accurately determined. Accurate measurement of dendritic capacitance, voltage-gated currents, and synaptic currents are all likely to be compromised by space-clamp problems.
The accuracy of capacitance measurements is sensitive to the quality of the recordings. Noise has a modest effect in our models (e.g., 5% white noise introduces <1% error in our current-clamp step protocol estimates). However, signal transients, drifts, and other unstable behavior can significantly affect the estimates obtained with all of these protocols, particularly if voltage-gated currents are activated. Slow changes in the membrane potential will greatly affect capacitance measurements using the current-clamp protocol since it relies on an accurate estimation of the slowest time constant. In contrast, fast signal changes primarily affect voltage-clamp step protocol estimates of capacitance. Low sampling rates (aliasing) can greatly reduce the accuracy of the measurements in voltage clamp, especially with the voltage-clamp step protocol. The accuracy and the rate of the membrane potential change during a voltage-clamp step increases with an increase in the voltage-clamp gain. However, as the rate of voltage change increases, a fixed low sampling rate may introduce aliasing effects that will result in an underestimation of the total measured charge and thus the capacitance estimate. The voltage-clamp step protocol therefore requires high sampling rates depending on the voltage-clamp gain. In contrast, current-clamp measurements would not be as affected by aliasing problems. Short-duration voltage-clamp steps are usually used when this method is preferred under the assumption that the membrane capacitance charges quickly. This is indeed the case in isopotential cells, especially if the clamp gain is set high. However, in nonisopotential cells, there is significant current flow into distal compartments; charging of the capacitor of such distal compartments takes time and is influenced by the axial resistance between the proximal and distal compartments (Eq. 9; see the appendix). Therefore longer voltage-clamp pulses will yield larger (and more accurate) estimates of the total membrane capacitance.
The discrepancy between estimated capacitance values in current- versus voltage-clamp methods can intuitively be understood as follows: voltage-clamp methods control the membrane potential of a restricted area of the membrane near the electrode. Electrotonically distant regions, however, are not clamped to the same voltage due to lack of space clamp (Breneman et al. 2009; Prinz and Fromherz 2003; Spruston 1993). The errors in the total membrane capacitance estimates originate from the assumption that the clamped membrane potential measured at the point of electrode penetration is maintained throughout the cell surface. Since the voltage difference drops with distance, less charge accumulates at distant points than would accumulate if the voltage at these distant points was the same as that imposed at the soma—thus the underestimate. The lack of space clamp also explains why voltage-clamp ramp capacitance estimates depend on the slope of the membrane potential change. At higher dV/dt values, the membrane potential in distant regions differs more from that of the point of penetration due to the membrane-filtering properties, thus producing larger errors in the capacitance estimates. The same argument explains why the fast voltage-clamp ramps lead to larger errors than those of voltage-clamp steps. In the appendix we provide a derivation of equations for the simple two-compartment model shown in Fig. 8A, showing that the contribution of distal compartments is identically affected in both voltage-clamp methods by the electrotonic distance of the soma to this compartment (represented by the resistance Ra) and the leakiness of the distal compartment (represented by Rf; Eqs. A25 and A31). The methods depend differently on the duration of the voltage-clamp steps and ramps. However, these equations clearly show that long voltage pulses and slow voltage ramps are necessary to minimize the capacitance measurement errors when using these methods.
The charge from a current step is rapidly equalized throughout the cell structure, but affects the average membrane potential more slowly. This can be seen, for example, in the equations describing membrane potential in a finite cable with a sealed end (Eq. 1), which is given by an infinite series of exponentially decaying terms, the slowest of which corresponds to the membrane time constant (Holmes et al. 1992; Rall 1977). Although for very long cables this description breaks down, it still holds for finite cables of varying terminating resistances (Holmes et al. 1992; Rall 1977), which explains the accuracy of the capacitance measurements in cells that can be described with a ball-cable-ball model as long as the cable is not excessively long (see Fig. 4).
In summary, our results show that membrane capacitance can be measured with remarkable accuracy using the current-clamp step method, even in cells with complex architectures. With highly complex neurons the current-clamp step method can underestimate the capacitance due to numerical errors introduced by multiexponential fitting methods. It is important to note again that the voltage amplitude term V0 in Eq. 1 divided by the input current corresponds to a resistive term that must be used to calculate the total membrane capacitance. The input resistance of the cell, which is often used instead, is the incorrect parameter to use in nonisopotential cells. On the other hand, the methods most commonly used to measure capacitance (voltage-clamp step or ramp protocols) yield significant errors for neurons whose membrane structure is not electrotonically compact and should be used with caution. When measurements are done with both current- and voltage-clamp steps, long pulses should be used, rather than brief pulses, as is commonly done, especially with voltage-clamp pulses.
GRANTS
This work was supported by National Science Foundation Undergraduates in Biological and Mathematical Sciences Training Grant DUE-0436244 and National Institutes of Health Grants MH-64711 to J. Golowasch, MH-60605 to F. Nadim, NS-50928 to A. L. Taylor, and MH-46742 to A. L. Taylor.
ACKNOWLEDGMENTS
Present address of G. Thomas: Drexel University College of Medicine, Department of Neurobiology and Anatomy, Philadelphia, PA 19129.
APPENDIX: A TWO-COMPARTMENT MODEL
Here we demonstrate that the current-clamp estimate of the total membrane capacitance is a good approximation (and that the voltage-clamp estimates deviate from this value) to the actual total capacitance of our simplest model in which two spheres, one representing the soma (the “near” compartment, characterized by Cn and Rn) and one representing the dendrite (the “far” compartment, characterized by Cf and Rf) are coupled by a simple resistor Ra, representing the resistance of a cablelike structure such as a neurite (Fig. 8). The current-clamp estimate of capacitance is given by τ0/R0, where τ0 and R0 are as defined earlier in Eq. 1. It has been shown before that capacitance can be accurately determined in this manner for neurons of arbitrarily complex architectures, at least in the absence of somatic shunt (Major et al. 1993a). Our goal is to derive values for these quantities in terms of the circuit parameters that can provide a clear and intuitive understanding of the sources of error when using the voltage-clamp protocols described herein. We begin with τ0. The input impedance of the cell can be written as (Siebert 1986)
| (A1) |
where s is the complex frequency. The right side of this equation can be rearranged, yielding
| (A2) |
The impedance of a system that responds to a current step in the manner described by Eq. 6 is given by the expression (Siebert 1986)
| (A3) |
Multiplying this out and rearranging, we obtain
| (A4) |
Equation A4 has the same form as that of Eq. A2 and so we can infer that the coefficients of each term for Z(s) must be identical. Thus we write a system of four equations relating the circuit parameters (Cn, Cf, Rn, Rf, Ra) to the “kernel” parameters (R0, τ0, R1, τ1).
If we assume that RnCn = RfCf, as would be the case for a cell with uniform specific membrane conductance and capacitance, this adds a fifth equation to this system and we can define a common time constant τc = RnCn = RfCf, yielding
| (A5) |
| (A6) |
| (A7) |
| (A8) |
Equations A7 and A8 comprise a system of two equations in the two unknowns τ0 and τ1 that can be reduced to a single quadratic equation in τ0. Since Eqs. A7 and A8 are symmetric in τ0 and τ1, we adopt the standard convention that τ0 is the larger of the two. Thus
| (A9) |
| (A10) |
where
and
After some algebra, this reduces to
| (A11) |
| (A12) |
Next we solve Eqs. A5 and A6 using Eqs. A11 and A12 for R0 and R1, yielding
| (A13) |
| (A14) |
As for τ0 and τ1, R0 and R1 are expressed in terms of circuit parameters. Using Eqs. A11 and A13, the current-clamp estimate of capacitance is thus given by
| (A15) |
This shows that, for the simple case of a two-compartment model in which the near and the distant compartments are coupled by a resistor, the current-clamp method gives an accurate measurement of the total capacitance.
Next we derive the response of the two-compartment model to a voltage-clamp step v(t) = ΔVm (see Eq. 8). Using Eq. A4, the current response of the system is given by
| (A16) |
The current response is given by the inverse Laplace transform of I(s) and can be written as
| (A17) |
where
| (A18) |
| (A19) |
| (A20) |
| (A21) |
The charge delivered by the transient part of Eq. A17 is given by
| (A22) |
Dividing out by ΔVm yields the estimate of capacitance using a voltage-clamp step
| (A23) |
This equation clearly shows that the estimate of cm,vc depends on the duration of the voltage pulse, tp, with very short pulses yielding an estimate of cm,vc = Cpulse, which after substitution in terms of circuit parameters simplifies to cm,vc = Cn—i.e., the capacitance of the near compartment only. For very long pulses, the exponential term approaches zero and cm,vc = Cpulse + Gdecayτvc, which can be written in terms of the kernel parameters (R0, τ0, R1, τ1) by substitution, using Eqs. A18, A20, and A21
| (A24) |
Substituting in the expressions for τ0, τ1, R0, and R1 in terms of circuit parameters (Eqs. A11–A14) and simplifying leads
| (A25) |
which is Eq. 9. Equations A23 and A25 show that the total capacitance measured using the voltage-clamp step protocol strongly depends on the duration of the voltage pulse, but is also dominated by the capacitance of the near compartment (typically the soma), especially for large values of axial (coupling) resistance Ra. The contribution from the far compartment drops as either the resistance of the far compartment, Rf, decreases (e.g., if its surface increases; Fig. 3) or Ra increases (e.g., if the neurite gets longer; Fig. 4C).
Another way of looking at the error generated when using the voltage-clamp protocol is to calculate the ratio of the VC_step estimate to the CC_step estimate in terms of the kernel parameters (R0, τ0, R1, τ1). The ratio can be defined (using Eqs. A15 and A24) as
| (A26) |
where Rin = R0 + R1.
A similar approach can be used to derive the response of our two-compartment model (Fig. 8A) to a voltage-clamp ramp. To determine the total membrane capacitance we first find the response of the circuit to a single voltage ramp given by vramp(t) = m·t·u(t), where m is the slope of the ramp and u(t) is a step function as before. The response of the circuit can be shown, via Laplace transforms, to be
| (A27) |
In our VC_ramp protocol, a depolarizing voltage ramp is followed by an identical hyperpolarizing ramp. The capacitance estimate in this case is given by
| (A28) |
if we sample the current at the midpoint of both ramps (T is the ramp duration). Since the system is linear and shift invariant, the current response of the system can be written
| (A29) |
By combining Eqs. A27, A28, and A29 and simplifying, we obtain
| (A30) |
where
Substituting the kernel with circuit parameters (and T with ΔVramp/m, where ΔVramp is the amplitude of the ramp, m is the slope), this expression becomes
| (A31) |
and
Notice that when m is large (i.e., a ramp is very fast), the term tends to zero and the capacitance estimate reduces to that of the near compartment only, just as with very short voltage-clamp steps. With very small m, the term tends to 1, and we obtain the same expression as with long voltage-clamp steps, as shown numerically in Fig. 3B for the ball-stick-ball model (compare green, red lines).
REFERENCES
- Breneman KD, Highstein SM, Boyle RD, Rabbitt RD. The passive cable properties of hair cell stereocilia and their contribution to somatic capacitance measurements. Biophys J 96: 1–8, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bucher D, Johnson CD, Marder E. Neuronal morphology and neuropil structure in the stomatogastric ganglion of the lobster, Homarus americanus. J Comp Neurol 501: 185–205, 2007 [DOI] [PubMed] [Google Scholar]
- Chklovskii DB, Mel BW, Svoboda K. Cortical rewiring and information storage. Nature 431: 782–788, 2004 [DOI] [PubMed] [Google Scholar]
- Dougherty KJ, Sawchuk MA, Hochman S. Properties of mouse spinal lamina I GABAergic interneurons. J Neurophysiol 94: 3221–3227, 2005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Golowasch J, Marder E. Ionic currents of the lateral pyloric neuron of the stomatogastric ganglion of the crab. J Neurophysiol 67: 318–331, 1992 [DOI] [PubMed] [Google Scholar]
- Haedo RJ, Golowasch J. Ionic mechanism underlying recovery of rhythmic activity in adult isolated neurons. J Neurophysiol 96: 1860–1876, 2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris FJ. Multirate Signal Processing for Communication Systems. Upper Saddle River, NJ: Prentice Hall, 2006 [Google Scholar]
- Harris-Warrick RM. Dynamic Biological Networks: The Stomatogastric Nervous System. Cambridge, MA: MIT Press, 1992, p. xvii, 328 [Google Scholar]
- Hartline DK, Castelfranco AM. Simulations of voltage clamping poorly space-clamped voltage-dependent conductances in a uniform cylindrical neurite. J Comput Neurosci 14: 253–269, 2003 [DOI] [PubMed] [Google Scholar]
- Hodgkin AL, Huxley AF. A quantitative description of membrane current and its application to conduction and excitation in nerve. J Physiol 117: 500–544, 1952 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holmes WR, Segev I, Rall W. Interpretation of time constant and electrotonic length estimates in multicylinder or branched neuronal structures. J Neurophysiol 68: 1401–1420, 1992 [DOI] [PubMed] [Google Scholar]
- Iwasaki S, Chihara Y, Komuta Y, Ito K, Sahara Y. Low-voltage-activated potassium channels underlie the regulation of intrinsic firing properties of rat vestibular ganglion cells. J Neurophysiol 100: 2192–2204, 2008 [DOI] [PubMed] [Google Scholar]
- Johnson SL, Thomas MV, Kros CJ. Membrane capacitance measurement using patch clamp with integrated self-balancing lock-in amplifier. Pflügers Arch 443: 653–663, 2002 [DOI] [PubMed] [Google Scholar]
- Joshi C, Fernandez JM. Capacitance measurements. An analysis of the phase detector technique used to study exocytosis and endocytosis. Biophys J 53: 885–892, 1988 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khorkova O, Golowasch J. Neuromodulators, not activity, control coordinated expression of ionic currents. J Neurosci 27: 8709–8718, 2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koch C. Biophysics of Computation: Information Processing in Single Neurons. New York: Oxford Univ. Press, 1999 [Google Scholar]
- Major G, Evans JD, Jack JJ. Solutions for transients in arbitrarily branching cables: I. Voltage recording with a somatic shunt. Biophys J 65: 423–449, 1993a [DOI] [PMC free article] [PubMed] [Google Scholar]
- Major G, Evans JD, Jack JJ. Solutions for transients in arbitrarily branching cables: II. Voltage clamp theory. Biophys J 65: 450–468, 1993b [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nadim F, Golowasch J. Signal transmission between gap-junctionally coupled passive cables is most effective at an optimal diameter. J Neurophysiol 95: 3831–3843, 2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nadim F, Olsen OH, De Schutter E, Calabrese RL. Modeling the leech heartbeat elemental oscillator. I. Interactions of intrinsic and synaptic currents. J Comput Neurosci 2: 215–235, 1995 [DOI] [PubMed] [Google Scholar]
- Neher E, Marty A. Discrete changes of cell membrane capacitance observed under conditions of enhanced secretion in bovine adrenal chromaffin cells. Proc Natl Acad Sci USA 79: 6712–6716, 1982 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pineda RH, Knoeckel CS, Taylor AD, Estrada-Bernal A, Ribera AB. Kv1 potassium channel complexes in vivo require Kvbeta2 subunits in dorsal spinal neurons. J Neurophysiol 100: 2125–2136, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prinz AA, Fromherz P. Effect of neuritic cables on conductance estimates for remote electrical synapses. J Neurophysiol 89: 2215–2224, 2003 [DOI] [PubMed] [Google Scholar]
- Puil E, Gimbarzevsky B, Miura RM. Quantification of membrane properties of trigeminal root ganglion neurons in guinea pigs. J Neurophysiol 55: 995–1016, 1986 [DOI] [PubMed] [Google Scholar]
- Rabbah P, Golowasch J, Nadim F. Effect of electrical coupling on ionic current and synaptic potential measurements. J Neurophysiol 94: 519–530, 2005 [DOI] [PubMed] [Google Scholar]
- Rall W. Core conductor theory and cable properties of neurons. In: Handbook of Physiology. The Nervous System. Cellular Biology of Neurons. Bethesda, MD: Am. Physiol. Soc., 1977, sect. 1, vol. I, pt. 1, p. 39–98 [Google Scholar]
- Royeck M, Horstmann MT, Remy S, Reitze M, Yaari Y, Beck H. Role of axonal NaV1.6 sodium channels in action potential initiation of CA1 pyramidal neurons. J Neurophysiol 100: 2361–2380, 2008 [DOI] [PubMed] [Google Scholar]
- Selverston AI, Russell DF, Miller JP. The stomatogastric nervous system: structure and function of a small neural network. Prog Neurobiol 7: 215–290, 1976 [DOI] [PubMed] [Google Scholar]
- Siebert W. Circuits, Signals, and Systems. Cambridge, MA: MIT Press, 1986 [Google Scholar]
- Solsona C, Innocenti B, Fernandez JM. Regulation of exocytotic fusion by cell inflation. Biophys J 74: 1061–1073, 1998 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Soto-Trevino C, Rabbah P, Marder E, Nadim F. Computational model of electrically coupled, intrinsically distinct pacemaker neurons. J Neurophysiol 94: 590–604, 2005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spruston N, Jaffe DB, Williams SH, Johnston D. Voltage- and space-clamp errors associated with the measurement of electrotonically remote synaptic events. J Neurophysiol 70: 781–802, 1993 [DOI] [PubMed] [Google Scholar]