Motion Perception During Variable-Radius Swing Motion in Darkness

Abstract

Using a variable-radius roll swing motion paradigm, we examined the influence of interaural (y-axis) and dorsoventral (z-axis) force modulation on perceived tilt and translation by measuring perception of horizontal translation, roll tilt, and distance from center of rotation (radius) at 0.45 and 0.8 Hz using standard magnitude estimation techniques (primarily verbal reports) in darkness. Results show that motion perception was significantly influenced by both y- and z-axis forces. During constant radius trials, subjects' perceptions of tilt and translation were generally almost veridical. By selectively pairing radius (1.22 and 0.38 m) and frequency (0.45 and 0.8 Hz, respectively), the y-axis acceleration could be tailored in opposition to gravity so that the combined y-axis gravitoinertial force (GIF) variation at the subject's ears was reduced to ∼0.035 m/s² – in effect, the y-axis GIF was “nulled” below putative perceptual threshold levels. With y-axis force nulling, subjects overestimated their tilt angle and underestimated their horizontal translation and radius. For some y-axis nulling trials, a radial linear acceleration at twice the tilt frequency (0.25 m/s² at 0.9 Hz, 0.13 m/s² at 1.6 Hz) was simultaneously applied to reduce the z-axis force variations caused by centripetal acceleration and by changes in the z-axis component of gravity during tilt. For other trials, the phase of this radial linear acceleration was altered to double the magnitude of the z-axis force variations. z-axis force nulling further increased the perceived tilt angle and further decreased perceived horizontal translation and radius relative to the y-axis nulling trials, while z-axis force doubling had the opposite effect. Subject reports were remarkably geometrically consistent; an observer model-based analysis suggests that perception was influenced by knowledge of swing geometry.

INTRODUCTION

Spatial orientation in humans requires central multi-sensory integration of motion cues (Lackner and DiZio 2005; Mayne 1974; Young 1984) from both sensory (e.g., vision, vestibular organs, and proprioception), and nonsensory sources (e.g., efferent copy, cognition). One reason for this is that sensory information in isolation can be ambiguous. For example, the otolith organs, like all linear accelerometers, cannot intrinsically separate linear acceleration from gravity. Rather they measure the combined gravitoinertial force (GIF), defined as the difference between gravity and acceleration (GIF = g − a). Therefore additional information is required to disambiguate tilt from translation in darkness.

Motions experienced in everyday life combine tilts and translations that require us to distinguish them. For example, a typical child's swing introduces an off-axis sinusoidal pitching motion where in the steady state the nasooccipital component of linear acceleration is cancelled almost exactly by the nasooccipital component of gravity. Motions combining tilt and translation above or below an axis of rotation are common in aircraft and flight simulators. Even more universal is the reverse situation, where the head is above the rotation axis, and the forces combine in the inverted-pendulum gait mechanics exemplified by walking. How do we resolve these tilt and translation cues?

In many cases of combined tilts and translations, the otolith signal along the axis of motion cannot be the main source of tilt and translation estimates because the net GIF is close to zero (e.g., in some swing motions). This implies a necessary contribution of information from other sensors (e.g., semicircular canals) or from the otoliths along a different axis (e.g., the z axis) to resolve our motion. It has been shown that angular acceleration cues provided by the semicircular canals and gravitoinertial cues provided by the otoliths are primary contributors to tilt and translation perception (Glasauer 1995; Lewis et al. 2008; Merfeld et al. 2005a,b; Stockwell and Guedry 1970; von Holst and Grisebach 1951) and also contribute to vestibuloocular reflexes (Angelaki et al. 1999; Merfeld et al. 1999). However, studies to date have generally only considered the contribution of otolith stimuli in the horizontal head plane (i.e., oriented perpendicular to gravity along the y-axis). Here we consider also the contribution of otolith stimuli along the dorsoventral axis (i.e., parallel to gravity along the z-axis).

For roll swing motions like those utilized in our previous study (Merfeld et al. 2005b), when the head is displaced from the rotation axis, it is both tilted and translated, yielding varying y- and z-axis (Fig. 1) force cues and roll rotation cues. When this motion is sinusoidal, it is possible to choose paired sets of frequencies and radial arm lengths such that the y-axis force from the linear acceleration opposes the y-axis component of gravity (Merfeld et al. 2005b) so that the sum at the level of the ears is reduced below the perceptual threshold. The y-axis force is thus perceptually “nulled,” and the only remaining cues are the modulating z-axis forces and semi-circular canal rotation cues.

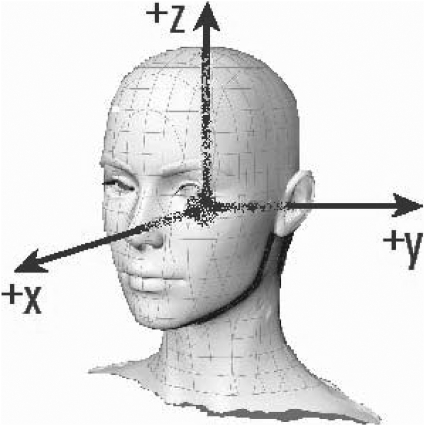
Fig. 1.

Experimental coordinate frame. The y and z axes align with subject interaural and dorsoventral axes.

To what extent do the z-axis forces that remain contribute to perceived tilt and translation? Specifically, what happens when, in addition to the y-axis force nulling, there is no z-axis force modulation? For swing motions, the z-axis force modulation occurs at twice the harmonic frequency of the tilt and translation stimuli, so it would not be expected to be sufficient to distinguish tilt from translation without other information, yet theoretically these z-axis forces provide a motion cue that is correlated with the overall motion pattern. Therefore we hypothesized that this z-axis cue might influence the perception of tilt and translation, particularly when y-axis forces were nulled.

We have found only one study that examined the influence of such z-axis forces. MacDougall and colleagues compared ocular torsion evoked by two motion paradigms: roll-tilt motions on a tilt-chair and centripetal linear acceleration during constant velocity rotation on a fixed-chair centrifuge (MacDougall et al. 1999). The magnitude of the y-axis force component was the same for both paradigms, but the z-axis forces were different. They found that the static ocular torsion (ocular counterolling) was significantly higher during centrifugation (where there was a higher z-axis force) and suggested that the z-axis force might play a role in resolving the tilt-translation ambiguity for vestibular action (VOR). Given that human perception can be influenced by mechanisms different from those that drive VOR (Merfeld et al. 2005a,b), would such z-axis forces also influence perception of tilt and translation?

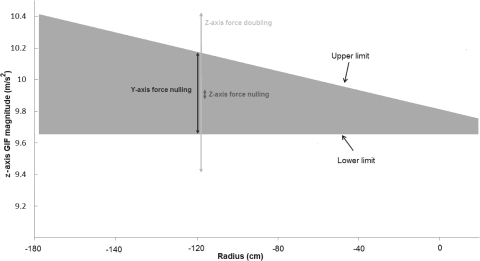
To examine the perceptual role of z-axis forces, we designed novel motion paradigms to expand on the previously published y-axis “nulling” profile (Merfeld et al. 2005b). Perceived tilt and translation responses evoked at two frequencies (0.45 and 0.8 Hz) were studied over a wider range of radial arm lengths. In some profiles when the y-axis GIF was nulled, we also introduced sinusoidal radial translations at twice the tilt frequency. In one case, the phase of the z-axis acceleration was chosen so that this acceleration cancelled the z-axis force modulations caused by the centrifugal and gravitational forces. In the second case, the phase of z-axis acceleration was chosen such that it doubled the z-axis GIF modulations (Fig. 2 ).

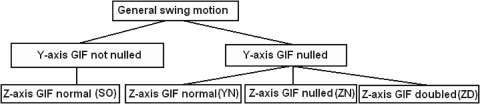
Fig. 2.

Our motion profiles. SO, swing only; YN, y-axis force nulling; ZN, z-axis force nulling; ZD, y-axis force doubling.

METHODS

Using a motorized, servo-controlled swing device [Massachusetts Eye and Ear Infirmary (MEEI) tilt device, Neurokinetics, Pittsburgh, PA], we utilized a motion paradigm that combined tilt and translation to generate a y-axis GIF that varied with radial arm length. The peak tilt angle was 10°, and the subject's ear canal position with respect to the rotation center was varied from 20 cm above (+20 cm) to 122 cm below (−122 cm). For some trials (Fig. 2, categories YN, ZN, and ZD), we matched the tilt frequency with a specific radial distance (−38 cm for 0.8 Hz and −122 cm for 0.45 Hz, respectively) from the center of rotation to the subject's ear so that the y-axis otolith signal (GIF) was nulled below threshold. Additionally, for some of these trials (Fig. 2, ZN and ZD), we applied a phase-locked sinusoidal radial translation at twice the frequency tilt motion.

We selected 0.8 Hz for direct comparison to a previous study (Merfeld et al. 2005b) and 0.45 Hz because it was the lowest frequency where it was possible to null the y-axis force using our tilt device. This makes the radius and translation for y-axis nulling as large as possible, which, in turn, makes the subject reports as large as possible, which we expected to increase the signal-to-noise ratio (see magnitude estimation in the following text). Each trial included ramp-up and -down periods of ∼1 min each, and a steady-state component of ∼1.5 min.

MEEI tilt device

The MEEI tilt device is capable of linear motion (translation) along the subject's z axis as well as tilt motion about the center of rotation as shown in Fig. 3. The device could command tilt with an accuracy of less than a tenth of a degree, and translation with an accuracy of around a tenth of a millimeter. Subjects were restrained by side clamps, a five-point harness, and by an MRI shoulder and head mask (Aquaplast, thermoplastic, 4.8-mm disposable S-frame: No. RT-1992SD) individually molded to each subject, which minimized head movement.

Fig. 3.

Massachusetts Eye and Ear Infirmary (MEEI) tilt device motion capability.

Motion paradigms

While seated in an upright position, subjects were passively swung in roll tilt with their external ear canals at predetermined distances between +20 cm (above) and −122 cm (below) the center of rotation. The swing-only (with no radial translation) motion paradigm was similar to the one used in the previous experiment (Merfeld et al. 2005b). The derivation, simulation, and experimental validation of the paradigm are presented in detail in the appendix. Because the roll motion was sinusoidal with a peak tilt angle of 10°, the y-axis gravity force component was predominantly sinusoidal and had the same amplitude for all trials (1.70 m/s²). The y-axis acceleration contributed by the steady-state sinusoidal motion was also sinusoidal, but the amplitude varied with radius (i.e., the location of the subject's ear height relative to the center of rotation). The y-axis acceleration opposed gravity when the subject' ear was below the axis of rotation and added to gravity when the subject's ear was above the axis of rotation, where the total y-axis GIF reached a maximum of almost 2 m/s² (at +20 cm).

Y-axis nulling (Fig. 2, nategory YN).

When the subject's ear was below the center of rotation, the y-axis acceleration was always in opposition to the y-axis component of gravity, and they almost completely cancelled at the nulling radius (−122 cm for 0.45 Hz or −38 cm for 0.8 Hz). However, a Taylor series small-angle approximation of the y-axis gravitational force sensed by the otoliths, noise, and ramp-up considerations (see appendix) meant that the y-axis GIF could not be completely eliminated but instead reduced below the putative detection threshold. These thresholds depend on the orientation of subjects relative to gravitational vector and apparatus used (Greven et al. 1974; Gundry 1978), but for motions similar to our profiles, reported thresholds are around 0.063, 0.057, and 0.15 m/s², in the x, y, and z axes, respectively (Benson et al. 1986, 1989; Jongkees and Groen 1946).

Theoretical calculations predicted that the y-axis GIF amplitude at the tilt frequency should be <0.035 m/s², which was confirmed by accelerometer measurements. The z-axis GIF amplitude at twice the tilt frequency was 0.25 m/s². Intermittent and transient components, especially those of high-frequency, are stochastic (i.e., noisy and/or random) and therefore unlikely to provide information sufficient for motion discrimination. Note that the total resultant GIF variation was also around 0.25 m/s² for both 0.45 and 0.8 Hz (see appendix for details).

Z-axis nulling (Fig. 2, category ZN)

For some trials in which the y-axis force variations were nulled, we added an additional z-axis acceleration using a simultaneous phase-locked radial sinusoidal translation at twice the frequency of the tilt oscillation (± 2 mm at 1.6 Hz for the 0.8 Hz tilt and ± 6.3 mm at 0.9 Hz for the 0.45 Hz tilt). The acceleration generated by this radial motion always opposed the combined z-axis gravity component and centripetal acceleration. With this additional radial acceleration, the total resultant z-axis GIF summed to a constant mean value of 9.88 m/s² (mildly hypergravic) with theoretically predicted variations having an amplitude of 0.012 m/s² for both 0.45 and 0.8 Hz. The y- and z-axis forces are phase-locked and vary with different frequencies. The y-axis force reaches it maximum when the z-axis force deviation from the mean is zero and vice versa. Therefore the maximal variations in the resultant force are the same as the y-axis force component.

Z-axis doubling (Fig. 2, category ZD)

We also tested subjects using a z-axis force doubling profile where we reversed the phase of the additional z-axis translation. Similar to the z-axis nulling, this doubling profile increased the mean z-axis GIF slightly (9.88 m/s²) but yielded an increase in the z-axis variations to an amplitude of 0.5 m/s², well above any purported thresholds for detection. We chose to modify the z-axis force only when the y-axis force was nulled to avoid confounds with the y-axis otolith signals and because pilot studies indicated that z-axis forces might have the greatest effect when the y-axis forces provided less information.

Subjects and instructions

Ten healthy subjects (4 male, 6 female) were prescreened as “normal” via standard clinical vestibular tests (caloric, rotation, EquiTest posturography, and Hallpike positional testing). All subjects signed an informed consent consistent with institutional procedures prior to participation. The subjects were between 23 and 64 yr old [32 ± 11 (SD) yr] and half of them (4 male, 1 female) had experience in other motion experiments at MEEI.

Subjects were instructed on the capabilities of the motion device and familiarized with the range of motions. They then took a pencil and paper distance and angle estimation test where they received feedback regarding the distances and angles after the test. They were then instructed about reporting motion perception. Specifically, five questions were asked during training and during the experiment. Subjects were explicitly instructed to report motions relative to the bridge of their nose. 1) What is the maximal side-to-side translation you are experiencing? 2) If you feel like you are tilting, what is your best estimate of the distance to the center of rotation? 3) Relative to the floor, what is the maximal vertical difference between the top and bottom of your motion path? 4) What is the maximal head tilt to the left you are experiencing? 5) What is the maximal head tilt to the right you are experiencing?

These questions were expanded from a set used in a previous experiment (Merfeld et al. 2005b). Question 2 was added because the roll radius remains fixed throughout a motion profile (unlike tilt angle and position) and can only be determined by combining multiple sources of sensory information. We therefore surmised that it would be a good indicator of a subject's awareness of their overall motion. The majority of the subjects were most familiar in reporting distances in inches, so all subjects were required to report all distances in inches and all angles in degrees, although distances have been converted into SI units for presentation.

In addition to the verbal reports, each subject's dynamic tilt perception was recorded by having them keep a somatosensory tilt bar level with their perceived earth horizontal (Park et al. 2006). The somatosensory signals were measured using a potentiometer and sampled at 60 Hz for an angle discriminate of less than a tenth of a degree. This task also served to maintain subject alertness and verify compliance.

Magnitude estimation and training

Subject reports were based on a direct estimation magnitude estimation task using real values (inches) rather than ratios. Without training, this method often yields nonlinear scaling errors as the expansion of the perception domain increase with the increase in stimulus magnitude [Class I stimulus as defined by Stevens for his psychophysical law: sensation = A × (stimulus)ⁿ (Stevens 1957)]. To counteract this, some previous studies have used a subject-selected modulus and ratio scaling (Parker et al. 1979); however, these studies have often shown higher expansion moduli (1.4–2.2) than studies that used a directly familiar scale such as inches. While lack of knowledge about a device expands the estimation range and increases reporting variance, experience and knowledge (i.e., training) have been demonstrated to shrink the range and reduce variance by reducing cognitively mediated biases (Burgard and Kuznicki 1990; Laming 1997; Stevens 1957; Wertheim et al. 2001). We therefore expected untrained subjects to have high reporting variances, and implemented a training regime to reduce them.

For the experimental sessions, the subjects were trained on 12 representative motion profiles (6 in light followed by 6 in darkness) over the entire range of radial distances and for peak tilt angles between 5 and 25°, even though only 10° was examined in the experiment (see Table 1). During training, subjects were asked to report their perceived motion by answering questions 1–2 and 4–5. Question 3 was omitted during training because the subjects could see that the vertical translation was very small during the lighted trials, and we didn't want the subjects to learn to expect small vertical translations. Before the second and third sessions, a shorter training session consisting of six trials (3 light, 3 dark) was administered to re-familiarize the subjects with the device capabilities and to recalibrate their perceived motion reports.

Table 1.

Training (T) and experimental protocol

Order	Category	Frequency, Hz	Radius, cm	Tilt Angle°	Light
T1	SO	0.45	−122	30	Y
T2*	SO	0.45	−122	20	Y
T3	YN	0.45	−122	10	Y
T4*	SO	0.45	0	15	Y
T5	SO	0.8	0	10	Y
T6*	SO	0.8	20	5	Y
T7*	SO	0.45	−20	10	N
T8	YN	0.8	−38	10	N
T9*	SO	0.45	−40	15	N
T10	SO	0.45	−122	20	N
T11*	SO	0.8	0	15	N
T12	SO	0.8	−40	5	N
1	SO	0.45	−20	10	N
2	YN	0.45	−122	10	N
3	SO	0.8	0	10	N
4	ZN	0.45	−122	10	N
5	SO	0.45	0	10	N
6	YN	0.8	−38	10	N
7	SO	0.45	−40	10	N
8	ZN	0.8	−38	10	N
9	ZD	0.45	−122	10	N
10	SO	0.45	20	10	N
11	SO	0.45	−80	10	N
12	ZD	0.8	−38	10	N

The training sessions marked *were omitted for the second and third session. The motion categories refer to Fig. 2 Y = Yes; N = No.

The training was successful in helping subjects to accurately report their perceived motion in light and dark. The experienced subjects performed much better at the start of training than the inexperienced subjects, but by the end of the training session, all subjects were consistently reporting with <10% error in the dark (down from >50% in some cases) except for questions 1 and 2 in the y-axis nulling cases (T3 and T8) as also observed during the experiment (see results). The errors on subsequent training sessions started out much lower, indicating that the influence of training persisted for at least two to three days, which was typically the time between test sessions.

We also tested six untrained subjects for comparison. The untrained subjects showed the same patterns as trained subjects although their reporting variance was indeed much higher. Training significantly reduced the average SD of perceived angle, translation, and radius reports from 13.7 to 8.8° (P < 0.01), 37 to 19 cm (P < 0.02), and 71 to 49 cm (P < 0.05), respectively using paired t-test. Untrained subjects also had a much greater tendency to overestimate their tilt angle (by 8° on average compared with 3° in trained subjects).

Experiment Sessions

The experiment consisted of three sessions of training followed by 12 randomly ordered (but the same across subjects) trials: four at 0.8 Hz for and eight at 0.45 Hz (See Table 1). Each subject was tested about the same time each day, and were requested to avoid alcohol consumption during the prior 24 h (and asked about compliance).

Statistical Analysis

Paired t-test were performed in Systat (v. 12, Systat Software, San Jose, CA) to determine significance of the independent variables on the dependent variables. Additionally, a hierarchical mixed regression model was used to quantify the magnitude of these effects.

RESULTS

The manipulation of y- and z-axis forces had a significant effect on subject perception. Nulling the y-axis forces significantly decreased the reported horizontal translation and rotation radius, particularly in the 0.45 Hz tilt and translation profile. Additionally, nulling the z-axis forces further decreased the reported horizontal translation and rotation radius, whereas doubling the z-axis forces had the opposite effect. The vertical translations reported by subjects (question 3) were very small throughout and generally consistent with the swing motions experienced.

Angle of Tilt: Verbal Report

Subjects generally reported their angle of tilt in the 5 to 15° range (See Fig. 4A). When questioned afterward, no subject had realized that the peak tilt angle was always 10°. Additionally, although some subjects occasionally reported asymmetric tilt motion, no subject reported significant biases to either side.

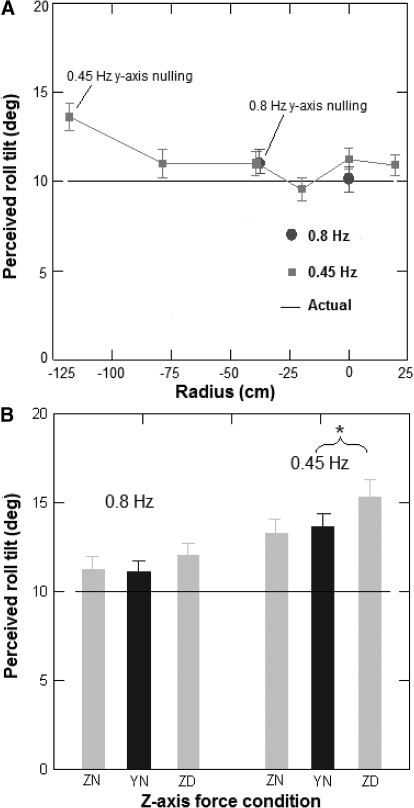
Fig. 4.

A: subject reported mean tilt perception for the swing-only condition. B: comparison of mean tilt perception for the y-axis force nulling profiles grouped by z-axis nulling condition. —, the actual tilt angle. Error bars represent SE. *, significant effects (P < 0.05).

Tilts for the 0.8-Hz profile were slightly overestimated at the nulling radius, though not significantly, which was consistent with results obtained in the previous experiment (Merfeld et al. 2005b). The effects of z-axis nulling and doubling were not significant at 0.8 Hz. At 0.45 Hz, subjects significantly overestimated their tilt angles with y-axis nulling (t = 2.5; df = 58; P > 0.001). Additional z-axis force doubling at 0.45 Hz showed a significant overestimation of tilt angle (t = 1.6; df = 58; P > 0.002) as compared with y-axis nulling only, but z-axis force nulling did not significantly decrease the perceived angle of tilt (t = −0.6; df = 58; P = 0.28; See Fig. 4B).

Horizontal translation: verbal reports

The actual horizontal translation in the experiment varied between 0 and 43 cm, depending on the distance from the center of rotation. The 0.8-Hz results (Fig. 5A) were consistent with results obtained in the previous experiment (Merfeld et al. 2005b). There were no significant effects of z-axis nulling or doubling at 0.8 Hz.

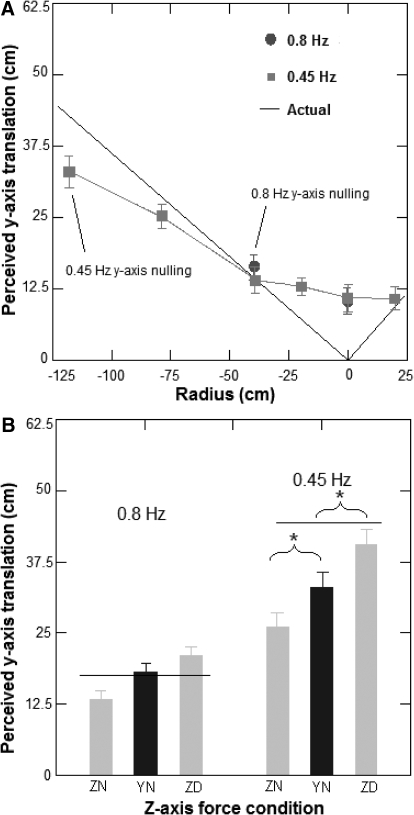
Fig. 5.

A: subject reported mean horizontal translation perception for the swing-only condition. B: comparison of mean stranslation perception for the y-axis force nulling profiles grouped by z-axis nulling condition. —, actual translations. Error bars, SE; *, significant effects (P < 0.05).

At 0.45 Hz, subjects generally reported their horizontal translation accurately except at the y-axis nulling radius (where the translation was underestimated, although not quite to the point of significance, P = 0.055) and at the center of rotation (where the translation was overestimated, probably as an artifact, see discussion). The additional z-axis force doubling significantly increased horizontal translation reports as compared with swing only (t = 11.9; df = 58 P < 0.01), and the z-axis force nulling profile significantly reduced the horizontal translation perception compared with swing-only (t = −4.1; df = 58; P < 0.05; see Fig. 5B).

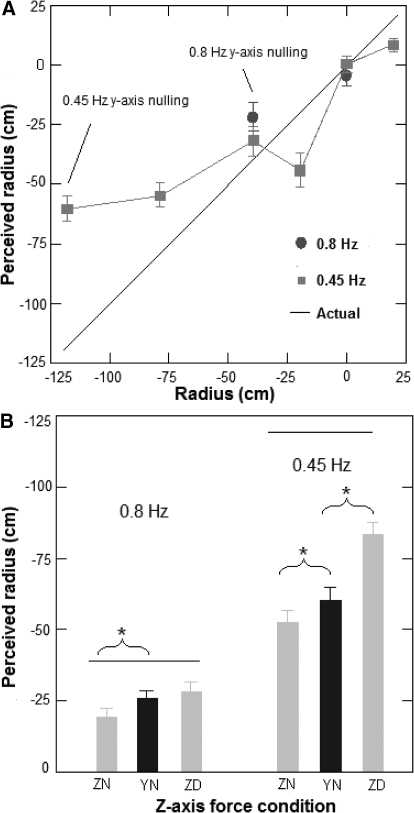
Rotation radius: verbal reports

The actual radius from the center of rotation to subject ear-center in the experiment varied between 20 cm above the center (+20 cm) and 122 cm below the center (−122 cm). Unlike for horizontal translation, subjects would report if they were above or below the center of rotation (positive or negative). Subjects generally reported rotation radius accurately for profiles lacking y-axis nulling. However, subjects underestimated the (negative) rotation radius consistently (by almost 50% on average) at the y-axis nulling radius (for both 0.8 and 0.45 Hz; P < 0.01; Fig. 6A).

Fig. 6.

A: subject reported mean radius perception for the swing-only condition. B: comparison of mean radius perception for the y-axis force nulling profiles grouped by z-axis nulling condition. —, actual radius error bars, SE; *, significant effects (P < 0.05).

For both 0.8 and 0.45 Hz, z-axis force nulling significantly reduced the perceived rotation radius compared with swing only (t = −9.7; df = 58; P < 0.05 and t = −8.4; df = 58; P < 0.05). The z-axis force doubling increased the perceived rotation radius, which was significant at 0.45 Hz (t = 22.6; df = 58; P < 0.01) but not quite significant at 0.8 Hz (t = 7.1; df = 58; P = 0.07; see Fig. 6B).

Mixed regression analysis

A mixed regression model was developed to estimate the combined effects of radius, y-axis nulling, and z-axis nulling and doubling on subject reports for both frequencies. This fit a linear model to each dependent variable (i.e., perceived tilt angle, perceived horizontal translation, and perceived radius) of the form V_D = Aw + Bx + Cy + Dz + E, where A–D are the coefficients on the independent variables w–z (i.e., radius, y-axis nulling, z-axis nulling, and z-axis doubling) while minimizing the least-square residuals. For example, z-axis nulling had the effect of decreasing the perceived mean center of rotation estimate by 12.7 cm (toward the center), and z-axis doubling of increasing the estimate by 16.8 cm. Each of the four independent variables (see Table 2) had a significant effect (P < 0.05) on at least two of the three dependent variables. In total, 9 effects of 12 possible effects were significant.

Table 2.

Mixed regression effects model

	Dependent Variable (VD)
	Perceived Angle of Tilt°	Perceived Horizontal Translation, cm	Perceived Radius, cm
Independent Variable
Radius (A), cm	−0.4	0.2*	0.7*
y-axis nulling (B)	0.9	−0.76	−17.0*
z-axis nulling (C)	−0.4	−7.4*	−12.7*
z-axis doubling (D)	1.1	9.4	16.8*
Intercept (E)	10.7	11.4	−3.3

The effect of the independent variables and intercept on the dependent variables (V_D) can be expressed as V_D + Aw + Bx + Cy + Dz + E., where x, y, and z are 0 (absent) or 1 (present). Significant (P < 0.05) effects are marked *. y-axis nulling was marginally significant for horizontal translation (P = 0.055).

This regression model accounted for over 95% of the variance (see Table 2). Additionally, a Kolmogorov-Smirnov test (KS test) showed that the residuals for the fit were not significantly different from a normal distribution (P = 0.21). Note that for translation, the absolute value of radius was considered because both positive and negative radii tended to increase the translation.

Other Effects

There was no significant effect of subject experience on reports of horizontal translation or radius, although the experienced subjects reported significantly less error for angle of tilt (P < 0.05). Performance during training and on the written test did not significantly correlate with errors in estimating tilt angle, horizontal translation, or distance from center of rotation.

Some subjects performed significantly better during some sessions compared with their others that generally corresponded to reported “off-days” where they felt they performed poorly. There was a significant effect of the randomized order of trials (P < 0.045) for the radius estimate. However, trial order did not have a significant effect on any other dependent variables, so it is likely that this was coincidental. In eight z-axis force nulling trials, subjects reported that the motion was “very confusing,” and one reported mild motion sickness. No confusion was reported in other trials.

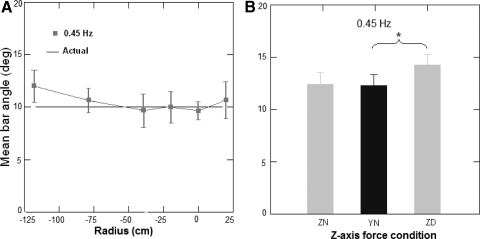
Angle of Tilt: Somatosensory Bar

The somatosensory bar traces were fitted to sinusoids using a least-squares linear regression technique discussed in a previous work (Park et al. 2006). At 0.45 Hz, the somatosensory bar results (Fig. 7A) were generally in good agreement with the verbal reports (Fig. 4A). For the 0.45-Hz condition, the phase error was usually relatively small (under 10°). By contrast, the 0.8-Hz somatosensory results often showed high phase errors (≥90°) due to the rapid swing motion making it difficult for the subjects to achieve good phase-locked responses, although the magnitudes generally were in good agreement with the verbal reports. Because subjects were unable to perform the task well during the 0.8-Hz profiles, these data are not presented.

Fig. 7.

A: somatosensory bar angle as a function of radius from least-squares linear regression to a sinusoid for 0.45 Hz. B: comparison of the somatosensory bar angle results for the z-axis force profiles for the y-axis nulling condition. Error bars, SE; *, significant effects (P < 0.05).

The additional z-axis force doubling increased the tendency to overestimate tilt angle (t = 4.6; df = 58; P < 0.04) as compared with swing-only, but the z-axis force nulling profile did not significantly decrease the perceived angle of tilt (t = −0.13; df = 58; P = 0.35; see Fig. 7B). There was no significant double-frequency component of the somatosensory data for the trials where z-axis force was manipulated, suggesting that the subjects interpreted the z-axis modulations as an integral part of the overall motion. These results are similar to the verbal reports of tilt angle (see Fig. 4).

DISCUSSION

Based on the overall regression results, we found significant effects of both y- and z-axis forces on subjects' perception of motion. In the cases where only the y-axis forces were nulled, subjects overestimated tilt angle (P < 0.05) and underestimated roll radius (i.e., thought they were closer to the center of rotation; P < 0.01). z-axis force nulling caused additional incremental underestimates in horizontal translation and roll radius relative to y-axis nulling alone (both P < 0.05). Conversely, z-axis force doubling caused incremental overestimates in tilt angle, horizontal translation, and roll radius (all P < 0.05). These results suggest that both y- and z-axis components of GIF are important for overall subject motion perception.

Geometric consistency

Although some profiles subjects reported their motion with significant errors, even for these cases their reports were remarkably internally geometrically consistent. For example, at 0.45 Hz: 1) the swing-only y-axis nulling profile had a mean reported radius of 61 cm and a mean reported horizontal translation of 33 cm. These are consistent with a tilt angle of 15.7°, which compares well with the mean reported tilt of 14°. 2) The z-axis nulling profile had a mean radius of 53 cm and a mean reported horizontal translation of 25 cm. These are consistent with a tilt angle of 13.8°, which compares very well with the mean reported tilt of 13°. And finally 3), the z-axis doubling profile had a mean reported radius of 86 cm and a mean reported horizontal translation of 43 cm. These are consistent with a tilt angle of 14.5°, which compares very well with the mean reported tilt of 15°.

Geometric consistency was a general feature throughout the experiment for both 0.8 and 0.45 Hz (summarized in Table 3). Is it reasonable to assume that subjects' perception of distance from the center of rotation was therefore based, at least in part, on knowledge of swing geometry?

Table 3.

Summary of geometric consistency

Frequency	Category	Perceived Radius, cm	Horizontal Translation, cm	Consistent Angle, °	Perceived Angle, °
0.45 Hz	YN	61	33	15.7	14
	ZN	53	25	13.8	13
	ZD	86	43	14.5	15
0.8 Hz	YN	26	14	15.1	11.5
	ZN	22	12	16.4	11.5
	ZD	30	18	16.7	12

“Consistent angle” is computed from perceived radius and horizontal translation assuming geometric consistency is preserved. Note that although there are quantitative differences at 0.8 Hz, geometry was overall still preserved for individual reports (not significantly different from geometrically consistent, P = 0.41). Also see the discussion sections on verbal reports: tilt angle degree translation and roll radius for an explanation of differences between tilt angle and horizontal translation reports at 0.45 and 0.8 Hz.

Previous studies have demonstrated that knowledge of the capabilities of motion devices can influence subject perception (Wertheim et al. 2001). Specifically, in sled studies where some subjects had prior knowledge that the device could only translate, their tilt sensations were smaller than those experienced by subjects without prior knowledge.

For our study, this geometric consistency was tested using a paired t-test where geometrically consistent distances to the center of rotation were calculated from the horizontal translation and tilt angle reports. A comparison of these derived values with the verbal reports showed no significant difference at either 0.8 Hz (t = −3.2; df = 143; P = 0.12) or 0.45 Hz (t = −4.2; df = 214; P = 0.41). For this analysis, trials with reported tilt angles of <5° (around just 5% of total cases) were excluded because their derived radii became very high (≥8 SD from the mean).

By contrast, a comparison of reported versus actual radius did show a significant difference for both 0.45 Hz (t = −38.6; df = 239; P < 0.01) and 0.8 Hz (t = 19.8; df = 143; P < 0.05), providing further evidence that that the perception of motion was driven by a geometrically consistent multidimensional internal model rather than separate motion components. This geometric consistency was likely reinforced by the informed consent process, familiarization with the device capabilities, and training. This is demonstrated by less geometric consistency in naïve untrained subjects' reports. Nonetheless, two of the six naïve untrained subjects clearly demonstrated this consistency. Both of these subjects demonstrated a clear understanding of the capabilities of the device (by asking questions and even in 1 case overtly discussing the motion geometry without prompting) even with the minimal amount of familiarization allowed by the informed consent process and in the absence of any explicit training.

Verbal Reports

Subjects didn't report any sensations of radial motion when asked after the experiment. This implies that their internal models of swing motion may have had a fixed radius (i.e., the variation in z-axis forces were interpreted as being caused by tilt angle and centripetal acceleration rather than by radial translation). This would also be a more likely interpretation based on commonly experienced tilt motion. The constant z-axis DC force (1.008 G) did not apparently deter this interpretation.

The reports showed some evidence of regression of estimates to the mean although this tendency was significantly attenuated by training. This effect is ubiquitous in magnitude estimation studies: subjects regress estimates toward the mean both to reduce errors across a broad range of stimuli and based on experience. For example, Mittelstaedt and Glasauer found that subjects experiencing self-motion slower than a walking pace overestimated their translation, whereas subjects moving faster than a walking pace underestimated their translation (Mittlestaedt and Glasauer 1991).

Tilt angle

Subjects in the experiment overestimated the tilt angle at 0.45 Hz, especially when the y-axis forces were nulled, in both verbal reports and somatosensory bar results. Subjects overestimated more with z-axis doubling and overestimated less with z-axis nulling.

Overestimation of tilt angle has been reported for parallel swing studies (Guedry and Harris 1963) and also for passive yaw rotation and active roll tilt studies (Isreal et al. 1995; Ivanenko et al. 1997). Overestimation may be a strategy adopted by the nervous system in situations when otolith cues are less reliable or the consequences of underestimation would carry a high penalty. For example, subjects have been known to anticipate rear- and downward translations so that potential losses of balance or falls can be preempted (Malcolm and Jones 1974). This might also explain why the overestimation was more pronounced in the y-axis nulling case.

Why were the estimated tilt angles smaller at 0.8 Hz than at 0.45 Hz? These differences agree qualitatively with the Park study, which showed that tilt angle estimates were lower at higher frequencies (Park et al. 2006). It is also possible that subjects' estimates might be influenced by the same factors that cause angular visual illusions. Studies have shown that angles subtending longer line segments appear to be larger than angles subtending short segments (Werkhoven and Koenderink 1993). This suggests a possible radius dependence of tilt angle estimation where subjects interpreted an increase in radius as correlating with an increase in tilt angle. Additionally, it has also been shown that estimated tilt displacement during self-rotation in the dark decreases with increasing tilt velocity (Jurgens and Becker 2006). This effect could account for a 10–15% increase in tilt estimation gain at 0.45 Hz as compared with 0.8 Hz at the average angular velocities of 32°/s (0.8 Hz) and 16°/s (0.45 Hz) in our study (or higher gains for the peak for the peak velocities).

The additional tilt angle overestimation observed when the y- and z-axis forces were nulled may have resulted from a preservation of geometric consistency with an internal model (i.e., larger tilt angle perceptions were driven by smaller perceptions of radius).

Translation and roll radius

Horizontal translation and roll radius reports were generally veridical for profiles lacking y- or z-axis nulling except the horizontal translation was overestimated near the center of rotation. This local overestimation was likely an artifact of the absolute value calculation: if a subject thought they were either just above or below the center of rotation, they would report a positive value for horizontal translation in either case. This contrasts with radius, where subjects could report either a positive or negative value. Therefore near the center of rotation, positive and negative errors across subjects and trials would cancel for radius but sum for translation.

Y-axis nulling caused roll radius to be underestimated, likely because the primary motion cue in this case was the semi-circular canal cue, and the nulling removed the dynamic and phase-locked confirming y-axis otolith cues. As angular sensors, the semicircular canals cannot provide information about rotation radius. Thus the only remaining radius cue was the z-axis otolith stimulus. However, even with a rotation radius of zero, there would still be a small z-axis modulation due to the tilting motion.

Similarly, z-axis force nulling decreased perceptions of horizontal translation at 0.45 Hz and roll radius at both frequencies, whereas z-axis force doubling had the opposite effect. While the trend was the same, we were unable to find a significant effect of y-axis nulling on horizontal translation estimates at 0.8 Hz; this may have been a result of regression to the mean, where subjects would be more likely to overestimate the small translation at 0.8 Hz.

It is likely that the estimates of radius and translation were affected by the inherit ambiguity of the y- and z-axis cues. The lack of confirming otolith signals could tend to reduce the magnitude of perceived motion. With z-axis nulling, although the average z-axis otolith signal is the same as in the swing-only case, the variation over the motion profile is consistent with roll tilt at a radius closer to the center (see Fig. A3). These conflicting signals—the average z-axis force suggesting tilt rotation at the actual radius and the variation suggesting tilt nearer the center of rotation—combine to generate an overall perception of rotation between the center and actual radius. Additionally, this might explain why some subjects indicated that the z-axis nulling profiles were “confusing”: y-axis nulling would be expected below the axis of rotation, whereas z-axis nulling would be expected above the axis of rotation. The situation is reversed for the z-axis doubling case, where the z-axis cues would suggest rotation farther from the center of rotation.

There was also some potential ambiguity for reporting radius: mathematically, as the center of rotation increases, the perceived tilt decreases to the point that if no tilt is perceived, the correct report for center of rotation is infinity, not zero. It was therefore possible that subjects perceiving no tilt at all would report a radius of zero rather than the mathematically correct infinite or indeterminate. However, this was only observed in a few cases when subjects reported a low angle of tilt and large horizontal translation, and this had only a marginal effect on reducing the reported radii.

Observer model

Several models have been proposed for how the brain might disambiguate tilt from translation, from a simple filtering of otolith signals (Mayne 1974; Paige and Tomko 1991; Paige et al. 1998) to using internal models of motion ( Borah et al. 1979; Merfeld et al. 1993, 1999; Vingerhoets et al. 2006; Zupan and Merfeld 2005). In simple filtering, low-FM of GIF is interpreted as arising from tilt, whereas high-frequency GIF modulation is interpreted as arising from translation. For swing motion, if translation estimates were derived from a simple filtering of otolith signals, then translation perception close to zero would be expected at the nulling radius when the y-axis GIF was close to zero. By contrast, if the tilt-translation ambiguity was resolved using an internal model, then translation estimates would instead be close to zero when the head was centered on the axis of rotation (a more accurate solution).

The fact that the estimates of horizontal translation were not close to zero when the y-axis forces were nulled suggests that they were resolved using an internal model; however, this does not preclude the possibility that a simple filtering of otolith signals could have played a role in attenuating the estimates.

The experimental results were compared with simulations of an observer model originally developed by Merfeld (BMerfeld and Zupan 2002; Merfeld et al. 1993) and further elaborated by Haslwanter and Vingerhoets (BHaslwanter et al. 2000; Vingerhoets et al. 2006). The observer model used was an extension proposed by Newman and Oman (Newman 2009), and it also predicted perceived translational velocities and displacements via “leaky” integration with time constants that were shorter in the direction of the perceived vertical. This observer model predicted many of the response characteristics measured (for example, tilt overestimation for y-axis nulling). However, the model did not account for the effect of z-axis nulling or doubling.

There are several possible explanations for these shortcomings. First, our observer model did not incorporate biological noise or simulate the effects of perceptual thresholds. Such effects are probably important when modeling the y- and z-axis nulling cases. Second, the observer model we used did not include any nonvestibular sensory modalities, such as haptic (e.g., “seat of the pants”) receptors that could provide additional information on the gravitoinertial acceleration gradient along the body and thus potentially provide information on body centrifugal acceleration.

Finally, the internal model incorporated into the observer assumed the subjects were na|$$|Adive and knew nothing about the motion constraints of the tilt device. However, as a result of seeing the device and being informed of the types of motion they were likely to experience—part of the informed consent process—it is likely that subjects develop expectations regarding the geometric constraints on possible motion profiles. Such expectations would likely be reinforced by training and by the magnitude estimation questions asked. Therefore our subjects very likely assumed that their motions were constrained to swinging. Just as similar cognitive influences can affect the VOR (Barr et al. 1976), it is reasonable to suggest that this knowledge may have influenced the subjects' magnitude estimation. In fact, as discussed earlier, cognitive information regarding the motion device has been reported to alter tilt/translation processing (Wertheim et al. 2001).

To model the effect of geometric constraints, predictions made by the “nāve” observer model were used to estimate the corresponding swing motion by using a post hoc fitting where the z-axis gravitational force oscillations were interpreted as arising from changes in swing radius (instead of actual z-axis motion), and the model output was modified to a swing motion minimizing the least-square errors of angle, translation, and radius. This allowed subject expectations to constrain—to some extent—predicted motion trajectories, and seemed to approximate experimental results reasonably well (see Table 4). However, this post hoc fitting is probably not how the brain actually imposes geometry in an internal model. A more parsimonious approach would be to add internal geometric constraints to the observer model that would model either situational-dependent geometry or a generalized geometry built up over time by incorporating memory into the model. The authors are exploring such alternatives.

Table 4.

Observe model parameters and model predictions

Observer Model Parameters
Semicircular canals and otoliths					Feedback gains
SCC time constant	SCC adaptation constant				SCC gain (Kω)				GIF gain (Kf)				GIFω gain (Kωf)				Acceleration gain (Ka)
5.7	80				3.0				2.0				2.0				−2.0
Observer Model Results
	Parameter
	Peak y-axis linear velocity, cm/s				Peak Angular velocity, °/s				Horizontal translation, cm				Tilt angle, °				Distance from rotation center, cm
	C	YN	ZN	ZD	C	YN	ZN	ZD	C	YN	ZN	ZD	C	YN	ZN	ZD	C	YN	ZN	ZD
Actual	0	60	60	60	28	28	28	28	0	42	42	42	10	10	10	10	0	−122	−122	−122
Model output	10	38	38	38	27	27	27	27	3	31	31	31	10.5	11	12	13	0	−70	−25	−130
Fit to swing geometry	N/A	N/A	N/A	N/A	N/A	N/A	N/A	N/A	0	36	24	46	10.5	12	12.6	12.1	0	−86	−55	−110
Experiment results	N/A	N/A	N/A	N/A	N/A	N/A	N/A	N/A	11	33	25	43	9.5	14	13	15	0	−60	−53	−86

Columns are arranged by nulling condition (C = subject's ears are at the center of rotation; YN = y-axis nulling; ZN = z-axis nulling; ZD = z-axis doubling). GIF, gravito-inertial force; SCC, semicircular canals.

Summary

The results highlight the importance of both y-axis and z-axis GIF in human motion perception. Although in the absence of y-axis accelerations, z-axis signals don't ultimately provide sufficient information to accurately estimate rotation radius, they nevertheless had a significant influence. These results (e.g., geometric consistency, effect of z-axis forces) suggest that subjects' motion perception was derived from an internal model that not only comprises all sensory signal components, but also takes into account known geometric constraints.

GRANTS

Funding for this experiment was generously provided by National Aeronautic and Space Administration Grant NNJ04HF79G and National Institute of Deafness and Other Communications Disorders Grant R01 DC-04158.

APPENDIX

Derivation, simulation, and experimental validation of the motion paradigm

Motion must initiate from zero velocity and zero acceleration, and for sine waves, velocity must be 90° out of phase with acceleration. Therefore either acceleration or velocity must be discontinuous if steady-state motion commenced from a stop. We eliminated this discontinuity by multiplying the sinusoidal velocity by a linear ramp with an initial value of zero and a value of 1 when the steady state began.

If the duration of the ramp-up period is limited to a positive integer number of half-cycles, a number of simplifying characteristics emerge: specifically, the position, velocity, and acceleration are all “continuous.” All motion profiles in this experiment were ramped up from zero to eliminate any suprathreshold discontinuities; each profile lasted 50 ramp-up, 80 steady-state, and 50 ramp-down cycles. The steady-state tilt angle was 10°, giving a peak angular velocity of 27°/s.

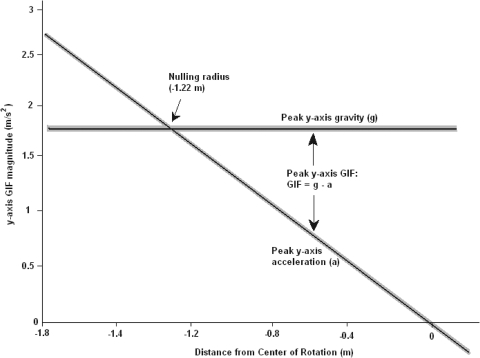
The steady-state y-axis gravitational force measured by the otolith organs can be expressed as g_y(t) = −G sin[Θ_max cos(ωt)] ≈ [−;G Θ_max cos(ωt)] by Taylor series expansion for small angles, where G is −;9.8 m/s², Θ_max is the maximum tilt angle (10°), ω is the roll frequency (ω = 2πf), and f is the oscillation frequency. The tangential acceleration varies with radial distance from the rotation axis, and can be expressed as a_y(t) = −;R Θ_max ω² cos(ωt), where R is the radial distance between the rotation axis and ear level. When the head is below the axis of rotation, the tangential acceleration approximately cancels the y-axis gravitational force (a_y ≈ g_y) when R = −;G/(ω)² (Fig. 2, categories B–D). This gives a radius of R = −;1.22 m for 0.45 Hz and R = −;0.38 m for 0.8 Hz.

In addition to the y-axis force, the otoliths measure a z-axis component of the GIF that is composed of components from gravity and the centripetal acceleration in the steady state. The z-axis gravitational force variation can be expressed as g_z(t) = −;G cos[Θ_max cos(ωt)], which for small angles can be simplified by second-order Taylor series expansion as g_z(t) = −;G {1 − 1/4 Θ_max² [1} cos (2ωt)]}. The centripetal acceleration can be expressed as a_z(t) = −;R (ω Θ_max)² 1/2 [1 −; cos (2ωt)], so that combined force per unit mass is f_z(t) = g_z(t) − a_z(t) = [1/2 R (ω Θ_max)² − G (1 − 1/4 Θ_max²)] + [G 1/4 Θ_max² − 1/2 R (ω Θ_max)²] cos(2 ωt). The time-invariant DC component [1/2 R (ω Θ_max)² − G (1 −; 1/4 Θ_max²)] in this case is approximately −;1.008 G (−;9.88 m/s²), and the time-varying component [G 1/4 Θ_max² − 1/2 R (ω Θ_max)²] has an amplitude of ≈0.023 G (0.23 m/s²) for either 0.45 or 0.8 Hz.

It is not possible to eliminate this z-axis GIF because the contribution from gravity and centripetal acceleration will always be in the same direction. However, it is possible to add an additional z-axis acceleration component to interfere with the sinusoidal variation in GIF. This complementary radial motion contributes maximum accelerations upwards and downwards at the swing endpoints, and center, respectively. This makes the z-axis acceleration profile remain constant near the average of the z-axis GIF [i.e., effectively nulling the variation in GIF (Fig. 2, category ZN)].

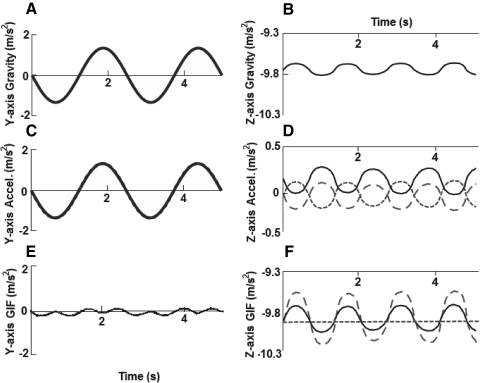
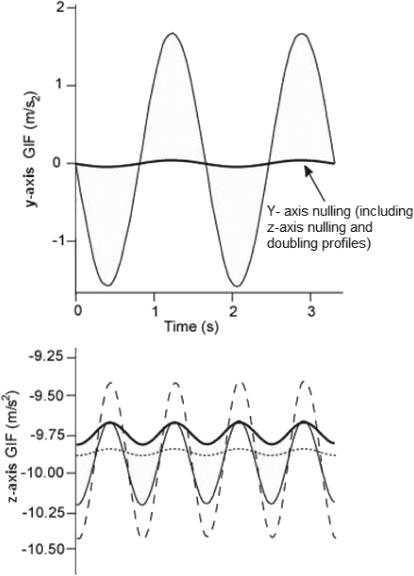
With the z-axis force doubling profile, instead of nulling the z-axis GIF, the z-axis GIF variation from the swing midpoint to center was doubled (Fig. 2, category ZD). Note that the swing-only, z-axis shear force nulling, and z-axis shear force doubling profiles all have the same average z-axis force measured by the otoliths; only the variation changes. The doubling profile introduces z-axis GIF variation amplitudes of around 0.5 m/s² (>3 times the z-axis discrimination threshold), for either frequency. The theoretical, simulated, and experimentally determined y-axis and z-axis forces are shown in Figs. A1–A4.

Fig. A1.

y-axis (IA) and z-axis (DV) forces and accelerations for the various motion paradigms calculated from equations in text. Left: y-axis components; right: z-axis components. y-axis (A) and z-axis (B) gravitational force (g) components are shown. y-axis (C) and z-axis (D) acceleration are shown for the y-axis nulling (—), z-axis force nulling (…), and z-axis force doubling (- - -). y-axis (E) and z-axis (F) components of the total resultant specific force (f = g − a) are shown (2nd row trace subtracted from the 1st).

Fig. A2.

Peak steady-state amplitude components of gravity, accleration, and combined gravitoinertial force (GIF) during the 0.45-Hz swing paradigm for a 10° tilt. As shown the peak y-axis gravity component depends only upon tilt angle and is independent of radius; the amplitude of the linear acceleration component increases with radius (a_t = rα). As shown graphically, the difference between the 2 yields the GIF (f = g − a). The y-axis contributions of gravity and linear acceleration cancel one another at a radius of −1.22 m at 0.45 Hz. The effect is similar for the 0.8-Hz paradigm. Line thickness represents mechanical vibrations and other noise. Note that the amplitude (maximum) is shown in this figure. Minimum values are the negative of those shown in this plot.

Fig. A3.

Maximum and minimum z-axis GIF at steady state for the 0.45-Hz swing paradigm as a function of radius. At the y-axis nulling point (circa −1.2 m), a substantial z-axis force variation, predominantly at 0.9 Hx, remains. This component can be reduced by simultaneously applying a phase-locked radial linear acceleration at 0.9 Hz (z-axis force nulling). It can also be increased by simultaneously applying the same z-axis acceleration but with the phase altered by 180° (z-axis force doubling). The effect is similar for 0.8 Hz. Note that minimum and maximum values are shown (instead of the amplitudes as in Fig. A2).

Fig. A4.

Sinusoids regressed to accelerometer measurements of the 4 motion profiles for the 0.45-Hz paradigms: head center (bold line), swing-only y-axis nulling (solid line), z-axis nulling (dotted line), and z-axis doubling (dahsed line). Results were similar for the 0.8-Hz paradigm. The actual measurements also showed vibrational components at higher frequencies (mostly at 5 and 15 Hz).