Abstract
The study of learning and memory at the single-neuron level has relied on the use of many animal models, most notably rodents. Although many physiological and anatomical studies have been carried out in rats, the advent of genetically engineered mice has necessitated the comparison of new results in mice to established results from rats. Here we compare fundamental physiological and morphological properties and create three-dimensional compartmental models of identified hippocampal CA1 pyramidal neurons of one strain of rat, Sprague–Dawley, and two strains of mice, C57BL/6 and 129/SvEv. We report several differences in neuronal physiology and anatomy among the three animal groups, the most notable being that neurons of the 129/SvEv mice, but not the C57BL/6 mice, have higher input resistance, lower dendritic surface area, and smaller spines than those of rats. A surprising species-specific difference in membrane resonance indicates that both mouse strains have lower levels of the hyperpolarization-activated nonspecific cation current Ih. Simulations suggest that differences in Ih kinetics rather than maximal conductance account for the lower resonance. Our findings indicate that comparisons of data obtained across strains or species will need to account for these and potentially other physiological and anatomical differences.
INTRODUCTION
The mammalian hippocampus is a region of the medial temporal lobe that has been implicated in various aspects of memory. Rodents with lesions to the hippocampus show impaired trace eyelid conditioning, contextual fear conditioning, and spatial learning (Logue et al. 1997; Morris et al. 1982; Sutherland et al. 1982). Neurons of this region demonstrate functional plasticity, which is a presumed substrate for information storage (Morris et al. 1990). In addition, pharmacological or genetic manipulation of protein function in the hippocampus can disrupt both long-term cellular plasticity and certain forms of learning and memory (Chen et al. 2006; Nolan et al. 2004; Zeng et al. 2001).
Anatomical, physiological, and theoretical studies of CA1 pyramidal neurons, the primary output of the hippocampus proper (Witter and Amaral 2004), have predominantly been performed in rats (Golding et al. 2005; Harris and Stevens 1989; Megías et al. 2001; Poirazi et al. 2003). The development of genetic methods that alter protein expression in specific neurons, however, most often uses mouse models and has resulted in numerous studies related to learning and memory being carried out in mice (Chen et al. 2006; Nolan et al. 2004; Picciotto and Wickman 1988). Although mice are closely related to rats, there are important differences that complicate direct comparisons between species. Behavioral studies suggest that mice have different strategies for learning spatial information. For example, on the Morris water maze, a spatial memory task in which rodents use spatial cues to navigate through a circular pool to a hidden platform (Morris 1984), mice do not perform as well as rats (Frick et al. 2000; Whishaw 1995) and use simpler strategies than rats do to locate the platform (Whishaw et al. 2001).
The behavioral disparities between rats and mice could stem from anatomical and/or physiological differences in CA1 pyramidal neurons. At the anatomical level, these differences may include: neuronal size reflected by total dendritic length, surface area, or volume; spatial distribution or branching of the dendritic arbor; or dendritic spine size or density. At the physiological level, distinctions could include: passive membrane properties such as resting membrane potential (Vm), input resistance (RN), and membrane time constant (τ); and active membrane properties such as those contributing to action potential generation as well as subthreshold membrane resonance.
Individual studies have reported passive physiological properties of mouse or rat CA1 neurons (Biscoe and Duchen 1985; Staff et al. 2000), but the combined morphological and physiological properties of CA1 pyramidal neurons have not been systematically compared between rats and mice. Observations from rats and single-cell models created from rat neuron morphologies should not be generalized to explain data obtained from mice without evidence that the CA1 pyramidal neurons of both species are similar in structure and function. In this study, we performed a systematic analysis of rats and two common strains of mice used for genetic manipulations, C57BL/6 and 129/SvEv, comparing gross hippocampal anatomy, dendrite and spine morphology, passive and active membrane properties, and membrane potential resonance. In addition, we created animal-specific, single-neuron models that incorporate the unique physiological and morphological properties of the CA1 pyramidal cells from the different species and strains. This study reveals significant differences between mouse strains, as well as between mice and rats. A major difference between the two species is that mice have less Ih active at resting membrane potentials than rats.
METHODS
Slice preparation
All animals used in this study were males aged 5–7 wk. This range was chosen to facilitate comparison with other physiological studies in both rat (Magee 1999; Poolos et al. 2002; Staff et al. 2000) and mouse species (Chen et al. 2006; Nguyen et al. 2000a,b; Nolan et al. 2004; Tsay et al. 2007), as well as a behavioral study comparing hippocampal-dependent learning in rats and mice (Whishaw and Tomie 1996). Sprague–Dawley rats, C57BL/6Jax mice, and 129/SvEvTac mice were anesthetized with a ketamine/xylazine mixture (90/10 mg/ml) and intracardially perfused with ice-cold artificial cerebral spinal fluid (aCSF) consisting of the following (in mM): 2.5 KCl, 1.25 NaH2PO4, 25 NaHCO3, 0.5 CaCl2, 7 MgCl2, 7 dextrose, and 205 sucrose, bubbled with 95% O2-5% CO2 to maintain a pH of about 7.4. The brain was removed, the cerebellum was cut away, and a cut was made longitudinally down the central fissure to separate the hemispheres. A blocking cut was made along the dorsal surface of each hemisphere at an angle of about 75° referenced to vertical to maximize the dendritic projections within the plane of the slice. Each section was mounted on its dorsal surface, rostral end toward the blade, and sliced on a vibrating tissue slicer (Vibratome 3000, Vibratome, St. Louis, MO). Because rats have larger brains and hippocampi relative to those of mice (Kalisch et al. 2006; Kovacevic et al. 2005; Ma et al. 2005; Sahin et al. 2001), horizontal slices were cut 350 μm thick in rats and 300 μm thick in mice to obtain approximately the same number of slices across the dorsoventral axis from each species. Typically four to six sections were harvested from the middle of the hippocampus relative to the dorsoventral axis. Slices were held for about 45 min at 37°C in a holding chamber of aCSF solution containing (in mM) 125 NaCl, 2.5 KCl, 1.25 NaH2PO4, 25 NaHCO3, 2 CaCl2, 2 MgCl2, 10–25 dextrose, 1.3 ascorbic acid, and 3 sodium pyruvate, bubbled with 95% O2-5% CO2. Incubation beyond 45 min was at room temperature (∼22°C). All methods were approved by the University of Texas at Austin Institutional Animal Care and Use Committee.
Whole cell recordings
Whole cell current-clamp recordings were performed on slices submerged in a chamber filled with aCSF heated to 32–34°C, flowing at a rate of 1 to 2 ml/min (same as holding aCSF, minus pyruvate and ascorbate). Neurons were visualized using an Olympus microscope (Model BX51WI) fitted with differential interference contrast optics using infrared illumination (Stuart et al. 1993). Patch pipettes (4–7 MΩ) were pulled from capillary glass of external diameter 1.65 mm (World Precision Instruments), using a Flaming/Brown micropipette puller (Model P-97, Sutter Instruments), and filled with an internal solution containing the following (in mM): 120 K-gluconate, 20 KCl, 10 HEPES, 4 NaCl, 7–14 Tris-phosphocreatine, 0.3 Tris-GTP, and 4 Mg-ATP. Neurobiotin (Vector Labs) was included (0.1–0.2%) for subsequent histological processing. Data were acquired with a Multiclamp 700B amplifier (Molecular Devices) and digitized at 20–50 kHz with an ITC-18 (Instrutech) computer interface and Axograph 6.0 (AxoGraph Scientific) acquisition software. Membrane properties were measured on each cell in the presence of 1) synaptic blockers (50 μM 2-amino-5-phosphonovaleric acid [ APV ], 10 μM 6-cyano-7-nitroquinoxaline-2,3-dione [ CNQX ], 10 μM bicuculline, 10 μM picrotoxin) and 2) synaptic blockers plus an h channel blocker [ 5 mM CsCl or 20 μM 4-(N-ethyl-N-phenylamino)-1,2-dimethyl-6-(methylamino) pyridinium chloride (ZD7288) ] . All drugs were made up as stock solutions in water, DMSO, NaOH, or ethanol (final concentration of each solvent ≤0.1%). At least 5 to 10 min were allowed for solutions to wash in before taking measurements. CsCl and ZD7288 caused a change in Vm, so a holding current was applied to hold the cells at the initial Vm measured in synaptic blockers. Because many of our measurements are critically dependent on minimization of recording artifacts, pipette capacitance was compensated for, and the bridge was balanced manually prior to each recording run. Injected currents used for this purpose were typically 50% larger than those used for data collection to further minimize errors. Series resistance was 8–25 MΩ for all recordings and experiments were terminated if this range was exceeded.
Input resistance was calculated as the slope of the linear fit of the voltage–current plot between −40- and + 40-pA current injections for rats and C57BL/6 mice. In 129/SvEv mice, the line was fit between −60 and + 20 pA because neurons had larger input resistances and were more likely to fire action potentials with current injections above + 20 pA. Membrane time constant traces were analyzed using Igor (WaveMetrics), and slow and fast time constants were calculated from a double-exponential fit of the averaged voltage decay resulting from 100 trials of identical 1-ms, −400-pA current injections. Active membrane properties were calculated as the average spike threshold, maximum dV/dt, peak, amplitude, and half-width of five individual action potentials. Threshold was defined as the voltage at the time corresponding to the first maximum of the third derivative of the voltage response. Action potential amplitude was measured from threshold to peak, with the half-width measured at half this distance. The sag ratio was calculated as the proportion of steady-state to maximum voltage transients resulting from hyperpolarizing current injections. Resonance was measured using a sinusoidal current injection of constant amplitude and linearly spanning 0–15 Hz in 15 s, and the impedance amplitude profile was determined by taking the ratio of the Fourier transform of the voltage response to the Fourier transform of the current stimulus (Narayanan and Johnston 2007; Puil et al. 1986). Resonance frequency was measured as the frequency of the peak impedance, and resonance strength was the ratio of the peak impedance to the steady-state impedance at a frequency of 1 Hz.
Cellular morphology
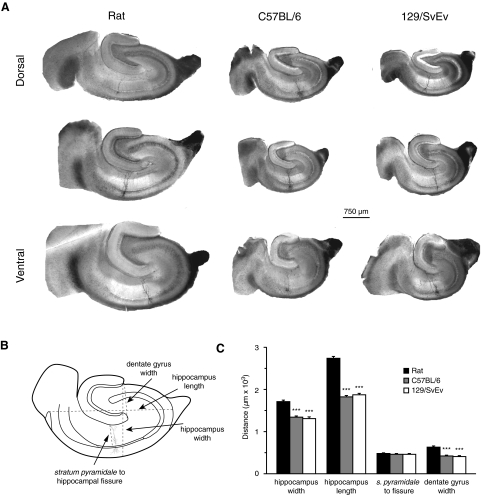
Slices were fixed in 3% glutaraldehyde in 0.1 M phosphate buffer (pH 7.4) and stored at 4°C for ≤3 mo. They were processed using an avidin–horseradish peroxidase system activated by diaminobenzidine (DAB, Vector Labs). DAB-processed slices were mounted on slides in glycerol and viewed with a compound (Leitz Diaplan) microscope. Dimensions of a sample of slices were measured in vitro, prior to fixation, and again after DAB processing, and no significant shrinkage of tissue was observed (<1%). The length of the hippocampus in a slice was measured as the maximum distance from the apex of CA3 to the angular bundle, and the width was measured across the extent of the granule cell layer from each of the blades of the dentate gyrus and across CA1 to the alveus. The width of the dentate gyrus was measured as the distance between the ends of the granule cell body layer. To account for differences in hippocampal geometry due to slicing across the dorsoventral axis, processed slices were ranked from 1 to 11 (ventrodorsal), according to their shape, to represent their position along this axis. The average location of slices was in the middle of the dorsoventral axis (ranked 6) and was not different among the three groups.
For illustrative purposes, images of the cells were created from z-stacks of photos taken at ×10 or ×100 and processed using Helicon Focus Pro software (Helicon Soft). Neurons were reconstructed using a ×40 objective with a computer-controlled indexing system running Neurolucida 6.0 imaging software (MicroBrightField). Whole cell, three-dimensional (3D) reconstructions included the soma and dendritic shafts, but not dendritic spines. To quantify dendritic anatomy, all morphological measurements were done in Neurolucida Explorer (MicroBrightField). Total dendritic length, membrane surface area, and cell volume included the sum of the lengths, surface areas, and volumes of all dendritic segments. Dendritic branching patterns were analyzed using Sholl (1953) analyses, in which a set of nested concentric spheres of linearly increasing radius were centered at the cell body, and noncumulative counts of intersections and dendritic lengths were measured for each sphere. The number of intersections refers to the number of times the processes intersect an individual Sholl sphere and the length refers to the total length of all processes within a sphere, not including length in smaller spheres. Due to variation in total dendritic length, the radius of the smallest Sholl sphere that encompassed all dendritic processes ranged from 480 to 740 μm (to the nearest 20 μm) for different cells. To compare Sholl analyses across this large range of lengths, we used a different set of radii for each cell, scaled to give a total of 20 Sholl spheres for each cell. For example: a cell extending ≤600 μm from the soma would have 20 spheres of radii incrementing by 30 μm, whereas a cell extending 480 μm would have 20 spheres with 24 μm increments to the radii.
To compare spine densities among groups, samples of dendritic segments including spines were reconstructed at ×100. These segments were randomly chosen but met the following criteria: 1) having a dark stain and clearly discernible spines, 2) being 25 to 50 μm long, 3) including no branch points, and 4) the dendrite being planar along the horizontal axis. Because spine density varies with location (Megías et al. 2001), we looked at dendritic segments from six of the seven spiny regions of the CA1 neurons, described in Megías et al. (2001): lacunosum-moleculare thin (LMt) and medium (LMm), radiatum thin (Rt), radiatum thick distal (RTd) and medial (RTm), and oriens distal (OD). The lacunosum-moleculare thick spiny segments described by Megías et al. (2001) were not included because their small length (1 μm) made their location difficult to determine. The average distance from the soma of each reconstructed segment was measured by linear distance. Each spine was reconstructed as a cylinder, with its length defined as the distance from the edge of the dendritic shaft to the end of the spine and its diameter defined as the diameter of the spine head. More accurate measures of spine length and head diameter were obtained by serial-section electron microscopy (Harris and Stevens 1989) for comparison. The light microscope reconstructions enabled us to analyze a large number of dendritic segments. Spine densities were calculated as the number of spines divided by the length of the segment. To account for spines obscured from view by the dendritic shaft, spine densities were corrected using the geometric equation derived in Feldman and Peters (1979)
where N is the estimated spine density; n is the raw spine density, before accounting for hidden spines; Dr is the radius of dendrite; Sl is the average length of spines [ (mean ± SD) Rat: 0.69 ± 0.29 μm; C57BL/6: 0.71 ± 0.27 μm; 129/SvEv: 0.62 ± 0.25 μm ] ; Sd is the average diameter of spine head [ (mean ± SD) Rat: 0.35 ± 0.16 μm; C57BL/6: 0.35 ± 0.15 μm; 129/SvEv: 0.35 ± 0.14 μm ]
N, n, and Dr were determined individually for each segment, whereas Sl and Sd were determined as the average values for each animal group.
Simulations Effect of Ih on Resonance and “sag.”
Simulations were performed on a single-compartment model (cylinder of 100-μm diameter and 100-μm length) using the NEURON simulation environment (Hines and Carnevale 1997). Membrane properties were set to: Cm = 1 μF/cm2 and Rm = τslow/Cm (from τslow = RmCm, and using mean τslow from experiments). Kinetics of the h conductance were: τact = 47 ms and V1/2 = −82 mV (Magee 1998). The maximal conductance (ḡh) was set to 22 μS/cm2, to yield a resonance frequency (fR) similar to that observed in the rat. To simulate the lower fR observed in mice, we either reduced ḡh or jointly increased τact and reduced V1/2. To match experimental observations, we simulated membrane potential sag at −65 mV and resonance at −75 mV using current injection waveforms identical to those used experimentally.
Passive models of reconstructed neurons
Whole cell reconstructions were imported into the NEURON simulation environment (Hines and Carnevale 1997), and models were created by pairing each cell's digitized anatomy with its measured τslow (recorded in synaptic blockers plus either ZD7288 or CsCl). Default membrane parameters for each cell were set to Cm = 1 μF/cm2, Ri = 150 Ω-cm, and Rm = τslow/Cm. No active conductances were included. The whole cell reconstructions were based solely on dendritic diameter and length and did not include spines. To account for the extra surface area in spines, Rm was divided and Cm was multiplied by a “spinescale” parameter (Golding et al. 2005; Stuart and Spruston 1998), which was defined as the ratio of the total surface area, including spines, to the surface area without spines, according to the following equation
where SAshaft is the surface area of dendritic shaft for a 1-μm-long segment; SAspines is the surface area contributed by spines in a 1-μm-long segment; d is the average diameter of dendritic shaft; N is the estimated spine density from the Feldman and Peters (1979) equation; and A is the average surface area of an individual spine.
The average surface area of an individual spine in rats and C57BL/6 was set to 0.85 μm2, which is the sum of the head and neck surface areas reported for rats in Harris and Stevens (1989). The individual spine surface area in 129/SvEv was set to 0.83 μm2, which was obtained by scaling the Harris and Stevens (1989) neck surface area by 90%. Spines in 129/SvEv were shorter than, but had head diameters similar to, those of the other groups, so we reasoned that differences in spine length and surface area were due to a shorter spine neck.
Statistical analyses
A two-factor ANOVA test, Bonferroni-corrected (InStat 3.0; GraphPad Software), was used to assess the differences among the three animal groups and between pharmacological treatments. Where ANOVA revealed significant differences, a Student's t-test was performed to assess the significance between groups. When SDs across groups were significantly different according to Bartlett's test, a Dunn-corrected, nonparametric ANOVA was used. Data are reported as means ± SE.
RESULTS
Quantitative morphology
Because rats have larger brains with larger hippocampi than those of mice (Kalisch et al. 2006; Kovacevic et al. 2005; Ma et al. 2005; Sahin et al. 2001), we first compared gross hippocampal anatomy, as measured from our slices. As expected, slices of rat hippocampi were larger than those from mice, with larger average lengths and widths (Fig. 1; ANOVA, Bonferroni-corrected; length: P < 0.0001; width: P < 0.0001). Surprisingly, the mean distance from individually labeled soma along the apical dendritic tree to the hippocampal fissure was similar across groups (Fig. 1, ANOVA, P = 0.248). The observed similarities were not due to a dorsoventral sampling bias because the mean slice positions along the dorsoventral axis were not different among groups (see methods for quantification detail). The findings suggest that the apical dendritic lengths of CA1 pyramidal neurons may be conserved across these two species, despite differences in total hippocampal volume. Although the extent of area CA1 was similar in rats and mice, the width of the dentate gyrus was smaller in mice (Fig. 1C, nonparametric ANOVA, Dunn-corrected; P < 0.001), which contributes to a difference in total hippocampal volume across species.
Fig. 1.
Geometry of hippocampal slices taken from rats and C57BL/6 and 129/SvEv mice. A: photos of slices showing hippocampal geometry across the dorsoventral axis in the 3 groups. A neurobiotin-filled cell is visible in CA1 of each slice. B: diagram of a typical measurement of hippocampal width, length, soma-to-hippocampal fissure distance, and dentate gyrus width. C: average measure of hippocampal width and length in slices with stained neurons; average distance from each visible soma to the hippocampal fissure, as measured along the apical dendritic tree; and average width of the dentate gyrus. ***P < 0.001. (n = 22 rats, 21 C57BL/6 mice, and 14 129/SvEv mice).
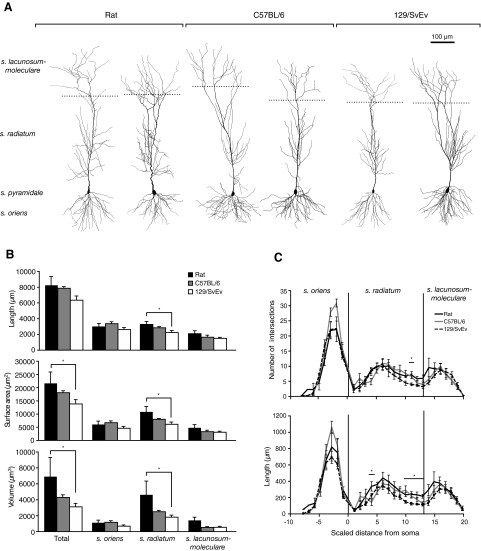
We further quantified dendritic morphology using 3D reconstructions of DAB-processed neurons (Fig. 2A). Total dendritic length was similar across all animal groups, but neurons of 129/SvEv mice appeared slightly shorter due to a decreased dendritic length within stratum radiatum compared with that of rats (Fig. 2, A and B; nonparametric ANOVA, Dunn-corrected; total length: P = 0.012; length in s. oriens: P = 0.186; length in s. radiatum: P = 0.019; length in s. lacunosum-moleculare: P = 0.098). Total membrane surface area and volume were also significantly reduced in the 129/SvEv mouse strain compared with those of rats, due to differences within stratum radiatum (Fig. 2B; nonparametric ANOVA, Dunn-corrected; total surface area: P = 0.004; surface area in s. oriens: P = 0.029; surface area in s. radiatum: P = 0.002; surface area in s. lacunosum-moleculare: P = 0.091; total volume: P = 0.002; volume in s. oriens: P = 0.025; volume in s. radiatum: P = 0.001; volume in s. lacunosum-moleculare: P = 0.124). Neurons of C57BL/6 mice were intermediate to both rats and 129/SvEv and were not significantly different from either. Consistent with these data, Sholl analyses performed on the neuron reconstructions revealed that the number of intersections and dendritic length were decreased in distal stratum radiatum of 129/SvEv mice compared with those in rats (Fig. 2C). Additionally, C57BL/6 had less dendritic length in proximal stratum radiatum and at the stratum radiatum/stratum lacunosum-moleculare border.
Fig. 2.
Morphology of CA1 pyramidal neurons of rats and C57BL/6 and 129/SvEv mice. A: representative reconstructed neurons from each animal group. Dotted lines represent the borders between stratum radiatum and stratum lacunosum-moleculare for each cell. B: average dendritic length, membrane surface area, and volume within different strata of CA1. *P < 0.05. C: Sholl analyses for intersections and dendritic length. Radius of concentric circles was different for each cell and was set to give a total of 20 apical circles. Scaled distance from soma refers to the number of Sholl spheres, increasing from 1 to 20 with distance from the soma. Negative distances refer to the basal dendrites. Stars represent regions of significant difference (P < 0.05). Rat vs. 129/SvEv mice: difference in intersections at Sholl distance 11 and in dendritic length at Sholl distances 11–13. Rat vs. C57BL/6 mice: difference in dendritic length at Sholl distances 4 and 13. C57BL/6 vs. 129/SvEv: differences in dendritic length at Sholl distances 10–11. n = 5 rats, 6 C57BL/6 mice, and 8 129/SvEv mice.
Analysis of spines
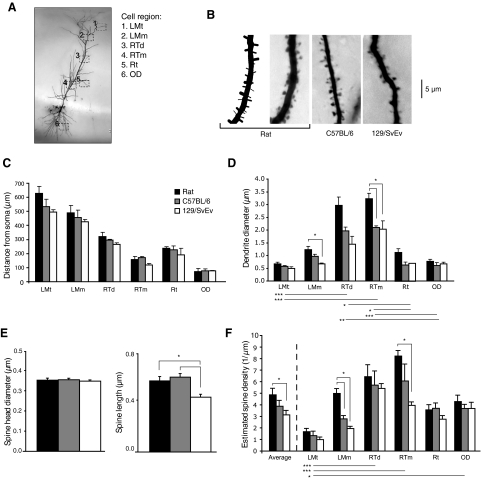
Whole cell reconstructions provide a measure of the membrane surface area along the dendritic shaft. Because dendritic spines also significantly contribute to the membrane surface area and cell volume, we quantified spine density across the dendritic arbor in each of the three groups. Spiny segments were reconstructed from six different regions across the dendritic tree in the three animal groups (Fig. 3, A and B; n = 3 segments per region per animal, 54 total). Average distances from the soma differed slightly but not significantly between rats and mice for the same cell regions (Fig. 3C; standard ANOVA; LMt: P = 0.153; LMm: P = 0.635; RTd: P = 0.244; RTm: P = 0.111; Rt: P = 0.608; OD: P = 0.957). Dendrite diameter was larger in rats than that in 129/SvEv mice in LMm and larger in rats than that in both mice in RTm (Fig. 3D) (Across animal species: ANOVA, Bonferroni-corrected; LMt: P = 0.174; LMm: P = 0.011; RTd: P = 0.080; RTm: P = 0.016; Rt: P = 0.035; OD: P = 0.482. Across region: nonparametric ANOVA, Dunn-corrected: P < 0.0001). The spine head diameter was similar across all three groups, but total spine length was reduced in 129/SvEv compared with that in both rats and in C57BL/6 mice (Fig. 3E; ANOVA, Bonferroni-corrected; head diameter: P = 0.729; spine length: P < 0.0001). Spine densities of the different regions were determined by counting the number of visible spines per μm length. However, this method of counting will be affected by dendrite diameter because more spines will be obscured from view by larger diameter dendrites than smaller ones. We used the geometric equation of Feldman and Peters (1979) to correct for spines that were hidden by the dendritic shaft. This approach allowed us to compare across groups of animals, regardless of average diameter, and to give us more accurate spine density approximations for modeling. Corrected values revealed larger spine densities in rats than 129/SvEv mice in radiatum/thick/medial and larger densities in rats than both mice in lacunosum-moleculare/medium (Fig. 3F) (Across animal species: standard ANOVA, Bonferroni-corrected; average: P = 0.039; LMt: P = 0.227; LMm: P = 0.001; RTd: P = 0.569; RTm: P = 0.031; Rt: P = 0.130; OD: P = 0.407. Across cell region: nonparametric ANOVA, Dunn-corrected: P < 0.0001).
Fig. 3.
Spine densities in CA1 pyramidal neurons of rats and C57BL/6 and 129/SvEv mice. A: sample cell and regions where spiny reconstructions were made. 1: lacunosum-moleculare thin (LMt); 2: lacunosum-moleculare medium (LMm); 3: radiatum/thick distal (RTd); 4: radiatum/thick medial (RTm); 5: radiatum thin (Rt); 6: oriens distal (OD). n = 3 rats, 3 C57BL/6 mice, and 3 129/SvEv mice reconstructions for each of the 6 regions (total of 54 reconstructed segments). B: sample photos of spines from LMm from the 3 groups. The rat spiny segment is accompanied by the 2D image of its corresponding 3D reconstruction. C: average distance from the soma for the reconstructed spiny segments of the different cell regions. D: average dendritic diameter of the reconstructed spiny segments. Significance bars above the graph show significance across animal groups within a single-cell region. Bars below show significance across cell regions for all animal groups. E: average spine length and spine head diameter of all spines reconstructed within each animal group. F: average estimated spine densities derived by correcting raw spine counts to account for hidden spines using the Feldman and Peters (1979) geometric equation. Significance bars above the graph show significance across animal groups within a single-cell region. Bars below show significance across cell regions for all animal groups. *P < 0.05, **P < 0.01, ***P < 0.001.
Resting membrane properties
Dendritic geometry will determine cellular physiology, given that membrane surface area is inversely proportional to RN (Rall 1977). Because CA1 pyramidal neurons of 129/SvEv mice had less surface area than those of rats, we hypothesized that they might also be physiologically distinct from rat neurons. We measured passive membrane properties in the three animal groups in the presence of CNQX, APV, bicuculline, and picrotoxin to block fast glutamatergic and GABAergic transmission. Rat neurons had passive membrane properties similar to those previously reported by our lab and by others (Table 1; Fan et al. 2005; McDermott et al. 2003; Staff et al. 2000). C57BL/6 neurons had a more hyperpolarized resting membrane potential (Vm) than that of the other two groups (Table 1; ANOVA, Bonferroni-corrected; P = 0.0001). 129/SvEv neurons had significantly larger input resistances (RN) than those of the other groups, as might be predicted from their smaller membrane surface area (ANOVA, Bonferroni-corrected; P = 0.0001). Both fast and slow time constants (τfast, τslow) were similar across all animal groups (ANOVA, Bonferroni-corrected; τslow: P = 0.103; τfast: P = 0.810; 50 neurons total; rat: 20; C57BL/6: 16; 129/SvEv: 14).
Table 1.
Passive properties in control ACSF
| Property | Rat (n = 20) | C57BL/6 (n = 16) | 129/SvEv (n = 14) |
|---|---|---|---|
| Membrane potential, mV | −64.6 ± 0.8 | −67.5 ± 0.6* | −62.8 ± 0.6 |
| Input resistance, MΩ | 65.6 ± 4.4 | 65.4 ± 1.7 | 93.1 ± 6.7* |
| Slow time constant, ms | 22.4 ± 1.5 | 22.2 ± 0.9 | 26.1 ± 1.6 |
| Fast time constant, ms | 0.8 ± 0.1 | 0.8 ± 0.0 | 0.8 ± 0.0 |
Values are means ± SE.
Significantly different from the other two groups.
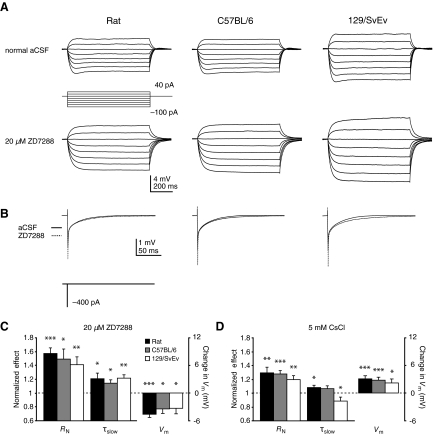
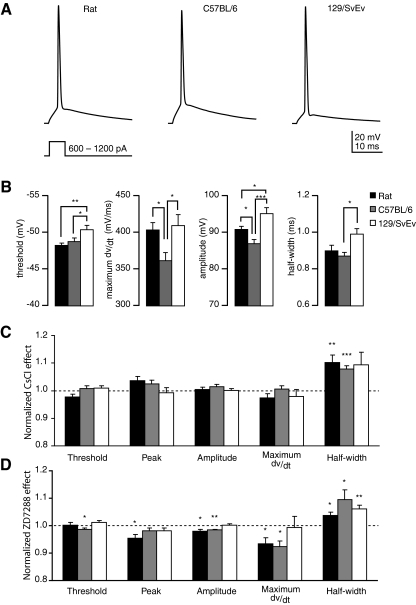
Because Ih is a prominent contributor to Vm, RN, and τ, we also measured these parameters in the presence of the Ih blockers ZD7288 or CsCl. The Ih blocker ZD7288 had similar effects on the passive properties for neurons of all groups. ZD7288 increased RN, increased τslow, and hyperpolarized Vm (Fig. 4, A–C), as would be expected after blocking Ih. CsCl likewise increased RN. However, in CsCl-treated cells, τslow increased only in rats, whereas in C57BL/6 it did not significantly change, and in 129/SvEv it decreased. Wash-in of CsCl also resulted in depolarization of Vm in all three groups of animals (Fig. 4D). For consistency, after drug wash-in, we held the cells at the Vm measured before drug application.
Fig. 4.
Effect of ZD7288 or CsCl on passive membrane properties of CA1 pyramidal neurons in rats and C57BL/6 and 129/SvEv mice. A and B: stimulus protocols used to measure the input resistance (A) and membrane time constant (B), and representative traces in normal artificial cerebrospinal fluid (aCSF) and after wash-in of 20 μM ZD7288. C and D: mean amount of change in input resistance, slow membrane time constant, and membrane potential after wash-in of 20 μM ZD7288 (C) or 5 mM CsCl (D), normalized to values obtained in normal aCSF. *P < 0.05, **P < 0.01, ***P < 0.001. ZD7288: n = 8 rats, 7 C57BL/6 mice, and 9 129/SvEv mice. CsCl: n = 20 rats, 16 C57BL/6 mice, and 14 129/SvEv mice.
Action potential properties
In addition to passive properties, we also measured certain active properties. Active properties of CA1 pyramidal neurons in control aCSF varied widely among the three groups of animals. The action potential amplitude measured in rats was consistent with previously reported values (Staff et al. 2000; Fig. 5B). Compared with rats, C57BL/6 had a hyperpolarized peak and decreased maximum dV/dt, resulting in an action potential of smaller amplitude (Fig. 5, A and B). In contrast, 129/SvEv neurons had a hyperpolarized threshold and an action potential of larger amplitude compared with that of rats. 129/SvEv neurons also had a larger half-width than that of neurons of C57BL/6 (Fig. 5B; ANOVA, Bonferroni-corrected; threshold: P = 0.003; max dV/dt: P = 0.014; amplitude: P < 0.0001; half-width: P = 0.035).
Fig. 5.
Active membrane properties of CA1 pyramidal neurons of rats and C57BL/6 and 129/SvEv mice. A: stimulus protocol and representative action potentials from each group showing threshold, peak, and amplitude differences. B: action potential threshold, maximum dV/dt, amplitude, and half-width in normal aCSF. C and D: amount of change in active properties after wash-in of 5 mM CsCl (C) or 20 μM ZD7288 (D), normalized to values obtained in normal aCSF. *P < 0.05, **P < 0.01, ***P < 0.001. CsCl: n = 20 rats, 16 C57BL/6 mice, and 14 129/SvEv mice. ZD7288: n = 8 rats, 7 C57BL/6 mice, and 9 129/SvEv mice.
The inclusion of compounds intended to block Ih affected active properties uniquely, depending on the compound used and animal group. CsCl increased action potential half-width in rats and C57BL/6, but not in 129/SvEv (Fig. 5C). ZD7288 decreased amplitude, decreased maximum dV/dt and increased half-width in rats and C57BL/6. It also increased threshold in rats and decreased peak amplitude in the C57BL/6 mice. The only measured effect of ZD7288 in 129/SvEv mice was an increase in the action potential half-width (Fig. 5D).
Membrane resonance
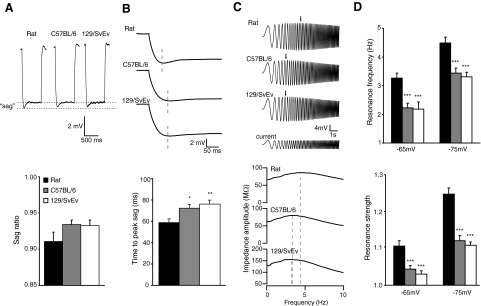
Ih blockers affected both the passive and active membrane properties of rat and mouse CA1 pyramidal neurons. Additional information on Ih in the different species was obtained by analyzing the voltage “sag,” which results from the membrane charging more rapidly than the activation or deactivation of Ih. The sag ratio and timing of the peak hyperpolarization can reveal differences in the amount of active Ih at rest. Sag ratios were not significantly different in the three groups of animals, although there appeared to be a trend with rats having more sag (Fig. 6A; ANOVA; P = 0.293). The time-to-peak of the sag, however, was significantly longer for both mouse groups than that for the rats (Fig. 6B; standard ANOVA, Bonferroni-corrected; P = 0.001), suggesting there may be some difference in Ih. In addition to voltage sag, Ih causes the membrane potential to resonate at a frequency that is directly related to the amount of active Ih (Hu et al. 2002; Hutcheon and Yarom 2000; Narayanan and Johnston 2007). To further explore possible differences in Ih between rats and mice, we measured the intrinsic resonance properties of the neurons in control aCSF using a “chirp” stimulus (Narayanan and Johnston 2008). Because Ih activation and membrane resonance are voltage-dependent, we measured resonance at two different potentials: −65 and −75 mV. At both of these membrane potentials, rats had significantly higher resonance frequencies and strengths than those of both strains of mice (Fig. 6, C and D; ANOVA, Bonferroni-corrected; frequency at −65 mV: P < 0.0001; frequency at −75 mV: P < 0.0001; strength at −65 mV: P < 0.0001; strength at −75 mV: P < 0.0001).
Fig. 6.
h resonance of CA1 pyramidal neurons of rats and C57BL/6 and 129/SvEv mice. A: membrane “sag” shown in voltage responses to hyperpolarizing current injections, and average sag ratios of neurons in control aCSF. B: same voltage responses in A, expanded to show time-to-peak hyperpolarization and average time-to-peak for each group. C: impedance amplitude profile stimulus protocol and representative traces and impedance amplitude profiles at Vm = −75 mV from neurons of each group. The peak impedance is indicated by the arrows (top) and dashed lines (bottom). D: mean resonance frequency and resonance strength measured in control aCSF while cells were held at −65 and −75 mV. *P < 0.05, **P < 0.01, ***P < 0.001, significantly different from the rat. n = 22 rats, 21 C57BL/6 mice, and 21 129/SvEv mice.
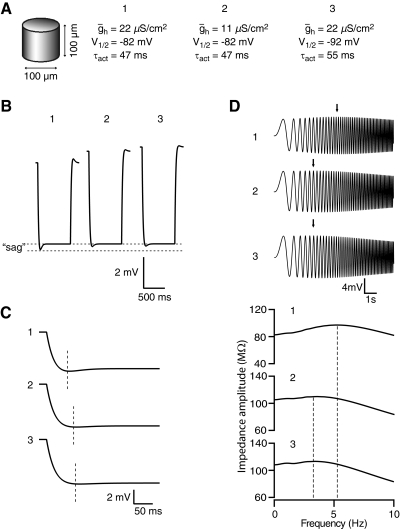
The observed lower resonance frequency in mice suggested that mice may have less active Ih near rest, relative to that of rats. This could be the result of either fewer total h channels or a difference in h channel kinetics, effectively reducing any h conductance (gh) available to influence resonance (Narayanan and Johnston 2007). To distinguish between these two possibilities, we simulated the effects of either reducing maximal h conductance (ḡh), or altering the biophysical properties of h channels (half activation voltage, V1/2; and activation time constant, τact) as might be expected if mice were to have a reduced HCN1:HCN2 ratio relative to rats (Chen et al. 2001; Ulens and Tytgat 2001). Using a single compartment model with Rm = 22 kΩ-cm2 (our measured value in rats), and experimentally determined properties of gh (V1/2 = −82 mV, and τact = 47 ms; Magee 1997), we were able to reproduce the sag ratio, time-to-peak, and resonance values observed in rats (Fig. 7, model 1) by setting ḡh to 22 μS/cm2. Lowering ḡh (Fig. 7, models 2), or changing V1/2 and τact (Fig. 7, model 3) were both able to reproduce reduced sag ratio, delayed time-to-peak, (Fig. 7, B and C), and lower resonance frequencies (Fig. 7D), similar to our observations in mice. Similar shifts in resonance frequency could also be obtained by altering V1/2 and τact in isolation (data not shown). Changing Rm to 26 kΩ-cm2 (our measured value in 129/SvEv) did not affect resonance or membrane voltage sag (data not shown).
Fig. 7.
Simulations of single-compartment neuron models with varying h-channel properties. A: representation of the cylindrical compartment used in the models. Rm was 22 kΩ-cm2 (taken from our rat τslow data) and h channels were modeled with 3 different sets of parameters: 1, using previously reported values for V1/2 and τact measured in rats, and ḡh required to obtain the experimental fR; 2, decreasing ḡh in half and keeping V1/2 and τact the same; 3, keeping ḡh the same but hyperpolarizing V1/2 and increasing τact. B: “sag” from a single hyperpolarization in each of the 3 models. C: same voltage responses as in B, expanded to show time to peak. D: “chirp” voltage response and impedance amplitude profiles of the 3 model cells in A. The peak impedance is indicated by the arrows (top) and dashed lines (bottom).
Simulations using passive membrane models
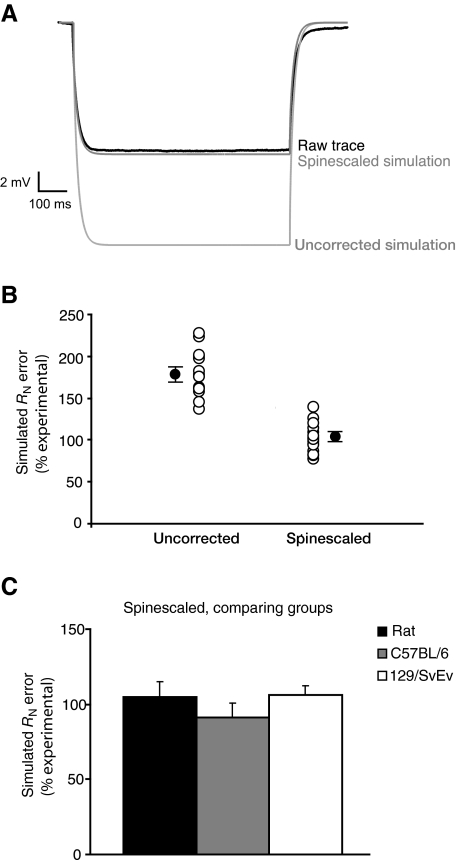
Because of the many differences reported here among rats and the two mouse strains, we used our morphological and physiological data to create models of mouse CA1 neurons for use in future studies done on C57 and 129 strains of mice. We used τslow measured in CsCl or ZD7288 to calculate Rm for each cell, and individual cell morphology was combined with its calculated Rm, to create a single-cell model in NEURON. When compared with the experimental data, models that did not account for spine surface area gave RN values approximately twofold larger than the actual experimental values (Fig. 8, A and B). To account for the surface area contributed by spines, an additional model was created for each neuron by dividing Rm and multiplying Cm in a region-dependent manner by the spinescale values shown in Table 2. These spinescales were calculated using our corrected spine densities, dendritic diameters, and previously reported spine surface area measurements (Harris and Stevens 1989). After applying the spinescale, RN closely fit the experimental values for all groups, despite significantly different passive membrane properties, cell morphologies, and spine densities across animal groups (Fig. 8, B and C; no difference across groups: standard ANOVA, P = 0.490).
Fig. 8.
Simulations from single-cell models incorporating passive physiological properties and morphologies of individual neurons and the species and strain-appropriate spinescale corrections for Cm and Rm. A: simulated voltage responses to a −100-pA current injection in a spinescaled and nonspinescaled model cell (gray), compared with the actual experimental voltage response (black). B: percentage error in input resistance of each model cell compared with the actual experimental values. Open circles = individual models. Closed circles = means ± SE. C: mean percentage error in modeled input resistances, separated by group.
Table 2.
Spinescale values for each segment
| Segment | Rat | C57BL/6 | 129/SvEv |
|---|---|---|---|
| S. oriens distal | 2.51 | 2.74 | 2.45 |
| S. radiatum thick/medial | 1.69 | 1.78 | 1.56 |
| S. radiatum thick/distal | 1.60 | 1.81 | 1.74 |
| S. radiatum thin | 1.86 | 2.69 | 2.04 |
| S. lacunosum-moleculare medium | 2.10 | 1.78 | 1.78 |
| S. lacunosum-moleculare thin | 1.71 | 1.66 | 1.53 |
DISCUSSION
In this study we compared the cellular morphologies and passive and active membrane properties of CA1 pyramidal neurons of rats, C57BL/6 mice, and 129/SvEv mice. Neurons from rats and C57BL/6 mice had similar structure, with few differences in dendritic morphology and membrane physiology. In contrast, we discovered several distinguishing anatomical and physiological characteristics of the 129/SvEv mouse strain. Moreover, based on measurements of membrane resonance and voltage sag, we report the amount of active Ih at rest to be a significant difference between rats and both mouse strains.
Similarities across species and strains
We observed surprising similarities in area CA1 between the two species. On the gross hippocampal level, the CA1 region appears to be very similar in rats and mice. Despite mice having smaller hippocampi, the distance from CA1 stratum pyramidale to the hippocampal fissure is conserved and total dendritic length of CA1 pyramidal neurons is comparable between the two species. This might imply the difference in hippocampal size may be the result of fewer neurons as opposed to similar numbers of smaller neurons. Alternatively, our observations suggest the CA1 pyramidal neurons appear to be more densely packed, so the number of neurons might be similar because of an increased density in mice relative to that of rats. At the single-neuron level, the membrane time constant was also conserved across animal groups. The membrane time constant is an important factor affecting the spread of voltage signals in these neurons (Rall 1977) and it provides an underlying similarity in the way that rats and mice may temporally process inputs.
Also surprising was how well our single-cell models—which incorporated a variety of morphological and physiological measurements—re-created experimental steady-state RN measurements across species. This attests to the accuracy of our physiological measures of τslow, our whole cell morphological measurements, and our spine density approximations. It also suggests that there was no factor affecting passive membrane properties uniquely in mice compared with rats that we did not account for in the models. Our mouse neuron models provide the first mouse CA1 pyramidal cell models to date.
Neurons from 129/SvEv mice are morphologically and electrophysiologically distinct from neurons from rats
Although the mouse strains exhibited both similarities and differences to the rat in various parameters, differences at the cellular level were more pronounced in the 129/SvEv strain than those in the C57BL/6 strain, which generally had characteristics intermediate to the rat and 129/SvEv. 129/SvEv mice had smaller neurons than those of rats, with less dendritic length, membrane surface area, and cell volume in stratum radiatum. In addition, they had thinner diameter dendrites and lower spine densities in regions lacunosum-moleculare/medium and radiatum/medial than rats, as well as a shorter average spine length than that of both rats and their C57BL/6 counterparts. The combination of these factors suggests that they had fewer spines and less surface area in these regions compared with those of rats. Consistent with these data and combined with the observation of a longer membrane time constant compared with that of both rats and C57BL/6, 129/SvEv had larger input resistances. In contrast to the 129/SvEv strain, the C57BL/6 strain exhibited fewer and more limited morphological distinctions. These included decreased dendritic length at the stratum radiatum/stratum lacunosum-moleculare border, decreased dendritic diameter in RTm, and decreased spine density in LMm. Physiological differences between rats and C57BL/6 included a hyperpolarized Vm and differences in active properties. These differences are suggestive of potentially important species- and strain-specific attributes of hippocampal connectivity.
The 129/SvEv mouse strain also exhibited a unique pharmacological response relative to that of the two other groups—neurons from the 129/SvEv animals displayed a decrease in τslow in CsCl. This is inconsistent with the expected increase that would occur if a resting conductance (i.e., Ih) is blocked. One possible explanation is a species/strain-specific difference in the affinity of the Na+ /K+ -ATPase for extracellular Cs+ . In addition to blocking h channels, Cs+ is also known to compete with K+ to be transported across the membrane via the Na+ /K+ -ATPase (Sachs 1977), block inwardly rectifying K+ channels (Fukushima 1982), reduce uptake of intracellular Ca2+ by SERCA pumps (Kargacin et al. 2005), and interfere with K+ buffering in glia (Janigro et al. 1997). Cs+ can also cause a depolarization of Vm (Fernandez et al. 2001; Ghamari-Langroudi and Bourque 2001). The 129/SvEv mice may be more sensitive to some of these effects relative to the two other groups. Additionally, whereas ZD7288 affected the action potential amplitude of rats and C57BL/6, the action potential amplitude of 129/SvEv mice remained unaffected.
It is interesting that we found significant differences between these two strains of mice. In contrast to these findings, one previous study reported that passive membrane properties were similar between C57 and 129 strains (Nguyen et al. 2000b). However, methodological differences, most notably blind versus visualized patching and recording at room temperature versus physiological temperature, may explain these discrepancies.
Mice of the 129 strain have been reported to have deficiencies in long-term potentiation (LTP) (Nguyen et al. 2000a) and have a mixed history with the Morris water maze. Some variants perform well on the maze (Brooks et al. 2005; Contet et al. 2001; Montkowski et al. 1997), whereas other variants perform poorly (Owen et al. 1997). In contrast, C57 strains have generally been reported to perform well in the Morris water maze (Montkowski et al. 1997; Stavnezer et al. 2002). The combined morphological and physiological differences observed in 129/SvEv CA1 pyramidal neurons could negatively affect neuronal information processing and the animal's performance in hippocampal-dependent learning tasks. Differences in dendritic surface area or branching could affect action potential propagation (Vetter et al. 2001) or firing patterns (Mainen and Sejnowski 1996) of these neurons, whereas morphological alterations at the level of the dendritic spine could influence the compartmentalization of Ca2+ signals (Majewska et al. 2000). Additionally, the differences in passive and active membrane properties could affect the charge transfer across the membrane and alter action potential output (Rall 1977).
We chose the C57 and 129 variants because they are widely used in studies of learning and memory in which genetic manipulations are used. Embryonic stem cells are most commonly derived from the 129/SvEv strain (Brook and Gardner 1997) for the generation of mutants resulting from homologous recombination (Thomas and Capecchi 1990). Because 129 strains have various behavioral deficits (Balogh et al. 1999), mutant lines created in this strain are typically crossbred with C57 animals. Our results suggest careful consideration is necessary when comparing the physiology between strains and across species.
Both mouse strains have less Ih active at rest than rats
The differences in anatomical and physiological properties observed among the groups do not appear to be species specific with one exception—membrane resonance. C57BL/6 and 129/SvEv had lower resonance frequencies and strengths than those of rats at both membrane potentials tested. The membrane potential resonance observed in CA1 pyramidal neurons occurs in the theta-frequency range (Leung and Yu 1998; Pike et al. 2000) and is critically dependent on the distribution and characteristics of ion channels expressed throughout the membrane, most notably, channels of the HCN family (Hu et al. 2002; Hutcheon and Yarom 2000). At membrane potentials near rest, the resonance frequency is dependent primarily on the interaction of Rm, Cm, and Ih (Narayanan and Johnston 2008). Because the three animal groups had a similar τslow, and Cm is similar for several neuron types (Chitwood et al. 1999; Gentet et al. 2000), and given the relationship τslow = RmCm, we propose that the differences in resonance frequency between rats and mice are due to differences in Ih. Because resonance frequency is directly related to the magnitude of Ih, the lower resonance frequencies observed in mice suggest they have less Ih than that of rats.
The magnitude of Ih is determined by its maximal conductance (ḡh), its voltage dependence of activation (V1/2), and its activation time constant (τact; Narayanan and Johnston 2008). The level of expression of h channels will determine ḡh, whereas the molecular identity of the channels will largely determine V1/2 and τact. We modeled both scenarios in our single-compartment simulations and found that either decreasing ḡh or shifting τact and V1/2 resulted in membrane voltage transients displaying sag and resonance similar to experimental observations from mice, consistent with the hypothesis that less Ih is active at the resting membrane potential in mice than that in rats.
Our results suggest that mice have either a lower ḡh or a different h-channel subunit composition. Although membrane resonance is useful for detecting local differences in Ih, steady-state RN provides the best indicator of ḡh because it more efficiently engages Ih distal to the recording site. Because the steady-state RN of rats and mice was increased to a similar degree in the presence of h-channel blockers, this suggests our observations were not due to a difference in ḡh. We propose that the differences in membrane resonance and sag are more likely due to h-channel subunit composition. In both rats and mice, pyramidal neurons in CA1 have h channels composed of HCN1 and HCN2 isoforms (Moosmang et al. 1999; Shin and Chetkovich 2007). Channels comprised of HCN2 activate at a more hyperpolarized Vm and are slower to activate relative to channels made up of HCN1 alone (Chen et al. 2001; Santoro et al. 2000; Ulens and Tytgat 2001). Heteromerization of the two subunits in CA1 pyramidal neurons is also possible (Much et al. 2003), resulting in channels having properties intermediate to the two (Ulens and Tytgat 2001; but see Chen et al. 2001). Mice would have less Ih active at rest than that of rats if they had a decreased HCN1:HCN2 ratio.
Finally, because neurons from the 129/SvEv group had larger RN and a slightly higher Rm, it was not clear whether the decrease in fR was attributable to Rm as opposed to altered Ih. Simulations revealed that there was little effect on fR caused by increasing Rm from 22 to 26 kΩ-cm2 (data not shown), suggesting that the lower fR in the 129/SvEv group, like the C57BL/6 group, was due to less active Ih.
Several studies show that mice do not perform as well as rats on the Morris water maze. Rats use complex spatial strategies to find the hidden platform in the maze (Frick et al. 2000; Lipp and Wolfer 1998), whereas mice use simpler, route-dominated techniques (Whishaw et al. 2001). On both the single-cell and hippocampal network levels, a decrease in Ih could hinder the spatial processing abilities of the mouse CA1. The density of Ih is distributed in a gradient across the apical tree of CA1 pyramidal neurons. Along the apical trunk in stratum radiatum, there is a sevenfold linear increase in current density relative to the soma (Magee 1998), increasing to 60-fold in distal stratum lacunosum-moleculare (Lorincz et al. 2002). Ih affects signal processing of CA1 pyramidal neurons in several ways. By attenuating distal signals (Golding et al. 2005) and normalizing temporal summation (Desjardins et al. 2003; Magee 1999), it removes the location dependence of inputs integrated at the soma. Additionally, it inhibits dendritic (Poolos et al. 2002) and cellular (Fan et al. 2005) excitability, decreases the amplitude and duration of distal Ca2+ spikes (Tsay et al. 2007), and constrains LTP at perforant path synapses (Nolan et al. 2004). The inhibitory effects of Ih on signal propagation may provide a way for the neuron to respond dynamically to a wide range of physiological inputs (Nolan et al. 2004). Ih also preferentially filters low-frequency inputs (Nolan et al. 2004; Poolos et al. 2002), conferring on CA1 pyramidal neurons high-pass filtering capabilities. In combination with the low-pass filtering caused by passive properties of the cell membrane, Ih helps tune individual CA1 neurons to frequencies in the theta range (Hu et al. 2002; Hutcheon and Yarom 2000). The somatodendritic gradient in Ih also mediates gradients in optimal tuning frequency (Narayanan and Johnston 2007) and intrinsic phase response along the somatoapical trunk (Narayanan and Johnston 2008). However, it should be noted that, because a majority of the studies identifying the properties and distribution of Ih have used rats (Desjardins et al. 2003; Fan et al. 2005; Golding et al. 2005; Hu et al. 2002; Hutcheon and Yarom 2000; Lorincz et al. 2002; Magee 1998, 1999; Narayanan and Johnston 2007; Poolos et al. 2002), whereas some of the functional aspects of dendritic Ih have relied on mice (Nolan et al. 2004; Tsay et al. 2007), extrapolation of these results across species and strains should be performed with caution.
There is also evidence that Ih may affect the overall expression of the hippocampal theta oscillation as well as theta-related phenomena in CA1 pyramidal neurons. Forebrain-specific HCN1 knockouts show enhanced theta power (Nolan et al. 2004). Interestingly, when compared with rats, mice also show enhanced theta power (Buzsáki et al. 2003). Ih may also play a role in the generation of phase precession in CA1, a phenomenon in which a neuron will fire progressively earlier in the theta cycle as an animal traverses space (O'Keefe and Recce 1993; Skaggs et al. 1996). Two rhythm generators oscillating at slightly different frequencies could cause such a phase shift (O'Keefe and Recce 1993), with the mechanism likely involving either a network or intrinsic oscillation or both (Maurer and McNaughton 2007). Because mouse pyramidal neurons resonate at lower frequencies than those of neurons in rats, phase precession could be altered in mice, possibly affecting their spatial memory processing.
Conclusions
The differences we found in CA1 pyramidal neurons across rodent species and strains may significantly influence hippocampal function, highlighting the necessity of considering animal type in the design and interpretation of experiments on CA1 pyramidal neurons. This study presents several anatomical and physiological distinctions that exist between a single rat strain and two strains of mice. There are likely to be many more differences that were not directly measured here, as well as differences in other strains of rats and mice. In light of our results, researchers should be cautious about overgeneralizing phenomena observed in a single species and strain.
GRANTS
This work was supported by the National Institutes of Health Grants MH-48432, MH-44754, and NS-37444 to D. Johnston.
ACKNOWLEDGMENTS
We thank M. Caffarelli and D. Moulik for help with slice processing and neuron reconstructions, Drs. Darrin Brager, Payne Chang, and Rishikesh Narayanan for helpful comments on a draft of this manuscript, and all members of the Johnston Laboratory for technical support with this project.
REFERENCES
- Balogh SA, McDowell CS, Stavnezer AJ, Denenberg VH. A behavioral and neuroanatomical assessment of an inbred substrain of 129 mice with behavioral comparisons to C57BL/6J mice. Brain Res 836: 38–48, 1999 [DOI] [PubMed] [Google Scholar]
- Biscoe TJ, Duchen MR. An intracellular study of dentate, CA1 and CA3 neurones in the mouse hippocampal slice. Q J Exp Physiol 70: 189–202, 1985 [DOI] [PubMed] [Google Scholar]
- Brook FA, Gardner RL. The origin and efficient derivation of embryonic stem cells in the mouse. Proc Natl Acad Sci USA 94: 5709–5712, 1997 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brooks SP, Pask T, Jones L, Dunnett SB. Behavioural profiles of inbred mouse strains used as transgenic backgrounds. II. Cognitive tests. Genes Brain Behav 4: 307–317, 2005 [DOI] [PubMed] [Google Scholar]
- Buzsáki G, Buhl DL, Harris KD, Csicsvari J, Czéh B, Morozov A. Hippocampal network patterns of activity in the mouse. Neuroscience 116: 201–211, 2003 [DOI] [PubMed] [Google Scholar]
- Chen S, Wang J, Siegelbaum SA. Properties of hyperpolarization-activated pacemaker current defined by coassembly of HCN1 and HCN2 subunits and basal modulation by cyclic nucleotide. J Gen Physiol 117: 491–504, 2001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen X, Yuan L-L, Zhao C, Birnbaum SG, Frick A, Jung WE, Schwarz TL, Sweatt JD, Johnston D. Deletion of Kv4.2 gene eliminates dendritic A-type K+ current and enhances induction of long-term potentiation in hippocampal CA1 pyramidal neurons. J Neurosci 26: 12143–12151, 2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chitwood RA, Hubbard A, Jaffe DB. Passive electrotonic properties of rat hippocampal CA3 interneurones. J Physiol 515: 743–756, 1999 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Contet C, Rawlins JNP, Bannerman DM. Faster is not surer: a comparison of C57BL/6J and 129S2/Sv mouse strains in the watermaze. Behav Brain Res 125: 261–267, 2001 [DOI] [PubMed] [Google Scholar]
- Desjardins AE, Li Y-X, Reinker S, Miura RM, Neuman RS. The influences of Ih on temporal summation in hippocampal CA1 pyramidal neurons: a modeling study. J Comput Neurosci 15: 131–142, 2003 [DOI] [PubMed] [Google Scholar]
- Fan Y, Fricker D, Brager DH, Chen X, Lu H-C, Chitwood RA, Johnston D. Activity-dependent decrease of excitability in rat hippocampal neurons through increases in Ih. Nat Neurosci 8: 1542–1551, 2005 [DOI] [PubMed] [Google Scholar]
- Feldman ML, Peters A. A technique for estimating total spine numbers on Golgi-impregnated dendrites. J Comp Neurol 188: 527–542, 1979 [DOI] [PubMed] [Google Scholar]
- Fernandez N, Andreasen M, Nedergaard S. Influence of the hyperpolarization-activated cation current, Ih, on the electrotonic properties of the distal apical dendrites of hippocampal CA1 pyramidal neurones. Brain Res 930: 42–52, 2001 [DOI] [PubMed] [Google Scholar]
- Frick KM, Stillner ET, Berger-Sweeney J. Mice are not little rats: species differences in a one-day water maze task. Learn Mem 11: 3461–3465, 2000 [DOI] [PubMed] [Google Scholar]
- Fukushima Y. Blocking kinetics of the anomalous potassium rectifier of tunicate egg studied by single channel recording. J Physiol 331: 311–331, 1982 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gentet LJ, Stuart GJ, Clements JD. Direct measurement of specific membrane capacitance in neurons. Biophys J 79: 314–320, 2000 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghamari-Langroudi M, Bourque CW. Ionic basis of the caesium-induced depolarization in rat supraoptic nucleus neurones. J Physiol 536: 797–808, 2001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Golding NL, Mickus TJ, Katz Y, Kath WL, Spruston N. Factors mediating powerful voltage attenuation along CA1 pyramidal neuron dendrites. J Physiol 568: 69–82, 2005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris KM, Stevens JK. Dendritic spines of CA1 pyramidal cells in the rat hippocampus: serial electrol microscopy with reference to their biophysical characteristics. J Neurosci 9: 2982–2997, 1989 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hines ML, Carnevale NT. The NEURON simulation environment. Neural Comput 9: 1179–1209, 1997 [DOI] [PubMed] [Google Scholar]
- Hu H, Vervaeke K, Storm JF. Two forms of electrical resonance at theta frequencies, generated by M-current, h-current, and persistent Na+ current in rat hippocampal pyramidal cells. J Physiol 545: 783–805, 2002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hutcheon B, Yarom Y. Resonance, oscillation and the intrinsic frequency preference of neurons. Trends Neurosci 23: 216–222, 2000 [DOI] [PubMed] [Google Scholar]
- Janigro D, Gasparini S, D'Ambrosio R, McKhann, Guy, DiFrancesco D. Reduction of K+ uptake in glia prevents long-term depression maintenance and causes epileptiform activity. J Neurosci 17: 2813–2824, 1997 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kalisch R, Schubert M, Jacob W, Kessler MS, Hemauer R, Wigger A, Landgraf R, Auer DP. Anxiety and hippocampus volume in the rat. Neuropsychopharmacology 31: 925–932, 2006 [DOI] [PubMed] [Google Scholar]
- Kargacin GJ, Aschar-Sobbi R, Kargacin ME. Inhibition of SERCA2 Ca2+-ATPases by Cs+ . Pflügers Arch 449: 356–363, 2005 [DOI] [PubMed] [Google Scholar]
- Kovacevic N, Henderson JT, Chan E, Lifshitz N, Bishop J, Evans AC, Henkelman RM, Chen XJ. A three dimensional MRI atlas of the mouse brain with estimates of the average and variability. Cereb Cortex 15: 639–645, 2005 [DOI] [PubMed] [Google Scholar]
- Leung LS, Yu H-W. Theta-frequency resonance in hippocampal CA1 neurons in vitro demonstrated by sinusoidal current injection. J Neurophysiol 79: 1592–1596, 1998 [DOI] [PubMed] [Google Scholar]
- Lipp HL, Wolfer DP. Genetically modified mice and cognition. Curr Opin Neurobiol 8: 272–280, 1998 [DOI] [PubMed] [Google Scholar]
- Logue SF, Paylor R, Wehner JM. Hippocampal lesions cause learning deficits in inbred mice in the Morris water maze and conditioned-fear task. Behav Neurosci 111: 104–113, 1997 [DOI] [PubMed] [Google Scholar]
- Lorincz A, Notomi T, Tamás G, Shigemoto R, Nusser Z. Polarized and compartment-dependent distribution of HCN1 in pyramidal cell dendrites. Nat Neurosci 5: 1185–1193, 2002 [DOI] [PubMed] [Google Scholar]
- Ma Y, Hof PR, Grant SC, Blackband SJ, Bennett R, Slatest L, McGuigan MD, Benveniste H. A three-dimensional digital atlas database of the adult C57BL/6 mouse brain by magnetic resonance microscopy. Neuroscience 135: 1203–1215, 2005 [DOI] [PubMed] [Google Scholar]
- Magee JC. Dendritic hyperpolarization-activated currents modify the integrative properties of hippocampal CA1 pyramidal neurons. J Neurosci 18: 7613–7624, 1998 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Magee JC. Dendritic Ih normalizes temporal summation in hippocampal CA1 neurons. Nat Neurosci 2: 508–514, 1999 [DOI] [PubMed] [Google Scholar]
- Mainen ZF, Sejnowski TJ. Influence of dendritic structure on firing pattern in model neocortical neurons. Nature 382: 363–366, 1996 [DOI] [PubMed] [Google Scholar]
- Majewska A, Tashiro A, Yuste R. Regulation of spine calcium dynamics by rapid spine motility. J Neurosci 20: 8262–8268, 2000 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maurer AP, McNaughton BL. Network and intrinsic cellular mechanisms underlying theta phase precession of hippocampal neurons. Trends Neurosci 30: 325–333, 2007 [DOI] [PubMed] [Google Scholar]
- McDermott CM, LaHoste GJ, Chen C, Musto A, Bazan NG, Magee JC. Sleep deprivation causes behavioral, synaptic, and membrane excitability alterations in hippocampal neurons. J Neurosci 23: 9687–9695, 2003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Megías M, Emri Z, Freund TF, Gulyás AI. Total number and distribution of inhibitory and excitatory synapses on hippocampal CA1 pyramidal cells. Neuroscience 102: 527–540, 2001 [DOI] [PubMed] [Google Scholar]
- Montkowski A, Poettig M, Mederer A, Holsboer F. Behavioral performance in three substrains of mouse strain 129. Brain Res 762: 12–18, 1997 [DOI] [PubMed] [Google Scholar]
- Moosmang S, Biel M, Hofmann F, Ludwig A. Differential distribution of four hyperpolarization-activated cation channels in mouse brain. Biol Chem 380: 975–980, 1999 [DOI] [PubMed] [Google Scholar]
- Morris R. Developments of a water-maze procedure for studying spatial learning in the rat. J Neurosci Methods 11: 47–60, 1984 [DOI] [PubMed] [Google Scholar]
- Morris RGM, Davis S, Butcher SP. Hippocampal synaptic plasticity and NMDA receptors: a role in information storage? Philos Trans R Soc Lond B Biol Sci 329: 187–204, 1990 [DOI] [PubMed] [Google Scholar]
- Morris RGM, Garrud P, Rawlins JNP, O'Keefe J. Place navigation impaired in rats with hippocampal lesions. Nature 297: 681–683, 1982 [DOI] [PubMed] [Google Scholar]
- Much B, Wahl-Scott C, Zong X, Schneider A, Baumann L, Moosmang S, Ludwig A, Biel M. Role of subunit heteromerization and N-linked glycosylation in the formation of the functional hyperpolarization-activated cyclic nucleotide-gated channels. J Biol Chem 278: 43781–43786, 2003 [DOI] [PubMed] [Google Scholar]
- Narayanan R, Johnston D. Long-term potentiation in rat hippocampal neurons is accompanied by spatially widespread changes in intrinsic oscillatory dynamics and excitability. Neuron 56: 1061–1075, 2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Narayanan R, Johnston D. The h channel mediates location dependence and plasticity of intrinsic phase response in rat hippocampal neurons. J Neurosci 28: 5846–5860, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nguyen PV, Abel T, Kandel ER, Bourtchouladze R. Strain-dependent differences in LTP and hippocampus-dependent memory in inbred mice. Learn Mem 7: 170–179, 2000a [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nguyen PV, Duffy SN, Young JZ. Differential maintenance and frequency-dependent tuning of LTP at hippocampal synapses of specific strains of inbred mice. J Neurophysiol 84: 2484–2493, 2000b [DOI] [PubMed] [Google Scholar]
- Nolan MF, Malleret G, Dudman JT, Buhl DL, Santoro B, Gibbs E, Vronskaya S, Buzsáki G, Siegelbaum SA, Kandel ER, Morozov A. A behavioral role for dendritic integration: HCN1 channels constrain spatial memory and plasticity at inputs to distal dendrites of CA1 pyramidal neurons. Cell 119: 719–732, 2004 [DOI] [PubMed] [Google Scholar]
- O'Keefe J, Recce ML. Phase relationship between hippocampal place units and the EEG theta rhythm. Hippocampus 3: 317–330, 1993 [DOI] [PubMed] [Google Scholar]
- Owen EH, Logue SF, Rasmussen DL, Wehner JM. Assessment of learning by the Morris water task and fear conditioning in inbred mouse strains and F1 hybrids: implications of genetic background for single gene mutations and quantitative trait loci analyses. Neuroscience 80: 1087–1099, 1997 [DOI] [PubMed] [Google Scholar]
- Picciotto MR, Wickman K. Using knockout and transgenic mice to study neurophysiology and behavior. Physiol Rev 78: 1131–1163, 1988 [DOI] [PubMed] [Google Scholar]
- Pike FG, Goddard RS, Suckling JM, Ganter P, Kasthuri N, Paulsen O. Distinct frequency preferences of different types of rat hippocampal neurones in response to oscillatory input currents. J Physiol 529: 205–213, 2000 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poirazi P, Brannon T, Mel BW. Arithmetic of subthreshold synaptic summation in a model CA1 pyramidal cell. Neuron 37: 977–987, 2003 [DOI] [PubMed] [Google Scholar]
- Poolos NP, Migliore M, Johnston D. Pharmacological upregulation of h-channels reduces the excitability of pyramidal neuron dendrites. Nat Neurosci 5: 767–774, 2002 [DOI] [PubMed] [Google Scholar]
- Puil E, Gimbarzevsky B, Miura RM. Quantification of membrane properties of trigeminal root ganglion neurons in guinea pigs. J Neurophysiol 55: 995–1016, 1986 [DOI] [PubMed] [Google Scholar]
- Rall W. Core conductor theory and cable properties of neurons. In: Handbook of Physiology. The Nervous System. Cellular Biology of Neurons Bethesda, MD: Am. Physiol. Soc, 1977, sect. 1, vol. I, pt. 1, p. 39–97 [Google Scholar]
- Sachs JR. Kinetic evaluation of the Na-K pump reaction mechanism. J Physiol 273: 489–514, 1977 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sahin B, Aslan H, Unal B, Canan S, Bilgic S, Kaplan S, Tumkaya L. Brain volumes of the lamb, rat, and bird do not show hemispheric asymmetry: a stereological study. Image Anal Stereol 20: 9–13, 2001 [Google Scholar]
- Santoro B, Chen S, Lüthi A, Pavlidis P, Shumyatsky GP, Tibbs GR, Siegelbaum SA. Molecular and functional heterogeneity of hyperpolarization-activated pacemaker channels in the mouse CNS. J Neurosci 20: 5264–5275, 2000 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shin M, Chetkovich DM. Activity-dependent regulation of h channel distribution in hippocampal CA1 pyramidal neurons. J Biol Chem 282: 33168–33180, 2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sholl DA. Dendritic organization in the neurons of the visual and motor cortices of the cat. J Anat 87: 387–406, 1953 [PMC free article] [PubMed] [Google Scholar]
- Skaggs WE, McNaughton BL, Wilson MA, Barnes CA. Theta phase precession in hippocampal neuronal populations and the compression of temporal sequences. Hippocampus 6: 149–172, 1996 [DOI] [PubMed] [Google Scholar]
- Staff NP, Jung H-Y, Thiagarajan T, Yao M, Spruston N. Resting and active properties of pyramidal neurons in subiculum and CA1 of rat hippocampus. J Neurophysiol 84: 2398–2408, 2000 [DOI] [PubMed] [Google Scholar]
- Stavnezer AJ, Hyde LA, Bimonte HA, Armstrong CM, Denenberg VH. Differential learning strategies in spatial and nonspatial versions of the Morris water maze in the C57BL/6J inbred mouse strain. Behav Brain Res 133: 261–270, 2002 [DOI] [PubMed] [Google Scholar]
- Stuart G, Spruston N. Determinants of voltage attenuation in neocortical pyramidal neuron dendrites. J Neurosci 18: 3501–3510, 1998 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stuart GJ, Dodt HU, Sakmann B. Patch-clamp recordings from the soma and dendrites of neurons in brain slices using infrared video microscopy. Pflügers Arch 423: 511–518, 1993 [DOI] [PubMed] [Google Scholar]
- Sutherland RJ, Kolb B, Whishaw IQ. Spatial mapping: definitive disruption by hippocampal or medial frontal cortical damage in the rat. Neurosci Lett 31: 271–276, 1982 [DOI] [PubMed] [Google Scholar]
- Thomas KR, Capecchi MR. Targeted disruption of the murine int-1 protooncogene resulting in severe abnormalities in midbrain and cerebellar development. Nature 346: 847–850, 1990 [DOI] [PubMed] [Google Scholar]
- Tsay D, Dudman JT, Siegelbaum SA. HCN1 channels constrain synaptically evoked Ca2+ spikes in distal dendrites of CA1 pyramidal neurons. Neuron 56: 1076–1089, 2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ulens C, Tytgat J. Functional heteromerization of HCN1 and HCN2 pacemaker channels. J Biol Chem 276: 6069–6072, 2001 [DOI] [PubMed] [Google Scholar]
- Vetter P, Roth A, Häusser M. Propagation of action potentials in dendrites depends on dendritic morphology. J Neurophysiol 85: 926–937, 2001 [DOI] [PubMed] [Google Scholar]
- Whishaw IQ. A comparison of rats and mice in a swimming pool place task and matching to place task: some surprising differences. Physiol Behav 58: 687–693, 1995 [DOI] [PubMed] [Google Scholar]
- Whishaw IQ, Metz GAS, Kolb B, Pellis SM. Accelerated nervous system development contributes to behavioral efficiency in the laboratory mouse: a behavioral review and theoretical proposal. Dev Psychobiol 39: 151–170, 2001 [DOI] [PubMed] [Google Scholar]
- Whishaw IQ, Tomie JA. Of mice and mazes: similarities between mice and rats on dry land but not water mazes. Physiol Behav 60: 1191–1197, 1996 [DOI] [PubMed] [Google Scholar]
- Witter MP, Amaral DG. Hippocampal formation. In: The Rat Nervous System ( 3rd ed.), edited by Paxinos G.San Diego, CA: Elsevier Academic Press, 2004, p. 635–704 [Google Scholar]
- Zeng H, Chattarji S, Barbarosie M, Rondi-Reig L, Philpot BD, Miyakawa T, Bear MF, Tonegawa S. Forebrain-specific calcineurin knockout selectively impairs bidirectional synaptic plasticity and working/episodic-like memory. Cell 107: 617–629, 2001 [DOI] [PubMed] [Google Scholar]