Whole-Motion Model of Perception during Forward- and Backward-Facing Centrifuge Runs

Abstract

Illusory perceptions of motion and orientation arise during human centrifuge runs without vision. Asymmetries have been found between acceleration and deceleration, and between forward-facing and backward-facing runs. Perceived roll tilt has been studied extensively during upright fixed-carriage centrifuge runs, and other components have been studied to a lesser extent.

Certain, but not all, perceptual asymmetries in acceleration-vs-deceleration and forward-vs-backward motion can be explained by existing analyses. The immediate acceleration-deceleration roll-tilt asymmetry can be explained by the three-dimensional physics of the external stimulus; in addition, longer-term data has been modeled in a standard way using physiological time constants. However, the standard modeling approach is shown in the present research to predict forward-vs-backward-facing symmetry in perceived roll tilt, contradicting experimental data, and to predict perceived sideways motion, rather than forward or backward motion, around a curve.

The present work develops a different whole-motion-based model taking into account the three-dimensional form of perceived motion and orientation. This model predicts perceived forward or backward motion around a curve, and predicts additional asymmetries such as the forward-backward difference in roll tilt. This model is based upon many of the same principles as the standard model, but includes an additional concept of familiarity of motions as a whole.

1. Introduction

Rotation in a centrifuge gives a window into perception and misperception of self-motion during complex linear and angular accelerations. In a fixed-carriage centrifuge run, the subject is in a fixed orientation—for example, facing forward in the direction of motion—at the end of the centrifuge arm while the centrifuge accelerates, and then later decelerates. Without vision, subjective reports of self-motion during the acceleration, and especially during the deceleration, are not typically veridical [8, 9, 10, 15, 16, 21, 22, 45, 53]. To explain these non-veridical subjective reports, models have been developed that formally implement principles of self-motion perception, matching experimental data [6, 15, 16, 36, 37, 40, 44, 52, 60]. Certain components of the perceived self-motion, especially roll tilt, can thus be explained by the models, but other aspects are still not explained.

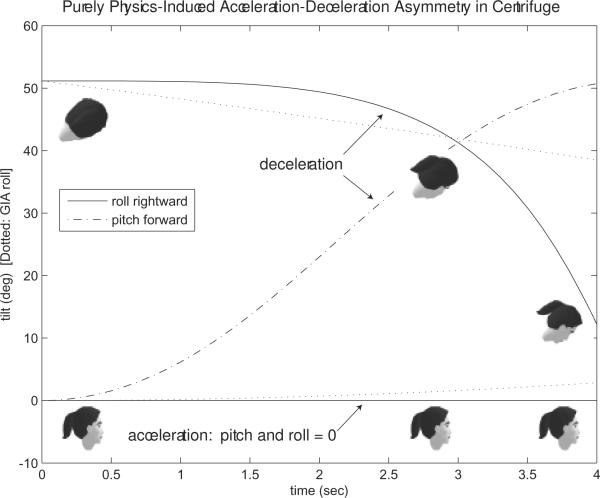
A well-studied component of perceived self-motion is roll tilt. During centrifuge acceleration with the subject facing forward in the direction of motion, the roll angle---as measured from straight upward---of the gravito-inertial acceleration (GIA) changes, eventually pointing diagonally upward and inward toward the centrifuge axis (Fig. 1); the GIA is the sum of the centripetal acceleration inward and the “pseudo-acceleration” upward due to the presence of gravity, indistinguishable by physical laws from an actual acceleration (a fact that in neuroscience is often referred to as Einstein's Principle of Equivalence). Later, during deceleration, the roll angle of the GIA decreases, reaching zero again when the centrifuge stops. Subjects in a centrifuge typically perceive a change in their own roll orientation, with perceived roll angle similar to the GIA angle, as though the GIA is interpreted as the direction of upward. However, the perceived roll angle lags behind the GIA angle during centrifuge acceleration, but not as much during centrifuge deceleration whether indicated by a visual measure [16, 21, 22, 45] or a somatosensory measure [9, 10, 45]. This acceleration-deceleration asymmetry can be explained in the short term (in the first few seconds of the acceleration or deceleration) by a model of the three-dimensional consequences of the stimulus itself [26] (Fig. 2) without appealing to special longer-term properties of the physiological system, or by models that include physiological properties [6, 15, 16, 36, 40, 44, 52, 60]. The latter models can also predict ongoing perception of roll tilt whose time course is consistent with experimental data.

Figure 1.

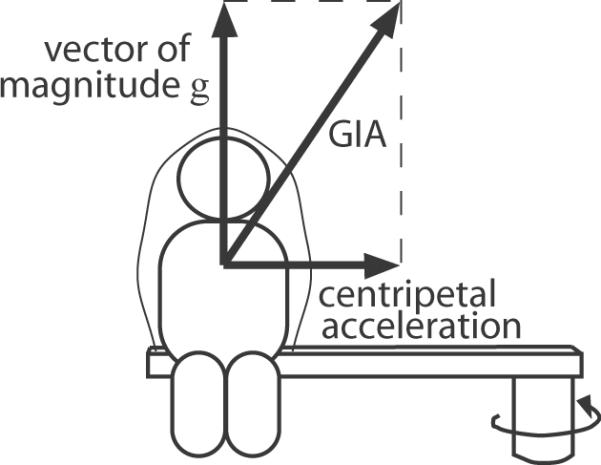
The roll tilt of the gravito-inertial acceleration (GIA) vector during rotation of a subject in a fixed-carriage centrifuge. The GIA is the sum of the centripetal acceleration and an Earth-upward vector of magnitude g (equaling that of the gravitational acceleration), as explained in the text.

Figure 2.

Laws-of-physics-only predicted perceived roll and pitch tilt during first 4 s of counterclockwise-rotating 1-m radius centrifuge acceleration and deceleration at 10°/s²; initial velocity before deceleration is 200°/s², so a deceleration to stop would take 20 s. Both roll and pitch tilt exhibit an acceleration-deceleration asymmetry. Because the centrifuge deceleration begins with a perceived head orientation of roll tilt (to match the GIA), the clockwise angular acceleration from centrifuge deceleration causes the head's perceived orientation to rotate clockwise in yaw, into a pitch-down and less-roll orientation. Head orientations relative to vertical are shown next to the curves. Roll tilt of the GIA is shown by the dotted lines.

Not explained, however, by these models are differences in roll perception during forward-facing versus backward-facing runs. In addition, the three-dimensional shape of predicted perceived motion has not been displayed. During centrifuge acceleration, backward-facing experimental subjects have been found to report faster roll tilt change than do forward-facing subjects, whether indicated by a visual measure [45] or a somatosensory measure [9,10] (though in [45], no difference was found with a somatosensory measure). The existing models do not exhibit this forward-backward difference in roll, although it has been possible to model forward-backward differences in horizontal eye movements by considering additivity of angular and linear stimuli [40, 44, 60] and a gaze-centering mechanism [51, 55]. Another suggested explanation for forward-backward differences is the orientation of the vestibular system in the head [17], although this theory is still open to investigation.

1.1. The Role of Familiarity

Throughout the study of perception, principles of familiarity and meaning have been demonstrated in various contexts (reviewed in [5]). Gestalt psychologists incorporated the ideas of familiarity and meaningfulness in their laws (e.g. [12], reviewed in [20]). Most relevantly, familiar movements are more readily perceived than unfamiliar movements: In one example, subjects were visually presented two drawings in quick succession [11]. If the two drawings were of a man “saluting”, i.e. an arm in two positions, then subjects typically reported movement of the arm. However, if the two drawings were of line segments, then subjects were less likely to report movement [11]. Knowledge of and familiarity with stimuli allow one to perceive motion more quickly, proficiently, and comprehensively than one otherwise would with a novel stimulus (reviewed in [33]).

The concept of familiarity also underlies the scientific understanding of self-motion perception. First, the three-dimensional laws of physics are familiar—in the sense of everyday experience with the three-dimensional relationships between linear and angular accelerations, velocities, position and orientation—and certain perceptual phenomena can be explained simply by the consequences of the nervous system's likely understanding of these laws of physics. For example, these basic laws give an acceleration-deceleration difference in perceived roll in a centrifuge [26]. In particular, because the deceleration begins with perceived non-zero roll tilt, the angular acceleration imposed by the centrifuge deceleration causes a change in perceived roll orientation, even by a perfect processor of acceleration information (Fig. 2). Other perceptual phenomena, as well, can be explained by the stimulus itself, i.e. the external physics, including perceived tumbling in a centrifuge whose carriage swings out [27], and differences in perceptual disturbances during vestibular coriolis cross-coupling, depending on the axis of rotation [28, 30], tilt axis [29], gravitational environment [28, 29,30], acceleration or deceleration of rotation [29], and direction of head movement [28, 30].

Beyond the laws of physics, specific components of perceived motion have well-known properties wherein perceived motion and orientation move toward “likely” values. The idea that components of perception move toward likely values has been formalized using a Bayesian approach [36] in which probability distributions called “priors” essentially consider perception as favoring familiar states. The general idea of perception moving toward likely values underlies other models as well. Three examples: (1) upon lack of angular acceleration, perception moves toward “not rotating”, (2) upon lack of linear acceleration, perception moves toward “not translating”, and (3) upon sustained linear acceleration, perception moves toward an orientation such that the GIA is vertical because in everyday experience a constant GIA is usually that from gravity. These principles are widely recognized in research on self-motion perception (reviewed in [23]), and have been implemented in three-dimensional models for human centrifuge runs [6, 15, 16, 36, 40, 44, 52, 60]. The core of these models consists of the basic physics along with the components' tendencies as described above, whether implemented by Kalman filters, transfer functions, Bayesian modeling, or differential equations with time constants. This core can be called the “Standard Model”, representing the main themes of current scientific understanding of self-motion perception.

During complex motion, however, “likely” motions might not simply be combinations of likely values of the individual components. In perceived self-motion induced by optic flow, subjects have been found to report perceived motions that are simpler overall than the presented motion, despite the fact that the individual components are already simple [3]. For example, optic flow indicating simultaneous simple components of 180° yaw rotation and straight linear motion was instead perceived in a way that simplified the motion as a whole: the perceived path was curved with perceived orientation remaining approximately fixed relative to the path. In addition, yaw rotation and horizontal translation tend to be linked in optically-induced perception, and subjects' perceptions are most accurate when the orientation while traveling along a curvilinear path is fixed tangentially [2].

1.2. Explaining Subjective Perception

To understand complex self-motion perception, it may be necessary to consider familiarity in a more whole-motion manner than that tied to individual components of motion. The goal of the present research was to compare the standard type of three-dimensional model that uses component-wise tendencies with a three-dimensional model motivated by the concept of whole-motion familiarity. In the process, the research investigated to what extent experimental data on centrifuge runs could be explained by (1) the physics consequences of the stimulus itself, by (2) the standard component-tendencies approach, by (3) a component-tendencies approach with different time constants for forward and backward motion, or instead by (4) a small number of whole-motion principles. The principles implemented in the whole-motion model were motivated by the concept of familiarity, and were taken to be as minimal as possible. The principles were that (i) the interpretation of the GIA takes into account centripetal acceleration whenever the perceived path is curvilinear, (ii) acceleration that is initially forward or backward leads to forward or backward translation without sideways slippage in the absence of sudden substantial sideways acceleration, (iii) forward motion tends to be sustained for longer than backward motion, and (iv) vertical translation is not perceived, or is perceived only transiently. All of these principles are based upon everyday experience, including in vehicles. Because of their simplicity, experimental data are not available for most of them, and they may vary between individuals. However, the GIA principle, (i), is a specialized form of a well-known hypothesis about the gravito-inertial force (GIF, the “force”-phrased version of the “acceleration”-phrased GIA): the GIF-resolution hypothesis states that the GIF is resolved by the nervous system into the sum of the gravity-associated and the translation-associated forces, a hypothesis that has been supported by experimental and modeling research [1, 6, 26, 40, 41, 43, 46]. Because much of this research has been on eye movements or central neuron responses, the GIF-resolution hypothesis could use more testing with respect to perception itself.

The focus here is on qualitative results: Can either the Standard Model or the Whole-Motion Model predict the roll-tilt difference between forward- and backward-facing runs? Does either or both models predict the roll-tilt difference between acceleration and deceleration? What three-dimensional shape of perceived motion does each model predict? Quantitative results were used to ensure that values fell within the ranges that had been found experimentally.

2. Methods

Two different models were compared for perception of self-motion during fixed-carriage centrifugation without an external visual reference. The inputs to the models were angular and linear acceleration. In subjects, these accelerations may be detected by a combination of senses such as vestibular and somatosensory, and the models implicitly include all such detection of acceleration of the body as a whole. Both models were run for a forward-facing and a backward-facing subject, each for both the centrifuge acceleration and the centrifuge deceleration.

2.1. Experimental Data

Published experimental data were used for testing the models. For centrifuge runs in which the GIA tilted 45° [9, 45] or 51.2° [10], perceived roll tilt showed a faster change during backward-facing acceleration than during forward-facing acceleration. For centrifuge runs in which the GIA tilted 10° [22], 13.8° [21], 20° [22], 30° [16, 22], 34.3° [21], 40° [16], 45° [9, 45] or 51.2° [10], perceived roll tilt showed a faster change during deceleration than during acceleration.

Forward-facing versus backward-facing acceleration: At the end of the acceleration stage, the average perceived roll angle when forward-facing was between 55% and 95% of the value when backward-facing, and was between 30% and 70% of the GIA angle; the average roll angle when backward-facing was between 45% and 100% of the GIA angle, depending upon the experiment. More specifically, for acceleration at 10°/s² to 200°/s at 1 m radius (giving GIA roll of 51.2°), average roll tilt reported using a visual measure when forward-facing was approximately 55% of that when backward-facing, and the average time constant of decay for roll when backward-facing was 72% of that when forward-facing (27.0 s vs. 37.4 s to reach 90% of the final value); when reported using a somatosensory measure, average roll tilt at the end of acceleration when forward-facing was approximately 60% of that when backward-facing [10]. For acceleration at 25°/s² to 250°/s at 0.54 m radius (giving GIA roll of 45°), average roll tilt reported using a visual measure when forward-facing was approximately 65% of that when backward-facing, and the average time constant of decay for roll when backward-facing was 56% of that when forward-facing (14.6 s vs. 28.1 s when clockwise and 16.4 s vs. 27.5 s when counterclockwise); when reported using a somatosensory measure, average roll tilt at the end of acceleration when forward-facing was not statistically significantly less than that when backward-facing, and the difference in time constants was not statistically significant [45]. For acceleration at 26°/s² to 254°/s at 0.5 m radius (giving GIA roll of 45°), average roll tilt reported using a somatosensory measure when forward-facing was approximately 80% of that when backward-facing, and the average time constant of decay for roll when backward-facing was 65% of that when forward-facing (24.6 s vs. 37.7 s to reach 95% of the maximal value) [9].

Deceleration versus acceleration: For the deceleration stage of the centrifuge run, experimental results showed a faster change in perceived roll tilt than during the acceleration stage regardless of the centrifuge parameters, using centrifuge radii of 0.5m [9], 0.54 m [45], 1 m [10], 1.9 m [22], 6.1 m [21] and 10 m [16]. The perceived roll had time course and magnitude similar to that of the GIA roll, though the potential for reporting lag has precluded exact measurements of timing for this fast change. Therefore, the relevant result is that perceived roll changes faster during deceleration than during acceleration.

2.2. Standard Model

The Standard Model implements well-known tendencies of perception by means of time constants superimposed upon the laws of physics (Fig. 3A), mirroring existing models [18, 29, 60, and related ones]. Most three-dimensional models of self-motion perception effectively have this core, which also accomplishes frequency segregation as a side effect of the time constants: high-frequency acceleration is interpreted more as translation while low-frequency acceleration is interpreted more as tilt. Here, the Standard Model extends most existing models by including output of position and orientation, including heading. The values of position and orientation are computed as the natural consequences of the computed linear and angular velocity (which are the more common outputs of such models). It is worth mentioning, however, that there are models with additional notable elements that are omitted in this Standard Model. One example is additional explicit frequency segregation [4, 25], and another example is otolith-mediated detection of rotation [35]. Neither of these elements would have significant effects, however, during centrifuge acceleration and deceleration, nor would they affect the general behavior of the model's output for the present conditions.

Figure 3.

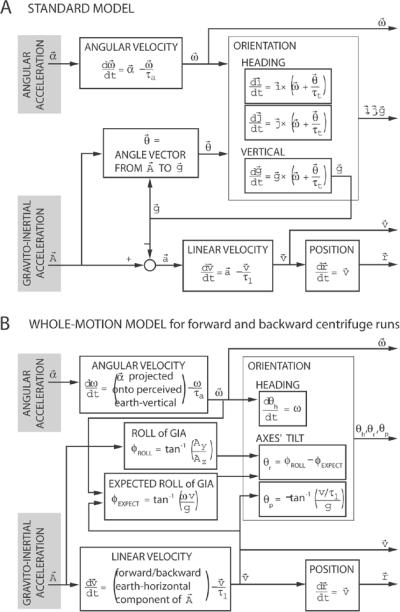
Model comparison. (A) Standard Model, consisting of the core of many models in the literature. Change in perceived angular velocity is given by angular acceleration and decays with time constant τ_a. Change in perceived linear velocity is given by perceived linear acceleration, as derived by subtracting the perceived gravity vector from the GIA, and decays with time constant τ_l. Change in perceived position is given by perceived linear velocity. For perceived orientation, vectors $\overrightarrow{g}$, $\overrightarrow{i}$, and $\overrightarrow{j}$ are earth-fixed vectors given in head coordinates, indicating upward and any perpendicular pair of headings such as “north” and “west”, respectively. Change in perceived orientation is given by perceived angular velocity but with an additional factor: $\overrightarrow{\theta }$ gives direction angle, according to the right-hand rule, used in simulating the tendency for perceived vertical to move toward the GIA direction, with time constant τ_t. Arrows indicate which variables are used in which equations. (B) Whole-Motion Model motivated by the concept of familiarity during forward and backward motion. Perceived angular velocity is about the perceived earth-vertical axis, and heading is based upon angular velocity. Perceived roll angle θ_r of the subject's y-axis (interaural axis) from earth-horizontal, and pitch angle θ_p of the subject's x-axis (naso-occipital axis) from earth-horizontal, are those that match the GIA: θ_r matches the unexpected portion of the GIA roll, given the perceived centripetal acceleration, and θ_p is based upon the portion of the GIA not used toward linear velocity because of the linear time constant. Here, GIA roll and θ_r are positive when GIA tilts toward the centrifuge axis and perceived roll is outward from the centrifuge axis, respectively, while GIA pitch and θ_p are positive when tilted toward the direction of motion. Linear velocity is forward or backward depending on whether the initial change in GIA is forward or backward, and the value of the linear time constant depends on whether the motion is forward or backward, as explained in the text. Magnitude of angular velocity, linear velocity, and gravitational acceleration are given by ω, v, and g, respectively. Subscripts on A indicate head-leftward (y) or head-upward (z) components of the GIA.

For perceived angular velocity, a time constant of 20 s was used. Experimental measures of the angular time constant can vary [24, 57], and depend upon centrifugal force [47, 48]. Fortunately, the current research was not sensitive to the angular time constant, so a value of 20 s was chosen, being a typical choice and within the range found experimentally. For perceived linear motion, time constants of 10 s for forward motion and 3 s for backward motion were chosen to match those in the Whole-Motion Model as described below. A linear time constant of this order of magnitude was also used by Bos et al. [7]. For tilt, the time constant was determined as explained under Results and in the next paragraph, giving 0.4 s as the necessary value to reasonably fit experimental data. Once the tilt time constant was determined, tests for robustness were performed by runs with angular time constant 15 s, 20 s and 25 s.

It is worth noting that previous similar modeling of roll tilt in a centrifuge [36, 44, 52, 60] focused on the general pattern and did not extract and report a tilt time constant. Historically, before the role of the angular stimulus had been recognized, the time constant was considered to be on the order of 5 s. However, variable-radius centrifugation has now indicated a tilt time constant less than 1/3 previously thought [53] based upon studies of perceived time-to-peak in variable-radius versus fixed-radius centrifuge, while an analysis of pure linear oscillation derived a value of 2.8 s [6]. The present modeling tests have shown that an even smaller value is required to give results in the experimentally observed ranges for fixed-carriage centrifugation, which includes rotation. Because the goal was to test the Standard Model's ability to fit the data, the tilt time constant was tuned for fixed-carriage centrifugation here. Even though the resulting value of 0.4 s seems short relative to the time course of the acceleration and deceleration, it is competing with linear-angular interaction, and this balance leads to an appropriate predicted time course of perceived roll tilt.

2.3. Whole-Motion Model

The Whole-Motion Model also has a laws-of-physics foundation, but with different rules from the Standard Model for implementing the tendencies of perception. (Note that the Standard Model is also for “whole motion” but tendencies of components are implemented differently.) The development of the Whole-Motion Model is based upon the overall shape of motion in three dimensions (Fig. 3B). It takes into account what could be considered expectations from everyday experience with components such as forward/backward motion and centripetal acceleration.

The detected linear acceleration forward or backward, depending on whether the subject is forward- or backward-facing and whether the centrifuge is accelerating or decelerating, is interpreted as a change in forward or backward velocity (i.e. by the laws of physics), mitigated by a time constant of decay of linear velocity perception. This time constant is implemented in the same way as in the Standard Model. For present purposes of modeling the greater familiarity of forward motion, the time constants were taken to be 10 s for forward translation and 3 s for backward translation. The difference in value is motivated by the concept of familiarity, and the values chosen were based upon testing the model in comparison with existing published data on roll tilt, but are naturally available for additional tuning to future experimental data. Additional tests were performed with other combinations of values of these time constants.

The detected angular acceleration is interpreted (again, by the laws of physics) as a change in angular velocity about the perceived earth-vertical axis. The perceived angular velocity is taken to be in the perceived earth-vertical direction because the GIA is not tumbling about the subject. When the perceived orientation of the head and therefore angular acceleration are not earth-vertical, only the component in the earth-vertical direction is used to compute angular velocity. In addition, a time constant of 20 s was used for decay of perceived rotation, just as in the Standard Model, and tests for robustness were performed by runs with angular time constant 15 s, 20 s and 25 s.

The interpretation of the GIA takes into account centripetal acceleration in the amount familiar from everyday experience, as explained here. According to the laws of physics, as well as everyday experience, curvilinear motion is always accompanied by centripetal acceleration of magnitude equaling the product of the angular and linear velocity magnitudes, so the GIA is tilted in roll accordingly. If the subject is also in a roll-tilted orientation, then the roll angle of the GIA is correspondingly greater or less. Therefore, in the present Whole-Motion Model, if the subject's perception is of moving around a curve, and if the detected GIA reflects the centripetal acceleration to be expected during such a curve, then the subject does not perceive roll tilt. The subject perceives roll tilt only to the extent that the roll angle of the GIA is greater or less than that expected during the perceived curve.

Perceived pitch tilt also takes into account linear acceleration. Specifically, perceived pitch angle is given as the difference between the pitch angle of the detected GIA and the pitch angle of GIA that should correspond to the perceived forward/backward linear acceleration. The difference between these two angles depends only upon the linear velocity and the time constant of decay of perceived translation. Note that the noncommutativity of rotations is handled implicitly by the fact that perceived roll and pitch angles are specified directly at any given time, rather than as the result of roll and pitch rotation. The operation of rotation does not commute in more than one dimension, but this model uses the rotation operation only for heading (dθ_h/dt in Fig. 3B). Roll (θ_r) and pitch (θ_p) are specified directly and are well-defined in the range 0° to 90° for the GIAs that occur in the centrifuge.

A technical note: The subject's x, y and z axes are defined as the naso-occipital, inter-aural and head-vertical axes, respectively, and roll and pitch angles are defined by the projection of the GIA onto the subject's xz-plane and yz-plane, respectively.

A side effect of the rule about centripetal acceleration and roll tilt is that modeled subjects do not perceive sideways slippage during the forward or backward motion, unlike in the Standard Model. Such model predictions are presented to be available for comparison with future experimental research. In the Standard Model, tilt is determined instead by a tilt time constant, regardless of whether the detected GIA already corresponds to perceived accelerations and velocities. As a consequence, when the Standard Model computes translation, sideways linear acceleration may arise from roll-tilt mismatch between the GIA and perceived roll.

An additional principle implemented in the Whole-Motion Model is that the subject perceives translation only in an earth-horizontal plane. This hypothesis is undoubtedly too strict for the most general case of self-motion, but is inspired by the concept of familiarity, at least for centrifuge acceleration. This hypothesis might not apply at the beginning of centrifuge deceleration [26], and is presented here as open to testing and modification based upon experimental research.

2.4. Centrifuge Parameters

Centrifuge parameters were chosen to match those of [10], with radius 1 m, centrifuge acceleration/deceleration 10°/s², and maximum angular velocity 200°/s. Each of the acceleration and deceleration therefore lasted 20 s. The initial perception of the subject was considered to be upright and stationary before the acceleration, and tilted by the amount of the GIA before the deceleration, at 51.2°. The centrifuge was considered to rotate counterclockwise.

An additional set of tests was performed with radii of 0.5 m and 6 m, each at 10°/s², and with radius 1 m at each of 5°/s² and 20°/s².

3. Results

3.1. Standard Model

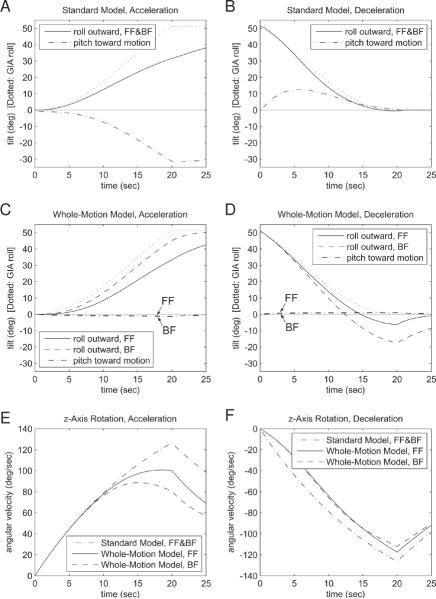
In roll tilt, the Standard Model exhibits differences between acceleration and deceleration, but not between forward- and backward-facing runs (Fig. 4A,B). By using a very short tilt time constant of 0.4 s, the simulated perceived roll tilt increases to more than half the GIA roll tilt in the 20 s of centrifuge acceleration (Fig. 4A), and makes a smooth descent upon deceleration (Fig. 4B), without being drawn more quickly downward, or later oscillating, by the natural physics consequences of the three-dimensional stimulus (Fig. 2). Specifically, at the end of the acceleration, the roll tilt has increased to 62% of the GIA roll tilt, within both the forward-facing range of 30–70% and the backward-facing range of 45–100% reported experimentally. However, the fact that the model's roll tilt when forward-facing is equal to 100% of that when backward-facing (i.e. they are equal) is inconsistent with most experimental results (as described under Experimental Data in Methods). In summary, the physics of the stimulus itself gives the acceleration-deceleration difference in which the roll more closely follows the GIA during deceleration, the short time constant gives the roll's long-term approach toward the GIA, but forward-facing/backward-facing differences are not found.

Figure 4.

Results from both models, showing individual components of predicted perceived motion for centrifuge acceleration and deceleration. (A) Standard Model roll and pitch tilt during acceleration forward-facing (FF) and backward-facing (BF). The pitch values are negative, indicating pitch away from the direction of motion, i.e. pitch-back during FF and pitch-forward during BF acceleration. (B) Standard Model roll and pitch tilt during deceleration. Pitch is forward during FF and back during BF deceleration. (C) Whole-Motion Model roll and pitch tilt during acceleration. Pitch is just slightly greater in magnitude during BF than during FF acceleration. (D) Whole-Motion Model roll and pitch tilt during deceleration. Pitch is just slightly greater in magnitude during FF than during BF deceleration. (E) Angular velocity about the head's vertical (z) axis during acceleration, both Standard Model and Whole-Motion Model. (F) Angular velocity about the head's vertical (z) axis during deceleration, both Standard Model and Whole-Motion Model.

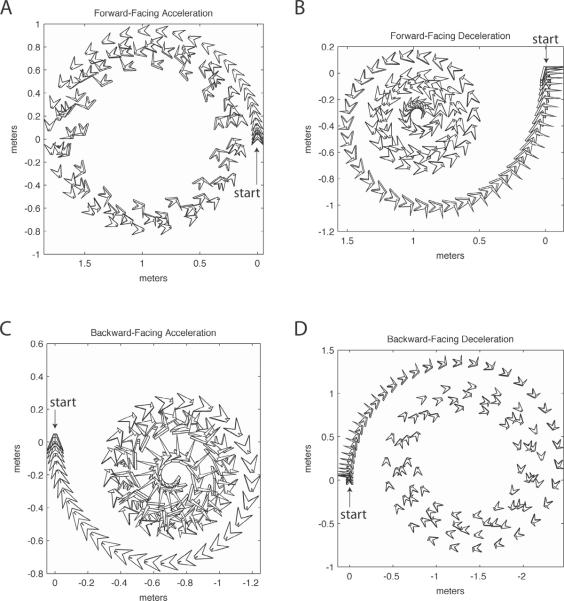
The three-dimensional simulated perceived motion for both acceleration and deceleration spirals sideways (Fig. 5) and upwards (not shown) while including significant pitch tilt (Fig. 4A,B). Forward- and backward-facing accelerations give similar spirals, but facing outward for the former and inward for the latter (Fig. 5C,E). Forward- and backward-facing decelerations both give significant translation turning into a spiral or loop (Fig. 5D,F). Additional tests (not shown) indicate that shorter linear time constants give earlier spirals, while longer linear time constants give later loops and/or ongoing translation.

Figure 5.

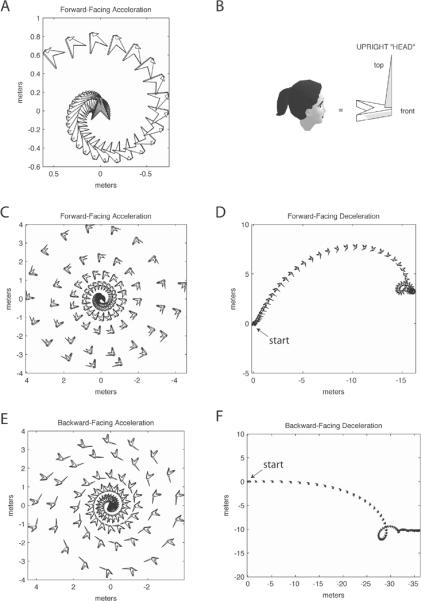
Standard Model: three-dimensional display of predicted perceived motion. Parts C,D,E,F correspond to Fig. 6A,B,C,D for the Whole-Motion Model, though head sizes are adjusted for better viewability as indicated in each part. (A) First 10 s of forward-facing centrifuge acceleration, top view in an Earth-fixed reference frame. The “head”, which is a polyhedron as indicated in Part B, is displayed in time-lapse format with a time step of 0.25 s. The head starts at (0,0) and spirals outward in a counterclockwise manner while rotating counterclockwise. The head generally moves leftward around the spiral. (B) The polyhedral “head” used in Figures 5 and 6, to facilitate views of orientation. The “head” is arrow-shaped with a blunt point at the nose and a sail sticking up from the front. (C) Extension of Part A, for a total of 25 s with “head” scaled x2. This is the same 25 s shown in Fig. 4A. The head spirals outward in an approximately sideways manner. (D) Forward-facing deceleration, same conventions as in Part C (head scaled x2), for the 25 s shown in Fig. 4B. The head translates significantly before turning into a clockwise spiral. (E) Backward-facing acceleration, head scaled x2 from Part B, for the 25 s shown in Fig. 4A. The head starts at (0,0) and spirals outward counterclockwise, facing inward and moving sideways head-rightward. (F) Backward-facing deceleration, head scaled x2 from Part B, for the 25 s shown in Fig. 4B. The head translates significantly before turning temporarily into a loop and then a slowing translation (more densely placed heads in the time-lapse format, at the right end of the plot). Though not clearly discernible, the head is rotating clockwise at an increasing rate as it moves. NOTE: In all of Parts A, C, D, E, and F, there is significant upward earth-vertical motion not visible in these top views. Also, there are pitch and roll components more easily discerned from Fig. 4A,B.

This is the general shape of perceived motion (Fig. 5) that would be predicted by models that are based upon decay of perceived angular and linear velocity, and tilt moving toward the GIA, assuming that the velocity output of the models indicates corresponding changes of position and orientation.

3.2. Whole-Motion Model

In roll tilt, the Whole-Motion Model exhibits differences between acceleration and deceleration, as well as between forward- and backward-facing runs (Fig. 4C,D). The simulated perceived roll tilt significantly lags the GIA upon acceleration, and quickly follows the GIA upon deceleration, even overshooting the GIA tilt. During acceleration, roll tilt more closely follows the GIA for backward-facing than for forward-facing runs. Specifically, at the end of the acceleration, the roll tilt when forward-facing has reached 65% of the GIA roll tilt, and when backward-facing has reached 88% of the GIA roll tilt. The roll tilt when forward-facing is 79% of that when backward-facing, well within the range 55–95% found experimentally. During deceleration, the roll tilt closely follows the GIA for both backward- and forward-facing runs, then gradually exhibits overshoot in both, greater in the backward-facing run than in the forward-facing run.

The amount of z-axis angular velocity (which is related to horizontal eye movements) during acceleration has a lower peak for backward-facing than for forward-facing runs, though the graphs rise similarly at first (Fig. 4E). However, during deceleration, there is little difference in z-axis angular velocity between forward- and backward-facing runs (Fig. 4F). These contrast with the Standard Model's output, which is the same for forward- and backward-facing runs (Fig. 4E,F).

The three-dimensional simulated perceived motion begins as a forward- or backward-facing turn which either continues at a radius or becomes a nearly on-axis turn (Fig. 6), with roll tilt as explained above, and with a very small amount of pitch tilt (Fig. 4C,D). During acceleration, the simulated perceived turn remains at a radius for the forward-facing run but becomes essentially on-axis for the backward-facing run (Fig. 6A,C). During deceleration, the opposite occurs, with the perceived rotations being more on-axis for the forward-facing run (Fig. 6B,D).

Figure 6.

Whole-Motion Model: three-dimensional display of predicted perceived motion. Parts A,B,C,D correspond to Fig. 5C,D,E,F for the Standard Model, though head sizes are adjusted for better viewability as indicated in each part. (A) Forward-facing centrifuge acceleration, top view in an Earth-fixed reference frame, for a total of 25 s in time-lapse format with a time step of 0.25 s, with polyhedral “head” as shown in Fig. 5B scaled ½ size. This is the same 25 s shown in Fig. 4C. The head starts at (0,0) and moves in an approximate circle forward-facing counterclockwise, while tilting rightward in roll. (B) Forward-facing deceleration, same conventions as in Part A (head from Fig. 5B scaled ½ size), for the 25 s shown in Fig. 4D. The head starts at (0,0) in a rightward-roll orientation, and moves backward into an approximately on-axis clockwise spin. The spin is approximately upright, as discerned better from Fig. 4D. (C) Backward-facing acceleration, head scaled ½ size, for the 25 s shown in Fig. 4C. The head starts at (0,0) and moves backward into an approximately on-axis counterclockwise spin. During the spin, the head is tilted in roll, as discerned more easily from Fig. 4C. (D) Backward-facing deceleration, head scaled ½ size, for the 25 s shown in Fig. 4D. The head starts at (0,0) and moves in a forward-facing clockwise spiral while roll tilt changes from outward roll to inward roll (as also discerned in Fig. 4D). NOTE: No earth-vertical motion exists in these four simulations.

3.3. Additional Sets of Parameters

The results were confirmed with additional tests using radii 0.5 m and 6 m at 10°/s², and using radius 1 m at 5°/s² and 20°/s² (not shown). Perceived motion predicted by the Whole-Motion Model exhibits the same asymmetries as when using the original parameters. In particular, during acceleration, roll more closely follows the GIA for backward-facing runs than for forward-facing runs, and z-axis rotation peaks at a lower velocity for backward-facing runs. The largest asymmetries occur at the greatest radius.

Robustness was confirmed by testing with variations of the time constant values. For the Standard Model, angular time constants of 15 s, 20 s and 25 s all result in forward-facing runs and backward-facing runs giving the same roll tilt (equaling 69%, 62%, and 57%, respectively, of the GIA roll) at the end of the acceleration. Variation of the tilt time constant had already been performed in the original fitting; another choice of value would still fail to give forward/backward-facing differences. For the Whole-Motion Model with angular time constants of 15 s, 20 s and 25 s, the roll tilt at the end of the acceleration when forward-facing is 78%, 74% and 71%, respectively, of that when backward-facing, confirming the robustness of the model. In addition, variations of the time constants for forward and backward translation were found to allow fitting of more precise experimental data when desired. For example, time constants of 40 s for forward velocity and 10 s for backward velocity result in simulated perceived roll tilt of 39% and 65%, respectively, of the GIA tilt at the end of the acceleration. In this simulation, the roll tilt when forward-facing is 60% of the roll tilt when backward-facing, consistent with experimental data using a somatosensory measure for the same centrifuge parameters, 10°/s²acceleration to 200°/s at 1 m radius [10]. Because numerical results differ between experimental studies, precise fitting was not performed; instead, the main point was that the Whole-Motion Model can reproduce forward-facing/backward-facing roll tilt differences well within the ranges reported experimentally, whereas the Standard Model cannot.

4. Discussion

Modeling whole-motion properties is shown here to be more consistent with perception in a centrifuge than is the standard approach of combining component-wise tendencies. The Whole-Motion Model makes predictions that the Standard Model cannot. For the Whole-Motion Model, only a few basic principles are required, all falling under the umbrella of the concept of familiarity: the interpretation of the GIA takes into account centripetal acceleration, forward or backward acceleration lead into translation only forward or backward, and forward motion is more familiar than backward motion. The Whole-Motion Model developed with these principles displays acceleration-deceleration roll tilt differences just as with the “Standard” model that uses component-wise tendencies, while also exhibiting differences between forward-facing and backward-facing runs, and giving predicted perceived motions forward- or backward-facing around a curve or on-axis. The Standard Model, on the other hand, cannot exhibit roll-tilt differences for forward-facing versus backward-facing runs, even when the greater familiarity of forward motion is implemented. However, the basic asymmetry in roll tilt between acceleration and deceleration can be explained over the first few seconds by the physics consequences alone, without requiring either the Standard Model or the Whole-Motion Model.

4.1. Familiarity

For other sensory modalities as well, familiarity plays a role in perception and action. This idea has been implemented in the study of vision by Bayesian probability theory and models, which allow mathematical prediction of what the optimal human observer perceives by combining prior knowledge about the scene and important features of the stimulus [31, 32]. These same ideas have been shown applicable to combined visual-haptic perception [13] and in sensorimotor tasks [34]. Norris [49] also used the Bayesian model to show that word frequency affects perception while making the optimal choices using all available information.

For passive self-motion perception in fixed-carriage centrifuges, previously existing models have already included to a certain extent the concept of familiarity. This concept has been implemented by the Bayesian method [36], by highlighting the optimization process [52] and by models that use optimization or its equivalent [6, 15, 16, 40, 44, 60]. The Whole-Motion Model presented here extends these ideas to the motion as a whole, rather than focusing on components separately.

4.2. Roll Tilt

The Whole-Motion Model is consistent with experimental data on roll tilt, including forward-backward differences. Experiments on perception have found a faster roll tilt change during backward-facing than during forward-facing acceleration [9, 10, 45], as given by the model (Fig. 4C). During deceleration, the model also exhibits fast roll tilt change for both backward- and forward-facing runs, with an overshoot past upright appearing especially for the backward-facing orientation (Fig. 4D). Experimental subjects' reports have also included this overshoot, either for both forward- and backward-facing runs [21] or for mainly backward-facing runs [10, 45].

The forward-backward differences in roll were not explicitly programmed into the model, nor is the overshoot a “second effect” arising from a higher-order differential equation. Instead, both are consequences of the hypothesis that perception understands centripetal acceleration. Indeed, the nervous system must understand centripetal acceleration during running, bicycling, and riding in vehicles in everyday life.

To the model, the greater linear velocity during forward-facing motion (motivated by the greater familiarity of forward motion) implies that more centripetal acceleration should exist, so the tilted GIA is interpreted as making sense, and is interpreted less as actual tilt; thus, perceived roll is less during forward-facing than during backward-facing acceleration. Upon deceleration, as well, the perceived roll is exactly that required to make sense of the GIA. The overshoot is not a physiological “second effect”, but is due to the fact that a subject going through a curve must be tilting into the curve if the GIA is vertical through the body. At the end of the centrifuge deceleration, the GIA is vertical through the body, so the (perceived) turning subject reports appropriate tilt. This tilt looks like overshoot in the graph (Fig. 4D), but is physically logical.

An experimental observation worth follow-up is the occasional subjective report of roll tilt that oscillates more times than just the overshoot and recovery [6]. As mentioned in 3.1, the physics consequences of the three-dimensional stimulus would predict such an oscillation, which has also been modeled with a three-dimensional model of perception [6].

4.3. Three-Dimensional Motion

The natural shape of turning or rotating arising from the Whole-Motion Model (Fig. 6) is a consequence of its treatment of the GIA. While the Whole-Motion Model resolves the GIA into translation and tilt, as do other three-dimensional models [6, 15, 16, 36, 40, 44, 52, 60], it approaches the resolution differently. Most models compute tilt based upon a tendency toward the GIA, and then, in effect, compute translation from the remaining GIA (and a number of models have been shown to be the same in this respect [6, 18]). This approach leads to predicted perceived sideways linear velocity. The Whole-Motion Model, on the other hand, computes linear velocity first, and then computes tilt from the remaining GIA. This approach leads to a predicted perceived forward or backward linear velocity.

Although it is tempting to suspect that the Standard Model could be made to predict only forward or backward perceived velocity by a different choice of parameter values, it could not. Any nonzero roll time constant would cause a roll lag and thereby a sideways velocity, while a zero roll time constant would fail to give the experimentally-reported lag.

4.4. Additional Components of Motion

The Whole-Motion Model predicts possible forward-backward differences in perceived z-axis angular velocity, pitch orientation, and linear velocity. However, the paucity of published experimental data makes comparison of the models unreasonable for these components. The results of the present research also suggest further study of basic hypotheses, for example that the perception of linear motion is more sustained when the acceleration is forward than when it is backward.

It is worth noting that other models [6, 15, 16, 36, 40, 44, 51, 52, 55, 60] have predicted forward-backward differences in horizontal eye movements for reasons different from the Whole-Motion Model's forward-backward differences in perceived z-axis angular velocity. (Also, it is worth noting that monkey data and models [41, 51, 56] differ from those for humans.) In the eye-movement models, the differences are due to combined linear and angular stimuli and/or a special gaze-centering mechanism. In the Whole-Motion Model, the z-axis angular velocity, itself, differs due to the simulated subject's perceived roll angle; although total predicted perceived angular velocity is similar for forward- and backward-facing runs, the greater roll tilt in the backward-facing run (Fig. 4C) causes less of the angular velocity to be about the head's z-axis (Fig. 4E). Experimental findings on horizontal eye movements could be related to perceptual differences in roll, although it is worth noting that eye movements and perception do not always align [38, 39, 42, 47, 50, 58].

For pitch, one study investigated perception [9], and found perceived change of pitch in the backward-facing run, but not in the forward-facing run. This finding is consistent with the Whole-Motion Model's output of greater pitch for the backward-facing than for the forward-facing acceleration (Fig. 4C). However, the model's output is quite small, and the published experimental reports were scaled and were not based upon explicit subjective tilt. Rather, the instructions were to “imagine that the plate you are holding is supporting several glasses filled with water: you must maintain it perfectly horizontal so that the liquid does not spill” [9], which effectively means to report the GIA instead of the subjective vertical. Nevertheless, forward-backward differences were found both experimentally and slightly in the Whole-Motion model. The Standard Model had much greater pitch tilt, as also seen in previous models with the same foundation [6, 36, 40, 44, 60].

Additional experimental research suggested by the current investigation is on perception of linear motion in a centrifuge. Straight linear motion has been studied to compare the ability to reproduce passive forward and backward motion, with two subjects [14]. Backward distance was more accurately reproduced, with slightly greater estimates than for forward distance, but backward velocity estimates were variable and inaccurate compared to forward velocity estimates. Further research would be desirable on this topic because distance and velocity estimates have been found to be differentially affected by potential distortion of perceived time [19]. In addition, perceived translation may be more governed by nondirectional cues such as vibration and sound than by linear accelerations [59]. Vertical eye movements have also been found to be less consistent during backward translation than during forward translation [54]. For a centrifuge, the question then arises whether perception of linear motion would be less consistent, perhaps through intersubject variability, during those conditions in which the subject experiences backward acceleration. Conditions with greatest potential for experimental linear-perception mismatch with the models would then be those of acceleration when backward-facing and deceleration when forward-facing. The models also generate questions of whether or how much sideways and/or earth-vertical motion is perceived.

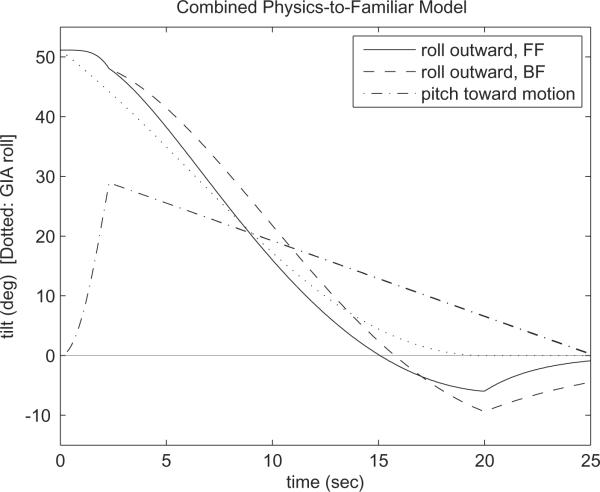
A potential modification to the Whole-Motion model, and to our understanding of self-motion perception, could stem from further experimental research, including that on perceived vertical motion at the beginning of the centrifuge deceleration. The physics of the stimulus alone predicts perceived vertical motion [26]. In the present paper, the principles motivated by whole-motion familiarity are applied immediately, but experimental investigation can help determine whether or how the pure laws of physics might govern perception at the start. In fact, pitch tilt is another component that would be predicted to be substantial soon after the start of deceleration, based upon the laws of physics. A combined model would be reasonable, in which physics-based beginnings of perception change into more familiar long-term perceptions of whole motion. In such a model for a centrifuge, physics could govern roll and pitch at the start, and then whole-motion principles could take over roll when the physics-induced perceived roll tilt matches that consistent with the roll expected from centripetal acceleration (Fig. 7). Pitch could then transition over a period of time from that predicted by pure physics to that predicted by whole-motion principles.

Figure 7.

Possible output for predicted perception during deceleration, from a rudimentary model incorporating physics-based predictions at the beginning and familiarity-based predictions in the long term. For the centrifuge parameters here, of 1 m radius, 200°/s initial velocity, and 10°/s² deceleration, the match between physics and familiarity for roll occurs at the 2.3 s point: the roll tilt predicted from physics matches the roll tilt expected by familiarity of centripetal acceleration. The graph shows roll and pitch output from a pure physics-based model (as in Fig. 2) for the first 2.3 s, followed by roll output from the Whole-Motion Model which takes over the simulation at the 2.3 s point. Pitch values after the 2.3 s point are plotted as a decreasing weighted average of the physics output at the 2.3 s point and the Whole-Motion Model output at the 25 s point; otherwise pitch would exhibit a discontinuity, unlike roll, upon which the 2.3 s transition was based. Pitch is essentially the same magnitude for the forward-facing (which gives pitch-forward) and backward-facing (which gives pitch-back) decelerations.

4.5. Conclusion

The purpose of modeling is to test and further develop scientific understanding of phenomena, and to raise experimental questions by identifying gaps in our knowledge. Although certain components of perceived self-motion in centrifuges have been previously understood and modeled successfully, the present research demonstrates that an approach that considers the shape of three-dimensional motion as a whole can better predict additional aspects of perceived self-motion. Perception may be significantly influenced by familiarity, which for complex motions may take a whole-motion form as proposed here rather than a component-wise form as is typically used. Ultimately, the concept of whole-motion familiarity may apply to a wide range of other complex motions as well.