Solute partitioning and filtration by extracellular matrices

Abstract

The physiology of glomerular filtration remains mechanistically obscure despite its importance in disease. The correspondence between proteinuria and foot process effacement suggests podocytes as the locus of the filtration barrier. If so, retained macromolecules ought to accumulate at the filtration barrier, an effect called concentration polarization. Literature data indicate macromolecule concentrations decrease from subendothelial to subepithelial glomerular basement membrane (GBM), as would be expected if the GBM were itself the filter. The objective of this study was to obtain insights into the possible role of the GBM in protein retention by performing fundamental experimental and theoretical studies on the properties of three model gels. Solute partitioning and filtration through thin gels of a commercially available laminin-rich extracellular matrix, Matrigel, were measured using a polydisperse polysaccharide tracer molecule, Ficoll 70. Solute partitioning into laminin gels and lens basement membrane (LBM) were measured using Ficoll 70. A novel model of a laminin gel was numerically simulated, as well as a mixed structure-random-fiber model for LBM. Experimental partitioning was predicted by numerical simulations. Sieving coefficients through thin gels of Matrigel were size dependent and strongly flux dependent. The observed flux dependence arose from compression of the gel in response to the applied pressure. Gel compression may alter solute partitioning into extracellular matrix at physiologic pressures present in the glomerular capillary. This suggests a physical mechanism coupling podocyte structure to permeability characteristics of the GBM.

the physiology of glomerular permselectivity, that is, the ability of the kidney's filters to retain large proteins in the blood while allowing salt, water, and toxins to escape into the urine, has historically been described in terms of structure-function correlations. The glomerular filter is a three-layer structure comprised of capillary endothelium, a 250- to 300-nm-thick glomerular basement membrane (GBM), and a layer of specialized epithelial cells, called podocytes. The present understanding of glomerular physiology can be described in a few conflicting observations. First, the appearance of protein in the urine is usually but not invariably associated with ultrastructural changes in the podocyte, and several studies have demonstrated that disruption of the podocyte barrier through a variety of podocyte-targeted experiments produces proteinuria (4, 16, 26, 33, 34, 45, 56). Genetic disorders affecting protein constituents of the podocyte slit diaphragm are associated with a nephrotic phenotype (33). Electron microscopy studies failed to reveal an accumulation of macromolecules immediately underlying the podocyte layer. Studies by Farquhar, Ryan, Ghitescu, and Fujigake (6, 20, 21, 28, 48, 49) show spatially varying penetration of macromolecules into the basement membrane, with concentrations of macromolecules decreasing within the GBM from endothelium to epithelium, as seen within semipermeable membranes. Third, clinical illnesses that appear limited to an individual layer of the capillary wall provide intriguing clues to the filter. Diseases that appear to be lesions of the capillary endothelium such as preeclampsia and hemolytic-uremic syndrome, or lesions of the basement membrane alone, such as thin GBM disease, Pierson syndrome, and Alport's syndrome are not associated with massive proteinuria, except for Pierson syndrome, where podocyte architecture is also disrupted (1, 19, 22, 24, 25, 27, 29, 36, 41, 54).

Despite these observations, the role of the podocyte slit diaphragm as a molecular sieve retaining macromolecules in the blood stream is unproven. Wherever the barrier to passage of macromolecules actually lies, one would expect macromolecules to accumulate upstream from the barrier, much like peas in a colander. Electron microscopy studies have mapped solute concentrations within the glomerular capillary wall and can thus provide us a clue as to the location of the main barrier. Interestingly, these studies fail to reveal any accumulation of macromolecules immediately underlying the podocyte layer, and in fact show limited to negligible penetration of macromolecules into the basement membrane. No increase in solute concentration in the subepithelial GBM is seen in Fujigaki's data, nor in that of Ryan and Karnovsky. If the podocyte layer has been damaged, macromolecules are observed throughout the entire thickness of the GBM (6, 20, 28, 48, 49). If the podocytes were the filtration barrier, one would expect a concentration polarization in the subepithelial GBM, but the data do not show a concentration polarization: they show exactly the opposite. Fujigaki measured a decreasing solute concentration from subendothelial GBM to subepithelial GBM, very similar to how Deen draws the profile within a semipermeable membrane (12). When presented in this manner, it is very difficult to implicate the podocyte slit diaphragm as the only size-selective barrier in the glomerulus, and very tempting to consider the GBM as having an additional role in the selectivity barrier. However, a recent paper by Tanner et al. (55) uses two-photon intravital microscopy of fluorescent tracers in the Necturus kidney to argue that the podocyte slit diaphragm is the primary barrier to albumin transport across the glomerulus. Interestingly, no hint of a concentration polarization was reported in that manuscript, either. In an accompanying editorial, Navar (35) suggests that Tanner's data do not exclude exclusion of macromolecules by the GBM. This is similar to the conclusions presented by Edwards et al. (14) a decade earlier in her modeling of the multilayer glomerular filter. The endothelial and epithelial contributions to the GBM may differ from each other in protein or glycosaminoglycan composition, but the rapidity with which a variety of insults (vascular clamps, antibodies to slit diaphragm proteins) causes a redistribution of solutes argues strongly against a fixed structural cause within the GBM for the observed spatial variation (20, 48).

This leads to a “podocyte paradox”: the distribution of macromolecules within the GBM is most consistent with the GBM being the locus of size selectivity, yet filtration appears insensitive to defects in the GBM and exquisitely sensitive to changes in podocyte structure. This suggests that podocytes in some way regulate the filtration characteristics of the GBM. Several investigators proposed transport models that could explain this apparent paradox, including Oliver Smithies, and an elegant series of abstracts by Somers (50–53). Smithies' model has been challenged on several points, and Somers' model has disappointingly not yet appeared in manuscript form. In contrast, work by Comper and colleagues (8, 32, 46, 47) postulates high-volume albumin transport across the glomerular filter, although this remains a point of contention. An earlier model of GBM behavior by Robinson and Walton (44) predates but informs the present emphasis on podocyte biology and motivated the experiments discussed below.

Could the basement membrane have size-selective transport properties? Robinson and Walton (44) explored the role of the GBM as a compressible ultrafilter using a gel of sedimented glomerular skeletons and noted both mechanical compression of the gel and increasing rejection of proteins with progressively greater degrees of compression. Compression of the gel is thought to bring gel fibers closer together, effectively increasing the concentration of the gel and reducing the size of the interstices between fibers. The minimum sieving coefficient that Robinson observed for albumin was ∼0.034, two orders of magnitude higher than is generally accepted for the intact glomerulus, although Comper et al. (9) argue that this figure is approximately correct for the entire glomerular filtration barrier. Edwards and colleagues (13, 15) investigated transport properties of extracellular matrix (ECM) and observed size selectivity of GBM and of pelleted glomerular ECM. The generalizability of their data and that of Robinson is limited by the nonphysiologic high-pressure sedimentation technique employed to obtain a homogeneous layer of ECM for filtration experiments and the inevitable inclusion of mesangial proteins into their matrix. Wolgast and colleagues (57, 58) published a highly detailed gel model incorporating structure and charge, and validated it using neutral and charged equine myoglobin, but their results focus on charge density analysis, without any detailed analysis of the molecular architecture of the GBM. Klaentschi et al. (30) investigated dextran filtration by thin layers of Matrigel, a commercially available extract of ECM produced by Englebreth-Holm-Swarm (EHS) cell tumors. This commercially available product is primarily laminin, nidogen-1, and perlecan; the α1α2 collagen IV is imperfectly crosslinked in the animals and is poorly retained in the commercial extraction. Klaentschi et al. observed size-dependent rejection of dextrans and a small pressure-dependent decrease in hydraulic permeability attributed to compression of the gel in response to increased hydrostatic pressure. Dextran's utility as a probe for glomerular investigation has been challenged on the basis of its conformation. Ficoll is an approximately spherical copolymer of sucrose and epichlorohydrin which is freely filtered and does not appear to be metabolized or taken up by the renal tubule, and consequently has been used to probe glomerular permselectivity (38). Moreover, filtration data using Ficoll and its derivatives, and sulfated dextrans as used by Klaentschi, differ in the apparent effect of negative charge (3, 7, 23, 30, 31). We sought to reproduce and confirm Klaentschi's observations using Ficoll and develop a model describing a structural basis for solute partitioning in the GBM. If gel compression is a significant effect at physiologic pressures within the glomerulus, this might illuminate a mechanism by which podocytes alter the transport characteristics of the GBM.

Could experiments to assess the relative contributions of GBM and podocyte to permselectivity be conducted in vivo? Experimental data from in vivo experiments can be difficult to interpret. Mass transport within the capillary lumen is difficult to control and assess during such experiments, as it will depend on renal blood flow (RBF), glomerular filtration rate (GFR), and the intrinsic characteristics of the glomerular capillary wall. While saline loading, dehydration, or drugs may alter GFR, it is difficult to document the precise effects on RBF and filtration fraction within individual glomeruli, and whether such effects are uniform or heterogeneous throughout the cortex. Thus, it can be difficult to draw valid conclusions about the mode of molecular transport, and quite challenging to decipher the contribution of individual layers. The data from Ryan and Karnovsky, Fujigaki, and more recently, Miner (5, 20, 25, 48) show that in vivo interventions directed at one layer can materially affect the other layers: podocyte-targeted interventions alter fluid flow through the GBM; GBM-targeted interventions can alter podocyte architecture. These challenges have encouraged our laboratory to develop in vitro models of glomerular filtration that can isolate the transport properties of ECM gels. That said, experiments that test the structure of the GBM, rather than testing hemodynamic variations in glomerular perfusion, may provide insight into the contribution of the GBM to the filtration barrier.

How can we resolve the apparent paradox that the GBM appears to be the main barrier to protein transport across the glomerular capillary wall with the histopathology data that consistently show that podocyte-targeted manipulations produce nephrotic syndrome, whereas major defects in the GBM largely produce relatively minor proteinuria? A mechanism coupling podocyte structure to GBM characteristics would add to our understanding of the filtration barrier. If the GBM truly functions as a compressible ultrafilter, podocyte foot process effacement might alter the mechanical forces on the GBM, changing the transport properties of the GBM. To that end, our group continued to explore pressure-permeability relationships in a spectrum of model ECMs.

EXPERIMENTAL PROCEDURES

Numerical simulations.

For visualization and simulation purposes, it is helpful to idealize the geometric configuration of a gel as a collection of cylindrical “struts” of varying length and radius comprising a “unit cell” (37). However, even given this simplified description, determining the excluded volume fraction through direct or numerical integration can be a significant and often impractical challenge. This task is even more daunting when many combinations of lattice configurations and shapes must be examined quickly. Our group found success approximating the excluded volume fraction using the Monte Carlo method. In our solution, many spheres of a given radius are stochastically placed within a specific sampling space (e.g., the bounding box) around the collection of cylindrical struts (the wireframe). The ratio of the number of spheres that do not intersect any strut to the number of total spheres placed then approximates the available volume fraction. This method does not presently include sphere-sphere interactions nor electrostatic effects and is applicable only to very dilute solutions, but is easily adapted to capture such effects.

Use of the Monte Carlo method has many benefits over trying to directly compute the volume fraction through integration. The method is quite fast, and, depending on the configuration of struts, converges to a stable result in only a few tens or hundreds of thousands of samples (which takes mere seconds on modern CPUs). It is therefore easy to change simulation parameters, including the size, shape, and placement of the sampling space or the configuration of struts, and immediately examine the result. This is particularly useful when the exact configuration of the lattice is unknown but empirical data are available, as many approximate configurations can be tried and compared with the experimentally determined volume fraction. It is also straightforward to substitute spheres with more complex shapes, allowing for future examination of different types of solutes. It would also be possible to incorporate more complicated intersection models that take into account the physical interactions between different types of materials. A small binary executable is available from the corresponding author upon request.

Structural models of GBM molecular architecture can provide insight into solute partition coefficients and transport. Following Ogston's approach, we can model partition coefficient as the volume of gel that is available for a given solute to occupy (37). The rules that govern whether a solute may occupy a given location in the gel may be as simple as the solute not overlapping a gel fiber, or as complex as necessary to predict results accurately.

To validate the numerical method, hard-sphere steric hindrance-based partition coefficients from the Monte Carlo model were compared with those predicted by Ogston's analytic formula. Microsoft Excel's random number generator was used to generate coordinates for 1,000 fibers of radius 1 and length 426 [chosen as the putative length of a collagen fibril (61)] randomly oriented and placed with centers randomly positioned within a cube 800 × 800 × 800. The spreadsheet was exported as a text file and formed the structure for a Monte Carlo simulation of partitioning. The parameters used in Ogston's formula

$$f=e^{\left(2\pi vL{r}^2+\frac{4\pi }{3}\text{v}{r}^3\right)}$$ (1)

may be directly extracted from the input parameters to the Excel spreadsheet. The length of fiber 2L = 426; the density of fiber centers ν = 1,000*(800)⁻³ and r is the radius of the test solute plus the radius of the fiber. The analytic and numerical results agreed perfectly (Fig. 1).

Fig. 1.

Comparison of analytic and numeric predictions of steric hindrance partitioning into a random fiber array. x-axis, solute radius in arbitrary units; y-axis, partition coefficient. Ogston's formula predictions (black line) were well-matched by a Monte Carlo simulation (dashed line).

Using size data from structures visualized by Yurchenco (59, 62), we constructed an extremely simple three-dimensional (3-D) model of an idealized laminin gel, shown in Fig. 2. This model departs from previous published models which depict laminin molecules as forming a plane-filling pattern of tessellated hexagons; such models did not incorporate interactions that would permit an ordered 3-D structure (59). The model which we tested maintains trimeric attachment between the short arms of three laminin molecules and permits the long arm to be unbound, and also incorporates a nidogen linkage to the B1 chain of laminin. The structure of the model permits idealization of the gel as a repeated series of 3-D space-filling structures. Rigid sphere excluded volume partitioning was numerically simulated for the idealized laminin gel shown in Fig. 2. The number of fiber centers per unit volume, the fiber lengths, and the fiber radii were read directly from the text file input to the software routine for comaprison to Ogston's analytic model for a random array of fibers. The software completed 10⁵ random test placements of a solute of given radius within a bounding box governed by the network geometry and repeated for rigid spheres from 20 Å to 120 Å radius in 1-Å steps.

Fig. 2.

Three-dimensional model of laminin polymerization. Yellow, laminin; green, nidogen. The 3 short arms of laminin form heterotrimeric interactions while the long arm does not interact with adjacent molecules.

Macromolecular partitioning into ECMs.

As a test platform to explore solute partitioning into ECM, we chose two systems that are easily handled in vitro and have historical relevance to the understanding of basement membrane biology. First, two commercially available ECM products, Matrigel (Cat. no. 354234, BD Biosciences, Franklin Lakes, NJ), and laminin (Cat. no. 354259, BD Biosciences), were selected as ECM gels, as EHS tumor matrix has been a source of materials for structural studies of basement membrane components. Matrigel and BD's laminin are extracts of ECM produced by EHS tumors grown in mice (ATCC Number CRL-2108). Second, bovine lens basement membrane (LBM), the kind gift of Dr. B. Hudson, was selected as a rare example of an intact basement membrane that can be handled in the laboratory. The commercially available Matrigel is primarily laminin-111, nidogen-1, with some perlecan but little type IV collagen (α1₂α2[IV] chain composition). The collagen is largely crosslinked and therefore extracts poorly. The commercially available laminin is similarly collagen poor (P. Yurchenco, unpublished results). Ficoll, a globular polydisperse polysaccharide, was labeled with FITC after the method of Ohlson et al. (38). Matrigel and laminin were thawed to 5°C, where they become liquid, and pipetted in aliquots at full strength (8–9 mg/ml, considerably in excess of minimum gel concentration) onto chilled commercially available 12-well plates and allowed to gel by gentle warming to 37°C. Gels were rinsed with warmed phosphate-buffered saline with 1 mM calcium chloride (PBSC) and incubated for 48–72 h with 3 ml of 1 mg/ml FITC-Ficoll 70. The FITC-Ficoll solution was aspirated and the gels were incubated with an equal volume of warmed PBSC for 72 h. The supernatants were collected and analyzed by size-exclusion chromatography as previously described (18). Partition coefficients were calculated from simple mass balance as

$$\Phi =\frac{C_{\text{s}}}{C_{\text{f}}-C_{\text{S}}}$$ (2)

where C_f and C_s are the Ficoll concentrations in the feed and supernatant solutions, respectively.

Derivation of the calculation is presented in appendix 1. To examine partitioning into a collagen-rich basement membrane in its native configuration, Ficoll partitioning into lens basement membrane (LBM) was measured in the same way. Patches of LBM were incubated overnight in a large excess of feed solution, removed, and equilibrated with 200 μl of PBSC (“supernatant”). Feed and supernatant were analyzed by size exclusion chromatography. A three-component partitioning model was developed to account for droplets of feed solution adherent to the LBM patches when they were removed from feed and placed in supernatant (see appendix 1). The volume of the LBM patch was estimated by multiplying the area of the patch as determined by digital planimetry of a photomicrograph by the thickness of the LBM. LBM thickness was estimated by sandwiching LBM between two coverslips and measuring the thickness with a micrometer, and then subtracting the thickness of the coverslips alone.

RESULTS

Partitioning.

Ficoll partitioning coefficients into Matrigel or laminin were highly similar and decreased with increasing Ficoll radius, from a partition coefficient of ∼0.78 ± 0.053 for 20-Å radius molecules to 0.47 ± 0.026 for 140-Å radius molecules (Fig. 3, solid lines). Control wells without Matrigel showed minimal signal. The numerical simulation (Fig. 3, open circles) was qualitatively similar to the experimental data. The difference might be explained by errors in estimation of gel volume, which we estimate to be in the range of 5–8% based on volume displacement and microscopic techniques. The number of fibers per unit volume and the fiber geometries were counted from the text file that generated the gel architecture for the numerical simulation and were used to calculate partition coefficients from Ogston's formula (Fig. 3, solid circles).

Fig. 3.

Solute partitioning into Matrigel and laminin: x-axis, Ficoll radius; y-axis, partition coefficient. Ficoll 70 partitioning into thin sheets of Matrigel (gray) and laminin (black) is graphed with solid lines of means (thick) ± SE (thin lines). Weak size dependence is evident. A numerical simulation of excluded volume partitioning into a simple idealized laminin gel predicted actual partitioning well (○). Ogston's random fiber partitioning model predicted partitioning poorly (●). Of note is that the numerical simulation produces discontinuous data points, whereas the polydisperse tracer is separated by size exclusion chromatography, and so experimental data appear as the continuous line.

Partitioning in LBM was strongly size dependent and rejected macromolecules much more stringently than did either of the commercially available extracts (Fig. 4, solid lines). Partition coefficients ranged from 0.296 ± 0.028 at 20 Å to −0.002 ± 0.002 at 140 Å radius. As the general shape of the partitioning curve resembled that of Ogston's formula, the random fiber numerical simulation described in experimental procedures was fitted to the experimental data by varying the number of randomly placed fibers and their radius. Interestingly, the best fit was achieved when a random fiber array was superposed on the laminin network used for numerical simulation of the Matrigel and laminin gels (Fig. 4, open circles). The best fit was achieved for 2.32 × 10¹⁶ fibers/ml, with a fiber radius of 4.2 nm, corresponding to a volume fraction of ∼0.54.

Fig. 4.

Solute partitioning into lens basement membrane: x-axis, Ficoll radius; y-axis, partition coefficient. Ficoll 70 partitioning into lens basement membrane is graphed as solid lines (thick, mean of 3 experiments, thin, means ± SE). A numerical simulation combining the laminin mesh of Fig. 2 and a random fiber array similar to that used to generate Fig. 1 achieved the best fit to the experimental data (○). Of note is that the numerical simulation produces discontinuous data points, whereas the polydisperse tracer is separated by size exclusion chromatography, and so experimental data appear as the continuous line.

Sieving by Matrigel gels.

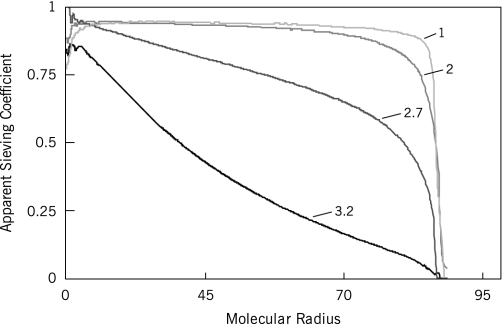
The hydraulic permeability of the Matrigel membrane varied with applied transmembrane pressure (Fig. 5). As transmembrane pressure increased, hydraulic permeability decreased. At the highest membrane flux tested, the Matrigel membrane displayed size-dependent rejection of Ficoll (Fig. 6, black line), whereas the control frit and cellulose support membrane did not reject any solute, consistent with the 200-nm-pore size of the cellulose support (data not shown). At progressively higher membrane fluxes, the size-dependent hindrance of Ficoll transport became increasingly apparent (Fig. 6, gray lines). In particular, the sieving coefficient for a 36 Å radius Ficoll decreased from 0.975 at 0.5 psi to 0.559 at 2.0 psi (25.8–103.4 mmHg).

Fig. 5.

Hydraulic permeability of Matrigel membrane. y-axis, filtration flux; x-axis, transmembrane pressure in PSI. At increasing pressures, the slope of the flux-pressure curve decreases, suggesting membrane compression. To convert PSI to mmHg, multiply by 51.71.

Fig. 6.

Size-dependent filtration by extracellular matrix as a function of membrane flux, in m/s. y-axis, apparent sieving coefficient; x-axis, molecular radius in Angstroms. At low membrane fluxes, little size selectivity is observed (light gray line). As membrane flux increases (progressively darker lines), size selectivity is more pronounced. The ripples evident at lower molecular weights are attributed to noise due to the low solute concentrations in the feed and permeate solutions at those molecular weights. Experimental errors are similar to those depicted in Figs. 3 and 4, but the additional lines to show standard errors have been removed for clarity.

The flux dependence of the Ficoll sieving coefficient can arise from three distinct phenomena: concentration polarization, solute diffusion, and gel compressibility. Concentration polarization refers to the accumulation of retained solutes at the upstream surface of the Matrigel membrane arising from the convective ultrafiltrate flux. The magnitude of the polarization effect is determined by the ratio of the ultrafiltrate flux (J_v) to the bulk mass transfer coefficient (k_m), with the latter a function of the device geometry and the hydrodynamic conditions (63). Previous estimates of the mass transfer coefficient indicate that concentration polarization effects are likely to be small in this system (C_wall/C_bulk < 1.3) (18), and this phenomenon would actually lead to an increase in the ultrafiltrate concentration at high ultrafiltrate flux (or transmembrane pressure), which is opposite of what is observed experimentally.

The rate of solute transport across the membrane has contributions from both convection and diffusion. At high ultrafiltrate flux, Ficoll transport is dominated by the pressure-driven convective flow. As the ultrafiltrate flux decreases, Ficoll diffusion will become more significant, increasing the Ficoll concentration in the ultrafiltrate. The relative contributions of convection and diffusion are determined by the membrane Peclet number

$$\text{Pe=}\frac{J_{\text{v}}{\delta }_{\text{m}}{K}_{\text{c}}}{K_{\text{d}}D}$$ (3)

where δ_m is the thickness of the Matrigel membrane, D is the Ficoll diffusion coefficient, and K_c and K_d are the hindrance factors for convective and diffusive transport, respectively. The calculated values of Pe for our experiments range from 100 to 330 for the 45 Å radius Ficoll (with K_c/K_d = 1), indicating that diffusion is unimportant over the entire range of ultrafiltrate flux. The Peclet number would be even larger for the larger size Ficolls due to the reduction in the Ficoll diffusion coefficient and the increase in magnitude of K_c/K_d due to the greater effect of hydrodynamic interactions on diffusion compared with convection (11).

The hydraulic permeability data in Fig. 5 provide clear evidence that the Matrigel is compressible, with the effective pore size decreasing with increasing transmembrane pressure. The gel compressibility would cause a reduction in the Ficoll sieving coefficient at high ultrafiltration flux (i.e., high transmembrane pressures), consistent with the experimental measurements. The effective pore size (s) of a porous network can be estimated from the measured value of the hydraulic permeability (L_p) as

$$s={\left(\frac{2{\delta }_{\text{m}}{L}_{\text{p}}}{\epsilon }\right)}^{1/2}$$ (4)

where ε is the porosity of the gel (40). The hydraulic permeability is defined as the slope of a plot of the filtration velocity (in m/s) as a function of the transmembrane pressure (in Pascals) multiplied by the solution viscosity (in kg·m⁻¹·s⁻¹). The inclusion of the solution viscosity in the definition of the hydraulic permeability makes L_p independent of the solution properties. The parameter s is equal to the specific area of the pores, defined as the ratio of the total pore volume to the total pore surface area. Thus, for a porous material with a uniform array of cylindrical pores, s = r_pore/2. The hydraulic permeability of the Matrigel, evaluated from the slope of the ultrafiltrate flux vs. pressure data in Fig. 5, varies from ∼2.3 × 10⁻¹² m at 0.5 psi to 1.0 × 10⁻¹² m at 2 psi corresponding to an effective pore size of s = 500 to 330 Å (assuming a Matrigel porosity of 90% and a thickness of 500 μm). This is remarkably similar to the model structure, where the “unit cell” of the tessellated structure is ∼700 Å across, but has an irregular protrusion extending 200 Å into the center of the unit cell.

DISCUSSION

Starting with size and structure measurements made on individual laminin molecules, we constructed a 3-D model of a laminin-nidogen gel that seems consistent with prior imaging studies (59, 60, 62). We simulated rigid-sphere excluded-volume partitioning into gels composed of EHS tumor extracts and compared our predictions with experimental data using FITC-Ficoll. Numerical simulation and experimental results matched well. We then directed attention to an actual basement membrane and measured strongly size-dependent partitioning into LBM as well. Unlike the Matrigel and laminin gels, partitioning into LBM was better simulated by a random fiber model than by a structured lattice alone. We also quantified Ficoll rejection by a Matrigel membrane and observed a pressure and flux dependence to the sieving coefficients.

Molecular architecture and numerical simulation.

What relevance could our observations have to glomerular filtration? Some limits of our model system are clear. Our numerical simulation only included dilute hard-sphere excluded volume considerations and a small subset of GBM constituents. Electrical charge and solute-solute interactions, both thought important in glomerular filtration, were not explicitly calculated, although we are seeking funding to incorporate these phenomena into our simulations. We previously argued that modeling Ficoll as a rigid sphere fails to completely capture the features of this tracer molecule (18).

That said, our physical model system was designed to simplify numerical simulation by excluding several phenomena: FITC-Ficoll is widely taken to be very weakly anionic and so electrostatic interactions between this tracer and the gel are unlikely to dominate; the fluorescent label permits very low concentrations of solute to be used, effectively eliminating solute-solute interactions. The details of Ficoll's distribution of shapes, and whether as we previously suggested, shear-induced deformation is responsible for its hyperpermeability, remain unknown. Our own data suggest that Ficoll sieving closely matches predicted hindrances for a rigid sphere in a slit pore, except where the Ficoll is about the same size as the pore. While our present numerical model doesn't capture that subtlety, our physical model doesn't share the physical features of the previously reported sieving experiment. Our numerical simulation technique lends itself to incorporating more sophisticated interactions, such as electrostatics and more complicated solute and gel geometries.

The overestimation of partition coefficient could be explained by experimental errors in estimating gel volume or by factors not included in our simple excluded volume model. Gel volume was calculated as the volume of liquid gel pipetted into the well, not the actual volume of the gelled material. We used volume displacement techniques and area thickness measurements to attempt to measure gel volumes more accurately, and these measurements seemed to be repeatable to 5–8%, and suggested that the actual gel volumes were slightly smaller than the aliquots of supernatant used in the experiment. Consequently, 10% shrinkage in volume could partly account for the observed discrepancy, despite our efforts to measure gel volumes carefully. Electrostatics were not included in our model, and the fluorescein isothiocyanate is likely not entirely electrically neutral. In fact, a recent paper by Tanner et al. (55) used fluorescein as an anionic modifer to dextran. Electrostatic contributions to partitioning, whether considered as direct charge-charge interactions between solute and gel, or in terms of a Donnan equilibrium between the gel and the bulk solution, could contribute to the difference between calculated and measured partitioning. Another possibility is that the structures we proposed may not have captured the structural features of laminin gels. Electrostatic interactions between solute and gels and structural insight into laminin gels are rich subjects for further investigation.

The geometry of the fibers used to simulate partitioning into LBM is only loosely based on actual estimate of collagen fibril geometry. In particular, the radius of 4.2 nm seems quite large compared with the 1.2-nm-wide structures reported by Adachi, but may be entirely consistent with helical lateral interactions between collagen molecules as reported by Yurchenco (2, 60, 61). Previous efforts to relate partitioning predictions based on steric hindrances alone to measured data have modeled electrostatic effects as an “effective radius” equal to the sum of solute radius and Debye length with some success (17). The artificially large fiber diameters needed for this model to predict hindrances in LBM may constitute an effective radius incorporating multiple phenomena.

Previous efforts to explain and predict partitioning and hindrance in experimental systems using Ogston's model have been challenging, as noted by Deen et al. (13): “Extensive efforts were made to interpret our diffusive and connective hindrance factors for Ficoll using those fiber-matrix theories. The theories were found to be largely unsuccessful in correlating our data…”. The molecular architectures explored here may prove more tractable. The striking difference between the partition coefficients predicted by our numerical simulation and those predicted by Ogston's theory lies in the very sharp size dependence of the partition coefficient. Intuitively this makes good sense: the highly structured architecture we proposed is largely open space, whereas a random pattern of fibers has little open spaces; similarly, the gel architecture we propose has no acute angles in it; a solute has to be very large to be excluded from the region surrounding the intersection of two or more fibers. In contrast, a random array of fibers has many acute angles where fibers pass close to each other, excluding macromolecules. This is the structure suggested for collagen gels, based on Yurchenco's rotary-shadowed electron microscopy data, and indeed our measurements of LBM bear this out (62). Neither our simulation nor Ogston's model captures hydrodynamic effects. Three significant challenges in rendering our approach useful in a theory of glomerular permeability will be developing a framework that incorporates other basement membrane components, incorporates electrostatic effects, and that can predict frictional resistance to solute movement.

Gel compression and glomerular filtration.

We explored pressure-driven filtration by Matrigel and observed size-dependent permselectivity that varied as a strong function of ultrafiltrate flux; at low fluxes there was minimal Ficoll retention while at higher fluxes the size dependence of membrane transport was unmasked. The mechanism of the flux dependence for the Matrigel appears to be related to the compressibility of the gel at high pressures. The effects of Ficoll diffusion on the sieving coefficients appear to be negligible due to the large values of the Peclet number in our model. However, it is important to note that the Matrigel used in these experiments (∼500 μm in thickness) is three orders of magnitude thicker than the human GBM (0.3 μm); thus, these results do not imply that solute diffusion is unimportant in determining physiologic transport rates across the glomerular filter. We explored hydrostatic pressures normally present in the proximal glomerular capillary, suggesting that gel compression of extracellular matrices could be important in vivo (42). This result has been reported several times before in the literature for glomeruli. Robinson and Walton (44) reported similar findings with a gel prepared from acellular glomeruli but observed much more stringent albumin exclusion (θ ≅ 0.03) than we observed for a similarly sized Ficoll molecule (θ ≅ 0.55). Robinson also noted a more pronounced effect of pressure; the sieving coefficient of albumin in GBM decreased from 0.175 to 0.034 with increasing pressure, a decrease of 80%, whereas the sieving coefficient for a 36 Å Ficoll in Matrigel decreased by less than half in our hands (44). This could be explained in part by albumin's significant anionic charge, which greatly alters partitioning and filtration (10). Correlation of our observations with in vivo or ex vivo filtration data remains challenging. Our experimental system is largely convection based; the Peclet number for our system is quite high, even for small molecules, whereas in vivo, the Peclet number in the GBM is thought to be quite low for albumin and similarly sized molecules. In general, the complex mass transport inside the glomerular capillary in response to physiologic disturbances, such as salt loading or hydropenia, is difficult or impossible to tease out. Rippe et al. (43) published results that are generally consistent with our hypothesis: he found that the sieving coefficient for Ficoll decreased with increasing GFR, an effect that might be consistent with gel compression, although the size dependence of filtration appeared blunted at higher GFR. However, the interpretation of in vitro data as evidence for or against a single physiologic mechanism in a complex negative feedback system must be considered speculative.

In Ohlson's sieving measurements using the chilled isolated perfused kidney (cIPK) model two trends are observed, a decrease in fractional clearance for smaller Ficoll with increasing GFR and an increase in fractional clearance for albumin and larger Ficoll with increasing GFR, which the authors interpret in terms of the classic two-pore model for the filtration barrier (39). The decrease in sieving with increased GFR would be consistent with gel compression; the increase for large molecules might represent isolated regions of the capillary loop where in the chilled model podocytes no longer are the force resisting dilation of the capillary loop, and leakage occurs. The very nature of the disconnect between data obtained in the cIPK model and Rippe's in vivo data speaks to the need for mechanistic descriptions of the phenomena.

The ECM gels described here showed only slight size selectivity, compared with the glomerulus. There are many possible explanations for this, the most obvious of which is that the gels tested in this report are far from complete basement membranes, lacking collagen and proteoglyans. Second, the glomerular filtration barrier is a complex multilayer filter comprising endothelial glycocalyx, endothelial cells, basement membrane, and podocytes. The live animal studies and the cIPK necessarily test all components and their interactions, and the live animal studies are complicated by renal autoregulation. The direct effects of volume loading of an animal or increasing perfusate flow rate in a cIPK on mass transport in the nephron are not clear. Increased RBF may dilate the capillary while pressurizing it, mixing compressive and tensile forces on the basement membrane.

Similarly, Edwards, Daniels, and Deen (13) explored pressure-sieving relationships in a gel of compacted acellular glomerular proteins. Edwards reported a similar trend of decreasing θ with increasing pressure, albeit with sieving coefficients of ∼0.1 in their model system, significantly less than in the laminin gel studied here. One would expect a priori that gels composed of collagen and laminin would exhibit much more stringent size exclusion than one of laminin alone, perhaps by orders of magnitude. Collagen and laminin appear to be present in basement membranes in 1:1 stoichiometric ratios. As collagen subunits are much larger than those of laminin (400 vs. 75 nm), a model incorporating both molecules would necessarily include strands of many collagen molecules crossing the “unit cell” of the laminin mesh. This is consistent with Yurchenco's images (62). The implication is that steric exclusion alone will lead to solute partition coefficients that are significantly smaller than those measured and modeled in this report. This report expands on the previous literature in several ways. Klaentschi's and Robinson's important work has been expanded from dextrans and albumin to a globular polydisperse polysaccharide that is presently used as a glomerular probe. The continuous polydispersity of this probe allows more detailed comparison with numerical models than a single globular protein (albumin) or a random-coil (dextran) permit.

The significance of gel compression as a potential mechanism coupling podocyte behavior to filtration characteristics of the GBM has not been widely discussed. If, as has been proposed, the podocyte cytoskeleton holds the capillary loop in place against the hydrostatic pressure of blood, then the endothelial glycocalyx and the GBM are compressed against the podocytes by circulating blood. If the normally circumferential podocyte foot processes are rearranged by drugs or disease, the pressure of circulating blood in the capillary loop will be borne by the GBM and the endothelium. Thus, the GBM, and possibly other layers of the glomerular capillary wall, is in radial compression in health and in circumferential tension in disease. The data here and previously published by other groups suggest that solute partitioning and transport change with varying mechanical forces applied to the GBM. This conceptual framework has the potential to explain results by Miner and Kalluri (25, 26) which have previously been difficult to reconcile with models wherein a single layer of the glomerular capillary wall dominates the filtration barrier. Mutations in laminin and nephrin, when studied carefully, can result in proteinuria with morphologically normal appearing foot processes. Kalluri (26) asserted that “studies with nephrin-deficient mice demonstrate that massive proteinuria can be observed without any defects in the GBM, glomerular endothelium, or podocyte foot processes…all three components of the glomerular filtration barrier are in constant molecular and biochemical communication with each other…”. To this statement we might add mechanical communication as well. Much further work exploring partitioning and hindrance into mechanically stressed gels of ECM is needed to explore whether this proposed mechanical coupling can explain observations to date.

APPENDIX 1

Calculation of the partition coefficient.

In our calculation of the partition coefficient, we exploit two experimental parameters to simplify calculation. First, we assume that the initial incubation of the gel is in such an excess volume of feed solution that concentrations in the feed solution are not affected by solute partitioning into the gel. Second, the supernatant with which the gel is rinsed has the same volume as the gel itself; that is, V_s = V_gel. From those starting points, we have

$$\Phi \equiv \frac{C_{\text{gel}}}{C_{\text{feed}}}$$ (1)

$$C_{\text{gel}(\text{initial})}=\Phi C_{\text{f}}$$ (2)

$$C_{\text{gel}(\text{final})}=\Phi C_{\text{s}}$$ (3)

By mass balance,

$$C_{\text{gel}(\text{final})}{\text{V}}_{\text{gel}}+C_{\text{s}}{\text{V}}_{\text{s}}=C_{\text{gel}(\text{initial})}{\text{V}}_{\text{gel}}$$ (4)

Since we have set V_gel and V_s equal as closely as possible, we can obtain

$$C_{\text{gel}(\text{final})}+C_{\text{s}}=C_{\text{gel}(\text{initial})}$$ (5)

Combining Eqs. 2 and 5

$$C_{\text{gel}(\text{final})}+C_{\text{s}}=\Phi C_{\text{f}}$$ (6)

Combining Eqs. 3 and 6

$$\Phi C_{\text{s}}+C_{\text{s}}=\Phi C_{\text{f}}$$ (7)

And rearranging we obtain:

$$\Phi =\frac{C_{\text{s}}}{C_{\text{f}}-C_{\text{s}}}$$ (8)

For the case of LBMs, it was difficult to remove the supernatant trapped between folds of the tissue without extensive manipulation. A multicompartment model to account for this effect was developed based on the assumption that the largest Ficolls in solution did not partition into the matrix at all. We justified that assumption by the observation that the size-dependent component of the partition coefficient appeared highly repeatable from sample to sample and from run to run, but a size-independent partitioning varied widely from sample to sample and from run to run. We used the measured partition coefficient for the largest Ficoll to estimate the volume of supernatant retained on the surface of the lens membranes. From that, it was straightforward to calculate partitioning into the basement membranes.

GRANTS

This work was supported by Grants 1K08 EB003468 [National Institute of Biomedical Imaging and Bioengineering, National Institutes of Health (NIH)], 1R01 EB008049-01 (National Institute of Biomedical Imaging and Bioengineering, NIH), and R37-DK-36425 (National Institute of Diabetes and Digestive and Kidney Diseases, NIH).