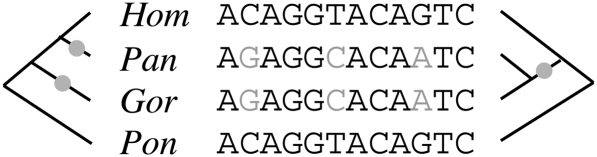Phylogenomics of primates and their ancestral populations

Abstract

Genome assemblies are now available for nine primate species, and large-scale sequencing projects are underway or approved for six others. An explicitly evolutionary and phylogenetic approach to comparative genomics, called phylogenomics, will be essential in unlocking the valuable information about evolutionary history and genomic function that is contained within these genomes. However, most phylogenomic analyses so far have ignored the effects of variation in ancestral populations on patterns of sequence divergence. These effects can be pronounced in the primates, owing to large ancestral effective population sizes relative to the intervals between speciation events. In particular, local genealogies can vary considerably across loci, which can produce biases and diminished power in many phylogenomic analyses of interest, including phylogeny reconstruction, the identification of functional elements, and the detection of natural selection. At the same time, this variation in genealogies can be exploited to gain insight into the nature of ancestral populations. In this Perspective, I explore this area of intersection between phylogenetics and population genetics, and its implications for primate phylogenomics. I begin by “lifting the hood” on the conventional tree-like representation of the phylogenetic relationships between species, to expose the population-genetic processes that operate along its branches. Next, I briefly review an emerging literature that makes use of the complex relationships among coalescence, recombination, and speciation to produce inferences about evolutionary histories, ancestral populations, and natural selection. Finally, I discuss remaining challenges and future prospects at this nexus of phylogenetics, population genetics, and genomics.

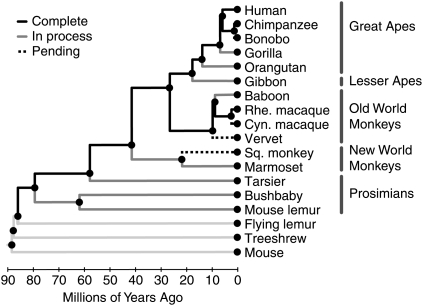
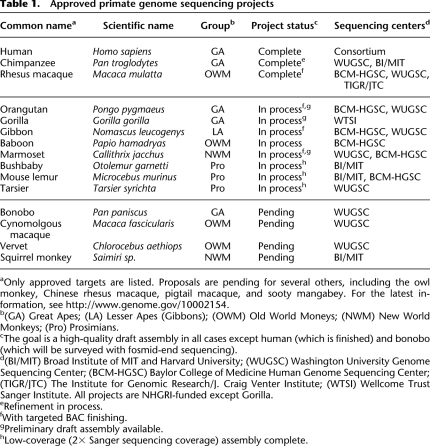
The genome sequence of “Susie,” a female Sumatran orangutan from the Gladys Porter Zoo in Brownsville, Texas, will soon be published (Orangutan Genome Sequencing and Analysis Consortium, in prep.), bringing the total number of sequenced primate species to four (human, chimpanzee, rhesus macaque, and orangutan). Preliminary genome assemblies, with various levels of sequencing coverage, are also available for the gorilla, marmoset, bushbaby, mouse lemur, and tarsier genomes, and work is underway to sequence the gibbon and baboon genomes. Moreover, four additional primate species have been approved for sequencing by the National Human Genome Research Institute (NHGRI) (Fig. 1; Table 1). Thus, genome sequences for at least 15 primate species are expected to be available within the next few years, making the primates one of the most comprehensively sequenced groups on the tree of life.

Figure 1.

Phylogeny of primates, showing species for which sequencing is complete, in process, or approved but pending. Three nonprimates—the flying lemur, treeshrew, and mouse—are shown as outgroups. (Cyn. macaque) Cynomolgous macaque, (Rhe. macaque) Rhesus macaque, (Sq. monkey) Squirrel monkey. An approximate time scale, based on estimated dates of divergence from Janecka et al. (2007) (dates >25 Mya), Goodman (1999) (dates 3–25 Mya), Caswell et al. (2008) (chimpanzee/bonobo), and Morales and Melnick (1998) (rhesus/cynomolgous macaque) is shown at the bottom of the figure. Note that the estimated numbers of years before the present reflect DNA sequence divergences and represent upper bounds on speciation times. Nodes are indicated by circles to emphasize that the phylogeny represents both ancestral and extant species, as well as their evolutionary relationships. Note that the prosimians do not form a proper clade but are paraphyletic.

Table 1.

Approved primate genome sequencing projects

^aOnly approved targets are listed. Proposals are pending for several others, including the owl monkey, Chinese rhesus macaque, pigtail macaque, and sooty mangabey. For the latest information, see http://www.genome.gov/10002154.

^b(GA) Great Apes; (LA) Lesser Apes (Gibbons); (OWM) Old World Moneys; (NWM) New World Monkeys; (Pro) Prosimians.

^cThe goal is a high-quality draft assembly in all cases except human (which is finished) and bonobo (which will be surveyed with fosmid-end sequencing).

^d(BI/MIT) Broad Institute of MIT and Harvard University; (WUGSC) Washington University Genome Sequencing Center; (BCM-HGSC) Baylor College of Medicine Human Genome Sequencing Center; (TIGR/JTC) The Institute for Genomic Research/J. Craig Venter Institute; (WTSI) Wellcome Trust Sanger Institute. All projects are NHGRI-funded except Gorilla.

^eRefinement in process.

^fWith targeted BAC finishing.

^gPreliminary draft assembly available.

^hLow-coverage (2× Sanger sequencing coverage) assembly complete.

Among other things, these new genome sequences will help to identify the genetic basis of differences between primate species, including the genomic features that differentiate humans from other primates (Clark et al. 2003; Pollard et al. 2006b; Prabhakar et al. 2008), to identify and characterize functional sequences present in primates but not other mammals (Boffelli et al. 2003), and to catalog the genomic similarities and differences between humans and nonhuman primates widely used in biomedical research, such as the baboon and rhesus macaque (Rhesus Macaque Genome Sequencing and Analysis Consortium 2007). They will also help to clarify the molecular evolutionary context for human diseases such as AIDS, Alzheimer's, cancer, and malaria (McConkey and Varki 2000; Rhesus Macaque Genome Sequencing and Analysis Consortium 2007; Degenhardt et al. 2009). In short, these new sequence data will put within reach the grand vision of comprehensive genomic resources for primates that was first articulated nearly a decade ago (McConkey and Varki 2000; Boffelli et al. 2003; Enard and Paabo 2004; Goodman et al. 2005).

Perhaps the most informative approach available for comparative genomic analyses of multiple closely related species is to take an evolutionary and phylogenetic perspective—a technique that has been dubbed “phylogenomics” (Eisen and Fraser 2003; Murphy et al. 2004). By explicitly considering the phylogeny by which the species in question are related, phylogenomic methods not only capture the relationships among present-day genomes, but also reveal information about ancestral genomes, and about the lineages on which evolutionary changes have occurred. Moreover, phylogenomics opens up a two-way street between functional and evolutionary analyses, with evolutionary patterns providing information about the potential functions of genomic elements, and functional annotations allowing for richer and more realistic models of evolutionary dynamics. Phylogenomics has been applied widely in many groups of species, including mammals (e.g., Thomas et al. 2003; Rat Genome Sequencing Project Consortium 2004; The ENCODE Project Consortium 2007), yeasts (Cliften et al. 2003; Kellis et al. 2003), drosophilids (Clark et al. 2007; Stark et al. 2007), nematode worms (Stein et al. 2003), and various plants (Yu et al. 2002; Wang et al. 2008). It has already been used extensively within the primates (Boffelli et al. 2003; Rhesus Macaque Genome Sequencing and Analysis Consortium 2007) and is expected to be applied broadly as additional primate genomes become available.

Nevertheless, there is an important—and, perhaps, underappreciated—challenge in applying phylogenomic methods to groups of closely related species such as the primates. Most phylogenomic methods inherit from phylogenetics the assumption that there is a single “correct” species phylogeny that holds across the genomes in question, and that present-day genomes have arisen by a stochastic process that operates along the branches of this phylogeny. This modeling approach ignores variation among individuals of the same species, implicitly assuming that it is negligible relative to variation across species. Within the primates, however, this assumption does not hold. Because species divergence times are short relative to ancestral population sizes, population genetic effects become significant, and variation in local genealogies across loci can be considerable. To take one prominent example, it has been estimated that the canonical ((human chimp) gorilla) species phylogeny holds across only about two-thirds of the genome, with the two alternative tree topologies occurring about one-third of the time, due to deep coalescences of ancestral lineages (Patterson et al. 2006; Hobolth et al. 2007; Burgess and Yang 2008). Population genetic effects, of course, are not limited to the primates—they also impact comparative genomics of other groups of interest, such as the drosophilids (e.g., Pollard et al. 2006a)—but my focus here will be on their implications in primate phylogenomics.

In this article, I will examine the assumptions that underlie phylogenomic analyses from a population genetic point of view, and discuss their limitations within groups of species, such as the primates, that have experienced short intervals between ancestral speciation events relative to their population sizes. These limitations potentially have important consequences for inferences of rates and patterns of mutation, of positive or negative selection, and of the locations of functional elements. After introducing some basic concepts, I will review several pioneering papers from an emerging literature on “population-aware” phylogenomics, which not only consider interspecies comparisons in a more accurate and realistic way, but also shed light on modes of speciation, ancestral populations, and selective forces within the primates. Finally, I will discuss remaining challenges and future prospects at the intersection of phylogenetics and population genetics.

Phylogenetics and species phylogenies

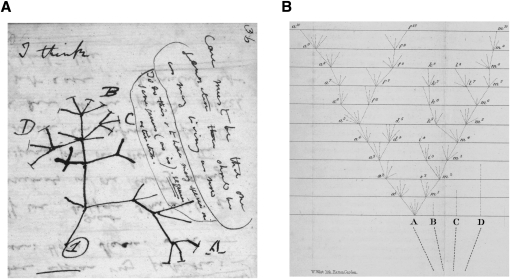
At the core of phylogenetics is the assumption that groups of present-day species are related by a species phylogeny—a tree in which present-day species appear as leaf nodes and ancestral species as internal nodes (Fig. 1). Darwin himself sketched species phylogenies in his celebrated notebooks, and displayed one as the sole figure in The Origin of Species (Fig. 2). While the concept of a phylogenetic tree is now recognized to have limitations—it cannot, for example, accommodate horizontal gene transfer or hybridization between species (Keeling and Palmer 2008)—it remains widely used in evolutionary analysis. This is particularly true for animal species, for which hybridization and horizontal transfer seem to be fairly rare events.

Figure 2.

(A) Sketch of a phylogeny from Charles Darwin's “Notebook B” (1837–1838). (Reproduced with permission from the Syndics of Cambridge University Library.) (B) A portion of the phylogeny that later appeared as the sole figure in The Origin of Species (the version from the first edition is shown). (Reproduced with permission from John van Wyhe ed., The Complete Work of Charles Darwin Online [http://darwin-online.org.uk/]). Darwin seemed quite taken with the metaphor of a tree, and wrote “limbs divided into great branches…were themselves once, when the tree was small, budding twigs; and this connection of the former and present buds by ramifying branches may well represent the classification of all extinct and living species in groups subordinate to groups.” Note that Darwin drew his phylogenies like real trees, with roots at bottom and leaves at top. In contrast, the phylogenies elsewhere in this article (like most in the literature today) are drawn so that time proceeds either from left to right, or from top to bottom.

With the advent of molecular phylogenetics, the concept of the species phylogeny has become central in mathematical models of sequence evolution. These models typically assume that an individual sequence, originally present in an ancestral species at the root of the phylogeny, changes along the branches of the tree from root to leaves, by well-defined string-editing operations that correspond to genetic mutations (e.g., point mutations, insertions, deletions, or inversions). A phylogeny, ancestral sequences, and/or a sequence alignment can be estimated by minimizing an appropriate cost function (Sankoff 1975; Fitch 1977; Felsenstein 1981).

The most widely used statistical model for phylogenetics, originally proposed by Felsenstein (1981) (see also Neyman 1971), allows character substitutions to occur along the branches of a phylogeny by a Poisson (or, more generally, a continuous-time Markov) process, in a branch-length-dependent way. The tree topology, the branch lengths, the parameters of the substitution process, and a prior distribution at the root of the tree define a probability distribution over columns in a multiple alignment, and therefore can be estimated from sequence data by maximum likelihood. The model can be used not only for the estimation of trees, alignments, and ancestral sequences, but also to gain insight into the substitution process (Whelan et al. 2001), to compare competing models, and for hypothesis testing (Huelsenbeck and Rannala 1997). In phylogenomics, it forms the basis of methods for detecting evolutionary conservation (Boffelli et al. 2003; Cooper et al. 2005; Siepel et al. 2005), positive selection (Clark et al. 2003; Nielsen et al. 2005), accelerated evolution (Pollard et al. 2006b), and protein-coding potential (Siepel and Haussler 2004; Gross and Brent 2006). Moreover, it extends readily to non-sequence data, including gene family size (Hahn et al. 2005), categories of protein function (Engelhardt et al. 2005), and protein–protein interactions (Barker and Pagel 2005).

ARGuments for considering population dynamics

By modeling genome evolution as a process by which a single genome sequence mutates along the branches of a species phylogeny, standard phylogenetic models reduce entire populations to single points in genotypic space. In reality, of course, these populations consist of many individuals with similar but nonidentical genomes. Furthermore, these individuals—or, more precisely, chromosomes belonging to these individuals—are related by trees of genetic ancestry known as genealogies (Fig. 3A), whose shapes are influenced by factors such as population size, population substructure, and natural selection. (For simplicity, let us start by ignoring recombination and imagine that whole chromosomes are passed from parents to children; recombination will be introduced below.) These genealogies, and the associated patterns of genetic variation, are traditionally the domain of population genetics, just as species phylogenies and patterns of interspecies divergence are the domain of phylogenetics. Nevertheless, despite their different areas of emphasis, population genetics and phylogenetics are ultimately concerned with the same biological and historical processes. The Felsenstein model can be thought of as an abstraction of these processes that focuses on interspecies divergence and ignores intraspecies variation. Conversely, the coalescent—the predominant model for genealogies (Kingman 1982a,b; Hein et al. 2005; Wakeley 2009)—is an abstraction that focuses on intraspecies variation and ignores interspecies divergence.

Figure 3.

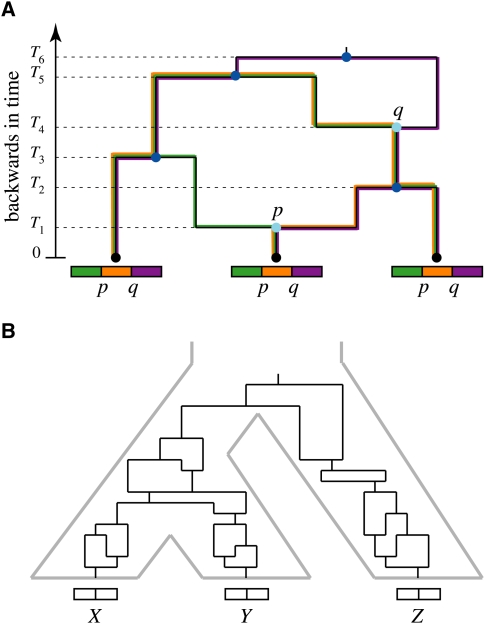
(A) Illustration of a genealogy under the simple Wright–Fisher model. Each row of circles represents the set of individual (nonrecombining) chromosomes in a constant-sized population during a discrete generation. Edges between circles represent inheritance relationships. Under this model, each individual chromosome randomly samples a parent from the previous generation. As a result, the present-day individuals are related by a tree, known as a genealogy, consisting of those individuals and all of their ancestors (black). Notice that many ancestral chromosomes have no present-day descendants. (B) Population genetic interpretation of speciation, assuming discrete generations. At a time τ generations before the present, the population was abruptly partitioned, and the precursors of species X and Y became genetically isolated. Individuals from the two species are related by a genealogy that reflects both this speciation event and the genealogy of their ancestors in the population at the time of speciation. Their time to most recent common ancestor (t) can be decomposed into a time since speciation (τ) and a time since coalescence (T). (C) A three-species phylogeny for species X, Y, and Z, with ancestral species XY and XYZ. Individuals x₁, y₁, and z₁ have a genealogy that reflects the species tree (light gray), but individuals x₂, y₂, and z₂ have a genealogy with a discordant topology (dark gray).

The distinction between the phylogenetic and population genetic perspectives begins to erode when the intervals between speciation events become small relative to ancestral population sizes. This is because the coalescence time—the time backward to the point of common origin—between two randomly selected chromosomes, in a diploid population with effective size N_e, is approximately exponentially distributed with mean 2N_e (in units of generations). Thus, the time t to the most recent common ancestor of chromosomes from species X and Y can be divided into two components: the speciation time τ, or time since complete genetic isolation of X and Y, and the coalescence time T for the ancestors of the selected chromosomes at the time of speciation (Fig. 3B). Assuming an abrupt and complete speciation, τ is a constant for all chromosomes, while T is an exponentially distributed random variable, T ∼ exp(2N_e), whose value depends on the chromosomes sampled. If τ ≫ 2N_e, then t = τ + T is approximately equal to τ and it is reasonable to treat the divergence between individual chromosomes as an estimator of speciation time. Similarly, if τ ≪ 2N_e, then t ≈ T and the situation is approximately that considered by the coalescent. However, if 2N_e and τ are similar in magnitude, then both τ and T make significant contributions to t, and both ancestral population dynamics and interspecies divergence must be considered.

To see how population dynamics can impact phylogenetic inference, consider a phylogeny for three species, X, Y, and Z, with ancestral populations XY and XYZ, corresponding speciation times of τ_XY and τ_XYZ (measured in generations), and ancestral effective population sizes of N_XY and N_XYZ (Fig. 3C). For concreteness, imagine that X, Y, and Z represent human, chimpanzee, and gorilla, respectively. Suppose this phylogeny and its branch lengths are to be inferred from randomly selected chromosomes, one from each of the three species, and, for simplicity, assume the divergence times t_XY and t_XYZ can be estimated from sequence data with high accuracy. If N_XY and N_XYZ are small, then τ_XY and τ_XYZ will be well approximated by t_XY and t_XYZ and the tree will be easily estimated. However, if N_XY and N_XYZ are larger, then t_XY = τ_XY + T_XY and t_XYZ = τ_XYZ + T_XYZ will depend strongly on the exponentially distributed coalescence times, T_XY and T_XYZ, and the branch lengths of the inferred phylogeny will vary substantially depending on the chromosomes that are sampled.

Importantly, the inferred topology as well as the branch lengths may differ from the species phylogeny. The reason is that it is possible for chromosomes from species X and Y to coalesce so deeply that a coalescence between one of them and a chromosome from Z can occur before they coalesce with each other—a phenomenon known as “incomplete lineage sorting” (ILS; see Fig. 3C). Traditionally, ILS is said to produce a difference between a “gene tree” and a “species tree,” although the “gene,” of course, could be any genomic segment of interest. The probability that X and Y coalesce before the speciation of Z is simply given by the cumulative distribution function for the exponential distribution: 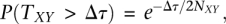where Δτ = τ_XYZ − τ_XY is the interval between speciations. Given that a coalescence of such depth has occurred, the lineages leading to the chromosomes from X, Y, and Z must have been distinct in the X Y Z ancestral population, and, by symmetry, all three possible coalescences of these lineages are equally likely. Thus, the probability of ILS in this three-species phylogeny is 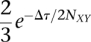(Hudson 1983a; Nei 1987; Pamilo and Nei 1988). Notice that this quantity depends only on the ratio of the interspeciation interval to the ancestral population size, and approaches a maximum value of 2/3 as Δτ approaches zero, or as N_XY approaches infinity. When the ratio Δτ/2N_XY is very small, all topologies are essentially equally likely.

So far we have considered only the case of nonrecombining chromosomes, but in sexually reproducing organisms, meiotic recombination has a major effect on genealogical histories. When tracing lineages backward in time, recombination is in a sense the inverse of coalescence: Instead of causing two lineages to come together to form one (the shared parent of two chromosomal segments), a recombination event makes a single lineage split into two (the parental chromosomes that recombined). There is a slight twist, however, in that these two parent chromosomes are associated with different portions of the descendant chromosome—the segments to the left and the right of the recombination event. As a result, at each position the chromosomes have a tree-like genealogy, but these genealogies will change at positions at which recombination events have occurred. This behavior is captured in a graph called the “ancestral recombination graph,” or ARG (Fig. 4A; Griffiths and Marjoram 1997; Hein et al. 2005). When reading the ARG backward in time, lineages can be seen to coalesce, as in ordinary genealogies, but also to split. The graph as a whole is not a tree, but a tree can be extracted from it at any position by following either the left or right fork at each recombination event, depending on whether the position falls to the left or right of the corresponding event. Thus, the ARG contains a set of marginal genealogies as subgraphs, with a distinct genealogy for each nonrecombining genomic segment. Notably, the ARG must eventually converge on a single chromosome, called the global most recent common ancestor (GMRCA), because (again, going backward in time) the rate of coalescence is quadratic, while the rate of recombination is only linear, in the number of active lineages.

Figure 4.

(A) An ancestral recombination graph (ARG) for three individuals. As the graph is followed backward in time, edges can be seen to merge (times T₂, T₃, T₅, and T₆, dark blue), where descendant lineages coalesce at common ancestors, or to split (times T₁ and T₄, light blue), where descendants derive from recombining ancestors. (By assumption, at most one event occurs at each instant in time, so all internal nodes have three adjacent edges.) Ultimately, coalescences overwhelm recombinations and the graph is reduced to a single node (the global most recent common ancestor). Each recombination node is associated with a point along the sequence at which the recombination event occurred (p or q). For any nonrecombining segment of the sequence (green, orange, and purple), a genealogy can be extracted by choosing the left or right edge exiting each recombination node, depending on the position of the segment relative to the recombination point. Thus, the graph defines a set of marginal genealogies for the nonrecombining segments (traced here in colors matching the segments). (B) A “phylogenetic ARG” for three individuals from different species (X, Y, and Z). This graph is the same as the ARG for individuals in a single interbreeding population except that both recombination and coalescence events are prohibited from occurring across species boundaries (gray). Its marginal genealogies will in general exhibit differences in branch length and topology that reflect ancestral population dynamics and historical recombination.

When the chromosomes under study are drawn from individuals of different species, the genetic isolation of species prohibits interspecific coalescence or recombination events. A kind of constrained ARG results, with constraints reflecting the species phylogeny (Fig. 4B). This “phylogenetic ARG,” as it will be called here, contains a rich store of both phylogenetic and population genetic information. Suppose the phylogenetic ARG is known for a set of samples drawn from different species, with one chromosome per species. As one traverses the chromosome, the marginal genealogies of the ARG will vary both in topology and in branch lengths. The reason is that the modern chromosomes are essentially stitched together, by recombination, from fragments of ancestral chromosomes that have different coalescent histories. In a sense, multiple chromosomes from ancestral populations are sampled as one moves along the chromosome, despite that only one chromosome from each species is represented in the data. As a result, it is possible to perform population genetic analyses on ancestral populations using the phylogenetic ARG, as discussed below.

Implications for phylogenomics

A population-aware view of phylogenetics has numerous implications in phylogenomics. One example is in the reconstruction of species phylogenies from large-scale genomic data, which typically depends on the assumption that the species phylogeny can be directly inferred from sequence data for one individual per species. This approach is reasonable when ancestral population sizes are small relative to interspeciation intervals (i.e., Δτ/2N_e is small), so that the phylogenetic ARG is well approximated by a tree. (Imagine stretching the gray-outlined branches in Figure 4B, whose length corresponds to Δτ and whose width corresponds to N_e, until the ARG contained within them is forced into a tree-like configuration.) When Δτ/2N_e is large, however, a typical method for phylogenetic inference will recover some average over marginal genealogies, which themselves will be highly variable and differ considerably from the species tree. Indeed, it is possible that none of these marginal genealogies will equal the species phylogeny, in terms of both branch lengths and topology. Rather, the species phylogeny exists only as a kind of meta-property of the phylogenetic ARG, with approximate speciation times defined by minima over the corresponding coalescence times in the marginal genealogies.

The “average” phylogeny obtained in phylogenetic reconstruction will depend on the distribution of marginal genealogies present in the sample. Remarkably, it turns out that, even when the assumptions of the coalescent hold, this distribution can favor genealogies with the “wrong” (non-species) topology over ones with the “right” topology (Rosenberg 2002; Degnan and Rosenberg 2006). This circumstance cannot arise with three species, but it is possible with four if interspeciation intervals are short relative to population sizes and if the species topology is asymmetric (which is disfavored by the coalescent). Moreover, it is possible for any topology of five or more species (Degnan and Rosenberg 2006). This fact has an important implication for widely used “concatenated genes” or “supergene” methods for phylogenetic inference, whereby a tree is estimated from sequence data pooled across loci. If the most frequent topology is discordant with the species phylogeny, these methods can converge on the wrong phylogeny. In other words, even a statistically consistent genealogy estimator may be inconsistent as an estimator of the species phylogeny, as has been shown by simulation in the case of maximum likelihood estimation (Kubatko and Degnan 2007). Deriving a consistent estimator may require deeper consideration of the phylogenetic ARG (Liu and Pearl 2006).

The conditions for inconsistency identified by Degnan and Rosenberg (2006) are fairly extreme, and probably do not hold in reality for the primates. However, ILS may still be a significant contributing factor in some persistent ambiguities in phylogenetic inference, particularly in cases in which alternative phylogenies differ by short branches deep in the tree, as with the Euarchonta, Glires, and Laurasiatheria (Thomas et al. 2003; Nishihara et al. 2006); the Afrotheria, Xenarthra, and Boreoeutheria (Murphy et al. 2007); and the Primates, Scandentia, and Dermoptera (Janecka et al. 2007). It is fairly likely in these cases that the ratio Δτ/2N_e was small enough for certain ancestral branches that significant numbers of loci exhibit ILS, perhaps helping to explain the conflicting reconstructions reported by various groups. It has also been argued that ILS may explain widespread discordance in drosophilid phylogenies (Pollard et al. 2006a).

The phylogenetic ARG also has implications for phylogenomic methods that make use of inferred rates and patterns of mutation along the branches of a phylogeny in identifying functional elements or detecting selection. Examples include phylogenomic methods for detecting protein-coding genes (Siepel and Haussler 2004; Gross and Brent 2006), RNA secondary structures (Pedersen et al. 2006), evolutionarily conserved noncoding elements (Boffelli et al. 2003; Cooper et al. 2005; Siepel et al. 2005), or protein-coding genes under positive selection (Nielsen and Yang 1998). Most of these methods assume the Felsenstein model of sequence evolution and a single species phylogeny for the entire genome. If, in contrast, there is significant variation across the genome in local genealogies, complex biases and elevated false-positive/false-negative rates may result (Fig. 5).

Figure 5.

Aligned human (Hum), chimpanzee (Pan), gorilla (Gor), and orangutan (Pon) sequences, showing substitutions (gray) that would each require at least two events to explain under the species phylogeny (left) but only one under a local genealogy resulting from incomplete lineage sorting (right). In a phylogenomic analysis that assumes the species phylogeny holds across the genomes, the observed substitutions will be overcounted, resulting in inflated substitution rates on the branches leading to chimpanzee and gorilla. This type of overcounting can produce complex biases in the prediction of genes or other functional elements, the detection of negative or positive selection, the reconstruction of ancestral genomes, or other phylogenomic analyses (see, e.g., Anisimova et al. 2003).

Embracing the ARG

The previous sections have emphasized the complex relationship between the species phylogeny and the ARG, and the challenges these relationships pose in phylogenomic analyses. However, a population genetic approach to phylogenomics also opens up new opportunities to gain insight into the nature of ancestral primate populations. In recent years, a number of pioneering papers have begun to bridge the gap between phylogenomics and population genetics and, in various ways, to unlock information embedded in the phylogenetic ARG.

Ancestral population sizes

The core idea of using variation in local genealogies to disentangle speciation times and ancestral population sizes has been in circulation for some time (Takahata 1986; Nei 1987). Two simple, but ingenious, approaches were proposed early on, both of which exploited the fact that, with sparse sampling across the genome, the loci under study were likely to be unlinked, and their genealogies could be assumed to be statistically independent. The first method, by Takahata (1986), derived information about ancestral population sizes from the variance in the estimated divergence times for pairs of orthologous sequences. The second, by Wu (1991) (see also Hudson 1983a; Nei 1987), made use of the variance in tree topologies estimated from three or more orthologous sequences. Takahata's method essentially estimated τ_XY and N_XY from the variance in estimates of t_XY at multiple loci (in the notation above), while Wu's method estimated N_XY from the relative frequency of topological inconsistency in reconstructed gene trees.

From the beginning, interest focused on applying these methods to primates, but until the late 1990s this endeavor was hampered by a deficiency of sequence data. An early attempt at a “phylogenomic” analysis was the paper by Takahata and Satta (1997), who were able to scrape together sequences for a few dozen orthologous pairs of genes from human, chimpanzee, gorilla, and various Old World and New World monkeys. Using previously published methods (Takahata et al. 1995), Takahata and Satta obtained estimates of divergence times for the major groups of primates that have held up remarkably well. In addition, they found reasonably strong evidence that ancestral hominoid populations were substantially larger (one to two orders of magnitude) than the current effective human population size of ∼10⁴, although their confidence intervals were large. This research area received a major boost a few years later, when Chen and Li (2001) sequenced 53 autosomal intergenic nonrepetitive regions (totaling ∼24,000 nucleotide sites) from orthologous regions of the human, chimpanzee, gorilla, and orangutan genomes. Assuming an orangutan outgroup, Chen and Li found strong support in a pooled data set for a ((human, chimpanzee), gorilla) topology, but found that 22 of the 53 segments (42%) supported an alternative topology. By Wu's method, they arrived at estimates of 52,000–96,000 for the effective population size of the ancestral population common to humans and chimpanzees, and dates of 4.6–6.2 and 6.2–8.4 million years ago (Mya), respectively, for the chimpanzee and gorilla speciations, in reasonable concordance with Takahata and Satta (1997) (see also Satta et al. 2004). It should be emphasized that these estimates of absolute time and population size, like similar estimates discussed below, require particular values for generation times, mutation rates, and/or certain speciation times to be assumed. In this case, the method was calibrated by assuming an orangutan speciation time of 12–16 Mya and generation times of 15–20 yr.

Following the pioneering work of Takahata and Satta (1997) and Chen and Li (2001), there was a burst of interest in improved statistical methods for joint estimation of ancestral population sizes and speciation times. In particular, it was observed that a failure to account for sources of variance other than coalescence—such as variation in the mutation rate across loci or error in topology reconstruction—could lead to overestimates in ancestral population sizes (Yang 1997, 2002). Indeed, methods designed to consider such variance, when applied to Chen and Li's data, produced substantially reduced estimates of the human/chimpanzee ancestral population size, of ≤30,000 (Yang 1997, 2002; Rannala and Yang 2003; see also Jensen-Seaman et al. 2001)—although the investigators conceded that these estimates could be quite sensitive to their modeling assumptions (concerning, for example, the distribution of mutation rates). The issue of intralocus recombination, which had been ignored by previous methods, was also examined. Wall (2003) reanalyzed Chen and Li's data using summary-likelihood methods based on the coalescent with recombination (Hudson 1983b), and estimated an effective population size for the ancestral human/chimpanzee and human/chimpanzee/gorilla populations of ∼40,000–70,000. In general, these more sophisticated analyses agreed on the point that the effective population sizes of ancestral hominoids were larger than that of present-day humans, but failed to pin down absolute sizes for these populations with any certainty.

Incomplete lineage sorting

As discussed above, local genealogies discordant with the species phylogeny, due to incomplete lineage sorting (ILS), are expected to occur at non-negligible frequencies when ancestral population sizes are large relative to interspeciation intervals, as with the great apes. Indeed, Chen and Li's (2001) study suggested that signatures of ILS are highly prevalent in the human, chimpanzee, and gorilla genomes. Recent studies have further examined ILS in hominoid genomes.

Patterson et al. (2006) approached the issue of ILS in an interesting and innovative way. Working with a data set much larger than any considered previously—consisting of 9.3 million aligned bases from orthologous regions of the human (H), chimpanzee (C), gorilla (G), orangutan (O), and rhesus macaque (M) genomes—they identified sites at which exactly two alleles were observed in the five species (for example, an “A” in human and chimp, and a “G” in the other species), and partitioned these “divergent sites” based on the pattern of allele assignments in the five species. For example, all sites in which human and chimpanzee had one allele and the other species had another allele went in one class (denoted HC sites), while sites in which human differed from the remaining species went in another class (H sites). Patterson and colleagues then considered average properties of sites near each class of divergent sites, focusing in particular on the HC sites and their neighbors, which should reflect the canonical phylogeny for human, chimpanzee, and gorilla, and the HG and CG sites and their neighbors, which should be enriched for ILS. They used various filters and corrections to control for alignment errors, recurrent mutations, mutation rate variation, and other potential sources of bias. They were particularly careful to correct for recurrent mutations, which can easily produce HG and CG sites under the canonical topology, and can lead to biases in downstream analyses without an appropriate correction.

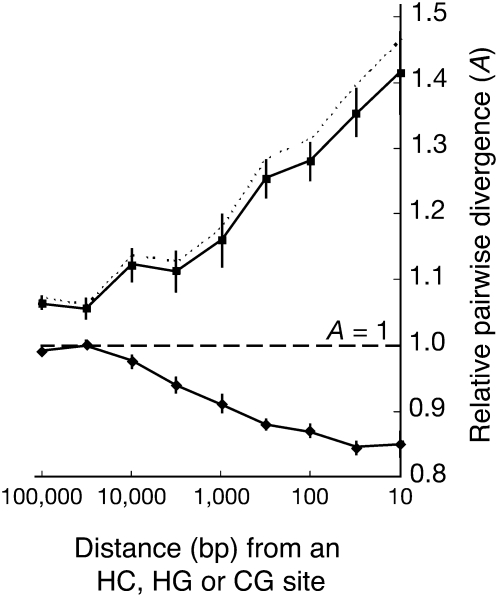
Patterson and coworkers found that human–chimpanzee divergence was substantially reduced in the neighborhood of HC sites and was increased in the neighborhood of HG and CG sites—to 86% and 147% of the autosomal average, respectively (Fig. 6). This observation can be understood in terms of the phylogenetic ARG: The HC sites should be enriched for local genealogies with shallow human–chimpanzee coalescences (see Fig. 3C), and, owing to linkage disequilibrium, so should their neighboring sites. In contrast, HG and CG sites and their neighbors should be enriched for deep human–chimpanzee coalescences. Both of these effects decline with distance (Fig. 6), as local genealogies become decorrelated through the effects of recombination. By a related calculation, Patterson and colleagues estimated that a noncanonical human–chimpanzee–gorilla topology (implying ILS) applies for 18%–29% of the genome. Thus, they were able to shed light on properties of the phylogenetic ARG not by modeling it directly, but by pooling sites expected to have similar genealogies and analyzing them in a relatively straightforward way.

Figure 6.

Average human–chimpanzee divergence near an HC site (upper solid line) and near an HG or CG site (lower solid line) as a function of distance, based on the five-way (HCGOM) alignments of Patterson et al. (2006). Distances are measured as fractions of the genome-wide average (represented by A = 1). The dotted line reflects a correction for recurrent mutations. (Adapted with permission from Macmillan Publishers Ltd. © 2006, Patterson et al. 2006.)

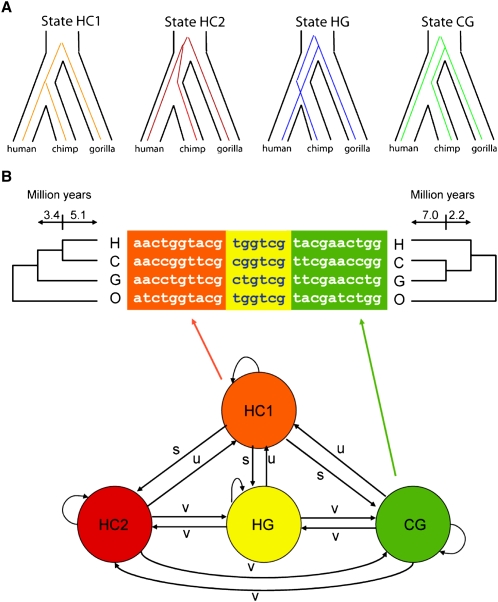
A more direct approach was taken by Hobolth et al. (2007), who approximated the phylogenetic ARG for human, chimpanzee, gorilla, and an orangutan outgroup using a phylogenetic hidden Markov model (HMM). Hobolth and colleagues' HMM consists of four states, one representing a recent coalescence of human and chimpanzee (after the gorilla speciation), and the other three representing the possible genealogies that can occur with deeper human/chimpanzee coalescences (Fig. 7). Transitions between these states represent recombination events, and are parametrized accordingly. The model is approximate in two ways: First, it does not attempt to capture variation in the branch lengths (coalescence times) among the genealogies represented by each state, but simply uses their expected values under the coalescent; and, second, it assumes the transitions between genealogies are Markovian as one traverses the sequence, which, strictly speaking, is not true for the ARG (Wiuf and Hein 1999; McVean and Cardin 2005). Nevertheless, unlike previous models for estimating ancestral population sizes, this “coal-HMM” allows recombinations to occur freely, and makes use of the spatial distribution of informative sites. It not only allows all parameters of interest to be estimated from the data by maximum likelihood, but it also permits efficient computation of posterior probability distributions over the four genealogy classes at each position along the genome.

Figure 7.

(A) The four genealogy types associated with the states of the hidden Markov model of Hobolth et al. (2007). State HC1 describes the case in which the human/chimpanzee coalescence occurs subsequent to the gorilla speciation. States HC2, HG, and CG describe the three possible topologies when the human/chimpanzee coalescence occurs prior to the gorilla speciation. Notice that states HC1 and HC2 both have the species topology, but with shallow and deep human/chimpanzee coalescences, respectively, while states HG and CG represent cases of incomplete lineage sorting (ILS). The orangutan is not shown here, but it is used as an outgroup in the analysis. The branch between the human/chimpanzee/gorilla and orangutan ancestors is assumed to be sufficiently long that ILS in this part of the phylogeny can be ignored. (B) The state-transition diagram for the HMM and an example alignment, with alignment blocks colored to match the states that generated them. The transition parameters s, u, and v, which are estimated from the data, reflect the rates of recombinations that convert one genealogy type to another. (Reprinted from Hobolth et al. 2007.)

Hobolth et al. (2007) applied their coal-HMM to four autosomal human–chimpanzee–gorilla–orangutan alignments, covering a total of 1.9 Mbp, and obtained estimates of speciation times and effective population sizes similar to those from previous studies. For example, they estimated 65,000 ± 30,000 for the ancestral human–chimpanzee effective population size, 45,000 ± 10,000 for the ancestral human–chimpanzee–gorilla effective population size, 4–5 Mya for the human–chimpanzee speciation, and 6–7 Mya for the gorilla speciation (assuming an orangutan divergence time of 18 Mya). In addition, they found evidence for extensive ILS on the autosomes. The HC1 state was predicted for only ∼50% of sites, with the remaining sites proportioned roughly equally among the other three states, so that the HG and CG states (which represent ILS) accounted for about one-third of all sites. Thus, despite the use of quite different methods, Patterson et al. (2006) and Hobolth et al. (2007) arrived at fairly similar estimates for the prevalence of ILS in hominoid genomes.

Mode of speciation

So far, this article has assumed a very simple model of speciation, in which a single ancestral population is abruptly subdivided into two descendant populations at a particular point in time. These two populations are henceforth isolated genetically, and they gradually diverge into separate species. This “instantaneous speciation” model may be reasonable in cases of allopatric speciation, meaning that a geographic barrier has prevented gene flow between nascent species, but it is not appropriate when gene flow between nascent species continues to occur for some time, as in parapatric speciation (Mayr 1963). From the point of view of the phylogenetic ARG, parapatric speciation would produce a porous, rather than an impervious, boundary between species (Fig. 4B). Because different models of speciation make different predictions about the patterns of nucleotide divergence between species, DNA sequence comparisons may be informative about the mode by which particular species have emerged. This idea has been explored extensively by Wakeley, Hey, Nielsen, and colleagues (Wakeley 1996; Wakeley and Hey 1997; Nielsen and Slatkin 2000; Nielsen and Wakeley 2001; see also Beerli and Felsenstein 2001). However, their approach relies on ancestral polymorphisms shared between descendant populations and, hence, is better suited for very closely related species than for species as distant as the great apes.

Recently, there have been several attempts to use alternative models of sequence divergence to shed light on the process of human/chimpanzee speciation. An early approach, by Osada and Wu (2005), was based on the idea of “speciation genes,” which can contribute to speciation through hybrid incompatibility or differential adaptation (Wu and Ting 2004). Osada and Wu conjectured that different estimated speciation times for coding and noncoding regions might be indicative of parapatric speciation (assuming speciation genes occurred at high enough frequency, and noncoding elements of similar effect were rare). Applying a likelihood ratio test to several hundred human, chimpanzee, and gorilla sequences, they found evidence to support such a difference with humans and chimpanzees and suggested it was due to a prolonged genetic exchange. However, their analysis did not consider the effects of selection on the relative coalescence times of coding and noncoding regions (see next section), and it relied on a prominent role for speciation genes. More recently, Innan and Watanabe (2006) developed a model for gradual speciation, in which, starting at speciation, the rate of gene flow increases linearly with time as it is measured backward from the present. This model contains instantaneous speciation as a special case (with a slope of infinity for the linear function), and therefore allows the hypotheses of instantaneous and gradual speciation to be compared by a likelihood ratio test. Based on about 40,000 genomic sequence fragments from human and chimpanzee, Innan and Watanabe (2006) were not able to reject the null hypothesis of an instantaneous human–chimpanzee speciation event, in apparent contrast with the findings of Osada and Wu (2005).

Patterson et al. (2006) were led to the issue of the mode of speciation by observations on the X chromosome. In their study of human/chimpanzee divergence across the genome, they found a striking reduction on the X in comparison with the autosomes, with the X exhibiting only ∼83.5% the average divergence level of the autosomes, along nearly its entire length. (Some reduction is expected because of the reduced effective population size of the X chromosome, but this effect alone would predict a ratio of X to autosome divergence of ∼93%.) An analysis of human and gorilla, in contrast, showed no excess reduction in divergence, indicating that the observations were not due to an anomalously low mutation rate. Patterson and colleagues took these observations to indicate that the human–chimpanzee divergence was significantly more recent on the X than in most regions of the autosomes. Consistent with this hypothesis, they found dramatically reduced evidence for ILS on the X. (Hobolth et al. [2007] obtained similar results when applying their HMM to Patterson and colleagues' X chromosome data.) Patterson and colleagues argued that the peculiar reduction of divergence on the X, together with the large variance in divergence on the autosomes, suggested that the human and chimpanzee lineages may have initially separated, and, roughly a million years later, exchanged genes before separating permanently.

Patterson et al. (2006) noted two side benefits of their hybridization theory. First, a recent divergence of the X would help to resolve a puzzle involving anomalously high estimates of the ratio of male-to-female mutation rates (called α) in human–chimpanzee comparisons. Second, the hybridization scenario would help to explain an apparent conflict between genetic evidence suggesting a speciation date of ≤ 5.4 Mya and the existence of the 6.5–7.4 Myr old Toumaï fossil, which exhibits hominin dental features and evidence of bipedalism. Patterson and coworkers suggested that perhaps the Toumaï represents an early human-like lineage that arose after an initial speciation event, while most of the current human and chimpanzee X chromosomes derive from a subsequent hybridization event. Strong selection on the X from hybrid incompatibility loci might explain why nearly the whole chromosome reflects the more recent event.

Patterson and coworkers' deliberately provocative conjecture had the intended effect of generating controversy within the evolutionary genomics community. In particular, their article elicited critical responses from Barton (2006) and Wakeley (2008). Barton argued that the observation of a large variation in divergence on the autosomes was itself not strong evidence for parapatric speciation, and could as easily be explained by an abrupt (allopatric) speciation event and a large ancestral population size. Indeed, he claimed that the observed variation was consistent with an ancestral population of 45,000, which would make Patterson and colleagues' observations reasonably concordant with numerous previous studies (e.g., Takahata and Satta 1997; Chen and Li 2001; Wall 2003). Barton conceded that the markedly decreased divergence on the X chromosome was puzzling, but argued that this was not the expected effect of hybrid incompatibility, which should reduce gene flow and hence increase divergence times. Similarly, Wakeley (2008) objected that, by Patterson and coworkers' own methods, the human–chimpanzee speciation time estimated from the autosomes predated the average divergence time on the X chromosome, so the reduced divergence on the X was not strictly incompatible with the null model of a simple speciation. He noted that a proper statistical test would have to consider variation in the male-to-female mutation rate ratio α, as well as variation in coalescence times, and such a test had not been applied. Citing various estimates of α in mammals, Wakeley (2008) argued that this quantity could have changed sufficiently during primate evolution to explain the differences between Patterson and colleagues' human–chimpanzee and human–gorilla observations. Patterson et al. (2006) replied, in turn, that their argument for complex speciation rested on their observations on the X chromosome, not the autosomes, and that after recalculating α by Wakeley's methods, they still found the human–chimpanzee versus human–gorilla differences to be unrealistically large. They also pointed out that a mutational explanation would not explain the near absence of ILS on the X chromosome.

Recently, Burgess and Yang (2008) reanalyzed the data of Patterson et al. (2006) in perhaps the most careful attempt to date to estimate hominoid speciation times and ancestral population sizes. Burgess and Yang worked with an updated, realigned, and curated version of the data of Patterson and colleagues, which included the latest chimpanzee and macaque genome assemblies and which was passed through a series of conservative filters to avoid misalignments, rearrangements, and sequencing errors. Applying the Bayesian framework of Rannala and Yang (2003) to this data set, they performed a wide-ranging analysis, considering the effects of sequencing error, the type of neutral sites selected, intralocus recombination, and alternative models for rate variation on estimates of the evolutionary parameters of interest. In addition, they used their Bayesian coalescent model to investigate Patterson and colleagues' observations involving the X chromosome. Their results suggested, in general, that the key evolutionary parameters of interest were fairly insensitive to the subsets of sites considered and to modeling choices for matters such as rate variation and recombination. Based on this larger data set, they obtained estimates of key parameters that were comparable to those of previous studies; for example, N_HC = 100,000, N_HCG = 55,000, N_HCGO = 85,000, τ_HCG = 6.4 Mya, τ_HCGO = 14.6 Mya, and τ_HCGOM ≈ 25–30 Mya, (where H = human, C = chimpanzee, G = gorilla, O = orangutan, M = macaque; these estimates assumed a date of 4 Mya for the HC speciation and a generation time of 15 yr). Like Patterson et al. (2006), they found that estimates of X–autosome divergence ratios were substantially lower for human–chimpanzee than for other pairs of apes. However, they took the additional step of expressing this ratio in terms of ratios of mutation rates, speciation times, and population sizes, drawing on parameter estimates from their Bayesian model. They found little support for reduced human/chimpanzee X–autosome ratios in mutation rates (e.g., due to changes in α) or speciation times (e.g., due to complex speciation), and concluded instead that the most likely cause of the reduced divergence ratios was an unusually small effective population size for the X chromosome in the HC ancestor. They considered several possible causes for such a reduction, rejecting some of them—such as a highly unbalanced sex ratio or high variance in reproductive success in females—as biologically unrealistic, and favoring instead an explanation due to selection at linked loci (see following section).

What can be concluded from Patterson and colleagues' controversial study and the investigations that have followed it? First, it seems clear that Patterson and colleagues' finding of large variation in divergence (and frequent ILS) on the autosomes, while notable for the genome-wide scope of their analysis, is not in itself surprising, but rather is concordant with the results of several previous studies. Furthermore, the studies that followed have agreed that these observations can be explained by realistically large ancestral population sizes, without the need to hypothesize a complex speciation event. Even Patterson and coworkers' estimate of a human/chimpanzee speciation time of <6.5 Myr, while earlier than estimates based on the fossil record, is well in line with most other estimates from genomic data (e.g., Takahata and Satta 1997; Chen and Li 2001; Glazko and Nei 2003; Burgess and Yang 2008). However, Patterson and colleagues' observations of a substantial reduction in human/chimpanzee divergence on the X chromosome are surprising, and do seem to imply something unusual about the ancestral population that split to form the human and chimpanzee lineages. While their hypothesis of delayed introgression and hybrid incompatibility has been controversial, many alternative explanations—for example, involving large changes in the degree of male mutation bias, highly unbalanced sex ratios, high variance in the reproductive success of females, or repeated selective sweeps on the X chromosome—are arguably no more parsimonious. Patterson and colleagues' proposal is seductive in that it resolves several issues simultaneously, including the important problem of an apparent inconsistency between the fossil record and the genetic data. As conjectured by Burgess and Yang and explored further in the next section, a compelling alternative case can be made in terms of selection at linked sites, but many open questions remain in explaining these peculiar observations. In any case, there is no debating the impact that Patterson and colleagues' study has had in stimulating thought and discussion about an important evolutionary puzzle.

Background selection

Recently, McVicker et al. (2009) have explored another topic with implications for Patterson and colleagues' puzzling observations regarding the X chromosome, and, more generally, for the ways in which natural selection has shaped primate genomes. McVicker and coworkers began by observing that evidence of ILS among the great apes was less pronounced near genes than in other regions of the genome. In attempting to explain this observation, they had the insight that reduced ILS near genes could be caused by background selection (BGS), or a reduction in diversity at neutral sites due to linkage with sites under selection (Charlesworth et al. 1993). The connection between BGS and ILS derives from the fact that background selection acts to produce a local decrease in the effective population size of a neutral site that is in linkage disequilibrium (LD) with sites under selection, essentially because a fraction of chromosomes in the population are eliminated owing to deleterious mutations at linked sites. As a result, BGS distorts the phylogenetic ARG in the neighborhood of functional elements, reducing ancestral coalescence times, and, hence, the rate of ILS. The degree of distortion is determined by the collection of selected sites that are in LD with the neutral site, the strength of selection at these sites, and the amount of LD. (Hitchhiking [HH] on advantageous alleles has a similar effect [Maynard Smith and Haigh 1974], but McVicker and colleagues focused on the case of negative selection; see below.) With widespread selection on noncoding functional elements as well as protein-coding genes (Mouse Genome Sequencing Consortium 2002), the effect of background selection could be quite pronounced across the genome. It also may have a disproportionately large influence on the X chromosome, and may help to explain Patterson and colleagues' observations (see below).

McVicker and coworkers undertook a systematic search for signatures of BGS in hominid genomes, working with various data sets, including Patterson and coworkers' alignments of five primate genomes (which they augmented with their own PCR-based sequence data), carefully filtered human–chimpanzee–macaque and human–dog alignments, and human polymorphism data from several sources. Their approach was based on their own classification of sites in the human genome—and, by extension, aligned sites in the other genomes—as being “conserved” (under long-term purifying selection) or “neutral” (free of selective constraint), depending on their degree of phylogenetic divergence across the placental mammals. They compared neutral sites near and far from their conserved sites, in terms of their patterns of divergence within the great apes and their diversity in human populations. In addition, they adapted a theoretical model of BGS (Nordborg et al. 1996) for their purposes, and fitted it to their data by maximum likelihood, conditioning on their predictions of conserved sites and separately estimated recombination rates. This model allowed estimation at each site of a quantity called B, which represented the expected reduction in diversity (or, equivalently, the reduction in the local effective population size) from BGS, relative to pure neutrality (0 ≤ B ≤ 1). The estimates of B considered all linked sites designated as being under selection and a distribution of selective effects, assuming that selection acts multiplicatively and is sufficiently strong that homozygotes for deleterious alleles can be ignored. Selection at exonic and non-exonic sites was modeled separately, to allow for differences in their effects.

McVicker and colleagues found that both human diversity and human/chimpanzee divergence were significantly reduced in the neighborhood of conserved sites, even after normalizing for human/macaque or human/dog divergence to control for mutation rate variation and unidentified selected sites. They also found a significant reduction near conserved sites in the density of human–gorilla (HG) and chimpanzee–gorilla (CG) sites (as defined by Patterson et al. 2006). Both of these observations are consistent with a reduced local effective population size due to BGS. Their quantitative model fit the data well and produced estimates of speciation time, effective population size, mean selection strength, and mutation rates that were, in most respects, consistent with previous estimates (for example, 6 Myr for the human/chimpanzee speciation event, and 99,000 for the effective size of their ancestral population). Their estimates of the overall reduction in diversity due to selection were strikingly high: 22% on the autosomes and 38% on the X chromosome. Thus, indirect effects of selection—whether through BGS or HH—appear to have played a major role in shaping hominid genomes.

McVicker and colleagues were particularly interested in the effects of BGS on the X chromosome, in part because of the findings of Patterson et al. (2006). The X chromosome is notable both for a reduction in the rate of recombination (which, except for the pseudoautosomal regions, can occur in females only) and for its hemizygosity in males, which should produce an increase in the average strength of selection. These properties are expected to conspire to increase the importance of BGS (and HH) on the X, and together may account for McVicker coworkers' much larger estimates for reduction in diversity due to BGS on the X as compared with the autosomes (38% vs. 22%). Indeed, McVicker and colleagues found that the estimated effective population size for the X chromosome under their model was only 24% that of the autosomes, in contrast to the 75% expected under random mating, suggesting that BGS/HH—rather than hybridization or changes in male mutation bias—might explain the decreased human/chimpanzee divergence on the X. However, the uncertainty in McVicker and coworkers' parameter estimates was large, and they could not establish that the effective population size was significantly different from 75%. In addition, if BGS is responsible for the human/chimpanzee observations, then other factors have to be invoked to explain why similar patterns are not seen with gorilla—for example, differences in ancestral population sizes or in the degree of population substructure. Interestingly, there is some evidence for reduced effective population sizes at the time of the human/gorilla speciation relative to those at the human/chimpanzee speciation (Hobolth et al. 2007; Burgess and Yang 2008), which may have led to a proportionally smaller effect of BGS on the X–autosome ratio for human/gorilla than for human/chimpanzee. Current primate behavior also suggests the possibility of a more strongly subdivided ancestral population for human/gorilla than for human/chimpanzee, which would have a similar effect. (These points were made in review by D. Reich and P. Green, respectively.) However, it is not clear whether these effects would be strong enough to produce the striking differences that are observed in comparisons of human with chimpanzee and gorilla.

While McVicker and coworkers' quantitative model generally seemed to fit the data well, it produced two anomalous parameter estimates. The first was the mean selection strength for non-exonic conserved sites, which was estimated to be extremely low, suggesting that many such elements are either false-positive predictions or no longer under selection in hominids (see Keightley et al. 2005). The second parameter was the deleterious mutation rate at exonic selected sites, which was estimated to be several times higher than previous estimates. Essentially, it seems the model is unable to account for the large reduction in sequence divergence observed near exons without positing an unrealistically strong effect from BGS, which is accomplished through an inflated deleterious mutation rate in exons. McVicker and colleagues surmise that this behavior results from some combination of unidentified selected sites and modes of selection not considered by their model, such as positive or fluctuating selection. Indeed, others have argued that HH may provide a better explanation than BGS for observed patterns in the data (Burgess and Yang 2008; Hellmann et al. 2008; see also Macpherson et al. 2007). However, it may be possible to explain the observed patterns completely in terms of negative selection, by considering both incomplete annotation of functional sites and mutational events not captured by the model, such as transposable element insertions (P. Green, pers. comm.).

Future prospects

For all of McVicker and coworkers' accomplishments, their difficulty with the exonic deleterious mutation rate underscores the challenges that remain in interpreting patterns of polymorphism and divergence in primate genomes. It is clear that genomic data sets contain valuable information about evolutionary history, the locations of functional elements, and the forces that have shaped primate genomes. However, it is exceedingly difficult, when attempting to extract this information, to disentangle the effects of mutation, selection, recombination, and ancestral population dynamics. Consequently, most attempts to make inferences about one or more aspects of the evolutionary process have involved strong simplifying assumptions about other aspects, sometimes to their detriment.

The observation of dramatically reduced divergence on the X chromosome presents a particular challenge, because of the unique pattern of inheritance of the X. As discussed, a reduced effective population size of the X relative to the autosomes, male mutation rate bias, background selection/hitchhiking, and introgression combined with hybrid incompatibility all provide possible explanations for reduced divergence on the X. Other effects could potentially contribute as well, such as differences in demographic and mating patterns of males and females, leading to further differences in effective population size between the X chromosome and the autosomes (Hammer et al. 2008; Keinan et al. 2009). Ideally, all of these factors would be modeled simultaneously, and a larger body of sequence data—including, for example, the full gorilla, orangutan, and neanderthal genomes—would be analyzed. Even then, it is not clear whether the puzzle of the X chromosome divergence will be solvable from genetic data alone.

At the heart of many problems of evolutionary reconstruction is the fact that the ARG is essentially unreconstructable from present-day genomic sequences alone. If the phylogenetic ARG could be inferred genome-wide with high accuracy, many properties of interest—such as the rate of ILS, the sizes of ancestral populations, and the species phylogeny—would become trivial to estimate, while others—concerning, for example, modes of speciation, the locations of functional elements, and sites under positive or negative selection—would be much easier to estimate than they are now. However, reconstruction of the ARG is well known to be a formidable statistical and computational problem (Griffiths and Marjoram 1996; Kuhner et al. 2000; Hein et al. 2005; Song and Hein 2005). There are at least two major obstacles: First, the problem of searching the space of ARGs is computationally intractable, even in a restricted, parsimony-based formulation (Wang et al. 2001); and second, the data typically provide only weak information about which ARG is most likely, so that the posterior distribution over possible ARGs (to put the matter in Bayesian terms) is diffuse. Inference of the ARG is further complicated by poorly understood and difficult-to-model heterogeneities in the biological processes that give rise to it, such as differences among species in recombination hot spots (Winckler et al. 2005), and variation in mutation rates and patterns across sites and across branches of the phylogeny (Yang 1994; Hwang and Green 2004). Thus, the appealing strategy of first reconstructing the ARG to high accuracy, and then using it to address various evolutionary and functional questions of interest, does not seem to be feasible.

Is the enterprise of evolutionary genomics then hopeless? Of course not. There are many possible ways to incorporate histories of recombination and coalescence into phylogenomic analyses without explicitly reconstructing the ARG. These range from approaches that gain power by pooling data across loci (as Patterson and coworkers did), to approximate models that operate, in a sense, on a “collapsed” or marginalized ARG (like the model of Hobolth et al. 2007), to full Markov chain Monte Carlo sampling approaches that effectively integrate out “nuisance” variables irrelevant to the problem at hand (Kuhner et al. 2000). In some cases, progress may be achieved by a “divide and conquer” strategy, in which key variables or parameters are estimated in separate analyses (as with McVicker and colleagues' conserved elements and recombination rates). For some analyses, it may be enough to work with a “minimal ARG” approximated by an efficient algorithm (Song and Hein 2005). Statistical power may be improved by considering indels, rearrangements, and duplications as well as substitutions. Finally, in some cases, it may be sufficient to be aware of population-level effects when performing conventional phylogenomic analyses—for example, by excluding regions of the genome that show evidence of ILS in analyses in which they may produce biases.

Molecular evolution is a forbiddingly complex process, involving the interplay of forces that operate at multiple scales in space and time, on molecules, organisms, populations, and species. It is unlikely that there will ever be a unified model that captures all aspects of this process and provides a ready answer to any question of interest. Instead, it will continue to be necessary to make use of abstractions that capture certain aspects of the process in detail, but dramatically simplify others. Nevertheless, increases in sequence data, computational power, and modeling sophistication will allow for the use of increasingly rich and complex models. As demonstrated by the papers discussed here, the time is ripe for breaking down the remaining barriers between traditional phylogenetic and population genetic models of molecular evolution, and for applying unified models to the wealth of newly available sequence data for primates.