Pyramidal Neuron Number in Layer 3 of Primary Auditory Cortex of Subjects with Schizophrenia

Abstract

Individuals with schizophrenia demonstrate impairments of sensory processing within primary auditory cortex. We have previously identified lower densities of dendritic spines and axon boutons, and smaller mean pyramidal neuron somal volume, in layer 3 of the primary auditory cortex in subjects with schizophrenia, all of which might reflect fewer layer 3 pyramidal neurons in schizophrenia. To examine this hypothesis, we developed a robust stereological method based upon unbiased principles for estimation of total volume and pyramidal neuron numbers for each layer of a cortical area. Our method generates both a systematic, uniformly random set of mapping sections as well as a set of randomly rotated sections cut orthogonal to the pial surface, within the region of interest. We applied our approach in twelve subjects with schizophrenia, each matched to a normal comparison subject. Primary auditory cortex volume was assessed using Cavalieri’s method. The relative and absolute volume of each cortical layer and, within layer 3, the number and density of pyramidal neurons was estimated using our novel approach. Subject groups did not differ in regional volume, layer volumes, or pyramidal neuron number, although pyramidal neuron density was significantly greater in subjects with schizophrenia. These findings suggest that previously observed lower densities of dendritic spines and axon boutons reflect fewer numbers per neuron, and contribute to greater neuronal density via a reduced neuropil. Our approach represents a powerful new method for stereologic estimation of features of interest within individual layers of cerebral cortex, with applications beyond the current study.

Introduction

In subjects with schizophrenia, the processing of sensory information within the primary auditory cortex is impaired (Javitt, Doneshka, Grochowski, and Ritter, 1995; Javitt, Shelley, and Ritter, 2000; Javitt, Steinschneider, Schroeder, Vaughan, and Arezzo, 1994; Javitt, Strous, Grochowski, Ritter, and Cowan, 1997; Rabinowicz, Silipo, Goldman, and Javitt, 2000). These impairments manifest as the reduced ability to discriminate tones (Javitt, Shelley, and Ritter, 2000; Strous, Cowan, Ritter, and Javitt, 1995; Wexler, Stevens, Bowers, Sernyak, and Goldman-Rakic, 1998), and impaired generation of auditory event-related potentials (Ahveninen, Jääskeläinen, Osipova, Huttunen, Ilmoniemi, Kaprio, Lönnqvist, Manninen, Pakarinen, Therman, Näätänen, and Cannon, 2006; Javitt, Doneshka, Grochowski, and Ritter, 1995; Javitt, Grochowski, Shelley, and Ritter, 1998; Laurent, Garcia-Larréa, d’Amato, Bosson, Saoud, Marie-Cardine, Maugière, and Dalery, 1999; O’Donnell, Vohs, Hetrick, Carroll, and Shekhar, 2004; Salisbury, Kuroki, Kasai, Shenton, and McCarley, 2007; Shelley, Silipo, and Javitt, 1999). Tone discrimination deficits are evident even in the absence of an inter-tone interval (Javitt, Strous, Grochowski, Ritter, and Cowan, 1997), and as such are unlikely to be secondary to impairments in cognitive functions such as working memory that depend on non-auditory cortex. Impaired tone discrimination correlates with selective impairments in the ability to discriminate spoken emotion (prosody) (Leitman, Foxe, Butler, Saperstein, Revheim, and Javitt, 2005), a core negative symptom in individuals with schizophrenia (Shea, Sergejew, Burnham, Jones, Rossell, Copolov, and Egan, 2007), that impairs the ability to recognize and convey important cues for successful social interactions (Leitman, Ziwich, Pasternak, and Javitt, 2006). Deficits in tone discrimination are also correlated with impairments in phonemic processing and reading attainment in subjects with schizophrenia, thus potentially contributing to cognitive impairments in these individuals (Aspromonte, Saccente, Ziwich, Javitt, and Revheim, 2008).

Subjects with schizophrenia similarly show deficits in auditory cortical structure. The auditory cortex in humans is located within the Sylvian fissure on the superior temporal gyrus (STG). Within the STG, the primary auditory cortex is located on the first transverse (Heschl’s) gyrus, while the auditory association cortices are posterolateral to the primary cortex, within Heschl’s sulcus and on the planum temporale (Bailey and von Bonin, 1951; Braak, 1980; Garey, 1999; Hackett, Preuss, and Kaas, 2001; Nakahara, Yamada, Mizutani, and Murayama, 2000; Rivier and Clarke, 1997; Sweet, Dorph-Petersen, and Lewis, 2005; von Economo and Koskinas, 1925; Wallace, Johnston, and Palmer, 2002). In vivo studies using magnetic resonance imaging have found that reduced gray matter volume of the STG is the most consistently reported change in cortical gray matter volume in subjects with schizophrenia (as summarized in (Honea, Crow, Passingham, and Mackay, 2005; McCarley, Wible, Frumin, Hirayasu, Levitt, Fischer, and Shenton, 1999)). STG gray matter volume reductions do not seem to be an artifact of illness duration or antipsychotic treatment because they are already present in subjects with schizophrenia at the time of their first psychotic episode (Hirayasu, McCarley, Salisbury, Tanaka, Kwon, Frumin, Snyderman, Yurgelun-Todd, Kikinis, Jolesz, and Shenton, 2000; Hirayasu, Shenton, Salisbury, Dickey, Fischer, Mazzoni, Kisler, Arakaki, Kwon, Anderson, Yurgelun-Todd, Tohen, and McCarley, 1998; Kasai, Shenton, Salisbury, Hirayasu, Onitsuka, Spencer, Yurgelun-Todd, Kikinis, Jolesz, and McCarley, 2003), and in some subjects at high risk for onset of schizophrenia (Rajarethinam, Sahni, Rosenberg, and Keshavan, 2004). Furthermore, gray matter volume reductions in STG are not found in psychotic bipolar disorder subjects (Hirayasu, McCarley, Salisbury, Tanaka, Kwon, Frumin, Snyderman, Yurgelun-Todd, Kikinis, Jolesz, and Shenton, 2000; Hirayasu, Shenton, Salisbury, Dickey, Fischer, Mazzoni, Kisler, Arakaki, Kwon, Anderson, Yurgelun-Todd, Tohen, and McCarley, 1998), and are not prominent in subjects with alcohol dependence (Mathalon, Pfefferbaum, Lim, Rosenbloom, and Sullivan, 2003; Sullivan, Mathalon, Lim, Marsh, and Pfefferbaum, 1998), suggesting that these reductions reflect the disease process of schizophrenia. Several studies have examined gray matter reductions specifically within Heschl’s gyrus of subjects with schizophrenia. Though an early report indicated no change in volume (Barta, Pearlson, Brill II, Royall, McGilchrist, Pulver, Powers, Casanova, Tien, Frangou, and Petty, 1997), subsequent studies conducted in individuals at first episode of psychosis indicated modest reductions in Heschl’s gyrus gray matter volume in subjects with schizophrenia relative to normal controls and to subjects with affective psychosis (Hirayasu, McCarley, Salisbury, Tanaka, Kwon, Frumin, Snyderman, Yurgelun-Todd, Kikinis, Jolesz, and Shenton, 2000; Kasai, Shenton, Salisbury, Hirayasu, Onitsuka, Spencer, Yurgelun-Todd, Kikinis, Jolesz, and McCarley, 2003; Salisbury, Kuroki, Kasai, Shenton, and McCarley, 2007).

The above functional and structural abnormalities in subjects with schizophrenia both point to impairments in layer 3 of primary auditory cortex (Lewis and Sweet, 2009). In a series of postmortem studies in subjects with schizophrenia we have identified a reduction in several constituents of the gray matter microcircuitry within this layer of primary auditory cortex which may contribute to both the observed functional and volume deficits. In deep layer 3 of the primary auditory cortex we observed reductions in mean pyramidal neuron somal volume (Sweet, Bergen, Sun, Sampson, Pierri, and Lewis, 2004) and in densities of markers of axon boutons (Sweet, Bergen, Sun, Marcsisin, Sampson, and Lewis, 2007) and dendritic spines (Sweet, Henteleff, Zhang, Sampson, and Lewis, 2009). All of these findings could be attributable to a smaller number of layer 3 pyramidal neurons in subjects with schizophrenia. For example, if the number of large pyramidal neurons in layer 3 was reduced in schizophrenia, one would expect a smaller mean pyramidal neuron somal volume, as well as the loss of their dendritic spines and the boutons arising from their intrinsic axon collaterals, which terminate extensively within this layer (Ojima, Honda, and Jones, 1991). Although we did not observe reduced pyramidal neuron density in our study of somal volume (Sweet, Bergen, Sun, Sampson, Pierri, and Lewis, 2004), this finding would not preclude reduced pyramidal neuron numbers if primary auditory cortex layer 3 volume was also reduced. We therefore sought to estimate the total pyramidal neuron number in layer 3 of primary auditory cortex in subjects with schizophrenia.

Definitive identification of pyramidal neurons by their morphological features requires sections that are cut orthogonal to the pial surface. Robust stereological estimation based upon unbiased principles of sampling requires this criterion to be met throughout the full extent of the convoluted cortical region of interest, in this case the primary auditory cortex. To accomplish this end, we developed a novel approach, combining the determination of primary auditory cortex volume using the Cavalieri method (Gundersen and Jensen, 1987) with the preparation of Fixed Axis VErtical Rotator (FAVER) (Dorph-Petersen and Gundersen, 2003) sections to examine layer 3; in the latter step the tissue was oriented such that all resultant sections were orthogonal to the pial surface, allowing identification of pyramidal neurons and enhancing identification of the boundaries of all six cortical layers.

Results

Primary Auditory Cortex and Layer Volumes

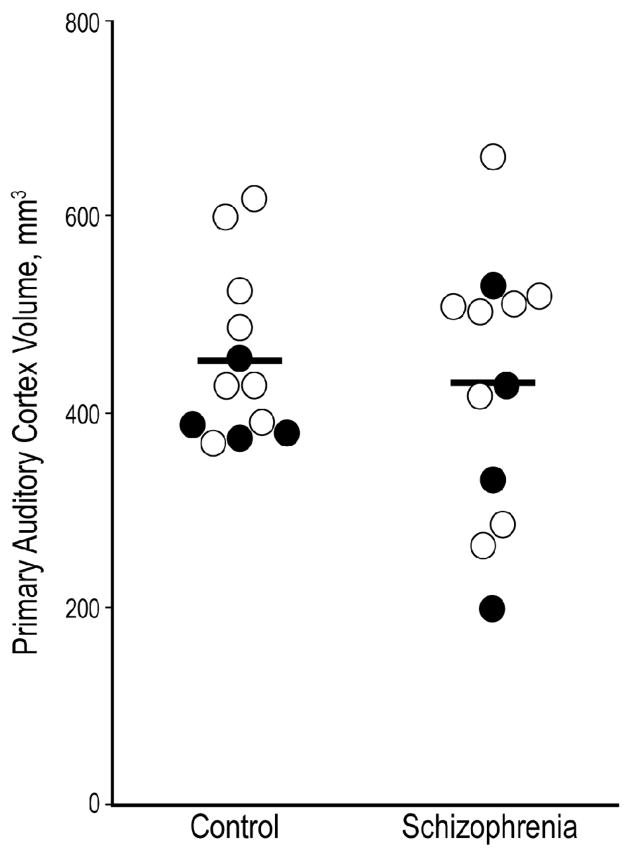
Gray matter volumes of the primary auditory cortex for the 12 subject pairs are shown in Figure 1. The mean (CV) volume of the primary auditory cortex gray matter in subjects with schizophrenia was 428 mm³ (0.32). The corresponding value in the comparison subjects was 451 mm³ (0.19) (F_1,10 = 0.3; p = 0.59). The V_V and V_{Tot Layer} for the individual cortical layers are shown in Table 1. Neither of these measures significantly differed between the schizophrenia and control subjects in any layer. The V_V and V_{Tot Layer} for layer 3 are shown in Figure 2, A–B.

Figure 1. Volume of primary auditory cortex in subjects with schizophrenia and normal comparison subjects.

Gray matter volume was unchanged in the primary auditory cortex of subjects with schizophrenia. Pairs with affected subjects diagnosed with schizophrenia are shown as open circles; pairs in which the affected subject was diagnosed with schizoaffective disorder are shown as filled circles. Horizontal bars denote group means.

Table 1.

Volumes of individual layers of the primary auditory cortex in subjects with schizophrenia and normal control subjects.

	Volume Fraction (VV) Mean (CV)			Volume (VTot Layer), mm3 Mean(CV)
	Control	Schizophrenia	F1,10, p	Control	Schizophrenia	F1,10, p
Layer 1	0.111 (0.14)	0.117 (0.22)	0.14, 0.71	49.81 (0.21)	48.35 (0.31)	0.31, 0.59
Layer 2	0.087 (0.19)	0.090 (0.14)	0.10, 0.76	39.13 (0.27)	38.07 (0.33)	0.10, 0.75
Layer 3	0.356 (0.12)	0.343 (0.12)	0.46, 0.51	158.62 (0.17)	144.04 (0.29)	1.47, 0.25
Layer 4	0.095 (0.15)	0.098 (0.15)	0.84, 0.38	43.00 (0.29)	42.30 (0.38)	0.02, 0.88
Layer 5	0.134 (0.16)	0.127 (0.18)	0.53, 0.48	59.99 (0.20)	55.04 (0.41)	0.40, 0.54
Layer 6	0.218 (0.24)	0.225 (0.24)	0.21, 0.65	100.26 (0.37)	99.70 (0.45)	0.00, 0.95
			Total	451 (0.19)	428 (0.32)	0.30, 0.59

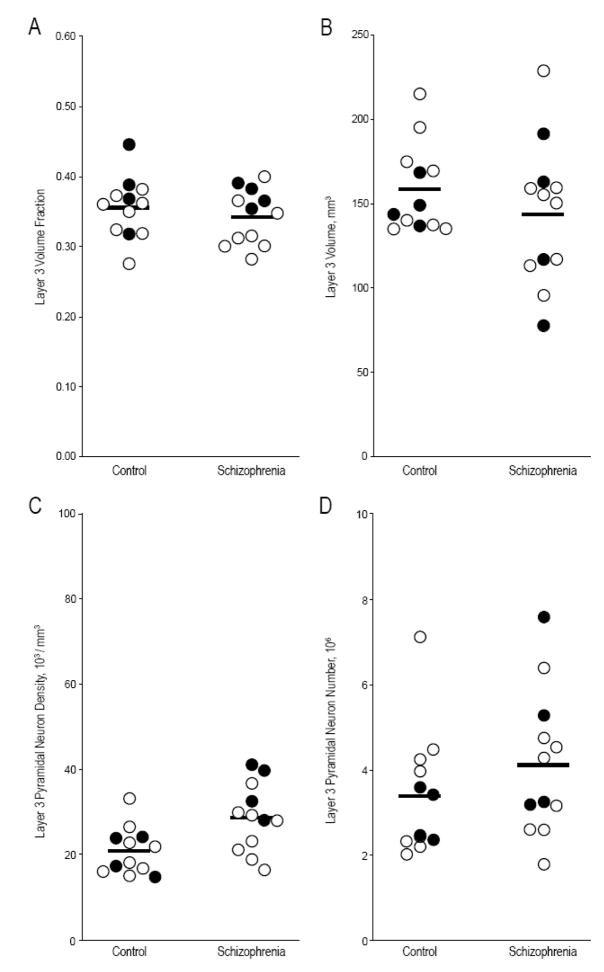
Figure 2. Layer 3 volume fraction, volume, pyramidal neuron density, and pyramidal neuron number in primary auditory cortex of subjects with schizophrenia and comparison subjects.

Only pyramidal neuron density differed significantly between subjects with schizophrenia and comparison subjects (see text). Pairs with affected subjects diagnosed with schizophrenia are shown as open circles; pairs in which the affected subject was diagnosed with schizoaffective disorder are shown as filled circles. Horizontal bars denote group means.

Pyramidal Neuron Number

Mean (CV) layer 3 pyramidal neuron N_V in comparison subjects was 20.7 ×10³/mm³ (0.27) (Figure 2). In subjects with schizophrenia the corresponding value was 28.6 ×10³/mm³ (0.28), an elevation of 38.0% which was significant (F_1,10 = 10.52; p = 0.009). However, mean (CV) layer 3 pyramidal neuron number (N) for comparison subjects was 3.38 ×10⁶ (0.43) while in subjects with schizophrenia it was 4.11 ×10⁶ (0.41), a non-significant difference (F_1,10 = 1.25; p = 0.29).

Precision of estimates

The CEs for the main estimates are shown in Table 2. It is apparent, that all CEs are small compared to the respective observed CVs. This suggests that the various estimates are robust, and that most of the observed variation in our results is due to biological variation across subjects.

Table 2.

Estimates and sources of methodologic error contributing to determinations of layer 3 pyramidal neuron N and N_V in the primary auditory cortex of subjects with schizophrenia and normal control subjects (see text for significance tests).

		Control			Schizophrenia
Estimator	Mean	CV	CE (Lower, Upper)	Mean	CV	CE (Lower, Upper)
VPrimary, mm3	451	0.19	0.035	428	0.32	0.036
VV Layer 3	0.356	0.12	0.068, 0.087	0.343	0.12	0.060, 0.077
VTot Layer 3, mm3	158.62	0.17	0.075, 0.093	144.04	0.29	0.070, 0.085
NV, 103/mm3	20.7	0.27	0.059, 0.077	28.6	0.28	0.065, 0.085
N, 106	3.38	0.43	0.096, 0.121	4.11	0.41	0.096, 0.12

Discussion

Implications for auditory function and development in subjects with schizophrenia

In a different cohort, we had previously identified lower pyramidal cell mean somal volume and lower densities of axon boutons and dendritic spines in deep layer 3 of primary auditory cortex (Sweet, Bergen, Sun, Marcsisin, Sampson, and Lewis, 2007; Sweet, Bergen, Sun, Sampson, Pierri, and Lewis, 2004; Sweet, Henteleff, Zhang, Sampson, and Lewis, 2009), a set of findings which could result from fewer layer 3 pyramidal neurons. The current findings, though subject to potential limitations as discussed below, do not support this hypothesis. The two groups did not significantly differ in pyramidal neuron number, a finding consistent with prior stereologic studies finding no global change in neuron number across the cerebral cortex (Pakkenberg, 1993), in the prefrontal cortex (Thune, Uylings, and Pakkenberg, 2001), or in the anterior cingulate gyrus (Stark, Uylings, Sanz-Arigita, and Pakkenberg, 2004) in subjects with schizophrenia.

Thus, the current findings would indicate our prior observations regarding spine and bouton densities likely result from a lower number of spines and boutons per pyramidal neuron. This explanation with regards to dendritic spines is consistent with studies conducted using Golgi preparations to examine layer 3 pyramidal neurons in other cortical regions, which have found lower spine density per unit dendritic length in subjects with schizophrenia (Garey, Ong, Patel, Kanani, Davis, Mortimer, Barnes, and Hirsch, 1998; Glantz and Lewis, 2000). Reduced numbers of excitatory synapses per pyramidal neuron might then serve to reduce current flow within layer 3 primary auditory cortex circuits in individuals with schizophrenia, a process consistent with physiologic observations (Javitt, Grochowski, Shelley, and Ritter, 1998; Javitt, Steinschneider, Schroeder, Vaughan, and Arezzo, 1994).

The lack of altered pyramidal neuron number in auditory cortex layer 3 differs from the finding of reduced neuron number in the primary visual cortex in subjects with schizophrenia (Dorph-Petersen, Pierri, Wu, Sampson, and Lewis, 2007). In that region, reduced neuron number resulted from a smaller cortical surface area allocated to primary visual perception (Dorph-Petersen, Pierri, Wu, Sampson, and Lewis, 2007), suggesting the existence of a schizophrenia-related change in cortical parcellation. Because cortical parcellation in primates reflects an in utero neurodevelopmental process (Mai and Ashwell, 2004), such findings, as well as other lines of evidence (Lewis and Levitt, 2002), potentially point to an in utero timing of altered visual cortex development in subjects with schizophrenia. In contrast to the visual cortex, gray matter volume reductions of the primary auditory cortex appear to be progressive at or around the time of disease onset in late adolescence and early adulthood, and associated with progressive impairments in cortically generated MMN (Kasai, Shenton, Salisbury, Hirayasu, Onitsuka, Spencer, Yurgelun-Todd, Kikinis, Jolesz, and McCarley, 2003; Salisbury, Kuroki, Kasai, Shenton, and McCarley, 2007). This developmental period is instead characterized by reductions in neuropil elements, predominantly loss of axospinous synapses (Rakic, Bourgeois, Eckenhoff, Zecevic, and Goldman-Rakic, 1986). We have similarly observed reduced densities of pre- and post-synaptic neuropil structure components in deep layer 3 of primary auditory cortex in subjects with schizophrenia (Sweet, Bergen, Sun, Marcsisin, Sampson, and Lewis, 2007; Sweet, Henteleff, Zhang, Sampson, and Lewis, 2009). The loss of neuropil would not be expected to impact neuronal number, though it might contribute to increased neuronal density via a reduction in the regional and layer volumes, a pattern consistent with the observed increase in pyramidal neuron density in our sample. Regardless, the difference in findings between auditory and visual cortex at least raise the possibility that cortical abnormalities which contribute to functional deficits in subjects with schizophrenia may arise via multiple mechanisms, with different developmental timings.

Methodologic Considerations

We have for the current study successfully developed a novel stereological design for robust estimation of volume and cell number of individual layers of specific regions of the cerebral cortex. Similar to existing approaches (Bussière, Giannakopoulos, Bouras, Perl, Morrison, and Hof, 2003; van Kooten, Palmen, von Cappeln, Steinbusch, Korr, Heinsen, Hof, van Engeland, and Schmitz, 2008), our method generates standard anatomical mapping sections for reliable delineation and robust estimation of the total volume of the region of interest. Our approach also generates a set of FAVER sections from blocks sampled uniformly random across the whole region of interest. These sections, which are unique for the current design, are all orthogonal to the pial surface, resulting in several advantages relative to prior approaches. Our FAVER sections facilitate delineation of all cortical layers in their full 3D-extent, a process which can be challenging in standard coronal sections which may intersect a region of interest at varying degrees of orientation relative to the cell layers. As a result, this set of sections may be used with a range of existing stereological probes to generate layer- and region-specific estimates. As a consequence of their consistent orientation orthogonal to the pial surface, our FAVER sections also provide for robust identification of pyramidal cell morphology throughout the region and layers of interest, allowing unbiased quantification of this important cell type. It is also possible to use FAVER sections to directly estimate total pyramidal neuron numbers and layer volumes using a fractionator approach. However, in a fractionator design it is likely that a higher number of FAVER blocks need to be generated to ensure sufficient precision. Finally, the set of FAVER sections generated in the current approach (i.e. from a set of randomly rotated blocks with uniformly random position within the region of interest) should also provide for robust estimates of cell volume using the nucleator or rotator (Gundersen, 1988; Vedel Jensen and Gundersen, 1993). This is unique for the current design, not a general feature of FAVER sections (Dorph-Petersen and Gundersen, 2003).

The current method is somewhat similar to a stereological design previously published by one of us (Dorph-Petersen, 1999), with the important difference that the current method allows for reorientation of the tissue blocks to ensure optimal visualization of all six cortical layers. It should be noticed that the current method is only applicable in almost prismatic cortical regions —i.e. in cortical regions like the STG, where the cortex shows limited curvature in one dimension (here, in the direction parallel to Heschl’s Gyrus). This allows the initial cut slabs to be performed almost orthogonal to the pial surface and subsequently the generation of usable FAVER blocks containing all six cortical layers. The latter would not be possible in a cortical region with extensive curvature in all three dimensions.

The sampling principle of the current method allows unbiased estimation of the total volume and the total number of all identifiable cell types in each cortical layer. However, it should be emphasized that the method also allows for unbiased estimation of the respective mean densities. This is less trivial than it may seem: The local cortical densities vary as a function of the gyrational pattern (e.g. bottom of sulci vs. top of gyri) and global gradients across the region of interest may be present. Therefore, the cell or volume density of a cortical layer measured in an arbitrary section is not representative for the whole region of interest and cannot form the basis of an unbiased estimate of the relevant mean density. Also, due to the convoluted nature of the human cerebral cortex, series of sections cut with some fixed orientation, e.g. coronal, will virtually always contain some parts of the cortex cut obliquely or tangentially, rendering less reliable the delineation of the individual cortical layers and preclude consistent identification of certain structural elements such as pyramidal neurons. This effectively prevents unbiased estimation of features within layers, or of pyramidal neurons. Furthermore, the unavailable parts of the cortex, cut obliquely or tangentially, will be located in certain specific positions depending on the gyration, which may show systematic differences between study groups (Chance, Tzotzoli, Vitelli, Esiri, and Crow, 2004). These potential biases apply to the two prior studies of neuron density in auditory cortex of subjects with schizophrenia, which relied upon a limited set of sections cut in a fixed, coronal, orientation. We previously reported unchanged pyramidal neuron density in deep layer 3 of primary auditory cortex in one such study, (Sweet, Bergen, Sun, Sampson, Pierri, and Lewis, 2004) while a study of layer 3 neuron density in Heschl’s gyrus also found no significant differences between subjects with schizophrenia, normal controls, or subjects with mood disorders (Cotter, Mackay, Frangou, Hudson, and Landau, 2004). In contrast, the method presented here is robust to these problems. Whether due to these methodologic factors, or differences in the cohort studied, using our robust approach we found layer 3 pyramidal cell density in auditory cortex of subjects with schizophrenia to be significantly increased, consistent with multiple reports examining other brain regions in this disease (Selemon and Goldman-Rakic, 1999).

Despite these substantial strengths in comparison to existing methods, this initial implementation has several limitations, resulting in reduced precision. The primary auditory cortex was present in fewer slabs than expected. This limited both the number of mapping sections for Cavalieri’s method as well as the number of slabs for FAVER blocks. Because other studies based upon a larger number of sections have found the primary auditory cortex to have a smooth shape (Hackett, Preuss, and Kaas, 2001), the impact of only having a few sections available is expected to be limited. Based upon our current knowledge of the small size of the region, it would be desirable to cut slabs thinner than 3mm if technically feasible. In addition it may be possible to select mapping sections from both the rostral and the caudal surface of the sampled slabs, doubling the number of sections for Cavalieri’s method and improving precision. In such a design, slabs could be cut with interchanging thicknesses with thicker mapping slabs and thinner FAVER slabs to keep the resulting intersectional distance of the mapping sections as constant as possible to improve the estimator precision further (Baddeley, Dorph-Petersen, and Vedel Jensen, 2006). Alternatively, it may be possible to cut vibratome sections for mapping from the rostral surface of each slab and the FAVER blocks then subsequently cut from the remainder of the slabs (Dorph-Petersen, 1999). It should be noticed that these concerns would likely not apply to other cortical regions which are substantially larger than the primary auditory cortex (e.g. visual cortex (Dorph-Petersen, Pierri, Wu, Sampson, and Lewis, 2007)).

Ideally, the FAVER blocks (and resulting FAVER sections) would either be completely contained within the boundaries of the region of interest, as deduced from the mapping sections, or the boundaries would be identifiable in the individual FAVER sections. In our application, most FAVER blocks, cut based upon the mapping sections, contained only the region of interest. However, the FAVER blocks cut rostral to the first or caudal to the last mapping sections, respectively, contained both the region of interest as well as tissue from the neighboring region. We treated this problem by weighting the data from these blocks by 1/3. Layer thicknesses and cell densities only shift modestly across the relevant regional boundaries in the current study (Galaburda and Sanides, 1980; Hackett, Preuss, and Kaas, 2001; Sweet, Dorph-Petersen, and Lewis, 2005). As a consequence, though the boundaries were not recognizable in the limited extent of cortex present in the FAVER sections, our weighting approach would be expected to provide a robust solution. We expect this limitation would also have been reduced if more mapping sections had been available, thereby providing a better extrapolation from the most rostral and caudal sections to the then relatively fewer extreme FAVER blocks. In general, the regional boundaries of other cortical regions may be easily recognizable in the FAVER sections, potentially by the use of specific stains.

Another potential limitations of our implementation should be noted. It is a requirement of the N_V × V_Ref approach that mapping and FAVER sections have identical tissue shrinkage due to processing, or that any difference in shrinkage is assessed and corrected for in the calculations. In the current implementation, we only monitored the areal shrinkage of the mapping sections, not the FAVER sections. As the shrinkage was limited, and because the mapping and FAVER sections underwent identical processing it is likely a robust assumption that both kinds of sections shrank to the same degree with no need for correction.

Though not specific to the method we applied, our study may also have been limited by its small sample size, which restricts the power to detect differences between groups. It is thus possible that with a larger sample the small decreases in primary auditory cortex and layer 3 volumes, may have become significant. The latter would be consistent with the evidence of gray matter volume reductions reported in vivo, which while frequently replicated have generally been modest in magnitude, ranging from 6%–20% reductions of relative volume in subjects with schizophrenia (Hirayasu, McCarley, Salisbury, Tanaka, Kwon, Frumin, Snyderman, Yurgelun-Todd, Kikinis, Jolesz, and Shenton, 2000; Kasai, Shenton, Salisbury, Hirayasu, Onitsuka, Spencer, Yurgelun-Todd, Kikinis, Jolesz, and McCarley, 2003; Salisbury, Kuroki, Kasai, Shenton, and McCarley, 2007). Another limitation of the small sample is that it precludes meaningful evaluation of the relationship to the outcome of interest of possible clinical confounds affecting subgroups of individuals, such as the four included subjects diagnosed with schizoaffective disorder. In particular, all of our subjects with schizophrenia had a lifetime history of antipsychotic medication use, and all but one were taking these medications at the time of death. In a monkey model, longterm antipsychotic exposure resulted in reduced volumes of cortical gray matter (Dorph-Petersen, Pierri, Perel, Sun, Sampson, and Lewis, 2005), primarily due to reductions in numbers of astroglia (Konopaske, Dorph-Petersen, Sweet, Pierri, Zhang, Sampson, and Lewis, 2008) without (as assessed in a separate cohort) effects on axon bouton or dendritic spine densities (Sweet, Bergen, Sun, Marcsisin, Sampson, and Lewis, 2007; Sweet, Henteleff, Zhang, Sampson, and Lewis, 2009). Thus, longterm antipsychotic use may have affected the measures of gray matter volume and neuronal density. However, longterm antipsychotic exposure has not been shown to effect neuron number (Konopaske, Dorph-Petersen, Pierri, Wu, Sampson, and Lewis, 2007) and thus it is unlikely to have impacted our principal finding of unchanged layer 3 pyramidal neuron number.

In summary, we present a novel stereologic method, optimized for the quantification of pyramidal neurons within individual layers of the cerebral cortex. Using this method, we found pyramidal neuron number to be unchanged in layer 3 of primary auditory cortex of subjects with schizophrenia. Previous observations of lower axon bouton and dendritic spine densities in primary auditory cortex in individuals with schizophrenia do not appear to be a simple consequence of a deficit in number of pyramidal neurons. Instead they are likely to result from a lower number of spines and boutons per pyramidal neuron, potentially contributing to impairments in auditory sensory processing and auditory event-related potentials in schizophrenia.

Experimental Procedure

Tissue Specimens

Brain specimens from all subjects were obtained during autopsies conducted at the Allegheny County Medical Examiner’s Office after receiving consent from the next-of-kin. An independent panel of experienced clinicians made consensus DSM-IV diagnoses using a method previously described (Glantz and Lewis, 2000). All subjects were determined to be without postmortem evidence of neurodegenerative disorders. Thioflavin-S staining revealed infrequent neuritic plaques in one subject (Case 685) and another subject had evidence of limited amyloid beta deposits detected on immunohistochemistry (Case 1088), but neither subject met clinical or neuropathological criteria for Alzheimer disease (Mirra, Heyman, McKeel, Sumi, Crain, Brownlee, Vogel, Hughes, van Belle, and Berg, 1991). Twelve subjects diagnosed with either schizophrenia (n = 8) or schizoaffective disorder (n = 4) were each matched to one comparison subject for sex, age, and post-mortem interval (Table 3). All comparison subjects were free of lifetime psychiatric illness, with the exception of Case 987, who had a history of post-traumatic stress disorder which had been in full remission for 39 years prior to death. Procedures were approved by the University of Pittsburgh Committee for Oversight of Research Involving the Dead and Institutional Review Board.

Table 3.

Study subject characteristics.

Control Subjects								Schizophrenic Subjects
Pair	Case	Sex/Age	Race	Hand¤	PMI•	Storage Time†	Cause of Death	Case	Diagnosis	Sex/Age	Race	Hand¤	PMI*	Storage Time†	Cause of Death
1	700	M / 42	W	R	26.10	63.53	ASCVD°	533	Chronic Undifferentiated Schizophrenia	M / 40	W	R	29.10	88.60	Accidental asphyxiation
2	806	M / 57	W	R	24.00	45.40	Pulmonary Thrombo- embolism	665	Chronic Paranoid Schizophreniaa	M / 59	B	R	28.10	69.53	Intestinal Hemorrhage
3	739	M / 40	W	R	15.80	59.67	ASCVD°	1088	Undifferentiated Schizophreniaa,g	M / 49	W	R	21.50	27.66	Accidental combined drug overdose
4	822	M / 28	B	L	25.30	43.70	ASCVD°	787	Schizoaffective Disordere	M / 27	B	L	19.20	49.93	Suicide by gunshot
5	727	M / 19	B	R	7.00	61.93	Trauma	829	Schizoaffective Disordera,h,i	M / 25	W	NA‡	5.00	42.80	Suicide by drug overdose
6	659	M / 46	O*	R	22.30	72.77	Peritonitis	930	Continuous Disorganized Schizophreniab,h	M / 47	W	R	15.30	23.13	ASCVD°
7	1047	M / 43	W	R	13.80	17.43	ASCVD°	933	Disorganized Schizophrenia	M / 44	W	NA‡	8.30	35.77	Myocarditis
8	852	M / 54	W	R	8.00	51.70	Cardiac Tamponade	722	Undifferentiated Schizophreniaf,h	M / 45	B	R	9.10	76.80	Upper GI Bleed
9	685	M / 56	W	R	14.50	83.70	Hypoplastic Coronary Artery Disease	1105	Schizoaffective Disorderd	M / 53	W	R	7.90	10.93	ASCVD°
10	686	F / 52	W	R	22.60	84.33	ASCVD°	802	Schizoaffective Disordera,f	F / 63	W	A~	29.00	64.37	Right Ventricular Dysplasia
11	987	F / 65	W	R	21.50	29.80	ASCVD°	917	Chronic Undifferentiated Schizophrenia	F / 71	W	NA‡	23.80	42.97	ASCVD°
12	1092	F / 40	B	R	16.60	14.37	Mitral Valve Prolapse	1010	Chronic Undifferentiated Schizophrenia**	F / 44	B	L	18.70	27.03	Sudden Unexpected Death [in Epilepsy]

^¤Hand indicates handedness;

^•PMI indicates postmortem interval in hours;

^†Storage time is in months;

^°ASCVD indicates atherosclerotic coronary vascular disease;

^‡NA indicates not available;

^~A indicates ambidextrous;

^*Asian Indian;

^**Mild Mental Retardation;

^aAlcohol dependence, current at time of death;

^bAlcohol dependence, in remission at time of death;

^cAlcohol abuse, current at time of death;

^dAlcohol abuse, in remission at time of death;

^eOther substance dependence, current at time of death;

^fOther substance dependence, in remission at time of death;

^gOther substance abuse, current at time of death;

^hOther substance abuse, in remission at time of death;

ⁱOff antipsychotic medication at time of death.

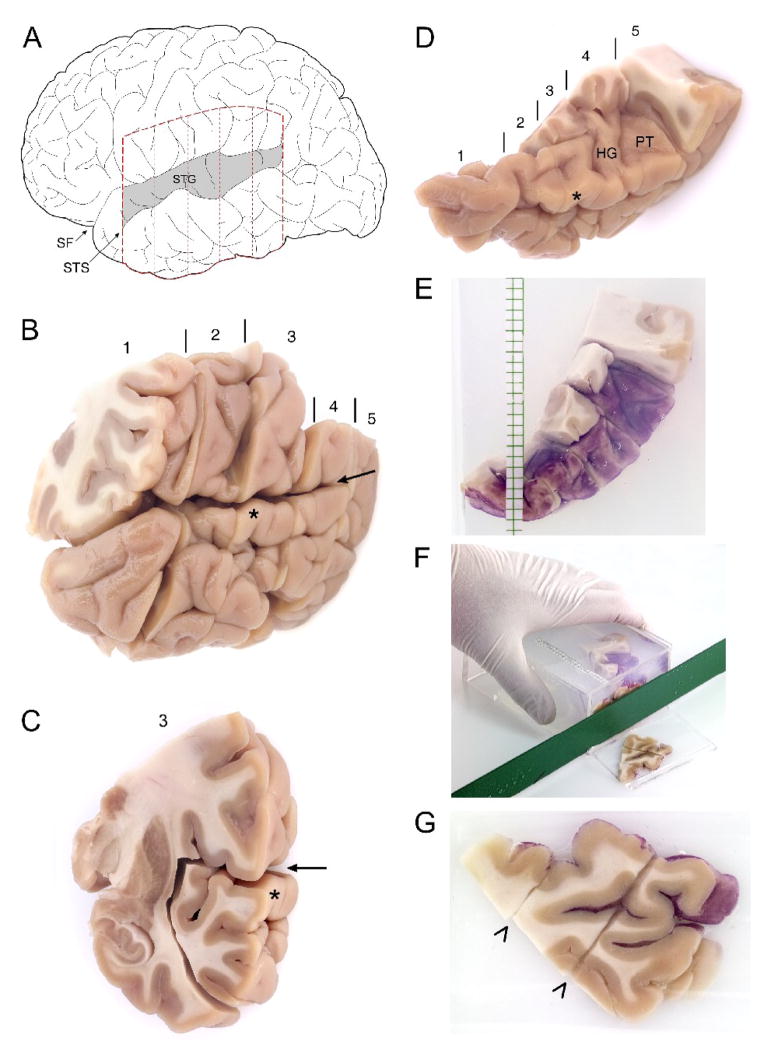
The left hemisphere of each subject brain was initially blocked coronally at ~1.5 cm intervals, immersed in ice-cold 4% paraformaldehyde in phosphate buffer for 48 hours, washed in a graded series of sucrose solutions, and stored in an antifreeze solution at −30°C. All blocks containing the left STG, from a point rostral to the lateral origin of Heschl’s gyrus to the termination of the Sylvian fissure, were selected for further processing (Figure 3, A–B). The STG was dissected from all blocks in each subject and the antifreeze solution removed by washes in 18% sucrose solution in phosphate buffered saline (PBS).

Figure 3. Processing of human postmortem tissue for mapping and unbiased estimation of volumes of the primary auditory cortex.

(A) Schematic of a lateral view of the left hemisphere in human. The Superior Temporal Gyrus (STG) is shaded. STS, Superior Temporal Sulcus; SF, Sylvian Fissure. Dashed lines indicate approximate boundaries of coronal blocks containing the entire STG in human subjects, shown in (B). (B) Fixed coronal blocks of tissue containing the left STG. Blocks are numbered from rostral to caudal, with vertical lines indicating boundaries between adjacent blocks. The sylvian fissure is denoted by the arrow. In (C), block 3 is shown. The wide margins used to dissect the STG from this block are clearly visible as cuts through the insular and inferior temporal grey matter and the subjacent white matter. (D) All STG pieces dissected from the coronal blocks are shown. Blocks are numbered, with separating lines, as in (B). Heschl’s Gyrus (HG) and the Planum Temporale (PT), separated by Heschl’s Sulcus are clearly visible after the overlying parietal cortex has been removed. The asterisk indicates the STG at the same level as in (B) and (C). (E) The individual STG pieces seen in (D) are then “glued” together, the pial surface painted with hematoxylin, to aid in identification of this surface during later processing, and embedded in a mold using 7% agarose solution. The STG is reoriented when placed into the agarose to allow cutting into slabs orthogonal to the long axis of HG. At the time of embedding, 3 mm graph paper is also placed in the mold to guide cutting into slabs of uniform thickness. (F) A cut made through the reoriented embedded STG, at approximately the level of the asterisk from (D) is shown. An identical size plastic mold with one side removed, serves as a cutting guide. (G) The rostral face of the slab seen cut in (F). The lateral surface of the STG is to the upper right. Diagonal cuts through the tissue (arrowheads) indicate where the original coronal blocks were apposed during the embedding process.

For each subject, the pial surface of the STG in each block was painted with hematoxylin to aid in identification of this surface during later processing. The blocks were then reassembled into their in vivo orientation using a 7% solution of low melting point agarose (BioWhittaker Molecular Applications; Rockland, ME). After reassembly, the STG was embedded in 7% low melting point agarose and cut, with a random starting position, into systematic, uniformly random 3-mm slabs oriented orthogonal to the long axis of Heschl’s gyrus and, to the extent possible, to the pial surface of the superior temporal plane (Figure 3, F–G). Consecutive slabs were randomly separated into two alternate uniform random series, with every other slab part of the same series (Figure 4, A–B). Each slab in one of the series (randomly chosen) was mounted flat with the Precision Cryoembedding system (Pathology Innovations, Wyckoff, New Jersey) (Peters, 2003) sectioned exhaustively on a cryostat at 60 μm, and the slabs in the second series were reserved for later dissection of regions of interest. All sections and slabs were stored in antifreeze solution at −30°C until histologic processing.

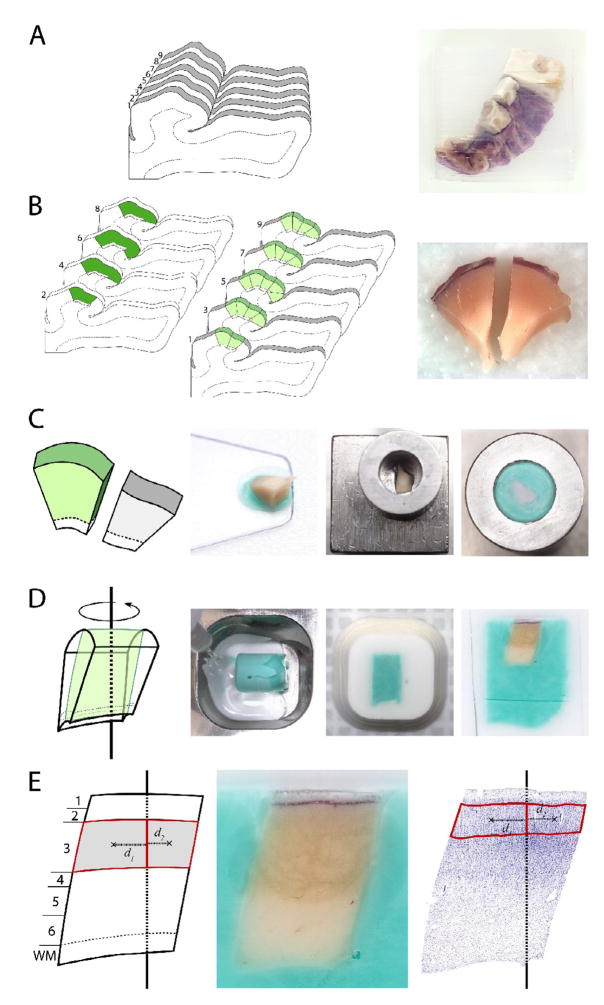
Figure 4. Generation of FAVER sections orthogonal to the pial surface for estimation of layer volumes.

(A) The reassembled STG embedded in agarose was cut into uniform random 3-mm slabs oriented orthogonal to the long axis of Heschl’s gyrus and to the pial surface of the superior temporal plane. (B) The complete set of slabs was separated into two series. One series was sectioned exhaustively, and a systematic uniform random series of three adjacent sections from the rostral surface of each slab was processed for Nissl substance, acetylcholinesterase and parvalbumin immunoreactivity to map the primary auditory cortex, shown in dark green. Using these maps, the corresponding regional boundaries were identified in the second series of slabs (shown in light green) and the primary auditory cortex was dissected from the slab and divided into smaller blocks of ~3mm. (C) A systematic random sub-sample of these blocks was selected for further processing. The selected block was placed with the pial-surface down and transferred onto a cold stainless steel block, ensuring an orientation of the final cut sections orthogonal to this surface. A hollow stainless steel cylinder was placed over the block, and the remaining exposed tissue was covered with a colored OCT solution. In the image at right, the cylinder has been inverted, show that this results in the pial surface of the block being oriented orthogonal to the long axis of the cylinder. (D) The embedded block was then removed from the cylinder, placed into a well, randomly rotated about the central axis of the cylinder, fixed in this position with a clear OCT solution, and mounted on a chuck for cutting in a cryostat, parallel to the long axis of the cylinder. (E) Shows the orientation of the resulting central section, clearly cut orthogonal to the pial surface. All cortical layers are readily distinguishable, with the borders of layer 3 delineated in the image at right. The centroids of each of hemi-contours are indicated by an x and their respective distances to the central axis indicated by d₁ and d₂, respectively.

Delineation of Auditory Cortex and Estimation of Primary Auditory Cortex Volumes

One complete section from each slab was selected for each subject, thus resulting in a systematic, uniformly random series of cut sections through the region of interest which were then processed (see below) for Nissl substance. Series of sections adjacent to the Nissl-stained series were selected for processing for acetylcholinesterase (AChE) and parvalbumin (PV), respectively (Sweet, Dorph-Petersen, and Lewis, 2005). These sections were used to map the primary auditory cortex according to cyto– and chemoarchitectonic criteria, and to estimate its volume (V_Primary) according to the Cavalieri method, as described previously (Sweet, Dorph-Petersen, and Lewis, 2005). This approach resulted in a mean (SD) of 3.5 (0.7) mapping sections containing primary auditory cortex per subject. Though fewer than the 8–12 sections generally recommended for use of Cavalieri’s method, the number of sections was still useful for estimation because of the ovoid shape of the region of interest (see, for example, delineations of primary auditory cortex using similar criteria, but with more closely spaced sections, in (Hackett, Preuss, and Kaas, 2001)). The order of delineations and volume determinations was blocked by pair, with sections coded to mask subject numbers and randomly ordered with regard to diagnosis. For the eight normal comparison subjects who had unpaired estimates of regional volumes used in our prior study (Sweet, Dorph-Petersen, and Lewis, 2005) (cases 659, 685, 700, 727, 739, 806, 852, and 1047), sections were recoded prior to blocking within pairs.

Estimation of Volumes of Primary Auditory Cortex Layers

Because of the extensive curvature of the cortical surface, it is not possible using only the above approach to generate uniformly random sections orthogonal to the pial surface without any layers cut obliquely. To achieve this goal, a second set of sections was generated: the boundaries for primary auditory cortex marked on the Nissl-stained mapping sections were transferred to the pial surface of each unsectioned slab immediately rostral to the Nissl-stained section. For the most rostral and most caudal section to contain each region of interest, the boundaries were extended rostrally and caudally onto the adjacent unsectioned slabs, respectively (Figure 4B). The primary auditory cortex was then separated from each slab by cuts perpendicular to the pial surface along these regional boundaries as well as by undercutting the gray matter. Each primary auditory cortex piece was then further subdivided into ~3-mm wide blocks. Targeting a total of 6–10 blocks/subject, every block (17 subjects), or every other block (7 subjects), was selected with a random start for further processing. Each selected block was placed using a thin layer of OCT (Sakura Finetek, Torrence, CA 90501) onto a stainless steel block (Precision Cryoembedding System, Pathology Innovations, LLC; Wyckoff, NJ) at −20°C with the pial-surface down (Figure 4C). A hollow stainless steel cylinder was placed over the block, and the remaining exposed tissue was covered with the colored OCT solution. The embedded tissue block was allowed to freeze at −20°C and was then removed from the cylinder. The block was placed into a stainless steel well, randomly rotated about the central axis of the cylinder, and then fixed in this position with a clear OCT solution. Each embedded block was sectioned exhaustively on a cryostat at 50 μm. All sections were stored in antifreeze solution at −30°C. The central section from each block qualifies as a FAVER section, i.e. a randomly rotated section through the center of the block (Dorph-Petersen and Gundersen, 2003). These sections, which are free of oblique cuts through the cortex (Fig 5), were immersed for 24 hours in cold 4% buffered paraformaldehyde, mounted on gelatin-coated slides, and processed for Nissl substance with thionin, with all sections from each pair processed together. In two cases, (727 and 806), a single block was damaged during tissue processing and was unavailable for further analysis. In the current design, the random loss of these blocks increases estimator noise but does not introduce a bias.

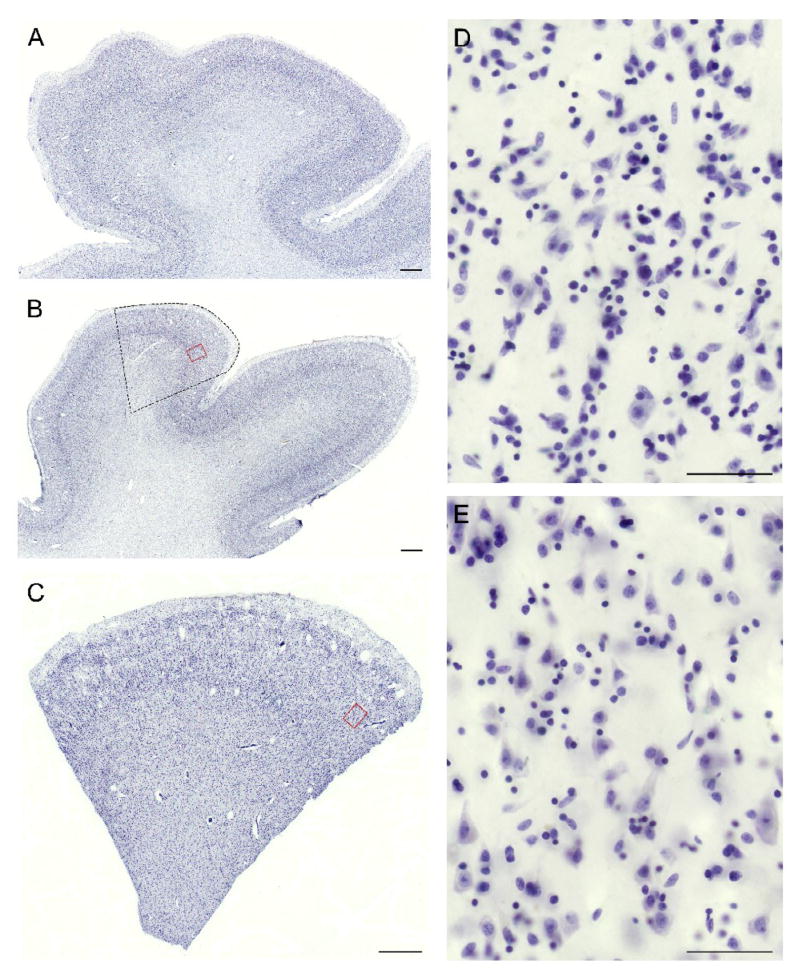
Figure 5. Tissue sections oriented orthogonal to the pial surface for robust estimation of pyramidal neuron number.

(A) A section through Heschl’s gyrus from a coronal tissue block that was not embedded in agarose and reoriented prior to sectioning. It can be seen that the angle of sectioning relative to the pial surface varies extensively, from orthogonal to substantially tangential. (B) A section through Heschl’s gyrus from a slab cut after embedding in agarose and reorienting as shown in Fig 4A. Though the angle of cut relative to the pial surface is more uniformly orthogonal, some tangential areas remain, for example in the region of the red rectangle. The dashed outline shows the approximate location of a small block which was dissected out and further reoriented orthogonal to the pial surface, using the approach shown in Fig. 4B and 4C. (C) A section through the dissected and reoriented block corresponding to the outlined region in (B). (D) and (E) show at higher magnification a portion of the regions contained within the red rectangles in (B) and (C). In (E), but not (D), sampling is clearly orthogonal to the pial surface, as indicated by the improved representation of pyramidal cell morphology with triangular somal profiles and apical dendrites visible within the plane of section. Scale bar = 1mm in A-C. Scale bar = 50μm in D and E.

The borders of layers 1 to 6 in the primary auditory cortex were identified and delineated on the Nissl-stained FAVER sections using cytoarchitectonic criteria (Sweet, Dorph-Petersen, and Lewis, 2005). Sections were visualized on an Axioplan 2 microscope (Zeiss, Thornwood, NY) equipped with a motorized specimen stage (Ludl Electronic Products, Hawthorne, NY), an object rotator, and an MT12 microcator with ND281 readout (Heidenhain, Germany). A three-chip CCD cooled camcorder (DEI-750T, Optronics, Goleta, CA) connected to a computer was mounted on the top of the microscope. The computer, fitted with a frame grabber (I-Color, Foresight Imaging, Lowell, MA) and a 19″ Trinitron monitor (Dell, Round Rock, TX), ran the Stereo Investigator stereology software package (v. 7.5, MicroBrightField, Williston, VT). Using 1.25x (0.035 NA) and 5x (0.15 NA) Plan-Neofluar objectives, with final on-screen magnifications of 58× and 220x, respectively, a contour was drawn around each cortical layer. Each contour was then subdivided along the central axis of the block (Figure 4E), resulting in a total of ~2250 hemi-contours in the 24 subjects.

Determination of the volumes for each layer used FAVER (Dorph-Petersen and Gundersen, 2003), a general and unbiased method for estimation of total volume and particle number from randomly rotated central sections through a region of interest.

First, the volumes of the individual cortical layers for each block were estimated from the areas of each delineated hemi-contour using Pappus’ theorem:

$$V_{\mathit{Layer}}:=\pi ·\sum (A_{\mathit{Layer}}·d),$$ (1)

where V_Layer is the volume of the layer of interest within the tissue block; A_Layer the area of the hemi-contour; d the distance of the hemi-contour’s centroid to the fixed central axis. The sum is across the two hemi-contours of the block. Here and elsewhere, := indicates that the quantity at the left is estimated by the expression at the right. The areas of traced contours are reported by the Stereo Investigator, while the coordinates of the centroids can easily be calculated from the coordinates of the vertices of the polygonal contours. The contour coordinates was extracted from the raw data files of the Stereo Investigator.

Subsequently, the volume fraction V_V of each of the six cortical layers within the primary auditory cortex was estimated as:

$$V_{V\mathit{Layer}}:=\frac{{\displaystyle \sum _{i=1}^n}\left(V_{\mathit{Layer}}·w_i\right)}{{\displaystyle \sum _{i=1}^n}\left(V_{\mathit{Block}}·w_i\right)},$$ (2)

where V_Block is the total cortical volume for each block (i.e. the sum of all six layer volume estimates for the block), and the sums are across the all the n blocks sampled from that subject. Notice, we used weighted sums in the above ratio estimator. The weights, w_i, were 1 for all blocks except for blocks from the most rostral or caudal slabs of the region of interest—i.e. from blocks more rostral or caudal than the first or last mapping section, respectively. For these blocks (on average 2.75 per subject) a weight of 1/3 was used reflecting that these blocks only partly contained the region of interest.

Finally, the total volume of each of the six layers of the primary auditory cortex was estimated by the product of the respective volume fraction and the total volume of the region of interest:

$$V_{\mathit{Tot}\mathit{Layer}}:=V_{V\mathit{Layer}}·V_{\mathit{Primary}}.$$ (3)

Shrinkage of tissue due to histological processing was monitored in the mapping sections via point counts of the initial area of tissue present on the rostral surface of each 3-mm slab and the corresponding final slide mounted mapping sections. Because mean areal shrinkage was small at (4.4%), and did not differ between groups (t₂₂ = 0.49, p = 0.62), estimates were not corrected for shrinkage.

Estimation of Layer 3 Pyramidal Neuron Number

The following criteria for pyramidal neurons were used: 1) an identifiable nucleolus, 2) an abundance of Nissl-stained cytoplasm, 3) a vertical apical dendrite, and 4) a triangular shape. We used the nucleolus of the pyramidal neurons as the sampling unit, and no pyramidal neuron with two nucleoli were observed. Pyramidal neuron numbers were estimated in the same FAVER sections stained for Nissl substance used to determine the layer 3 volumes. The contours of layer 3 for each block traced during the volume estimations above were reloaded into the Stereo Investigator and carefully realigned to each section. Measurements were obtained using a 100x (1.4NA) oil immersion objective, with visualization on a computer monitor at a final magnification of 4500x. In each section layer 3 was subsampled systematic, uniformly random by unbiased counting frames (Gundersen, 1977) of 50 × 35 μm in a square grid with random rotation. For each subject the step-length and resultant area sampling fraction was individually selected to target at least 300 sites/subject, using the layer 3 contour areas determined for estimation of layer 3 volume. At each frame, the sections were subsampled in the z-axis by optical disectors (Gundersen, 1986) with a disector height h = 12μm. At each sampling site, the section thickness was determined by focusing from top to bottom, and the disector placed so its center was halfway between the section top and bottom surfaces leading to symmetric top and bottom guard zones of 4.5μm on average, corresponding to ~10.7μm in the original 50μm cut section. This sampling approach was determined after the conduct of a pilot calibration study of randomly selected sections from several subjects. In the calibration study, pyramidal neuron nucleoli were sampled systematic uniformly random as described above, but without guard zones (i.e., in the full thickness of the section), and their z-positions recorded together with the respective local section thickness measured centrally in the counting frame. A uniform distribution of nucleoli was observed in the center of the section. Near the top and bottom of the sections, corresponding to ~5 μm in the initial 50-μm sections, fewer nucleoli were observed, indicating the effect of lost caps (Andersen and Gundersen, 1999). As a quality control, plots of the z-positions of all nucleoli sampled across all brains in the study were inspected and confirmed sufficient guard zones as well as linear shrinkage in the z-axis (see Fig. 4 in (Dorph-Petersen, Caric, Saghafi, Zhang, Sampson, and Lewis, 2009) for a more detailed description of this kind of pilot calibration study and quality control). Our approach resulted in mean (range) of 404 (330–562) frames sampled across 7.8 (5–12) blocks per subject, and a mean (range) of 504 (278–1285) pyramidal neurons sampled per subject.

The total number of layer 3 pyramidal neurons were estimated using the N_V × V(ref) approach, also known as an optical disector design (Dorph-Petersen, Nyengaard, and Gundersen, 2001; Gundersen, 1986). The numerical density N_V of layer 3 pyramidal neurons was estimated for each subject across all sampled blocks as:

$$N_V:=\frac{{\overline{t}}_{wd}}{h}·\frac{\sum \left(\sum {\left(d_j\right)}_i·w_i\right)}{BA·a·\sum \left(\sum {\left(d_p\right)}_i·w_i\right)}$$ (4)

$${\overline{t}}_{wd}:=\frac{\sum \left(t_j·d_j·w_i\right)}{\sum \left(d_j·w_i\right)},$$ (5)

where a = 1750μ² is the area of the counting frames, d_j is the distance of the j’th pyramidal neuron to the fixed axis of the respective block, Σ(d_j)_i is the sum of these distances across all sampled pyramidal neurons in the i’th block, d_p is the distance of the p’th associated point (upper right corner of each frame) hitting the region of interest to the fixed axis of the respective block, Σ(d_p)_i is the sum of these distances across all sampled points in the i’th block, BA = 50μm is the cryostat block advance (Dorph-Petersen, Nyengaard, and Gundersen, 2001), t̄_wd is the block-and-distance-weighted mean section thickness, t_j is the local section thickness measured centrally in the frame sampling the j’th pyramidal neuron. w_i is the block weight—i.e. either 1 or 1/3 as in eq. 2. The outer sums in eq. 4 are across the sampled blocks while the sums in eq. 5 are across all sampled neurons in all blocks (or in a systematic, uniformly random subset thereof). This version of the density estimator is robust to the marked and varying z-axis shrinkage seen in cryostat sections. We observed a final mean section thickness of 20.9μm, corresponding to a z-axis shrinkage of 58%, with a site to site coefficient of variation (CV) of 0.19 and an intersubject CV of 0.07. We did not observe any systematic difference in final section thickness between the two subject groups.

The total number N of Layer 3 pyramidal neurons was estimated for each subject by the product of the numerical density and the total volume of layer 3:

$$N:=N_V·V_{\mathit{Layer}3}=N_V·V_{V\mathit{Layer}3}·V_{\mathit{Primary}},$$ (6)

Precision of Measurements

We determined the coefficient of error (CE) for each of the stereological estimates to assess their precision. For the Cavalieri estimate of the total volume of the primary auditory cortex CE_Cavalieri was determined using the methods described by Gundersen et al. (Gundersen, Jensen, Kiêu, and Nielsen, 1999) We used the equations based upon smoothness class m = 1 in the terminology of Gundersen et al., (Gundersen, Jensen, Kiêu, and Nielsen, 1999) reflecting the smooth 3D shape of the region of interest (Hackett, Preuss, and Kaas, 2001). The CEs of V_V and N_V, estimated in eqs. 2 and 4 above were calculated using the general approach for stereological estimators of ratios R estimated by:

$$R:=\frac{\sum x}{\sum y}=\frac{\overline{x}}{\overline{y}},$$ (7)

where x and y in the context of the current paper reflects the terms within the sums in the numerator and denominator, respectively, of eqs. 2 and 4. The CE of such a ratio can be approximated, e.g. see pg 155 in (Cochran, 1977); see also (Kroustrup and Gundersen, 1983), and eq. 10.32 in (Howard and Reed, 1998):

$${CE}_R^2\approx \frac{n}{n-1}·\left(\frac{\sum x^2}{{\left(\sum x\right)}^2}+\frac{\sum y^2}{{\left(\sum y\right)}^2}-2·\frac{\sum \left(x·y\right)}{\sum x·\sum y}\right),$$ (8)

where n is the number of items (here blocks), and the sums are across all items (blocks). However, this equation does not take into account the high block sampling fraction (sf) of ½ or ¼ of the current study, where half of the slabs were cut into blocks of which either all or a half were sampled. Using the standard statistical approach of multiplying with (1−sf) would overcorrect the estimated CE: Eq. 8 reflects the combined CE of all levels of sampling from blocks and below—i.e. including the CEs of sampling sections within blocks, fields within sections, and test systems (disectors) within the fields—and only the CE of the block sampling level should be corrected. Therefore, it is easily seen that:

$$(1-sf)·{CE}_R^2\le {CE}_{R,\mathit{true}}^2\le {CE}_R^2,$$ (9)

where CE_R is approximated by eq. 8 and CE_{R, true} is the true (but approximated) CE of the ratio estimate. Thus, it is from eq. 9 possible to calculate bounds for the CE of the V_V and N_V estimates obtained by eqs. 2 and 4. Assuming independence of the errors in the various step of estimation, the CE of the estimate of total volume of a layer can be expressed as:

$${CE}_{V_{\mathit{Tot}\mathit{Layer}}}^2={CE}_{V_{V\mathit{Layer}}}^2+{CE}_{\mathit{Cavalieri}}^2,$$ (10)

and the CE of the estimated total number of layer three pyramidal neurons as:

$${CE}_N^2={CE}_{N_V}^2+{CE}_{V_{V\mathit{Layer}3}}^2+{CE}_{\mathit{Cavalieri}}^2,$$ (11)

By combining eq. 9 with eqs. 10 and 11 it is then easy to calculate bounds for the two CEs.

Note, as mentioned in the previous, our Cavalieri estimates of the total volume of the region of interest were based upon very few sections. Despite the smoothness and regularity of the primary auditory cortex, it is not known to what extent the assumptions inherent in the approach devised by Gundersen et al. (Gundersen, Jensen, Kiêu, and Nielsen, 1999) hold when less than 8–12 sections are used. Therefore, it is possible that we underestimated the CE_Cavalieri used in eqs. 10 and 11.

Also, the reader should be reminded, that ratio estimators as eq. 2 and 4 are biased but consistent, i.e. a small bias is present, but it is typically negligible and decreases rapidly as more items (here blocks) are sampled (see e.g. page 210 in (Baddeley and Vedel Jensen, 2005) and chapter 6.8 in (Cochran, 1977)). To verify robustness of the estimators we calculated the mean CE of the respective denominators of eq. 2 and eq. 4 for each subject group.

Finally, as discussed in our previous paper, the delineation of the primary auditory cortex is nontrivial (Sweet, Dorph-Petersen, and Lewis, 2005). However, the CEs calculated above do not include the variance component due to imprecision in the delineation of the region of interest, as it is unknown. Therefore, the true total methodological CE of our estimated totals (V_Primary, V_{Layer 3}, and N) are likely slightly higher than reported here.

Statistical Methods

The response variables of interest were primary auditory cortex volume (V_Primary), layer volume (V_{Tot Layer}), layer volume fraction (V_V), pyramidal neuron number (N), and pyramidal neuron density (N_V). Analysis of covariance (ANCOVA) was used to detect the diagnosis effect between schizophrenia and control groups for each of the response variables. Two ANCOVA models were utilized: a primary model with diagnosis, pair as a blocking factor and, because subjects were not paired on tissue storage time, tissue storage time as a covariate; and a secondary model with diagnosis, sex, age, PMI and tissue storage time entered as covariates with subject pairings ignored. Analyses were implemented in SAS PROC GLM. All statistical tests were two-sided and conducted with an alpha level = 0.05. Because the results of all analyses were congruent between the two models, only the primary model results are reported.