Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2009 Nov 11.
Published in final edited form as: J Biomech. 2008 Dec 6;42(2):158–163. doi: 10.1016/j.jbiomech.2008.10.020

Rotator Cuff Tendon Strain Correlates with Tear Propagation

Nelly Andarawis-Puri 1, Eric T Ricchetti 2, Louis J Soslowsky 3
PMCID: PMC2775924  NIHMSID: NIHMS143998  PMID: 19064267

INTRODUCTION

Rotator cuff tears are common soft-tissue injuries and a source of pain and disability. In the general population, the prevalence of full-thickness and partial-thickness supraspinatus tendon tears ranges from 5-39% and 13-37%, respectively (Breazeale and Craig 1997; Fehringer et al. 2008; Fukuda et al. 1990; Fukuda et al. 1994; Fukuda 2003; Matsen 2008; Milgrom et al. 1995; Neer 1983;; Sher et al. 1995; Yamaguchi et al. 2006). Ideally, surgery should be indicated based on data that identifies tears at high risk of progression, for which non-surgical management would result in larger, less manageable defects. However, in the absence of such data, surgery is typically only indicated after failure of an initial period of non-operative treatment (Breazeale and Craig 1997; Matava et al. 2005). While this approach is successful in the management of some tears, for others, the delay in surgery results in larger, more difficult tears to manage and increases the risk of failure of the repair (Habernek et al. 1999; Feng et al. 2003).

In the absence of treatment criteria based on likelihood of tear propagation, initial rotator cuff tear size primarily influences clinical decision making. Typically, surgery is indicated for tears that extend through more than 50% of the tendon (Flatow et al. 1997; Peterson and Altcheck 1996). However, the supraspinatus tendon is structurally inhomogeneous (Clark and Harryman 1992) with region specific mechanical properties (Nakajima et al. 1994; Itoi et al. 1995), making tear size not an optimal criteria. In this context, surgery may be unnecessarily indicated for some large tears that are unlikely to propagate, while non-operative management will be chosen for some small tears that progress into less manageable tears. The use of a mechanical measurement, such as strain surrounding the tear, to predict the behavior of the tear under loading is therefore necessary. An understanding of the relationships between tear size, tendon loading, and strain adjacent to a rotator cuff tear would provide important insight into identifying tears that are likely to propagate, influencing clinical treatment.

To further understand tear etiology, studies investigated the effect of full and partial-thickness insertion site tears on the remaining intact portion of the tendon (Hatakeyama et al. 2001; Bey et al. 2002; Reilly et al. 2003; Reilly et al. 2003). Tissue strain was quantified in intact and torn supraspinatus tendons to evaluate the load bearing capacity of the tissue and predict likelihood of tear propagation. As expected, significant changes in tendon strain resulted following introduction of a rotator cuff tear. In addition, the effect of a tear on strain in the supraspinatus tendon was masked at certain glenohumeral abduction angles (Bey et al. 2002), emphasizing the effect of factors other than tear size on the loading environment of the torn tendon. In these studies, conclusions regarding the likelihood of tear propagation rely on the assumption that increase in tendon strain correlates with increase in risk of tear propagation. However, none of these studies explicitly investigated the relationship between tear size, tendon loading and tendon strain adjacent to a rotator cuff tear. Therefore, the objective of this study was to quantify two-dimensional strain fields adjacent to a tendon tear under loading to failure to assess relationships between strain and tear size. We hypothesized that: (1) Increase in average maximum and decrease in average minimum principal strain will correlate with an increase in tear size; (2) Tears will propagate in the direction of highest average maximum and lowest average minimum principal strain; and (3) Larger tears will result in higher average maximum and lower average minimum principal strain per load than smaller tears.

METHODS

The sheep infraspinatus tendon was utilized as a model for rotator cuff injury because of its established similarity to human supraspinatus tendon in shape and size, as well as through histological and mechanical evaluation (Coleman et al. 2003; Gerber et al. 1994; Gerber et al. 1999; Gerber et al. 2004). Although sheep infraspinatus tendons exhibit less structural variability than human supraspinatus tendons, this model adequately illustrates the behavior of a tear under various strain configurations and allows evaluation of the relationship between strain and tear propagation. Ten pairs of skeletally mature cadaveric sheep shoulders (2 males and 8 females) were dissected, retaining only the humerus and infraspinatus tendon. The infraspinatus muscle was removed, exposing the entire tendon. Specimens were subjected to 1 freeze-thaw cycle prior to dissection and mechanical testing.

The length and width of each tendon was measured and the location at the midpoint of each parameter was chosen as the surgical injury site. To ensure accuracy, 3 measurements of tendon width were taken 1mm proximal to the insertion site, and at the musculotendinous junction. Mean width was calculated at both locations, and the midpoint of each was marked. Tendon length was measured from the insertion site to the musculotendinous junction at the superior and inferior edges of the tendon and midtendon (passing through previously marked midpoints of width), and then used to mark the length midpoint. In one shoulder of each animal, an 8mm mid-substance circular defect (centered at the marked midpoint of length and width), representing 44.0±3.3% of the width of the tendon, was made in the infraspinatus tendon using a biopsy punch in a reproducible manner. In the contralateral shoulder of the same animal, a 12mm mid-substance circular defect, representing 66.0±6.0% of the width of the tendon, was similarly made. Inclusion of a control group of intact specimens was unnecessary because the objective of this study and associated hypotheses were to evaluate relationships between tendon strain, tear size, and risk of tear propagation, necessitating the existence of a tear in all experimental groups.

Each tear group was randomly assigned an equal number of left and right shoulders. The bursal-sided surface of the tendons was air-brushed with fine black paint to create a speckled texture for strain analysis using Vic2D (Version 4.4.1, Correlated Solutions Inc., Columbia, SC). Surface strain analysis could be used to reasonably reflect overall tendon strain because the infraspinatus is a non-sheathed tendon and loose, non-tendinous material was dissected off the tendon surface prior to air-brushing. Vic2D utilizes a texture correlation algorithm (Bey et al. 2002) to determine displacements of pixels in undeformed and deformed images. Briefly, displacement is calculated through optimization of the sum of squared differences function between a pixel with its surrounding region in deformed and undeformed image pairs. Strain is calculated from partial derivatives of the displacements using the lagrangian strain tensor equations. The user prescribes the size of the region surrounding each pixel to be used in the correlation analysis, and whether the analysis is conducted for every pixel or pixels are evenly skipped. Finally, the size of the neighborhood over which the derivatives of the displacement fields are calculated for strain analysis is chosen based on the desired amount of smoothing (larger values result in greater smoothing). Optimal analysis parameters were chosen and used for all specimens based on a parametric study that demonstrated a plateau in sensitivity of strain measurements to small changes in parametric values or region of interest, assuring repeatability of the analysis and robustness against image noise artifacts.

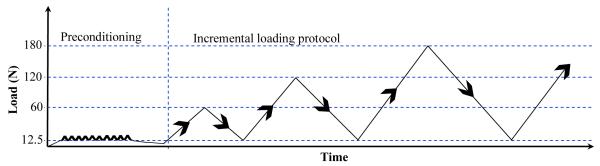
Each humerus was mounted in polymethylmethacralate (PMMA) in custom grips and the infraspinatus tendon was attached to an Instron testing machine (5543, Instron, Norwood, MA). The loading protocol was applied along the longitudinal axis of the tendon with the humerus positioned perpendicular to the direction of loading, in physiologically neutral position defined by 0° humeral abduction, rotation and flexion. The tendon grip was attached most proximally on the tendon and then rotated, wrapping the tendon around the grip, until it lined up with the start of the musculotendinous junction. This gripping technique improved load distribution near the grip eliminating slipping at the grip at higher loads. Mechanical testing was conducted in a 37° Celsius PBS bath. Preconditioning consisted of cyclical loading between 12.5N and 25N (approximately 1% ultimate load) 10 times at an approximate rate of 0.1% times the length of the tendon followed by constantly loading it with 12.5N for 5 minutes. The loading protocol was then applied at an approximate rate of 0.1% times the length of the tendon and consisted of a cyclic testing protocol to increasing load levels as follows (Figure 1): constant ramp from a nominal load (12.5N) to a peak of 60N, back to 12.5N; then ramp to 120N, and back to 12.5N; and so on to increasing peak levels in 60N increments until failure (denoted by inability to reach the next load level). Image capture software (custom written in Labview) and software to control Instron loading (Merlin) were synchronized, allowing isolation of images corresponding to loads of interest. Digital images were taken at each peak and valley of the loading protocol. Lagrangian strains were calculated between the initial valley image (12.5N) and each peak load using Vic2D.

Figure 1.

Figure 1

Open in a new tab

Loading protocol applied to the infraspinatus tendon. After preconditioning, the infraspinatus tendon was cyclically loaded to increasing load levels in 60N increments until failure at a rate of 0.04 mm/sec.

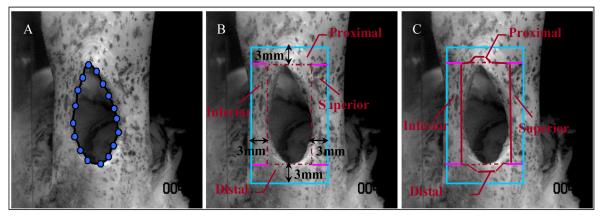
Percent increase in tear size was quantified at each valley, to determine the effect of strain level reached at the previous peak on tear size. To quantify tear size, an ImageJ (Version 1.33, National Institute of Health, Bethesda, MD) plug-in was used to place a spline curve around the edge of the tear at each nominal load image (Figure 2A) by an operator blinded to experimental condition. Changes in perimeter of the tear, indicating tear propagation from the previous load level, were determined from the spline curve. A 3mm area of interest around each infraspinatus tendon tear was defined and sub-divided into four regions (proximal, distal, superior, inferior) for strain analysis. The superior and inferior regions were marked by rectangles immediately superior or inferior to the tear, respectively, with a width of 3mm and a length equivalent to the length of the tear. The proximal and distal regions were marked by rectangles immediately proximal or distal to the tear, respectively, with a length of 3mm and a width extending to the borders of the defined superior and inferior regions (Figure 2B). The distal border of the proximal region directly contacted the proximal edge of the tear. Similarly, the proximal border of the distal region directly contacted the distal edge of the tear. To prevent tear propagation from affecting strain calculation, the proximal and distal regions were modified to exclude points whose surrounding texture used for measurement included the edges of the tear (Figure 2C). Since tear propagation occurred along and not across tendon fibers, the proximal and distal regions were the only regions altered by tear propagation. Close examination of the images captured at each valley support our approach, as the texture in the superior and inferior regions was deformed but conserved with increasing loads. Since average tendon length was 32.2±3.8mm, strain in the proximal and distal regions was evaluated in a region that was 7.1-10.1mm (12mm tear group) and 9.1-12.1mm (8mm tear group) away from the grip.

Figure 2.

Figure 2

Open in a new tab

A sample specimen exhibiting a 12mm mid-substance tear at 12.5N load. (A) Edges of tear are traced and the perimeter is calculated. (B) A 3mm region of interest around the tear is defined and sub-divided (proximal, distal, superior, inferior). (C) Points whose surrounding texture fell within the tear were excluded. Image resolution is 0.065 mm/pixel.

To test our first hypothesis, at each load, average strain and tear size for all specimens within a tear group was calculated and the correlation between percent increase in tear size and both average maximum and minimum principal strain was evaluated. To evaluate the second hypothesis, two independent repeated measures ANOVAs with a post-hoc Bonferroni were conducted to evaluate the effect of region around the tear on both average maximum and minimum principal strain. To evaluate the third hypothesis, the 8mm and 12mm tear groups were compared for both the average maximum and minimum principal strains using paired t-tests. For statistical analyses associated with the first and third hypotheses, significance (denoted by *) was set at p ≤ 0.05 and a trend (denoted by #) at p ≤0.1. For statistical analysis associated with the second hypothesis, significance was conservatively set at p ≤ 0.008 and a trend at p ≤ 0.02 to account for multiple comparisons.

Results

In 9 of the 10 shoulder pairs, the tendon with the 12mm tear failed at a lower load than the contralateral 8mm torn tendon. Mean failure load was significantly higher for the 8mm tear group (542N±130) than for the 12mm tear group (354N±132). During mechanical testing, all tendons failed due to propagation proximally, from the proximal edge of the tear towards the tendon grip. Since at least 4 tendons from the 12mm and 8mm tear groups reached a load of 240N and 480N before failure, respectively, these were the maximum load levels analyzed for each group.

Correlation between tear size and strain

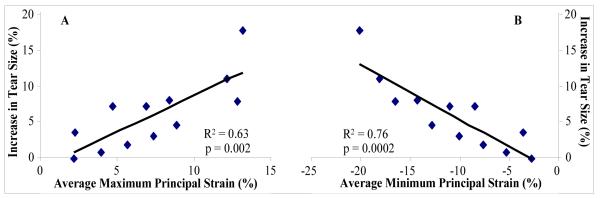
Supporting our first hypothesis, percent increase in tear size significantly correlated with both, average maximum principal strain (positive correlation, shown in Figure 3a) and average minimum principal strain (negative correlation, shown in figure 3b). A linear fit gave significant R2 values of 0.63 and 0.76 for the correlation between percent increase in tear size and average maximum and minimum principal strains, respectively. Since our results also showed that for each load level, strain was higher surrounding the 12mm than the 8mm tears, in figure 3, data was not pooled over both tear groups.

Figure 3. (A) A significant positive correlation between increase in tear size and average maximum principal strain. (B) A significant negative correlation between increase in tear size and average minimum principal strain.

Figure 3

Open in a new tab

Each point in represents an average of 10 specimens. Of the 12 points shown, 8 points are from data representing the 8mm tear group (corresponding to all loads up to 480N) and 4 points are from data representing the 12mm tear group (corresponding to all loads up to 240N).

Effect of regional strain on direction of tear propagation

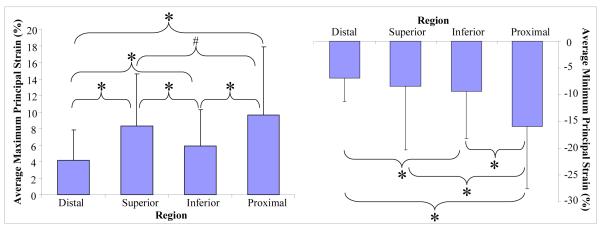
All tears propagated from the proximal tip of the tear into the proximal region, which had the highest average maximum and lowest average minimum principal strain, supporting our second hypothesis (Figure 4). Large standard deviations in Figure 4 are attributable to the large differences in strain values in each region surrounding the tear that are exhibited throughout the range of conditions that are pooled in this analysis (i.e., range of load). The repeated measures analysis (repeating over location per specimen) accounted for the large variability between specimens and ensured that data was evaluated in the context of each specimen. A post-hoc power analysis for maximum and minimum principal strains verified that for the number of data points, averages and standard deviations in this graph, differences between the four regions can be detected with a power of 0.8 and an alpha level (probability of a type I error) of 0.05. Table I reports the p values associated with comparisons between all 4 regions (proximal, distal, superior, inferior) surrounding the tear for average maximum and minimum principal strains.

Figure 4. The proximal region has significantly higher average maximum (right) and significantly lower average minimum (left) principal than the other regions (H2).

Figure 4

Open in a new tab

Shown data for strain at each region surrounding the tear, pooled over all loads and both tear sizes.

Table I.

Statistical analysis of strain per 3mm region around the tear (shown p values). T ears propagated proxim ally, into the region w ith highest strain. Significance w as conservatively set at p ≤ 0.008 and a trend at p ≤ 0.02 to account for m ultiple com parisons.

Average Maximum Principal Strain (% )
Distal Superior Inferior
Superior p ≤ 0.001
Inferior p ≤ 0.001 p ≤ 0.001
Proximal p ≤ 0.001 0.02 p ≤ 0.001
Average Minimum Principal Strain (% )
Distal Superior Inferior
Superior 0.055
Inferior 0.001 0.208
Proximal p ≤ 0.001 p ≤ 0.001 p ≤ 0.001
Open in a new tab

The proximal region had a significantly larger average maximum principal strain than the distal and inferior regions. In addition, the proximal region showed a trend toward a greater average maximum principal strain in comparison to the superior region.

As hypothesized, average minimum principal strain was significantly lower in the proximal region than in the distal, superior, or inferior regions.

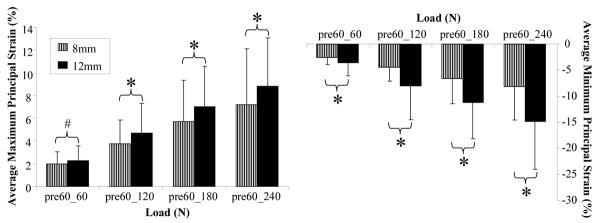
Effect of tear size on tendon strain

As hypothesized, average maximum principal strain was significantly higher for the 12mm tear group than the 8mm tear group at loads of 120N, 180N and 240N. A trend supporting a higher strain for the 12mm than the 8mm tear was observed at 60N (Figure 5). Similarly, average minimum principal strain was significantly lower for tendons with the 12mm than the 8mm tear at 60N, 120N, 180N and 240N (Figure 5).

Figure 5.

Figure 5

Open in a new tab

The 12mm tear group caused a significantly higher average maximum (right) and lower average minimum (left) principal strain than the 8mm tear group (H3). Shown strain between the first nominally loaded image (pre60) and each of loaded images (60N, 120N 180N and 240N).

Table II reports the p values associated with comparisons between the 12mm and 8mm tendon tears for average maximum and minimum principal strains at each load.

Table II.

Statistical analysis of the effect of tear size at each incremental load. Maximum and minimum principal strains adjacent to the 12mm tear were respectively significantly higher and lower than that of the 8mm tear.

Load p Values for Average p Values For Average
Increments (N) Maximum Principal Strain Minimum Principal Strain
60 0.093 0.005
120 0.017 0.001
180 0.031 p ≤ 0.001
240 0.041 p ≤ 0.001
Open in a new tab

DISCUSSION

The objective of the current study was to quantify strain fields adjacent to a rotator cuff tendon tear under loading to failure and to assess associations between tendon strain and tear size. In support of our first hypothesis, a positive linear correlation significantly fit the data supporting a direct relationship between increase in maximum principal strain and increase in tear size. Similarly, a negative linear correlation significantly fit the data supporting a direct relationship between decrease in minimum principal strain and increase in tear size. Interestingly, while percent increase in tear size increased with greater maximum and smaller minimum principal strains, tear propagation occurred at low maximum and high minimum principal strains. These findings validate the use of local strain adjacent to a rotator cuff tear as an indicator of risk of tear propagation and emphasize the importance of understanding the relationship between local strain environment and likelihood of tear propagation.

Results support our second hypothesis that tears will propagate in the direction of highest average maximum and lowest average minimum principal strain into the region that deformed most under loading, becoming the most likely site for further failure. This behavior was expected based on crack propagation theory of non-biological isotropic materials (Tada et al.2000) and has now been shown for the rotator cuff tendon. In normal physiological activity, the tendon to bone insertion site is subjected to complex loading, resulting in high strains that cause further propagation along the insertion site. However, many rotator cuff tears clinically propagate proximal to the insertion site, forming U, L or crescent shaped patterns. This type of behavior leads to proximal tendon retraction, resulting in a tear that is more difficult to repair. Thus, in evaluating the likelihood of tear propagation, measurement of the principal strain components can indicate the region into which the tear is most likely to propagate, thereby potentially impacting clinical treatment.

Finally, the results support our third hypothesis, demonstrating that for a given load, a larger tear will cause greater average maximum and smaller average minimum principal strain than a smaller tear. Additionally, larger tears resulted in a lower failure load than contralateral smaller tears. While intuitive, this supports the concept that larger rotator cuff tears subject the remaining intact tendon to higher loads and cause detrimental tendon strains at much lower loads than smaller tears. While it is reasonable to expect that a larger rotator cuff tear is at greater risk for propagation based on these findings, our results also showed that tear propagation occurred at low maximum and high minimum principal strain, implying that even moderate strains, such as those associated with a small load or small tear, may cause further tear propagation. Note the large standard deviations associated with this data are attributable to specimen variability. The repeated measures design of this experiment ensured that data was evaluated in the context of each specimen, accounting for the large range of strains per load resulting from specimen variability.

Mid-substance, circular tears were evaluated in this study to determine the relationship between tendon loading, tendon strains and tear propagation. These intratendinous defects differ from the insertion site tears that are clinically observed in the supraspinatus tendon. For instance, the difference in loading environment surrounding these two types of tears would result in lower,strains surrounding a mid-substance than an insertion site tear. Despite differences in magnitude, relationships established in this study between strain and tear propagation are expected to be applicable to an insertion site tear. This simplified model allowed us to isolate and establish basic relationships between tear propagation, strain and load, without confounding effects associated with more complex insertion site tears. For example, utilizing an intratendinous, circular defect eliminates any initial bias for tear propagation or high strain in any region because of its lack of sharp edges. Additionally, complexities associated with the curved surface of the insertion site were absent in this model, as strains were evaluated surrounding a tear in a region that anatomically exhibits no curvature.

In this study, the effect of cross-sectional area was not evaluated because it had no impact on the relationship between strain and tear propagation, or on the effect of tear on strain in the four regions surrounding the tear (1st and 2nd hypotheses). Cross-sectional area differences between specimens would impact the effect of load on strain. This relationship (3rd hypothesis) was considered in evaluating the effect of the two tear sizes on strain in the surrounding regions at each load. However, each tear group was randomly assigned an equal number of left and right shoulders. Additionally, each animal had one shoulder with an 8mm tear, and one shoulder with a 12mm tear. This paired data design within each animal used to compare the two tear groups, coupled with the random assignment of equal numbers of left and right shoulders in each tear group, eliminated any effect of cross-sectional area on this data.

The rotator cuff tears investigated in this study were surgically introduced in healthy sheep infraspinatus tendons, excluding factors present in chronic rotator cuff tears, such as tissue degeneration and remodeling due to injury and repair. Chronically degenerated and torn tendon is expected to exhibit diminished mechanical properties, resulting in higher strains under loading than healthy tissue. While the current study evaluates a different loading environment than that associated with chronic rotator cuff tears, we expect that relationships established between strain, tear propagation and loading are applicable in explaining the behavior of chronic supraspinatus tendon tears.

In conclusion, findings from this study provide insight into the relationships between strain, tear propagation and tendon loading. While results demonstrated an association between tear size and propagation, the correlation between strain and tear propagation also shows that factors other than tear size are important in predicting risk of tear propagation. Data from this animal model may readily be extrapolated to provide insight into the behavior of the more complex, clinical insertion site tears. Measurement of local strains around a rotator cuff tear may be used to provide information regarding the likelihood and direction of further tear propagation.

ACKNOWLEDGEMENTS

This study was supported by a grant from the NIH/NIAMS (AR050176) and the NIH/NIAMS supported Penn Center for Musculoskeletal Disorders (AR050950).

Footnotes

CONFLICT OF INTEREST STATEMENT: There are no conflicts of interest to disclose for all authors.

REFERENCES

  1. Bey MJ, Ramsey ML, Soslowsky LJ. Intratendinous strain fields of the supraspinatus tendon: Effect of a surgically created articular-surface rotator cuff tear. J Shoulder Elbow Surg. 2002;11(6):562–9. doi: 10.1067/mse.2002.126767. [DOI] [PubMed] [Google Scholar]
  2. Bey MJ, Song HK, Wehrli FW, Soslowsky LJ. A noncontact, nondestructive method for quantifying intratissue deformations and strains. J Biomech Eng. 2002;124(2):253–8. doi: 10.1115/1.1449917. [DOI] [PubMed] [Google Scholar]
  3. Breazeale NM, Craig EV. Partial-thickness rotator cuff tears. Pathogenesis and treatment. Orthop Clin North Am. 1997;28(2):145–55. doi: 10.1016/s0030-5898(05)70275-3. [DOI] [PubMed] [Google Scholar]
  4. Clark JM, Harryman DT., 2nd Tendons, ligaments, and capsule of the rotator cuff. Gross and microscopic anatomy. J Bone Joint Surg Am. 1992;74(5):713–25. [PubMed] [Google Scholar]
  5. Coleman SH, Fealy S, Ehteshami JR, MacGillivray JD, Altchek DW, Warren RF, Turner AS. Chronic rotator cuff injury and repair model in sheep. J Bone Joint Surg Am. 2003;85(12):2391–402. doi: 10.2106/00004623-200312000-00018. [DOI] [PubMed] [Google Scholar]
  6. Fehringer EV, Sun J, Vanoeveren LS, Keller BK, Matsen FA., 3rd Full-thickness rotator cuff tear prevalence and correlation with function and comorbidities in patients 65 years and older. J Shoulder Elbow Surg. 2008:1–5. doi: 10.1016/j.jse.2008.05.039. Epub. [DOI] [PubMed] [Google Scholar]
  7. Feng S, Guo S, Nobuhara K, Hashimoto J, Mimori K. Prognostic indicators for outcome following rotator cuff tear repair. J Orthop Surg (Hong Kong) 2003;11(2):110–6. doi: 10.1177/230949900301100202. [DOI] [PubMed] [Google Scholar]
  8. Flatow EL, Altchek DW, Gartsman GM, Iannotti JP, Miniaci A, Pollock RG, Savoie F, Warner JJ. The Rotator Cuff. Commentary. Orthop Clin North Am. 1997;28:277–94. doi: 10.1016/s0030-5898(05)70286-8. [DOI] [PubMed] [Google Scholar]
  9. Fukuda H. The management of partial-thickness tears of the rotator cuff. The Journal of Bone and Joint Surgery (Br) 2003;85-B(1):3–11. doi: 10.1302/0301-620x.85b1.13846. [DOI] [PubMed] [Google Scholar]
  10. Fukuda H, Hamada K, Nakajima T, Tomonaga A. Pathology and pathogenesis of the intratendinous tearing of the rotator cuff viewed from en bloc histologic sections. Clin Orthop Relat Res. 1994;(304):60–7. [PubMed] [Google Scholar]
  11. Fukuda H, Hamada K, Yamanaka K. Pathology and pathogenesis of bursal-side rotator cuff tears viewed from en bloc histologic sections. Clin Orthop Relat Res. 1990;(254):75–80. [PubMed] [Google Scholar]
  12. Gerber C, Meyer DC, Scheeberger AG, Hoppeler H, von Rechenberg B. Effect of tendon release and delayed repair on the structure of the muscles of the rotator cuff: an experimental study in sheep. J Bone Joint Surg Am. 2004;86(9):1973–82. doi: 10.2106/00004623-200409000-00016. [DOI] [PubMed] [Google Scholar]
  13. Gerber C, Schneeberger AG, Perren SM, Nyffeler RW. Experimental rotator cuff repair. A preliminary study. J Bone Joint Surg Am. 1999;81(9):1281–90. doi: 10.2106/00004623-199909000-00009. [DOI] [PubMed] [Google Scholar]
  14. Gerber C, Schneeberger AG, Beck M, Schlegel U. Mechanical strength of repairs of the rotator cuff. J Bone Joint Surg Br. 1994;76(3):371–80. [PubMed] [Google Scholar]
  15. Habernek H, Schmid L, Frauenschuh E. Five year results of rotator cuff repair. Br J Sports Med. 1999;33(6):430–3. doi: 10.1136/bjsm.33.6.430. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Hatakeyama Y, Itoi E, Pradhan RL, Urayama M, Sato K. Effect of arm elevation and rotation on the strain in the repaired rotator cuff tendon. A cadaveric study. Am J Sports Med. 2001;29(6):788–94. doi: 10.1177/03635465010290061901. [DOI] [PubMed] [Google Scholar]
  17. Itoi E, Berglund LJ, Grabowski JJ, Schultz FM, Growney ES, Morrey BF, An KN. Tensile properties of the supraspinatus tendon. J Orthop Res. 1995;13(4):578–84. doi: 10.1002/jor.1100130413. [DOI] [PubMed] [Google Scholar]
  18. Matava MJ, Purcell DB, Rudzki JR. Partial-thickness rotator cuff tears. Am J Sports Med. 2005;33(9):1405–17. doi: 10.1177/0363546505280213. [DOI] [PubMed] [Google Scholar]
  19. Matsen FA., 3rd Clinical practice. Rotator-cuff failure. N Engl J Med. 2008;358(20):2138–47. doi: 10.1056/NEJMcp0800814. [DOI] [PubMed] [Google Scholar]
  20. Milgrom C, Schaffler M, Gilbert S, van Holsbeeck M. Rotator-cuff changes in asymptomatic adults. The effect of age, hand dominance and gender. J Bone Joint Surg Br. 1995;77(2):296–8. [PubMed] [Google Scholar]
  21. Nakajima T, Rokuuma N, Kazutoshi H, Tomastu T, Fukuda H. Histologic and biomechanical characteristics of the supraspinatus tendon: Reference to rotator cuff tearing. J Shoulder Elbow Surg. 1994;3:79–87. doi: 10.1016/S1058-2746(09)80114-6. [DOI] [PubMed] [Google Scholar]
  22. Neer CS., 2nd Impingement lesions. Clin Orthop Relat Res. 1983;173:70–7. [PubMed] [Google Scholar]
  23. Peterson CA, Altchek DW. Arthroscopic treatment of rotator cuff disorders. Clin Sports Med. 1996;15:715–36. [PubMed] [Google Scholar]
  24. Reilly P, Amis AA, Wallace AL, Emery RJ. Mechanical factors in the initiation and propagation of tears of the rotator cuff. Quantification of strains of the supraspinatus tendon in vitro. J Bone Joint Surg Br. 2003;85(4):594–9. doi: 10.1302/0301-620x.85b4.12062. [DOI] [PubMed] [Google Scholar]
  25. Reilly P, Amis AA, Wallace AL, Emery RJ. Supraspinatus tears: Propagation and strain alteration. J Shoulder Elbow Surg. 2003;12(2):134–8. doi: 10.1067/mse.2003.7. [DOI] [PubMed] [Google Scholar]
  26. Sher JS, Uribe JW, Posada A, Murphy BJ, Zlatkin MB. Abnormal findings on magnetic resonance images of asymptomatic shoulders. J Bone Joint Surg Am. 1995;77(1):10–5. doi: 10.2106/00004623-199501000-00002. [DOI] [PubMed] [Google Scholar]
  27. Tada HPPC, Irwin GR. The Stress Analysis of Cracks Handbook. 3rd edition American Society of Mechanical Engineers; New York: 2000. Crack-Tip Stress Fields for Linear-Elastic Bodies; pp. 2–26. [Google Scholar]
  28. Yamaguchi K, Ditsios K, Middleton WD, Hildebolt CF, Galatz LM, Teefey SA. The demographic and morphological features of rotator cuff disease. A comparison of asymptomatic and symptomatic shoulders. J Bone Joint Surg Am. 2006;88(8):1699–704. doi: 10.2106/JBJS.E.00835. [DOI] [PubMed] [Google Scholar]

RESOURCES