On Image Reconstruction from a Small Number of Projections

Abstract

Image reconstruction from projections suffers from an inherent difficulty: there are different images that have identical projections in any finite number of directions. However, by identifying the type of image that is likely to occur in an application area, one can design algorithms that may be efficacious in that area even when the number of projections is small. One such approach uses total variation minimization. We report on an algorithm based on this approach, and show that sometimes it produces medically-desirable reconstructions in computerized tomography (CT) even from a small number of projections. However, we also demonstrate that such a reconstruction is not guaranteed to provide the medically-relevant information: when data are collected by an actually CT scanner for a small number projections, the noise in such data may very well result in a tumor in the brain not being visible in the reconstruction.

1. Introduction

In an application of image reconstruction from projections, the image is typically represented by a function f of two variables of bounded support. The values of this function are elements of the set of real numbers ℝ and they represent some physical property (e.g., linear X-ray attenuation coefficient in computerized tomography (CT) or Coulomb potential in electron microscopy (EM) of molecules) in a cross-section of the object to be reconstructed. The projections are usually taken with the help of some rays (e.g., X-rays or electron beams) and can be thought of mathematically as collections of line integrals of the function. The mathematical problem is to reconstruct the function from its (noisy and incomplete) projections [14, 25].

We define the projection in direction ϑ ∈ [0, π) as follows. Let (s₁, s₂) denote the coordinates of the point r = (r₁, r₂) ∈ ℝ² in the coordinate system rotated by ϑ. Then the projection of f in the direction ϑ (the ϑ-projection of f) is defined as that function [Rf](•, ϑ) of the variable s₁ for which

$$[Rf](s_1,\vartheta )={\int }_{L_{s_1,\vartheta }}f(r)d{s}_2,$$ (1)

where L_s,ϑ is the line at the distance s from the origin that makes the angle ϑ with the r₂-axis. It can be said that the transform R defined by (1) gives the ϑ-projections of f for any ϑ ∈ [0, π). The transform R is called the Radon transform of f, after J. Radon who studied this kind of transform in [27].

Let us suppose for now that we have taken projections of f for directions ϑ in the finite set Θ. Let, for s ∈ ℝ and ϑ ∈ Θ, g(s, ϑ) denote the approximation to [Rf](s, ϑ) that we obtain based on our measurements. For any ϑ ∈ Θ, we use S_ϑ to denote the set of all s for which we have a projection data item g(s, ϑ). In practice, the sets S_ϑ have to be finite, but in this paper we also deal with the mathematical idealization in which, for all ϑ ∈ Θ, S_ϑ is the set of all real numbers. (The point that we will make is that even such overabundance of data, as compared to what can be obtained in practice, is not in general sufficient for determining f uniquely.) Then we consider the following reconstruction task: Suppose f is an unknown image and we are given g(s, ϑ) for ϑ ∈ Θ and s ∈ S_ϑ, such that

$$[Rf](s,\vartheta )\approx g(s,\vartheta ),\text{for all}\vartheta \in \Theta ,s\in S_{\vartheta },$$ (2)

(where ≈ stands for approximately equal), we need to find an image f* that is a “good” approximation of f.

Our topic is an investigation of this task when the size of Θ is small. In applications such as CT and EM, the number of projections is often in the thousands; here we restrict our attention to cases in which that number is less than a hundred, or even only two or three. It has been shown (and this is discussed and further illustrated below) that good reconstruction results can be obtained from a small number of projections for certain (usually not realistic) restricted classes of images and data collection modes.

However, one has to be careful not to assume that similar methodologies can be usefully applied in actual applications of image reconstruction from projections. For example, the earliest application of CT in diagnostic medicine was the imaging of the human brain inside the head [18]. It is unlikely that whatever assumption is made about the nature of images in order to achieve good reconstructions from a small number of projections will be satisfied by all the possible images in such an application. In addition, CT is used to image the brain because one suspects a possible abnormality (e.g., a malignant tumor); even if it were the case that healthy brains satisfied a mathematical property that can be used for achieving reconstructions from a small number of views, forcing reconstructions to be consistent with this property may result in missing an abnormality present in the brain. In addition, physically collected data are unlikely to satisfy the mathematical assumptions that make reconstructions from a few projections possible, we demonstrate below that this by itself can result in the invisibility of a tumor in the brain when reconstructed from a small number of physically realistic projections.

Our paper is organized as follows. The next section discusses the essential notions of digital images, digitization of images, and what we call the “digital assumption,” together with an overview of discrete tomography (DT), which is a methodology that has been used to obtain good reconstructions from a small number of projections when the digital assumption is satisfied. The following section presents an alternative methodology that can be used to obtain good reconstructions from a small number of projections for certain classes of images and data collection modes: namely, total variation minimization. In Section 4 we specify the algorithms that we use in our paper for total variation minimization and for norm minimization. Section 5 presents two actual brain cross-sections and discusses why such images may not be in the special classes of the previous sections. It also presents the concept of ghosts, which are invisible from given projection directions. Section 6 presents two mathematical phantoms: the difference between them is a ghost for 22 projection directions. This ghost to some extent mimics a malignant tumor. Because the tumor is a ghost, the projection data for the given 22 directions are the same for the brain with and without the tumor and so no reconstruction algorithm could possibly distinguish between the presence and absence of this tumor in the brain. On the other hand, it is shown that such distinction can clearly be made if ideal (in the sense of satisfying some mathematical assumptions) data are collected for more (in our case 60 additional) projections. However, when data are collected in a realistic fashion (in the sense of simulating what happens in an actual CT scanner), the tumor again becomes invisible when using the same algorithm to reconstruct from the 82 views. Conclusions are given in Section 7.

2. Digitization and Discrete Tomography

In discussing our concepts it is essential to have the notion of an N × N digital image p, which is defined as a function from [0, N − 1]² into the real numbers, for a positive integer N. As it is customary in this context, elements of [0, N − 1]² are denoted by row vectors (t₁, t₂) and we consider that (t₁ + 1, t₂) is “below” and (t₁, t₂ + 1) is “to the right of” (t₁, t₂). This can be made mathematically precise by the introduction of a positive real number d, referred to as the sampling interval. Given a positive integer N and such a d, we associate with each (t₁, t₂) ∈ [0, N − 1]² a subset of the plane ℝ², which is called the pixel associated with (t₁, t₂), defined as

$$\begin{array}{c}pi{x}^{N,d}(t_1,t_2)=\{(r_1,r_2)\in {ℝ}^2|-\frac{(N-2t_2)d}{2}<r_1\le -\frac{(N-2-2t_2)d}{2}\\ \text{and}\frac{(N-2-2t_1)d}{2}\le r_2<\frac{(N-2t_1)d}{2}\}.\end{array}$$ (3)

Given an image f, a positive integer N and a sampling interval d, we define the N × N digital image $p_f^{N,d}$ by

$$p_f^{N,d}(t_1,t_2)=\frac{1}{d^2}\underset{pi{x}^{N,d}(t_1,t_2)}{\int }f(r)dr,$$ (4)

for any (t₁, t₂) ∈ [0, N − 1]². So, the N × N digitization $p_f^{N,d}$ with sampling interval d of f is provided by the averages of f over the pixels. An N × N digital image p and a d > 0 gives rise to an image ${\text{f}}_p^d$ that is defined by

$${\text{f}}_p^d(r)=\{\begin{array}{cc}p(t_1,t_2),& \text{if}r\in pi{x}^{N,d}(t_1,t_2)\text{for some}\\ \hfill & (t_1,t_2)\in {\left[0,N-1\right]}^2,\hfill \\ 0,\hfill & \text{otherwise}.\hfill \end{array}$$ (5)

For any N × N digital image p and any sampling interval $d,p_{\left[{\text{f}}_p^d\right]}^{N,d}=p$. However, it is generally not the case that, for an image f, positive integer N, and sampling interval $d,f_{\left[p_f^{N,d}\right]}^d=f$, even if the N and the d are chosen large enough so that f(r) = 0 whenever max {|r₁|, |r₂|} ≥ Nd/2. However, for a “reasonable” image f, there should be an N and a d, such that $f_{\left[p_f^{N,d}\right]}^d\approx f$.

A common approach to solving the reconstruction task is to assume that the image to be reconstructed is ${\text{f}}_p^d$ for some N × N digital image p and sampling interval d. We will refer to this as the digital assumption. The reason why this is helpful is the following. Let us use an alternative representation of the digital image p as an n-dimensional vector (i.e., an element of ℝⁿ) x_p, where n = N² and, for 1 ≤ i ≤ n, the ith component of x_p is p(t₁, t₂), where (t₁, t₂) ∈ [0, N − 1]² and i = t₁N + t₂ + 1. Note that such a t₁ and t₂ are uniquely determined by i and so we may denote them by $t_1^i$ and $t_2^i$ respectively. Using this notation, it is easy to see that in such a case we have that, for any ϑ ∈ Θ and any s ∈ S_ϑ,

$$[R{\text{f}}_p^d](s,\vartheta )=\langle a,x\rangle ,$$ (6)

(as usual, 〈a, x〉 denotes ${\sum }_{i=1}^n{a}_i{x}_i$, where a is the n-dimensional vector whose ith component is the length of the segment of the line L_s,ϑ that lies in the pixel $pi{x}^{N,d}\left(t_1^i,t_2^i\right)$ (in other words, it is the length of the intersection of the line with the ith pixel). In this fashion, each (approximate) equality in (2) gets replaced by an (approximate) linear equation in the unknown vector x. Let x* denote a “solution” of this system of (approximate) linear equations and let p* denote the (unique) N × N digital image such that x_p* = x*. Then one may consider $f^{\ast }=f_{p^{\ast }}^d$ to be a potential solution of the original problem. The important point here is that we obtain such a solution by solving a system of (approximate) linear equalities, and there is an extremely well-established field of numerical mathematics for solving such systems (see, e.g., [32]).

There is, however, a problem with such an approach. Even in the idealized case when there is no noise in the data (i.e., we have equalities, rather than approximate equalities, in (2)), the methodology can lead to a very inaccurate reconstruction due to the digital assumption. That is, the digital assumption can be a source of error: even though this methodology may lead to a unique reconstruction from perfect (noiseless) data, the result is not identical to either the image for which the data have been collected or to its digitization. The error can however be reduced by finer sampling and more data, but since an image may not correspond exactly to any digital image, we cannot expect a perfect reconstruction no matter how finely we digitize and how much data we use. To restate this in other words: just because a method can be shown to solve accurately the system of algebraic equations (6), one must not conclude that it will also perform well (in the sense of providing a good approximation of f) if the left hand sides of (6) were replaced by the g(s, ϑ) of the integral equations (2). To draw such a conclusion would be an inverse crime, which is defined in [19] as “the procedure of first simplifying the model, developing an estimator based on this model and then testing it against data produced with the same simplified model.”

That high quality (and sometimes even exact) reconstructions can be obtained from a small number of projections for certain class of images has been known for quite a while; for example, the whole field of discrete tomography (DT, see [15, 16]) is devoted to this topic. In DT it is assumed that all values in the images to be reconstructed come from a known finite set (maybe containing only two elements, in which case we use the term binary tomography), and this knowledge is then used in the reconstruction process to recover the images from a small number of projections. The first papers explicitly dealing with DT appeared in the early 1970s [21].

It is typical in discrete tomography to make the digital assumption. However, there are exceptions to this rule (e.g., [20]). In fact, there is a whole field referred to as geometric tomography [12] that may roughly be described as binary tomography without the digital assumption. The relationship between DT and geometric tomography is discussed in [21].

Using the digital assumption, powerful results have been obtained in DT. For example, Aharoni, Kuba, and Herman [1] provided a characterization (using ideas from linear programming) of those pixel locations in a binary digital image where the value is uniquely determined by the given data. There are additional assumptions that one can make that can be very useful to resolve the ambiguities at locations where the value is not uniquely determined by the data alone. One of these is to assume a prior distribution (such as a Gibbs distribution [31]) representative of the class of digital images in the specific application area. An example is provided by [24]), whose approach combines optimization (that is based on the data and the assumed prior distribution) with the linear programming characterization of [1]. That this approach is robust enough to be applicable to real data (in which the images are not generated by the assumed Gibbs prior and the measurements are not perfect) is demonstrated in [8] by the reconstruction of cardiac angiographic images from three projections. When the assumptions of DT are strictly met, it is often possible to recover exactly values in the image to be reconstructed. However, in practice it tends to be the case that the assumptions are only approximately satisfied and so perfection can no longer be guaranteed, but nevertheless reported experience indicates that even then DT can be efficaciously applied for reconstruction from a few projections in a variety of applications.

3. Total Variation Minimization

In the report on SIAM Imaging Science 2006 (SIAM News, v. 39(7), September 2006) it is stated: “A lot of credit for the excitement goes to Candes, who with Justin Romberg (Caltech) and Terence Tao (UCLA), proved an impressive result about the possibility of perfect reconstruction, given small amounts of data.” Indeed, a recent paper by these authors [5], they “Consider a simplified version of the classical tomography problem in medical imaging,” they reconstruct an image from data that corresponds to having only 22 projections and they report that “The reconstruction is exact” (their italic) and go on to say that they “obtained perfect reconstructions on many similar test phantoms.” And, yet again, the caption of Figure 1 of the front-page article in SIAM News, v. 39(9), November 2006 states: “When Fourier coefficients of a testbed medical image known as the Logan-Shepp phantom (top left) are sampled along 22 radial lines in the frequency domain (top right), a naive, ‘minimal energy’ reconstruction setting unobserved Fourier coefficients to 0 is marred by artifacts (bottom left). Surprisingly, ℓ₁-magic reconstruction (bottom right) is not just better - it's perfect!”

Figure 1.

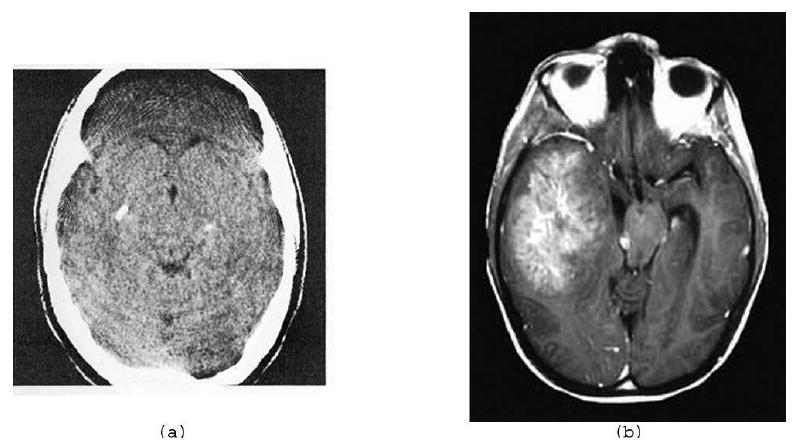
Two actual brain cross-sections. (a) Fig. 4.2 of [14]. (b) From the Roswell Park Cancer Institute website www.roswellpark.org/Patient_Care/Types_of_Cancer/Brain_Pituitary_Spine/BrainTumorFacts.

As we have seen in the previous section, “the possibility of perfect reconstruction, given small amounts of data” using DT has been known for over 35 years. However, claims of “perfection” and “exactness” in a real tomography application have not been made before. This is for a good reason, such claims are only tenable in artificial environments in which the underlying mathematical assumptions are strictly satisfied: as soon as we get to a physical image reconstruction problem, such claims cannot possibly be true (we carefully illustrate this in what follows). However, even though the reconstructions produced by the approach referred to in the first paragraph of this section cannot be guaranteed to be “exact” in more realistic situations, nevertheless they are sometimes efficacious (as compared to some alternative approaches), as is demonstrated for example in [30] and also later in our paper. First we discuss more carefully the nature of the approach.

In [5] the discussion concentrates on N × N digital images. The special property that is stated there as the one that allows reconstruction from a few projections is that the digital images should be “mostly constant”; which can be mathematically defined by saying that

$$\begin{array}{c}|\{(t_1,t_2)|0\le t_1,t_2<N-1\text{and}\\ p(t_1+1,t_2)\ne p(t_1,t_2)\text{or}p(t_1,t_2+1)\ne p(t_1,t_2)\}|\le B,\end{array}$$ (7)

where the size of the smallest such integer B gives a meaning to “mostly” (presumably, it is much less than N²).

In [5], the recovery of such a digital image is discussed from its discrete Fourier transform (DFT), sampled on a “small” subset of its domain (whose full size is N²). The recovery is achieved by defining the functional total variation (TV) (introduced by Rudin et al. [28] to the field of image restoration) that associates, with every N × N digital image p, a real number

$$\Vert p{\Vert }_{\text{TV}}=\sum _{t_1=0}^{N-2}\sum _{t_2=0}^{N-2}\sqrt{{(p(t_1+1,t_2)-p(t_1,t_2))}^2+{(p(t_1,t_2+1)-p(t_1,t_2))}^2},$$ (8)

and then choosing a digital image that has a minimal TV among all the ones that have the given DFT values at the sample points. A rough way of describing the consequences of the results of [5] is that there is a number S such that if SB log N (or more) sample points are randomly selected in the DFT domain, then the probability that the recovery approach described above will result in anything but the given digital image is small. It can be made smaller, by increasing S.

An objection to the relevance of this result to image reconstruction from projections, as practiced for example in CT, is that the underlying assumption of (7) is unlikely to be fulfilled for any B that is significantly less than N². This is the subject matter of Section 5. However, as is illustrated in the section after that, TV minimization can be quite efficacious even if (7) is violated for any B significantly smaller than N². Hence TV minimization has a wider range of applicability than what is implied by the result of the last paragraph.

Now we list some additional concerns.

1. In practice, we have at our disposal only approximations of the values of the DFT of f. This is both because practical projection data are noisy and because the data collection geometry allows us estimation only on radial lines and this will have to be followed by an interpolation to get at the required samples (see Section 9.2 of [14]).

2. The recovery procedure described above is only a mathematical formulation, we still need an algorithm that finds the minimizer of TV subject to the given constraints. Such an algorithm is likely to be an iterative method (see, e.g., Algorithm 6 of [10], and we describe the one that we use in this paper in the next section) that has to be stopped at some point, at which we will have only an approximation to the minimizer.

3. The claim made above is probabilistic; we can never be absolutely certain that the particular case with which we are dealing is not one of the unlikely cases.

In view of these concerns, the adjectives “perfect” and “exact” describing reconstructions that can be obtained by such approaches in the practice of medical imaging seem exaggerated. To use them in that context based on results obtained from data produced by the assumed simplified model of that actual situation is an example of committing an inverse crime [19], as discussed in the the previous section. In fact, in Section 6 it is demonstrated (using the mostly constant approximation of a cross-section of a human head shown in Fig. 2(b)) that the image that minimizes TV subject to even idealized perfect projections for 82 directions is not exactly the image for which the projection data were calculated. (The image in Fig. 3(a) satisfies the projection data extremely closely, and yet its TV is less than that of the given digital image in Fig. 2(b).) Nevertheless, we confirm that our TV-minimizing iterative procedure produces high quality reconstructions from a small number of projections that are calculated assuming some unrealistic physical conditions (detailed examples are given below). However, when we apply our TV-minimizing algorithm to realistic data from the same small number of projections, the result that we obtain is quite unacceptable from the medical point of view. We illustrate this in Fig 5(a) where the tumor becomes totally invisible in the reconstruction (we give the complete details to the experimental result in Section 6). As far as we can tell, this problem can be overcome only by the collection of data for additional projections: good quality reconstructions are obtained when using the same realistic data collection mode, but for a larger number of projections (something more similar to the number of projections that would be used in a clinical CT scanner).

Figure 2.

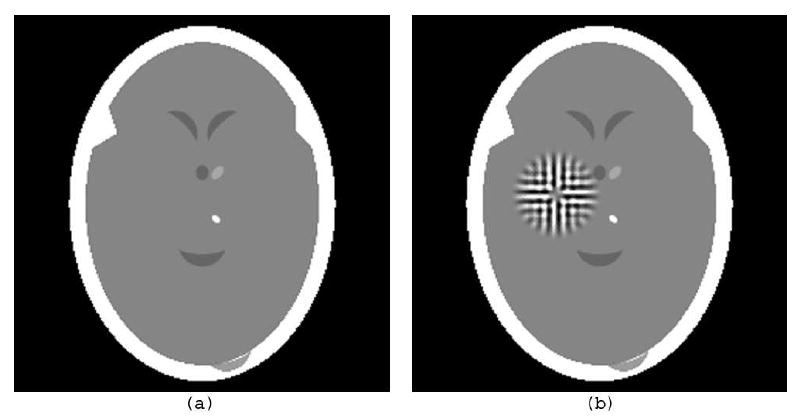
(a) Digitization $p_b^{243,0.0752}$ of the head phantom b based on Fig. 1(a), similar to Fig. 4.4 of [14]. (b) The same with a “tumor” g (which is a ghost for 22 projections) added to it.

Figure 3.

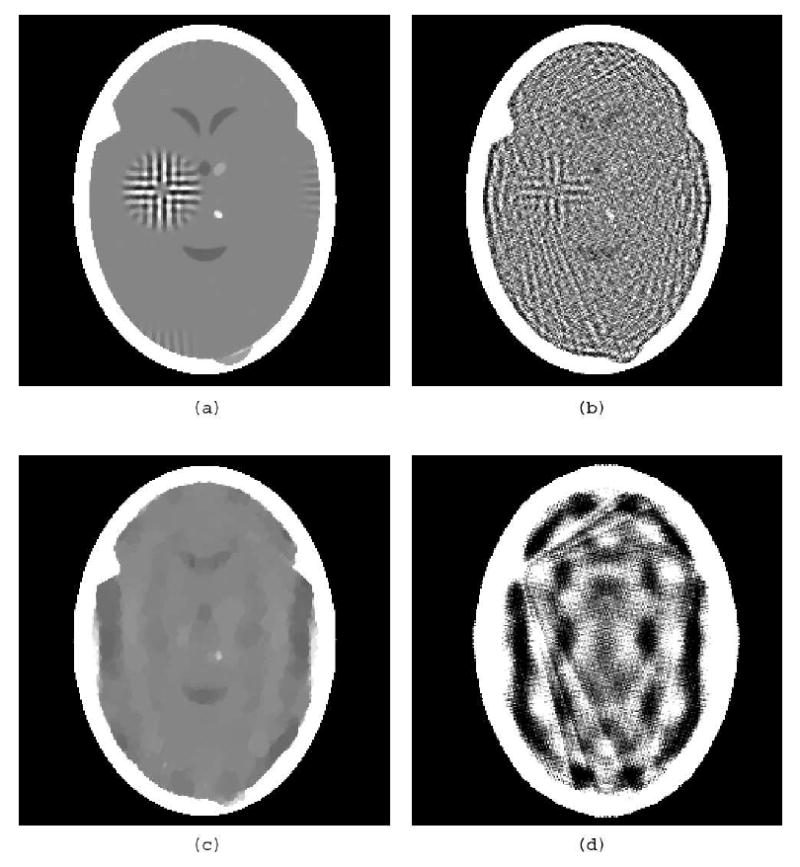
(a) TV-minimizing reconstruction by our algorithm from 82 noiseless idealized projections of the head phantom with a tumor in Fig. 2(b). (b) Norm-minimizing reconstruction by our algorithm from the same data. (c) The same as (a), but using only 22 projections. (d) The same as (b), but using only 22 projections.

Figure 5.

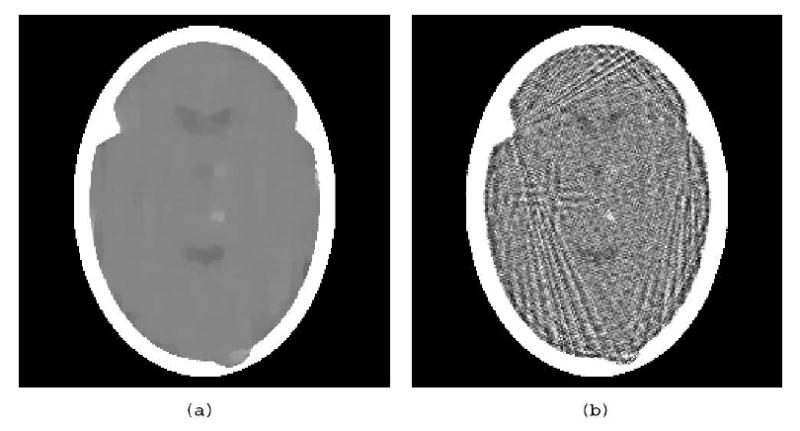
(a) TV-minimizing reconstruction from 82 realistically simulated projections of the head phantom with a tumor and variability in Fig. 4(a). (b) Norm-minimizing reconstruction from the same data.

4. The Minimization Algorithms

In this section we present the algorithms that are used in Section 6 to produce reconstructions from projections. Based on (6), consider the consistent system of equations

$$\langle a^i,x\rangle =b_i,$$ (9)

where aⁱ ∈ ℝⁿ, b_i ∈ ℝ, ‖aⁱ‖ > 0, and ${\text{a}}_j^i\ge 0$, for 1 ≤ i ≤ m and 1 ≤ j ≤ n. We wish to find an x ∈ ℝⁿ that is a solution to this linear system of equations. For any nonempty B ⊆ {1, …, m} we define an operator P_B : ℝⁿ → ℝⁿ by

$${\text{P}}_{B}x=x+\frac{1}{\left|B\right|}\sum _{i\in B}\frac{b_i-\langle a^i,x\rangle }{\Vert a^i{\Vert }^2}{a}^i,$$ (10)

where |B| is the cardinality of B and, as usual, the norm ‖•‖ is defined to be $\sqrt{\langle •,•\rangle }$. Suppose that ϑ₁, ϑ₂, …, ϑ_T are all the projection directions in Θ and, for 1 ≤ t ≤ T, B_t consists of all the indices i associated with the measurements taken in direction ϑ_t; see (6). We define the operator P : ℝⁿ → ℝⁿ by

$$\text{P}x={\text{P}}_{B_T}\cdots {\text{P}}_{B_2}{\text{P}}_{B_1}x.$$ (11)

We claim that the following holds.

Theorem. Let {β_k}_k∈ℕ be a sequence of positive real numbers such that ${\sum }_{k=0}^{\infty }{\beta }_k<\infty$, let {v^k}_k∈ℕ be bounded sequence of vectors in ℝⁿ and let x⁰ ∈ ℝⁿ. Then the sequence generated by

$$x^{k+1}=\text{P}(x^k+{\beta }_k{v}^k),\text{for}k\in \mathbb{N},$$ (12)

converges to a solution of (9).

We do not give the details of our proof. It consists of two parts.

In the first part of the proof it is shown that the Theorem holds if β_k = 0, for k ∈ ℕ. This is proved along the lines of proofs of similar results in [9, 11]. In addition, by choosing x⁰ to be the zero vector (which is what we do in all the reconstructions on which we report), we see that in this case each of the x^k is a linear combination of the a_i, and so convergence to a solution in fact implies convergence to the solution with minimal norm (see, e.g., [14] Section 11.2).

The second part of the proof shows that the convergence to a solution is maintained even in the presence of the summable perturbations in (12). This part is similar to a convergence proof provided in [4] and it relies on results from [2, 3].

The Theorem guarantees convergence even if the calculation of the iterates is affected by summable perturbations. We can make use of this property to steer the iterates towards the minimizer of a given convex function φ. That is, given a function φ : ℝⁿ → ℝ and a consistent system of equations (as in (9)), our algorithm aims at an x ∈ ℝⁿ that minimizes φ among the solutions of (9). The heuristic provided below is not guaranteed to achieve actual convergence to a minimizer of φ. However, it proceeds so that the value of the given function tends to be reduced and yet convergence to a solution of (9) is not compromised. The usefulness of this is illustrated in Section 6 for image reconstruction with φ is defined so that, for a digital image p, φ(x_p) = ‖p‖_TV.

For any k ∈ ℕ, let s^k ∈ ∂φ(x^k) be a subgradient of φ at x^k and

$$v^k=\{\begin{array}{cc}-\frac{s^k}{\Vert s^k\Vert },& \text{if}{s}^k\ne 0,\\ 0,& \text{if}{s}^k=0.\end{array}$$ (13)

The sequence {v^k}_k∈ℕ is bounded. Hence, by the Theorem, for any summable sequence of positive real numbers {β_k}_k∈ℕ, the {x^k}_k∈ℕ generated as in (12) converges to a solution of (9). We generate {β_k}_k∈ℕ as follows. Let, for x ∈ ℝⁿ,

$$Re\text{s}(x)=\sqrt{{\sum _{i=1}^m\left(\frac{b_i-\langle a^i,x\rangle }{\Vert a^i\Vert }\right)}^2},$$ (14)

The size of Res(x) indicates how badly x violates the given system of equations. To approximate the solution of the optimization problem (for φ) it is desirable to find an x for which Res(x) is small, and among all x with similar (or smaller) value of Res(x), the φ(x) should be small relative to the others. Guided by this principle, we initialize β to be an arbitrary positive number, which we denote by β₋₁. (We have always used β₋₁ = 1.) In the iterative step from x^k to x^k+1, we update the value of β, which is (in the notation of (12)) β_k−1 at the beginning of the step and β_k at its end. This is done according to the pseudocode (in which v^k is defined by (13)):

1:	logic = true
2:	while (logic)
3:		z = xk + βvk
4:		if (φ(z) ≤ φ(xk))
5:			then
6:				xk+1 = Pz
7:				if (Res(xk+1) < Res(xk))
8:					then logic = false
9:					else β = β/2
10:			else β = β/2

The iterative process is stopped when Res(x^k) < ε, where ε is a user-specified positive number. To avoid infinite loops in which Res(x^k + 1) < Res(x^k) always fails but at the same time φ keeps being reduced, we also incorporated an additional stopping criterion based on β getting smaller than some user-specified value; however, in all the experiments reported in Section 6 stopping was due to the criterion Res(x^k) < ε.

Let us put our proposed algorithm into the context of existing literature. In addition to the already mentioned [4, 5, 10, 28, 30], there are numerous papers relevant to TV reconstruction in medical imaging: for example, [26]. Of particular interest from the point of view of our paper is that TV can be usefully combined with DT: [6] proposes the use of discretization applied to a reconstruction obtained using a TV constraint as the solution to the DT reconstruction problem from a few noisy projections. Since we have not performed any comparative evaluations, we do not claim that the approach proposed in this section is superior by some criterion to those previously published. The main point of our paper are the results rather than the algorithm, the algorithm just happens to be the one that we use to obtain our results; we include its description because it has not been previously published. The algorithm falls into the class of block-iterative projection methods; such methods have a long and successful history in the field of image reconstruction from projections [9, 11]. They are closely related to the well-known ART algorithm (or Kaczmarz' method; see, for example, [17] or Chapter 11 of [14]). The difference is that in ART instead of using in (11) B_t that consist of all the indices i associated with the measurements taken in direction ϑ_t, we use B_t that consist of the index associated with a single measurement. The Theorem is new, no convergence result for a perturbed version of a block-iterative projection method has been previously published (although a corresponding theorem for ART is proved in [4]). A useful feature of such projection methods is their computational attractiveness in the context of image reconstruction from projections: since ${\text{a}}_j^i=0$ except when the the ith line intersects the jth pixel, typically ${\text{a}}_j^i$ is nonzero only for a small fraction of the j (in the examples discussed in Section 6 this fraction is less than 1%) and, for 1 ≤ i ≤ m, the list of such j and the corresponding values of ${\text{a}}_j^i$ can be efficiently calculated when they are needed. Such information leads to efficient evaluation of (10) with minimal demand for computational storage. These are the considerations that led us to use the proposed algorithm.

The complete algorithm consists of (12) with the v^k defined by (13) and the β_k defined by the pseudocode that makes use of (14). The algorithm is heuristic, we have no proof of convergence to the optimizer of φ under the given constraints; all we know is that it steers the x^k so as to reduce the φ(x^k) (see Step 4 of the pseudocode), while attempting to maintain the convergence to the feasible region, as guaranteed by the Theorem for a proper choice of the sequence {β_k}_k∈ℕ (see Step 7 of the pseudocode). Because of the specified stopping criterion, the aim of the algorithm can be stated as that of finding an x such that Res(x) < ε and φ(x) is “small.” While we have no precise mathematical result corresponding to this fuzzy aim, in all but one of the experiments reported in Section 6 the TV of the image produced by our algorithm is less than that of the image from which the projection data were generated. In those cases it follows that even if by the use of another algorithm we could have obtained an image with a smaller TV, this result would likely to be less useful than ours form the practical point of view, since it would differ more from what we wished to reconstruct as measured by the similarity of TV values. The one case where our algorithm did not produce a reconstruction with this desirable property is the unrealistic one in which the phantom satisfies (7) for a small B and the input consists of idealized perfect projections for 22 directions.

5. Brains and Ghosts

In Fig. 1 we show two actual brain cross-sections. Except for the region outside the head, it is unlikely that there are any (t₁, t₂) for which the condition that “p(t₁ + 1, t₂) ≠ p(t₁, t₂) or p(t₁, t₂ + 1) ≠ p(t₁, t₂)” is not satisfied. Thus, in these images B is a large fraction of N².

One may argue that the images shown in Fig. 1 are produced by some medical imaging devices and the local variations that we observe are entirely due to noise in the data collection, errors in the reconstruction, etc. We do not believe this for a minute (a brain is far from being homogeneous: it has gray matter, white matter, blood vessels and capillaries carrying oxygenated blood to and deoxygenated blood from the brain, etc.), but even if we were to stipulate for the sake of argument that healthy brains might give rise to images for which (7) is satisfied with a small B, we cannot avoid the fact that one is not in the business of imaging healthy brains: the reason why a CT scan of a brain is taken is that there is a suspicion of an abnormality. This abnormality may be a malignant tumor (such as the one in the left half of Fig. 1(b)) and may have a highly textured appearance. One of our main points is this: reconstructing from a few projections (using TV minimization or any other method) may make the tumor disappear, defeating the whole purpose of diagnostic CT!

To illustrate that such a thing can really happen we recall the idea of ghosts (images that are invisible from given projection directions). The existence of ghosts have been known and studied since the earliest days of CT; see, e.g., Section 16.4 of [14]. Here we discuss how to generate ghosts for digital images. Let ϑ be a direction in the plane. We say that a digital image p is a ghost for direction ϑ if, for every s ∈ ℝ and d > 0, $\left[R{\text{f}}_p^d\right](s,\vartheta )=0$.

Our particular way of producing ghosts for this paper is based on an idea that we first published over 35 years ago [13]. For this method it is necessary that the directions ϑ should be of the form arctan (u/v), where u and v are integers, not both zero.

Suppose that we are given L pairs of such integers (u₁, v₁), …, (u_L, v_L). We now construct an image that is a ghost for each of the directions arctan(u_ℓ/v_ℓ), for 1 ≤ ℓ ≤ L. The construction defines a sequence h⁰, h¹, …, h^L of real-valued functions of two integer arguments of finite support (i.e., for 0 ≤ ℓ ≤ L, there are only finitely many pairs of integers (t₁, t₂) for which the value of h^l is not zero). We can select h⁰ to be any such function and then define, for 1 ≤ ℓ ≤ L and all pairs of integers (t₁, t₂),

$$h^{\ell }(t_1,t_2)=h^{\ell -1}(t_1,t_2)-h^{\ell -1}(t_1+u_{\ell },t_2+v_{\ell }).$$ (15)

Clearly, all the functions defined in this way will be of finite support. Now suppose that there exist integers w₁ and w₂ such that h^L (t₁, t₂) ≠ 0 implies that w₁ ≤ t₁ ≤ w₁ + N − 1 and w₂ ≤ t₂ ≤ w₂ + N − 1. (Such w₁ and w₂ can always be found, provided only that N is large enough.) If we now define, for all (t₁, t₂) ∈ [0, N − 1]²

$$g(t_1,t_2)=h^L(w_1+t_1,w_2+t_2),$$

then the N × N digital image g is a ghost for the directions arctan(u₁/v₁), …, arctan(u_L/v_L).

6. Results

Based on the medical image in Fig. 1(a), we created an image b (a head phantom) exactly as described in Section 4.3 of [14]. (The description consists of the specification of fifteen geometrical shapes, with a value assigned to each of them. At any point r ∈ ℝ², b(r) is defined to be the sum of the values of those geometrical shapes that cover r.) In Fig. 2(a), we show the digitization of the image b where N = 243 and d = 0.0752 (we will denote it for the rest of the paper by $p_b^{243,0.0752}$). This digitization was produced by the software Snark05 [7], where the digitization was approximated by using a Riemann sum calculation based on 11 × 11 points in each pixel. (In showing $p_b^{243,0.0752}$, we display any value that is 0.1945 or less as black and any value that is 0.22 or more as white. The range of values in $p_b^{243,0.0752}$ is from 0.0 to 0.5641; thus the displayed range is less than 5% of the actual range. Such a display mode is necessary so that we can see the details inside the skull. The same mapping of values into displayed intensities is used for all the images that are discussed below.) Clearly, $p_b^{243,0.0752}$ satisfies (7) with a relatively small B.

To illustrate the claim that it is in-practice dangerous to rely on reconstructions from a small number of projections, we added a ghost g for 22 projections. The resulting digital image is shown in Fig. 2(b). The ghost is a not unreasonable approximation of a tumor, compare it to Fig. 1(b). (The specific construction of this ghost was as follows. We selected 22 reasonably evenly spaced projection directions by choosing the pairs (4,3), (4,2), (4,1), (4,0), (4,-1), (4,-2), (4,-3), (3,4), (2,4), (1,4), (0,4), (-1,4), (-2,4), (-3,4), (3,2), (3,1), (3,-1), (3,-2), (2,3), (1,3), (-1,3), and (-2,3) as the values for (u₁, v₁), …, (u₂₂, v₂₂). The function h⁰ was selected to be a digitized blob, a generalized Kaiser-Bessel window function [22], with its free parameters assigned to be the default values selected by Snark05 [7] weighted so that the range of values in the ghost is less than 7% of the range of values in the image that is displayed in Fig. 2(a). Another way of saying this is that the range of the difference between the images represented by Figs. 2(a) and 2(b), is less than 7% of the range within either of those images.)

To specify the projection data, let (for now) Θ consist of the 22 directions arctan(u/v), where the pairs (u, v) are defined in the previous paragraph. Because g is a ghost for each direction in Θ, we have that, for any ϑ ∈ Θ and s ∈ ℝ,

$$[R(b+f_g^{0.0752})](s,\vartheta )=[Rb](s,\vartheta ).$$ (16)

This implies that even if we were able to obtain perfect measurements for all ϑ ∈ Θ and s ∈ ℝ, we would still not be able to distinguish between the brain phantom with and without the ghost (which resembles a tumor). Any reconstruction method would produce identical results from such data for the brain with and the brain without the tumor.

To see if the tumor becomes recoverable with a larger number of projections (for which it is no longer a ghost), we generated idealized perfect projection data of the image represented by Fig. 2(b) for 82 directions: the 22 specified above and 60 directions at 3° increments from 1° to 178° with the first axis. Thus here (and from now on) |Θ| = 82. We selected, for each ϑ ∈ Θ, S_ϑ = {ld|l is an integer and − 172 ≤ l ≤ 172}, where d = 0.0752 is the sampling distance of the digitization. As an idealization of the data we calculated, for each ϑ ∈ Θ and s ∈ S_ϑ, $[R{f}_{\left[p_b^{243,d}+g\right]}^d]$ (s, ϑ) (these are exact line integrals through the digitization, such as represented in Fig. 2(b), of the head phantom with tumor). With these values on the left-hand-side of (6) we get a consistent system of equations, since $x_{\left[p_b^{243,d}+g\right]}$ will clearly be a solution.

The TV minimization approach indicates that we should try to find a 243 × 243 digital image p* such that x_p* satisfies the system of equations and, for any 243 × 243 digital image p such that x_p satisfies the system of equations, ‖p*‖_TV ≤ ‖p‖_TV. We used the algorithm that is described in the Section 4 with the stopping criterion ε = 0.05 to produce an approximation to such a p*, it is displayed in Fig. 3(a). (Since Res(x⁰) = 330.62, the choice of the stopping criterion implies that, when we stop, the value of Res is less than 0.02% of its initial value.) While the reconstruction is definitely not perfect, the tumor is clearly recognizable in it. We cannot expect much, if any, improvement by a “better” TV-minimizing algorithm, since the TV of the digital image represented in Fig. 3(a) is 427.35, which is already smaller than 430.98, the TV of the head phantom with tumor in Fig. 2(b). This shows that, in particular in this instance, TV minimization fails to produce a “perfect” or “exact” reconstruction: Even though we have a digital phantom (Fig. 2(b)) and we have collected error-free data as defined by (1), we have found that there is another digital image (Fig. 3(a)) that satisfies the data within Res error less than 0.05 whose TV is less than that of the phantom.

As comparison we look at the alternative approach of minimizing the norm ‖p‖₂ of the N × N digital image p, as defined by

$$\Vert p{\Vert }_2=\sqrt{\sum _{t_1=0}^{N-1}\sum _{t_2=0}^{N-1}{(p(t_1,t_2))}^2}.$$ (17)

As discussed in Section 4, a variant of our TV-minimizing algorithm can be used to approximate the minimum norm solution of a consistent system of equation. The result produced by this algorithm, also using the stopping criterion ε = 0.05, is displayed in Fig. 3(b). Clearly, while the approximation to TV minimization does not (and, in fact, cannot) recover exactly the digital image in Fig. 2(b), it is a much better approximation to it than what is provided by approximate norm minimization from the same data.

To demonstrate that the tumor is indeed a ghost function, we display in Figs. 3(c) and (d) reconstructions by our algorithm's TV-minimizing and norm-minimizing variants, respectively. All parameters were selected as in the three preceding paragraphs, except that the input consisted of projections in only those 22 directions for which the tumor is a ghost. Not surprisingly, there is no evidence of the tumor in these reconstructions. Of additional interest is that the reconstruction in Fig. 3(c) provides us with an example in which our TV-minimizing algorithm failed in the sense that it produced an image whose TV is higher than that of the phantom, which is shown in Fig. 2(b).

Next we investigate the validity of the statement that a digital image should be “mostly constant” to be recoverable from a small number of views; see (7). For this purpose, we take the digital image $p_b^{243,0.0752}+g$ (the brain phantom with the tumor, displayed in Fig. 2(b)) and, for (t₁, t₂) ∈ [0,242]² we altered the value $\left[p_b^{243,0.0752}+g\right](t_1,t_2)$ at that pixel by adding to it a number randomly selected from a zero-mean normal distribution whose standard deviation is $\rho \left[p_b^{243,0.0752}+g\right](t_1,t_2)$, where the factor of proportionality ρ was selected by examining the variability in actual brain scans. The resulting digital image is displayed in Fig. 4(a). Idealized perfect projection data were generated for the same 82 projection directions that were specified above, and both the TV-minimizing and the norm-minimizing algorithms were run with ε=0.05; the results are shown in Fig. 4(b) and (c). Again, the output of the TV minimizing algorithm is much superior. In fact, comparing it to Fig. 3(a), one cannot but conclude that the likely clinical usefulness of the two images is just about the same, even though in one case the “mostly constant” assumption is totally violated. We also ran the TV-minimizing algorithm with ε=0.005, which means that when the algorithm is stopped the result is more consistent with the data (but, of course, it is likely to have a slightly larger TV). The result is shown in Fig. 4(d), it does not much differ from Fig. 4(b). The important conclusion here is that the performance of the TV-minimizing algorithm does not depend in an essential way on the “mostly constant” condition.

Figure 4.

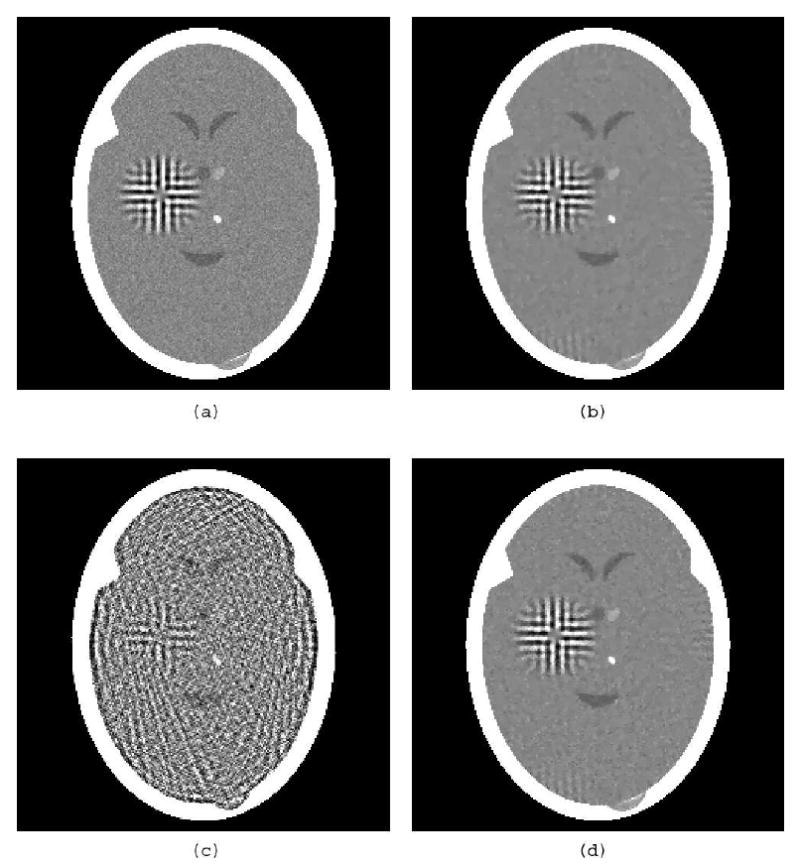
(a) Head phantom with tumor and variability. (b) TV-minimizing reconstruction from 82 noiseless idealized projections, ε=0.05. (c) Norm-minimizing reconstruction from the same data, ε=0.05. (d) TV-minimizing reconstruction from the same data, ε=0.005.

Until now all the reconstructions were from data sets in which the line integrals were calculated exactly based on digital images. The reconstruction algorithms that we used were in fact developed on the assumption that this is indeed the nature of the data. Real data in applications of image reconstruction will not be such for the following (and other, here not listed) reasons.

1. The natural (or even artificial) images that we wish to reconstruct are extremely unlikely to satisfy the digital assumption.

2. Detectors used in the instruments for collecting data will have a width and so, even if they were otherwise perfect, they could not be used for measuring line integrals exactly.

3. Measurements are stochastic in nature; in CT, for example, the total attenuation is estimated by the use of a, by necessity, finite number of X-ray photons, resulting in statistical noise in these estimates.

We now investigate what happens when we attempt to reconstruct from data that are realistic from these points of view.

The software Snark05 [7] allows us to calculate line integrals of the head phantom b based on its original geometrical description, rather than on its digitization. This can be combined with the calculation of the line integrals for the tumor and the variations in the phantom (indicated in Fig. 4(a)), which are digital images. In order to simulate the width of the detector, for each line for which the algorithm assumes that the data had been collected, we introduce 10 additional lines (five on both sides) with spacing d/11 between them. (Recall that d = 0.0752 is the assumed distance between the lines for which data are collected.) The stochastic data collection is simulated using 500,000 photons for estimating each data item g (s, ϑ). The details of how this is done in Snark05 are explained in Section 4.4 of [14].

The results of reconstructions from such realistic data generated for the 82 projection directions for the head phantom with tumor and variability (displayed in Fig. 4(a)) are shown in Fig. 5. The stopping criterion for both algorithms was ε = 1.5, which is reasonable since for this noisy data set the value of Res for the phantom is actually slightly more than 1.5. While TV minimization does a good job from the point of view of its aim (the TV of the reconstruction displayed in Fig. 5(a) is 444.17, while the TV of that displayed in Fig. 5(b) is 1,287.33), this mathematical success does not translate into medical usefulness. The TV-minimizing algorithm, when applied to the realistic data, totally eliminated the tumor, while the tumor is visible in the norm-minimizing reconstruction (in spite of its much more noisy-looking nature). The TV of the phantom in Fig. 4(a) is 488.17 and the phantom slightly violates the condition Res(x) < 1.5, while the reconstruction in Fig. 5(a) satisfies this condition and has a lower TV. All we can say about this is that the combined mathematical criteria of reducing the values of Res and TV do not guarantee medically useful images when applied to realistic data. If we desire to recover the phantom exactly using our algorithm, then the ε of the stopping criterion has to be at least as large as the Res of the phantom, which in the case of noisy data is sufficiently large that minimizing TV subject to Res(x) < ε will result in an image without some of the high frequency components of the phantom. This seems to be in the nature of minimizing TV as defined in (8), and the retention of such high frequencies seems to mandate an alternative function φ to be minimized. It is interesting to note that the algorithm of Section 4 is applicable irrespective of how this φ is chosen.

7. Conclusions

Total variation minimization can produce good results if the images to be reconstructed and the data collection meet some (usually unrealistic) mathematical criteria. The algorithms that we presented in Section 4 were developed based on the digital assumption. As is demonstrated above, as long as the data are collected in a way that is consistent with this assumption, the TV-minimizing algorithm can, but is not guaranteed to, give useful results even if the number of projections is small. However, when realistic data collection is simulated (violating the digital assumption), then reconstruction from a small number of views is likely to fail to deliver essential information.