Extension of the Tryptophan χ^2,1 Dihedral Angle - W3 Band Frequency Relationship to a Full Rotation: Correlations and Caveats

Abstract

The correlation of the UVRR νW3 mode with the tryptophan χ^2,1 dihedral angle (1-3) has been extended to a full, 360° rotation. The three-fold periodicity of the relationship (cos 3χ^2,1) over 360° results in up to six dihedral angles for a given νW3. Consideration of a Newman plot of dihedral angles for proteinaceous tryptophans taken from the Protein Data Bank shows that sterically hindered ranges of dihedral angle reduce the possible χ^2,1 to one or two. However, not all proteinaceous tryptophans follow the νW3-χ^2,1 relationship. Hydrogen bonding at the indole amine, weaker, electrostatic cation-π and anion quadrapole interactions and environmental hydrophobicity are examined as possible contributing factors to noncompliance with the relationship. This evaluation suggests that cumulative weak electrostatic and nonpolar interactions characterize the environment of tryptophans that obey the νW3-χ^2,1 relationship, matching that of the crystalline tryptophan derivatives used to derive the relationship. In the absence of methods to quantify these weak interactions, measurement of the full width half maximum bandwidth (FWHM) of the W3 band is suggested as a primary screen for evaluating the applicability of the νW3 - χ ^2,1 relationship.

The utility of spectroscopy with respect to protein structure lies in its predictive value in the absence of crystallographic structure. In UV resonance Raman spectroscopy, tryptophan residues are structural bellwethers because they can be selectively probed at 229 nm. Tryptophan vibrational band are good markers for hydrophobic interaction (3-6), hydrogen bonding (5, 6) and conformation (1, 2, 6-8). The intensity ratio, I₁₃₆₀/I₁₃₄₀, of the tryptophan Fermi ‘doublet’ (also known as the W7 mode) serves as a good marker for hydrophobic interactions (2, 4, 9). A rise in the ratio indicates an increasingly hydrophobic environment for the indole ring. Several tryptophan modes, W2, W4, W6, and W17 are sensitive to hydrogen bonding. The stronger the hydrogen bonding the higher is νW2, νW4 and νW6 (2) and the lower is νW17 (8). One mode, the W3 mode, is of great interest because it tracts the conformation of tryptophan. The W3 mode is a hybrid mode consisting of indole C₂=C₃ stretching (50%), N₁-C₂ (23%) stretching and C₂-H (19%) bending vibrations (2, 6), yet its frequency depends on the χ^2,1 dihedral or torsion angle about the C_α–C_β–C₃=C₂ linkage (2). A systematic study of the W3 mode frequency (νW3) for several crystalline tryptophan analogs revealed that νW3 varies with the χ^2,1 torsion angle according to the empirically derived equation (1):

$$\nu W3=1542+6.7{\left(cos3\left|{\chi }^{2,1}\right|+1\right)}^{1,2}$$ (1)

Deuteration of the tryptophan ring d₅ carbon affects the relationship of νW3 with the χ^2,1 torsion angle (8), and a similar equation can be written (1, 7):

$$\nu Wd3=1514+7.5{\left(cos3\left|{\chi }^{2,1}\right|+1\right)}^{1,2}$$ (2)

These equations are derived using the absolute value of the torsion angle, |χ^2,1|, within a range of 60-120° (3). It is apparent that the angular dependence for νWd3 is greater than for νW3 as the angular coefficient for νWd3 is larger.

In this work, we extend and modify the relationship, νW3(χ^2,1), to cover a full 360° rotation since all dihedral angles are plotted in the same rotational direction. We show that the relationship is not single-valued---and therefore not a function---and has a three-fold periodicity over 360° due to the three-fold steric overlap of the indole residue with moieties bound to C_α. Thus, a single νW3 corresponds to as many as six dihedral angles. This follows intuitively from a consideration of a Newman diagram for dihedral steric clashes as discussed below. νW3-χ^2,1 data points for single tryptophan wild-type and mutant proteins, multiple tryptophan proteins where the W3 band has been resolved into components, fibrillar peptides (fd and Pf3 virion coat peptides) and two model tryptophan-containing peptides, the bee venom peptide, melittin, and the caged tryptophan peptide, exendin-4 TC5b, have been added to the original νW3 plot for crystalline tryptophan analogs (1, 7). This plotting suggests that three ranges of dihedral angle are poorly populated, attributable to steric interference with the protein backbone.

At the same time, the νW3-χ^2,1 data points for the proteins and model peptides show that the cosine-based relationship can only provide a rough guide to the tryptophan dihedral angle, even for tryptophans in a hydrophobic, constrained environment similar to that of the crystalline tryptophan derivatives used to derive the νW3-χ^2,1 relationship. For some of the peptides and proteins, the UV resonance-Raman determined νW3, coupled with a χ^2,1 dihedral angle taken from an x-ray crystal structure, constitutes a data point that lies off the cosine-dependent curve. In particular, we examine the influence of hydrogen bonding at the indole amine on νW3 compliance with the cosine-dependent relationship through density function theory (DFT) calculations. For these calculations, we focus on the S. cerevisiae mutant enzyme, TIM Trp90Tyr Trp157Phe, bound to the ligand, 2-phosphoglycolate (PGA), because all other structural information gleaned from the UVRR data correlates with previously published results for TIM. DFT calculations based on model systems are utilized to understand the deviation of TIM νW3 from Eq. (1).

We also examine the weak, noncovalent cation-π and anion-quadrapole interactions of proteinaceous tryptophans as the source of noncompliance with the νW3-χ^2,1 relationship. Tryptophan dihedral angles for these proteins are taken from x-ray crystal or NMR structures available in the Protein Data Bank while νW3 values are taken from the literature or have been measured. We compare the indole C₂=C₃, C_β–C₃, and C₂–N₁ bond lengths for the νW3-χ^2,1 relationship-compliant versus noncompliant tryptophans. This information is also gleaned from structures in the Protein Data Bank, and is relevant because the νW3 depends upon C₂=C₃ and C₂–N1 stretching, and the C_β–C₃ bond length has been found to vary inversely with |χ^2,1| (1, 2). Hydrophobicity of the tryptophan environment is indicated by measure of the W7 1360 cm^-1:1340 cm^-1 band ratio (4, 5). As the crystalline tryptophan derivatives used to formulate the νW3-χ^2,1 relationship are expected to reside in a hydrophobic environment, the W7 ratio was examined for model peptides and relationship-compliant and noncompliant proteins.

The purpose of this analysis is to expose the specific tryptophan interactions and indole structural factors that contribute to deviations of νW3-χ^2,1 data points from the relationship given in Eq. (1). We find that numerous weak electrostatic and nonpolar interactions accumulate to create an environment about the indole of tryptophan that is both constrained and hydrophobic, like the environment of the crystalline tryptophan derivatives from which the νW3 - χ ^2,1 relationship was derived. In the absence of methods to quantify these weak interactions, measurement of the FWHM bandwidth of the W3 band is suggested as a primary screen for evaluating the applicability of the νW3 - χ ^2,1 relationship.

Materials and Methods

All reagents used were purchased from either Sigma-Aldrich Co. (St. Louis, MO) or Fluka (Milwaukee, WI) with the exception of glycerol-3-phosphate dehydrogenase, which was purchased from Boehringer Mannheim Ltd. (Indianapolis, IN). The model peptide, exendin-4 TC5b, was synthesized according to the protocol given in (10). S. cerevisiae TIM (Trp90Tyr Trp157Phe; hereafter referred to as the TIM mutant or simply TIM) was expressed and purified as described before (11). The kinetic parameters of the mutant are not distinguishable from those of the wild type TIM (12). Enzymatic activity was determined by the conversion of GAP to DHAP in the presence of TIM and glycerol 3-phosphate dehydrogenase as described by Putman and Knowles (13).

TIM enzyme samples employed in UV resonance Raman spectroscopy were at a concentration of 0.3 mM TIM in 50 mM Tris-HCl, 50 mM NaCl buffer, pH 7.8. Four samples were measured: unbound TIM and TIM bound to PGA (5 mM) in the aqueous buffer given above, and deuterium solutions of TIM bound to Pi (50 mM) and G3P (10 mM) with buffer conditions as above. Exendin-4 TC5b (1 mM) was spun cast in a silica gel matrix. Following gelation, the gel was bathed in 15 mM phosphate buffer, pH7.0. The method of silica gel preparation is given in (14). The melittin peptide was dissolved in 20 mM Tris buffer, pH 7.4 to a concentration of 2 mM.

UV Resonance Raman Spectroscopy

All UVRR spectra were acquired with CW 229 nm excitation at an incident power of 1.8 mW. The UVRR instrument has been described elsewhere (15). For each sample, three acquisitions of three minutes, collected over an 805-1680 cm^-1 frequency window, were summed. The sample-containing quartz tube was rastered vertically, spun and chilled to 16°C to minimize protein exposure to potentially denaturing UV radiation. UVRR peak positions were calibrated against the known peaks of indene. The resulting calibration-limited accuracy is ± 1 cm^-1. Curvefitting analysis was carried out via the GRAMS/AI software package. All curvefits were carried out with the minimal number of Gaussian-Lorentzian peaks (optimally 50 -70 % Lorentzian) necessary to yield a χ²< 3.

Crystallographic Measurements

Dihedral angles, bond lengths, and intermolecular distances were measured from the indicated Protein Data Bank structures using the UCSF Chimera package from the Resource for Biocomputing, Visualization, and Informatics at the University of California, San Francisco (supported by NIH P41 RR-01081) (16).

Raman Data Simulations

A series of calculations were performed using DFT-based simulations with Gaussian03W (17). A DFT approximation implementing the Becke's three-parameter exchange functional (18). in combination with the Lee, Yang, and Parr correlation (19) function (or B3LYP) was used. As a compromise between accuracy and applicability to large molecules, the 6-31G(d) basis set was used. Smaller basis sets are enough in DFT based calculations because the basis functions do not have to describe correlating orbitals (20, 21). For all systems the geometry was first optimized before the frequency calculations. All calculated frequencies were scaled by a factor of 0.963 (20, 22). GaussView (23) was used to visualize the atomic displacements correlating to each of the simulated Raman peaks. Using normal coordinate analysis, the displacement vectors associated with each different vibrational mode of skatole (6), a tryptophan analog, and skatole-d⁵ (1) were previously assigned. To identify the W3 or Wd3 mode in the simulated Raman spectra, we compared the visualized atomic displacements to the displacement vector-W3 mode relationship for skatole and skatole-d⁵. A series of calculation were made to prove that the assignment was correct. First, a full geometry optimization and frequency calculation at fixed |χ^2,1| torsion angles of 60.6 °, 78.0 °, 83.5 °, 88.0 °, 98.7 °, 105.1 ° and 116.5° were carried out. These χ^2,1 torsion angles were chosen because they correspond to the values used to generate Eq. (1). Second, we made a similar set of calculations using Trp-d⁵ to generate a relationship similar to Eq. (2). Finally, we performed unconstrained simulations on a Trp molecule, a Trp-d⁵, and a Trp analog where the indole N had been replaced by an isotope, ¹⁵N. As defined, the W3 mode should have very minimal contribution from the indole N (2, 6).

Results and Discussion

Four 229 nm.-excited UVRR spectra for the S. cerevisiae mutant enzyme, TIM (Trp90Tyr Trp157Phe), in the 800 – 1550 cm^-1 range are shown in Figure 1. These include results for the ligand-free enzyme (Fig. 1a, trace 1), and the enzyme bound to the tight-binding transition state analog, PGA (Fig. 1a, trace 2). UVRR results for deuterium solution are also given for TIM ligated to G3P (Fig. 1b, trace 1) and phosphate (Pi)-ligated TIM (Fig. 1b, trace 2). The many peaks represent resonantly-enhanced vibrational modes for the several tyrosines in the TIM sequence, and most importantly, the single tryptophan residue, Trp-168, which is critically situated at the substrate binding loop hinge. The Fig. 1 inset shows a close-up view of the W3 bands for these spectra.

Figure 1.

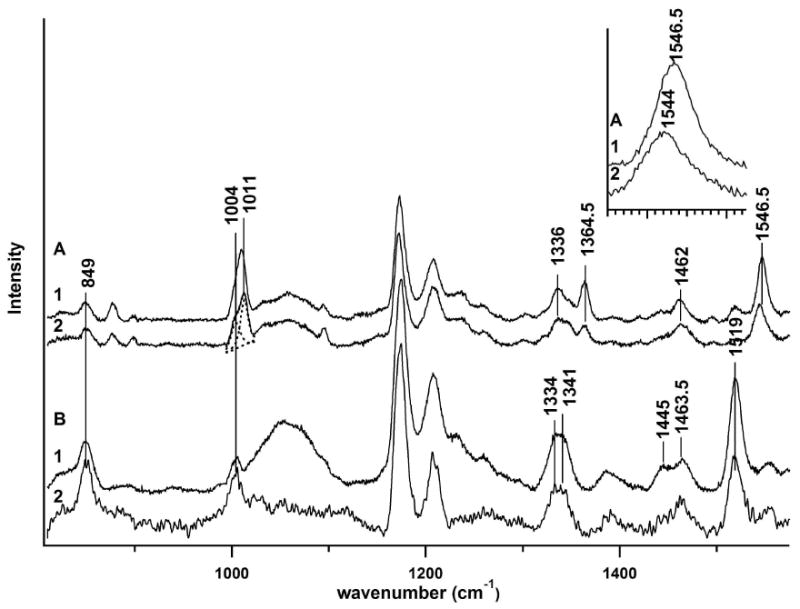
UVRR spectra for TIM in aqueous and deuterium solution with and without ligands. a. Aqueous solution. 1. ApoTIM 2. TIM ligated to PGA. Inset displays the W3 mode for apoTIM and PGA bound TIM. b. Deuterium solution 1. TIM ligated to G3P 2. TIM ligated to phosphate.

The UVRR data (Figure 1a) present a picture of the immediate environment of Trp-168 in TIM. The intensity ratio, I₁₃₆₀/I₁₃₄₀, of the W7 mode peaks has been linked to the hydrophobicity of the tryptophan environment, where a value less than one for the ratio corresponds to a hydrophilic environment, and conversely, a value greater than one indicates a hydrophobic one (4). The value of the νW17 (876 cm^-1) for TIM in both the bound and unbound conformations indicates weak hydrogen bonding at the indole amine while the W6 band position at 1420 cm^-1 corresponds to a non-hydrogen bonded state (2). Like W3, the W1 mode, located at 1620 cm^-1, depends upon indole ring stretching, but νW1 is buried beneath the intense tyrosine Y8a/b bands at ∼1614 cm^-1 (not shown) and is therefore undecipherable. Concomitantly, the significance of tyrosine band changes accompanying binding loop motion---such as those for the Y9a mode at 1173 cm^-1---are difficult to interpret due to the presence of nine tyrosine residues in TIM. However, the importance of the Y208 residue to enzyme activity has been realized (12, 24).

The W3 Mode (1542 – 60 cm^-1) and the Dihedral Angle, χ^2,1 for Trp-168 of TIM

While x-ray crystal studies of the bound and unbound binding loop conformers of TIM show that a backbone hydrogen bond network enforces a rigid loop movement between the two binding states (25), subsequent solid-state TIM NMR studies (11, 26) and T-jump studies of solution phase TIM (27) show that Trp -168 has some local mobility. The Trp-168 W3 mode (∼1542 – 1560 cm^-1) is expected to report on the local dihedral angle changes of Trp-168 that accompanying loop motion according to the νW3-χ^2,1 relationship discussed above. The x-ray crystal structure, 1YPI, of apo TIM with Trp-168 in the loop unbound position reveals the χ^2,1 torsion angle to be -79.65° (28). When TIM is bound to the PGA transition state analog, x-ray crystallography reveals (PDB file: 7TIM), the χ^2,1 torsion angle of Trp-168 to be -99.61° (25).

The W3 Mode - Dihedral Angle, χ^2,1 Relationship Extends over a Full Rotation

A problem arises when we try to reconcile the observed W3 frequencies and corresponding χ^2,1 torsion angles as derived from Eq. (1) (2) with that obtained from the x-ray crystal structures. Binding of the transition state analogue, PGA, to TIM downshifts the W3 mode from 1547 cm^-1 to 1544 cm^-1 (Fig. 1a, trace 4). According to Eq. (1), this νW3 corresponds to a change in |χ^2,1| from 83° to 78°, a -5 ° dihedral angle change in going from the apo to holo enzyme conformation. The x-ray diffraction derived dihedral angle for apo TIM is -79.6° (PDB:1YPI; (28)), which is within the error bounds defined by Eq. (1). However, for PGA-bound TIM, the x-ray diffraction-obtained value for χ^2,1 is -99.6° (PDB:7TIM; (25)), far from the value of ±77.6° predicted by Eq. (1). The resulting apo-to-holo dihedral angle change predicted from the crystal structures is -20 °. While the magnitude of the dihedral angle change predicted from crystal structures is four-fold higher, the sign of the change is the same as for the UVRR data.

These discrepancies between χ^2,1 values predicted by the relationship given in Eq. (1) and those available from crystallographic structures suggest that plotting νW3 against x-ray crystallographic dihedral angles for proteins would reveal the general validity of Eq. (1). This is of interest because the relationships reproduced in Eqs. (1) and (2) are often used to predict tryptophan dihedral angles from νW3 results for proteins. Table 1 lists several tryptophan-bearing peptides and proteins with their corresponding νW3 and crystal structure-derived χ^2,1 dihedral angles. According to the convention used in calculating these angles, values are reported within the range of ± 0 - 180°. These dihedral angle values have been recalculated so they can be plotted in the same rotational direction. Thus a negative value of χ^2,1 is recalculated as 360° + χ^2,1. Furthermore, given the three-fold redundancy---3 cos χ^2,1---of the relationship given in Eq. 1 over a full rotation, the angular values of 1-120°, 121-240° and 241-360° are degenerate, and all dihedral angles have been reduced to a value between 0-120 ° (Table 1).

Table 1.

W3 mode frequencies and χ^2,1 torsional angle for Tryptophan in Peptides and Proteins

Protein System/Trp No.	Trp residue	νW3 (cm-1)	χ2,1, degree	Reduced χ2,1 (0 - 120°)	PDB #
glyceraldehyde 3-phosphate dehydrogenase	84	1557a	127.61	7.6	1GD1j
Gyrase B with Novacin	128	1556b	-106.13	14	1KIJk
Gyrase B with chlorobiocin	170	1555b	-98.1	22	1KZNl
Bacteriorhodopsin	182	1550c	36	36	2BRDm
	189	1553c	106	106
Pf3 virion coat protein	38	1546d	142	22	1IFPn
fd virion coat protein	26	1560e	87	87	2C0Xo
apo TIM mutant	168	1546f	-79.6	40.4	1YPIp
PGA-TIM mutant	168	1544f	-99.6	20.4	7TIMq
apoPTPase	354	1549g	-71.2	48.8	1YPTr
Tungstate PTPase		1559g	-4	116	1YTWs
COHb	β37	1547h	92i	92	1LJWt
	β15	1558h	115i	115
	α14	1558h	122i	2
deoxyHb	β37	1548h	93i	93	4HHBu
	β15	1558h	104i	104
	α14	1558 h	100i	100
horse heart cytochrome C	59	1552i	114.5	114.5	1HRCv
melittin	19A	1547 f	95.3		2MLTw
	19B	1547 f	89.2
exendin-4 TC5b W/P cage	25	1546 f	73.2		1JRJx

^aAustin et al., 1989 (45)

^bCouling et al., 1998 (46)

^cHashimoto et al., 1997 (36)

^dWen and Thomas Jr., 2000 (43)

^eWen and Thomas Jr., 2000 (43)

^fThis paper

^gJuszczak et al., 1997 (44)

^hRodgers et al., 1992 (47)

ⁱJordan et al., 1995 (42)

^jSkarzynski et al., 1987 (48)

^kLamour et al., 2002 (49)

^lLafitte et al., 2002 (50)

^mGrigorieff et al., 1996 (51)

ⁿWelsh et al., 1998 (38)

^oMarvin et al., 2006 (37)

^pLolis et al., 1990 (28)

^qLolis and Petsko, 1990 (25)

^rStuckey et. al, 1994 (52)

^sFauman et al., 1996 (53)

^tSafo et al., 2002 (54)

^uFermi, G. et al., 1984 (55)

^vBushnell et al., 1990 (56)

^wTerwilliger et al., 1982 (35)

^xNeidigh et al., 2001 (34)

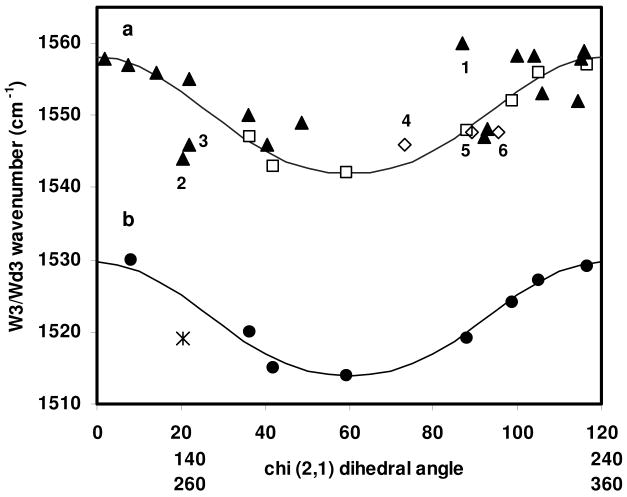
The reduced χ^2,1 dihedral angles given in Table 1 are plotted against the corresponding UVRR-determined νW3 in Figure 2a (solid triangles). Also included are data points (open squares) for the crystalline tryptophan analogs from which Eq. 1 was derived (1), and data points (open diamonds) for model tryptophan-containing peptides, melittin conformers A and B (labeled 5 and , respectively) and the truncated exendin-4 TC5b W/P cage peptide (labeled 4). Data points for Trp-bearing proteins that lie far from the fitted curve are also numbered as follows: 1. fd virion coat protein, 2. TIM mutant Trp90Tyr Trp157Phe ligated to PGA, 3. Pf3 virion coat protein. The relationship given by Eq. (1) has been modified (see discussion below) to fit the experimental data points given in Table 1, and is also plotted in Fig. 2a as a solid line. The overlay of the three degenerate χ^2,1 dihedral angle ranges means that data points for proteins (Table 1) define the relationship over one full rotation (Fig. 2a). This has not been previously realized. Due to the χ^2,1 angular degeneracy and the fact that the fit relationship is not single valued, one νW3 can map to as many as six χ^2,1 dihedral angles, as can be seen from Fig. 2a. Therefore, νW3 would seem to be a poor predictor of the tryptophan χ^2,1 dihedral angle. However, as discussed below, large ranges of dihedral angle values for tryptophan are generally avoided in protein structures, greatly reducing the possible number of dihedral angles for any one νW3.

Figure 2.

Relationship between νW3 and the dihedral angle over a full rotation. a. Data points are for crystalline tryptophan derivatives (open squares) (2), proteinaceous tryptophan residues (solid triangles, see Table 1), and model peptides (open diamonds, see Table 1) for which νW3 is available (See Table 1). χ^2,1_360° is given by Eq. (3) where a= 1542 cm^-1 and b=7.0. As in reference (1), these parameters are empirically adjusted. Numbered points correspond to: 1. fd virion coat protein, 2. TIM mutant Trp90Tyr Trp157Phe ligated to PGA, 3. Pf3 virion coat protein, 4. the truncated exendin-4 TC5b peptide, 5, 6. melittin, two data points corresponding to dihedral angles W19A (point 6) and W19B (point 5) from crystal structure, 2MLT. b. Data points are for deuterated tryptophan derivatives (solid circles) (1), and the Pi/G3P ligated, deuterated TIM proteins (cross), which share the ligated, aqueous TIM dihedral angle given in Table 1. νWd3 taken from Fig. 1. The curve fit to this data is given by Eq. (3) where a= 1514 cm^-1 and b=6.8. As in reference (1), these parameters are empirically adjusted.

The νW3-χ^2,1 relationship was previously extended to deuterated tryptophan in UV Raman spectroscopic studies of deuterated, solid state tryptophan derivatives (1). The νWd3 - dihedral angle data pairs originally used to define this relationship are reproduced in Fig. 2b (solid circles). Additionally, a single data pair for deuterated, phosphate and G3P ligated TIM is shown (star) as the same dihedral angle as used for aqueous, ligated TIM (Table 1) is used here. A plot of a modified νWd3 - dihedral angle relationship, fit to the data pairs for deuterated tryptophans, is also shown in Fig. 2b (solid line). As for G3P-ligated TIM in aqueous buffer (Table 1 and Fig. 2a), the experimentally determined νWd3 does not place the corresponding crystallographic dihedral angle value squarely on the modified curve fit discussed below. Possible reasons for deviations of protein νW3 and νWd3 - dihedral angle data points (Fig. 2 a, b) from the modified Eqs. (1) and (2) are discussed below.

Modification of the νWd3-χ^2,1 Relationship

In the first paper to discuss the νWd3-χ^2,1 relationship, the data was fit to an unspecified third order spline function (2). Subsequently, Eqs. (1) and (2) were introduced as empirical fits to the νW3 and νWd3 - dihedral angle data points (1). Expansion of the relationship given in Eq. (1) to cover a full rotation, and using the same rotational sense for all dihedral angles, χ^2,1, yields

$$\nu W3=a+b{\left(cos3{\chi }_{360}^{2,1}+1\right)}^{1,2}$$ (3)

Where for all negative values of dihedral angle, χ^2,1

$${\chi }_{360}^{2,1}=360°+{\chi }^{2,1}$$ (4)

And a and b are empirically-determined parameters that are determined from fitting to the νW3-χ^2,1 data pairs. The physical significance of the cos 3 ${\chi }_{360}^{2,1}$ dependence is now discussed.

Steric Hindrance result in Excluded Values for the Tryptophan χ^2,1 Dihedral Angle

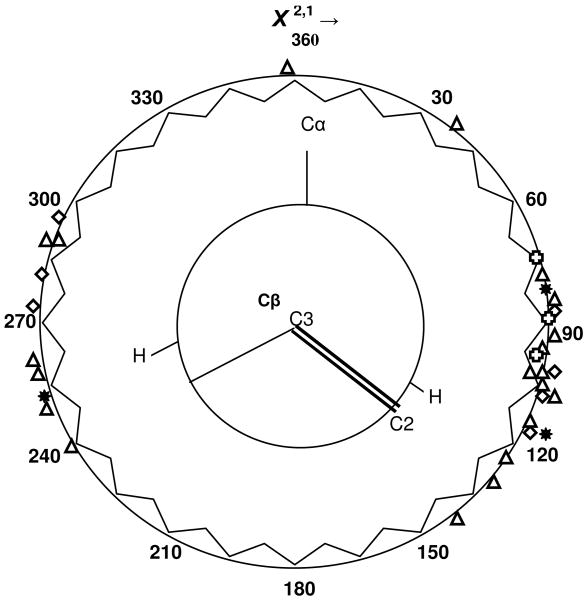
A circular plot of the crystallographically determined tryptophan dihedral angles for the proteins given in Table 1 reveals that certain ranges of dihedral angle are favored in protein structures. This plot is given in Figure 3. ${\chi }_{360}^{2,1}$ is plotted clockwise and all dihedral angles are plotted as positive angles in the 0 - 360° range. Dihedral angle values for tryptophans found in proteins in water solution (triangles; see Table 1) and those for crystalline tryptophan derivatives (diamonds) (2) are plotted. Dihedral angle values for two model peptides, melittin and exendin-4 TC5b (Table 1), are indicated by crosses. The three allowed tryptophan dihedral angles for an α helix, as determined from a dataset of 61 globular proteins in the Protein Data Bank, are also plotted (stars) (29). Concentric with this plot is a Newman diagram looking down the tryptophan C₃---C_β bond axis. The C₃== C₂ double bond is part of the indole pentagonal ring as is the fourth bond of C₃. The ${\chi }_{360}^{2,1}$ dihedral angle plot clearly shows that some angular ranges are preferred. C_α, and the protein backbone extending away from it (not shown), are a steric barrier to the free rotation of the bulky tryptophanyl indole, whose plane is roughly perpendicular to that formed by the protein backbone. Dihedral angles that line up the indole plane with the C_β— C_α bond will likely lead to steric clashes as the bulky indole encounters atoms attached to the backbone and the backbone itself. These sterically hindered dihedral angle ranges appear to extend over the ranges of approximately 0° - 75°, 150° -240°, and 300° – 360° (Fig. 3). Complementary to these are two sterically ‘favored’ dihedral angle ranges: 75° – 150° and 240° – 300°, resulting in the elimination of possible dihedral angles for any given νW3. Likely dihedral angles for any one νW3 are now reduced to one or two choices, as can be ascertained from the plot of the νW3-χ^2,1 relationship in Fig. 2a, suggesting the continued utility of the νW3 -- χ^2,1 relationship as given by Eqs. (3) and (4).

Figure 3.

Newman plot of tryptophan χ^2,1 dihedral angles for proteinaceous tryptophans (triangles) and model peptides (crosses), as given in Table 1, and for crystalline tryptophan derivatives (diamonds) from (2). The three allowed (stars) tryptophan dihedral angles for an α helix, as determined from a dataset of 61 globular proteins in the Protein Data Bank, are also plotted (29). All negative dihedral angles are plotted as χ^2,1_360° = 360° + χ^2,1. Concentric with the plot is a Newman diagram showing the disposition of the tryptophan indole C₂==C₃ bond with respect to the C_β ---C_α bond along the C_α–C_β–C₃=C₂ linkage.

Consideration of the Newman diagram makes plain the three fold cosine-dependency of the relationship given in Eq. (3). The highest νW3 is encountered whenever the indole plane coincides with one of three C_β bonds or when χ^2,1 assumes values of 0°, 120° or 240°. It is precisely at these angles that steric hindrance for the indole is greatest. Since the cosine depends on 3χ^2,1, the latter three angles become equivalent to 360 ° = 0 °, where the cosine value of these is unity, and the value of the relationship assumes its maximum value. The addition of one to the cosine 3χ^2,1 value is necessary to prevent subtractions from the minimal νW3 value given by the parameter, a (See Eq. (3)). The parameter, b, and the exponent value of 1.2 are empirically determined by fitting to the set of available experimental νW3 - χ^2,1 data pairs.

Exceptions to the Rule: Not all Protein Tryptophans Manifest the νW3 -- χ^2,1 Relationship

Scrutiny of the νW3 - χ^2,1 dihedral angle data pairs given in Table 1 and plotted in Fig. 2a shows that not all νW3 for proteinaceous tryptophans conform to the νW3-χ^2,1 relationship of Eq. (3). In particular, tryptophans found in the fibrillar viral coat proteins of fd (point 1, Fig. 2a) and Pf3 (point 3, Fig. 2a), are far from the curve defined by Eq. (3). The data point for the loop hinge Trp-168 in PGA-ligated TIM (point 2, Fig. 2a) also falls into this set. Even with an estimated uncertainty of ±10° (1), these data pairs would not lie on the curve defined by Eq. (3). Indeed, the νW3 for the fd virion coat protein (1560 cm^-1) has a value that is outside the range of the νW3-χ^2,1 relationship (1542-1558 cm^-1). Clearly, factors besides the χ^2,1 dihedral angle influence νW3 in both fibrillar and globular proteins. We now consider several parameters as a suitable criterion for reliable application of the νW3-χ^2,1 relationship.

Indole Bond Lengths with Respect to the νW3-χ^2,1 Relationship

Maruyama and Takeuchi have shown that the bond length of C₂-C₃ for the indole pentagonal ring increases with increases in |χ^2,1| for crystalline tryptophan derivatives while the bond length of C_β-C₃ decreases under these conditions (1). Taking this cue, C₂-C₃, C₂-N₁ and C_β-C₃ bond lengths of tryptophanyl indoles that greatly deviate from the 3(cosine) function were measured, and compared to bond lengths for tryptophans whose data pairs lie on the curve at the same dihedral angle (Fig. 2a) to look for trends in bond length with respect to data points that fell above or below the νW3-χ^2,1 curve. Specifically, the bond lengths for the viral coat protein, fd (Fig. 2a, point 1), are compared to those for melittin W19B and the crystalline tryptophan derivative, N-acetyl-L-tryptophan methyl ester (Ac-L-TrpME), whose data points are on the νW3-χ^2,1 curve at roughly the same dihedral angle (Fig.2a). The bond lengths for the tryptophans in PGA ligated TIM (Fig. 2a, point 2) and the viral coat protein, Pf3 (Fig. 2a, point 3) are compared to those for the tryptophan in gyrase B with clorobiocin, whose data point in Fig. 2a is just above the νW3-χ^2,1 curve at 22°, 1555 cm^-1. These bond lengths are given in Table 2. For this limited data set, the C₂-C₃ bond lengths show no apparent trend for tryptophans whose data points deviate from the νW3-χ^2,1 relationship The C₃--C_β bond length of the fd virion coat protein tryptophan is not significantly different from those of melittin or Ac-L-Trp ME while the C₃--C_β bond lengths of PGA-ligated TIM and Pf3 are shorter than those of gyrase B. The C₂-N₁ bond lengths of fd and PGA-ligated TIM are not significantly different from those of curve compliant proteins. Only the C₂-N₁ bond length of Pf3 shows any appreciable difference from that of curve compliant gyrase B. Indole bond lengths do not appear to be diagnostic of rule-breaking tryptophans. We next consider a specific case of disagreement between the crystallographic-determined tryptophan dihedral angle and that predicted by W3 band measurements, namely that for the PGA-ligated TIM mutant. DFT-based simulations are applied to explain the discrepancy with the expectation that these explanations may be generalized to other proteinaceous tryptophans that do not follow the νW3-χ^2,1 relationship.

Table 2.

Indole bond lengths for Tryptophan-containing Proteins and Derivatives

Tryptophan-containing Species	r(C3--Cβ)/pm*	r(C3---C2)/pm*	r(C2—N1)/pm*
Ac-L-TrpME	150.7	135.4	136.2
Melittin W19B	150.0	136.7	138.5
fd virion coat	149.5	135.8	137.2
Gyrase B/chlorobiocin	152.0	136.3	137.6
TIM/PGA	149.3	136.1	137.8
Pf3 virion coat	146.3	136.4	138.9

^*All bond lengths measured from corresponding Protein Data Bank file; see Table 1 for corresponding file; pm=picometer.

DFT Calculations Applied to the Discrepancy between the χ^2,1 Torsion Angle Predicted by νW3 versus X-ray Crystallography for Ligated TIM

To explain the low νW3 value obtained for PGA-ligated TIM (Fig. 2A, point 2), we first calculate the vibrational modes of skatole, a tryptophan analog, in order to verify the νW3-χ^2,1 relationship, and then proceed with molecular simulations of Trp-168 noncovalent interactions in the liganded and nonliganded forms of TIM. The results of the vibrational calculations indicate (Figure 4 and Table 3) that indeed we have assigned the correct simulated peak for the W3 mode. The simulated Raman data yield the following equation for νW3 and νWd3, respectively:

Figure 4.

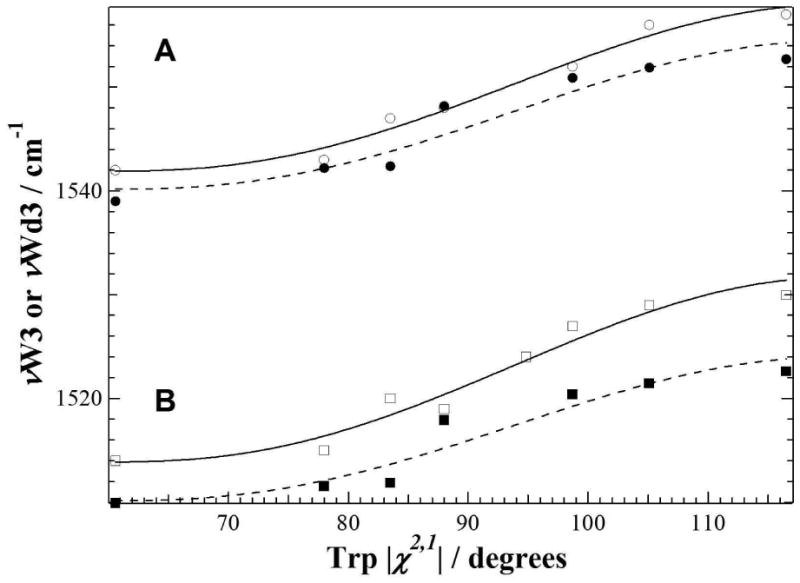
Simulated νW3 = (1540.2 ± 1.1) + (6.245 ± 0.853)(cos 3|χ^2,1|+1)^1,2 (Table 2, νW3_{calc scaled}; broken line trace and solid circles) and νWd3 = (1510.1 ± 1.1) + (6.041 ± 0.806)(cos 3|χ^2,1|+1)^1,2 (Table 2, νWd3_{calc scaled}; broken line trace and solid squares) as a function of the χ^2,1 torsional angles and where the errors associated with the intercept and coefficient values are fitting errors. Results of the simulations are very similar to the published data on the νW3 (solid line trace and open circles, from (2)) and the νWd3 (solid line trace and open squares, from (1)). All frequencies reported are calculated using DFT/B3LYP and 6-31g(d) with a scaling factor = 0.963 (20, 22).

Table 3.

Observed and calculated W3 mode frequency for Trp (νW3) and Trp-d⁵ (νWd3) as a function of the |χ^2,1| torsional angle.

|χ2,1|, deg	νW3, cm-1			νWd3, cm-1
	obsa	calcb	calcscaledc	obsd	calcb	calcscaledc
60.6	1542	1598.1	1539.0	1514	1568.0	1509.9
78.0	1543	1601.5	1542.2	1515	1569.6	1511.5
83.5	1547	1601.6	1542.4	1520	1570.0	1511.8
88.0	1548	1607.7	1548.2	1519	1576.2	1517.9
98.7	1552	1610.5	1550.9	1527	1578.8	1520.4
105.1	1556	1611.6	1551.9	1529	1579.9	1521.4
116.5	1557	1612.3	1552.7	1530	1581.1	1522.6

^aFrom (2)

^bBased on DFT/B3LYP and 6-31g(d) calculations.

^cScaling factor = 0.963 (20, 22)

^dFrom (1)

$$\nu W3=\left(1540.2\pm 1.1\right)+\left(6.245\pm 0.853\right){\left(cos3\left|{\chi }^{2,1}\right|+1\right)}^{1,2}$$ (5)

$$\nu Wd3=\left(1510.1\pm 1.1\right)+\left(6.041\pm 0.806\right){\left(cos3\left|{\chi }^{2,1}\right|+1\right)}^{1,2}$$ (6)

Where the errors associated with the intercept and coefficient values are the fitting errors. Not only have we reproduced Eqs. (1) and (2), but we have also shown that that the isotopic substitution on the indole nitrogen had very little effect on the νW3. Values of 1539.9 cm^-1 for the natural Trp and 1539.4 cm^-1 for ¹⁵N-Trp were obtained (Table 4). On the other hand, the unconstrained calculations for Trp-d⁵ yielded a νW3 downshifted from that of the natural Trp by 30 cm^-1 (Table 4). This peak shift is consistent with was previously reported (1). The simulated peak positions corresponding to the W6 and W7 tryptophan modes (Table 4) were also identified using the unconstrained calculations involving Trp, ¹⁵N-Trp, and Trp-d⁵.

Table 4.

Isotopic dependence of the calculated W3 mode frequency for Trp (νW3) and χ^2,1 torsional angle.^†

Samples	|χ2|, deg	νW3, cm-1	νW6, cm-1	high νW7, cm-1	low νW7, cm-1	Ihigh νW7/Ilow νW7	Inew νW7/Ilow νW7	νW17, cm-1
natural abundance Trp	39.9	1539.9	1467.2	1359.8	1334.7	0.386	0.735	856.8
Trp with indole N replaced by 15N (15N-trp)	39.8	1539.4	1457.8	1358.3	1332.8	0.318	0.691	849.2
ring deuterated Trp (Trp-d5)	39.9	1510.0	1376.9	----	----	----	----	781.1

^†All values presented are based DFT/B3LYP and 6-31g(d) and scaling factor = 0.963 (20, 22).

Noncovalent Interactions at the Trp-168 Indole - Hydrogen Bonding

With the assignment of the W3 mode ascertained, we attempt to reconcile the νW3 and x-ray crystallographic dihedral angle obtained for Trp-168 in PGA-ligated TIM. We examine specifically the hydrogen bonding and around Trp-168 in TIM, followed by more generalized considerations of weaker electrostatic interactions, steric hindrance and hydrophobic interactions.

To simulate hydrogen bonding in PGA-ligated TIM, we carried out calculations involving tryptophan and three different hydrogen bonding partners. These are: 1. a phenol, to mimic the interaction between Trp-168 and Tyr-164, 2. a carboxyl, to mimic the interaction of Trp-168 with Glu-129, and 3. a water molecule. The distances between the indole N–H and the hydrogen bonding partner were varied and fixed for each set of calculations. Varying the distance simulates the change in the extent of hydrogen bonding: the closer the distance, the greater is the hydrogen bonding. The angle of the hydrogen bond was set to 180°. No other constraints were used.

The set of Trp-H₂O simulations indicates that as the distance between the water molecule and the indole N–H narrows from 4 to 2 Å, the values of νW3 and χ^2,1 hardly change (Table 5), and are near the values obtained for the unconstrained Trp simulation (Table 3). Values of νW3 are around 1536.7 cm^-1 while the χ^2,1 are about 42.4°. The upshift in νW6 as the water is placed increasingly closer to the indole N-H group indicates that the extent of hydrogen bonding increases with closer approach (8). The insensitivity of νW3 to hydrogen bond length indicates that the extent of hydrogen bonding cannot explain the observed shifts in νW3. Similar results were observed when either phenol or a carboxylic group was used as the hydrogen bonding partner. This set of observations, and the frequency positions of the hydrogen bond markers, W6 and W17 (876 cm^-1, Fig. 1A) (2, 8), rule out strong hydrogen bonding as an explanation for the misfit of the PGA-bound TIM νW3 - χ^2,1 dihedral angle pair to Eq. (3). This supports the earlier finding of Maruyama and Takeuchi (1) that there is no direct correlation between νNH and νW3 for the crystalline tryptophan derivatives.

Table 5.

Calculated frequencies of some tryptophan modes and χ^2,1 torsional angle for the Trp-water complex. The effect of hydrogen bonding and steric strain. ^†

Distance of water from the indole	|χ2,1|, deg	νW3, cm-1	νW6, cm-1	high	low	Ihigh νW7/Ilow νW7	νW17, cm-1
N–H group, Å				νW7, cm-1	νW7, cm-1
1.5	40.4	1532.1	1442.1	1360.2	1341.5	1.088	871.6
2.0	42.3	1536.3	1431.2	1359.8	1338.6	0.707	857.5
2.5	44.2	1538.1	1420.9	1359.3	1336.6	0.497	856.1
3.0	42.6	1535.9	1413.2	1358.3	1335.7	0.424	858.2
4.0	42.3	1538.1	1413.7	1359.3	1335.2	0.406	857.8

^†All values presented are based DFT/B3LYP and 6-31g(d) and scaling factor = 0.963 (20, 22).

Noncovalent Interactions at the Trp-168 Indole: Anion-Quadrapole and Cation-π Interactions

Here, we explore the possibility that weaker, attractive electrostatic interactions influence the W3 mode. The anion-quadrapole interaction involves the electrostatic attraction between an anion and the partial positive charge surrounding an aromatic ring, here the indole ring (30, 31) while the cation-π interaction involves the attractive force between a cation and the π electron cloud on either face of the indole ring (32, 33). Typically, the anion in a proteinaceous anion-quadrapole interaction is a glutamate or aspartate while the cation in proteinaceous cation-π interactions is either arginine or lysine. As this weaker interaction is difficult to quantify in the presence of stronger hydrogen bond interactions, we look for the influence of these aromatic interactions on tryptophan discrepancies with the νW3-χ^2,1 relationship by examining the x-ray crystal structures. The results for the proteinaceous tryptophans discussed above are given in Table 6. We see that for proteins with tryptophans that follow the νW3-χ^2,1 relationship such as bacteriorhodopsin, gyrase B with cholorbiocin and melittin, electrostatic interactions are common and multiple. It is noteworthy that for the enzymes, TIM and PTPase, the ligand state which best conforms to the νW3-χ^2,1 relationship has more than one such electrostatic interaction. While weak, the cumulative effect of these interactions can be significant (31). On the other hand, the relationship-compliant tryptophan in the model peptide, exendin-4 TC5 with a caged tryptophan, has no such electrostatic interactions, while the noncompliant tryptophan in the Pf3 virion coat peptide does. As the evidence accumulates, it becomes clearer that no one factor is the bellwether for compliance with the νW3-χ^2,1 relationship. Rather, compliance appears to be based on a complex web of weak interactions that are difficult to quantify individually.

Table 6.

Noncovalent Interactions for Tryptophan in Several Proteins

Protein	PDB #	Molecular Coordinates	Distance (A)	Interaction
Gyrase B with chlorobiocin	1KZN	W170A CZ2 - R168 ANH1	3.96	Cation- π
		W170A CH2 - K129A NZ	3.96	Cation- π
apoTIM	1YPI	W168 CE2 – K134 N2	3.97	Cation- π
		W168 CZ2 - L174 N	5.79	Cation- π
+ PGA	7TIM	W168 CE2 – K134 N2	4.26	Cation- π
Yersinia PTPase/apo;WT	1YPT	W354 CE2 - R409 NH2	4.95	Cation- π
“ + vanadate	2I421	W354 CD2 - R409NH1	5.91	Cation- π
		W354 CD1 - T358 OG1	3.42	Anion-quadrapole
Pf3 virion coat	1IFP 1FPSF	W38 – R37 (interstrand)	NA	Cation- π
Fd virion coat	1IFJ	F42 - W26	NA	Aromatic face-edge
Melittin	2MLT	W19A CZ2 - K23A NZ	4.62	Cation- π
		W19B CE2 - K23B NZ	4.39	Cation- π
Bacteriorhodopsin W182	2BRD	W182 CZ2 – RET 216 het C20	4.14	Cation- π
		W182 CZ2 –RET 216 het C19	5.39	Cation- π

¹(57)

Noncovalent Interactions at the Trp-168 Indole: Hydrophobicity

The homogeneous composition of the crystalline tryptophan derivatives used to formulate the νW3-χ^2,1 relationship would seem to indicate a hydrophobic environment for the constituent indole rings. Hydrophobicity can be spectoscopically estimated from the intensity ratio, 1360 cm^-1:1340 cm^-1, which are νW7 bands, since a hydrophobic environment yields a band ratio greater than or approximately equal to one (4, 5). Estimate of this simple intensity ratio for the crystalline tryptophan derivatives is not straightforward because the W7 bands are not split into doublets but into triplets, quartets or even more component bands (2). Estimate or measurement of this W7 band ratio for the set of peptides and proteins under discussion here is somewhat more straightforward because W7 doublets are present or readily discernible from the UVRR results. W7 1360 cm^-1:1340 cm^-1 band ratios are given in Table 7. The ratios range in value from 0.8 to 1.7, with the fd virion peptide taking the maximum value. As the W7 band ratio for the ligated forms of both enzymes, TIM and PTPase, and horse heart cytochrome C, is lowest in value, the least hydrophobic environment for their respective tryptophans is indicated. W7 band ratios for skatole in solvents of varying polarity show that a band ratio of 0.17 is obtained in dimethyl formamide and 1.0 in benzene (4). Even at a 1360 cm^-1:1340 cm^-1 band ratio of 0.8, enzymatic tryptophans would seem to be in a fairly hydrophobic environment. The highest values in W7 band ratio are found for the virion coat peptides, fd and Pf3 (1.7 and 1.5, respectively), but the ratio for PGA-ligated TIM is 0.8, the minimum value found. As the νW3 - χ^2,1 data points for these peptides and protein all do not fall on the νW3 - χ^2,1 curve, hydrophobicity as measured by the W7 1360 cm^-1:1340 cm^-1 band ratio is not a good indicator of compliance with the derived relationship. Consideration of the W7 band ratio for the relationship compliant model peptides and proteins leads to the same conclusion.

Table 7.

W3 Bandwidth for Tryptophans in Peptides and Proteins

Trp-bearing species	W7 Band Ratio (1360 cm-1/1340 cm-1)	W3 Bandwidth (FWHM/cm-1)
Range of νW3-χ2,1 Relationship	-	16 (1542 - 1558)
Crystalline Trp derivatives	-	9 - 15
Exendin-4 TC5b W/P cage	1.1	16
Melittin	1.5	15
Horse heart cytochrome C	0.8	14
Fd virion peptide	1.7	18
Pf3 virion peptide	1.5	23
PTPase + tungstate	0.8	11
apoPTPase	2.0	17
TIM + PGA	0.8	16
apoTIM	1.3	13

Noncovalent Interactions at the Trp-168 Indole: Steric Hindrance

No one molecular interaction appears to account for the noncompliance of a given tryptophan with the νW3 - χ^2,1 relationship. The sum total of all weak interactions will determine whether the νW3 - χ^2,1 data point for any single tryptophan will follow the relationship. It should come as no surprise, therefore, that tryptophans with an environment similar to those of the crystalline tryptophan derivatives used to define the νW3 - χ^2,1 relationship will comply with it; that is, tryptophans in a constrained environment.

Tryptophans Compliant with the νW3 - χ^2,1 Relationship

NMR study of the tryptophan in the model truncated peptide, exendin-4 TC5b (point 4, Fig. 2a), shows that Trp-26 is encased by an extensive hydrophobic network of methyl groups and prolines on both faces of the indole and about its edge (34). The conformation of Trp-26 is also stabilized by hydrogen bonds both at the indole amine and backbone carbonyl and amine (34). This environment is very much like the environment of the crystalline tryptophan derivatives used to define the νW3 - χ^2,1 relationship: hydrophobic, constrained and in most cases, with hydrogen bonds to either the indole amine or the backbone carbonyl or amine. The environment of Trps-19A and B of the model peptide, melittin (points 6 and 6, Fig. 2a), is also hydrophobic and constrained. The tryptophans are aligned on the apolar face of the bent rod of 26 amino acids (35). Four peptide rods pack together in a bilayer sandwich, two rods per layer, with the hydrophobic faces packed together. This arrangement persists in the venom sack of the insect and in solution where the positive face of each rod accounts for aqueous solubility and prevents protein aggregation (35). All subunit contacts are hydrophobic, with tight interhelical packing of valine, leucine, isoleucine and tryptophan residues. Lys-23 in the same and an adjacent helix stabilize Trp-19 with cation-π interactions. Considering Trp-182 in retinal-bound bacteriorhodopsin, which also follows the νW3 - χ^2,1 relationship (data point 36°, 1550 cm^-1, Fig. 2a), the retinal cofactor both creates an hydrophobic environment for the indole ring and sterically hinders it via cation-π interactions (Table 6) (36).

Tryptophans Noncompliant with the νW3 - χ^2,1 Relationship

The fibrillar structure of the virion coat peptides, fd (point 1, Fig. 2a) and Pf3 (point 3, Fig. 2a), suggests a constrained, crystal-like, environment for their tryptophans. However, the interpretation of fiber x-ray structures of both of these coat proteins is clouded by the lack of resolution in the data (37). Welsh et al. (38) construct several possible structural models for Pf3 and Marvin and coworkers (37) refer to the Trp-26 dihedral angle values provided by Raman studies of fd in constructing their structure (39, 40). In models of Pf3, Trp-38 is directed to the central core of the fiber, which is occupied by viral DNA. There, multiple copies of Trp-38 are thought to help neutralize the negative charge of the DNA phosphates via anion-quadrapole electrostatic interactions, or by cation-π interactions bridged by a cation (38). Several of the models for Trp-38 place it in a polar environment, which would help explain the noncompliance of Trp-38 with the νW3 - χ^2,1 relationship. An earlier x-ray structure for the fd virion coat protein provided a dihedral angle of 290.1° for Trp-26 (41). With νW3 = 1560 cm^-1, the data point for Trp-26 would lie very far from the νW3 - χ^2,1 curve. Subsequent crystallographic study of fd (37) provides a dihedral angle of 87 °, bringing the data point for Trp-26 closer to the νW3 - χ^2,1 curve (point 1, Fig. 2a). As this angle was determined by reference to the dihedral angle values provided by Raman studies of fd (39, 40), there is uncertainty in the x-ray structural position of Trp-26. More to the point, however, is the value of νW3 for Trp-26, 1560 cm^-1, which is outside the possible value range of the νW3 - χ^2,1 relationship given in Eq. (3), namely 1542-1558 cm^-1. This narrow value range---only 16 cm^-1---suggests that νW3 bandwidth could be a useful guide in empirically determining steric hindrance for tryptophan, and therefore the utility of the νW3 - χ^2,1 relationship for predicting the χ^2,1 dihedral angle.

W3 Bandwidth as a Predictor of Compliance with the νW3-χ^2,1 Relationship

νW3 bandwidths for several of the peptide and protein data points shown in Fig. 2a are given in Table 7. νW3 bandwidths have been equated with the FWHM value for each peak. As published spectra were only available for FWHM measurements in some cases (virion peptides and horse heart cytochrome C), the values given are only a first order approximation. The FWHM value was also estimated from published spectra for each of the crystalline tryptophan derivatives used to construct the νW3-χ^2,1 relationship (2), and these are summarily reported as a range of values, 9-15 cm^-1. For these tryptophan derivatives, the widest νW3 bandwidth would seem to lie just inside the maximum value of the νW3-χ^2,1 relationship. Estimated FWHM values for relationship-compliant proteins, such as horse heart cytochrome C (42), fall just within the νW3-χ^2,1 relationship bandwidth boundaries while those for noncompliant fd and Pf3 virion coat proteins (43) do not. More valuable are FWHM measurements that can be made on the original data, as for exendin-4 TC5b peptide and melittin. Here, the FWHM bandwidths are 16 cm^-1 and 15 cm^-1, respectively (Table 7). Perhaps the most instructive measurements are those made on two different states of the same protein where one state follows the νW3-χ^2,1 relationship and the other does not. This is true for the liganded and nonliganded states of the enzymes, TIM and PTPase (44). The FWHM data for these enzymes provide a nice contrast because in one case, for TIM, the nonliganded state is compliant with the νW3-χ^2,1 relationship while for PTPase, the liganded state is relationship compliant. The FWHM measurements in Table 7 are in agreement with the νW3-χ^2,1 plot results. Data points for enzymatic states with the narrower FHWM bandwidths (nonligated TIM, FWHM =13 cm^-1 and ligated PTPase, FWHM=11 cm^-1) follow the relationship while states with wider FWHM bandwidths (ligated TIM, FWHM=16 cm^-1 and nonligated PTPase, FWHM=17 cm^-1) do not. Thus, FWHM measurements of νW3 provide an estimate of how constrained the tryptophan is with respect to the constrained environment of the crystalline tryptophan derivatives used to construct the νW3-χ^2,1 relationship, and thus can provide a rough guide to the utility of the relationship in predicting the χ^2,1 dihedral angle for any one tryptophan. It should come as no surprise that constraint on the motion of the indole ring of tryptophan, as measured by the FWHM of νW3, is relevant here. As discussed above and illustrated by the Newman projection in Fig. 3, the 3cosine dependence of νW3 stems from the three-fold steric hindrance encountered by the indole from moieties bonded to C_α. Clearly, this relationship would find great utility in Raman crystallographic studies where residue motion is minimized. Even with this spectroscopic guideline, the experimental value of νW3 for the fd viral coat protein still lies outside the boundaries of the νW3-χ^2,1 relationship. Science is an ongoing process, and undoubtedly refinements to this relationship will be made by others, advancing the utility of Raman spectroscopy for making structural predictions.

Conclusion

The νW3 - χ ^2,1 relationship (1-3) has been extended to a full, 360° rotation by plotting all dihedral angles in the same rotational direction, i.e., clockwise. As the period of the relationship given in Eq. (3) is three-fold (3cos χ ^2,1) the χ ^2,1 dihedral angle ranges 0° – 120°, 120° – 240°, 240° – 360°, are superimposable. It is clear from this plotting that as many as six dihedral angles correlate to a single νW3. A Newman plot of tryptophan dihedral angles gleaned from protein and tryptophan analog crystallographic data shows, however, that the χ ^2,1 dihedral angle ranges, 0° - 75°, 150° -240°, and 300° – 360°, are generally avoided because of steric clashes between the indole rings and the protein backbone. This elimination of dihedral angle ranges reduces the number of possible dihedral angles for any νW3 to two or even a single angle, suggesting a general utility for the νW3 - χ ^2,1 relationship. At the same time, νW3 - χ ^2,1 data points for some proteinaceous tryptophans do not conform to the relationship given in Eq. (3). For one of these proteins, the mutant enzyme TIM (Trp90Tyr Trp157Phe), DFT-based calculations and simulations are used to explore the possibility that hydrogen bonding, a strong, noncovalent interaction, at the indole amine is responsible for noncompliance of the ligated TIM νW3 - χ ^2,1 data point with the νW3 - χ ^2,1 relationship. In agreement with Maruyama and Takeuchi (1), our simulation results show no dependence of νW3 on hydrogen bonding at the indole amine. The χ^2,1 dependence on C₂-C₃, C₂-N₁ and C_β-C₃ bond lengths of tryptophanyl indoles, suggested earlier (1), is not found here for proteinaceous tryptophans that obey the νW3 - χ ^2,1 relationship. The effect of weaker anion-quadrapole and cation-π interactions on νW3 is evaluated through examination of x-ray crystal structures for several proteins for which νW3 is available. This evaluation suggests that multiple, weak electrostatic anion-quadrapole, cation-π, and aromatic face-edge interactions coupled with van der Waals interactions act in a cumulative fashion to stabilize the indole side chain of tryptophan. In the absence of methods to quantify or model the cumulative effect of these interactions, the environment about the crystalline tryptophan derivatives used to formulate the νW3 - χ ^2,1 relationship is considered. That environment is both constrained and hydrophobic. The hydrophobicity of the tryptophan environment can be evaluated from the W7 band ratio, 1360 cm^-1:1340 cm^-1, where a value greater than one indicates a hydrophobic environment (5), but band ratio measurements for the set of peptides and proteins considered here showed no correlation with the νW3 - χ ^2,1 relationship. Estimation of environmental constraint for tryptophan as measured by FWHM of the W3 band showed greater success in predicting compliance with the νW3 - χ ^2,1 relationship. For model peptides where the indole is stabilized through numerous noncovalent interactions and other relationship-compliant proteins, the νW3 - χ ^2,1 data point conforms to the νW3 - χ ^2,1 relationship. As the νW3 bandwidth of the νW3 - χ ^2,1 relationship is only 16 cm^-1, the FWHM of νW3 for the tryptophan under study should be no greater than this. Given this constraint, application of νW3 - χ ^2,1 relationship for predicting the tryptophan χ ^2,1 angle has some chance of success. Clearly, where a spectral bandwidth nearly matches the full range of the relationship used to predict a structural parameters, the error bars are large.

Abbreviations

DFT

density functional theory

DHAP

dihydroxy acetone phosphate

FWHM

full width half maximum

GAP

glyceraldehyde phosphate

G3P

glycerol 3-phosphate

PTPase

protein tyrosine phosphatase

PGA

2-phosphoglycolate

Pi

phosphate

PDB

Protein Data Bank

TIM

triose phosphate isomerase

UVRR

ultraviolet resonance Raman spectroscopy