Area under the Free-Response ROC Curve (FROC) and a Related Summary Index

Abstract

SUMMARY

Free-response assessment of diagnostic systems continues to gain acceptance in areas related to the detection, localization and classification of one or more “abnormalities” within a subject. A Free-response Receiver Operating Characteristic (FROC) curve is a tool for characterizing the performance of a free-response system at all decision thresholds simultaneously. Although the importance of a single index summarizing the entire curve over all decision thresholds is well recognized in ROC analysis (e.g. area under the ROC curve), currently there is no widely accepted summary of a system being evaluated under the FROC paradigm. In this paper we propose a new index of the free-response performance at all decision thresholds simultaneously, and develop a nonparametric method for its analysis. Algebraically, the proposed summary index is the area under the empirical FROC curve penalized for the number of erroneous marks, rewarded for the fraction of detected abnormalities, and adjusted for the effect of the target size (or “acceptance radius”). Geometrically, the proposed index can be interpreted as a measure of average performance superiority over an artificial “guessing” free-response process and it represents an analogy to the area between the ROC curve and the “guessing” or diagonal line. We derive the ideal bootstrap estimator of the variance which can be used for a resampling-free construction of asymptotic bootstrap confidence intervals and for sample size estimation using standard expressions. The proposed procedure is free from any parametric assumptions and does not require an assumption of independence of observations within a subject. We provide an example with a dataset sampled from a diagnostic imaging study and conduct simulations which demonstrate the appropriateness of the developed procedure for the considered sample sizes and ranges of parameters.

1. Introduction

The problem of detecting, locating and marking one or more abnormalities in the same subject is a common task in diagnostic imaging (e.g. detection of multiple nodules) or imagery of military targets (e.g. detection of multiple targets). A commonly used method of evaluating diagnostic performance in such an environment is a Free Response Receiver Operating Characteristic (FROC) approach (Egan, Greenberg, Schulman, 1961; Bunch et al., 1978) which entails placing on an examination (e.g. an image of a subject) an arbitrary number of rated marks each of which indicates the location of a suspected abnormality as well as the level of suspicion (indicated with a rating) regarding the specific abnormality at each marked location. The distinctive feature of FROC analysis is that not only the accuracy of ratings but also the number of marks is considered as one of the integral characteristics of the system.

Similar to the ROC paradigm, a higher rating indicates a higher degree of suspicion. However, in contrast to ROC, under the FROC paradigm considering all marks as “positive” regardless of their rating does not necessarily lead to identification of all abnormalities, since some abnormalities may not have been marked at all. Thus, the accuracy of the set of unrated marks (performance at a “find everything” mode) is another inherently important characteristic of the system.

Several approaches have been developed for analyzing FROC data. Two major parametric approaches for fitting the FROC curve (Chakraborty, 1989; Edwards, et al., 2002) model similar but formally different latent structures. Both approaches make an additional assumption of independence of the observations within the same subject. Some of the existing nonparametric methods for analysis of summary indices do not require independence (Chakraborty and Berbaum, 2004; Samuelson and Petrick, 2006), but these also have certain deficiencies as discussed below.

In recognition of the importance of a single summary measure of the overall performance of a free-response system, several indices have been proposed. One type of index characterizes the ROC-type diagnostic performance (subject as a basic unit) instead of the FROC-type diagnostic performance (a rated mark within a subject as a basic unit). Indices of this type characterize the ability to discriminate between actually positive (with at least one known abnormality) and actually negative (without known abnormalities) subjects using a specific method of forming a summary opinion on a subject as a whole from the collection of the rated marks within the examination (e.g. maximum rating of all marks, Chakraborty, 2006).

Another type of summary index attempts to characterize directly the FROC-type diagnostic performance. Some of the nonparametric procedures of this type suffer from disregarding information (e.g. JAFROC-2 ignores FP marks on actually positive examinations, Chakraborty and Berbaum, 2004), or from the absence of a well behaving statistical procedure for the analysis (e.g. JAFROC-1, Chakraborty and Berbaum, 2004). In addition, analogous to the ROC approach there are several summary indices of the FROC curve that relate to a subset of all possible decision thresholds. These include the True Positive Fraction (TPF) at a specific False Positive Rate (FPR) (Chakraborty, 1989) and the area under the FROC curve up to a specific FPR (Samuelson and Petrick, 2006). Similar to the corresponding indices in ROC analysis these indices suffer from the subjectivity of selecting the FPR range (or point), entail analytical complications associated with the uncertainty of the FPR-related threshold, and are potentially less precise than the indices that summarize over all decision thresholds (e.g. partial AUC versus AUC, Zhou, Obuchowski, McClish, 2002). We are unaware of any FROC summary index that simultaneously characterizes the FROC-type performance at all decision thresholds, uses all the available data, and has a well-developed procedure for statistical analysis.

In this manuscript we propose a new easily estimable and interpretable summary index of FROC-type diagnostic performance which uses all available data and incorporates important features of the FROC curves in a meaningful and explicit manner. We also develop a computationally-simple nonparametric method for statistical analysis that does not require the often difficult to justify assumption of independence among the observations within the same subject. The proposed methodology is applicable to the phases of evaluation of diagnostic systems where interest often lies in the overall performance of the system and in which the structure of the sample is controlled by design.

In Section 2 we outline the FROC approach and define an empirical FROC curve. Section 3.1 presents a convenient formulation for the area under the empirical FROC curve and discusses its limitations as an index of performance. We propose a new index of the overall performance in Section 3.2. In Section 3.3 we introduce a concept of a “guessing” free-response process and use it to provide a geometric interpretation for the proposed index. Section 3.4 briefly outlines a standard procedure for constructing an asymptotic confidence interval and estimating sample size using a newly derived closed-form estimator of the ideal bootstrap variance. In Section 4 we present simulation results for the ranges of parameters commonly encountered in diagnostic imaging. Section 5 illustrates the proposed procedure on a sample of experimentally ascertained diagnostic performance imaging data. A discussion follows in Section 6.

2. Free-Response Approach and FROC Curve

When evaluating a subject (e.g. patient, examination, image) under the FROC paradigm the diagnostic system places a number of marks indicating suspected locations of the abnormalities of interest and supplements every mark with a rating indicating a level of suspicion regarding abnormality at the marked location. In this paper we focus on retrospective studies where the number of subjects with and without abnormalities as well as the number of actual abnormalities on every image are often known and controlled (or fixed) by design. For simplicity of presentation we will describe the case where there are only two types of subjects evaluated by the FROC system: actually positive subjects with a fixed number of abnormalities τ=t and actually negative subjects with no abnormalities, τ=0. However, the formulations we present are generalizable to more than two types of subjects (e.g. τ=0,1,2,3...). The outline of the extension is given in Appendix.

Every mark placed on the image, regardless of the value of the assigned rating, can be classified as a True Positive (TP) or False Positive (FP) finding depending on whether or not it “contains” an actual abnormality. This classification of containment is typically determined by comparing the distance between the mark and the geometrical center of the actual abnormality to an acceptance radius R (radius of an “acceptance target”). The acceptance radius is a proximity criterion that is chosen at the design stage of the FROC study.

The data from the FROC study for the S₀ actually negative and S_t actually positive subjects can be summarized as follows:

$$\begin{array}{c}\hfill {\left\{x_{s^{\prime }{c}^{\prime }}^0\right\}}_{c^{\prime }=1}^{n_{s^{\prime }}^0},s^{\prime }=1,\dots S_0\leftrightarrow "\text{actually negative}"\tau =0\text{abnormalities}\\ \hfill ({\left\{x_{sc}^t\right\}}_{c=1}^{n_s^t},{\left\{y_{sc}^t\right\}}_{c=1}^{m_s^t}),m_s^t\le ts=1,\dots S_t\leftrightarrow "\text{actually positive}"\tau =t\text{abnormalities}\end{array}$$ (1)

where n^τ is the number of FP marks; m^τ is the number of TP marks; {x^τ} is the collection of ratings for the FP marks (vector of random length n); {y^τ} is the collection of ratings for the TP marks (vector of random length m) and τ is the number of abnormalities. We assume the data for a randomly selected subject can be described by a joint distribution of the random variables:

$$\begin{array}{c}\hfill (x^0,n^0)~F_{x,n}^0-"\text{actually negative}"\tau =0\text{abnormalities}\\ \hfill (x^t,y^t,n^t,m^t)~F_{x,y,n,m}^t-"\text{actually positive}"\tau =t\text{abnormalities}\end{array}$$ (2)

Each rated TP or FP mark can be classified as “positive” or “negative” based on comparison of its rating with a decision threshold ε. The performance of the FROC system at the decision threshold ε is conventionally characterized by the proportion of the abnormalities identified by the “positive” TP marks and by the average number of “positive” FP marks per subject. These two characteristics are termed correspondingly as True Positive Fraction (TPF) and False Positive Rate (FPR) and using our notation can be formulated as follows:

$$\begin{array}{c}FP{R}_{\rho °\pi }\left(\epsilon \right)=E\{n^0\times P(x^0>\epsilon \mid n^0)\}\times (1-\kappa )+E\{n^t\times P(x^t>\epsilon \mid n^t)\}\times \kappa \hfill \\ TP{F}_{\rho °\pi }\left(\epsilon \right)=\frac{E\{m^t\times P(y^t>\epsilon \mid m^t)\}}{t}\hfill \end{array}$$ (3)

where κ=S_t/(S₀+S_t) is the proportion of the actually positive subjects as determined by design. Throughout this paper we assume that all expectations are taken over all random quantities defined in (2) except for those which are conditioned upon (are to the right of |). The subscript ρ°π reflects the general interpretation of the FROC process as a composition of a pruning (or “candidate selection”) process π, and a rating-generating (or “candidate analysis”) process ρ (Edwards, et al., 2002). Note that for more than two types of subjects (e.g. τ=0,1,2) FPR will include more terms, and TPF will become a weighted average of the type-specific TPFs. We note that FPR is the “FP rate” and, unlike “TP fraction” (TPF), it can be greater than 1.

The FROC curve is a collection of points (fpr, tpf) residing in an infinite band [0,+∞)x[0,1]. The point fpr=0, tpf=0 corresponds to the operating mode where no marks are considered “positive”. With decreasing strictness of the decision threshold ε both TPF_ρ°π(ε) and FPR_ρ°π(ε) gradually increase. The operating point where all rated marks are considered “positive” has the following coordinates:

$$FP{R}_{\pi }=E\left(n^0\right)\times (1-\kappa )+E\left(n^t\right)\times \kappa TP{F}_{\pi }=\frac{E\left(m^t\right)}{t}$$ (4)

The above quantities are some of the very important characteristics portrayed by the FROC curve which we term as “pruning” characteristics.

Using the data collected for a sample of subjects we can estimate the TPF_ρ°π(ε) and FPR_ρ°π(ε) at every decision threshold ε and obtain an empirical FROC curve by connecting the estimated points (0,0), $\left\{(\widehat{FP{F}_{\rho °\pi }}\left(\epsilon \right),\widehat{TP{F}_{\rho °\pi }}\left(\epsilon \right))\right\}$, and $(\widehat{FP{F}_{\pi }},\widehat{TP{F}_{\pi }})$ with straight line segments. The empirical estimators of TPF and FPR are:

$$\begin{array}{c}\hfill \widehat{FP{R}_{\rho °\pi }}\left(\epsilon \right)=\frac{\sum _{s‘=1}^{S_0}\sum _{c‘=1}^{n_{s‘}^0}I(x_{s‘c‘}^0>\epsilon )+\sum _{s=1}^{S_t}\sum _{c=1}^{n_s^t}I(x_{sc}^t>\epsilon )}{S_0+S_t},\widehat{TP{F}_{\rho °\pi }}\left(\epsilon \right)=\frac{\sum _{s=1}^{S_t}\sum _{c=1}^{m_s^t}I(y_{sc}^t>\epsilon )}{t{S}_t}\hfill \\ \hfill \text{and}\hfill \\ \hfill \widehat{FPR\pi }=\frac{\sum _{s^{‘}=1}^{s_0}{n}_{s‘}^0+\sum _{s=1}^{s_t}{n}_s^t}{S_0+S_t}\widehat{TP{F}_{\pi }}=\frac{\sum _{s=1}^{s_t}{m}_s^t}{t{S}_t}\hfill \end{array}$$ (5)

The notations and computations used in (1) and (5) are illustrated in Web-Appendix C.

3. Area under the Empirical FROC Curve and a Related Index of Performance

3.1 Area under the Empirical FROC Curve

Applying straightforward algebra and using the formulations of the empirical estimators in (5) it can be shown that the area under the empirical FROC curve (FAUC) can be written as:

$$\begin{array}{c}\hfill {\widehat{A}}_{\rho °\pi }=\frac{1}{t{S}_t(S_0+S_t)}\sum _{\tilde{s}=1}^{S_0+S_t}\sum _{s=1}^{S_t}{w}_{\tilde{s}s}\hfill \\ \hfill \text{where}{w}_{\tilde{s}s}=\{\begin{array}{cc}\sum _{\tilde{c}=1}^{n_{\tilde{s}}}\sum _{c=1}^{m_s}\psi \left(x_{\tilde{s}\tilde{c}}\right)\hfill & n_{\tilde{s}}{m}_s\ne 0\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}\text{and}\psi (x_{\tilde{s}\tilde{c}},y_{sc})=\{\begin{array}{cc}1\hfill & x_{\tilde{s}\tilde{c}}<y_{sc}\hfill \\ 1∕2\hfill & x_{\tilde{s}\tilde{c}}=y_{sc}\hfill \\ 0\hfill & x_{\tilde{s}\tilde{c}}>y_{sc}\hfill \end{array}\phantom{\}}\hfill \end{array}$$ (6)

In (6) the index s̃ represents all subjects (actually positive and actually negative) and s represents only the actually positive subjects. Thus, w_s̃s corresponds to comparisons within the same actually positive subject when s̃ = s + S₀; between an actually negative and an actually positive subject when s̃ ≤ S₀; and between two different actually positive subjects when s̃ > S₀ and s̃ ≠ s + S₀. If either of the subjects corresponding to s or s̃ have no marks w_s̃s is equal to 0 by definition. We note that unlike the area under the ROC curve, the area under the empirical FROC curve in (6) is generally not bounded by 1 since the denominator may be less than the numerator.

The formulation in (6) is analogous to the representation of the area under the empirical ROC curve as a U-statistic (Bamber 1975; Hanley and McNeil, 1982). The FAUC can also be written as a product of the area under the empirical ROC curve for the clustered collection of ratings on TP and FP marks (A_ρ|π) and two pruning characteristics, namely:

$$\begin{array}{c}\hfill {\widehat{A}}_{\rho °\pi }={\widehat{A}}_{\rho \mid \pi }\times \widehat{TP{F}_{\pi }}\times \widehat{FP{R}_{\pi }}\hfill \\ \hfill \text{where}{\widehat{A}}_{\rho \mid \pi }=\left(\sum _{\tilde{s}=1}^{S_0+S_t}\sum _{s=1}^{S_t}{w}_{\tilde{s}s}\right)/\left\{\left(\sum _{s=1}^{S_t}{m}_s^t\right)\times \left(\sum _{s‘=1}^{S_0}{n}_{s‘}^0+\sum _{s=1}^{S_t}{n}_s^t\right)\right\}\hfill \end{array}$$ (7)

The representation of the area under the empirical FROC curve in (7) agrees with the presentation of the FROC curve as a scaled ROC curve under the assumption of independence of the rated marks within a subject (Edwards, et al., 2002). Although the formulation in (7) does not require this assumption, it will become useful if one desires a similar relationship to hold for the corresponding expected values (without ^) as well. The ideal bootstrap variance for Â_ρ°π is derived in Web Appendix A.

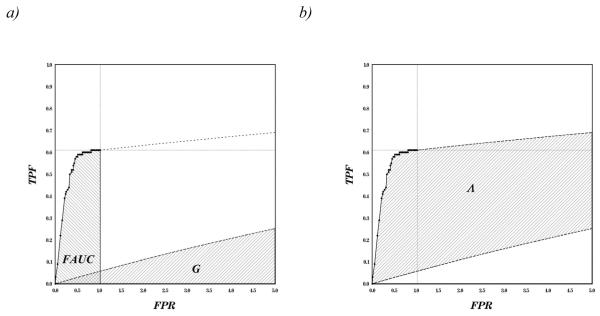
Although the area under the FROC curve summarizes the performance of the FROC system for all decision thresholds, in some instances the area under the FROC curve might be considered a suboptimal or, worse, a potentially misleading summary index of the overall performance of the system. For example, one FROC curve can be above another at all FPR where both curves are defined, achieve a higher TPF_π and yet have a smaller area under the curve. Figure 1 shows two such curves, namely an empirical FROC curve and a “guessing” curve truncated at FPR=5.

Figure 1. Empirical, augmented, guessing FROC curves and the areas corresponding to the FAUC and Λ indices computed from the data in the example.

On both plot a) and plot b):

The empirical FROC curve consists of dots connected with solid line segments.

The guessing FROC curve corresponding to φ=0.06 and its segment used for the augmentation are indicated with a dashed line.

On plot a):

“FAUC” indicates the area under the empirical FROC curve.

“G” indicates the area under the portion of the guessing FROC curve truncated at FPR=5.

On plot b):

“Λ” indicates the area between the augmented and guessing FROC curves which is numerically equivalent to the index formulated in (8).

3.2 A New Index of Performance of a Free-Response System

The inadequacy of the FAUC as an index of the overall performance can be attributed to the feature of the FAUC to reward for a higher rate of FP marks (FPR_π) instead of penalizing for it. In addition, both the FAUC as well as a conventional FROC curve itself, depend on the choice of the acceptance radius, R, since its increase may substantially increase the estimated performance by directly increasing the TPF_π. Naturally, the effect of the acceptance radius on performance increases with an increasing density of the abnormalities in the sample (i.e. decreasing image size or increasing number of the abnormalities).

We propose a new index, Λ, that, similar to the FAUC, rewards for higher ability to discriminate between FP and TP marks (A_ρ|π) as well as for the higher detection fraction (TPF_π). At the same time, the proposed index penalizes for a higher rate of FP marks (FPR_π) and for a larger effect of the acceptance radius (reflected in φ). The index can be written as follows:

$$\Lambda =A_{\rho °\pi }-FP{R}_{\pi }+\frac{TP{F}_{\pi }}{\phi }$$ (8)

The quantity φ reflects a general effect of the size of the acceptance target by combining the acceptance radius R and the density of the abnormalities in the sample. As our interest is in a general effect, we do not model the exact mechanism of the influence of the acceptance radius. Thus, we define the density of the abnormalities using a fixed-by-design dimensional size of the image (Σ) rather than the variable size of the “anatomical” area. We propose the following expression for the parameter φ:

$$\phi ={\left\{\frac{1}{\left(t\kappa /\Sigma \right)\left(\pi R^2\right)}-1\right\}}^{-1}$$ (9)

where tκ/Σ corresponds to the density of the abnormalities in the sample. The parameter φ can be interpreted (assuming no overlaps between TP targets for a given acceptance radius) as a maximum ratio of the average area coverable by the TP marks to the remainder of the image, i.e. φ=tκπR²/(Σ- tκπR²) (equivalently, φ/(φ+1) can be viewed as the largest fraction of the average area coverable by TP marks).

In general there are multiple approaches of combining the two quantities, acceptance radius and density of the abnormalities, into a single parameter. The specific structure of both φ and Λ permits us to relate the proposed index to a certain artificial “guessing” free-response process, which enables an intuitive graphical and numerical interpretation for Λ. As a result, Λ can be interpreted as a measure of the superiority of the system over an artificial “guessing” FROC process which randomly marks the same images with targets of the same size. Graphically, the Λ is equivalent to the area between the augmented empirical FROC curve and the FROC curve of the “guessing” free-response process. In the next section we will demonstrate that for a “reasonable” FROC process Λ varies between 0 and 1/φ, and the product of φ*Λ permits interpretation as the average improvement over the “guessing” process relative to the improvement achievable by a perfect free-response system.

3.3 Guessing, Augmented FROC Curves and Geometric Interpretation of Λ

In this section we introduce the concept of a “guessing” free-response (FROC) process that will lead to an intuitive interpretation of the proposed index Λ but which is not required for the methodology proposed beyond this section. A guessing FROC is an artificial process that does not represent an actual performance of an evaluated system but rather provides a lower bound for it.

We use the term “guessing” for a naïve theoretical free-response process which randomly places possibly multiple marks on the image in such a manner that each mark has the same probability (p=φ/(φ+1)) to cover (“hit”) an abnormality. We define a guessing FROC process operating at a specific decision threshold as a Poisson process with a certain rate that characterizes placing marks at random on the ensemble of images. tpf denotes the probability that at least one of the randomly placed marks covers a given abnormality, and fpr denotes the expected number of marks that do not cover any abnormality. By varying the rate from 0 to infinity we can plot the entire “guessing” FROC curve which acquires the following formulation:

$$tpf=1-e^{-\phi \times fpr}$$ (10)

The “guessing” FROC process has several uses which are of immediate interest in this paper. First, it enables us to define a “reasonable performance” as the performance that is better than a naïve guess. Then, a “reasonable” FROC curve is a curve which lies above the “guessing” curve at all fpr. Second, similar to the empirical ROC, the artificial “guessing” process can be used to extend (augment) the empirical FROC curve to the trivial point where there are no “negative” findings. We augment the observed FROC curve by the part of the guessing FROC curve which lies above TPF_π. As a result, the augmented FROC curve beyond the operating point (FPR_π, TPF_π) can be described as follows:

$$\forall fpr>FP{R}_{\pi }tpf=1-\{(1-TP{F}_{\pi })\times e^{\phi \times FP{R}_{\pi }}\}\times e^{-\phi \times fpr}$$ (11)

As noted previously, the concept of extending the operating characteristic curve beyond the last observed operating point with the aid of a guessing process is not new. In ROC analysis the extension of the empirical ROC curve from the last nontrivial operating point to the trivial point (1, 1) with a straight line can be viewed as an augmentation with a guessing process which randomly re-labels as “positive” some of subjects previously labeled as “negative” at the last nontrivial operating point.

One of the useful properties of the augmented FROC curve is that if the original FROC curve is “reasonable,” i.e. is above the guessing FROC for all fpr<FPR_π, the augmented FROC curve is also “reasonable”. Therefore, we can interpret the proposed index Λ as the area between the augmented and “guessing” FROC curves. Indeed, since the area above the entire “guessing” FROC curve is:

$${\stackrel{‒}{A}}^g={\int }_0^{\infty }{e}^{-\phi \times \mathrm{fpr}}d\mathrm{fpr}=\frac{1}{\phi }$$ (12)

and the area above the augmented FROC curve can be written as:

$${\stackrel{‒}{A}}_{\rho °\pi }^a=(FP{R}_{\pi }-A_{\rho °\pi })+\left[\{(1-TP{F}_{\pi })\times e^{\phi \times FP{R}_{\pi }}\}{\int }_{FP{R}_{\pi }}^{\infty }{e}^{-\phi \times \mathrm{fpr}}d\mathrm{fpr}\right]=FP{R}_{\pi }-A_{\rho °\pi }+\frac{1}{\phi }-\frac{TP{F}_{\pi }}{\phi }$$ (13)

the area between reasonable augmented FROC curve and the “guessing” FROC curve is:

$${\stackrel{‒}{A}}^g-{\stackrel{‒}{A}}_{\rho °\pi }^a=\frac{1}{\phi }-\left(\frac{1}{\phi }+FP{R}_{\pi }-A_{\rho °\pi }-\frac{TP{F}_{\pi }}{\phi }\right)=A_{\rho °\pi }-FP{R}_{\pi }+\frac{TP{F}_{\pi }}{\phi }=\Lambda$$ (14)

Thus, for a “reasonable” FROC curve the proposed index Λ ranges from 0 (negligible performance) to 1/φ (perfect performance). Additionally, (12-14) permit the interpretation of the product φ*Λ as the average relative improvement in performance over the guessing process.

3.4 Statistical Inferences

A nonparametric estimator for the proposed index is straightforward to obtain, by substituting into equation (8) the formulas for the nonparametric estimators of the area under the FROC curve A_ρ°π (6) and “pruning” characteristics TPF_π and FPR_π (5). In Web Appendix B we derive the closed-form expression for the ideal bootstrap variance of Λ under the bootstrap scheme where the entire subject is used as a sampling unit (Rutter, 2000; Samuelson and Petrick, 2006) and the data are stratified by the number of abnormalities. In agreement with the stratified sampling of subjects frequently used during the evaluation of an overall performance of a diagnostic system with FROC analysis, we consider bootstrapping within groups of subjects with the same number of abnormalities. The derivation of the ideal bootstrap variance is conceptually similar to the approach used in the ROC setting (Bandos, Rockette, Gur, 2007).

The estimator of Λ consists of a scaled generalized U-statistic and sample averages. The availability of the closed-form variance estimator allows one to use a simple procedure for the construction of the asymptotic confidence interval:

$$\widehat{\Lambda }\pm {\Phi }^{-1}\left(\frac{\alpha }{2}\right)\times \sqrt{V_B\left(\widehat{\Lambda }\right)}$$ (15)

where Φ represents a cumulative standard normal distribution function, α - a significance level, and V_B - the ideal bootstrap variance. For conditions where the distribution of Λ̂ is likely to be highly skewed (e.g. small sample size and high performance level) the confidence interval in (15) may be improved using an appropriate transformation.

Because of the tendency of the considered variance estimator to decrease at an approximate order of 1/S for equal numbers of actually positive and actually negative subjects (S₀=S_t=S), one can use a simple approach for sample size estimation. Specifically, one can estimate the size of a balanced sample which is needed to achieve a desired length, Δ, of a (1-α) confidence interval around Λ̂ using the following standard expression:

$$S^{\ast }=\frac{4{\Phi }^{-1}{\left(\frac{\alpha }{2}\right)}^2\times V_B\left(\widehat{\Lambda }\right)\times S}{{\Delta }^2}$$ (16)

4. Simulations

We conducted a simulation study where we generated the FROC datasets in which the observations were correlated within a subject and were drawn from the distributions with the parameters resulting in FROC characteristics in the general range consistent with the scenarios commonly encountered in diagnostic imaging. Our simulation model includes correlation structures which can not be handled by the existing parametric methods; but, it does not specifically address all known phenomena (e.g. “satisfaction of search”, Berbaum, et al., 1990). Furthermore, the levels of correlation we use in our simulations may not represent the correlations observed in all FROC breast imaging datasets. However, since the proposed statistical approach is based on bootstrapping subjects as a unit, it has approximately the same properties regardless of the specific within-subject correlation structure.

The number of False Positive marks, n, was generated from a binomial distribution (number of trials=5) with the average probability of success for actually positive subjects of 0.1 resulting in FPR_π^t of 0.5, and with an average probability of success for actually negative subjects of 0.1 or 0.3 resulting in FPR_π⁰ of 0.5 or 1.5 correspondingly. The overall FPR_π was 0.5 or 1 correspondingly. The number of True Positive marks, m, was generated from a binomial (number of trials t) with the average probability of success, TPF_π, of 0.4, 0.6 and 0.8. Marginally the ratings for the FP, x, and TP, y, marks were generated from normal distributions with equal variances and means chosen to achieve the average A_ρ|π (the probability that TP rating exceeds an FP rating) of approximately 0.7, 0.8, and 0.9.

The observations on the same subjects were correlated by relating the distributional parameters to the same realization of a random subject-specific deviate. The random variables n and m were correlated by displacing subject-specific “probabilities of success” from the average by a random variable uniformly distributed on (-0.05,0.05) (an increasing transformation of the subject-specific deviate). The ratings {x}, {y} were related to each other and to n and m by displacing means of the distributions of ratings by a normally distributed deviate (also an increasing transformation of the subject-specific deviate) with mean 0 and standard deviation chosen in such a manner that the correlation between the ratings on the same subject is 0.2.

We considered samples that included 100 and 200 actually positive subjects and the same number of actually negative subjects. For the samples including 100 actually positive subjects we considered scenarios with one and with two abnormalities per image (t=1,2). For the higher sample sizes only the scenario with a single abnormality was considered. We considered φ of 0.06 and 0.1. For each combination of the parameters we generated 10,000 independent datasets.

The coverage of the 95% confidence interval was estimated by the percentage of the generated confidence intervals that covered the sample average of 10,000 estimates of Λ. The estimated coverage along with the average length of the confidence interval for considered combinations of parameters are shown in Table 1. From the table one can observe that the characteristics of the asymptotic confidence intervals are affected by the sample size (S₀=S_t), by the number of abnormalities on actually positive subjects (t), and by the detection fraction (TPF_π). With increasing TPF_π the coverage of the asymptotic confidence interval decreases. This can be attributed to the increasing skewness of the estimator of TPF_π, since, for small φ, this estimator substantially affects the distribution of the estimator for Λ. The separation of the distributions of the ratings of FP and TP marks, A_ρ|π, has a slight effect on the length of the confidence interval but does not substantially affect coverage.

Table 1.

Estimated coverage and length (in parenthesis) of the asymptotic 95% confidence interval

					φ
TPFπ	FPRπt	FPRπ0	S0=St	t*	0.06			0.10
					Aρ|π			Aρ|π
					0.70	0.80	0.90	0.70	0.80	0.90
0.40	0.50	0.50	100	1	94.7% ( 3.251 )	94.7% ( 3.260 )	94.6% ( 3.268 )	94.3% ( 1.977 )	94.4% ( 1.987 )	94.7% ( 1.997 )
				2	94.7% ( 2.301 )	94.8% ( 2.308 )	94.6% ( 2.316 )	94.6% ( 1.403 )	94.8% ( 1.407 )	94.3% ( 1.414 )
			200	1	94.9% ( 2.304 )	95.0% ( 2.310 )	94.6% ( 2.317 )	94.9% ( 1.402 )	95.2% ( 1.409 )	94.5% ( 1.416 )
		1.50	100	1	94.7% ( 3.319 )	94.0% ( 3.336 )	94.5% ( 3.357 )	94.7% ( 2.048 )	94.1% ( 2.065 )	95.0% ( 2.085 )
				2	94.7% ( 2.350 )	94.4% ( 2.365 )	95.2% ( 2.377 )	94.7% ( 1.453 )	94.8% ( 1.465 )	94.7% ( 1.479 )
			200	1	95.3% ( 2.353 )	94.3% ( 2.365 )	95.1% ( 2.379 )	94.8% ( 1.452 )	94.7% ( 1.464 )	94.6% ( 1.478 )
0.60	0.50	0.50	100	1	94.9% ( 3.247 )	94.9% ( 3.257 )	94.7% ( 3.268 )	94.4% ( 1.976 )	94.2% ( 1.985 )	94.5% ( 1.994 )
				2	94.4% ( 2.299 )	94.8% ( 2.306 )	94.7% ( 2.313 )	94.2% ( 1.400 )	94.5% ( 1.406 )	94.6% ( 1.413 )
			200	1	94.5% ( 2.303 )	94.7% ( 2.309 )	95.0% ( 2.317 )	94.3% ( 1.401 )	94.8% ( 1.407 )	94.9% ( 1.414 )
		1.50	100	1	94.9% ( 3.317 )	94.5% ( 3.336 )	94.6% ( 3.353 )	94.6% ( 2.045 )	95.1% ( 2.064 )	94.4% ( 2.081 )
				2	94.7% ( 2.350 )	94.7% ( 2.360 )	94.6% ( 2.375 )	94.7% ( 1.451 )	94.5% ( 1.463 )	95.0% ( 1.475 )
			200	1	94.8% ( 2.352 )		94.7% ( 2.377 )	95.1% ( 1.450 )	94.7% ( 1.463 )	95.3% ( 1.476 )
0.80	0.50	0.50	100	1	94.3% ( 2.649 )	93.4% ( 2.650 )	93.8% ( 2.662 )	93.8% ( 1.609 )	93.6% ( 1.618 )	93.7% ( 1.623 )
				2	94.2% ( 1.877 )	94.5% ( 1.881 )	94.4% ( 1.887 )	94.2% ( 1.143 )	94.2% ( 1.147 )	94.4% ( 1.152 )
			200	1	94.5% ( 1.879 )	94.4% ( 1.885 )	94.2% ( 1.888 )	94.6% ( 1.142 )	94.1% ( 1.146 )	94.4% ( 1.154 )
		1.50	100	1	94.0% ( 2.703 )	93.8% ( 2.714 )	93.4% ( 2.731 )	94.3% ( 1.670 )	94.4% ( 1.679 )	93.8% ( 1.695 )
				2	94.4% ( 1.918 )	94.0% ( 1.927 )	94.2% ( 1.937 )	94.9% ( 1.186 )	94.6% ( 1.193 )	94.2% ( 1.204 )
			200	1	94.5% ( 1.919 )	94.4% ( 1.929 )	94.6% ( 1.938 )	94.8% ( 1.183 )	94.5% ( 1.193 )	94.2% ( 1.204 )

Table 2 shows the average sample sizes estimated to achieve the length of the 95% confidence interval which is equal to the average length of the 95% confidence interval shown in the corresponding cells of Table 1 for S₀=S_t=200, t=1. The sample sizes were estimated using expression (16) with the ideal bootstrap variance computed from the simulated datasets of size S₀=S_t=100, t=1. The results demonstrate that for the considered parameters the proposed procedure can be successfully used in combination with the standard approach to sample size estimation.

Table 2.

Average sample size predicted as necessary to achieve a targeted length of the asymptotic 95% confidence interval

			φ
			0.06			0.1
			Aρ|π			Aρ|π
TPFπ	FPRπ1	FPRπ0	0.7	0.8	0.9	0.7	0.8	0.9
0.4	0.5	0.5	200	200	199	199	199	200
		1.5	199	200	200	200	200	199
0.6	0.5	0.5	199	200	200	200	200	199
		1.5	200		200	200	200	200
0.8	0.5	0.5	200	199	200	200	201	199
		1.5	200	200	200	201	200	200

5. Example

The data represent the output of a radiologist’s readings of 200 mammographic breast examinations, 100 of whom depicted a single mass (t=1, S_t=100, S₀+S_t=200). These 100 actually positive and 100 actually negative subjects were selected at random from a larger dataset. In the original study the examinations were presented as a two view film mammogram with prior examinations available for comparison. All readings were done during a series of sessions (approximately 50 cases per session) in a clinically simulated environment (e.g. display, lighting in the reading room, workflow on a film alternator etc.) and the free-response rating paradigm was used. The radiologists had to identify all suspicious regions, mark the location of each one and rate the suspected abnormality as to the perceived “probability that it is actually present”. All data entries were computerized and the order of cases displayed was randomized for the dataset as a whole and within each session. The dataset was verified through an extensive protocol that used all source documents (e.g. pathology reports, follow up studies) and a series of independent reviews by multiple experienced radiologists. All negative examinations were verified by at least one follow-up negative mammogram and a minimum of two years of negative findings.

As a result of the evaluation there were a total of 204 False Positive marks on the examinations (53 on exams “with” and 151 on exams “without” a mass) resulting in an estimated FPR_π of 1.02 (0.53 and 1.51 for subjects with and without a mass respectively). On examinations with a mass there were 61 True Positive marks resulting in an estimated TPF_π of 0.61. The nonparametric estimator of the area under the ROC curve of ratings for TP and FP marks A_ρ|π (7) was 0.800. Using expression (9) and based on the dimensional size of the images, the size of the acceptance target and the number of abnormalities per subject, we computed φ to be approximately 0.06. The corresponding empirical, augmented and guessing FROC curves are shown in Figure 1. Λ is equivalent to the shaded region between the two curves. Similar computations are illustrated in Web Appendix C.

For φ=0.06 the estimate of Λ computed according to (8) is 9.64. This combination of φ and Λ allows us to interpret the average free-response performance of a radiologist as corresponding to 58% (9.64*0.06≈0.58) of the improvement achievable by a “perfect” over the “guessing” system. Using the algorithm for computing the ideal bootstrap variance of Λ described in Appendix we found the ideal variance to be 0.7161 resulting in the asymptotic 95% confidence interval for Λ of (7.99,11.30) with a length of 3.317, and the 95% confidence interval of (0.48,0.68) for Λ*φ.

We also estimated the sample size needed to achieve the targeted length of the 95% confidence interval. As a targeted length we chose 2.364, which is taken from the cell of Table 1 corresponding to the scenario where the simulation parameters are close to the ones estimated in this example, and sample size is S₀=S₁=200. The computed estimate of the sample size was 197.

The statistics computed from the data in this example closely agree with the simulation results presented in the previous section. For the simulated scenario with the parameters close to the estimates from the example the average length of the 95% confidence interval was 3.336 compared to 3.317 from the example; and the sample size estimated from the data in the example was 197 compared to targeted 200.

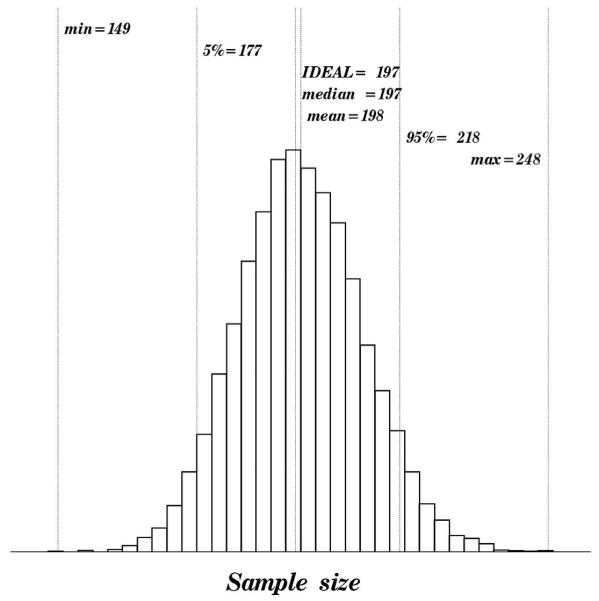
To quantitatively illustrate the gain in precision achieved by using an ideal instead of Monte Carlo (MC) bootstrap variance estimator we generated multiple realizations of the latter. Figure 2 demonstrates the distribution of the 10,000 estimates of the sample size needed to achieve length of the 95% confidence interval of 2.364 (each estimate was based on the MC bootstrap variance computed from 500 bootstrap samples). This figure demonstrates that with 500 bootstrap samples the MC approximation leads to the estimated sample size in a range from 149 to 248 and is not unlikely to produce estimated sample sizes between 177 and 218.

Figure 2. Distribution of the sample size estimated using the Monte Carlo bootstrap variance obtained by resampling of the data from the example.

The histogram is based on 10,000 estimates of the sample size. For each of the 10,000 replications the dataset from Section 5 was bootstrapped (re-sampled with replacement) 500 times, and for each of the 500 bootstrap samples the estimate of Λ was computed. The sample variance of 500 Λ’s (Monte Carlo bootstrap variance) was used to estimate the sample size (eq. 16) required to achieve the length of the 95% confidence interval of 2.364 (the length in the framed cell of Table 1).

The “IDEAL” estimate of the required sample size is obtained using the ideal bootstrap variance (Web Appendix B)

6. Discussion

In this paper we focused on a diagnostic task which requires detection and localization of possibly multiple abnormalities within a subject. We considered the evaluation of the diagnostic system under the FROC paradigm which enables gathering information on the total number of marks in addition to the proportion of “positive” marks at various decision thresholds. For the system evaluated under the FROC paradigm we have proposed a new summary index of the overall FROC-type performance of a diagnostic system. The advantages of the proposed index include: use of all decision thresholds simultaneously, a partial adjustment for the effect of the acceptance radius, relatively simple closed-form estimation, tractability of a simple nonparametric procedure for statistical inferences, use of all available data, and availability of a simple to visualize interpretation. The index can be interpreted as a measure of overall superiority over a “guessing” FROC process. It is analogous to the area between the empirical ROC and the diagonal “guessing” line, and as an index of performance it shares many advantages and limitations of the area under the empirical ROC curve. SAS code for the implementation of the proposed procedure is available from the authors.

The guessing free-response process and its FROC curve were introduced here to supplement the proposed index with a simple graphical interpretation. The guessing FROC curve (analogous of the diagonal ROC) represents the performance of an artificial guessing free-response process. The purpose of this process is not to model the performance of a diagnostic system but rather to provide a reference process for interpretation. We define an artificial guessing process on the entire image, rather than on a smaller “anatomical” area, and thus construct a more conservative, hence more universal, lower performance bound. Finally, analogous to the use of a guessing ROC process in the construction of an empirical ROC curve, we used the proposed guessing FROC process to extend the empirical FROC curve to the trivial point where there are no “negative” findings.

The proposed index Λ and guessing FROC process are related through the parameter φ which is a function of the acceptance radius (proximity criterion) and the density of abnormalities in the sample. Fundamental to the conventional FROC paradigm is that any index of performance estimated from FROC data depends upon the acceptance radius in combination with the density of the abnormalities in the sample. Because of this it is important to account for these parameters which are often selected at the design stage of a retrospective study. If one controls for these, φ is controlled automatically, otherwise φ accounts, at least partially, for the effect of differing design parameters on the estimated performance.

For the developed nonparametric estimator of the proposed index we derived the closed-form expression for the ideal bootstrap estimator of the variance (Efron, Tibshirani, 1993). This can be used to perform asymptotic bootstrap inferences avoiding the need for resampling and thereby eliminating Monte Carlo error. Other approaches to resampling-free variance estimation are also possible, for example an unbiased variance estimator may be also derived by extending the approach of Gallas (2006). The adopted nonparametric bootstrap approach also enables a statistical analysis which is free from strict structural or any parametric assumptions required by the existing parametric approaches. Specifically, the use of a subject as a bootstrap sampling unit allows one to ignore a specific correlation structure between the numbers of different types of marks and ratings within the same subject for the purpose of variance estimation.

In general, FROC data can be viewed as clustered ROC data with random and informative cluster size. The important difference between FROC analysis and conventional analyses of clustered ROC data is the use of the size of the clusters as an important characteristic of the diagnostic system (as opposed to a nuisance quantity). As shown in (7), FAUC is related to the area under the empirical ROC curve (AUC) for the clustered ratings of TP and FP marks. Several different approaches have been proposed for estimating the variance of the AUC for clustered data under different assumptions regarding the size of the clusters (Obuchowski, 1997; Rosner and Grove, 1999; Rutter, 2000) The ideal bootstrap covariances presented in Web Appendix A can be used to form an ideal bootstrap variance of the numerator of the AUC for clustered data in the presence of random cluster sizes.

APPENDIX

We briefly outline the idea of deriving the ideal bootstrap variance Λ. The key to the derivation is to decompose the index into a linear combination of simple quantities that are then grouped into ensembles of identically distributed random variables under the considered bootstrap scheme. The first component of Λ is the area under the empirical FROC curve (FAUC) that we previously presented as a sum of the random variables {W_s̃s} in (6). Depending on the type of subjects indexed by s̃ and s (i.e. actually positive, actually negative, same or different) {W_s̃s} can be partitioned into three sets of identically distributed variables, namely:

$$W_{\tilde{s}s}≔\{\begin{array}{cc}{\xi }_{jl}j=\tilde{s},l=s\hfill & \text{if}\tilde{s}>S_0\text{and}s\ne \tilde{s}-S_0\hfill \\ {\nu }_{jj}j=s\hfill & \text{if}s=\tilde{s}-S_0\hfill \\ {\eta }_{ij}i=\tilde{s},j=s\hfill & \text{if}\tilde{s}\le S_0\hfill \end{array}\phantom{\}}$$ (A1)

In the general case we denote the set of all types of actually positive subjects, i.e. all different values of t, in the dataset as T. In cases with more than one strata of actually positive subjects, i.e. |T|>1 (e.g. T={1,3}), each of the above variables will produce |T| sets ${\xi }_{jl}^t$,${\nu }_{jj}^t$ and ${\eta }_{ij}^t$, and there will appear another set of variables, $u_{jj‘}^{tt‘}$, corresponding to the comparisons between different strata of actually positive subjects, resulting in a total number of |T|² + 2 |T| i.i.d. sets. The general formula for the FAUC can then be written as follows:

$${\widehat{A}}_{\rho °\pi }=\frac{1}{\left(\sum _{t\in T}t{S}_t\right)\times \left(S_0+\sum _{t\in T}{S}_t\right)}\left\{\sum _{t\in T}\left(\sum _{j=1}^{S_t}\sum _{\begin{array}{c}\hfill l=1\hfill \\ \hfill l\ne j\hfill \end{array}}^{S_t}{\xi }_{jl}^t+\sum _{j=1}^{S_t}{\nu }_{jj}^t+\sum _{i=1}^{S_0}\sum _{j=1}^{S_t}{\eta }_{ij}^t\right)+\sum _{\begin{array}{c}t,t‘\in T\hfill \\ t\ne t‘\hfill \end{array}}\left(\sum _{j=1}^{S_t}\sum _{j‘=1}^{S_{t‘}}{u}_{jj‘}^{tt‘}\right)\right\}$$ (A2)

The variance of the index is the sum of the variances and covariances of all pairs of summations of the individual i.i.d. sets. These can be found by considering each pair of sets independently.

The formulae for the TPF_π and FPR_π can be derived from (5) in a similar manner. The variance of Λ is the sum of pairwise covariances between TPF_π, FPR_π and A_ρ°π. A detailed derivation of the ideal variance for the case of two strata (τ=0,1) is provided in Web Appendix A for FAUC and in Web Appendix B for Λ.