Membrane-Bending Mechanism of Amphiphysin N-BAR Domains

Abstract

BAR domains are highly conserved protein domains participating in a diversity of cellular processes that involve membrane remodeling. The mechanisms underlying such remodeling are debated. For the relatively well-studied case of amphiphysin N-BAR domain, one suggested mechanism involves scaffolding, i.e., binding of a negatively charged membrane to the protein's positively charged curved surface. An alternative mechanism suggests that insertion of the protein's N-terminal amphipathic segments (N-helices H0) into the membrane leads to bending. Here, we address the issue through all-atom and coarse-grained simulations of multiple amphiphysin N-BAR domains and their components interacting with a membrane. We observe that complete N-BAR domains and BAR domains without H0s bend the membrane, but H0s alone do not, which suggests that scaffolding, rather than helix insertion, plays a key role in membrane sculpting by amphiphysin N-BAR domains.

Introduction

Biological membranes are present in all cells and involved in virtually all functions of life—e.g., metabolism, signaling, cell division, fusion, and motility. Cellular membranes exist in many shapes that are persistent and dynamic, being in many cases sculpted actively by certain proteins (1–8). Such membrane sculpting occurs at the nanoscale, including components that are partly disordered (lipids in the membrane and some parts of the participating proteins), and involves many types of molecules with a wide range in density and arrangement, all of which makes studying membrane sculpting difficult. Nevertheless, impressive success has been achieved recently in characterizing membrane sculpting in cells, thanks to breakthroughs in experimental (3,5,9–15), theoretical (16,17), and computational (18–21) approaches.

Among membrane-sculpting proteins, the superfamily of BAR domains (22), which affect membrane bending from the cytosol, is remarkable, as these proteins exist in many organisms ranging from yeast to humans, are ubiquitous in various tissues, and participate in a large variety of cellular processes involving membrane remodeling, e.g., endocytosis, vesicle fusion, apoptosis, and cell-cell fusion. The amphiphysin N-BAR domain is particularly well studied (9,10,17–19,21,23–25), known to be involved in membrane remodeling in vivo, and can form high-curvature tubes (with radii R = 20–50 nm) and vesicles from low-curvature liposomes in vitro, but even for this protein the mechanism of membrane sculpting remains debated. The structure of the amphiphysin N-BAR domain (10) features bundles of α-helices capable of forming a dimer (Fig. 1 a), which possesses a concave surface with a high density of positively charged residues. At the N-terminus of each monomer one finds a ∼25-residue segment, unresolved in the crystal structure, that is predicted to form an amphipathic helix when interacting with the membrane, called N-helix or H0. The N-helix gives the N-BAR domain its name, to distinguish it from BAR domains lacking H0 either naturally or due to engineering of the protein sequence. One proposed mechanism for membrane sculpting by N-BAR domains involves scaffolding of the negatively charged membrane by the positively charged and concave surface of the protein. Another suggestion postulates, in the framework of the helix insertion mechanism, that H0 segments insert into one leaflet of the membrane, acting as wedges that increase the area of the leaflet, which leads to membrane bending. Both mechanisms probably take place in cases of various proteins (16), but to clarify the function of a representative and well-studied protein such as amphiphysin N-BAR domain, it is necessary to elucidate the actual mechanism in detail. Clarification of the mechanism employed by the amphiphysin N-BAR domain goes beyond just one important protein, since it will serve as a first step to deciphering mechanisms of membrane bending by other proteins at the molecular level.

Figure 1.

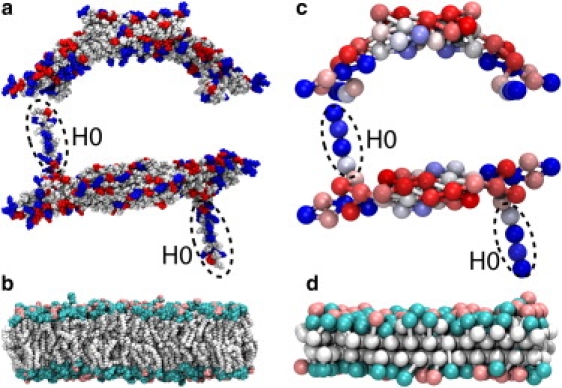
Amphiphysin N-BAR domain and lipid membrane. (a) The all-atom structure of the N-BAR domain, with charged residues highlighted in positive (blue) and negative (red). (b) The membrane composed of 70% DOPC (cyan) and 30% DOPS (pink) lipids. The SBCG models (c) of the N-BAR domains and (d) of the membrane; the SBCG beads of the N-BAR domains are colored according to their charge, on a linear scale from red at −2|e| to blue at 2|e|. The N-BAR domains in panels a and c are depicted as viewed from the side and from the top. The N-terminal segments H0 are highlighted by dashed ovals.

The scaffolding mechanism has been seen at work in simulations for N-BAR domains (18,19,21,23) and in experiments for another type of BAR domain, called F-BAR (14). The helix insertion mechanism, on the other hand, appears to be at work for many membrane sculpting proteins (16,26–28), but has not been confirmed yet for amphiphysin N-BAR, although it was suggested based on a mathematical model (17) that this mechanism alone should be sufficient to produce the experimentally observed membrane tubes with radii R = 20–50 nm. However, experiments (24,25) and simulations (25) of the H0 helix of amphiphysin N-BAR domain suggested that H0 should be rather flexible and partly disordered, making helix insertion difficult.

We had previously performed molecular dynamics simulations at both atomic and coarse-grained (CG) levels, the latter being of the shape-based type (29), to study membrane bending by Drosophila melanogaster amphiphysin N-BAR domains (19,21). The simulations (19,21) showed that individual N-BAR domains can bend a membrane locally (18,23), and, when arranged in specific formations or lattices on the membrane surface, can induce global membrane curvature with radii depending on the lattice type, e.g., lattice density. The action of N-BAR domains was found to depend critically on scaffolding (21). A similar action, but with different characteristic lattices, was observed experimentally for membrane tubes sculpted by F-BAR domains (14) via high-resolution cryo-electron microscopy reconstruction.

To distinguish the role of the crescent-shaped BAR domain and of the H0 segment in the action of the amphiphysin N-BAR domain, we extended the simulations reported in Yin et al. (21) to systems with only the H0 segments or only BAR domains without H0s. All-atom simulations were performed for a 2,300,000 atom system involving eight N-BAR domains (or their components) and covering 0.5 μs. Analogous shape-based coarse-grained (SBCG) simulations sampled a large ensemble of trajectories, each reaching 30 μs (accumulated time reaching 0.6 ms). We find that complete N-BAR domains and BAR domains lacking H0s maintain a prebent membrane, whereas H0s alone do not.

Methods

We performed both all-atom and SBCG simulations (29,30) using the program NAMD (31). Preparation and parameterization of the SBCG model was done with VMD (32), namely, the CGTools plugin.

In earlier studies of membrane bending by N-BAR domains (19,21), the SBCG model had been described and tested. Extensive simulations (19,21), including a 0.3-μs all-atom simulation of a 2,300,000 atom system that is being extended in this study, showed that the SBCG model is capable of describing overall features of membrane bending by N-BAR domains, as results of SBCG simulations agree well with those of the all-atom simulation and with information available from experiment.

All-atom simulations

The 0.3-μs all-atom simulation of eight N-BAR domains on a patch of DOPC/DOPS membrane (simulation “NBAR-init” in Table 1) had been reported in Yin et al. (21). The membrane patch is composed of 30% DOPS and 70% DOPC (Fig. 1 b), the preparation of which had been described earlier (19,21). The solvent was composed of TIP3P water (33), and Na⁺ ions were used to neutralize the net charge. The N-terminal segment, H0, defined here as residues 1–25 of Drosophila amphiphysin N-BAR domain, is modeled as a short helix and a flexible link (see Fig. 1) using the MOLEFACTURE plugin of VMD (32), based on the structure suggested in Gallop et al. (34). H0s were initially partially buried between lipid headgroups, so that their centerlines were at the level of lipid phosphates, and oriented perpendicular to the BAR domain main body. The position of H0s in the lipids was determined as described in Yin et al. (21) using steered molecular dynamics (35,36) to push the helices toward the level of phosphates and by equilibrating the resulting system.

Table 1.

Simulations performed

Name	Method	Nrun	Nparticle	Time (μs)	Result
NBAR-init	All-atom	1	2,304,973	0.3	Membrane bends (21)
noH0	All-atom	1	2,298,013	0.1	Bent membrane persists
H0	All-atom	1	2,273,949	0.1	Membrane flattens
CG-NBAR-init	SBCG	5	1883	5	Membrane bends (21)
CG-NBAR	SBCG	5	1883	30	Membrane bends
CG-noH0	SBCG	5	1845	30	Membrane bends
CG-H0	SBCG	5	1529	30	Membrane flattens
CG-mem	SBCG	5	1491	30	Membrane flattens

N_run is the number of independent simulation runs, N_particle is the total number of particles in each simulation (atoms in all-atom simulations or CG beads in SBCG simulations); “Time” is the simulated time for a single simulation in the series. Simulations NBAR-init and CG-NBAR-init have eight complete N-BAR domain dimers (“init” refers to “initial”; these simulations have been reported in (21)). Other simulations start from the conformations obtained at time t = 300 ns in NBAR-init and t = 80 ns in CG-NBAR-init.

A helical structure of the N-terminal segment was also suggested for human amphiphysin II N-BAR domain based on nuclear magnetic resonance studies (25). The first 25 amino acids of the two N-terminal segments exhibit 40% sequence identity and 52% similarity. The human H0 in Löw et al. (25) was found to maintain on average 76% helicity for the residues 1–33 studied, mainly due to the unfolding of residues 1–8. In our case, residues 1–25 of Drosophila H0 are initially modeled as mostly a helix, but the helical structure is partially lost during the simulations, with ∼80–90% helicity remaining. The loss of helicity occurs mainly at the termini of H0. The Drosophila H0 studied here and human H0 studied in Löw et al. (25) embed into the membrane in a similar fashion; the hydrophobic face of the amphipathic helix, whose edge is formed by residues Ala¹⁰, Val¹³, Ala¹⁷, Ala²⁰, and Ile²⁴ for Drosophila H0 and by residues Ala¹⁵, Val¹⁸, Val²², Ala²⁵, and Val²⁹ for human H0, is facing the hydrophobic interior of the membrane.

The system with eight N-BAR domains in simulation NBAR-init contains 2,304,973 atoms in a periodic cell of dimension 80 × 8 × 36 nm³. For this study, we branched the all-atom simulation, NBAR-init, after 0.3 μs. In one branch, the H0 helices were removed (simulation noH0 in Table 1); in the other branch, BAR domain main bodies were removed (simulation H0 in Table 1). Systems noH0 and H0 contain 2,298,013 atoms and 2,273,949 atoms, respectively, both of which inherit the periodic cell of dimension 75 × 8 × 37 nm³ from simulation NBAR-init after 0.3 μs. For both systems, water molecules were added to fill in the space emptied by the deletion of corresponding protein sections. Because of the newly added water molecules, the systems were equilibrated for 2 ns with heavy atoms of proteins and lipids being harmonically constrained (the constraints' spring constant was 1 kcal/(mol Ų)).

For the all-atom simulations, the CHARMM (37,38) force field was used, and periodic boundary conditions were assumed. Solution padding (∼8 nm long) was added on both sides of the long axis of the membrane to permit membrane bending (see Fig. 2 a). Simulations were carried out assuming an NpT ensemble (temperature 310 K and pressure 1 atm). A Langevin thermostat with a damping coefficient of 0.5 ps⁻¹ maintained temperature; pressure was maintained via a Langevin-piston barostat with a piston period and damping time of 2 ps each. Short-range nonbonded interactions were cut off smoothly between 10 and 12 Å. The PME algorithm was used to compute long-range electrostatic interactions. The implementation of these algorithms in NAMD is described in Phillips et al. (31). All-atom simulations were performed with an integration time step of 2 fs.

Figure 2.

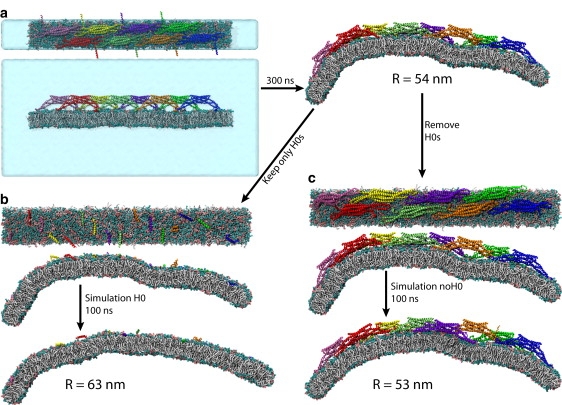
All-atom simulations of membrane bending by whole N-BAR domains and by their components. (a) Simulation NBAR-init (originally reported in (21)), (b) simulation H0, and (c) simulation noH0. The simulations are defined in Table 1. For each simulation, top and side views of the initial conformation, and the side view of the final conformation, are shown. In panel a, images of the initial conformation also include the water box, which is not shown in the remaining images.

Shape-based coarse-grained (SBCG) simulations

The SBCG model of N-BAR domains and membrane is described in detail in the literature (19,21); exactly the same model is used here. Briefly, a protein is represented by a number of CG beads arranged according to the protein's shape by a topology-conserving algorithm (39), with the number of beads specified by the user. In the case of N-BAR domains, 50 CG beads are used for each N-BAR domain dimer, corresponding to ∼150 atoms per CG bead (Fig. 1 c). Each H0 helix is represented by five beads. The CG beads are connected by harmonic bonds to maintain the protein shape. Each CG bead inherits the total mass and charge of the corresponding all-atom protein section that is represented by the CG bead. Interactions between beads are described by a CHARMM-like force field (37), i.e., bonded interactions are represented by harmonic bond and angle potentials, and the nonbonded potentials include 6-12 Lennard-Jones (LJ) and Coulomb terms. The choice of parameters for bonded and LJ interactions had been described earlier (19); the parameters are tuned to match the flexibility of the protein as observed in respective all-atom simulations, and to reproduce the hydrophobic/hydrophilic properties of the residues on the protein surface.

For the membrane, each leaflet of the bilayer is represented by two layers of CG beads, one for the lipid heads and one for the tails, a head-tail bead pair representing ∼2.2 all-atom lipid molecules (Fig. 1 d). The LJ and bond parameters for lipid beads are chosen, in general, to reproduce the area per lipid, bilayer thickness, and hydrophobic/hydrophilic properties (19). DOPC and DOPS in the SBCG model differ only in the charge and mass of their head beads (zero charge for DOPC and −2.2|e| for DOPS; mass of 864.75 amu for DOPC and 866.76 amu for DOPS). All tail beads have zero charge and a mass of 864.75 amu. To match the membrane charge, we introduced “ions,” each with a charge of ±2.2|e| and mass of 1000 amu, roughly corresponding to eight ions of mixed nature (such as both Na⁺ and Cl⁻) with their hydration shells.

Because electrostatic interactions play a key role in membrane bending by N-BAR domains, one wonders how well these interactions are reproduced by the SBCG model, and what salt conditions the model describes. The treatment of electrostatics in the SBCG model is rather simple: CG beads carrying charge interact via a Coulomb interaction with a uniform dielectric constant ɛ, whose value has been originally tuned to reproduce results of all-atom simulations (19) of one N-BAR domain (the appropriate value happens to be ɛ = 1; see discussion in (19,21)). Therefore, the model is appropriate for the conditions used in those all-atom simulations, such as the salt (NaCl) concentration of 80–150 mM (i.e., physiological concentration). The SBCG model does not represent all details of real charge screening, but here and in Yin et al. (21) we find that the SBCG model reproduces results of all-atom simulations of not only a single N-BAR domain, but also of multiple N-BAR domains (the latter without additional tuning). On the other hand, all details of charge screening (except atomic polarizability) are accounted for in the all-atom simulations reported here, which provide the ultimate test for the SBCG model.

The motion of CG beads is described by classical mechanics, assuming, however, Langevin equations of motion. The solvent is modeled implicitly, through Langevin terms (fluctuating and frictional forces) representing water viscosity. The damping constant for the Langevin equation is chosen to be γ = 2 ps⁻¹ for all beads (19) based on experimental diffusion constant values. A 35 Å cutoff was assumed for the nonbonded interactions. Periodic boundary conditions were used; the membrane was discontinuous in the longer dimension, as in the present all-atom simulations (see Fig. 2 a). Periodic boxes for all SBCG simulations were 75 × 8 × 50 nm³. The simulations were performed assuming constant volume and temperature, the latter being maintained at 310 K using a Langevin thermostat (31). The membrane was a randomized mixture of neutral and negative lipids, with 30% of negative lipids, as in all-atom simulations. N-BAR domains were placed on the flat membranes, the tips and N-helices of the proteins being at the level of the head beads of the membrane, which again (see all-atom simulations) corresponds to embedding the N-helices at the level of the lipid phosphate groups.

Visualization and analysis of simulations

Visualization and analysis were carried out with VMD (32). To determine the membrane curvature, the profile of the membrane was projected onto the x, z-plane, where the x axis is parallel to the long dimension of the membrane patch at time t = 0 and the z axis is perpendicular to this plane. The curvature was then computed as described in Yin et al. (21).

Results and Discussion

Simulations performed are listed in Table 1 and illustrated in Figs. 2 and 3. The new all-atom simulations, noH0 and H0, started from the all-atom simulation of one N-BAR lattice (NBAR-init), that involved eight N-BAR domains on a 64 × 8 nm² membrane patch and had been reported in Yin et al. (21); in NBAR-init the membrane bends within 300 ns from the flat conformation to a curved one with R = 54 nm (Fig. 2 a). SBCG simulations of the same system (CG-NBAR-init) showed (21) that over several microseconds the membrane bending for this lattice comes to a halt at R = 16 ± 4 nm. To investigate the role of H0s and BAR domains without H0s in membrane bending, we employed the final conformation from simulation NBAR-init, and modified the system by removing all H0 segments in one case (noH0) and by removing the rest of the protein and keeping only H0s on the membrane in the other case (H0). An analogous procedure was adopted for the SBCG simulations (CG-noH0 and CG-H0). As it was observed in Yin et al. (21) that in SBCG simulations of the studied lattice the curvature develops 3–4 times faster than in the all-atom simulation, the conformation for starting further simulations selected was the one reached at t = 80 ns, with R = 55 nm (Fig. 3 a). H0 segments were removed at the start of simulations CG-noH0, and the rest of the protein was removed while H0s were kept at the start of simulations CG-H0. We also investigated systems with complete N-BAR domains (CG-NBAR) and with all protein removed (CG-mem). For every SBCG system, five simulations of 30 μs duration were carried out.

Figure 3.

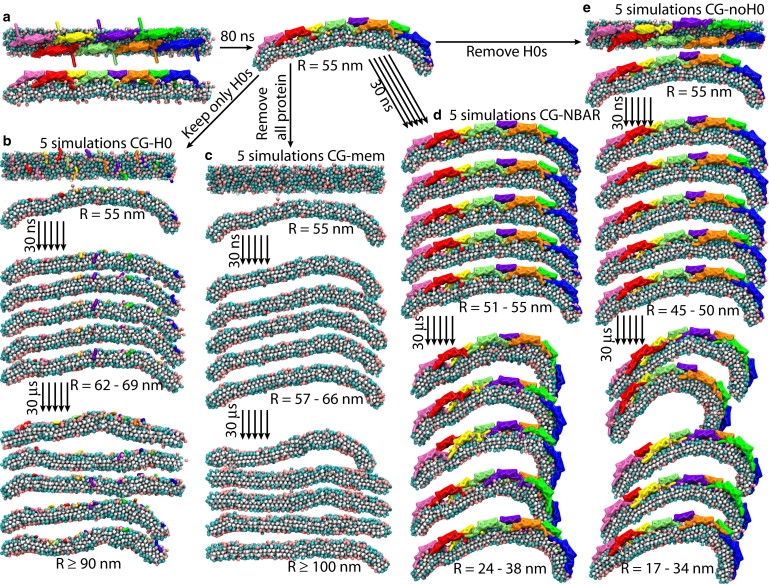
SBCG simulations of membrane bending by N-BAR domains and their components. (a) Simulation CG-NBAR-init. The conformation from this simulation at t = 80 ns is chosen as a starting point for other SBCG simulations, namely, (b) CG-H0, (c) CG-mem, (d) CG-NBAR, and (e) CG-noH0. See Table 1 for details. In each case, five SBCG simulations were performed, and the snapshots from each are shown at t = 30 ns (corresponding to ∼100 ns for all-atom simulation, see Fig. 2, b and c) and at t = 30 μs. Initial conformations for each simulation are shown from the top and from the side.

According to the theoretical work of Campelo et al. (17), H0s alone should induce a membrane curvature in the experimentally observed range, with R = 20–50 nm (10). Such curvature is expected (17) when the fraction of the membrane area covered by H0s is 7–10% (9–15% for a slightly different membrane model), and for a range of depths to which H0s are embedded into the membrane, including the depth used in our simulations where center lines of H0s are at the level of lipid phosphates. In Campelo et al. (17), the area of H0 in contact with the membrane is estimated to be 6 nm² and its width to be 1 nm; our measurement gives an H0 length of 4 nm and a width of 1.3 nm. Therefore, the area of H0 is 4–6 nm². In our simulations H0 and CG-H0, 16 H0s are placed on the membrane area of 512 nm², resulting in the occupied membrane area fraction of 12.5–18.8%, depending on the estimate for the actual H0 area. Thus, the occupied area fraction in our study is the same (or larger) as the one suggested in Campelo et al. (17) to induce membrane bending efficiently; the larger fraction for a given H0 embedding depth should lead to even higher membrane curvature according to the model of Campelo et al.

Results of all-atom simulations are shown in Figs. 2 and 4. The complete N-BAR domains are seen to bend the membrane steadily. BAR domains lacking H0s proceed to bend the membrane a little beyond R = 54 nm, which is the starting value. Since the determination of R is precise only within a few nanometers, it is not clear that the membrane continues to bend in this case, but BAR domains without H0s clearly maintain the membrane curvature at around the same value throughout the 100-ns simulation. H0s alone, on the other hand, fail to maintain this curvature. In simulation H0, the membrane flattens out significantly (Fig. 2 b), as the radius of membrane curvature experiences an increase by 10 nm within 100 ns (Fig. 4 b).

Figure 4.

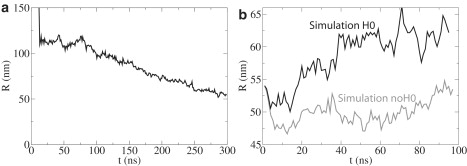
Radius of membrane curvature, R, versus time, t, from all-atom simulations. (a) R for simulation NBAR-init (see Fig. 2a). (b) R values for simulations H0 and noH0 (see Fig. 2, b and c).

In SBCG simulations (Table 1 and Figs. 3 and 5), the curved membrane is seen to be bent further by N-BAR domains and by BAR domains without H0s, reaching R = 17–40 nm at 30 μs, which agrees with experimental observations (10) and previous SBCG simulations (21). In the case of simulations of H0s only as well as of the membrane without any protein, the membrane relaxes to a flat conformation. In some cases, local ripples persist on the membrane within tens of μs, whereas in other cases the membrane curvature even changes its sign locally (Fig. 3 b), but on average it becomes flat. For almost flat membranes, an unambiguous determination of R becomes difficult. As the membrane length is 64 nm, once R is determined to be >100 nm, any circle with a radius larger than hundreds of nm can fit the membrane profile equally well. Therefore, the membrane can be considered simply flat for R > 100 nm and 100 nm is set as an upper limit in Fig. 5, b and c. In all simulations CG-mem and CG-H0, the value of R reaches ∼100 nm or more. Thus, all-atom and SBCG simulation results agree with regard to the ability of BAR domains or H0s to bend or not bend the membrane.

Figure 5.

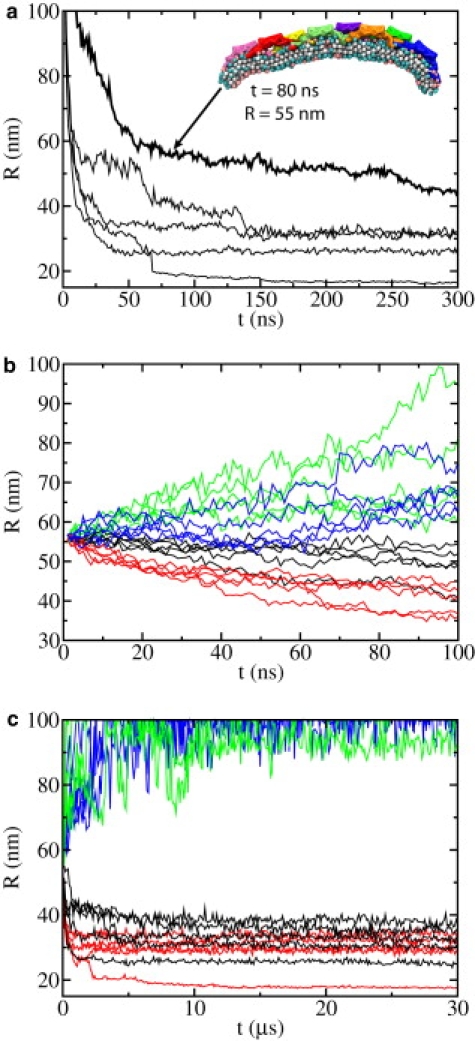
Radius of membrane curvature, R, versus time, t, in SBCG simulations. (a) Results from five SBCG simulations CG-NBAR-init (see also Fig. 4a). The thicker line is from the simulation that is most similar to the respective all-atom simulation (Fig. 2a). The arrow shows the moment at which the conformation is taken for the start of subsequent simulations CG-NBAR, CG-noH0, CG-H0, and CG-mem (see Fig. 3a). (b) Results from simulations CG-NBAR (black), CG-noH0 (red), CG-H0 (blue), and CG-mem (green) presented for the first 100 ns (see also Fig. 3, b–e, and Fig. 4b). (c) Results for times up to 30 μs.

Comparison of Fig. 5, a and b, with Fig. 4 shows that all-atom simulations are ∼3–4 times slower than the SBCG simulations in bending the membrane, as noticed before (21). Indeed, R assumes values of 46–54 nm during the 100-ns simulation noH0 and values of 45–54 nm during the first 30 ns of CG-noH0, whereas values of 54–66 nm are observed in the course of the 100-ns simulation H0 and 54–69 nm during the first 30 ns of CG-H0. Among simulations CG-NBAR-init, one trajectory at ∼t = 80 ns resembles that from NBAR-init at t = 300 ns closely (Fig. 5 a), almost like a mirror image (see Figs. 2 a and 3 a): seven N-BAR domains in these simulations are in a close contact with the membrane, while the eighth (different in the two cases) is not, leading to a strong bending on one side and a relatively flat membrane on the other. Therefore, the conformation from this SBCG simulation at t = 80 ns is chosen as a starting point for simulations CG-NBAR, CG-noH0, CG-H0, and CG-mem, in analogy with the starting conformations of simulations noH0 and H0.

Velocities of all atoms or CG beads in simulations starting from the final conformations of NBAR-init or CG-NBAR-init are reinitialized, i.e., they are newly assigned according to the Maxwell distribution (T = 310 K), and as a result the system loses the momentum of membrane bending that was accumulated in the simulations NBAR-init and CG-NBAR-init. This effect might be the reason why simulation noH0 does not produce significant membrane curvature within 100 ns. Indeed, for simulations CG-NBAR, which contain exactly the same system as CG-NBAR-init with only the velocities being reassigned, the membrane does not bend very quickly within the first 30 ns (Fig. 5 b); over a longer time the effect of reassigning velocities is overcome by bending forces stemming from the BAR domains.

Membrane bending solely by insertion of H0s has been observed in a prior simulation (23), however, only in a case where the H0 concentration on the membrane surface was very high. The simulation consisted of a membrane ∼315 nm² in area, with 10 H0s. The fraction of membrane area occupied by H0s was then 13–19%, but in fact H0s were concentrated locally on the membrane, and the curvature with R ≈ 25 nm also developed only locally. The actual area of H0 concentration was ∼200 nm², corresponding to an occupied area fraction of 20–30%. The 12.5–18.8% area fraction assumed in our simulations is close to the maximum concentration that can be realistically accommodated for complete N-BAR domains in all-atom representation, due to close protein packing already achieved in this case (Fig. 2), i.e., the H0 density assumed in Blood et al. (23) is unrealistically high. Even if complete N-BAR domains are pressed together to reach such a density, which can be achieved in SBCG simulations, our earlier study (21) showed that the membrane bends little in that case. It was found that the membrane bending becomes weak because scaffolding of the membrane by BAR domains is inhibited by tips and H0s of neighboring N-BAR domains, which at high N-BAR concentrations occlude the interaction between the BAR domain crescent and the membrane. Therefore, even if high concentration of H0s may lead to membrane bending, in the real case when complete N-BAR domains are present, such concentrations will correspond to weak bending.

Our observation that N-BAR and BAR domains bend membranes, while H0s do not, emphasizes the important role of the scaffolding mechanism. For the helix insertion mechanism one usually assumes a constant penetration depth and alignment of helices (16), but we observe here that H0s are highly dynamic and relatively disordered (Fig. 6). Indeed, the initially helical conformation of H0s becomes coiled and disordered, and the alignment of H0s, originally perpendicular to the long dimension of the membrane, is seen to change dramatically due to the shape fluctuations and rotational and translational diffusion on the membrane surface (however, the penetration depth remains constant for most of H0s throughout the simulations). The dynamic behavior of H0s described is found to be the same in the case when H0s are simulated alone or attached to BAR domains (Fig. 6). This dynamic nature of H0s has been characterized also in experiment (25) and noticed in previous simulations (21,23,25). Furthermore, the orientation of H0 with respect to the N-BAR domain main body is not known unambiguously, since the H0s were not resolved in the crystal structure (10). We modeled H0 as sticking out perpendicular to the main body of BAR domain (34), although other orientations have been proposed, such as one with H0 positioned under the BAR domain crescent or one with neighboring H0s forming antiparallel dimers (24). Nevertheless, even with possibly “incorrect” and highly fluctuating H0 orientation the membrane is bent successfully by N-BAR as well as BAR domains without H0s, but not by H0s alone.

Figure 6.

Dynamics of H0 segments in all-atom simulations. The arrangement of H0s at the beginning of simulation NBAR-init is shown at the top, the one by the end of simulation NBAR-init in the middle, and the one at the end of simulation H0 at the bottom. Only H0s are shown (e.g., BAR domains are present in simulation NBAR-init, but are not shown). Dimensions of the membrane are depicted schematically by a gray rectangle. All H0s are wrapped across the periodic cell boundaries, so that they all are viewed within the area of one periodic cell.

Thus, mobility and disorder may prevent H0s from bending the membrane efficiently. Additional studies should test the link between the disordered nature of H0s and their membrane-bending activity, for example, via simulations where the structure and orientation of H0s is constrained. At the time of this publication, one cannot state conclusively whether the disordered nature of H0s is the cause of their inability to bend the membrane in our simulations, as it is possible that even rigidly straight and perfectly aligned H0s would not bend the membrane either. It is clear from our simulations, though, that without constraints or other bias applied, H0s fail to bend the membrane, questioning the feasibility of the helix insertion mechanism in the case of amphiphysin N-BAR domain.

H0s may be involved in sensing membrane curvature, but this activity cannot be discerned from our simulations. A curvature-sensing function had been demonstrated for Ser/Thr-rich amphipathic helices (40), such as the ALPS motif of ArfGAP1, but given the low resemblance of H0 and the ALPS motif (8% sequence identity, 28% similarity, H0 contains only one Thr and one Ser whereas there are eight Ser and two Thr in ALPS), one may question a curvature sensing role of H0. However, the ALPS-like motifs, H0, and the membrane-embedding helices of ENTH form amphipathic helices, which may suggest a membrane-curvature sensing function for all.

Conclusion

Our study demonstrates the power of combining all-atom and coarse-grained simulations. SBCG simulations explore the long time behavior of membrane bending by N-BAR domains and permit sampling over several independent trajectories. All-atom simulations, on the other hand, are more accurate than SBCG simulations and furnish chemical detail. All-atom simulations performed here were carried out for a system of 2,300,000 atoms, with the overall simulated time reaching 0.5 μs. SBCG simulations were applied to the system of the same size (amounting to only 1000–2000 CG beads), and covered an accumulated time period of 0.6 ms.

Simulations show that N-BAR domains and BAR domains lacking H0s bend membranes efficiently, but H0s alone do not, suggesting that scaffolding is key for membrane bending by amphiphysin N-BAR domains. BAR domains without H0s bend the membrane after being prearranged in a lattice, and indeed our earlier study (21) showed that certain lattices are optimal for producing high membrane curvature, while H0s play a significant role in establishing connections between N-BAR domains within a lattice. Thus, an important biological function of H0 may be to increase the binding affinity of N-BAR domains to the membrane and to facilitate formation of optimal lattices, which may explain why BAR domains without H0s do not tubulate liposomes as efficiently as whole N-BAR domains do (25).

Our simulations address only one type of membrane (in regard to its composition and relative concentration of constituent lipids), cover times that are short in comparison with physiological timescales, and investigate only one N-BAR lattice. Furthermore, it is unclear how the observed effects will depend on the presence of different types of lipids (e.g., PIP2 instead of PS), or amphipathic helices from other proteins. Therefore, our results do not rule out the helix insertion mechanism altogether. Indeed, in numerous other proteins, such as Arf1 and ENTH domains, helices embedded into a membrane do appear to induce curvature (16,26–28); this may be the case also for endophilin N-BAR domain (34,41,42), which has four amphipathic helices per dimer versus two for amphiphysin. However, our study addresses the mechanism of membrane bending by amphiphysin N-BAR domains for realistic conditions and in a natural environment. Thus, even though for other conditions conclusions can be different, for the physiologically relevant conditions studied and for this specific protein, simulations reveal that the helix insertion mechanism plays a minor role in membrane bending.

Our results demonstrate the importance of detailed simulations in comparison with highly schematic theoretical models. Insertion of helices such as N-BAR domain's H0 was suggested on the grounds of theoretical analysis (17) to be sufficient to explain membrane bending by amphiphysin N-BAR domains, but our simulations, performed for the same conditions as in Campelo et al. (17), suggest that H0s cannot even maintain membrane curvature, and are unlikely to bend membranes. Our simulations and previous work (24,25) show that H0s do not exert a strong global bending force on the membrane, possibly because H0s are very dynamic and rather disordered (21,23,25).

Results obtained here are in line with a large body of recent simulations and experiments (10,14,18,19,21,23–25), and suggest that the scaffolding mechanism is much more powerful for bending membranes than the helix insertion mechanism, at least for the amphiphysin N-BAR domain. A possible scenario arising from this accumulated knowledge is that H0s help N-BAR domains to bind to the membrane and to arrange in a formation that is efficient for membrane bending. H0s may also be involved in sensing the existing curvature. The scaffolding mechanism, amplified by the appropriate arrangement of N-BAR domains, is then employed to sculpt membranes. How membrane sculpting by BAR domains actually works in cells is less clear, due to the multitude of additional factors acting in vivo. However, investigations of BAR domain activity in cells (9,10,14) do not contradict, but rather support, the idea that the scaffolding mechanism takes place in cells, too.