A Self-Consistent Description of the Conformational Behavior of Chemically Denatured Proteins from NMR and Small Angle Scattering

Abstract

Characterization of the conformational properties of unfolded proteins is essential for understanding the mechanisms of protein folding and misfolding. This information is also fundamental to determining the relationship between flexibility and function in the highly diverse families of intrinsically disordered proteins. Here we present a self-consistent model of conformational sampling of chemically denatured proteins in agreement with experimental data reporting on long-range distance distributions in unfolded proteins using small-angle x-ray scattering and nuclear magnetic resonance pulse-field gradient-based measurements. We find that standard statistical coil models, selected from folded protein databases with secondary structural elements removed, need to be refined to correct backbone dihedral angle sampling of denatured proteins, although they appear to be appropriate for intrinsically disordered proteins. For denatured proteins, pervasive increases in the sampling of more-extended regions of Ramachandran space {50°< ψ < 180°} throughout the peptide chain are found to be consistent with all experimental data. These observations are in agreement with previous conclusions derived from short-range nuclear magnetic resonance data from residual dipolar couplings, leading the way to a self-consistent description of denatured chains that is in agreement with short- and long-range data measured using both spectroscopic and scattering techniques.

Introduction

Despite the volume of structural information describing stable protein structures to high atomic resolution, the unfolded state occupies a conformational landscape that remains comparatively poorly understood. Development of an appropriate description of the conformational sampling of denatured proteins is essential for the study of protein folding, whereas the steadily increasing recognition of the biomedical relevance of natively unfolded proteins, for example in cancer-related signaling and neurodegenerative diseases (1–4), reinforce the need for relevant models of disordered molecular ensembles. Many intrinsically disordered proteins (IDPs) only adopt a stable conformation upon binding physiological partners (5–7), underlining the importance of understanding protein folding events occurring in the unfolded state.

Two models have been identified to explain the effects of chemical denaturants on folded proteins. The first invokes the different hydrogen-bonding properties of the denaturant relative to water in the vicinity of hydrophobic groups, such that it acts as a better solvent for hydrophobic groups that are normally buried in water-solvated proteins (8). An alternative model proposes that the denaturant binds directly to the protein backbone, presumably via hydrogen-bonding interaction with the amide groups, thereby destabilizing hydrogen-bonding networks that provide the origin of the stability of the native fold relative to the unfolded state (9). Both models stabilize the unfolded state in the presence of high concentrations of denaturant. The correct description of conformational sampling in the denatured state will surely provide crucial information on the molecular origins of chemical denaturation, thereby contributing to our understanding of protein folding and stability.

It has become clear over the last decade that rather than conforming to a simple random coil description, the conformational behavior of the unfolded protein can be extremely varied. The key question is not whether a protein is unfolded, rather how it is unfolded. To clarify these questions, conformational sampling in denatured proteins has been studied in detail using small-angle scattering (10,11), nuclear magnetic resonance (NMR) spectroscopy (12), and fluorescence correlation spectroscopy (13), as well as ensemble molecular simulation (14–19). Experimental and theoretical studies suggest that apparently diverse descriptions based on diverse experimental techniques probably derive from the sensitivity of the different approaches to local and long-range structure, underlining the strong complementarity of NMR and small-angle scattering techniques for the development of a self-consistent molecular description of the denatured state.

A popular approach used to analyze the conformational properties of disordered proteins is the use of explicit molecular descriptions of unfolded ensembles (17–22). To this end, explicit atomic-resolution ensemble models have been proposed on the basis of statistical coil sampling, extracted from backbone dihedral angles present in coil regions of protein databases. Amino-acid-specific behavior from these conformational distributions is then assumed to represent a Boltzmann distribution of dihedral angles in a statistical description of the unfolded polymer, such that an ensemble of conformers constructed on the basis of random sampling of these distributions can be considered to describe a representative ensemble. For these descriptions to yield useful information, they should be demonstrated to be accurate and relevant representations of the unfolded state. Ab initio and molecular dynamics simulations have indeed suggested that such approximations can be valid (23). In most cases, long-range interactions are reduced to a minimum, steric repulsion or excluded volume simplification, essentially to avoid chain overlap, with electrostatic and amino-acid-specific solvent effects ignored in the interest of efficiency. Nearest-neighbor effects can also be introduced to refine conformational behavior as a function of the nature of the neighboring amino acids.

One such approach, termed Flexible Meccano (FM; (24)), constructs conformational ensembles in this way. The algorithm uses a rudimentary spherical side-chain volume exclusion model, 20-amino-acid-specific conformational wells derived from coil regions of 500 high-resolution crystal structures, and additional conformational basins representing specific dihedral angle distributions such as pre-prolines, or prolines preceding prolines. The model has been validated against numerous types of experimental data: NMR residual dipolar couplings (RDCs) measured between covalently bound spins (24), reporting on orientational properties of internuclear vectors; NMR RDCs measured between protons (25), reporting on both distance and angular internuclear distribution functions; three-bond scalar couplings, reporting directly on backbone dihedral angles distributions (25); and small-angle scattering measurements, reporting on overall pairwise distribution functions and molecular dimensions (24). In addition, state-of-the-art molecular simulation technology, specifically the accelerated molecular dynamics approach (26,27) that allows for statistical sampling of the broad conformational subspace available to unfolded proteins, and critically, the reconstruction of Boltzmann-like sampling on an amino-acid-specific basis, reveals a very close reproduction of the conformational space described by the statistical coil database (28,29). These experimental and theoretical considerations allow us to propose that, although necessarily approximate, the FM approach provides a reasonable tool to allow the refinement of our understanding of the conformational properties of unfolded proteins in general and of denatured proteins in particular.

Partially aligned NMR spectroscopy has been shown to be a particularly powerful tool for studying molecular structure in both folded (30–32) and unfolded states (33–37). In recent years, we have used this parameter as a probe to derive an amino-acid-specific self-excluding model of the unfolded state. Explicit molecular ensemble analysis, using FM, successfully reproduced both spectroscopic and scattering data from protein X from Sendai virus, a protein that is natively partially unfolded (24), and RDCs from both apomyoglobin (34) and staphylococcal nuclease Δ131Δ (12) in high concentration of denaturant. This was subsequently used to identify conformational properties of several important IDPs involved in neurodegenerative diseases, the proteins τ (28) and α-synuclein (38), the tumor-suppressor p53 (29), and the unfolded C-terminal of the nucleoprotein of Sendai virus (39,40). Using the same conformational averaging approach, we have also recently developed further tools for refining the interpretation of small-angle x-ray scattering (SAXS) data from unfolded proteins in terms of average molecular dimensions (41) and the average surface accessibility of amino acids in unfolded proteins (42).

In a more recent study, up to seven RDCs per peptide unit could be determined for urea-unfolded ubiquitin, both between covalently bound and ¹H-¹H RDCs (25), allowing a detailed description of the angular and distance fluctuations of the unfolded state. The aim in this initial study was the calculation of complete conformational distributions of the unfolded or partially folded polypeptide chain that is in agreement with the available experimental data, resulting in the clear identification of enhanced sampling of two regions of Ramachandran space, in particular β-extended and polyproline II conformations. However, RDCs only report indirectly on the overall dimensions of the protein, thus a realistic description of the unfolded state should also reproduce experimental data reporting more directly on the overall dimensions of the protein. In this study, we demonstrate that this refined coil description provides a consistent description of the conformational behavior of chemically denatured proteins that is compatible with measurement of NMR RDCs, pulsed-field gradient (PFG) hydrodynamic measurements, and SAXS data.

Methods

The conformations used in this study to calculate the properties of the denatured state were built with Flexible Meccano (FM). To define the amino-acid-specific Ramachandran space, FM uses ϕ/ψ dihedral angles collected from 500 high-resolution (<1.8 Å) x-ray structures (43) where residues belonging to secondary structure elements were removed; this is the so-called standard (coil) library. Side chains for these conformations were added with the program SCCOMP (44).

SAXS properties of the different polypeptide chains were obtained from the averaging the individual scattering curves of 2000 atomic resolution conformations of each of the 23 proteins defined by their amino-acid sequence. The theoretical scattering profiles (s < 0.1 Å⁻¹) for each conformation were calculated with the program CRYSOL (45), and averaged to yield a final SAXS curve for each protein. Random Gaussian noise of an amplitude of 2% was added to the curves to produce more experimental-like data. R_g values were derived by analyzing the initial part of the curve (sR_g < 1.3) using Guinier's approach with the program PRIMUS (46).

Hydrodynamic properties of the denatured state were computed for eight proteins whose R_h values had been measured by PFG (47,48). For each of the eight proteins, an ensemble with 500 conformations was built as described above, and for each conformation the hydrodynamic radius was computed with a modified version of the program HYDROPRO (49) using an atomic element radius of 3.3 Å to define the volume of the conformation (50). The bead modeling strategy adopted by HYDROPRO has been proven to be efficient to calculate hydrodynamic properties for both rigid (51,52) and flexible (53) molecules. The averaged R_h was obtained as

$$\frac{1}{R_{\text{h}}}=\frac{1}{N}\sum _{i=1,N}\frac{1}{R_{\text{h},i}},$$ (1)

where N is the number of conformations of the ensemble (500) and R_h,i is the hydrodynamic radius of the conformation i.

The same calculations of SAXS and hydrodynamic properties were repeated for six additional ensembles with an enhanced population of extended conformations {50° < ψ < 180°} in the Ramachandran space. Databases with X = 1.5, 2.0, 2.5, 3.0, 3.5, and 4.0 times' higher populations for this range of ψ were created. Explicitly the same conformations with {50° < ψ < 180°} were repeated X times in the database to increase their possibility of being selected. Final databases have 68.3%, 74.2%, 78.2%, 81.2%, 83.4%, and 85.2% of the conformations in the extended region, respectively.

Results and Discussion

The overall dimensions of chemically denatured proteins, expressed in terms of an effective ensemble radius of gyration R_g, has been predicted and then shown to display a simple power-law dependence on chain length N that is in agreement with random-coil polymer behavior (54,55),

$$R_{\text{g}}=R_{\text{0}}{N}^v,$$ (2)

where R₀ is a constant that depends on the persistence length and ν is the exponential scaling factor. In a recent article, Kohn et al. measured and compiled the R_g obtained by SAXS for 28 proteins under different denaturing conditions, extracting a value of ν = 0.58 ± 0.11 (11). We have taken a set of 23 proteins from this list covering a broad range of chain lengths, from eight to 549 amino acids (see Table S1 in the Supporting Material). For each of the 23 amino-acid sequences, an ensemble of 2000 conformations was created using FM, and SAXS profiles were calculated from these ensembles (see Methods). The correlation between the experimental and simulated R_g values is shown in Fig. 1 a. A systematic deviation is observed, indicating that simulated ensembles underestimate the overall size of the denatured state.

Figure 1.

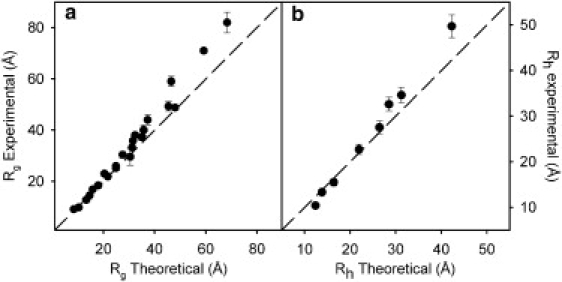
Correlation between experimental and theoretical values of (a) radius of gyration R_g, and (b) hydrodynamic radius R_h for the ensembles corresponding to the standard database. Dashed line represents slope equal to 1.0. Experimental values of R_g were obtained from Kohn et al. (11), and R_h values were obtained from Wilkins et al. (47) and Pan et al. (48).

Hydrodynamic measurements such as analytical ultracentrifugation, sedimentation coefficients, or translational diffusion coefficients have been used to obtain the hydrodynamic radius, R_h, for unstructured proteins (56,57). We have calculated the effective ensemble averaged hydrodynamic characteristics of eight proteins for which experimental data are available. The correlation between experimental and simulated averaged values is shown in Fig. 1 b. A systematic deviation on the correlation is observed when increasing the size of the polypeptide chain. This observation is coincident with the SAXS data and indicates an underestimation of the global structural parameters of the disordered chain under denaturing conditions when using the coil library to describe their conformational sampling.

The recent NMR study of urea-unfolded ubiquitin identified the need for an enhanced population of extended conformations, defined as a higher propensity to populate the region of Ramachandran space defined by {50° < ψ < 180°} (25). If true, this enhanced extendedness should be reflected in the overall dimensions of denatured proteins and therefore should be detectable by SAXS and hydrodynamic measurements. The overall population of extended conformations was systematically increased for each amino-acid-specific population in the database, by creating databases with X = 1.5, 2.0, 2.5, 3.0, 3.5, and 4.0 times higher populations for this range (see Methods). Taking into account that the coil database has 59.0% of conformations that are in the extended region, the new databases have 68.3%, 74.2%, 78.2%, 81.2%, 83.4%, and 85.2% of the conformations in the extended region, respectively. For each of the six new databases new ensembles of the same size for all proteins were computed and the R_g and R_h values were derived as explained for the standard (coil) database. The capacity of the ensembles to describe experimental R_g and R_h values was monitored via a reduced χ² value computed as

$${\chi }^2=\frac{1}{NP}\sum _{i=1,NP}\frac{{\left(R_{x,i}^{\text{exp}}-R_{x,i}^{\text{theo}}\right)}^2}{{\sigma }_i^2},$$ (3)

where R_x,i is either R_g or R_h for protein i, NP is the total number of proteins for the SAXS (23) and for the PFG data (8). The resulting χ² values for each database are shown in Fig. 2. Interestingly, for both experimentally measured parameters, R_g and R_h, the minimum value of the χ² function is obtained for the 2.0 database. R_g shows more sensitivity to the degree of extendedness than R_h that has a very flat χ² profile in the 68–78% range (1.5–2.5 databases). The presence of larger proteins in the dataset, and the different averaging processes governing the measured parameters, squared distance distribution functions compared to reciprocal, are possible reasons of this higher sensitivity found for R_g. The correlations between the experimental and simulated R_g and R_h values using the optimal database are displayed in Fig. 2, c and d, where a good agreement is observed. In this optimal database, the extended conformations represent 74.2% of the conformers—a significant enhancement when compared to the coil library, 59%. At this degree of extendedness, no systematic deviations are observed in the correlation plots, and both small peptides and large proteins are well described when using this database. Importantly, this optimal value of extendedness found by fitting overall parameters was also found when fitting a large dataset of residue-specific RDCs measured for urea-denatured ubiquitin (Fig. 3). It is also important to note that using this more extended conformational sampling gave very poor agreement for the RDCs (¹D_HN and ²D_CHN) measured in the intrinsically disordered protein X (25). Conversely, the standard coil database provides excellent agreement of both RDCs measured for the same protein. These results strongly suggest the existence of distinct conformational sampling in intrinsically and chemically denatured proteins that probe more extended conformations.

Figure 2.

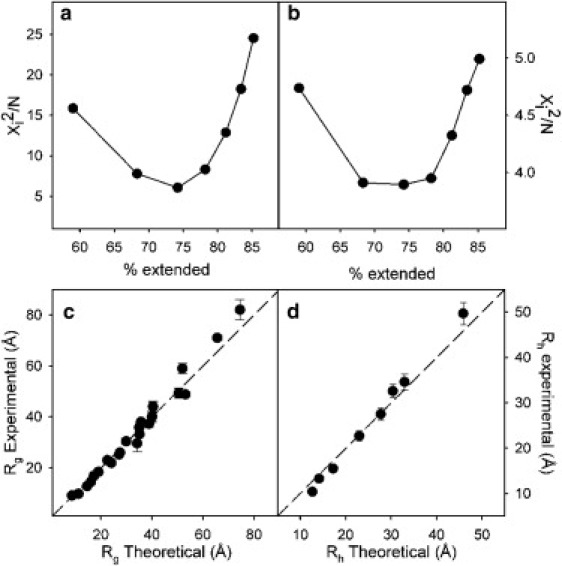
Optimal percentage of extended conformations. Agreement of the overall parameters (a) R_g and (b) R_h upon increasing the percentage of extended conformations in the database. Correlation between the experimental and theoretical (c) R_g and (d) R_h at the optimal database found, X = 2.0, which corresponds to a 74.2% of extended conformations. Dashed line again represents slope equal to 1.0.

Figure 3.

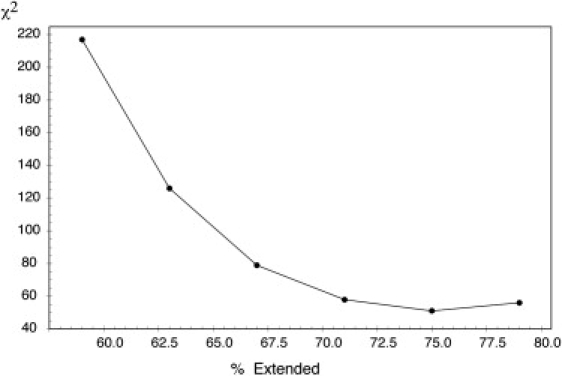
Reproduction of experimental residual dipolar couplings measured from urea unfolded ubiquitin at pH2 aligned in polyacrylamide gel using databases sampling different levels of extension. The χ² is measured over seven types of coupling: ¹D_NH, ¹D_CαHα, ¹D_CαC′, D_{HNHα (i,i-1)}, D_{HNHN (i,i+1)}, D_HNHN(i,i+2), and D_HNHα. Data taken from Meier et al. (25).

It is interesting to compare the level of extension with similar databases extracted using comparable approaches. Removing sheet and helical regions from a compilation of high-resolution structures resulted in the development of a database with 55% of conformers in the extended region (58), while similar results were found by Griffiths-Jones et al. (54% in this region excluding glycine) (59), and from two similarly constructed earlier, smaller coil databases (60,61). Compared to 59% in our database, these numbers are therefore slightly less extended, indicating that the current findings—that more extended conformers are necessary for chemically denatured proteins—are generally relevant for coil database descriptions.

Our results clearly suggest that parameters describing Flory's relationship (Eq. 2) for chemically denatured proteins are different to these describing IDPs. A parameterization of Flory's equation for IDPs was obtained from the simulated R_g and R_h values using the coil database with the length of the biopolymer chains (see Fig. 4). From the fitting of the data to the logarithmic form of Eq. 2, ν-values of 0.522 ± 0.01 and 0.449 ± 0.01 for the R_g and R_h parameters were obtained, respectively, and the R₀ values derived were 2.54 ± 0.01 and 3.53 ± 0.01 for the R_g and R_h, respectively. The ν-values obtained from the R_g and R_h data are notably smaller than the 0.6 and 0.588 values predicted for a random coil polymer with excluded volume (62), and experimentally calibrated values that are also close to these numbers (10,11,51).

Figure 4.

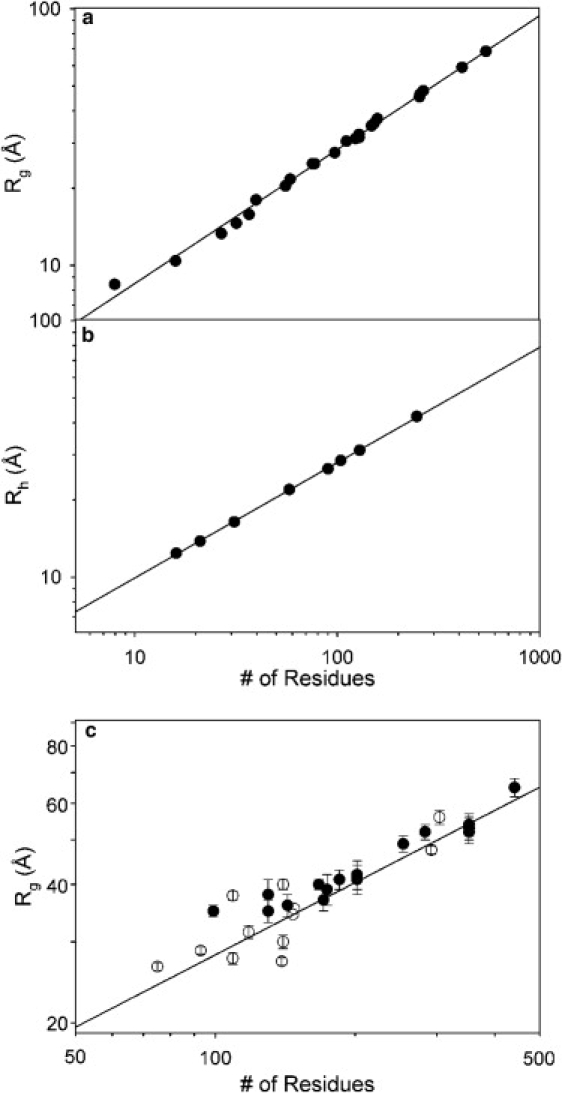
Relationship of the R_g (a) and R_h (b) values calculated using the standard database with the length of the protein chain N. From this correlation, the parameters of Flory's relationship (Eq. 1) were derived for both observables. From R_g, ν = 0.522 ± 0.01 and R₀ = 2.54 ± 0.01; and from R_h, ν = 0.449 ± 0.01 and R₀ = 3.53 ± 0.01. (c) R_g values compiled for protein τ (solid circles) and other IDPs (open circles), compared with the threshold values according to the calibration found in panel a (solid line). See the Supporting Material for the list of IDPs used in this plot.

The R_g values measured for different constructs of protein τ (63) and other IDPs have been collected from literature (see Table S2), and plotted as a function of the protein length in Fig. 4 c. The points are scattered around the line representing the previously described parameterization for IDPs indicating a broad agreement with the general law. Departures from the parameterized line are expected for IDPs, as they can often observe structuring phenomena that will modify the R_g values expected for a nonstructured chain of N residues. R_g values measured for different τ-protein constructs (63), solid circles in Fig. 4 c, appear above the line indicating that the conformational bias increases the overall stiffness of the protein. This general signature is more evident for K18 and K19 τ constructs that encompass the so-called repeat domain in which extended and turn regions have been identified in different NMR studies (28,64). Conversely, N-tail of measles virus nucleoprotein, a 139-residue-long IDP, appears as a more compact ensemble than the calibrated threshold (65). The SAXS data for this protein presents a Kratky plot with a clear bump at s = 0.08 Å⁻¹ that indicates a certain degree of compactness in a concrete region of the chain. A bioinformatics analysis predicts a 16-residue-long fragment to have a strong tendency to form an α-helix that is probably the origin of this partial compactation (66).

Conclusions

In conclusion, by comparing explicit molecular simulation with extensive experimental data reporting on the overall dimensions of highly disordered chains, we are able to refine the coil database to a level that agrees simultaneously with different and highly complementary biophysical measurements of local and long-range structure. We find that Ramachandran sampling, described using popular definitions of the statistical coil model that simply remove secondary structural elements from high-resolution crystallographic structures, is insufficient to describe protein conformational sampling under strongly denaturing conditions. On the basis of small-angle scattering and NMR data, we define a self-consistent model that enhances access to β-extended and polyproline II regions of Ramachandran space within native amino-acid-specific conformational wells. It is interesting to speculate that this model agrees qualitatively with a mechanism of denaturation that implicates urea binding to the polypeptide backbone (9), causing steric hindrance that would favor more extended local conformations, although it certainly does not disprove the importance of the side-chain solvation model (8).

Supporting Material

One table is available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(09)01436-2.