Coarse-Grained Brownian Dynamics Simulations of the 10-23 DNAzyme

Abstract

Deoxyribozymes (DNAzymes) are single-stranded DNA that catalyze nucleic acid biochemistry. Although a number of DNAzymes have been discovered by in vitro selection, the relationship between their tertiary structure and function remains unknown. We focus here on the well-studied 10-23 DNAzyme, which cleaves mRNA with a catalytic efficiency approaching that of RNase A. Using coarse-grained Brownian dynamics simulations, we find that the DNAzyme bends its substrate away from the cleavage point, exposing the reactive site and buckling the DNAzyme catalytic core. This hypothesized transition state provides microscopic insights into experimental observations concerning the size of the DNAzyme/substrate complex, the impact of the recognition arm length, and the sensitivity of the enzymatic activity to point mutations of the catalytic core. Upon cleaving the pertinent backbone bond in the substrate, we find that the catalytic core of the DNAzyme unwinds and the overall complex rapidly extends, in agreement with experiments on the related 8-17 DNAzyme. The results presented here provide a starting point for interpreting experimental data on DNAzyme kinetics, as well as developing more detailed simulation models. The results also demonstrate the limitations of using a simple physical model to understand the role of point mutations.

Introduction

DNA is now firmly entrenched with RNA and protein as an enzyme. Whereas double-stranded DNA does not appear to possess catalytic abilities, single-stranded DNA can act as an enzyme owing to its ability to form complex secondary (and tertiary) structures and bind to a nucleic acid substrate by Watson-Crick basepairing. In contrast to RNA and protein enzymes, these so-called deoxyribozymes or DNAzymes have yet to be found in vivo. Rather, deoxyribozymes (DNAzymes) catalyzing a range of reactions have been discovered by in vitro selection (1), most notably the RNA-cleaving 10-23 and 8-17 DNAzymes (2). These DNAzymes are so named because they were the 23rd (17th) clone of the 10th (8th) round of the selection process. The ability of the 10-23 DNAzyme to cleave mRNA at the start codon under physiological conditions (2) has opened up a number of possibilities for gene silencing (3). DNAzymes are easier to synthesize and more stable than comparable RNAzymes (4), and some of the issues related to delivery are being addressed through molecular design (5–8). Apart from promising clinical applications, the metalloenzyme properties of DNAzymes have led to their incorporation in sensitive sensors for detecting mercury (9–12), lead (13,14), copper (15), and uranium (16). DNAzymes also have served as components of molecular devices (17), in DNA computing systems (18), and as general laboratory reagents (1).

At the discovery level, in vitro selection is excellent at isolating and amplifying a catalytically active motif such as the 10-23 DNAzyme from a large random library (∼10¹⁴ candidate sequences), finding the proverbial enzyme in a haystack. However, this method for isolating the enzyme sequence does not readily furnish insights into its mechanism. For the latter task, the standard enzymology approach correlates the chemical functionality of the enzyme to the structure of its active state. This approach has been extraordinarily successful at elucidating the structure-function relationships for protein enzymes and catalytic RNA (19,20). Indeed, our understanding of the fundamentals of protein-mediated catalysis has reached the point where some protein enzymes can be designed de novo (21–23).

Such is not the case for DNAzymes in general, and the 10-23 DNAzyme in particular. Although a wealth of experimental data exist on the reaction rate, sensitivity to mutation, and end-to-end distance of the 10-23 DNAzyme (2,24–31), its active state appears resistant to crystallization (32,33). As a result, the powerful tools applied to understanding the mechanisms of protein enzymes and RNAzymes (19,20) cannot readily be employed for the 10-23 DNAzyme. In this contribution, we demonstrate how a simple physical model provides a glimpse into the tertiary structure of the 10-23 DNAzyme, thereby furnishing a starting point for obtaining the desired molecular-level understanding of the extant experimental data.

Modeling Approach

The DNAzyme and substrate system under consideration is depicted in Fig. 1, with an eye toward our eventual model. The DNAzyme sequence for most of our simulations is 5′-cgactcgtcaGGCTAGCTACAACGAtgcatctcga-3′, where the lowercase letters are 10 nucleotide recognition arms and the uppercase letters are the catalytic core of the 10-23 DNAzyme (2). In some simulations, we will consider shorter recognition arms by removing an equal number of bases from the 5′ and 3′ end; for example, a recognition arm length of 9 corresponds to removing the 5′ cytosine and 3′ adenine from the DNAzyme in Fig. 1. The RNA substrate is complementary to the recognition arms of the DNAzyme, with an unpaired adenine inserted between the two sequences that bind to the recognition arms. For simulations with shortened recognition arms, the corresponding complementary bases of the substrate are also removed. The cleavage reaction occurs at the 3′ end of the unpaired adenine.

Figure 1.

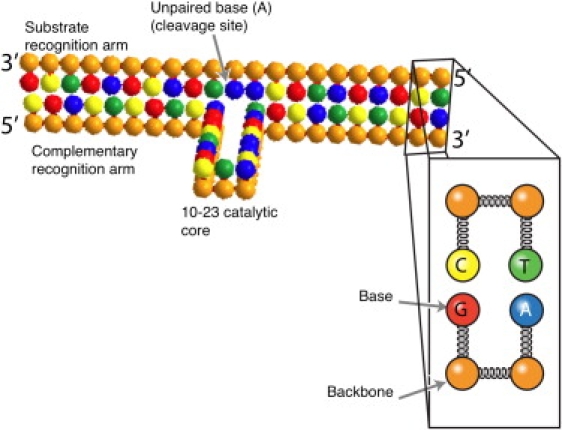
Schematic depiction of a two-bead model (37) of the 10-23 DNAzyme bound to its substrate. The inset highlights the bead-spring model. All beads interact with one another through excluded volume interactions, and connected beads are held together by a stiff spring. The finite stiffness of the backbone is enforced by a bending potential acting on contiguous backbone beads. The base beads further interact with one another through hydrogen bonding and stacking interactions. The coordinates of the beads in this figure were used to initialize the simulations. For simulations with shortened recognition arms, the bases at the ends of the DNAzyme and substrate are removed from the simulation. The DNAzyme sequence in our simulations is 5′-cgactcgtcaGGCTAGCTACAACGAtgcatctcga-3′. The substrate sequence is complementary to the recognition arms with an unpaired A in the center.

The schematic in Fig. 1 corresponds to the secondary structure proposed by Santoro and Joyce (2). Watson-Crick basepairing between the recognition arms brings the ends of the catalytic core into proximity, which leads to the formation of a loop in the DNAzyme. In what follows, we are interested in determining:

• 1.The most probable three-dimensional shape (tertiary structure) of this complex.
• 2.Fluctuations about the average state.
• 3.The dynamics of the complex following the cleavage of the substrate.

We will then see to what extent this information can provide molecular-scale interpretations of experimental data on the end-to-end distance of the bound DNAzyme, the impact of the recognition arm length and point mutations on the reaction rate, and the extension of the initial reaction product.

The ground state for the tertiary structure is thermodynamic in origin and could, in principle, be determined by an energy minimization routine. However, the standard methods used for this purpose, such as the one implemented in the Mfold server (34), are normally based on nearest-neighbor thermodynamic parameters and are limited to predicting secondary structure. Although the Mfold server is a powerful and computationally efficient method for predicting possible loop formation and other intramolecular bonds in a long sequence, it is not appropriate for the task at hand because the structure in Fig. 1 already approximates the minimum-energy secondary structure. Even if we had a way to extend these predictions to the tertiary structure, knowledge of the ground state does not provide any information about fluctuations or the transition to a new state after the cleavage reaction.

We could also, in principle, accomplish all three tasks using atomistically detailed molecular dynamics simulations with a package such as CHARMM (35). Such simulations would allow us to account for, among other factors, explicit solvent and salt. Unfortunately, molecular dynamics simulations incur substantial computational costs to reach even short timescales (e.g., (36)). Such a detailed simulation is only feasible if we start from a reasonable initial guess for the tertiary structure. As noted above, crystallization data cannot be used for this purpose (32,33). Likewise, the proposed structure in Fig. 1, in its normal two-dimensional incarnation, is likely to be far from the correct tertiary structure. Its relaxation would thus require significant computational resources.

In light of the limitations of the latter methods, we chose to use a coarse-grained model (37) that provides access to an approximation of the three-dimensional configuration at the nucleotide length scale while allowing us to reach the long timescales characterizing structural fluctuations and transitions. Coarse-grained simulations of nucleic acids have become increasingly popular for addressing a wide range of dynamic processes (37–45), as they often represent a reasonable compromise between computational cost and the complexity of the model. The relative merits of our model and others in the literature were discussed previously (37). As described in the Simulation Method and Kenward and Dorfman (37), the base-backbone model depicted in Fig. 1 constrains the beads to fixed interbead distances while accounting for excluded volume, backbone bending stiffness, basepairing, and base-stacking interactions. This off-lattice DNA model provides more degrees of freedom and mesoscale detail than its lattice counterparts (41,43), albeit with an increased computational cost. The latter potential fields are implemented in a Brownian dynamics (BD) routine that updates the chain configuration in time by integrating the corresponding Langevin equation. We are able to reach many microseconds of dynamics in our simulations on a reasonably powerful desktop computer. We can thus start from the initial configuration of Fig. 1, relax the DNA, and readily obtain thermodynamic data by measuring the time-averaged properties (and fluctuations thereabout) of the DNAzyme bound to its substrate, along with the corresponding dynamical data encoded in the system trajectory.

Although a coarse-grained model is attractive for our purposes, we also should recall its limitations. As a two-bead model, the simulations do not distinguish between the 3′ and 5′ end of the chain, apart from the 5′-3′ direction of the sequence. As a corollary, although the double-stranded regions of our chains are helical, the model does not resolve the major or minor groove, as would be the case in a three-bead model (44). Our model also treats DNA and RNA with the same potential energy functions (37), effectively assuming that the structural differences between these molecules are small compared to the generic nucleic acid features included in the model. Thus, we posit that although including a major/minor groove or distinction between DNA and RNA will alter our quantitative results, our key mechanistic conclusions should remain unchanged.

To retain a computationally efficient simulation, virtually all coarse-grained simulations of nucleic acids (37–41,43,44) use effective electrostatic interaction energies rather than accounting for explicit counterions. In the context of modeling metalloenzymes such as the 10-23 DNAzyme, this point deserves some further discussion beyond the computational issues. Metal ions are clearly a key part of the chemical mechanism leading to RNA cleavage by the 10-23 DNAzyme (2,24); indeed, such metalloenzyme chemistry is the basis of DNAzyme sensors (9–16). However, it is conceivable that the metal can assist in deprotonating the substrate (24) without simultaneously coordinating the tertiary structure of the DNAzyme. If the divalent counterion played an essential role in the coarse-grained structure by stabilizing two proximate phosphate groups, then we would expect the reaction rate to be roughly independent of the chemical identity of the counterion and second-order in counterion concentration. However, experimental data (24) indicate that the reaction rate roughly correlates with the pK_a value of the metal and the overall reaction obeys saturation kinetics (24). We thus proceed here on the assumption that, at the length scales resolved by our model, any contribution of metal coordination to the tertiary structure is small compared to those due to basepairing, stacking, excluded volume, and the semiflexible nature of the nucleic acids. We will return to this point after discussing the predictions of our model.

Simulation Method

The nucleic acid simulation model employed here, depicted schematically in Fig. 1, was described previously in the context of DNA hairpins (37). The model is a so-called two-bead model, where an individual sugar-phosphate/nucleoside (base) is represented as two beads, one for each of the entities. Interior and end backbone beads are connected to two or one other backbone beads, respectively, and each backbone bead is connected to a single base bead. The base beads provide the sequence information through their hydrogen-bonding and stacking interactions with other base beads, while the backbone beads confer connectivity and stiffness to the chain.

As described in Kenward and Dorfman (37), the excluded volume interactions are modeled with the repulsive part of the pairwise Lennard-Jones potential

$$U_{\text{LJ}}\left(r_{\text{ij}}\right)=\{\begin{array}{cc}4\epsilon \left({\left[\frac{\sigma }{r_{\text{ij}}}\right]}^{12}-{\left[\frac{\sigma }{r_{\text{ij}}}\right]}^6\right)+\epsilon ,& r_{\text{ij}}\le r_{\text{c}}\\ 0,& r_{\text{ij}}\ge r_{\text{c}}\end{array},$$ (1)

where r_c is the minimum of the Lennard-Jones potential and where r_ij is the distance between two species i and j. The other parameters, ɛ and σ, are the basic units for energy and length.

The elasticity is enforced by a finitely extensible nonlinear elastic (FENE) potential (46):

$$U_{\text{FENE}}\left(r_{\text{ij}}\right)=-\frac{\kappa }{2}{R}_0^2\ln \left(1-{\left[\frac{r_{\text{ij}}}{R_0}\right]}^2\right)\text{.}$$ (2)

The parameters κ = 30ɛ /σ² and R₀ = 1.5σ are the strength and minimum in the potential, respectively. They are chosen to be species-independent (37). The finite backbone stiffnesses of the molecules are modeled by a bending potential between contiguous backbone beads. This stiffness function is

$$U_{\text{b}}\left(\theta \right)=\frac{u_{\text{b}}}{2}{(\cos \theta -\cos {\theta }_0)}^2,$$ (3)

where θ₀ and u_b are the desired bending angle and the effective stiffness of the molecule. In all cases we use θ₀ = 0 and u_b = 18ɛ (37). No dihedral angle potential function is included, so the helicity in this model arises from the stacking potential.

The base beads interact by stacking potentials between contiguous bases (40,41) and hydrogen bonding between A-T/U (two bonds) and G-C bases (three bonds). Wobble pairs and non-Watson-Crick bonding are neglected. Hydrogen bonding between contiguous base i and j = i ± 2 on the same chain is not permitted to prevent the formation of three-member rings. The stacking and hydrogen-bonding potentials have the form (40)

$$U_{\text{k}}\left(r_{\text{ij}}\right)=-\epsilon u_{\text{k}}{\delta }_{\text{ij}}^{\text{k}}{\left[\exp \left(20\left[\frac{r_{\text{ij}}}{\sigma }-{\Gamma }_{\text{s}}\right]+1\right)\right]}^{-1},$$ (4)

where the subscript k is either k = stack or k = hbond for stacking and hydrogen bonding, respectively, and the strength of the potential is u_k. The particular type of base is prescribed by the δ^k_ij values. For the stacking and hydrogen bonding we use a value of Γ_s = 1.1, u_hbond = 2.0, and u_stack = 5.0. The stacking matrix Δ_ij^stack and bonding matrix Δ_ij^hbond are the same as in Kenward and Dorfman (37), with the assumption that the base U has the same bonding/stacking properties as T. The stacking matrix is given by

$${\mathbf{\Delta }}_{\text{ij}}^{\text{stack}}=\left[\begin{array}{cccc}{\delta }_{\text{AA}}^{\text{stack}}& {\delta }_{\text{AC}}^{\text{stack}}& {\delta }_{\text{AG}}^{\text{stack}}& {\delta }_{\text{AT}}^{\text{stack}}\\ {\delta }_{\text{CA}}^{\text{stack}}& {\delta }_{\text{CC}}^{\text{stack}}& {\delta }_{\text{CG}}^{\text{stack}}& {\delta }_{\text{CT}}^{\text{stack}}\\ {\delta }_{\text{GA}}^{\text{stack}}& {\delta }_{\text{GC}}^{\text{stack}}& {\delta }_{\text{GG}}^{\text{stack}}& {\delta }_{\text{GT}}^{\text{stack}}\\ {\delta }_{\text{TA}}^{\text{stack}}& {\delta }_{\text{TC}}^{\text{stack}}& {\delta }_{\text{TG}}^{\text{stack}}& {\delta }_{\text{TT}}^{\text{stack}}\end{array}\right]=\frac{1}{4}\left[\begin{array}{cccc}3& 2& 2& 3\\ 2& 1& 1& 2\\ 2& 1& 3& 3\\ 3& 2& 3& 4\end{array}\right],$$ (5)

whereas the bonding matrix has the form

$${\mathbf{\Delta }}_{\text{ij}}^{\text{hbond}}=\left[\begin{array}{cccc}0& 0& 0& {\delta }_{\text{AT}}^{\text{hbond}}\\ 0& 0& {\delta }_{\text{CG}}^{\text{hbond}}& 0\\ 0& {\delta }_{\text{GC}}^{\text{hbond}}& 0& 0\\ {\delta }_{\text{TA}}^{\text{hbond}}& 0& 0& 0\end{array}\right],$$ (6)

where δ^hbond_AT = 2/3 and δ^hbond_CG = 1 correspond to two and three hydrogen bonds formed, respectively.

The latter potential fields are implemented in a BD routine that updates the chain configuration in time by integrating the corresponding Langevin equation with a bead friction coefficient ξ. The dimensionless equation is formed with a length scale σ and timescale ξσ²/ɛ. All simulations are performed at a dimensionless temperature $\overline{T}=k_{\text{B}}T/\epsilon =0.1$ and integrated using a velocity Verlet algorithm (47) with time step δt = 0.01. Additional simulations performed at $\overline{T}=0.2$ yielded similar results for the end-to-end distance, whereas higher temperatures such as $\overline{T}=0.4$ lead to rapid fluctuations and dissociation of the complex. The simulations were performed without any parallelization on a MacPro with two 3 GHz quad-core Intel Xeon processors and 8 GB of 667 MHz DDR2 RAM.

The system was initialized using the configuration depicted in Fig. 1, which ensures that the desired basepairing occurs immediately after the start of the simulations. We thereby avoid complications due to possible secondary structure of the DNAzyme or the substrate alone. The bound system is allowed to relax for 100,000 BD time steps (t_BD = 1000) prior to acquiring structural data.

For the simulations with shortened recognition arms, bases are removed from each of the recognition arms to retain equal length recognition arms on the 3′ and 5′ sides of the DNAzyme. The homologous bases are also removed from the substrate. For the cleavage simulation data the spring force between the two relevant backbone beads at the cleavage site is set to zero for the dimensionless time t_BD ≥ 2500 to reflect the cleavage reaction.

Results and Discussion

Simulation temperature, time-, and length scales

One of the challenges in coarse-grained simulations is connecting the parameters in the simulation, which are necessarily in dimensionless form, to dimensional quantities. Although dimensionless results are ideal for developing scaling laws, we require appropriate conversion factors to compare our results to individual experimental datum. Our simulation model employs a basic length scale σ and energy scale ɛ, implying the dimensionless temperature $\overline{T}=k_{\text{B}}T/\epsilon$ and time t_BD ∼ ξσ²/ɛ, where ξ is the friction of a bead and k_BT is the thermal energy. The combination of excluded volume and the spring forces confines the beads to a dimensionless distance of σ = 0.97 ± 0.025, whereupon we associate this length scale with the typical spacing between nucleotides on the backbone, σ = 0.34 nm. We can obtain a reliable estimate for the energy scale by noting that a characteristic value of the hydrogen-bonding free energy is −1.5 kcal/mol/bond (48). The maximum value of the hydrogen-bonding potential (37,40) in our simulations is –ɛ u_hbond/3e per bond, leading to ɛ = 6.1 kcal/mol. With the choice u_hbond = 2.0, our dimensionless temperature $\overline{T}=0.1$ corresponds to an actual temperature of 310 K. If we approximate the bead friction by a sphere of radius σ in water, the dimensionless Brownian dynamics time, t_BD, corresponds to nanoseconds.

From the stacking matrix (37,41) and our value of ɛ, we find that the stacking energies used in our simulation range between −2.8 and −11.3 kcal/mol, depending on the particular combination of bases. We believe that these represent realistic estimates of the stacking energy. Stacking energies remain controversial and subject to significant experimental error, with reported values for polyA ranging from −3 to −13 kcal/mol (48).

DNAzyme bending and the active state

Fig. 2 depicts the evolution of the end-to-end distance of the DNAzyme recognition arms, starting from the configuration described in Fig. 1. After a period of rapid decay, the end-to-end distance reaches a relatively stable steady-state value. During the course of the trajectory, we obtain an average distance of (15.83 ± 1.19)σ, where the error represents 1 SD from the mean. Converting to dimensional units, the resulting distance of 5.4 ± 0.4 nm is close to the value of 6.00 nm obtained during bulk FRET measurements (30). After forming the complex, the DNAzyme remains bound to its substrate. This stability is consistent with the experimentally measured Michaelis-Menten kinetics, where the unbinding rate for the complex is effectively zero if the recognition arms are sufficiently long (24).

Figure 2.

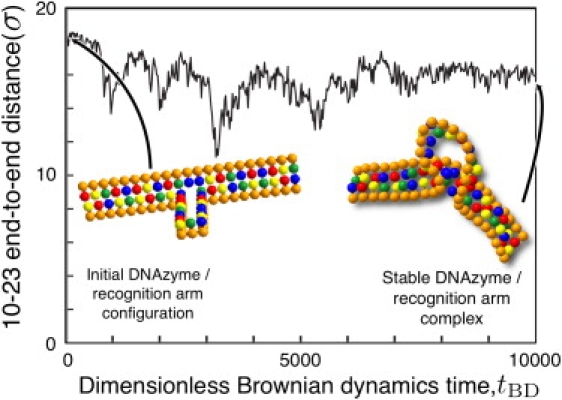
Evolution of the end-to-end distance of the substrate arms as a function of dimensionless simulation time. Distances are scaled with the simulation length scale σ. The average values (and standard deviations) are 15.83 (1.19), corresponding to dimensional values 5.4 (0.4) nm.

We propose that this stable state corresponds to the active state of the DNAzyme, so it is worthwhile to discuss the tertiary structure in detail. The binding to the substrate brings the ends of the catalytic core into close proximity. This introduces unfavorable bending into the loop comprising the catalytic core. The bending is relieved to some extent by buckling the catalytic core, which in turn could form a metal-ion binding pocket close to the scission site to aid in deprotonation of the RNA. The reduction in the end-to-end distance is the result of the recognition arms bending away from the catalytic core, which induces sufficient tension to partially unstack the unpaired base. The bending of the substrate is due to several factors, most notably the backbone stiffness. If the DNAzyme were to adopt the standard depiction in the literature, i.e., a fairly broad loop formed by the catalytic core and sharp bend at the attachment site to the complementary arms, the site of attachment of the recognition arms to the catalytic core would incur a substantial bending energy penalty. The combination of bending the substrate and partially unstacking the unpaired base minimizes steric hindrances and thus facilitates access to the reaction site.

Effect of recognition arm length

If we assume that the bending of the DNAzyme arms and the concomitant exposure of the reactive site are the essential features of the active state of the complex, we are also able to capture the qualitative dependence of the reaction rate on the length of the recognition arms (24). To this end, we systematically deleted the end base of each recognition arm (and the corresponding base of the substrate) and then measured the distribution of the angle between the cleavage site and the ends of the recognition arms. These data are plotted in Fig. 3 along with the corresponding experimental measurements of the Michaelis-Menten parameter k_cat by Santoro and Joyce (24). For the two largest recognition arms, we find that the average bending angle is unchanged and we thus postulate that their reaction rates would be similar. As the recognition arm length decreases, we observe a decrease in the bending angle. The fluctuations of the bending angle lead to transients where the bending angle of a shorter recognition arm is close to the average angle realized with the longer recognition arms. Hence, we would expect a finite but lower reaction rate for seven and eight nucleotide recognition arms. As the arms are shortened further, the complex becomes unstable and we expect that the reaction rate would vanish.

Figure 3.

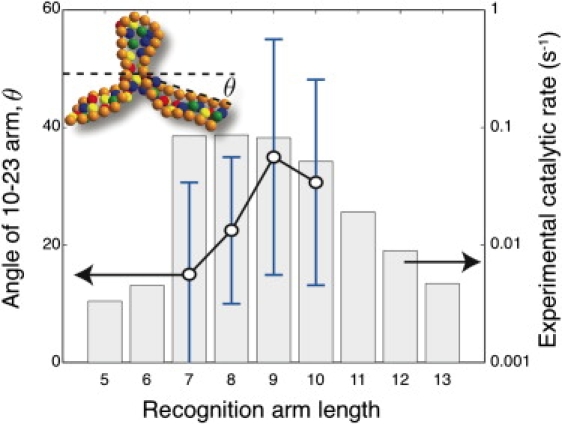
Average bend in the DNAzyme/substrate complex computed as θ = (180° – ϕ)/2, where ϕ is the angle formed by the two lines connecting the ends of the complex to the unpaired base A in the substrate. The inset shows a snapshot of the a DNAzyme with a recognition arm length of 7. The error bars correspond to 1 SD. The histogram reproduces the kinetic data of Santoro and Joyce (24) for k_cat (s⁻¹) as a function of the recognition arm length.

This basic trend was observed in experiments (24), but the boundaries between the different reaction rate regimes were shifted down by two nucleotides. Nevertheless, we can now provide an energetic interpretation for the reaction rate at the molecular scale. To achieve any reaction whatsoever, the recognition arms need to be sufficiently long so that the dissociation constant of the complex is small. However, simply realizing a strong bond between the DNAzyme and it substrate is not sufficient to ensure the optimal catalytic rate. Achieving the hypothesized active configuration also involves a decrease in configurational entropy and bending of the semiflexible chains. This energetic cost must be offset by the favorable free energy of basepairing.

The need for additional binding energy beyond that required for a small dissociation constant has implications for the design of DNAzyme recognition arms. At first glance, it would appear that the binding free energy for the recognition arms should be high enough to keep the complex together but not so large so that the reaction products cannot be released. However, our simulations indicate that the binding energy should be somewhat higher to provide the additional free energy needed to bend the substrate. Indeed, this may be the reason why the Michaelis-Menten kinetics for this system feature no dissociation of the complex—to observe a sensible reaction rate, the substrate must be strongly bound to the DNAzyme.

For very long arms, experiments also revealed a gradual quenching of the reaction rate that was attributed to the slow product release (24). We do not capture this regime of the experimental data, as we have not conducted simulations of sufficient duration to observe the unbinding of the reaction product from the recognition arms. Our discussion in the context of Fig. 6 indicates that reaching the unbinding stage would require increasing the simulation time by six orders of magnitude, which is not feasible.

Figure 6.

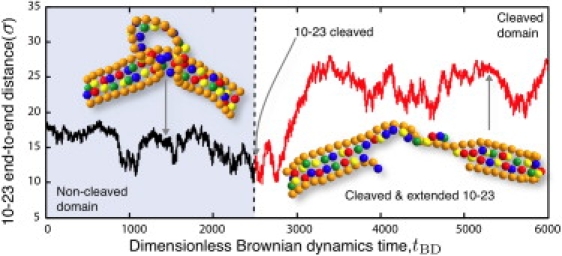
Evolution of the end-to-end distance of the substrate arms as a function of dimensionless simulation time. The snapshots depict the three-dimensional conformation of the bound DNAzyme/substrate complex at the indicated time. The substrate is cleaved at the simulation time t_BD = 2500. Distances are scaled with the simulation length scale σ.

We have made a testable prediction here about the relationship between the structure and function of the 10-23 DNAzyme. At present, there are no experimental data that we can use to confirm or refute our speculation. A starting point may be a series of trifluorophore FRET experiments similar to those performed by Liu and Lu (49) for the 8-17 DNAzyme. If these experiments were performed as a function of the recognition arm length and compared to the experimental rate data in Fig. 3, they could be used to validate our hypothesis.

Sensitivity to point mutations

Initial mutation studies of the 10-23 DNAzyme suggested that its catalytic core was relatively intolerant to mutation (2). However, systematic point mutations of each base in the core revealed a more complex behavior (28). To aid in our discussion here, we adopt the nomenclature of Zaborowska et al. (28): an A, T, C, G postfixed with a number {1–15} indicates the letter of the base and its position in the sequence of the DNAzyme catalytic core, from the 5′ to 3′ end. Table S1 in the Supporting Material lists the 45 possible point mutations of the wild-type 10-23 DNAzyme in order of their activity as measured by Zaborowska et al. (28). We divided these mutants into two groups. If the mutant cleaves at least 20% of the substrate in the reaction data of Zaborowska et al. (28), they are deemed to have reduced activity and are listed in order of descending activity. Otherwise, the mutant is deemed to have negligible activity. The latter mutants are not ranked by their activity. The (arbitrary) cutoff point of 20% was chosen to aid in reading the experimental data and our conclusions would not be changed by moving this cutoff to a different value.

There are five bases that have negligible activity for all possible point mutations (G1, G2, T4, G6, and G14). In light of these data, we expect that these bases would be in close proximity to the cleavage point. As illustrated in Fig. 4, we indeed find that the wild-type sequence possesses an asymmetric distribution of distances d_i, _A between the base i = 1–15 of the catalytic core and the unpaired base A at the cleavage site. The connectivity of the chain and the hydrogen bonding in the recognition arms leads to the first and last few bases of the catalytic core being located near the cleavage site. However, we found that the first six bases are proximate to the cleavage site. This structure contrasts sharply with the standard loop model of the 10-23 DNAzyme illustrated in Fig. 1, which would predict that the bases are distributed symmetrically about the cleavage site.

Figure 4.

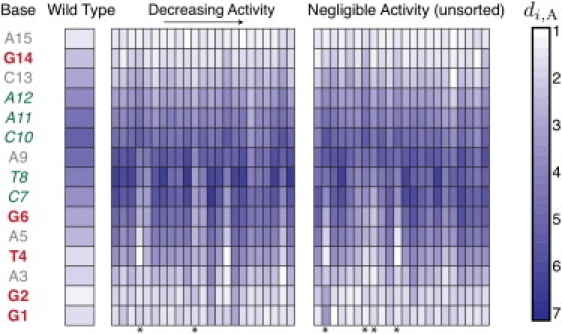
Average dimensionless distance d_i, _A between each base in the catalytic core and the unpaired base A in the substrate. The first column lists the bases of the catalytic core annotated in terms of the effect of their mutation. Any mutation of the bases in bold (red) leads to negligible activity. Any mutation of the bases in italics (green) leads to reduced activity. Some mutations of the bases in regular font (gray) lead to reduced activity, others lead to negligible activity. The first data column on the left corresponds to d_i, _A, for the wild-type sequence in Fig. 1. The remaining columns correspond to the point mutations studied in Zaborowska et al. (28). The mutants with reduced activity (>20% of the substrates cleaved in the experiments of (28)) are listed in order of descending activity as indicated in Table S1. The mutants with negligible activity are unsorted and listed in the order of Table S1. Distances are scaled with the simulation length scale σ. The asterisks indicate mutations where the base G6 is closer to the cleavage site than in the wild-type. These mutants are A12 → T, C3 → A, G1 → A, C7 → G, T4 → A, and A5 → T.

We indicated in Fig. 4 that most mutants of the central bases of the DNAzyme (C7-A12) retain some catalytic activity (28). Our simulation data for the wild-type indicate that these bases are generally far from the reactive site. We thus posit that these central bases provide a scaffold that keeps the key bases (G1, G2, T4, G6, and G14) in close proximity to the cleavage site. The particular 10-23 sequence identified by Santoro and Joyce (2) is likely the optimal scaffolding sequence but not the only possible choice.

We also wanted to explore whether our simulation model could provide insights into the lowered activity caused by point mutations. In Fig. 4, we plot the simulated distance d_i, _A between base i and the unpaired A in the substrate for each base in the 45 mutants studied by Zaborowska et al. (28). The sequences of these mutations are listed in Table S1. We observed two general trends in the structures of the mutants. First and foremost, the mutants frequently feature a lower value of d_{6, A} when compared to the wild-type. Indeed, of the 45 mutants that we studied, only the six marked by asterisks in Fig. 4 led to a decrease in d_{6, A} compared to the wild-type. (Two of the mutants involve the bases G1 and T4, which are fatal mutations.) As any mutation of G6 is fatal for the catalytic activity (28), it is reasonable to assume that this base is involved in the chemical mechanism. If the catalytic core of the DNAzyme formed a simple symmetric loop, which one might infer from the secondary structures appearing in the biochemistry literature (2,24), then G6 would be distal to the cleavage site. Our simulations indicate that the forces in the 10-23 catalytic core lead to an asymmetric loop that brings G6 into proximity of the cleavage site. Mutations of the catalytic core tend to disrupt this balance of forces, moving G6 away from the reactive site and reducing the catalytic rate.

The second trend we observed was that the asymmetric distribution of the distance to the cleavage point along the sequence is less pronounced among the mutants. To be quantitative, we computed the moment of the distance to the cleavage point as a function of the location relative to the middle of the sequence of the 15-base catalytic core,

$$M=\sum _{i=1}^{15}{d}_{i,\text{A}}(i-8)\text{.}$$ (7)

A positive moment indicates the bases with low values of i tend to be nearer to the cleavage site; a negative moment is the converse. The wild-type has a positive moment, with the first six bases close to the cleavage site. In contrast, the majority of the mutants (28 of 45) have a negative moment. Although this trend is not as clear as that for d_{6, A}, it is consistent with the reduced activity of the mutants.

We also investigated whether the mutations lead to a change in the bending angle θ of the complex. Fig. 5 plots the average bending angle of the 45 mutated complexes in the same order of activity as in Fig. 4 and Table S1. All of these mutants have the same 10 base recognition arms as the wild-type simulations used to generate the data in Fig. 3. The bending angle is not correlated with the mutation activity. Based on the data in Figs. 3–5, we propose that the decreased activity of the mutants is due to chemical factors (either the deletion of a critical base for the catalytic mechanism or the displacement of one of these bases from the active site), rather than the increased access to the reactive site engendered by the bending of the substrate.

Figure 5.

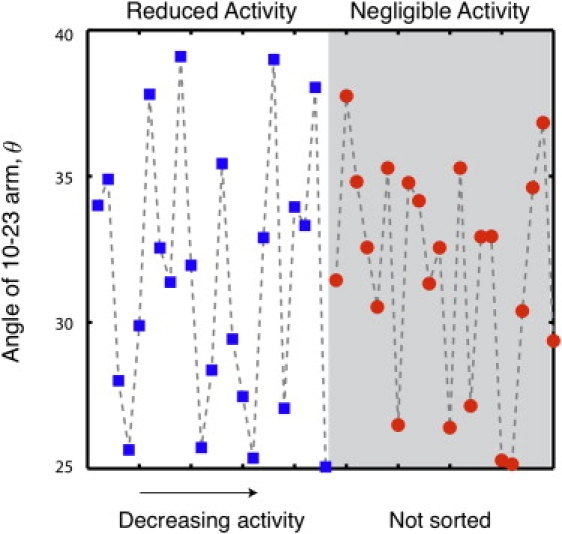
Average bend in the DNAzyme/substrate complex (as defined in Fig. 3) as a function of the mutant activity. The mutants are listed in the order of Table S1. The designations “reduced activity” and “negligible activity” are defined in Fig. 4.

Our discussion of the role of point mutations highlights a limitation in using coarse-grained physical models to study chemical rate data. We have been able to elucidate several generic structural features that we believe play a role in governing the chemistry, such as the role of the central bases as a scaffold and the importance of the proximity of G6 to the reactive site. However, our models do not allow us to make any definitive conclusions about why some mutations lead to deactivation whereas others lead to minor changes in the catalytic activity. As DNAzyme simulations mature, we hope that more-detailed models, such as those used for the hammerhead RNAzyme (50), can help guide mutation analysis.

Dynamics after cleavage

Thus far, we have used our coarse-grained simulation method to obtain data on the tertiary structure of the DNAzyme bound to its substrate, with a brief foray into the fluctuations of this structure in the context of the recognition arms in Fig. 3. However, one of the most useful aspects of a coarse-grained model is the ability to capture long-time diffusive behavior of the system. In this final set of results, we take advantage of the computational efficiency of our simulation method to study the large-scale conformational changes occurring in the DNAzyme/substrate complex after cleavage of the substrate. This task is readily accomplished by allowing the system to first relax to the state observed in Fig. 2 and then removing the spring force between the backbone beads located at the cleavage site. In performing this simulation we are not aiming to establish the reaction rate; this would require additional data on the chemical potential (in particular related to the activity of the metal ion (24)) that are not included in our model. Instead, we are interested in assessing the diffusive behavior of the system following the chemical reaction.

As seen in Fig. 6, the DNAzyme/substrate complex indeed undergoes a dramatic conformation change upon cleavage. When the potential U_hbond(r_ij) between complementary bases i and j is >10% of its maximum value, we count this as a single hydrogen bond. Before cleavage, the catalytic core fluctuates between one and five hydrogen bonds, with a typical value of 3. Once the substrate bond is broken, the ends of the DNAzyme catalytic core are no longer forced to remain in close proximity. The number of hydrogen bonds in the catalytic core rapidly drops to zero, with occasional fluctuations leading to the formation of a single hydrogen bond therein. In contrast, the double-stranded region in the recognition arm is fully hydrogen-bonded. As a result, the first effect of the reaction is an entropically favorable unwinding of the previously buckled catalytic core. Unwinding the catalytic core provides a number of newly available configurational states, but many of these do not lead to a significant increase in the end-to-end distance of the complex. During the exploration of this configuration space, the catalytic core eventually diffuses into a region of configuration phase space where it also begins to experience favorable stacking interactions between adjacent bases in the catalytic core. The stacking effectively increases the rigidity of the catalytic core and leads to an extension of the complex. As was the case with the uncleaved substrate, the ensuing structure of the reaction product is again relatively stable over the duration of our simulation. Thus, we can infer that the rate of reorganization of the complex following the reaction is much faster than the release of the products.

Although no such experimental data exist for the 10-23 DNAzyme, Kim et al. (51) reported single-molecule FRET data for the related 8-17 DNAzyme. In these experiments, the 8-17 DNAzyme was modified with a Cy5 fluorophore on the 5′ end and biotin on the 3′ end (for surface immobilization). The substrate was DNA with an inserted ribose base for cleavage; the substrate was 5′ labeled with Cy3. After the substrate was cleaved in Mg²⁺, the FRET energy rapidly decreased. The lower FRET energy is equipollent to an increase in the end-to-end distance, in agreement with our observation in Fig. 6. Our simulations further predict that this structural transition would occur over ∼10 μs; unfortunately, the comparable experimental timescale is difficult to ascertain from the published FRET signal (51). However, the experimental data indicate that the cleaved product remains bound to the DNAzyme for tens of seconds. In our simulation timescale, this corresponds to t_BD ≈ 10¹⁰. Thus, it is unsurprising that we do not observe any product release in our simulations.

Conclusions

Using a relatively simple nucleic acid model (37), we have obtained the first glimpses of the tertiary structure of the 10-23 DNAzyme bound to its substrate and the reorganization of the complex after cleavage. In doing so, we have been able to provide some molecular-level insights into a number of experimental observations on the reaction rate, end-to-end distance of the DNAzyme/substrate complex, and the impact of point mutations. We have also taken advantage of the computational efficiency of coarse-grained nucleic acid models to resolve the unwinding of the catalytic core and the mechanism underlying the subsequent extension of the complex after cleavage. Again, the predictions of our simulation are consistent with the pertinent experiments, lending credence to the overall modeling approach.

Our results represent an initial foray into the use of coarse-grained models to examine DNAzymes. At least at a qualitative level, it seems that many of the connections between DNAzyme physics and chemistry can be attributed to the generic properties of nucleic acids (stacking, Watson-Crick bonding, excluded volume, and semiflexibility), rather than the particular details of the functional forms used to model these interactions. This lends further support to the use of coarse-grained models (37–45) in general to elucidate the tertiary structure and transport properties of nucleic acids. Ultimately, as the field moves toward more detailed models, we anticipate that these future simulations will shed more light onto the key features of the coarse-grained structure of the 10-23 DNAzyme. For example, the three-bead model (44,45) more accurately captures the double-helical structure in the binding arms. As a result, we expect that this model might provide a more accurate measure of the bending angle. The absence of computational biophysical studies of DNAzymes makes it a fertile area for future work.

In light of its computational efficiency, the model used here should also be suitable for similar studies of related DNAzymes. However, coarse-grained DNAzyme simulations of this type are only the starting point for examining DNAzymes in silico. The tertiary structure produced by our coarse-grained simulations can serve as the initial conditions for atomistically detailed simulation models that resolve finer-scale features not captured by the extant coarse-grained models, such as explicit metal-ions, other salts, and explicit solvent. Indeed, we envision coarse-grained simulations as the first step in a hierarchical computational approach to elucidate the detailed structure of the nucleic acid complexes at the heart of both DNAzyme catalysis and emerging nanotechnology applications.

Supporting Material

One table is available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(09)01446-5.