Kinetics of the Multistep Rupture of Fibrin ‘A-a’ Polymerization Interactions Measured Using Atomic Force Microscopy

Abstract

Fibrin, the structural scaffold of blood clots, spontaneously polymerizes through the formation of ‘A-a’ knob-hole bonds. When subjected to external force, the dissociation of this bond is accompanied by two to four abrupt changes in molecular dimension observable as rupture events in a force curve. Herein, the configuration, molecular extension, and kinetic parameters of each rupture event are examined. The increases in contour length indicate that the D region of fibrinogen can lengthen by ∼50% of the length of a fibrin monomer before rupture of the ‘A-a’ interaction. The dependence of the dissociation rate on applied force was obtained using probability distributions of rupture forces collected at different pull-off velocities. These distributions were fit using a model in which the effects of the shape of the binding potential are used to quantify the kinetic parameters of forced dissociation. We found that the weak initial rupture (i.e., event 1) was not well approximated by these models. The ruptured bonds comprising the strongest ruptures, events 2 and 3, had kinetic parameters similar to those commonly found for the mechanical unfolding of globular proteins. The bonds ruptured in event 4 were well described by these analyses, but were more loosely bound than the bonds in events 2 and 3. We propose that the first event represents the rupture of an unknown interaction parallel to the ‘A-a’ bond, events 2 and 3 represent unfolding of structures in the D region of fibrinogen, and event 4 is the rupture of the ‘A-a’ knob-hole bond weakened by prior structural unfolding. Comparison of the activation energy obtained via force spectroscopy measurements with the thermodynamic free energy of ‘A-a’ bond dissociation indicates that the ‘A-a’ bond may be more resistant to rupture by applied force than to rupture by thermal dissociation.

Introduction

Fibrinogen is the precursor of fibrin monomer, a plasma protein that spontaneously polymerizes to form an insoluble branched network of fibrin fibers. The fibrin network serves as the structural scaffold of blood clots, which prevent blood loss and maintain the integrity of the cardiovascular system (1).

Fibrinogen is a 340-kDa glycoprotein consisting of two sets of three polypeptide chains, Aα, Bβ, and γ, that are linked together by 29 disulfide bonds forming three distinct structural regions. The central E region contains the N-termini of all six chains, whereas the two distal D regions both contain independently folded β- and γ-modules comprised of the C-termini of the Bβ and the γ chains, respectively (Fig. 1 A). The structural regions are connected by helical coiled coils consisting of all three chains to form a symmetrical D-E-D arrangement (2).

Figure 1.

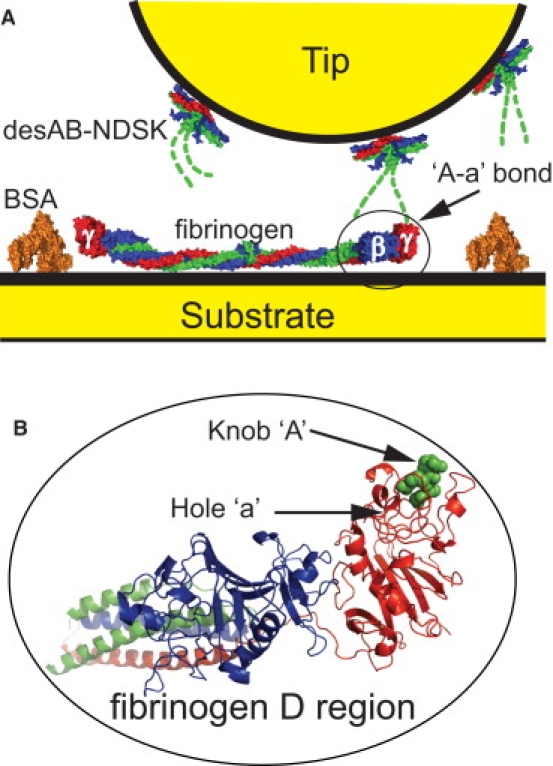
(A) Schematic of AFM experimental configuration. Space-filling models of fibrin fragment desAB-NDSK and fibrinogen colored by polypeptide chains α, β, and γ, and available in an online version of the article. The formation of an ‘A-a’ bond (circled) is shown between the γ-module of fibrinogen and knob ‘A’ of the desAB-NDSK fragment (dashed line). Knob ‘A’ (dashed line) does not appear in crystal structures and is thus approximated. Fibrin(ogen) knob ‘B’ and αC domains are not shown. (B) Detailed representation of ‘A-a’ bond showing fibrinogen D region (ribbons) with bound GPRP peptide (spheres). The GPRP peptide is knob ‘A’ peptide-mimetic. The following Protein Data Bank entries were used to generate protein models: 3GHG (fibrinogen), 2A45 (desAB-NDSK), 1BJ5 (BSA), and 1LTJ (fibrinogen D region with bound knob ‘A’). Scheme is not to scale. Protein models were generated with Pymol (DeLano Scientific, Palo Alto, CA).

Conversion of fibrinogen into fibrin monomer occurs when thrombin cleaves a short peptide from the N-terminus of each Aα chain, thus exposing the polymerization sites known as knobs ‘A’. Each knob ‘A’ noncovalently interacts with a complementary polymerization site known as hole ‘a’ in the γ-module of another fibrin molecule (Fig. 1). The ‘A-a’ knob-hole interaction results in the spontaneous formation of half-staggered, double-stranded fibrin polymers called protofibrils. Protofibrils grow and laterally aggregate to form an extensive branched network of fibrin fibers (2,3). During protofibril formation, thrombin also cleaves a short peptide from the N-terminus of each Bβ chain, exposing knobs ‘B’, which interact with complementary holes ‘b’ located in the β-module of other fibrin molecules. Although the ‘A-a’ interactions are known to be critical for fibrin polymerization, the role of the ‘B-b’ interactions, although important, remains less clear (4).

The fibrin polymer possesses unique mechanical properties that allow it to function in the flowing environment of blood; comprehensive reviews of mechanical properties of fibrin polymers can be found elsewhere (5–7). The response of the fibrin clot to mechanical force has been thought to be dependent on its architecture and on bending of individual fibers (8), although changes in the structure of the constituent monomers have also been implicated (9,10). Several complementary mechanisms involving different regions of the fibrin molecule have been proposed to account for the extensibility and elasticity of fibrin fibers, including full unfolding of the coiled-coil region (11,12), partial unfolding of the D regions (7,13), and extension of disordered repeat regions (12,14).

Since the fibrin network serves as the structural scaffold of a blood clot, it must routinely withstand the mechanical stresses associated with blood flow. This mechanical nature of the fibrin polymer is stimulating research aimed at understanding how each element of the supramolecular assembly responds to external forces. Therefore, both monomeric restructuring and the effects of force on intermolecular bonds should be examined. Herein, we focus on the ‘A-a’ knob-hole interactions as the most critical intermolecular interaction participating in the assembly of the fibrin polymer in that they initiate fibrin formation, ensure proper alignment of fibrin monomers, and influence the final polymer structure. In a previous study, using atomic force microscopy (AFM), we found that forced dissociation of the fibrin ‘A-a’ knob-hole bond was accompanied by a complex, reproducible force pattern consisting of several (2–4) rupture events (Fig. 2) (13). A rupture event (below also called an “event” for brevity) was defined as an abrupt change in force applied to the AFM probe, and each event corresponded to a change in the length of fibrinogen subjected to pulling force. We found that the pattern of events always exhibited a doublet of ruptures separated by ∼9 nm at pulling forces of ∼200 pN in magnitude. The rupture pattern may also contain a preceding and/or ensuing event of lower magnitude. The change in tip-substrate separation between each event was strikingly regular. We hypothesized that the ‘A-a’ interaction was solely responsible for the pattern, because the force pattern remained consistent when all known fibrin-fibrin interactions except for the ‘A-a’ interactions were eliminated. We have also shown that the structure of the knob-bearing molecule did not contribute to the pattern; however, changes in the structure of the D region were shown to influence the characteristic pattern, suggesting that unfolding of the D region of the fibrin molecule was responsible in part for the pattern of forced ‘A-a’ bond rupture.

Figure 2.

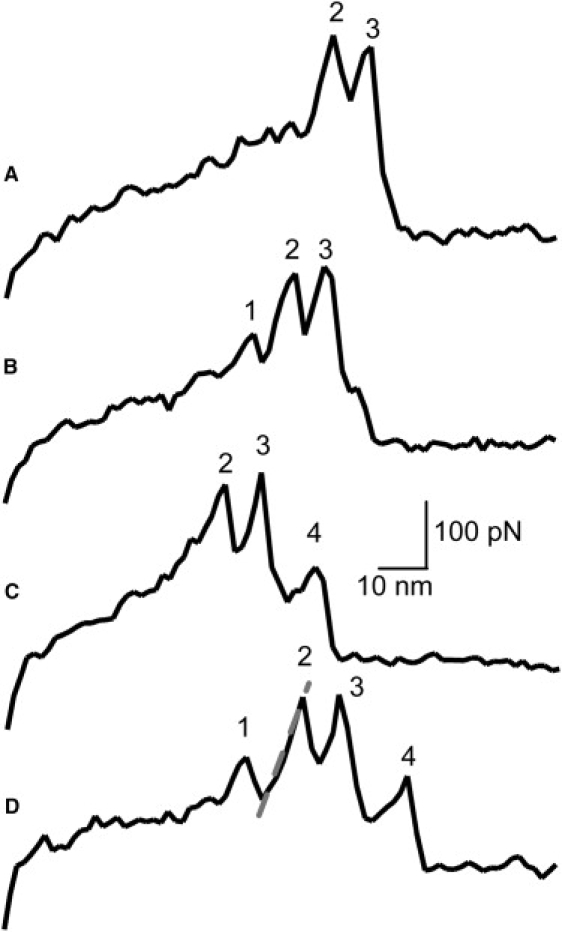
Force curves (restoring force in pN versus tip-substrate separation in nm) containing characteristic pattern of fibrin ‘A-a’ knob-hole forced dissociation. Four types of characteristic patterns were identified: doublet (A), doublet with preceding event (B), doublet with following event (C), and doublet with both preceding and following events (D). Event numbers are indicated. Linear approximation of slope before one event, as used for loading rate calculation, is shown as dashed gray line (the line is slightly offset for clarity).

In this study, in an attempt to gain molecular-level understanding about the mechanism of forced dissociation of ‘A-a’ bonds, several single-molecule force spectroscopy analysis techniques were utilized. First, the probability distributions of rupture forces were examined in an effort to understand the configuration of the bonds broken in each event. The extension of the protein before each event was then modeled as a freely jointed chain to obtain the changes in contour length after each event. Last, the kinetic parameters of each event were obtained using models from the arsenal of force spectroscopy techniques. Our data provide insight into the molecular mechanism of forced dissociation of the ‘A-a’ interaction and considerable extension of the D region under pulling force, and may further aid in elucidating the molecular mechanisms contributing to the mechanical properties of fibrin clots.

Materials and Methods

Materials

Reagents were of analytical grade and purchased from Sigma (St. Louis, MO) unless noted otherwise. Human plasma fibrinogen (FIB 1) and α-thrombin (HT 1002a) were purchased from Enzyme Research Laboratories (South Bend, IN). N-hydroxysuccinimide and 1-ethyl-3-(3dimethylaminopropyl) carbodiimide were purchased from Pierce Scientific (Rockford, IL). Water was purified with a Milli-Q UV Gradient A-10 system (Millipore, Bedford, MA) to a resistivity of 18.2 MΩ·cm.

Protein preparation

Normal (wild-type) recombinant fibrinogen was obtained as described elsewhere (15,16). Briefly, the fibrinogen was expressed in Chinese hamster ovary cells and purified using immunoaffinity chromatography on a column covalently modified with IF-1 monoclonal antibodies. After purification, the fibrinogen was dialyzed against HEPES-buffered saline (HBS, 20 mM HEPES and 150 mM NaCl, pH 7.4) buffer and stored at −80°C.

The desAB-NDSK fragment that represents the central region of fibrin and contains polymerization knobs ‘A’ and ‘B’ was obtained as described elsewhere (17). Briefly, plasma fibrinogen was clotted using thrombin, and the fibrin clot was digested by CNBr. The fragment was then separated using size-exclusion chromatography on a Superdex 200 column (Amersham Biosciences, Piscataway, NJ). The purified desAB-NDSK was characterized by sodium dodecyl sulfate polyacrylamide gel electrophoresis, dialyzed against HBS, and stored at −80°C.

AFM experiments

All surfaces for AFM experiments were prepared as described elsewhere (13). Briefly, clean glass microscope slides and silicon nitride DNP-S AFM cantilevers (Veeco Probes, Camarillo, CA) were coated with a 45-nm layer of gold as described elsewhere (18). Carboxylic-acid-terminated self-assembled monolayers were formed on the gold surfaces using a millimolar solution of 11-mercapto-undecanoic acid in absolute ethanol. For protein binding, the surfaces were activated using a mixture of equal volumes of 0.1 M N-hydroxysuccinimide and 0.4 M 1-ethyl-3-(3dimethylaminopropyl) carbodiimide in water for 30 min. Activated surfaces were then exposed to protein solutions in HBSC (20 mM HEPES, 150 mM NaCL, 3 mM CaCl₂, pH 7.4). The substrate was modified with a solution of equal parts recombinant fibrinogen (75 μg/mL) and bovine serum albumin (BSA) (100 μg/mL), whereas the cantilever was treated with the fragment desAB-NDSK (150 μg/mL). This protein arrangement meant that holes ‘a’ were on the substrate and knobs ‘A’ were on the tip (Fig. 1 A). The protein-modified surfaces were then washed with a series of buffers: first the AFM buffer (20 mM HEPES, 150 mM NaCl, 3 mM CaCl₂, 2 mg/mL BSA, and 0.1% Triton X-100, pH 7.4), then alternating high-salt (50 mM HEPES and 1 M NaCl, pH 7.4) and low-pH (50 mM NaOAc and 300 mM NaCl, pH 4.0) buffers to remove loosely attached protein.

AFM experiments were conducted using a Molecular Force Probe 3D instrument (Asylum Research, Santa Barbara, CA). Protein-coated substrates (tips and microscope slides) were allowed to equilibrate at room temperature in AFM buffer until the deflection signal stabilized (∼1 h). The spring constant was determined for each scan area before force curves were collected using the built-in thermal method. The average spring constant found for each probe was used in subsequent analysis. To vary the loading rate, each of the four cantilevers on the DNP-S chip was used, with spring constant measurements ranging from 45 to 240 pN/nm. In addition, the velocity of probe withdrawal was varied from 500 to 2000 nm/s, with the data sampling frequency varied simultaneously to maintain data density of 3 points/nm. With each combination of spring constant and retraction velocity, scans (32 × 32 arrays) consisting of 1024 force curves over at least three different 5 × 5-μm² surface areas were acquired.

Data analysis

Custom software written in MATLAB v. 7.1 (The MathWorks, Natick, MA) was used to analyze all data. The software first converted the cantilever deflection versus linear voltage displacement transformer signal into restoring force versus tip-substrate separation. Force events were then identified according to user-input filter criteria, described in the Supporting Material; ∼48% of all curves collected were identified as containing events. Since the focus of this study was the characteristic pattern of rupture of the fibrin ‘A-a’ bond (13), curves that did not exhibit this feature were excluded from the analysis. Curves containing the characteristic pattern were selected using multiple filters (for a full description, see Supporting Material). Examples of force curves not exhibiting the characteristic pattern are shown in Fig. S1 in the Supporting Material; ∼36% of the force curves exhibiting events contained the characteristic pattern and were included in the subsequent analysis. Four force-curve types were individually examined: those with just the doublet of events, those with the doublet and a preceding event, those with the doublet and a following event, and those with all four events. Neither the kinetic parameters nor the polymeric lengths for each event were found to be dependent on curve type. The numbers generated from each analysis method were averaged over all curve types, weighted by their respective errors (19).

Each force curve was modeled as a freely jointed chain (FJC) to extract the Kuhn length and contour length of the region of the protein that was lengthened by external force. The extension under force of a polymer approximated by the FJC model is described by

$$F=\left(k_{\mathrm{B}}T/a\right)L^{\ast }\left(R\right),$$ (1)

where a is the Kuhn length, k_BT is the thermal energy, R is the extension ratio (current end-to-end distance divided by the contour length), and L⁻¹(R)= y is the inverse Langevin function (the Langevin function is L(y) = coth(y) − 1/y). The current end-to-end distance was considered equal to the measured tip-substrate separation. The approximate closed-form function L⁻¹(R) = (1 − R)⁻¹ − (1 − R)² was used in the analysis (20). Each event in each curve was fit with this model using the least-squares regression analysis and allowing the Kuhn length, contour length, extension at rupture (i.e., length of the protein at the bond rupture), and slope from the rupture point to the baseline (i.e., the rate at which the AFM probe returns to the zero-deflection baseline, a constant determined by the spring constant of and viscous drag on the cantilever) to vary.

To examine whether events represented the extension of structures in series or in parallel, the extensions were modeled as either individual, independent functions (in the case of serial events) or sums of functions (in the case of parallel events), as described below (see also Fig. 3) (21). Once the curve was fit, the Kuhn length, contour length, rupture force, and position were recorded. The contour length and Kuhn length distributions were binned in 5- and 0.05-nm bins, respectively, and fit with Gaussian functions. The changes in contour length presented in Table 1, and the Kuhn lengths presented in Table S1 represent the averaged positions of the Gaussian fits for each event over all curve types, weighted by their respective standard deviations, as described above. If a distribution could not be fit with one Gaussian function with a positive position, it was fit with two Gaussian functions. The elastic energy stored in the molecule at rupture was calculated for each event in each curve using G = F_K × L_c × [ln(F/F_K) − ln(4π × sinh(F/F_K))], where L_c is the contour length and F_K = k_BT/a (22). The resulting energies were binned in 200-k_BT bins and fit with Gaussian functions.

Figure 3.

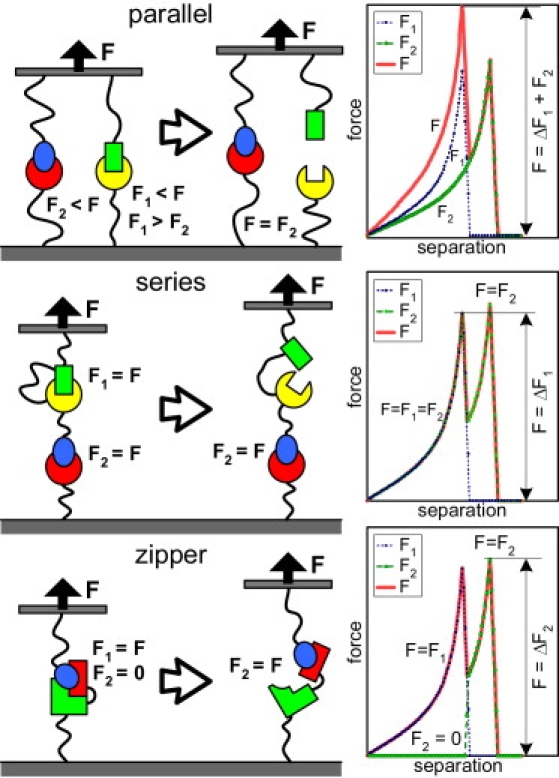
(Left) Schematic of parallel, series, and zipper bond configurations. The force experienced by each interaction (F₁ represents the first bond to rupture and F₂, the second), relative to total applied force (F), is indicated. (Right) Hypothetical force curves for each configuration, showing the total applied force (solid), F₁ (dotted), and F₂ (dashed). Select changes in restoring force in the force curves that correlate with the changes in force applied to each bond are indicated.

Table 1.

Contour lengths associated with each event in each curve type

Model	ΔL1 (nm)	ΔL2 (nm)	ΔL3 (nm)
Par	11 ± 6	6 ± 2	17 ± 6
Ser	3 ± 5, 36 ± 16	6 ± 2	16 ± 5

Increases in contour length obtained with events 1 and 2 in parallel (Par) and in series (Ser). Values represent averages of all curve types, weighted by the associated standard deviation. Errors represent the propagated standard deviation of each fitted parameter over n > 1000 force curves. Two values are given for populations that could not be fit with one Gaussian distribution centered at a positive value.

To examine the energy landscape of each event, a method introduced by Dudko et al. was used (23). This method was chosen for its ability to present force-spectroscopy data as dissociation rate (k_off) dependence on constant pulling force F. Such data representation is independent of loading rate, which may vary between and within experiments. Moreover, this approach automatically accounts for tether stiffening that might affect the extracted kinetic parameters (24). First, the force and loading rate distributions of each event in each curve type were converted into dissociation rate as a function of force by

$$k_{\text{off}}\left(F\right)=\frac{p\left(F\right)\dot{F}\left(F\right)}{\underset{F}{\overset{\mathrm{\infty }}{\int }}p\left(F\prime \right)dF\prime },$$ (2)

where p(F) is the normalized probability distribution and $\dot{F}$ is the loading rate (dF/dt). The data analysis was performed using a finite-difference version of Eq. 2 and force bins of 10 pN. Changing the bin size by twofold did not change the results significantly. The loading rate $\dot{F}$ associated with each force bin was defined as the median of the loading rate of the events with forces in the corresponding bin. The median loading rate was chosen to reduce the effect of outliers in the distribution. Results from different experiments (n = 18) were averaged, and the error in the dissociation rate was found as the error of the mean (19).

Because the log(k_off(F)) versus F trends for each event were curved, the Bell-Evans model was inadequate to extract information about the energy landscape of each rupture (25,26). Therefore, we used the model derived by Dudko et al. (27), which predicts a nonexponential dependence of dissociation rate on applied force:

$$k_{\mathrm{off}}\left(F\right)=k_{\mathrm{off}}\left(0\right){\left(1-\frac{\nu F{x}^{‡}}{\Delta G^{‡}}\right)}^{1/{\nu }^{-1}}\times \exp \left\{\beta \Delta G^{‡}\left[1-{\left(1-\frac{\nu F{x}^{‡}}{\Delta G^{‡}}\right)}^{1/\nu }\right]\right\},$$ (3)

where k_off(0) is the zero-force dissociation rate, ν is a scaling factor related to the shape of the energy well, x^‡ is the characteristic distance between the equilibrium state and the transition state at zero force, ΔG^‡ is the apparent activation free energy of the bond, and β = (k_BT)⁻¹ (27). A paraboloidal potential with a cusplike energy barrier (ν = 1/2) was assumed for all fits. The errors in the fit of each parameter were found with a covariance matrix (19).

Results

Force probability distribution

Since each event in a force curve represents some rupture on a molecular scale, the characteristic force curve shows that multiple inter- and/or intramolecular bonds are ruptured before final ‘A-a’ dissociation. The shape of the rupture force distribution of each event was used as a tool to determine the configuration of the bonds broken. The distribution of the force required to rupture a single bond has a typical shape (i.e., a single peak with a relatively long low force tail and a sharper drop-off at high forces) (28). If an event has a rupture force distribution exhibiting this shape, it most likely represents the rupture of a single bond.

We consider three possible arrangements of multiple interactions subjected to external force: in parallel, in series, or in a zipper configuration (Fig. 3). In a parallel configuration, the interactions share the load. In a series configuration, each interaction experiences the full load simultaneously. In a zipper configuration the interactions are arranged such that one interaction protects another from rupture; either one or both of the interactions may experience the full load. Therefore, bonds in series and zipper configurations will have rupture force distributions typical of a single bond, whereas bonds in parallel will not.

For comparison, Fig. 4 shows the rupture force distributions of each event in the characteristic pattern of ‘A-a’ bond rupture in a representative experiment. The force magnitude of event 1 was the most variable among experiments, suggesting that it may be in parallel with event 2. However, the experimental variation in the rupture force distribution of event 1 made this analysis inconclusive. The shapes of the rupture force distributions of events 2–4 were characteristic of single-bond ruptures. These results indicated that events 2–4 represented the rupture of bonds loaded in a series or zipper configuration, whereas there was not enough information to determine the configuration of event 1.

Figure 4.

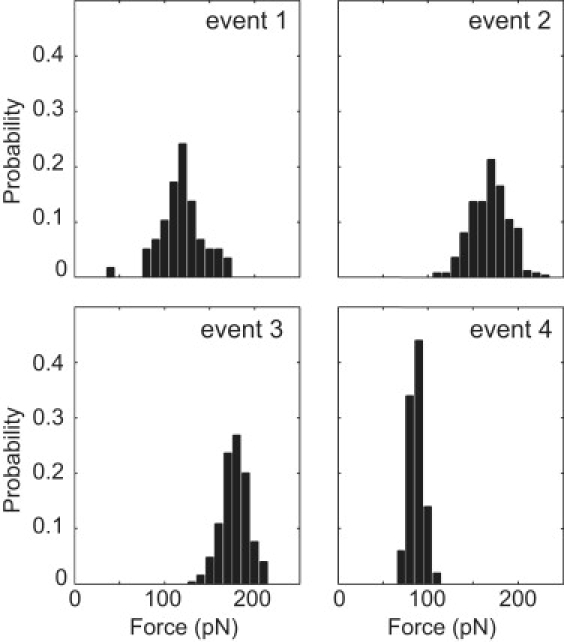
Probability distributions of the rupture forces in a representative experiment with tip retraction velocity of 1 μm/s and cantilever stiffness of 55 pN/nm.

For bonds in series, the weakest bond will break first, and bonds with approximately equal strength will have similar chances of first rupture. Bonds in a zipper configuration will always break in the same order. Events 2 and 3 were of the same force magnitude; however, they were followed by different changes in the length of the protein, indicating that they always occurred in the same order. Therefore, it is likely that these events were arranged in a zipper configuration. Since the rupture force of event 4 was much less than that of the previous events, it was also most likely in a zipper configuration.

Polymer modeling

To examine the polymeric extension of the protein at each event, the characteristic force curves were fit with the FJC model. Since the rupture force distribution of event 1 did not clearly define whether it occurred in series/zipper configuration or in parallel with event 2, both cases were examined. It was interesting to find that event 1 could be fit with either model (Fig. 5).

Figure 5.

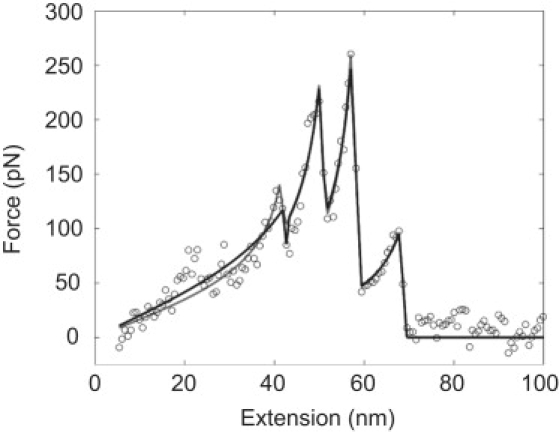
Representative four-event characteristic pattern force curve (circles) fit with the freely jointed chain model (lines). Least-square fits with event 1 in parallel (gray) and in series (black) with event 2 are shown. Events 2–4 were always fit in series configuration.

The contour length (i.e., end-to-end length of a fully extended protein) and Kuhn length (i.e., length of structural elements of the protein) of fibrinogen at each event were considered. The initial contour length was on the order of the molecular scale. However, our method of immobilization resulted in the protein attached at random orientation, causing large deviations in initial contour length (for examples, see Fig. 2). The changes in contour length after each event (ΔL) are shown in Table 1. Fig. S2 and Fig. S3 show the distributions and Gaussian fits of the contour length and Kuhn length parameters. The Kuhn length of each event is given in Table S1.

When the tip-substrate separation of each event relative to event 2 (i.e., relative separation) was plotted versus force, a characteristic fingerprint of the forced dissociation of fibrin(ogen) ‘A-a’ interaction was apparent (Fig. 6 A). Fig. 6, B and C, shows plots constructed with the force and FJC contour lengths obtained with event 1 in parallel and in series, respectively, with event 2. All events formed recognizable clusters when events 1 and 2 were in parallel, but event 1 was ill defined when events 1 and 2 were modeled in series. This indicated that events 1 and 2 most likely occur in a parallel configuration.

Figure 6.

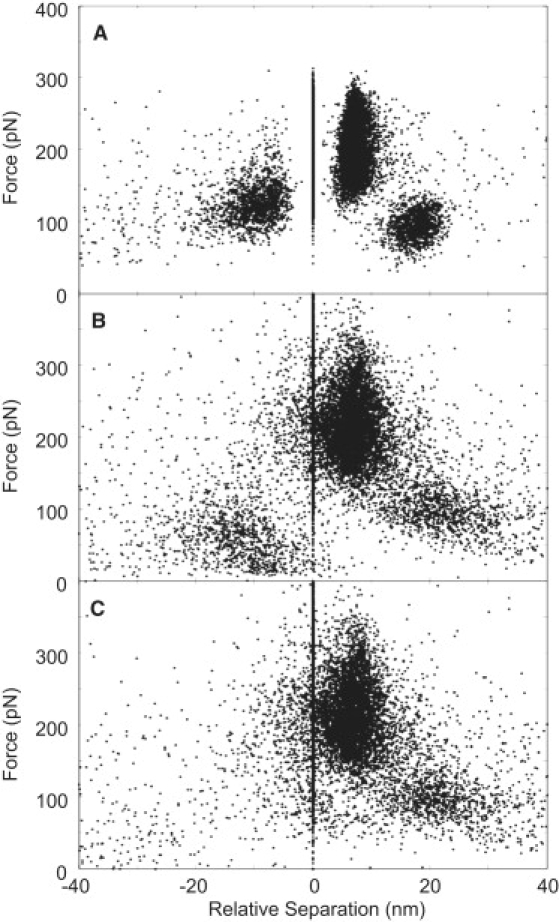
Characteristic force patterns of the rupture of interaction between fibrinogen and desAB-NDSK, where the rupture force is plotted versus relative separation (A) and versus relative contour length extracted from FJC fitted curves with events 1 and 2 modeled in parallel (B) and in series or zipper configuration (C).

Kinetic parameters

To examine the kinetic parameters of each event, the methodology suggested by Dudko et al. was used (23,27). The k_off(F) trends of each event are shown in Fig. 7. Since the characteristic pattern does not always include all four events, the dependence of each event's kinetic parameters on the presence of other events was examined. The events are apparently independent, as the difference in the “force spectra” between the curve types containing different numbers of events was less than the variation among experiments (Fig. 7 A). However, curves with all four events tended to have larger experimental error and were more scattered than other curve types. Such behavior was likely due to the relatively low population of this set, constituting ∼5% of the curves with a characteristic pattern of events. Also, events 2 and 3 were characterized by fewer data points at low forces in the presence of event 4 than in curves without event 4. Although we attribute this to the filter criterion that required events 2 and 3 to be at least 75 pN greater than event 4, this result did not affect the averaged k_off(F) dependencies of these events (see the Supporting Material for a full description of the data analysis procedure).

Figure 7.

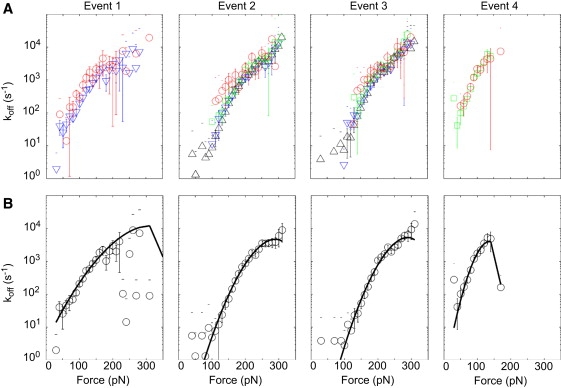
(A) Dissociation rates as a function of force for each event as it occurs in curves with just events 2 and 3 (▵), events 1–3 (▿), events 2–4 (^∗), and all four events (○), as identified in Fig. 2, where error bars represent error of the mean among experiments. (B) Dissociation rates as a function of force for each event, with curve types averaged and weighted by error (circles) and fit with Eq. 3 (line).

The averaged k_off(F) dependencies were fit with Eq. 3 using a least-squares regression (Fig. 7 B). Event 1 resulted in the fit with the largest root mean-square deviation from the data. The fit in the midforce region was good for each event, but deviated from the data at high- and low-force extremes. The low-force deviation was most likely due to lack of instrumental sensitivity in this regime. The high-force deviation was attributable to breakdown of the model used when the applied force approached the critical force, F_c = ΔG^‡/(νx^‡), where the energy barrier disappears. The F_c value calculated for each event (Table 2) was greater in magnitude than the majority of interactions observed, indicating that this model was appropriate for the force range of each interaction. The resulting kinetic parameters k_off(0), x^‡, and ΔG^‡, each of which was fit independently, are provided in Table 2. The resulting errors were not symmetric about the fit values; the first value corresponds to the negative error and the second value corresponds to the positive error.

Table 2.

Kinetic parameters for the forced dissociation of the ‘A-a’ interaction

	koff(0) (s−1)	x‡ (nm)	ΔG‡ (kBT)	Fc (pN)
Event 1	3.5 ± (3.7, 2.4)	0.21 ± (0.26, 0.08)	10.1 ± (5.6, 1.6)	400
Event 2	0.015 ± (0.005, 0.008)	0.41 ± (0.01, 0.02)	17.3 ± (0.5, 0.5)	350
Event 3	0.003 ± (0.001,0.002)	0.46 ± (0.04, 0.01)	19.1 ± (1.1, 0.3)	340
Event 4	0.27 ± (0.05, 0.007)	0.57 ± (0.01, 0.01)	11.7 ± (0.1, 0.3)	170

Discussion

The shape of the distribution of rupture forces for each event was examined to determine the configuration of the interactions broken at each instance (examples of considered configurations are shown in Fig. 3). Although it was not possible to determine the configuration of the bonds broken in event 1 using this analysis, the rupture force distributions of events 2–4 indicated that they were either in a zipper or series configuration. Of note, the shapes of the rupture force distribution for events 2–4 are indicative of single-bond ruptures; this result lends credence to the previous conclusion that the characteristic pattern represents the rupture of an interaction between a single pair of molecules. The invariable order of the last three events suggested that they were in a zipper configuration. By comparing the FJC model of events 1 and 2 when modeled in parallel and series, it became clear that event 1 likely represents extension of a structure parallel to event 2 (Fig. 6). The source of this parallel interaction remains unclear.

The initial contour length of the protein tether between the tip and substrate varied widely (data not shown), but was on the order of the length of fibrinogen and the desAB-NDSK fragment (∼45 nm and ∼10 nm in crystal structures, respectively). This dimension suggests that fibrinogen was often immobilized such that most of the molecule was available to extend in interactions exhibiting the characteristic event pattern. The increases in contour length after events 2 and 3 were ∼7 and 16 nm, respectively, for a total increase in contour length of ∼23 nm. Completely unfolding the globular region containing the hole (the γ-module) would contribute an increase of ∼38 nm in contour length, not including the disulfide loops and loops associated with binding of the knobs. It is assumed that the native length of this region is 2.4 nm and that individual peptides have a length of 0.35 nm. Therefore, an extension of 23 nm may reasonably be attributed to unfolding of portions of the γ-module.

Elastic energy stored by stretching the entire protein molecule before bond rupture can be estimated using parameters of the FJC model. Stored energy is ∼130, 1900, 2300, and 970 k_BT for events 1–4, respectively (Fig. S4). The stored elastic energy biases the energy landscape such that the bound species are in a metastable state. This stored energy is much larger than the energy barriers to dissociation of each event (Table 2). As seen from the sample force curves (Fig. 2), there is only partial relaxation of the elastic energy stored in the extended protein after each rupture. However, the magnitude of this relaxation is significant, making bond reformation unlikely. Therefore, the force-driven bond ruptures are likely irreversible in experiments when the tip-sample separation is monotonically increasing.

The kinetic parameters of events 2 and 3 are similar to the kinetic parameters of proteins unfolding by force (29,30). This observation substantiates the hypothesis that events 2 and 3 represent unfolding of the γ-module of fibrinogen. It is interesting to note that event 4, which represents final rupture of the ‘A-a’ knob-hole bond, was considerably less tightly bound than events 2 and 3, with a k_off(0) two orders of magnitude larger. The values of k_off(0) and x^‡ previously found for the ‘A-a’ knob-hole interaction by Litvinov et al. were 10⁻³−10⁻⁴ s⁻¹ and 0.3 nm, respectively (31). These values are comparable to the kinetic parameters returned for events 2 and 3 by our method. It is likely that the limited spatial resolution associated with optical tweezers did not allow Litvinov et al. to resolve both unfolding and unbinding events.

The thermodynamic free energy (ΔG) of fibrin polymerization has been reported to be in the range 13.4–21.6 k_BT/molecule, or 6.7–10.8 k_BT for the equivalent of one ‘A-a’ bond (32,33). The stepwise rupture of the ‘A-a’ bond in our system requires a series of energetic barriers associated with events 2–4 to be overcome before final dissociation of knob ‘A’ from hole ‘a’. The sum of the free energy differences (ΔG^‡) of these bonds is 36 (events 2 and 3)–48 k_BT (events 2–4), depending on whether final rupture of the ‘A-a’ bond occurs at event 3 or event 4. Therefore, the thermodynamic ΔG is a fraction of ΔG^‡ extracted from our pulling experiments, regardless of whether the ‘A-a’ bond breaks after event 3 or event 4. Simulations by Best et al. have indicated that ΔG^‡ might be considerably higher than the corresponding ΔG if mechanical pulling does not probe a “good” reaction coordinate (i.e., one that mimics thermodynamic behavior) (34). This suggests that the ‘A-a’ bond may be more resistant to mechanical force than to thermal dissociation.

We propose a mechanism to explain the phenomena represented by the four events in the characteristic force pattern. First, the fibrinogen molecule may reorient when pulled by the desAB-NDSK molecule attached to the tip, causing parallel extension and desorption from the substrate or from the tip of the probe (event 1). As the tip continues to pull away, force on the ‘A-a’ interaction results in partial unfolding of the region containing hole ‘a’ (events 2 and 3). Unfolding this region may destabilize the hole, leading to a weakened ‘A-a’ bond, and allow the knob to dissociate at a lower force, represented by event 4. We hypothesize that each event in the characteristic force curve may represent a structural intermediate in the unfolding pathway of the γ-module of fibrinogen when force is applied to the ‘A-a’ bond. That event 4 does not always occur suggests that the structure it represents constitutes a less populated intermediate than the structure represented by event 2, for example.

Our results indicate that each fibrin ‘A-a’ interaction can be maintained for strains of 50% (23 nm) before rupture. Future experiments are planned to investigate whether this unfolding mechanism is reversible, as it may contribute to the reversible extensibility of fibrin fibers that have not been ligated by Factor XIII. Such unfolding has been predicted in the literature (7). Furthermore, these results suggest that the ‘A-a’ interaction resists mechanical rupture more strongly than thermal dissociation. Although further investigation is necessary to determine precisely which domains unfold, the analysis presented herein provides a model and critical parameters to guide future studies.

Supporting Material

Data analysis and filtering, a table, and four figures are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(09)01433-7.