Wave Propagation in Lipid Monolayers

Abstract

Sound waves are excited on lipid monolayers using a set of planar electrodes aligned in parallel with the excitable medium. By measuring the frequency-dependent change in the lateral pressure, we are able to extract the sound velocity for the entire monolayer phase diagram. We demonstrate that this velocity can also be directly derived from the lipid monolayer compressibility, and consequently displays a minimum in the phase transition regime. This minimum decreases from v₀ = 170 m/s for one-component lipid monolayers down to v_m = 50 m/s for lipid mixtures. No significant attenuation can be detected confirming an adiabatic phenomenon. Finally, our data propose a relative lateral density oscillation of Δρ/ρ ∼2%, implying a change in all area-dependent physical properties. Order-of-magnitude estimates from static couplings therefore predict propagating changes in surface potential of 1–50 mV, 1 unit in pH (electrochemical potential), and 0.01 K in temperature, and fall within the same order of magnitude as physical changes measured during nerve pulse propagation. These results therefore strongly support the idea of propagating adiabatic sound waves along nerves as first thoroughly described by Kaufmann in 1989 and recently by Heimburg and Jackson, but already claimed by Wilke in 1912.

Introduction

The lipid monolayer is ubiquitously present in biology as one-half of the cell, organelle, or vesicle membrane. A complete understanding of the physical properties of lipid monolayers is therefore of fundamental interest to understand its role for biological bilayer systems.

Studying sound propagation in insoluble organic films the lipid monolayer obtains its attraction from the fact that most physical properties (lateral pressure, area per molecule, compressibility, surface potential, temperature, etc.) are easily accessible (1). Consequently lipid monolayers have been investigated very intensively from various viewpoints of physics and physical chemistry (see (1–4) and references therein). On the other hand, very few studies have addressed internal excitations or wave propagation within lipid monolayers (5). If, however, two-dimensional adiabatic excitations are present in simple lipid monolayer systems, their absence in complex biological lipid membranes appears very unlikely.

Here, we present both experimental and theoretical studies on adiabatic sound-wave propagation in lipid monolayers. Experimentally, lipid monolayers are excited by an alternating in-plane electric field (in-plane excitation electrodes, IPE) originating from a set of laterally patterned electrodes (interdigital transducers, IDT). For certain distinct frequencies f, we find pronounced changes in the lateral pressure that suggests electrical excitation with an underlying resonance phenomenon. This, in turn, allows us to extract, in detail, the variable sound velocity of the propagating wave by matching the excitation frequency f with the distance d between two planar electrodes, defining an imposed wavelength.

Thermodynamic analysis of the problem reveals that both the lateral pressure change and the sound velocity for the different thermodynamic states can be directly derived from the lipid monolayer phase diagram and gives clear evidence for the existence of a propagating, adiabatic sound wave. Order-of-magnitude estimates suggest that the origin of the decoupled propagation may be a consequence of the different sound velocities in two and three dimensions as well as the increased heat conductivity of the boundary water layer.

Materials and Methods

Lipids 1,2-dipalmitoyl-sn-glycero-3-[phospho-rac-(1-glycerol)] (DPPG) and 1,2-dipalmitoyl-sn-glycero-3-phosphocholine (DPPC) dissolved in chloroform were purchased from Avanti Polar Lipids (Birmingham, AL) and used without further purification.

All measurements were done on a standard film balance with a heat bath (NIMA, Coventry, England) modified by a small stage to position the excitation chips with the IDT structure. Standard isotherms could be recorded and the regulation circuit of the film balance allowed it to hold a specific pressure of the monolayer for measuring the area expansion coefficient α(T).

The IPE chips were produced by standard lithography method, using LiTaO3 as substrate for the gold electrodes. The interdigitated gold electrodes (finger spacing w ≈ 10 μm) were connected to an radio frequency (RF) amplifier (ZHL-2010+; Mini-Circuits, Brooklyn, NY), which was driven by a signal generator (SML 01; Rhode & Schwarz, Munich, Germany). Such chips are routinely used in our lab for surface acoustic wave studies, including microfluidic and sensor applications. Here, however, we operate the chips to generate RF electric fields coupling to the lipid monolayers only and at frequencies where no surface waves of the substrate are resonantly excited.

To obtain lipid mixtures, lipids dissolved in chloroform were mixed in the desired proportions. Before spreading the lipid monolayers on the air-water interface, the chip and the Wilhelmy plate were placed on the surface of the trough as described later in Fig. 2. Frequency sweeps between f = 0 and f = 27 MHz were performed during 30 min, whereas the pressure was recorded simultaneously.

Figure 2.

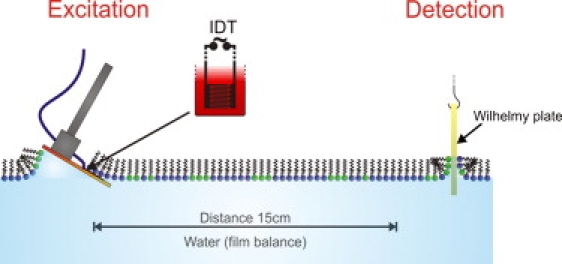
The IPE setup. A set of electrodes, IDTs, is used to create a local (electrode distance ≈10 μm) oscillating electric field in the plane of the lipid monolayer, which excites a propagating wave by local lateral polarization of the membrane. The substrate is LiTaO₃ being coated with SiO₂. For IPEs contacting directly from above the monolayer (not shown in the picture) the SiO₂ is additionally rendered hydrophobic for establishing a tight contact between the IPE chip and the lipid monolayer (silanized). The change in lateral pressure is determined by the force on a Wilhelmy plate dipped into the monolayer.

Results and Discussion

Theory

Fundamental thermodynamic relations

In Einstein's first publication in 1901, he approved our crucial assumption: applying a Carnot cycle to a free surface, he demonstrated that the interface of a water drop must have its own heat (heat capacity) and therefore its own entropy S^I (6,7). Our experiments as well as order-of-magnitude estimates will demonstrate that a lipid monolayer at the air/water interface has its own entropy S^I as well, and has, therefore, to be considered as an independent thermodynamic system. To realize the meaning of S^I for the experiment, it is very helpful to recall that it is the second derivative of S^I with respect to a thermodynamic variable x that is related to the generalized susceptibilities by (8)

$$k_{\mathrm{B}}{\left(\frac{{\partial }^2{S}^{\mathrm{I}}}{\partial x_{\mathrm{i}}^2}\right)}^{-1}\equiv -k_{\mathrm{B}}{\left(\frac{\partial x_{\mathrm{i}}}{\partial X_{\mathrm{i}}}\right)}_{X_{\mathrm{J}\ne \mathrm{i}}}\text{.}$$ (1)

Here k_B denotes the Boltzmann constant and

$$X_{\mathrm{i}}=-\frac{\partial S^{\mathrm{I}}}{\partial x_{\mathrm{i}}}\left(\text{e.g.},X_i=\frac{\pi }{T_{}},\frac{\mu }{T_{}},\dots \right),$$

the corresponding thermodynamic force. For x_i = A and constant temperature, this results in

$$k_{\mathrm{B}}{\left(\frac{{\partial }^2{S}^I}{\partial A^2}\right)}_{\mathrm{T}}^{-1}=-k_{\mathrm{B}}TA{\kappa }_{\mathrm{T}},$$ (2)

where

$${\kappa }_{\mathrm{T}}=-\frac{1}{A}{\frac{\partial A}{\partial \pi }|}_{\mathrm{T}}\text{.}$$ (3)

This is the lateral isothermal compressibility of the lipid monolayer, which can be directly derived from the pressure-area isotherm (Fig. 1). Hence, the mechanical properties of the lipid monolayer represent a measure of the susceptibility, i.e., inverse curvature of the entropy potential. A maximum in κ_T as observed in the phase transition regime corresponds to a flat entropy potential. It should be noted that different boundary conditions (keeping T, q, μ, or N, etc., constant) will result in different potentials, evidenced by, for example, different one-dimensional projections of the same n-dimensional potential.

Figure 1.

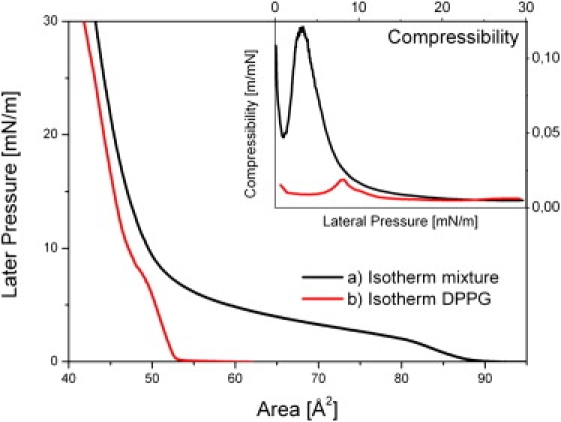
Isotherms of lipid monolayers for DPPG at 14°C and for a mixture of DPPC/DPPG as 10:1 at 20°C. Both isotherms show maxima in the compressibility at ∼8 mN/m for DPPG and at ∼2.5 mN/m for the mixture, whereas the later clearly corresponds to the phase transition regime. The inset shows the resulting compressibility of the corresponding monolayer. As for the IPE setup, a standard film balance was used for the measurements.

Estimation of ${\kappa }_{{\mathrm{S}}^{\mathrm{I}}}$ from κ_T

In principle, the velocity c₀ could be estimated within an order of magnitude by using κ_T. The easy accessibility of the thermal expansion coefficient α, however, enables us to get a better estimate of the adiabatic compressibility ${\kappa }_{{\mathrm{S}}^{\mathrm{I}}}$ using the thermodynamic relation (9)

$${\kappa }_{{\mathrm{S}}^{\mathrm{I}}}\approx {\kappa }_{\mathrm{T}}-\frac{T}{A{c}_{\pi }}{\left(\frac{\partial A}{\partial T}\right)}_{\pi }^2,$$ (4)

where c_π represents the heat capacity at constant pressure and

$$\alpha ={\frac{1}{A}\frac{\partial A}{\partial T}|}_{\pi }$$

the isobaric expansion coefficient. Even though this relationship is used quite commonly, it should be noted that it strictly holds only for a system defined by π, A, and T and will carry additional terms, when charge, dipole, chemical potential, etc., are included. Nevertheless, extracting κ_T and α_π from the experiment and approximating c_π by using the experimentally established correspondence between change in enthalpy ΔH and area ΔA (9),

$$\Delta H\approx \gamma \Delta A,$$ (5a)

and therefore,

$$\Delta c_{\pi }\approx \gamma {\left(\frac{dA}{dT}\right)}_{\pi }\text{.}$$ (5b)

Equation 4 can now be used to estimate the propagation velocity c₀ of a sound wave, which in the linear case is given from the fundamental thermodynamic relation

$$c_0=\sqrt{1/\rho {\kappa }_{{\mathrm{S}}^{\mathrm{I}}}}\text{.}$$ (6)

Here, ρ is the area per molecule, an experimentally well-controllable quantity. Since both κ_T as well as κ_T exhibit a maximum in the phase transition regime, the sound velocity is expected to undergo a minimum near the isothermal phase transition of the lipid monolayer. Clearly, inseparable from the excited sound wave, a temperature wave must propagate along the lipid monolayer as well. Knowing the propagating area density oscillation, an estimate of the accompanied temperature change can be extracted from the isothermal expansion and the heat capacity of the monolayer by (10)

$$\Delta T=T{c}_{0}vA\frac{{\alpha }_{\pi }}{c_{\pi }}\Delta \rho \approx T{c}_{0}v{\gamma }^{-1}\Delta \rho ,$$ (7)

where v is the particle velocity and Eq. 5b has been applied as well. Again, even commonly used, this strictly holds only for a system defined by π, A, and T.

Experiments

Excitation of sound waves by planar electrodes

When a thermodynamic system is forced out of its equilibrium position, the conservation of entropy requires a propagation phenomenon. In this sense, the observation of sound propagation in lipid monolayers would provide additional support such that the lipid membrane interface can be considered as a closed two-dimensional system, fairly well decoupled from the surrounding bulk bath. Qualitatively, a flat thermodynamic potential implies weak restoring forces and therefore a lower propagation velocity as for steep potentials.

In our experiments, the excitation of propagating sound waves along the lipid membrane was accomplished by incorporating a chip with a planar array of gold electrodes (in-plane excitation, IPE) in the plane of a negatively charged DPPG monolayer (Fig. 2). Traditionally, such IDTs are used as filters in RF applications or to create acoustic streaming in microfluidic systems (11,12). Another application of IDT: sensors comparable to the well-known quartz crystal microbalance (13,14). Here, however, we use such electrodes to excite in-plane waves on soft interfaces at various frequencies by electro-mechanical coupling to a polarizable membrane. We employ the fact that a lateral density oscillation ρ = ρ₀ + B · cos ωt creates a net pressure increase Δπ. This is due to a nonlinear pressure-area relationship π(A) and can be calculated with the help of the isotherm by simply integrating the pressure change over one period:

$$\overline{\Delta \pi }=\frac{\omega }{2\pi }\underset{0}{\overset{\frac{\omega }{2\pi }}{\int }}\pi \left(A\left(t\right)\right)dt-\pi \left(A\right)\text{.}$$ (8a)

The same expression can be written in terms of the mass density ρ:

$$\overline{\Delta \pi }=\frac{\omega }{2\pi }\underset{0}{\overset{\frac{\omega }{2\pi }}{\int }}\pi \left(\frac{m_{\text{Lipids}}}{{\rho }_0+B·\cos \omega t}\right)dt-\pi \left(\frac{m_{\text{Lipids}}}{{\rho }_0}\right)\text{.}$$ (8b)

Here, ω is the angular frequency of the traveling wave, B its amplitude, ρ₀ the lateral density in rest, and m_lipids the mass of the lipids forming the monolayer. The first term on the right side of Eq. 8 represents the time-averaged pressure change due to the modulation in the interface, whereas the second term denotes the undisturbed lipid monolayer.

If adiabatic propagation would indeed take place, Eq. 8 predicts a net increase in lateral pressure. The pressure spectrum of a DPPG monolayer shown in Fig. 3 confirms that such an increase takes place indeed. The average change in lateral pressure $\overline{\Delta \pi }$ detected during the excitation of the wave is plotted as a function of the stimulating frequency applied to the chip for three different configurations. Between f = 100 kHz and f = 27 MHz, a pure water surface does not produce any significant response. Nevertheless at a distance of 2 cm at ∼f = 33 MHz, pure water may also show a response. The origin of this signal is presently still unknown, but may be attributed to surface capillary water waves (15). The presence of a DPPG monolayer on this surface, however, results in a pronounced variation in $\overline{\Delta \pi }$ at ∼f = 11 MHz. Importantly, the response at f = 11 MHz is also not visible on the pure water surface at shorter distances between excitation and detection. We therefore conclude that the change of $\overline{\Delta \pi }$ at ∼f = 11 MHz can, ubiquitously, be attributed to the presence of the lipid membrane and will be used for further data interpretation.

Figure 3.

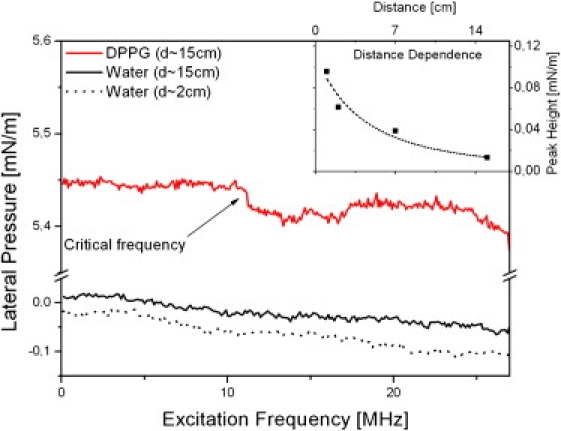
Frequency spectra of the nonlinear pressure change induced by the IPE chip in a DPPG lipid monolayer (red curve) or pure water for different distances d (black for d = 15 cm, solid line; and d = 2 cm, dotted line). At lower frequencies, the applied electric field does not affect the average lateral pressure, being measured by a Wilhelmy plate (see Fig. 1). However, at certain frequencies (here 10.9 MHz and 33 MHz), the lateral pressure significantly drops. The critical frequency (ν_crit) on the x axis can be changed by altering the overall lateral pressure. We calculate the propagation velocity (c₀ = λν_crit) from the finger spacing of the stimulating electrodes and the measured critical frequency ν_crit. The inset shows that attenuation is negligible. In fact, an exponential fit would lead to a decay length of ∼1 m.

Attenuation and amplitude of the wave

Considering the macroscopic (15 cm) distance between excitation and detection, the propagation of the wave does not seem to be significantly attenuated. To experimentally verify this finding, we measured the change in lateral pressure $\overline{\Delta \pi }$ as a function of distance from the source of excitation (see inset of Fig. 3). It turns out that the experimental data can be well fitted by a polynomial $\overline{\Delta \pi }\left(x\right)\propto -{\left(x-b\right)}^{-2}$, but not with an exponential decay function. This supports the idea of an adiabatic wave with decay due only to the geometry of the system but little dissipation.

Finally, the amplitude of the excited wave can be estimated by comparing the experimentally observed $\overline{\Delta \pi }$ to Eq. 8 and reveals a density variation B ≈ 0.02ρ₀ (± 0.005ρ₀). This, in turn, would result in a density modulation amplitude of ∼B ∼ 0.3 · 10⁻⁷ kg/m², which is well within reason for lipid monolayers.

Sound velocity from lateral pressure changes

The observed $\overline{\Delta \pi }$ clearly exhibits a frequency dependence (Fig. 3) with an apparent resonance-like feature at f = 11 MHz, indicating significant excitation at this point. It appears that sound velocity c₀, electrode spacing d, and stimulating frequency ν₀ are ideally matched at exactly this frequency to provide effective excitation. Taking the finger spacing between two electrodes d = 12 μm (therefore λ = 24 μm) and the resonance frequency ν₀ = 11 MHz from the experiment, we find a propagation velocity of c₀ = λν₀ = 260 m/s.

Following the same procedure, we repeated the experiment along the entire isotherm, also including the phase transition regime, and extracted the corresponding sound velocity. It turns out that the different thermodynamic states of the monolayer indeed exhibit different excitation frequencies ν₀, as can be seen in Fig. 4 for three different surface pressures.

Figure 4.

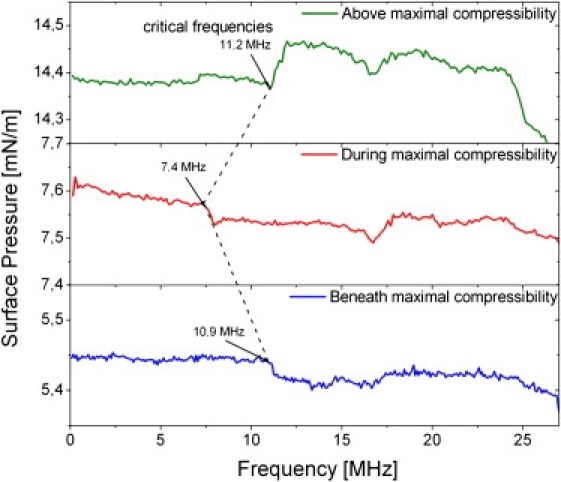
Frequency spectra of the lateral pressure change, measured for different surface pressures in a DPPG lipid monolayer at T = 14°C. The pressures are chosen to represent the different phases of the monolayer. The critical frequencies, where the nonlinear pressure change occurs for the first time, are marked. During maximum compressibility, the critical frequency is at a clearly lower value than for the other phase states. Note that $\overline{\Delta \pi }$ > 0 above the maximum compressibility, and $\overline{\Delta \pi }$ < 0 elsewhere. This is correctly predicted by the assumption of an oscillating density wave (Eq. 8).

A critical test whether the origin of the observed pressure change is indeed a lateral density oscillation arises from the fact that Eq. 8 predicts a negative change in $\overline{\Delta \pi }$ in and below the maximum compressibility, while $\overline{\Delta \pi }$ is positive for pressures above the maximum. Clearly, this behavior is qualitatively and quantitatively reproduced in Fig. 4, and does, therefore, strongly support our assumption of a propagating sound wave along the interface.

Sound velocity from the monolayer compressibility

The experiments described above enabled us to extract the sound velocities along the entire isotherm. If this represents indeed a two-dimensional sound wave, the velocity c₀ should directly depend on the adiabatic lateral compressibility (Eq. 6). Even though κ_T will produce the right order of magnitude for the sound velocity, we exploit the fact that all other susceptibilities appearing in Eq. 4 can be extracted from the monolayer isotherm as well, and will provide the basis to calculate a more accurate κ_S. Therefore α_π was measured from the A(T) isobars for different lateral pressures, to calculate a more accurate approximation of κ_S. c_π was calculated by applying Eq. 5, which should give a good estimate at least close to the phase transition regime (9). Finally, comparing the propagation velocities as being calculated from Eq. 6 and the measured sound velocities using c₀= λν₀, we find both qualitative and quantitative agreement within 10% or less (Fig. 5 a), confirming the existence of a propagating sound wave.

Figure 5.

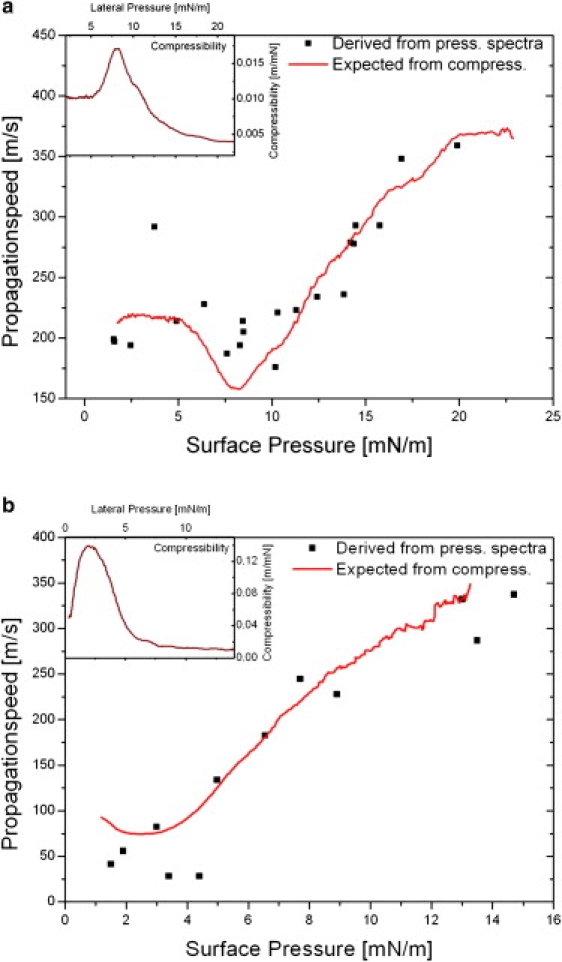
Propagation velocities along the lipid monolayer, measured as described in Fig. 2 (solid squares), and calculated from the adiabatic compressibility, as described in the text (line). The insets show the experimentally obtained isothermal compressibility used for the calculation of c₀. (a) Velocity curves for DPPG and (b) for a mixture of DPPG and DPPC (1:10). For high lateral pressures, the agreement between c₀ values as being predicted from the adiabatic compressibility and the experimentally determined velocity is within <5%. In the phase transition and for the lower pressure regime the deviation increases, but still falls within a 10% error bar. The origin of the deviation may be because the monolayer becomes less stable at low pressures. Note the larger errors around the maximum in compressibility. These probably correspond to the increased sensitivity of κ_s to oscillations in density in that region.

In particular, the minimum in propagation speed, because of the maximum in κ_T, is resolved. The same qualitative behavior is observed for a mixture of DPPG/DPPC (1:10). Again, excellent quantitative agreement is achieved between c₀ calculated from Eq. 4 and the experimental pressure spectra (Fig. 5 b). For this lipid, however, the minimum velocity predicted from the isotherm and confirmed experimentally is only c₀ = 50 m/s, corresponding to the phase transition regime between the liquid-expanded and liquid-condensed phases. This finding illustrates that both physical parameters (lateral pressure, temperature, etc.) and the composition of the monolayer control the propagation velocity.

On the coupling between monolayer and bulk

The only reasonable propagation mechanism for our system is one in which heat and entropy S_I (Eqs. 1–3) of the interface are approximately conserved (no exponential decay in wave energy). Therefore, the fact that only weakly damped wave propagation is experimentally observed (see inset of Fig. 3) calls for a decoupling between monolayer and bulk. Although, this is an experimental result and strongly supported by Einstein's early work on the heat of surfaces (7), we would like to outline another argument that assumes coupling but will demonstrate its insignificance at the same time. Following closely the book of Landau and Lifschitz (10), we present an order-of-magnitude estimate of why the lipid monolayer may be decoupled from the bulk.

When a wave propagates in media-1 (monolayer) at the interface to an adjacent media-2 (bulk water), the reflection coefficient R depends on the angle of incident θ, the density ρ, and sound velocity c of the two media (10):

$$R={\left[\frac{{\rho }_2{c}_2\cos \theta -{\rho }_1\sqrt{\left(c_1^2-c_2^2{\sin }^2\theta \right)}}{{\rho }_2{c}_2\cos \theta +{\rho }_1\sqrt{\left(c_1^2-c_2^2{\sin }^2\theta \right)}}\right]}^2\text{.}$$ (9)

If the incident wave forms an angle of less than the critical angle θ_c, where sinθ_c = c₁/c₂ (10), the entire wave is reflected (total internal reflection). Taking c₁ ∼100 m/s and c₂ ∼1500 m/s, we obtain a critical angle of θ₀ ≈ 5° for our arrangement. Lateral waves excited within the lipid monolayer will, therefore, be completely reflected. In this situation, Landau and Lifschitz (10) demonstrate that oscillations parallel to the interface of exponential decay in amplitude are created. These oscillations, however, do not provide significant dissipation as their exponential penetration into the bulk only resembles the energy distribution of the oscillating, propagating sound wave around the interface, and must not be mistaken as being the actual transport of energy out of the system, but as inseparable from the wave.

Similar arguments hold for the dissipation of heat. If the heat remains within the typical spatial extension of the sound wave, dissipation cannot be significant. As the temperature variations in the system are a direct consequence of the wave oscillations, the temperature changes perpendicular to the interface must be exponential as well (10),

$$T=T_0\exp \left(-z\sqrt{\frac{\omega }{2\chi }}\right)\exp \left(i\left[z\sqrt{\frac{\omega }{2\chi }}-\omega t\right]\right),$$ (10a)

where ω = 2πf, and χ is the thermometric conductivity which can be calculated from the heat capacity c_P, the density ρ, and the thermal conductivity k of the system (10)

$$\chi =\frac{k}{c_{\mathrm{P}}·\rho }\text{.}$$ (10b)

Following Landau and Lifschitz (10), the extension or viscous penetration depth δ in z direction (Fig. 6) can be estimated from

$$\delta =\sqrt{\frac{2\eta }{\rho \omega }},$$ (11)

where η is the dynamic and η/ρ the kinematic viscosity of water. Using standard numbers for water, this depth turns out to be δ ≈ 300 nm. To estimate whether thermal diffusion can add significantly to the dissipation process, we need to compare δ with the thermal penetration length ξ,

$$\xi =\sqrt{\frac{2\chi }{\omega }},$$ (12)

where χ denotes the thermometric conductivity (see Eq. 10b). This length scale describes over what distance a significant change in temperature takes place. Using c_p ≈ 4 kJ(kg K)⁻¹ and k ≈ 0.6 J(m Ks)⁻¹, we arrive at ξ ≈ 100 nm. Since δ ≥ ξ, the heat is, even when assuming coupling to the bulk, unable to escape the spatial extension of the sound wave within the timescale of compression (0.5 · 10⁻⁷ s here). In other words, Eq. 10a simply describes the reversible temperature oscillations inside the sound wave.

Figure 6.

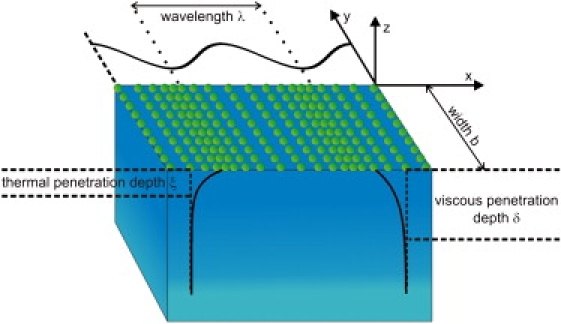
Schematic representation of the important length scales of the system. Both viscous (δ) and thermal (ξ) penetration depths and the geometry of the system are marked. While the lateral density wave propagates along the x-y plane, oscillations both in density and in temperature decay exponentially along the z direction. The density length scale (δ) is of the same order or larger than the thermal penetration depth (ξ), and therefore proposes negligible dissipation of heat into the bulk water.

Finally, heat could also dissipate within the monolayer plane. This is to be predicted from a two-dimensional shear viscosity observed in lipid monolayers. To estimate the corresponding loss inside the monolayer, we may also compare the length scale l of heat dissipation within the time of one compression/expansion cycle t = f₀⁻¹ to the wavelength λ. Only if the heat expands (diffuses) during t over a distance l, which is of the same order of magnitude as the wavelength λ, is significant dissipation to be expected. According to Landau, l can be calculated from the solution of the general equation of heat transfer (10),

$$l^2\approx \chi \tau ,$$ (13)

where χ is the aforementioned thermometric conductivity (Eq. 10b). Unfortunately, to our knowledge, no numbers for the heat conductivity k_I of lipid monolayers exist. However, k_I may be approximated by the heat conductivity of interfacial or boundary water, which has experimentally been observed on lipid membranes (16,17). Using k_I ≈ 6 J/m Ks (which is one order-of-magnitude larger than for bulk water) (18), then c_p ≈ 10 kJ/kg K (19), and τ ≈ t the lateral extension of heat due to thermal diffusion l ≈ 200 nm, which is ∼100 times smaller than the wavelength (λ ∼24 μm). Therefore, the heat cannot escape the propagating wave in the lateral direction either.

To summarize this paragraph, we would like to state that neither mechanical nor thermal coupling properties support the admittedly intuitive prejudice of a strongly attenuated (since coupled) wave, but are in agreement with our experimental observation of a propagating, only weakly attenuated sound wave.

Conclusion and Biological Impact

A new approach to excite and detect acoustic waves in lipid monolayers is presented. Moreover, the existence of adiabatic sound waves is experimentally confirmed and the corresponding sound velocities are extracted from our measurements. Comparison of our findings with theoretical predictions provide excellent agreement and reveal velocities between 300 m/s and 170 m/s for one-component, and 300 m/s to 50 m/s for two-component systems, with a distinct minimum in the phase transition regime. Considering the simplicity of our system, these values are in very good agreement with reported propagation velocities of action potentials in nerves, ranging between 10 and 100 m/s and depending not only on myelination but also on temperature, thickness, sodium concentration, etc. (20–23).

Our results provide an explanation of the well-known, yet still unresolved problem of a temperature variation that is observed during action potentials (24–27). Our findings even predict that such reversible changes must occur. Quantitative estimates in ΔT(t), calculated from static experiments and the modulation in area density ρ(t) using Eq. 7, propose temperature variations in the lipid monolayer of 0.01 K. Propagating changes in surface potential are expected as well. Taking surface potential measurements from static, isothermal experiments (2), the observed variation in area density ρ(t) predicts a change in ΔU between 1 mV and 50 mV propagating along the surface of the lipid monolayer. Our results are therefore in support of the idea of propagating sound waves in biological membranes as first discussed by Wilke (28) and Wilke and Atzler (29) in 1912, first thoroughly described by Kaufmann in 1989 (30,31), and recently discussed by Heimburg and Jackson in 2005 (24). The reported changes in temperature and pressure observed during nerve-pulse propagation (24–27) are at least in qualitative agreement with our predictions.