Effectiveness of Hair Bundle Motility as the Cochlear Amplifier

Abstract

The effectiveness of hair bundle motility in mammalian and avian ears is studied by examining energy balance for a small sinusoidal displacement of the hair bundle. The condition that the energy generated by a hair bundle must be greater than energy loss due to the shear in the subtectorial gap per hair bundle leads to a limiting frequency that can be supported by hair-bundle motility. Limiting frequencies are obtained for two motile mechanisms for fast adaptation, the channel re-closure model and a model that assumes that fast adaptation is an interplay between gating of the channel and the myosin motor. The limiting frequency obtained for each of these models is an increasing function of a factor that is determined by the morphology of hair bundles and the cochlea. Primarily due to the higher density of hair cells in the avian inner ear, this factor is ∼10-fold greater for the avian ear than the mammalian ear, which has much higher auditory frequency limit. This result is consistent with a much greater significance of hair bundle motility in the avian ear than that in the mammalian ear.

Introduction

With the mechanoelectric transducer (MET) channel strategically placed in their hair bundles, hair cells effectively convert mechanical signal into electrical signal. This transduction is supported by reverse transduction in hair cells that generates force in response to mechanical stimuli. Such a reciprocal process has been predicted by Gold (1) in 1948 as the requirement for counteracting viscous damping for the ear's performance. In recent studies, this effect is recognized as the basis of the cochlear amplifier (2,3), which is critical for the sensitivity and frequency selectivity of the ear in mammals (4–7) as well as in other vertebrates (8,9). Those motile responses of hair cells include electromotility in the cell body of outer hair cells (10–12), which is specific to the mammalian ear, and the motility called fast adaptation in hair bundles themselves (13–17), which is not specific to any animal species.

For the mammalian ear where outer hair cells with two motile mechanisms could be involved in reverse transduction, the relative significance of the two mechanisms is an important issue (18,19). The importance of electromotility is supported by the hearing deficit of mice, which have mutant prestin, the protein essential for electromotility (20), with its functional range outside the physiological range of the membrane potential (21). The significance of fast adaptation is supported by an innbsp;vitro experiment that showed the importance of Ca²⁺ entry through the transducer channels into hair cells on the vibration of the basilar membrane (19). Because the ear of nonmammalian vertebrates lacks electromotility, it has been assumed that hair-bundle motility is the basis of the cochlear amplifier in those animals (8,9).

Here we examine the effectiveness of two models for hair-bundle motility, which can function as the cochlear amplifier in the mammalian ear and the avian ear. One of the motile mechanisms, which is usually referred to as the channel re-closure model, assumes that Ca²⁺-binding to the cytosolic side of the MET channel on channel opening leads to closing of the channel (22). With this model, spontaneous oscillation and signal amplification by an individual hair bundle are described (22). This motile mechanism uses chemical energy in the form of Ca²⁺ gradient across the plasma membrane. This fast mechanism, which is called fast adaptation, is separate from myosin-based slow motility or slow adaptation (23–25), which controls the operating point of the MET channel.

Another model proposed by Tinevez etnbsp;al. (26) assumes that fast adaptation is not an independent phenomenon but it is the result of interplay between gating of the MET channel and ATP-dependent myosin motor, which is responsible for slow adaptation (23–25). This model (26) specifically assumes that myosin is a force generator with a built-in viscoelastic property. Let us tentatively refer to this model, for brevity, as the interplay model.

To study the effectiveness with which hair bundles function as an amplifier, previous treatments used equations of motion for the hair bundle and followed the amplitude (22,26). In those treatments, the amplitude is determined by a nonlinear term that appears in the local resonance. In this report, instead of solving equations of motion, we impose a small sinusoidal displacement on a hair bundle with a certain frequency and evaluate the work done by the motor in the hair bundle. If the work done by hair bundles exceeds energy loss by viscous damping, energy output is greater than energy input and the hair bundle can function as an amplifier. The validity of this condition is not limited to local resonance (27). The method of this comparison is similar to a previous attempt to examine the efficiency of electromotility (28).

This approach has several advantages. First, it is much simpler because we need to consider only linear terms in the perturbation method. Second, the effect of cochlear amplifier is significant only where the amplitude is small. Third, with small amplitude stimulation, the operating point will not be subjected to the effect of slow adaptation. This justifies omitting slow adaptation in the model. The main disadvantage is that with this method we only consider a necessary condition for amplification and not the sufficient condition. In addition, we cannot obtain such details of the amplifier gain, which depends on the nonlinearity of the system. When energy output exceeds energy input at a small amplitude, the oscillation grows out of linear range until the growth is stopped by the nonlinearity of the system.

Initially we describe the basic assumptions and an outline of the method. Next, we examine the effectiveness of a simplified channel re-closure model and interplay model as the cochlear amplifier. After examining these two mechanisms, we discuss their implications.

Assumptions

In the following we list and briefly describe our major assumptions. The assumptions specific to each model for hair bundle motility are described later.

Regarding the geometry of the hair bundle and the mechano-electric transducer (MET) channel, we make the following assumptions:

• 1.The structure of the hair bundle imposes an equal displacement to each tip-link in the bundle. This assumption allows our describing displacement of the hair bundle as if it has one tip-link (29). This condition can lead to negative stiffness of the hair bundles (30). To be precise, this displacement of tip-link is a displacement of tip-link assembly, which includes elements associated with tip link such as the MET and elastic elements other than tip-link itself. We do not discuss how the complex structure of a hair bundle can have such a property (31–33).
• 2.One MET channel with two states, open and closed, is associated with each tip link. This assumption is required to explain gating compliance and is in line with most theoretical treatments (26,29,34,35). Some experimental data are analyzed with one MET channel with three states, two closed and one open (36,37), which can be re-interpreted as two interacting two state channels (38). We do not consider such complex models here.
• 3.An MET is in series connection with a myosin motor, which interacts with actin filaments in the hair bundle and maintains the operating point of the MET channel.

  In addition, we make the following assumptions to simplify our analysis regarding the effectiveness of hair bundle motility:

• 4.
  The amplitude of tip-link displacement is periodic and small. We impose a tip-link displacement of angular frequency ω and amplitude δX,

  $$X\left(t\right)=\overline{X}+\delta X\sin \left(\omega t\right),$$ (1)

  where $\overline{X}$ is the steady-state value before stimulation and $\delta X\ll \overline{X}$. The force F_hb elicited in the hair bundle depends on the model, as will be described later. The leading term is linear in each model for the small amplitude stimulation. The mechanical energy generated by the hair bundle per cycle is then

  $$E_{\text{hb}}=\int F_{\text{hb}}·dX,$$ (2)

  which is proportional to δX².
• 5.The dominant viscous drag is due to shear in the gap between the tectorial membrane and the reticular lamina (subtectorial gap). That has been suggested for the mammalian cochlea (39), where surface of the tectorial membrane that faces the reticular lamina is smooth and planar. The morphology of the avian tectorial membrane is not as certain. Electron micrographs show cavities (domes) in the avian tectorial membrane near its contactnbsp;points with hair bundles and a thin structure of the tectorial membrane that descends to the microvilli surrounding each hair cell (40). However, fixation artifacts in those electron micrograph preparations of the avian tectorial membrane have been suggested (41,42). Here we evaluate the viscous loss in the avian ear in a manner similar to the mammalian ear. The assumptions involved would be that the thin structure of the tectorial membrane that surrounds each hair cell is thin enough not to have a significant internal shear, and that the dome above each hair bundle has no significant effect on viscous drag. The former assumption would lead to underestimation and the latter to overestimation of the drag.

• The tallest row stereocilia in the hair bundles of mammalian outer hair cells and the tallest row stereocilia of all avian hair cells are firmly attached to the tectorial membrane, capable of exerting force generated by those hair bundles. In those systems, the shear of the subtectorial gap is the same as the displacement X_s at the tip of the hair bundle, which is related to the displacement X at the tip-link by a geometrical factor g, i.e., X_s = X/g. For small displacement, we may use g ≈ s/h where s is rootlet separation and h the height of the tallest stereocilia (43).

  The gap, which can be approximated with the height h ofnbsp;the tallest stereocilia, is less than the thickness of a boundary layer (28). Thus, viscous drag F_d of the subtectorial gap per hair cell is proportional to the shear velocity,

  $$F_{\mathrm{d}}=\eta \frac{A}{h}\frac{d{X}_{\mathrm{s}}}{dt}\text{.}$$
• Here η is the viscosity of an external medium and A the area of the subtectorial gap per hair cell. For sinusoidal hair bundle displacement X in Eq. 1, the viscous loss E_d, energy loss by viscous damping during one cycle of the displacement is

  $$\begin{array}{l}{E}_{\mathrm{d}}=\int F_{\mathrm{d}}·d{X}_{\mathrm{s}}\\ =\pi \eta Ah\omega \delta X^2/s^2\text{.}\end{array}$$ (3)
• 6.
  Hair bundle energy must be greater than viscous loss. This condition,

  $$E_{\text{hb}}\ge E_{\mathrm{d}},$$ (4)

• leads to a frequency limit f_lim for the hair-bundle motility to be able to counteract viscous drag. Note that it does not depend on the amplitude because both E_hb and E_d are proportional to δX². If this frequency limit does not exceed the auditory frequency, the motile mechanism described by the model does not satisfy a necessary condition for the cochlear amplifier.

Channel re-closure model

Now we examine the channel re-closure model (22). This model assumes that elevation of cytosolic Ca²⁺ concentration due to opening of the MET channel, which does not have cation selectivity, leads to the binding of Ca²⁺ to the cytosolic side of the channel, which in turn leads to channel re-closure (14,15,17,23,29), thereby increasing the tension on the tip-link. This delayed tension increase can have amplifying effect on an oscillator with which the tip-link is in contact. Indeed, this mechanism can lead to spontaneous oscillation of hair bundles (22). The operating point of the MET channel is determined by a myosin motor, which is also triggered by an elevation of cytosolic Ca²⁺ concentration caused by channel opening.

Here we assume that the MET channel has only one Ca²⁺ binding site instead of two (22) for simplicity. For convenience, we assign each channel state with a number (Fig.nbsp;1). The channel in the open state may be either Ca-unbound (state 2) or Ca-bound (state 3). Closed state is either Ca-unbound (state 1) or Ca-bound (state 4).

Figure 1.

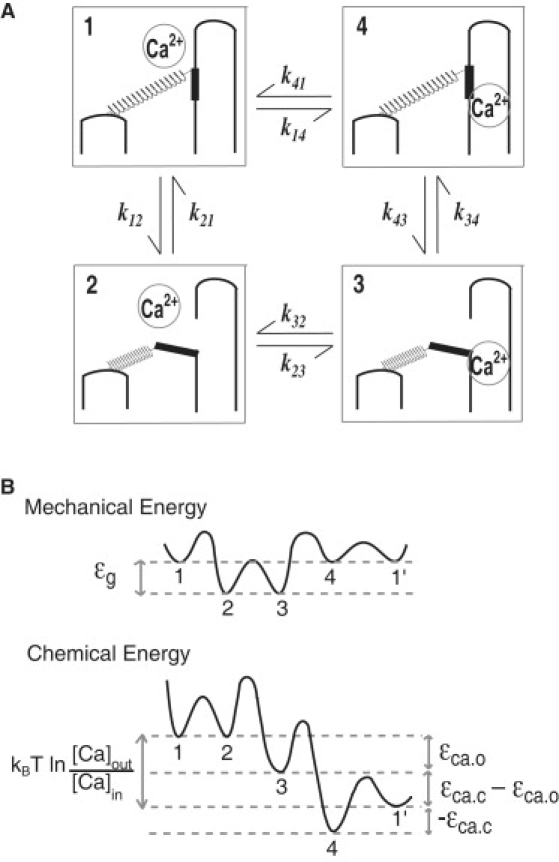
Channel re-closure model. (A) Schematic representation of transitions, which the mechanoelectric transducer channel undergoes. An opening of the channel (state 2) elevates Ca²⁺ concentration on the cytosolic side of the channel. The resulting binding of Ca²⁺ to a binding site leads to closure of the channel (state 3). Closure of the channel (state 4) reduces the cytosolic Ca²⁺ concentration, leading to dissociation (state 1). (B) Schematic representation of energy levels of these states. The mechanical energy level of open states 2 and 3 are the same and differs from the closed states 1 and 4 by gating energy ɛ_g. States 3 and 4 differs in the binding energy. These levels differ from unbound states 1 and 4. Directed transitions of the channels are supported by the expenditure of the chemical energy k_BT ln([Ca]_out/[Ca]_in) of Ca²⁺ after one cycle.

The probability P_i of the MET channel being in the i^th state follows a set of differential equations,

$$\frac{d}{dt}{P}_{\mathrm{i}}=-\left(k_{\mathrm{i}\mathrm{i}-1}+k_{\mathrm{i}\mathrm{i}+1}\right)P_{\mathrm{i}}+k_{\mathrm{i}-1\mathrm{i}}{P}_{\mathrm{i}-1}+k_{\mathrm{i}+1\mathrm{i}}{P}_{\mathrm{i}+1},$$ (5)

where the index i runs from 1 to 4. Here the index value 0 and 5 are, respectively, identical to 4 and 1. The quantity k_ij represents the transition rate from i^th state to j^th state. Open probability P_o is given by P₂ + P₃. Here the transition rates are to be determined by the energy barriers (Fig.nbsp;1 B) in the manner consistent with Arrhenius-Eyring equation (44,45), which is used for nonequilibrium systems (45,46).

The transitions between states 1 and 2 involve gating of the MET channel. The ratio of the transition rates is given by the difference of the free energy in the two states,

$$\frac{k_{12}}{k_{21}}=\exp \left[\beta {\varepsilon }_{\mathrm{g}}\right],$$ (6)

where β = 1/(k_BT) with Boltzmann's constant k_B and the temperature T. Gating energy ɛ_g can be expressed as

$${\varepsilon }_{\mathrm{g}}=K_{\mathrm{g}}{X}_{\mathrm{g}}\left(X-\frac{1}{2}{X}_{\mathrm{g}}\right)\text{.}$$ (7)

Here X is the displacement at the tip-link, K_g is the stiffness of gating spring, and X_g is the gating distance.

Both states 2 and 3 are open states. The transitions between them involve Ca²⁺ binding and unbinding. We have

$$\frac{k_{23}}{k_{32}}={\left[\text{Ca}\right]}_{\text{out}}\exp \left[\beta {\varepsilon }_{\text{ca,o}}\right],$$ (8)

assuming that the cytosolic Ca²⁺ concentration near the channel can be approximated by that of the external medium, [Ca]_out. Ca²⁺ binding energy of the open configuration is represented by −ɛ_{ca, o} (<0).

The transitions between states 3 and 4, both of which are Ca²⁺ bound, involve gating of the MET channel. However, the free energy of Ca²⁺ binding may depend on the conformation and may differ in these two states. On closing of the channel, Ca²⁺ level inside the cell ([Ca]_in) should immediately drop due to diffusion and Ca²⁺ buffers, aided by Ca²⁺ pumps (47,48), which maintains the low cytosolic Ca²⁺ concentration. Thus, we obtain

$$\frac{k_{34}}{k_{43}}=\exp \left[\beta \left({\varepsilon }_{\text{ca,c}}-{\varepsilon }_{\text{ca,o}}\right)\right]\exp \left[-\beta {\varepsilon }_{\mathrm{g}}\right],$$ (9)

where −ɛ_{ca, o} (<0) is Ca²⁺ binding energy of the channel when it is in closed configuration.

Transitions between states 4 and 1, which are both closed, involve only Ca²⁺ binding and unbinding. They are similar to transitions between states 2 and 3 except that the Ca²⁺ concentration is lower because the channel is closed. The ratio of the transition rates is given by

$$\frac{k_{41}}{k_{14}}=\frac{1}{{\left[\text{Ca}\right]}_{\text{in}}}\exp \left[-\beta {\varepsilon }_{\text{ca,c}}\right]\text{.}$$ (10)

The free energy change ɛ_cycle after one cycle is then

$${\varepsilon }_{\text{cycle}}=k_{\mathrm{B}}T\ln \frac{k_{12}{k}_{23}{k}_{34}{k}_{41}}{k_{21}{k}_{32}{k}_{43}{k}_{14}}\text{.}$$ (11)

Substitution of the transition rates using Eqs. 6 and 8–10 leads to

$${\varepsilon }_{\text{cycle}}=k_{\mathrm{B}}T\ln \frac{{\left[\text{Ca}\right]}_{\text{out}}}{{\left[\text{Ca}\right]}_{\text{in}}},$$ (12)

which is the difference of Ca²⁺ chemical potential inside and the outside of the cell. This result is consistent with nonequilibrium condition of this system, which uses chemical energy of a single Ca²⁺ per cycle.

These relationships between the transition rates allow usnbsp;to replace eight transition rates by six new parameters k₁, k₂, k₃, k₄, r₃, and r₄:

$$\begin{array}{l}{k}_{12}=k_1,k_{21}=k_1{e}^{-\beta {\varepsilon }_{\mathrm{g}}},\\ k_{23}=k_2,k_{32}=r_2{k}_2\\ k_{34}=k_3{e}^{-\beta {\varepsilon }_{\mathrm{g}}},k_{43}=r_3{k}_3,\\ k_{41}=k_4,k_{14}=r_4{k}_4,\\ r_2=\frac{1}{r_3{r}_4}\frac{{\left[\text{Ca}\right]}_{\text{in}}}{{\left[\text{Ca}\right]}_{\text{out}}}\text{.}\end{array}$$

Response of the MET channel

A small sinusoidal displacement X (See Eq. 1) of the hair bundle elicits a small periodic response in the channel. The probability P_i of the channel being in state i is, to the first-order terms,

$$P_{\mathrm{i}}\simeq {\overline{P}}_{\mathrm{i}}+\delta P_{\mathrm{i}}\sin \left(\omega t+{\varphi }_{\mathrm{i}}\right),$$ (13)

where ϕ_i is the phase, ${\overline{P}}_{\mathrm{i}}$ the probability of i state at the operating point (i.e., δX = 0), and the amplitude $\delta P_{\mathrm{i}}/{\overline{P}}_{\mathrm{i}}\ll 1$ for inbsp;= 1, 2, 3, and 4.

The applied displacement changes the transition rates k₂₁nbsp;and k₃₄ through its effect on the gating energy Δɛ_g (≡nbsp;K_gX_gδX sin ωt). The linearized forms are given by

$$k_{\text{ij}}\simeq {\overline{k}}_{\text{ij}}+\delta k_{\text{ij}}\sin \omega t,$$ (14)

where ${\overline{k}}_{\text{ij}}$ = κ_ij $\exp \left[-\beta K_{\mathrm{g}}{X}_{\mathrm{g}}\left(\overline{X}-1/2X_{\mathrm{g}}\right)\right]$ and $\delta k_{\text{ij}}=-{\overline{k}}_{\text{ij}}\beta K_{\mathrm{g}}{X}_{\mathrm{g}}\delta X$ with κ_ij being a prefactor.

With Eqs. 13 and 14, Eq. 5 leads to

$$\delta P_{\mathrm{i}}=\beta K_{\mathrm{g}}{X}_{\mathrm{g}}\delta X{\theta }_{\mathrm{i}},$$

where θ_i is a constant. The open probability P_o (= P₂ + P₃) is then expressed by

$$\begin{array}{c}{P}_{\mathrm{o}}={\overline{P}}_{\mathrm{o}}+\delta P_{\mathrm{o}}\sin \left(\omega t+{\varphi }_{\mathrm{o}}\right)\\ ={\overline{P}}_{\mathrm{o}}+\beta K_{\mathrm{g}}{X}_{\mathrm{g}}\delta X{\mathit{\theta }}_{\mathrm{o}}\sin \left(\omega t+{\varphi }_{\mathrm{o}}\right)\text{.}\end{array}$$ (15)

Constants θ_o and ϕ_o depend on the rates k₁, …, k₄, r₃, r₄, thenbsp;ratio [Ca]_out/[Ca]_in, and the open probability ${\overline{P}}_{\mathrm{o}}$ at the operating point.

Limiting frequency

The force F_hb produced by a hair bundle with N tip-links in response to the displacement X at each tip-link is expressed by

$$F_{\mathrm{hb}}=-N{K}_{\mathrm{g}}\left(X-X_{\mathrm{g}}{P}_{\mathrm{o}}\right)-N{K}_{\mathrm{s}}X,$$

where X_g is the gating distance, K_g is the stiffness of the gating spring of each MET channel, and K_s is the stiffness due to rootlet and side links.

The work E_hb done by the hair bundle during one cycle of stimulation is

$$E_{\text{hb}}=N{K}_{\mathrm{g}}{X}_{\mathrm{g}}{\int }_0^{\mathrm{T}}{P}_{\mathrm{o}}·dX,$$ (16)

because the work done by elastic elements drops off at the end of one cycle, leaving components of force with phase shifts. With Eq. 15, we obtain

$$\begin{array}{c}{E}_{\text{hb}}=N{K}_{\mathrm{g}}{X}_{\mathrm{g}}\delta P_{\mathrm{o}}\delta X{\int }_0^{\mathrm{T}}\sin \left(\omega t+{\varphi }_{\mathrm{o}}\right)\cos \omega td\left(\omega t\right)\\ =\beta N{\left(K_{\mathrm{g}}{X}_{\mathrm{g}}\delta X\right)}^2\Phi ,\end{array}$$ (17)

where Φ = πθ_o sin ϕ_o, which we call the phase factor.

With the aid of Eq. 3, the Assumption 6 that mechanical energy E_hb produced by the hair bundle must be larger than viscous loss E_d leads to a condition for the limiting frequency f_lim,

$$f_{\lim }=\beta M{\left(K_{\mathrm{g}}{X}_{\mathrm{g}}\right)}^2\Phi /\left(2{\pi }^2\eta \right),$$ (18)

below which viscous drag can be counteracted. This limiting frequency is obtained by dividing the corresponding angular frequency by 2π. A factor M is defined by

$$M=\frac{N{s}^2}{Ah}\text{.}$$ (19)

Notice that M can be determined by morphological data alone. For this reason, we call it the morphological factor.

The limiting frequency f_lim (Eq. 18) for the channel re-closure model is determined by gating force K_gX_g, the morphological factor M, and the phase factor Φ. Among these factors, the limiting frequency is particularly sensitive to gating force because of its second power dependence.

Optimal value of the phase factor

Since we are interested in the frequency limit, here we attempt to obtain the maximum value for the phase factor Φ. The numerical calculation is done using SciLab program (http://www.scilab.org) on Biowulf at the National Institutes of Health (http://biowulf.nih.gov), after normalizing four parameters k₁, k₂, k₃, and k₄, with respect to the operating frequency ω. The range of parameter values examined is shown in the Supporting Material.

Since the value for the steady-state open probability ${\overline{P}}_{\mathrm{o}}$ is fixed, the steady-state bundle displacement must be determined by solving a nonlinear equation for every set of transition rate values and the steady-state open probability ${\overline{P}}_{\mathrm{o}}$. We found that inclusion of displacement dependence in k₁ and k₃ renders the solution too lengthy to be accepted by the computer program. For this reason, we assume that k₁ and k₃ are constants. That is equivalent to assuming that the energy barriers for channel opening do not change with the tip-link displacement and would be somewhat unreasonable (36). This assumption may have significant effect where channel gating is rate-limiting. However, it will be much less significant where the phase factor is insensitive to the details of gating.

Preliminary trials show that the phase factor Φ is a monotonically increasing function of k₁/ω and k₃/ω, although it is virtually flat beyond 10⁶. That is illustrated by plotting Φ under the constraints of k₁ = k₃, parameters involved in gating, and k₂ = k₄, parameters involved in Ca²⁺-binding and unbinding (Fig.nbsp;2). The figure shows that gating with a rate close to the operating frequency has a damping effect. That is intuitively obvious, because gating is a mechanical relaxation. On the other hand, Ca²⁺-binding and unbinding at a rate near the operating frequency is effective in making a phase delay that has an amplifying effect.

Figure 2.

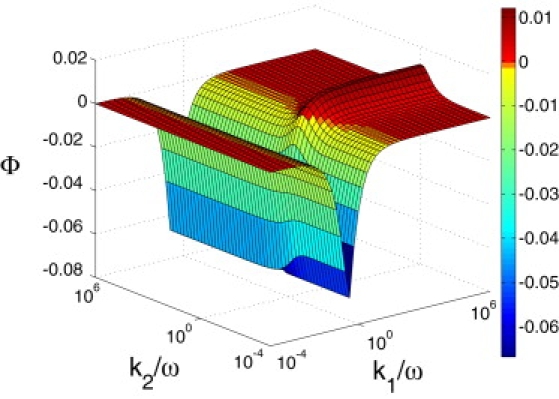
The phase factor Φ of the channel re-closure model. The phase factor Φ is plotted against k₁/ω and k₂/ω under the constraints k₃ = k₁ and k₄nbsp;= k₂. The range of the parameter values is in the Supporting Material. Each point represents the maximum value with respect to r₃ and r₄. The maximum value of Φ is 0.0086 at k₂/ω = 1.00. [Ca]_out/[Ca]_in = 100 and ${\overline{P}}_{\mathrm{o}}$ = 0.1.

For this reason, we can maximize Φ with respect to only four parameters, while giving large fixed values for k₁/ω and k₃/ω (i.e., k₁/ω = 10⁶, k₃/ω = 10⁶). The grid is iteratively recast in the optimal zone until the relative increment of the maximum value for Φ between the iteration falls below 1%.

If we assume that open probability at the operating point is ${\overline{P}}_{\mathrm{o}}$ of 0.1, the optimal value of Φ is 0.05 for the mammalian ear, which has the Ca concentration ratio of 10² (Table 1). The optimal parameter values k₂, k₄, r₃, and r₄ are 2.1, 0.3, 5 × 10⁻⁴, and 0.26. For the avian ear, which has ∼10 times higher endolymphatic Ca concentration (49), the optimal value is 0.07. The corresponding optimal parameter values are 2.5, 0.4, 5 × 10⁻⁴, and 0.08. The phase factor Φ also depends on the operating point. It has a maximum at ${\overline{P}}_{\mathrm{o}}$ ofnbsp;0.5, and the values are higher by ∼25% than that for ${\overline{P}}_{\mathrm{o}}$ of 0.1.

Table 1.

Parameter values for the basal end of the cochlea

Notation	Quantity	Mammal	Chicken	Unit
KgXg	Gating force	4.4∗	> 0.43†	pN
h	Height of tallest cilia	0.7 (61)	1.54 (53)	μm
s	Rootlet separation	0.5 (62)	0.45 (54)	μm
N	Number of tip-links/cell	60‡	187§
A	Subtectorial gap area/hair cell	125 (61)	19 (neural) (53)	μm2
			23 (abneural) (53)
[Ca]out	Endolymphatic [Ca2+]	23.7 (63)	240 (49)	μM
[Ca]in	Cytosolic [Ca2+]	0.2¶	0.2¶	μM

The viscosity coefficient η of the medium is assumed 1 mPa·s, same as water.

^∗Obtained from 500 fN force (37) at the tip of mouse outer hair cell and the geometric factor for h ≃ 4.4 μm (64).

^†Obtained from the value 40 fN (58,59) at the tip and h ≃ 4.8 μm (at the apex).

^‡At the midturn of the cochlea (65).

^§The number of stereocilia (53) multiplied by a ratio 0.8 (52).

^¶Median of estimated 60 nM and 300 nM (48).

Interplay model

The model proposed by Tinevez etnbsp;al. (26), which we refer to as the interplay model, assumes that fast adaptation is not based on a special structure or a mechanism but is a result of interplay between the MET channel and the myosin motor, which is a force generator and responsible for slow adaptation. While a release model (50,51) assumes that an element, which links the myosin motor with the MET channel, undergoes Ca²⁺-activated fast elongation, the interplay model assumes the actomyosin system that produces force has viscoelasticity. In the following we give a brief description of this model.

The distance X_a of the myosin motor from actin filaments obeys a differential equation,

$${\lambda }_{\mathrm{a}}\frac{d{X}_{\mathrm{a}}}{dt}=K_{\mathrm{g}}\left(X-X_{\mathrm{a}}-X_{\mathrm{g}}{P}_{\mathrm{o}}\right)-K_{\mathrm{e}}\left(X_{\mathrm{a}}-X_{\mathrm{e}}\right)-F_{\mathrm{a}},$$ (20)

where the myosin motor which generates isometric force F_a has an intrinsic pre-stressed Voigt-type viscoelastic element with viscosity λ_a and stiffness K_e (26) (Fig.nbsp;3). The degree of pre-stress is represented by X_e, which can serve as an adjustable parameter.

Figure 3.

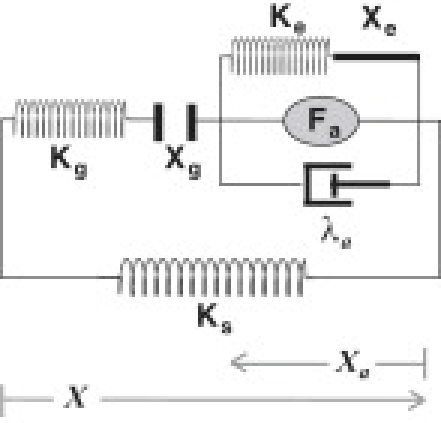
Interplay model. Gating of the MET channel is characterized by the stiffness K_g and distance X_g of the gate. Myosin, which produces force F_a, is connected with the MET channel through an element with stiffness K_e and friction coefficient λ_a. A parallel element has stiffness K_s.

The force F_a generated by unconventional myosin is a decreasing function of the cytosolic Ca²⁺ concentration, which is approximately proportional to open probability P_o of the MET channel (26). Hence it can be expressed to the first-order term,

$$F_{\mathrm{a}}=F_{\max }\left(1-S{P}_{\mathrm{o}}\right)\text{.}$$ (21)

The coefficient S can be expressed by

$$S=-\frac{{\left[{\text{Ca}}^{2+}\right]}_{\text{max}}}{F_{\text{max}}}\frac{d{F}_{\mathrm{a}}}{d\left[{\text{Ca}}^{2+}\right]}{|}_{\text{ref}}\text{.}$$ (22)

The channel's open probability P_o, that affects the cytosolic Ca²⁺ concentration, is expressed by a two-state Boltzmann function (26),

$$P_{\mathrm{o}}=\frac{1}{1+B\exp \left[-\beta K_{\mathrm{g}}{X}_{\mathrm{g}}\left(X-X_{\mathrm{a}}\right)\right]},$$ (23)

where B determines the open probability at rest.

Linearized response

A small sinusoidal displacement of the hair bundle, represented by Eq. 1, should give rise to a small displacement on the position X_a of the motor. This can be expressed as

$$X_{\mathrm{a}}={\overline{X}}_{\mathrm{a}}+\delta X_{\mathrm{a}}\sin \left(\omega t+\varphi \right),$$ (24)

where ${\overline{X}}_{\mathrm{a}}$ is the position at rest. For small periodical displacements, Eq. 23 becomes

$$P_{\mathrm{o}}={\overline{P}}_{\mathrm{o}}+\beta K_{\mathrm{g}}{X}_{\mathrm{g}}{\overline{P}}_{\mathrm{o}}\left(1-{\overline{P}}_{\mathrm{o}}\right)\left(\delta X\sin \omega t-\delta X_{\mathrm{a}}\sin \left(\omega t+\varphi \right)\right),$$ (25)

where the open probability ${\overline{P}}_{\mathrm{o}}$ at the operating point is given by

$${\overline{P}}_{\mathrm{o}}=1/\left(1+B\exp \left[-\beta K_{\mathrm{g}}{X}_{\mathrm{g}}\left(\overline{X}-{\overline{X}}_{\mathrm{a}}\right)\right]\right)\text{.}$$

Substitution of X_a and P_o into the differential equation Eq.nbsp;20, using Eqs. 24 and 25, leads to an expression fornbsp;the amplitude δX_a of the motor displacement,

$$\delta X_{\mathrm{a}}\sin {\varphi }_{\mathrm{a}}=-\frac{\left({\tilde{K}}_{\mathrm{g}}+K_{\text{ca}}\right)\omega {\lambda }_{\mathrm{a}}}{{\left({\tilde{K}}_{\mathrm{g}}+K_{\text{ca}}+K_{\mathrm{e}}\right)}^2+{\left(\omega {\lambda }_{\mathrm{a}}\right)}^2}\delta X,$$ (26)

where

$${\tilde{K}}_{\mathrm{g}}=K_{\mathrm{g}}\left[1-\beta K_{\mathrm{g}}{X}_{\mathrm{g}}^2{\overline{P}}_{\mathrm{o}}\left(1-{\overline{P}}_{\mathrm{o}}\right)\right],$$ (27)

which is the familiar form of gating stiffness (29) and can take negative values. The quantity K_ca defined by

$$K_{\text{ca}}=\beta K_{\mathrm{g}}{X}_{\mathrm{g}}^2{\overline{P}}_{\mathrm{o}}\left(1-{\overline{P}}_{\mathrm{o}}\right)S{F}_{\max }/X_{\mathrm{g}}$$ (28)

is the sensitivity of force production by the myosin motor to displacement. That is because a displacement X_g at the tip-link leads to an increase of $\beta K_{\mathrm{g}}{X}_{\mathrm{g}}^2{\overline{P}}_{\mathrm{o}}\left(1-{\overline{P}}_{\mathrm{o}}\right)$ in the open probability, which in turn causes a rise in the cytosolic Ca²⁺ concentration as described by Eq. 21, decreasing the motor force by the efficiency factor of SF_max.

Energy balance and frequency limit

In response to a tip-link displacement X, N tip-links of a hair bundle produce total force F_hb,

$$F_{\text{hb}}=-N{K}_{\mathrm{g}}\left(X-X_{\mathrm{a}}-X_{\mathrm{g}}{P}_{\mathrm{o}}\right)-N{K}_{\mathrm{s}}X\text{.}$$ (29)

For small periodical displacement as shown in Eq. 1, the work done by the hair bundle per cycle depends only on terms that include X_a and P_o, because elastic terms do not contribute. Only the term that is proportional to δX_a is nonelastic and remains in Eq. 25 after a full cycle. Thus, we have

$$\begin{array}{l}{E}_{\text{hb}}=N{\tilde{K}}_{\mathrm{g}}\int X_{\mathrm{a}}·dX\\ =N{\tilde{K}}_{\mathrm{g}}\delta X\delta X_{\mathrm{a}}{\int }_{\mathrm{0}}^{\mathrm{T}}\sin \left(\omega t+{\varphi }_{\mathrm{a}}\right)\cos \omega td\left(\omega t\right)\\ =\pi N{\tilde{K}}_{\mathrm{g}}\delta X\delta X_{\mathrm{a}}\sin {\varphi }_{\mathrm{a}}\text{.}\end{array}$$ (30)

With the aid of Eq. 26, we obtain

$$E_{\text{hb}}=-\frac{\pi N{\tilde{K}}_{\mathrm{g}}\left({\tilde{K}}_{\mathrm{g}}+K_{\text{ca}}\right)\omega {\lambda }_{\mathrm{a}}}{{\left({\tilde{K}}_{\mathrm{g}}+K_{\text{ca}}+K_{\mathrm{e}}\right)}^2+{\left({\lambda }_{\mathrm{a}}\omega \right)}^2}\delta X^2\text{.}$$ (31)

Note that the work E_hb done by the hair bundle can be negative. Under such conditions, the hair bundle behaves asnbsp;a damper. The condition E_hb > 0 requires ${\tilde{K}}_{\mathrm{g}}\left({\tilde{K}}_{\mathrm{g}}+K_{\text{ca}}\right)<0$. Since K_ca > 0 as shown in Eq. 28, This condition leads to

$$-K_{\text{ca}}<{\tilde{K}}_{\mathrm{g}}<0\text{.}$$ (32)

Namely, negative stiffness is a necessary condition for the hair bundle to function as an amplifier.

The condition for being an amplifier E_hb > E_d leads to ω > 2π f_lim with a linear-limiting frequency f_lim,

$$f_{\text{lim}}=\frac{1}{2\pi {\lambda }_{\mathrm{a}}}\sqrt{-{\tilde{K}}_{\mathrm{g}}\left({\tilde{K}}_{\mathrm{g}}+K_{\text{ca}}\right)\frac{{\lambda }_{\mathrm{a}}}{\eta }M-{\left({\tilde{K}}_{\mathrm{g}}+K_{\text{ca}}+K_{\mathrm{e}}\right)}^2}\text{.}$$ (33)

For a limiting frequency f_lim to exist, the terms inside the square root must be positive,

$$-\frac{{\left({\tilde{K}}_{\mathrm{g}}+K_{\text{ca}}+K_{\mathrm{e}}\right)}^2}{{\lambda }_{\mathrm{a}}{\tilde{K}}_{\mathrm{g}}\left({\tilde{K}}_{\mathrm{g}}+K_{\text{ca}}\right)}\frac{\eta }{M}<1\text{.}$$ (34)

Factors that determine the limiting frequency

The frequency limit for the interplay model depends on many parameters. Its sensitivity to operating point ${\overline{P}}_{\mathrm{o}}$ enters through ${\tilde{K}}_{\mathrm{g}}$ and K_ca. An example of the dependence on the operating point is shown in Fig.nbsp;4. Notice that E_hb has a symmetry axis ${\overline{P}}_{\mathrm{o}}$ = 0.5, where it has the maximum. The hair bundle energy E_hb is negative if ${\overline{P}}_{\mathrm{o}}$ is small. For a limiting frequency f_lim to exist, ${\overline{P}}_{\mathrm{o}}$ must be large enough to make E_hb > E_d, which is positive. The dependence of f_lim on its parameters is illustrated in Fig.nbsp;5.

Figure 4.

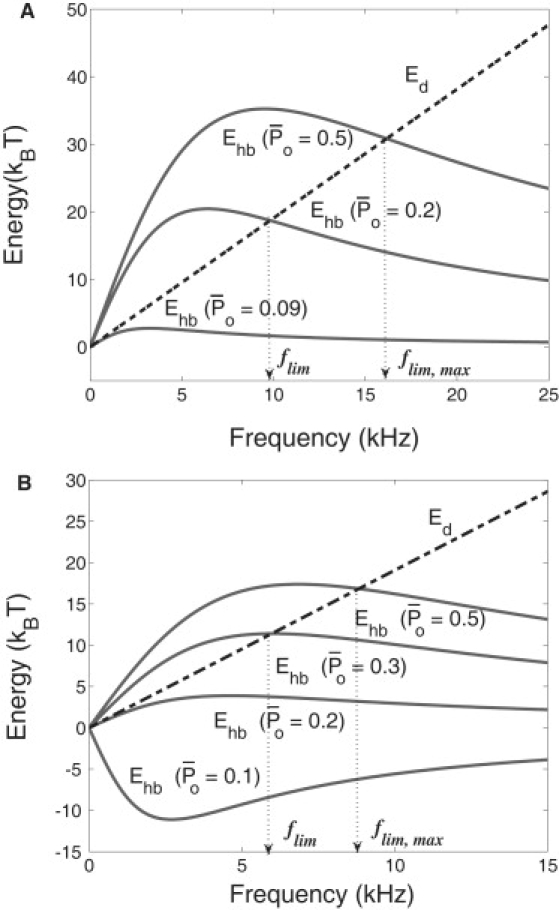
Hair bundle work E_hb and viscous loss E_d. Examples of E_d (dotted) and E_hb. (A) ${\overline{P}}_{\mathrm{o}}$ = 0.09 (or 0.91), 0.2 (or 0.8), and 0.5. E_hb > 0 requires 0.08 < ${\overline{P}}_{\mathrm{o}}$ < 0.92. E_hb > E_d requires 0.09 < ${\overline{P}}_{\mathrm{o}}$ < 0.91. (B) ${\overline{P}}_{\mathrm{o}}$nbsp;= 0.1 (or 0.9), 0.2 (or 0.8), 0.3 (or 0.7), and 0.5. E_hb > 0 requires 0.17 < ${\overline{P}}_{\mathrm{o}}$ < 0.83. The value E_hb > E_d requires 0.2 < ${\overline{P}}_{\mathrm{o}}$ < 0.8. Assumed parameter values: N = 60, K_g = 1.2 mN/m, X_g = 7 nm for panel A, 5 nm for panel B, F_m = 3 pN, S = 4, λ_a = 0.1 μN.s/m, K_e = 0.13 mN/m, η = 1 mPa.s, A = 100 μm², h = 1 μm, and s = 0.5 μm.

Figure 5.

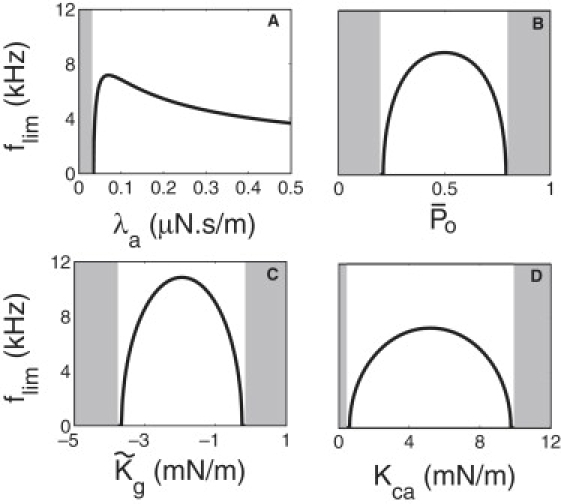
An example of parameter dependence of limiting frequency. The dependence on (A) λ_a, (B) ${\overline{P}}_{\mathrm{o}}$, (C) ${\tilde{K}}_{\mathrm{g}}$, and (D) K_ca. Limiting frequency f_lim does not exist in the shaded areas. Assumed parameter values are same as those for Fig.nbsp;4B.

The morphological factor M (Eq. 19) that appears in the channel re-closure model also appears in the frequency limit of the interplay model. Here we observe that the limiting frequency is an increasing function of this factor. The limiting frequency obtained is, however, quite sensitive to other factors (Fig.nbsp;5).

Morphological factor

The morphological features of the cochlea are represented by a single factor M in the limiting frequency for each of the two models. How do the values for this factor in the mammalian ear compare with those in the avian ear? The mammalian ear differs from the avian ear in having lower bundle height h and smaller number N of tip-links per bundle (see Tablenbsp;1). These two factors do not have significant influences on the morphological factor M because they work in the opposite directions in Eq. 19. The most important factor is the area A of the subtectorial gap per hair cell, which is much larger in the mammalian ear. For this reason, the morphological factor M for the avian cochlea is ∼10 times of that for the mammalian cochlea.

This large morphological factor M for the avian ear appears to indicate hair-bundle motility is more important in the avian ear than in the mammalian ear, when it is combined with the avian ear's lower auditory frequency limit, which is ∼1/10th of the mammalian one. Our result is that the limiting frequency is an increasing function of the morphological factor in the two models.

For this reason it is of interest to compare the mapping of the morphological factor along the avian basilar papilla with that of the characteristic frequency. In the chicken cochlea, each quantity that contributes to this factor has been carefully mapped along its longitudinal axis (52,53), although morphological data obtained from electron microscopy may need correction for sample shrinkage, which could be ∼30% in length (54,55) for scanning electron microscopy.

It has been shown that the height h of the tallest cilia in a hair bundle shows monotonic decrease from the apex to the base (Fig.nbsp;6 B). The number of stereocilia shows monotonic increases (53). The number N of tip-links in a hair bundle, which can be estimated by multiplying a factor 0.8 (52) to the number of stereocilia, is therefore an increasing function of the distance from the apex (Fig.nbsp;6 A). The surface area A of a single hair cell on the reticular lamina does not show monotonic dependence on the distance from the apex (Fig.nbsp;6 C) (53). It has a maximum at ∼50% from the apex on the abneural side (i.e., abneural hair cells) and it is relatively constant on the neural side (neural hair cells) (53).

Figure 6.

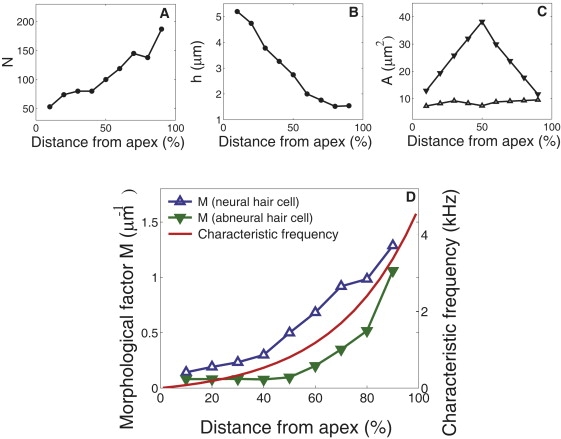
Morphological factor of the chicken cochlea. (A) Hair bundle height h, (B) the number N of tip-links, and (C) apical surface area A per hair cell on the neural (up-pointing open triangle) and abneural (down-pointing solid triangle) sides are plotted against the distance from the apex. Adopted from Tilney and Saunders (53). N is obtained by multiplying a factor 0.8 (52) to the number of stereocilia (53). Shrinkage factor is not considered. (D) Morphological factor M (= Ns²/A h) on the neural (blue) and abneural sides (green) are plotted together with the best frequency (red line). The value s is assumed to be 0.45 μm (54) (Tablenbsp;1). The best frequencies are adopted from Gleich and Manley (66).

The morphological factor M for the avian ear obtained from these experimental data is an increasing function of the distance from the apical end (Fig.nbsp;6 D), similar to the mapping of the characteristic frequency (Fig.nbsp;6 D). This observation is somewhat surprising because our condition to introduce the morphological factor is simply a necessary condition for an upper bound of characteristic frequency. However, this factor is always greater on the neural side than the abneural side at each longitudinal location. If one assumes that the role of abneural hair cells is similar to that of outer hair cells, this observation is somewhat paradoxical, because larger values of the morphological factor correspond to a greater effectiveness as the amplifier if other parameters are the same.

If we assume that achieving high frequency sensitivity is biologically costly, limiting frequency may have a correlation with the characteristic frequency. Then a relatively good correspondence of the morphological factor and the characteristic frequency along the longitudinal axis of the chicken ear appears consistent with the channel re-closure model, which predicts that the limiting frequency is proportional to the morphological factor. The difference in the morphological factor for neural and abneural cells could be attributed to either systematic difference in gating force in those cells or that in the open probability of the MET channel. Namely, gating force K_gX_g or the resting open probability ${\overline{P}}_{\mathrm{o}}$ of the channel could be somewhat larger in abneural cells than in neural cells.

The implication of the mapping of the morphological factor on the interplay model is more equivocal. The square-root dependence of the limiting frequency on the morphological factor indicates that the frequency limit predicted by the interplay model does not rise as sharply as the characteristic frequency along the longitudinal axis if all other parameters are constant throughout the cochlea. However, with so many parameters to which the limiting frequency is sensitive, such an assumption could be unrealistic. Rather, it could imply that other parameters need to change along the axis to make the rise of the limiting frequency sharper.

Alternatively, it is possible that the limiting frequencies that we obtained could be significantly higher than the characteristic frequency. If that is the case, our analysis is more effective in examining the validity of the re-closure model than in examining the interplay model because the re-closure model is more constrained by a smaller number of parameters.

Limiting frequency

For the channel re-closure model, gating force K_gX_g and the morphological factor M can be used to predict the limiting frequency if we can assume that the phase factor Φ is optimized. For the basal turn of the mammalian ear, gating force K_gX_g is 4.4 pN for mice (37), and the morphological factor at the base is 0.17 μm⁻¹ for the chinchilla. If we can use the value for mouse gating force for chinchilla, the limiting frequency is ∼2 kHz, much lower than the auditory frequency, which is 20 kHz for the chinchilla, 40 kHz for guinea pigs andnbsp;gerbil. It is also lower than the limiting frequency of ∼10 kHz, obtained from the condition for electromotility of outer hair cells to locally counteract viscous drag (28,56).

If we can assume that gating force for the chicken is ∼4.3nbsp;pN, similar to that of other animals, including ∼5.2 pN for frog (34) and ∼4.1 pN for turtle (57) (these values are based on s/h = 0.11), we obtain the limiting frequency of 20 kHz on the neural side and 17 kHz for the abneural side at the basal end. These frequencies are higher than the auditory range of ∼4 kHz, even after correcting for EM sample shrinkage that would reduce the morphological factor and thereby the limiting frequency by 50%. This observation is consistent with the hypothesis that hair bundles function as the cochlear amplifier in the avian ear. However, experimental values for the gating force measured at the tip of the hair bundle of the chicken are ∼40 fN (58,59), ∼1/10 of those in other animals, leading to 0.43 pN at the tip-link by considering the geometrical factor g ≈ s/h (Table 1). This lower value for gating force leads to the limiting frequency of 200 Hz for the neural side and 170 Hz for the abneural side, without correcting for sample shrinkage.

Why are the values for gating force of the chicken hair bundle so far obtained so small compared with those from other animals? A possible reason could be technical difficulties in experiments, specifically the time resolution must be high enough compared with measuring gating force in frogs (D. Bozovic, personal communication, 2008). Alternatively, it is possible that gating of channels in a single hair bundle may not be synchronous in the preparation, broadening channel opening with respect to bundle displacement (31,32). If the channel re-closure model, which predicts second power dependence of the limiting frequency on gating force, is correct, the gating force of chicken hair cells must be as high as that of other animals.

The predictions of the interplay model on the limiting frequency are difficult to make. It depends on a greater number of parameters such as λ_a, F_m, and S, which are related to the myosin motor and show considerable variability in their values (26). In addition, a relatively small uncertainty in parameter values tends to lead to a large uncertainty in the limiting frequency. For example, a 10% difference in either gating distance or gating stiffness can lead to >100% difference in the limiting frequency.

Conclusions

We assumed that viscous drag in the subtectorial gap must be counteracted by hair-bundle motility for small periodic stimulation and derived limiting frequencies of the ear for two models, the channel re-closure model (22) and the interplay model (26), of hair-bundle motility, each of which has been shown to work as an amplifier.

The limiting frequency obtained from the channel re-closure model is proportional to the phase factor, the morphological factor, and the square of gating force. The limiting frequency obtained from the interplay model is much more complex. Although it depends on the morphological factor, it is very sensitive to factors that characterize the gating of the mechanoelectric transducer channel as well as force production by the myosin motor.

The morphological factor is much larger for the avian ear than for the mammalian ear. For the chicken ear, this factor shows a longitudinal dependence similar to the tonotopic map. Such properties of the morphological factor can be derived by the channel re-closure model. However, gating force for the chicken must be larger than reported values. The limiting frequency predicted by the interplay model is not as specific, involving numerous parameters.

Supporting Material

One table is available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(09)01425-8.