A Second Look at Mini-Protein Stability: Analysis of FSD-1 Using Circular Dichroism, Differential Scanning Calorimetry, and Simulations

Abstract

Mini-proteins that contain <50 amino acids often serve as model systems for studying protein folding because their small size makes long timescale simulations possible. However, not all mini-proteins are created equal. The stability and structure of FSD-1, a 28-residue mini-protein that adopted the ββα zinc-finger motif independent of zinc binding, was investigated using circular dichroism, differential scanning calorimetry, and replica-exchange molecular dynamics. The broad melting transition of FSD-1, similar to that of a helix-to-coil transition, was observed by using circular dichroism, differential scanning calorimetry, and replica-exchange molecular dynamics. The N-terminal β-hairpin was found to be flexible. The FSD-1 apparent melting temperature of 41°C may be a reflection of the melting of its α-helical segment instead of the entire protein. Thus, despite its attractiveness due to small size and purposefully designed helix, sheet, and turn structures, the status of FSD-1 as a model system for studying protein folding should be reconsidered.

Introduction

Mini-proteins that contain <50 amino acids and fold independently of metal-binding centers or disulfide cross-linking sites are considered model structures for investigating the driving forces behind protein folding. These minimal model systems contain essential features of larger proteins: defined structures, important intramolecular contacts that stabilize the folded state, and, in some instances, cooperative folding and unfolding. At the same time, their small size makes it feasible to study folding pathways and protein-energy landscapes with long timescale, molecular dynamic (MD) simulations (1). Mini-proteins often serve as benchmarks for validating novel methods in molecular simulations such as replica-exchange molecular dynamics (REMD) (2–4). Insights gained from studying mini-protein folding can be applied to protein-structure prediction, de novo protein design, and the discovery of novel biologics for treating diseases.

The zinc-finger motif consists of an N-terminal β-hairpin and a C-terminal α-helix with the tertiary structure stabilized by a zinc metal center coordinated by two cysteines and two histidines. Mini-proteins designed to fold into the zinc-finger ββα motif independent of zinc binding are especially interesting because their folded structures contain the helix, sheet, and turn secondary structures of the parent zinc finger. Struthers et al. (5,6) iteratively designed the 23-residue BBA5 protein to adopt the ββα motif independent of zinc binding. A D-proline residue at position 4 was essential in stabilizing the β-hairpin in BBA5. Dahiyat and Mayo (7) used computational methods to design the 28-residue FSD-1 protein that also adopted the ββα motif independent of zinc binding (Fig. 1). They started with the backbone coordinates of the zinc-finger protein Zif268, and then selected side-chain rotamers to optimize side-chain/side-chain and backbone/side-chain interactions. The folding pathway, energy landscape, and stability of FSD-1 have been investigated by MD simulations in implicit and explicit solvent and by using improved sampling methods like REMD (8–13). These subsequent studies of FSD-1 were conducted mostly because of the small size of FSD-1, its sequence consisting of only natural amino acids, and the assumed accessibility of its thermal unfolding transition. However, the FSD-1 apparent melting temperature of 42°C and its reported NMR structure (7) have been assumed in previous studies without further experimental validation.

Figure 1.

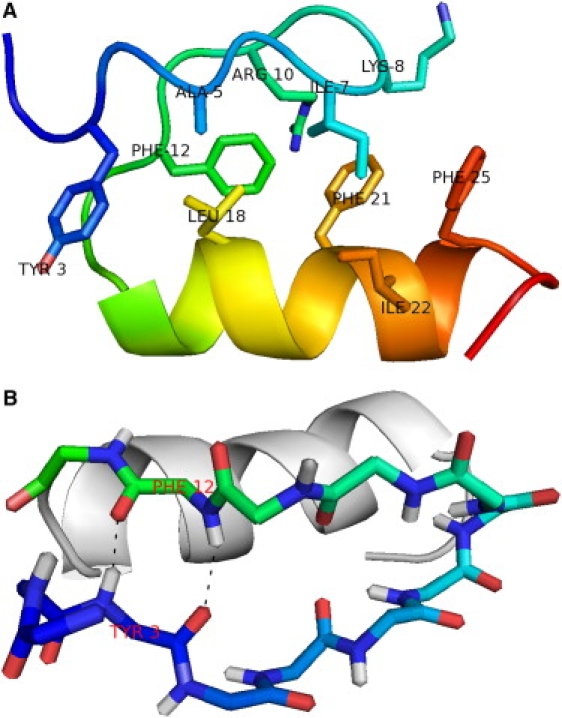
Structure of FSD-1 (PDB: 1FSD). (A) For clarity, side chains of selected residues are shown. (B) The main-chain atoms in the β-hairpin of FSD-1 are shown colors and the hydrogen bonds between Y3 and F12 highlighted by black dashes. The α-helix is shown in light gray. Figures were generated using PyMOL (33). Sequence: QQYTAKIKGRTFRNEKELRDFIEKFKGR.

In this study, we present a critical analysis of FSD-1 stability by studying its thermal unfolding and solution structure by circular dichroism (CD), differential scanning calorimetry (DSC), and REMD. Thermodynamics properties such as melting temperature and enthalpy of unfolding were determined by analyzing changes in ellipticity and excess heat capacity, as function of temperature, that were measured by CD and DSC experiments. REMD simulations provided structural details that suggested possible explanations for the unusually broad melting transition of FSD-1. The results suggest that an alternative interpretation that the apparent melting temperature was a reflection of a local helix-coil transition and not a protein unfolding transition is plausible and that FSD-1 may not necessarily be a robust model system for studying protein folding.

Materials and Methods

Peptide synthesis and purification

All reagents were obtained from commercial suppliers and used without further purification. FSD-1 was synthesized by solid-phase peptide synthesis using an automated microwave synthesizer (CEM Liberty, Matthews, NC). Fmoc amino acids were used. 2-Chlorotrityl resin was preloaded with Fmoc-Arg. The Fmoc groups were deprotected by treatment of 20% piperidine in 0.1 M N-hydroxybenzotriazole in N,N-dimetylformamide at 35 W at 75°C for 30 s followed by a second treatment at 35 W at 75°C for 3 min. Coupling was achieved with 5 equiv of Fmoc-amino acids, 5 equiv of 2-(1H-benzotriazole-1-yl)-1,1,3,3-tetramethyluronium hexafluorophosphate, and 10 equiv of diisopropylethylamine at 35 W at 75°C for 5 min. Arginine residues were first coupled at 0 W at 25°C for 25 min then at 20 W at 75°C for 5 min. A second coupling for arginine was carried out at 35 W at 75°C for 3 min. FSD-1 was cleaved from the resin by treatment with a mixture of 95% trifluoroacetic acid (TFA), 2.5% H₂O, and 2.5% triisopropylsilane for 2 h at room temperature. After filtration, TFA was removed by evaporation and the crude peptides precipitated with cold diethyl ether.

FSD-1 was purified by reversed-phase high performance liquid chromatography. Samples were prepared by dissolving the peptides in a 1:1 mixture of Solvent A (0.05% TFA in H₂O) and Solvent B (0.05% TFA, 10% H₂O in acetonitrile). The eluted samples were then monitored at 220 nm with a Gilson UV/VIS-155 (Gilson, Middleton, WI). A preparative VyDac C18 column (Cat# 218TP1022) was used with a linear gradient of Solvent A to Solvent B (5%–50% B) over 30 min with flow rate of 15 mL/min. The fraction containing the desired peptide was concentrated and repurified to >95% purity with a linear gradient of Solvent A to Solvent B (24.5% B to 25.5% B) over 30 min with a flow rate of 15 mL/min. Peptide purity was confirmed by NMR (Fig. S1 in the Supporting Material). Peptide identity was confirmed by electrospray mass spectrometry on a Waters Quattro micro (Watter, Milton, MA). The calculated average [M + H]⁺ mass was 3489 Da and the observed mass was 3489 Da.

CD

CD measurements were carried out on a Jasco J-810 (Easton, MD) equipped with a Jasco PTC-424S Peltier temperature controller. Protein concentration was determined by ultraviolet-visible absorbance at 280 nm using an extinction coefficient of 1490 M⁻¹ cm⁻¹. The protein concentration was 5 μM in 5 mM sodium phosphate buffer at pH 5.0 (7). Spectra were collected before thermal unfolding at 4°C and after thermal unfolding at 80°C in a 1-cm quartz cell, averaged over three scans from 260 to 190 nm with 2-s averaging, scanning speed of 20 nm/min, and data pitch of 1-nm increments. For thermal unfolding, a thermometer was placed inside the sample cuvette and the sample was constantly stirred. Thermal unfolding was monitored at 218 nm, with averaging time of 15 s, temperature increments of 1°C, and temperature slope of 30°C/h.

DSC

DSC measurements were carried out on a VP-DSC microcalorimeter from MicroCal (Northampton, MA). Samples were degassed under vacuum for 10 min before they were used for calorimetric analysis. The start and final temperatures were 10°C and 70°C, respectively, and the scan rate was 60°C/h. A 15-min prescan equilibration was used. The buffer was 50 mM sodium phosphate at pH 5.0, degassed. The sample cell was pressured to 25 PSI to prevent evaporation. A 0.5 mg/mL protein solution was prepared. Thirteen scans with the sample and buffer cell containing buffer were completed before the introduction of protein to the sample cell during a cooling cycle. Reheating runs were repeated to determine the calorimetric reversibility of the thermal-denaturation process. Data analysis was carried out using Origin 7.0 and the DSC add-on provided by MicroCal.

REMD

REMD simulations were carried out using Gromacs 3.3.1 (31). An energy minimized structure of FSD-1 (PDB code: 1FSV) was used as the starting structure for the simulations. The termini were charged and the net charge of the protein was +5. Five Cl⁻ ions were added in random locations to neutralize the system. The protein was solvated in a truncated dodecahedron box of TIP4P water where the minimum distance between a protein atom and the edge of the box was 12 Å. The system contained 19,881 atoms. The OPLS-AA/L 2001 force field was used. The system was minimized until the maximum force was <100 kJ mol⁻¹ nm⁻¹. Sixty-four temperatures were chosen with the average exchange rate of 20%. A 1-ns simulation was run to equilibrate the minimized system at each of the 64 temperatures. Each trajectory was assigned random initial velocities that were based on their respective temperatures. The NPT ensemble was used, the temperature was coupled to the Berendsen thermostat every 0.1 ps and the pressure was controlled by the Parrinello-Rahman method every 1.0 ps. REMD simulations are often carried out at constant volume (NVT), but constant pressure (NPT) was chosen to avoid extreme-pressure artifacts at higher temperatures (4). A potential problem of using the NPT ensemble is improper solvation due to lower densities at high temperatures. The box size at the highest temperature, 445.2 K, was 20% larger than the box size at the lowest temperature, 262.2 K. This indicates that the protein was solvated in a liquid-like environment at high temperatures. Bond lengths between hydrogen atoms and heavy atoms were constrained with LINear Constraint Solver. Timestep was 2 fs. For each temperature, the temperature-equilibrated system served as the starting coordinates. The resulting 64 structures were used as initial structures in the REMD simulations with attempted exchanges every 1000 timesteps (2 ps). Atomic coordinates were recorded every 2 ps for further analysis. A total of 76 ns were simulated for each replica that resulted in 4.8 μs of simulation time. The simulations were run on Teragrid (32) resources. Data from the last 75 ns were used in analysis.

To determine the distribution of target temperatures for the replicas, we followed a method described in Sanbonmatsu and Garcia (3) with minor modifications. The minimized system was equilibrated for 500 ps at temperatures 250, 300, 350, 400, 450, and 500 K. Their average potential energies, U, were calculated and fitted to a linear function (R²: 0.99).

$$P\left(exchange\right)=\text{exp}\left[\left(\frac{1}{k_{\text{B}}{T}_1}-\frac{1}{k_{\text{B}}{T}_2}\right)\times \left(U_1-U_2\right)\right]\text{.}$$ (1)

Equation 1 was solved iteratively for the temperature distribution using P(exchange) values of ∼0.10. k_B was the Boltzmann constant; T_i and U_i were the temperature and potential energy of replica I, respectively. Initial test simulations with the resulting temperature distribution actually resulted in an average exchange rate of 0.20. P(exchange) of 0.20 is recommended to produce ample exchanges between replicas. Temperatures below 273 K were chosen to help establish a baseline. The resulting temperatures were 262.2, 264.4, 266.6, 268.8, 271.1, 273.4, 275.7, 278.0, 280.3, 282.7, 285.1, 287.5, 289.9, 292.3, 294.8, 297.3, 299.8, 302.3, 304.8, 307.4, 310.0, 312.6, 315.2, 317.9, 320.6, 323.3, 326.0, 328.8, 331.6, 334.4, 337.2, 340.0, 342.9, 345.8, 348.7, 351.6, 354.6, 357.6, 360.6, 363.6, 366.7, 369.8, 372.9, 376.1, 379.3, 382.5, 385.7, 389.0, 392.3, 395.6, 399.0, 402.4, 405.8, 409.2, 412.7, 416.2, 419.7, 423.2, 426.8, 430.4, 434.1, 437.8, 441.5, and 445.2.

Curve fitting

Thermal-denaturation curves from CD melting and REMD melting were fit to a two-state model to determine T_m and ΔH_vH. The following function was used in the fitting procedures (15,16):

$$\begin{array}{l}f\left(T\right)=\frac{y_{\text{f}}+m_{\text{f}}T+(y_{\text{u}}+m_{\text{u}}T)\times K}{1+K}\\ K=\text{exp}\left(\frac{h}{RT}\times \left(\frac{1}{T_{\text{m}}}-\frac{1}{T}\right)\right),\end{array}$$ (2)

where f(T) was the observed signal, y_f was the folded-baseline intercept and m_f was the corresponding baseline slope, y_u was the unfolded-baseline intercept and m_u was the corresponding baseline slope, T was the temperature (K), h was the van 't Hoff enthalpy, R was the gas constant (1.987), and T_m was the temperature (K) in of the transition point. DSC data were fitted to a two-state model using Origin 7.0.

Results and Discussions

Circular dichroism

FSD-1 was synthesized by solid-phase peptide synthesis and purified to >95% purity by reverse-phase HPLC. Its molecular mass of 3488 Da was confirmed by mass spectrometry. The thermal unfolding of FSD-1 was monitored by CD spectroscopy at 218 nm. The starting temperature was 4°C and the final temperature was 80°C. The far-ultraviolet (UV) CD spectra of FSD-1 at 4°C, 80°C, and 4°C after melting are shown in Fig. 2 A. The CD spectra at 4°C before and after melting overlapped well, which confirms that FSD-1 unfolding is reversible as originally reported by Dahiyat and Mayo (7). Two minima observed at 207 nm and 220 nm for spectra recorded at 4°C indicated that FSD-1 contains a well-formed α-helical segment (14). However, the CD spectra provided little information about the formation of a β-hairpin. The CD spectra of a FSD-1 double mutant (I7PK8D-proline) exhibited similar minima at 207 nm and 220 nm (Fig. 2 B), but the double mutant did not contain a stable β-hairpin as determined by NMR (data not shown). The melting curve of FSD-1 measured at 218 nm was fit to a two-state model (Eq. 2) assuming a ΔC_p value of zero (15,16) (Fig. 3). The melting temperature (T_m) and van't Hoff enthalpy (ΔH_vH) were determined from the least-square fit to be 41°C and 18 kcal/mol, respectively. The T_m value reported by Dahiyat and Mayo was 42°C (7).

Figure 2.

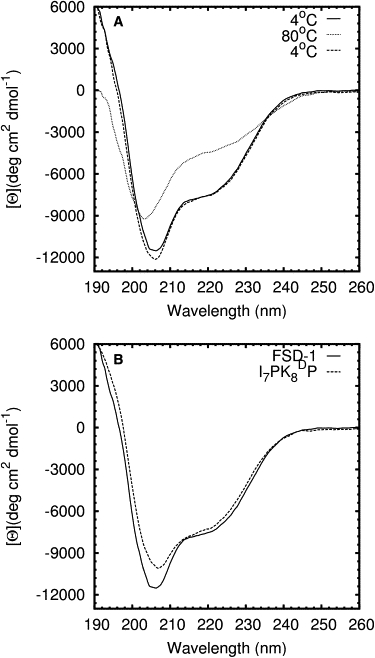
(A) Far-UV CD spectra of FSD-1 at 4°C and 80°C. Spectra were measured at 4°C premelting (solid) and postmelting (dotted). (B) Spectra of FSD-1 and an unfolded FSD-1 double mutant (I7PK^DP) at 4°C. ^DP denotes D-Proline.

Figure 3.

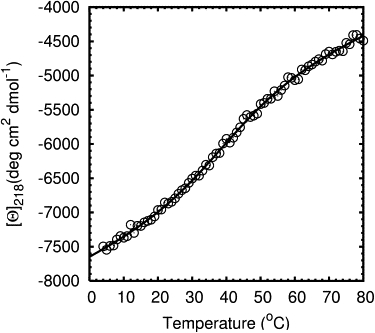
Thermal unfolding of FSD-1 monitored by CD at 218 nm. The melting curve was fitted to a two-state model and the resulting T_m was 41°C and ΔH_vH was 18 kcal/mol.

Thermal unfolding of FSD-1 was measured by CD. The mean residue ellipticity at 218 nm, [θ]₂₁₈, showed a broad transition with no clearly defined unfolded or folded baselines (Fig. 3). Lack of a baseline for the fully folded state indicated that FSD-1 was not well-folded even at 4°C. Because FSD-1 consists of only 28 residues, some flexibility was certainly expected, but a well-folded mini-protein should exhibit a better-defined baseline. For instance, the thermal unfolding of a 10-residue mini-protein (CLN025) designed, synthesized, and crystallized by Honda et al. (17) showed a well-defined, folded-state baseline and a T_m of 70°C. The broad transition of FSD-1 with undefined baselines was similar to helix unfolding (18–20). The broad melting transition observed by CD could be the result of the helix-to-coil transition in the α-helical part of FSD-1, rather than the unfolding of its proposed hydrophobic core between the helix and the hairpin.

Differential scanning calorimetry

DSC showed a broad melting transition for FSD-1 and its unfolding was reversible (Fig. 4). The broad transition made it difficult to determine the pre- and posttransition baselines necessary for a complete analysis of the calorimetric data. The unfolding of helical peptides also exhibits this behavior (18,19,21). An initial baseline was estimated by drawing a line connecting the heat-capacity values, C_p, at the lowest and highest temperatures. The resulting excess heat capacity curve obtained by subtracting the baseline was fit to a two-state model while assuming a ΔC_p value of zero. The least-square fit was poor and resulted in high sum of squares-of-residual values. To obtain better fits, the baseline was systematically lowered by increments of 25 cal^∗mol⁻¹K⁻¹. The estimated C_p baseline resulting in the lowest squares-of-residual value for the two-state fit was taken as the best; excess heat capacity values obtained from subtracting this baseline are shown in Fig. 4. Estimation of baseline by least-squares minimization was similar to that used by Scholtz et al. (18) in determining the baseline for the thermal melting of a 50-residue α-helix. For the two-state fit, T_m was 41°C and ΔH_cal was 15 kcal/mol. T_m values calculated from using different baselines were centered at 41°C and varied by less than a degree. However, ΔH_cal values varied depending on which baseline was used in calculating excess C_p; the values ranged from 12 to 15 kcal/mol.

Figure 4.

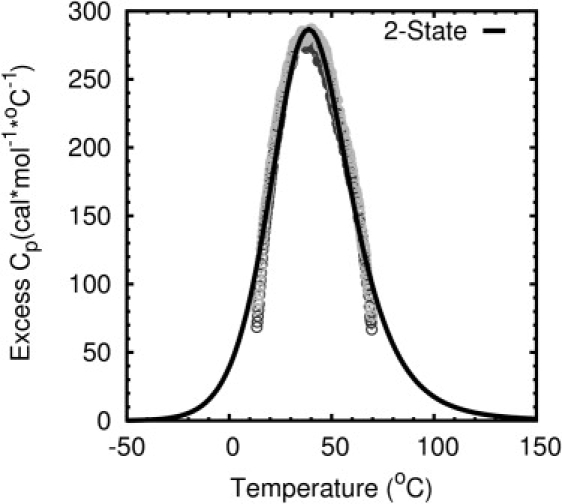
DSC melting curve fitted to a two-state model. T_m was determined to be 41°C and ΔH_cal was determined to be 15 kcal/mol. Dark and gray circles represent two back-to-back DSC scans.

The van't Hoff enthalpy determined by CD was 18 kcal/mol, which was 3 kcal/mol higher than the calorimetric enthalpy determined by DSC. The near unity ratio of ΔH_cal/ΔH_vH suggests that FSD-1 unfolding approximated a two-state transition (22). FSD-1 unfolding measured by DSC indicated that the unfolding transition began at near −20°C and ended at over 100°C. This broad transition is nearly identical to the helix-to-coil transition measured for a 50-residue α-helical peptide, Ac-Y(AEAAKA)₈-NH_2, by Scholtz et al. (18). They concluded that Ac-Y(AEAAKA)₈-NH₂ unfolding was far from being a two-state process because ΔH_cal ≫ ΔH_vH (18). GCN4brNC, a 29-residue α-helical peptide with covalently closed N- and C-terminal loops also exhibited a broad folding-unfolding transition ranging from 5°C to >80°C (19). The covalent loops between residues 1 and 5 at the N-terminus and between residues 25 and 29 at the C-terminus stabilized this helix. GCN4brNC unfolding was found to closely approximate a two-state transition (19). Unfolding of the 35-residue subdomain of the villin headpiece was examined by Godoy-Ruiz et al. (23). Its unfolding transition was much narrower, ranging from 40°C to 80°C. Its T_m was 65°C and it was reported to fold via a two-state mechanism. The broad unfolding transition of FSD-1 is more like the unfolding of α-helical peptides than that of the more stable 35-residue villin headpiece subdomain.

Molecular dynamics simulations

In CD and DSC melting experiments, measurements such as mean residue ellipticity or excess heat capacity are plotted as a function of temperature to calculate T_m. REMD simulations are analogous to thermal unfolding experiments in that a protein is simulated over a range of temperatures and measurements are recorded at each temperature. An advantage of molecular simulations is that atomic details are recorded during the simulation. In REMD, a replica starts at one temperature and exchanges its temperature, based on a Metropolis criterion, with a neighboring replica that has a different temperature (2). REMD-simulation temperatures were chosen so that potential-energy overlaps between replicas would be consistent across all temperatures and that there would be an optimal exchange rate near 20% (3). Fig. 5 shows that the energy overlaps were consistent throughout the temperature range for the last 10 ns of the simulation, which was representative of the entire 76-ns simulation.

Figure 5.

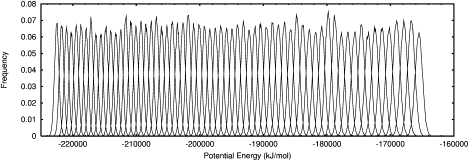
Potential-energy overlap between neighboring replicas during the last 10 ns of the simulation. Each distribution curve represents the potential-energy distribution at a single temperature. The left-most curve represents the potential energy of the lowest-temperature replica, and the right-most curve represents the potential energy of the highest-temperature replica.

The essence of REMD is high-sampling efficiency achieved by temperature exchanges between neighboring replicas. As shown in Fig. 6, top panel, a wide range of temperatures were sampled by three representative replicas. This indicates the high-quality sampling of the simulation. For example, replica 1 started at 262.2 K. Through a series of temperature exchanges, its temperature reached 445.2 K, the maximum temperature of the simulation, at time point 14.426 ns. Replica 1 continued to explore a wide range of temperatures throughout the simulation. Fig. 6, bottom panel, shows backbone root mean-square deviation (RMSD) between the native protein and trajectory snapshots of the corresponding replicas in Fig. 6, top panel,. A folding event was observed in replica 62 that started at 437.8 K with an unfolded structure (RMSD > 8 Å). In the first 40 ns of the simulation, the replica's temperature was limited to the upper half of the allowed temperature space and the protein stayed unfolded. A folding event occurred between 35 and 40 ns of the simulation, concurrent with replica 62 sampling much lower temperatures (Fig. 6). Unfolding events were observed in replica 1 and replica 31. Replicas 1 and 31 were examples of protein unfolding that is analogous to thermal denaturation. At lower temperatures, the conformations sampled were similar to the native structure, whereas at higher temperatures, unfolded ensembles of conformations were sampled.

Figure 6.

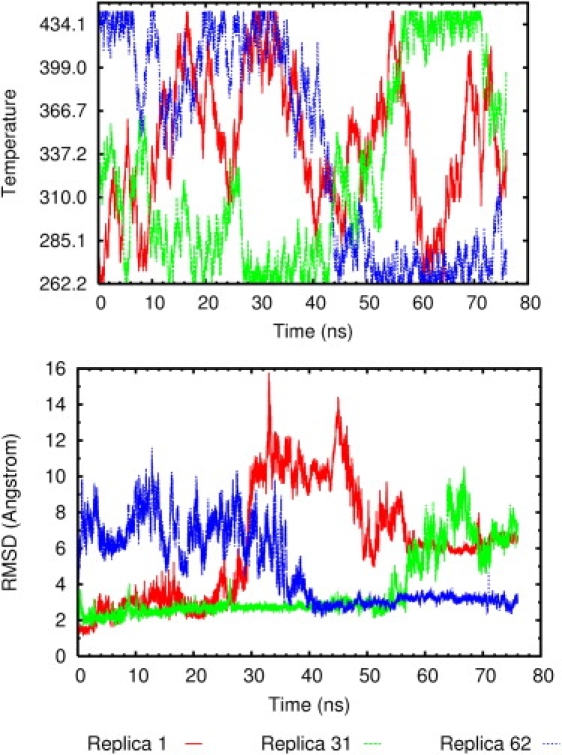
(Top) Temperatures sampled by 3 of 64 representative replicas during the course of the simulation. Replicas 1, 31, and 62 started at 262.2 K, 337.4 K, and 437.8 K, respectively. (Bottom) RMSD of three replicas during the course of the REMD simulation. A folding event is observed in replica 62, and unfolding events are observed in replicas 1 and 31.

Structural properties for each REMD trajectory were analyzed as a function of temperature. Backbone RMSD and C-α root mean-square fluctuation (RMSF) were calculated to provide different measures of protein unfolding (Fig. 7). RMSF is a measure of the average flexibility of an atom with respect to itself. High RMSF values indicate highly flexible atoms. Terminal residues 1, 2, and 26–28 were excluded from RMSF calculations because they were extremely flexible and distorted the flexibility of the entire protein. The RMSD and RMSF values were fit to a two-state model (Eq. 2) to predict the melting point of FSD-1. The average predicted T_m was 125°C, which was 84°C higher than the experimental T_m (41°C) determined by CD and DSC. The average FSD-1 T_m predicted by Li et al. (11) was 152°C, which was 111°C higher than the experimental T_m. Li et al. (11) used the NVT ensemble instead of the NPT ensemble used in this study. The NVT ensemble tends to stabilize the hydrophobic core at high temperatures (24,25). High T_m values were the results of the simulations overstabilizing proteins at high temperatures This may be because the force-filed parameters used were originally fit to room-temperature experimental values.

Figure 7.

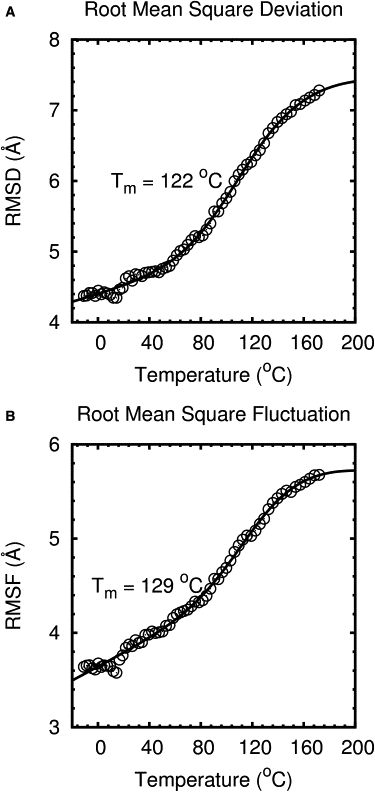
Thermal unfolding monitored by RMSD and RMSF. The data were fit to a two-state model. RMSF values were calculated for residues 3–25. The fitted melting temperatures T_m are shown in the panels.

Structural analysis

Experimental and simulation melting curves showed that FSD-1 exhibited a broad unfolding transition. There were difficulties in establishing a baseline for the folded state of FSD-1 in both simulation and experimental melting curves. In the REMD simulations, there were difficulties even though the lowest temperature was chosen to be −11°C to help establish a baseline for the folded state. These results suggest FSD-1 is only nominally stable even at −11°C, which is in agreement with DSC results. To further investigate, we examined hydrogen-bonding patterns and native contacts observed in the ensemble of FSD-1 NMR structures reported by Dahiyat and Mayo (7) (PDB ID: 1FSD) and in the ensemble of trajectory snapshots from the REMD simulation. In the NMR structures, residues 2–13 formed a β-hairpin and residues 5–10 formed an EbaaagbE reverse turn (26). The two β-stands in the hairpin were connected by this six-residue loop instead of the more common four residues in a traditional reverse turn. Two hydrogen bonds were formed between the amide and carbonyl groups of Y₃ and F₁₂ at 7°C as determined by NMR nuclear Overhauser effects (7) (Fig. 1 B). No other hydrogen bonds were observed between main-chain atoms of the hairpin residues. The fact that only two hydrogen bonds were observed in a hairpin of 12 residues indicates that the β-hairpin was minimally stable. For comparison, four interstrand hydrogen bonds were observed between residues in the 8-residue β-hairpin of BH17 (27), a 17-residue synthetic mini-protein containing independent helical and β-hairpin domains. A D-proline residue at position 13 nucleated the β-hairpin of BH17. For all temperatures of the REMD simulation, the highest average number of hydrogen bonds formed between the main-chain atoms of Y₃ and F₁₂ was 0.7 (Fig. 8). This suggested that the β-hairpin was formed only 35% (0.7/2.0) of the time even at low temperatures. The average number of hydrogen bonds formed between main-chain atoms of hairpin residues in strands one (residues 2–6) and two (residues 9–13) were also plotted in Fig. 8. At most 1.5 hydrogen bonds were formed. The expected number of interstrand hydrogen bonds for this β-hairpin of 12 residues would be six. Lack of detectable interstrand hydrogen bonds in the β-hairpin of FSD-1 contributed significantly to a hypothesis of its overall instability.

Figure 8.

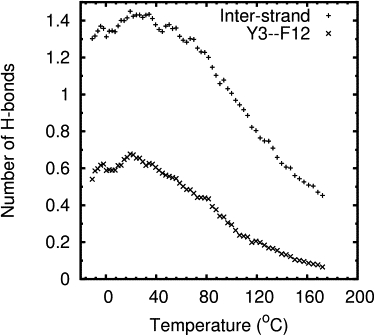
Average number of hydrogen bonds formed between main-chain atoms in residues Y₃ and F₁₂ (x) or between residues in strand 1 (residues 2–6) and strand 2 (residues 9–13) of the hairpin (+) during the REMD simulation.

The overall fold and topology of FSD-1 as designed depend mostly on the small hydrophobic core formed by residues Y₃, A₅, I₇, K₈, R₁₀, and F₁₂ in the β-hairpin and residues L₁₈, F₂₁, I₂₂, and F₂₅ in the α-helix (Fig. 1 A). Two residues were defined as in contact if their side chains have any two heavy atoms that are within 6.0 Å. Using this criteria, 185 contacts were found between residues in the α-helix (18,21,22,25) and those in the β-hairpin (3,4,7,8,10,12) in the ensemble of 41 NMR structures of FSD-1 reported by Dahiyat and Mayo (7). Contacts within the β-hairpin or α-helix were not considered. The maximum percentage of native hydrophobic-core contacts seen by REMD was 58% at −11°C. Li et al. (11) calculated the protein and β-hairpin native contacts for FSD-1 in their REMD simulation to be 60% for the entire protein, and 45% for the β-hairpin. Hydrogen-bond and native-contact information from the simulations of Li et al. (11), and the REMD reported herein, suggest that FSD-1 at low temperatures was very flexible and could adopt multiple conformations.

In MD simulations of FSD-1, it was found to be marginally stable at room temperature (9,10). The plasticity of the β-hairpin, especially reverse-turn residues 7, 8, and 9 were believed to contribute to the instability of FSD-1 (8,10). Li et al. (11) observed from their REMD simulations that the C-terminal α-helix was more stable than the β-hairpin by 33°C. For the α-helix, the C-terminal helical turn consisting of residues E₂₃, K₂₄, F₂₅, and K₂₆ was folded <10% of the time in their simulations. In five 200-ns simulations of FSD-1 at 300 K, Lei et al. (9) noted that the N-terminal β-strand (Y₃TAK) were mostly helical instead of forming the native β-strand. They concluded that this was probably due to the high helical propensity of A₅ and K₆ according to the Chou-Fasman scale (30).

Alternative interpretation

Results from CD, DSC, and REMD experiments showed that FSD-1 was only minimally stable even at low temperatures. The FSD-1 thermal unfolding curves measured by CD and DSC lacked baselines for the folded state, suggesting that FSD-1 adopts multiple conformations. MD simulations provided further evidence of the plasticity of the β-hairpin. The C-terminal residues (26–28) were also very flexible. The changes in ellipticity in the CD unfolding experiment and in heat capacity in the DSC unfolding experiment at low temperatures were likely caused by different dynamics of the β-hairpin and C-terminal residues. The broad melting transition observed by CD and DSC was probably the result of the helix-to-coil transition in the α-helical part of FSD-1, rather than the unfolding of its limited hydrophobic core. The melting temperature of FSD-1 was determined to be 41°C by CD and DSC. Given the minimal stability of the β-hairpin, it is quite plausible that the T_m reflects mostly the melting of the FSD-1 α-helix, rather than melting of the entire protein. Burial of hydrophobic groups of the FSD-1 amphiphilic α-helix by residues in the hairpin region, regardless of whether a hairpin was formed, likely shifted the helix's T_m to 41°C. Additional helix stability was gained by the presence of nine charged residues on the hydrophilic side of the 14-residue helical segment.

Conclusions

We have presented a critical analysis of FSD-1 stability by studying its thermal unfolding and structure by CD, DSC, and REMD. Thermal unfolding experiments and molecular dynamics simulations showed that the unfolding transition started at temperatures much lower than 7°C. The plasticity of the β-hairpin contributed significantly to the observed changes in ellipticity in the CD experiment and changes in heat capacity in the DSC experiment. We propose that the apparent melting temperature of FSD-1, 41°C, primarily reflects the melting of the FSD-1 α-helix, not the entire protein. Whereas its small size makes FSD-1 an attractive target for studying protein folding, these results question the status of FSD-1 as a robust model system.

Supporting Material

A NMR figure is available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(09)01439-8.