Dual Axis Target Mapping and Automated Sequential Acquisition of Dual Axis EM Tomographic Data

Abstract

Dual-axis electron microscopic tomography minimizes the missing wedge-induced resolution loss by taking two complementary tilt data sets of the same target along two orthogonal axes. The potential of this powerful approach has been hampered by the practical challenges inherent in finding the original targets that are dramatically displaced due to non-eucentric specimen rotation. Not only is the manual search for the original targets time consuming and tedious but the added dose during manual searching is uncontrollable. We have developed a hierarchical alignment scheme that allows tomographic data to be collected from an arbitrary number of target sites in one grid orientation and then to find and collect orthogonal data sets with little or no user intervention. Inspired by the successful multi-scale mapping in Leginon, our alignment is performed in three levels to gradually pinpoint the original targets. At the lowest level the grid lattice is used to determine the rotation angle and translational shift resulting from specimen rotation via auto- and cross-correlative analysis of a pair of atlas maps constructed before and after specimen rotation. The target locations are further refined at the next level using a pair of smaller atlas maps. The final refinement of target positions is done by aligning the target contained image tiles. Given the batch processing nature of this hierarchical alignment, multiple targets are initially selected in a group and then sequentially acquired. Upon completion of the data collection on all the targets along the first axis and after specimen rotation, the hierarchical alignment is performed to relocate the original targets. The data collection is then resumed on these targets for the second axis. Therefore, only one specimen rotation is needed for collecting multiple dual-axis tomographic data sets. The experiment of acquiring 20S Proteasomes dual-axis tomographic data sets in vitreous ice at 86000x CCD magnification on our FEI Tecnai Polara TF30 electron microscope has suggested that the developed scheme is very robust. The extra doses for finding and centering the original targets are almost negligible. This scheme has been integrated into UCSF Tomography software suite that can be downloaded at www.msg.ucsf.edu/tomography free for academic use.

1. Introduction

Single axis EM Tomography (EMT) has an intrinsic resolution limit set by the maximum angular range that specimens can tilt. The volume beyond this range is left unmeasured and commonly known as the “Missing Wedge”. For cryo-electron tomography the resolution is further deteriorated by the poor signal to noise ratio (SNR) images acquired at the very low doses necessary to preserve biological structures. Inspired by single particle reconstruction approaches, cryo-electron single particle tomography (CESPT) (Walz et al., 1997), minimizes resolution losses by averaging in 3D space. This approach has gained considerable interest since then (Bartesaghi et al., 2008, Bostina et al., 2007, Nicastro et al. 2006, Nicastro et al., 2005, Beck et al., 2004, Grunewald et al., 2003). CESPT relies in general on the premise that the particles are conformationally homogeneous and randomly oriented. Therefore, the missing wedge of one particle can be filled with the data of others settled in different orientations. SNR can also be improved because each point in 3D space is multiply sampled on various conformationally identical copies that contribute to the average. However, the ability to average identical structures is not applicable for larger entities such as cells and organelles. Dual-axis EMT is well suited for this class of problems by taking two perpendicular single axis EMT data sets (Penczek et al., 1995, Mastronarde et al., 1997, Iancu et al., 2005, Tong, et al., 2006, Arslan et al., 2006). For a tilt range of ±60°, 33 percent volume in reciprocal space is left unmeasured in single axis EMT versus 16 percent in dual axis EMT (Iancu et al., 2005).

Cryo EMT has drawn extensive interest because of its great potential to reveal unbiased structural information. However, challenges arise from vitreous specimen preparation, specimen loading, to the data acquisition at very low dose. Therefore, each loaded grid should be scanned thoroughly for accumulation of large numbers of particles and minimization of system idle time. Thus for both CESPT and dual-axis Tomography it is desirable to efficiently collect tomographic data from many different regions on the grid. Dual-axis Tomography has the additional challenge of requiring that the same target areas be precisely relocated after grid rotation. Owing to the large useful area and the limited CCD detector size, grid scanning is performed at very low magnifications. For example, the fully automated single particle data collection system, Leginon, scans grids by taking multiple images to form an initial montage map of the whole grid at a magnification as low as 120x (Potter et al., 1999, Carragher et al., 2000, Suloway et al., 2005). Due to limitations in stage accuracy, precisely relocating targets identified at very low magnifications and distributed over the entire grid to the CCD center at much higher magnifications poses a practical challenge (Pulokas et al., 1999). This process may involve hundreds of microns of stage displacement and more than forty-fold change in magnification. Even more challenging, tomographic approaches require very accurate optimization of z-height eucentricity, since each target is expected to tilt beyond ±60° at magnifications above 60,000x. Together these highly demanding yet repetitious operations are most suitable for automation, leading to not only a significant improvement in throughput but also dose reduction as well.

In one effort to facilitate tomographic acquisition of multiple data sets, UCSF Tomography has recently been integrated into Leginon (Suloway et al., 2009, to appear). However, given the particularly challenging demands of dual-axis tomography we have also extended UCSF Tomography to both include target selection suitable for CESTP and to efficiently relocate and collect tomographic data from target sites after grid rotation. The general strategy is to first collect data from all selected targets in one grid orientation and to then rotate the sample and resume data collection on the original targets. The non-eucentric in plane rotation can typically shift the targets a few hundred microns away from their original positions. While finding the original targets after specimen rotation is exclusive to dual-axis EMT, positioning targets to the CCD center with sufficient eucentric and focal accuracy is a shared challenge of both CESPT and dual-axis EMT. Thus, although we focus our discussion here on solving the problem of dual-axis EMT, it should be readily apparent that the same system is highly effective for collecting CESPT data sets and to facilitate EM acquisition of the same sample regions also imaged using light microscopy.

For the Polara microscope GATAN developed the so-called “flip-flop” rotation cartridge. This cartridge allows the specimen to be anchored at either the flipped or the flopped position, corresponding to 0 and 90 degrees orientation, respectively. Switching between the flipped and flopped positions is implemented via pushing on a tab extending from the cartridge (for a detailed description see Iancu et al., 2005). JEOL has recently introduced a similar rotation cartridge for its microscopes. In order to demonstrate the typical amount of shift induced by non-eucentric in-plane rotation of the Polara cartridge, two montage maps were constructed before and after rotation of a Maxtaform H6 235 pitch finder grid (Pelco) and are presented in Fig. 1.

Figure 1.

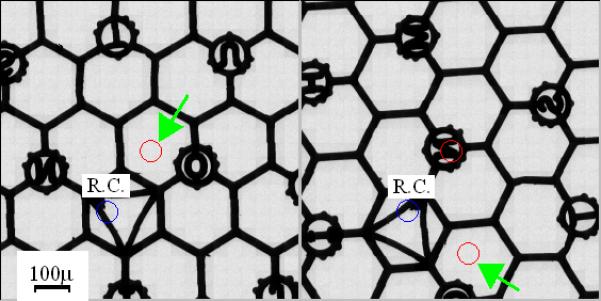
Montage maps of a Maxtaform H6 235 pitch finder grid (Pelco) before and after “flip-flop” specimen rotation at 990x nominal magnification. R.C. stands for rotation center. (a) Before rotation. The arrow points to the map center. (b) After rotation. The arrow points to the new location where the center of the pre-rotation map has been displaced. Both maps were constructed at the origin of stage xy plane.

Each map was made of 441 images acquired at 990x nominal magnification and centered at the origin of the Compustage xy plane and z eucentric height. This corresponds to a field view of 907 × 907 μm² on the grid. It is observed that the center of the pre-rotation map indicated by the red circle pointed by the green arrow in Fig. 1(a) has been shifted by more than 300 μm to its new location (Fig. 1(b), labeled by the green arrow). Manual hunting the original targets after rotation requires users to perform an exhaustive search within a large range of magnifications, very inefficient both in time and dose. In particular, it may place a prohibitive challenge to non-expert EM users and hence limit its general use.

Of course, the specimen rotation does not relocate the targets arbitrarily. Instead the new locations of targets are fully described by a rotation angle and a translational shift. Unfortunately, the rotation center typically does not correspond to the Compustage center (Fig. 1), and actually varies with each loading of the cartridge. Moreover the rotation angle varies from cartridge to cartridge. Therefore, the alignment parameters need to be determined for each sample and the large field of view is required to capture the very significant offsets (too large to be determined from a single image). By digitally stitching together a large number of images acquired at various stage coordinates both before and after specimen rotation into a pair of precise atlas maps, we can determine the required alignment parameters from a correlative analysis of the two maps. The pre-rotation coordinate of each target can then be mapped to the post-rotation coordinate system computationally and in principle, the new targets can be acquired simply by directing the stage to translate the specified coordinate to the CCD center. In reality, the situation is more complicated due to insufficient stage positioning accuracy and the large change between the magnification used for atlas construction and the magnification required for collecting the tilt data sets. In a typical setup, the magnification can vary from 480x to 60,000x. Therefore, each target has to be brought to the CCD center in several steps from low to high magnification. At each intermediate magnification the target position has to be refined to correct for the stage positioning error and any imperfect electron microscope alignment between the different magnifications. We have achieved this goal at the cost of only a small amount of extra dose. This scheme has been developed and integrated into the UCSF Tomography software system to enable sequential collection of multiple single- and dual-axis tomographic tilt series without any operator intervention. The longest continuous data collection session has exceeded 72 hours with a very high success rate.

2. Building the Atlas Map

Atlas maps provide a large-scale field of view by digitally stitching many images together, each representing a sub-area of the grid. Hereafter, images that form an atlas map are referred to as tile images. To build a precise map, each sub-area must be positioned to the CCD center accurately. Due to the large field of view, the required positioning is far beyond the deflection range of the image/beam shift coils. The only choice, is to use the computerized stage to mechanically position the sample. Unfortunately, the current commercial FEI Compustages are quite inaccurate at moving between two specified points. As a result, atlas maps so constructed will be aberrant, giving a deformed view of the grid. It is important to realize that building precise atlas maps is not just a cosmetic issue. The alignment parameters of dual-axis sequential tomographic data collection are derived from the correlative analysis of two maps constructed before and after specimen rotation. The deformation can undoubtedly bias the alignment parameters and affect how accurate the targets will be relocated afterwards. We therefore endeavored to improve the stage positioning accuracy in order to minimize the deformation. Efforts were directed towards stage calibration, backlash removal, and the strategy of building the atlas map in accordance with the stage behavior.

It was noticed that the major positioning error is along the stage x axis. As expected, additional error arises from the backlash that occurs when the stage movement reverses direction. We have developed a map building strategy that minimizes the effect from these errors. Given the fact that the stage y axis is more accurate and robust, the more frequent movement of the stage is directed along the y axis when a map is constructed and the less frequent along the x axis. Since the stage y axis is nearly parallel to the CCD x axis for magnifications in LM and M modes of FEI Tecnai electron microscopes, the map is constructed by putting the first image in the upper-left corner and proceeding from left to right. Once the first row has been assembled, the images in the second row are taken in the order from right to left. By so doing, the stage movement from one image to the next is always of same distance within the same row and from one row to the next. Thus we can precalibrate both the stage x and y movements with the induced shift set near to this distance. Since the vertical movement is always from top to bottom eliminating y-axis backlash, we can precalibrate the stage x movement in the same direction that the stage moves from one row to the next during map construction. To reduce backlash error resulting from reversing the direction of stage movement, we move the stage such that the target is always approached along the positive stage axes. Fig. 2 presents the hierarchical view of a grid acquired from 480x nominal magnification to 14500x. Fig. 2(a) shows an atlas map made of 121 images at 480x that covers near 980μm × 980μm of the grid. The map was built at 3000x magnification (the lowest M mode magnification on the Polara) and made of 81 images is given in Fig. 2(b). This M-mode map covers about 128μm × 128μm of the grid. Both Figs. 2(a) and 2(b) exhibit smooth edges of grid bars. In particular, the Quantifoil holes are well aligned as is shown in Fig. 2(b), suggesting that it is possible to build quite precise atlas maps via optimal integration of stage calibration and construction of atlas maps. The light blue arrow in Fig. 2(a) is used to mark the corresponding location of the map in Fig. 2(b). Fig. 2(c) shows one of the tile images that form the map in Fig. 2(b). Similarly the blue arrow indicates the corresponding location of this tile in Fig. 2(b). One of the holes in Fig. 2(c) was acquired at 14500x nominal magnification and given in Fig. 2(d).

Figure 2.

Hierarchical view of the specimen to show the process of finding the structures of interest. All images were acquired on FEI Tecnai Polara TF30 electron microscope equipped with a GATAN 4k UltraCam CCD camera. The blue square frames in the lower left corner of (a) and (b) represent the corresponding CCD imaging area, respectively. (a) Atlas map constructed at 480x nominal magnification. (b) Atlas map constructed at 3000x nominal magnification (M mode). (c) A tile image that forms the atlas map shown in (b). (d) An image taken at 14500x nominal magnification. The light blue arrows show where the location of the pointed map or images is originated in the precedent map or image.

3. Pipeline of Sequential Data Collection

Assuming the electron microscope is well aligned and all the necessary calibrations have been completed, the major preparations prior to starting sequential data collection are sketched in Fig. 3. First, an atlas map needs to be built with the user specified dimension and at any given stage location. In general, to keep the optical system stable it is preferred to build the map without turning off the objective lens or retracting the objective aperture. This condition can be realized by setting the electron microscope at the lowest magnification in M mode on FEI Tecnai electron microscopes. For example, in M mode (1700x) it takes 52 minutes to build an atlas of 800μm × 800μm on our FEI Tecnai T20 and Tecnai T12 electron microscopes under this setup. Since this avoids the need to restabilize the microscope after turning on the objective lens and provides a much higher magnification view for target selection, it is probably worth the time involved. However, due to a higher minimum M mode magnification (3000x) and slower camera readout, it would take an unacceptable amount of time to build maps of same size on our FEI Tecnai Polara TF30 G2 electron microscope equipped with a GATAN UltraCam 4k CCD camera and a GATAN lens-coupled energy filter. One solution is to build maps of reduced sizes at the same magnification. It takes nearly 58 minutes to build a map of 300μm × 300μm that contains total 441 1k images with 4x on-chip binning and 0.1s exposures. As an alternative, maps can be constructed at 480x magnification without the objective aperture inserted, as is shown in Fig. 2(a). This magnification is one of the few that do not need tuning of the EFTEM cross-over alignment. A map covering about 1000μm × 1000μm is then composed of 121 images and takes only 15 minutes to build with 0.1s exposures. This map is referred to as LM-mode map to distinguish from the maps built at a M-mode magnification. Upon completion of building the LM-mode map, the objective lens is turned on by switching to the lowest magnification in M mode and the objective aperture is reinserted. Since the magnification always changes between two fixed values (480x and 3000x in M mode for Tecnai TF30 electron micron scope, for example), it is in general that there is no need to tune the microscope alignment. The only extra work is to realign the objective aperture since we do not have a computerized objective aperture installed on our system. The overhead time of subsequent operations is used and in general sufficient to stabilize the objective lens.

Figure 3.

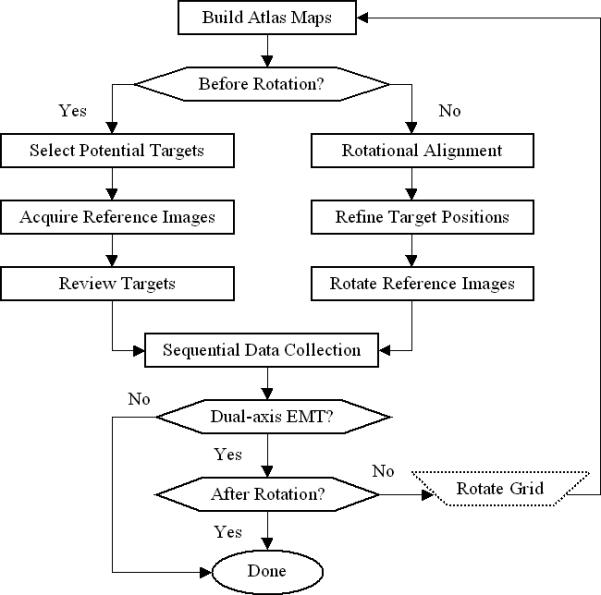
Major steps involved to achieve single- and dual-axis sequential electron microscopic tomographic data collection

Guided by the LM-mode map, we then build a smaller map of the promising area. This is shown in Fig. 2(b), composed of only 81 1k images with 4x on-chip binning and 0.1s exposure. This map took less than 11 minutes to build, and by the same convention, is named the M-mode map. In practice, if several promising areas are present but scattered in the LM-mode map, we build multiple M-mode maps, one for each identified area of the grid. This alternative strategy is most suitable for dual-axis tomographic data collection. The two LM-mode maps, one before and one after specimen rotation, will be used to derive the rotational alignment parameters including rotation angle, magnification change, and translational shift.

Upon completion of building the M-mode atlas map, the next step is to select potential targets. Users may examine potential sub-areas of appropriate ice thickness by clicking on the atlas map. As shown in Fig. 2(c) each click brings up a zoomed-in view of that sub-area by loading the nearest tile image that was saved during the map construction. In the meantime, a red circle is marked on the map to label the visited sub-area. Fig. 2(b), for example, indicates that a total of five sub-areas were visited. Candidate holes are then picked manually and marked on the rendered tile image shown in Fig. 2(c) where four holes were selected. A tile image with selected holes is referred to as target tile to distinguish those without any selection. The corresponding stage coordinate of the target tile along with the relative shift of each candidate hole is stored for later collection of images at intermediate magnifications, one per each selected hole. We also designate the first selection made on each target tile to be the site used only for tuning eucentric height, defocus, and energy filter zero-loss alignment, if installed. The red circle near the center in Fig. 2(c) is for this purpose. Candidate holes are always grouped together with a tuning site per target tile. This step is repeated until all sub-areas of interest on the map are examined. At the end, a list of stage coordinates is generated and each is associated with a sublist of relative positions of the candidate holes.

As can be seen in Fig. 2(c), 3000x magnification is generally too low to determine the presence of structures of interest within each hole. For this reason an image at an intermediate magnification is preferred (one per each selected hole) to provide a closer look with a very small amount of dose. Fig. 2(d) presents such an image acquired at 14000x magnification with 4x on-chip binning and 0.1s exposure. A large defocus can be applied to improve the contrast and facilitate the determination of the objects of interest. Such an image is referred to as a reference image because it will be used later to recenter the targets on the CCD during the sequential data collection. Acquisition of the reference images are automated by first recentering the sub-area of each target tile on the CCD. This can be implemented by taking a new image at the same stage location and magnification where the target tile is acquired. The stage positioning error is measured by correlative analysis between the target tile and this newly acquired image. This error along with the relative shift of each candidate hole is then compensated using the image/beam shift coils. A reference image is taken at the intermediate magnification for each centered hole. In practice, the induced misalignment by switching from the lowest magnification in M mode to the intermediate magnification should also be taken into account to ensure that the candidate holes are centered precisely. When all the candidate holes in this target tile have been imaged, the automation procedure then begins to process the next target tile and repeats until finished. A stack of images is generated and saved into an MRC file at the end of this step. It should be pointed out that the amount of the image/beam shift required to center each candidate hole on the CCD is converted to shifts in the stage coordinate system. When later the same candidate hole needs to be recentered during the sequential data collection, the stage movement is used to compensate for the amount of shift rather than the image/beam shift coils.

The last step prior to sequential data collection is a review of the acquired reference images to screen for structures of interest (targets). Any reference image with found targets is marked with red circles to label their locations relative to the image center. This image is referred to as target image to differentiate from those without targets. Only target images will be revisited during the following data collection while all other reference images are skipped. Fig. 2(d) shows a target image with a target selected at the center of the hole.

The complete selection of all target locations makes it possible to sequentially collect the tomographic data for each target without any user intervention. As mentioned earlier, targets are grouped with a tuning site per target tile. Since a target tile acquired at the lowest magnification in M mode covers only an area of 14μm × 14μm on the Polara electron microscope, we can reasonably assume that targets distributed within a target tile have the same eucentric height. Setting eucentric height is therefore performed only once per target tile. The automation is implemented in such a way that we first drive the stage to the tuning site to automatically set eucentric height and true focus. If an energy filter is installed, this tuning site is also visited for zero loss alignment prior to moving to a new target. The following task centers the next target on CCD within the current group. Since each target is associated with a target image in which the target is identified with the relative location to the image center, a new image is acquired at the same stage coordinate and magnification where the target image was acquired. The stage positioning error is then measured by correlating these two images. The sum of the stage positioning error and the relative shift of this target is compensated by deflecting the image/beam shift coils. This brings the target right to the CCD center due to the superior precision of the image/beam shift coils. For improved accuracy, the user specified defocus is then set by invoking the auto-focus routine at the target location but using an intermediate magnification and a short exposure to minimize the dose received (Zheng et al., 2006). This target is now centered on CCD at the desired eucentric height and properly defocused with the energy filter slit aligned to the zero loss peak and ready for tomographic data collection (Zheng et al., 2004). Upon completion of the data collection on current target, a zero loss alignment is performed again by shifting the stage to the tuning site. When finished, we then repeat the previous steps from centering the next target image all the way to acquiring the tomographic tilt series. When all targets linked to the current target tile are collected, the next target group is loaded into computer memory followed by setting eucentric height at its associated tuning site. The targets within this group are then centered, focused, and collected in the same fashion. This whole process continues until all targets have been collected.

4. Dual Axis Data Collection

4.1. Rotational Alignment

Fig. 2 also sketches the major steps involved after specimen rotation to find the original targets and resume the data collection for the second axis. The large target relocation shifts following specimen rotation necessitate the use of large-scale LM-mode atlas maps to track the shifts. Changes in the grid lattice in these two maps is used to measure the grid orientation and image magnification changes by performing auto-correlation of each atlas map. Figs. 4(a) and 4(b) present the auto-correlation images corresponding to the atlas maps in Figs. 4(c) and 4(d), respectively.

Figure.4.

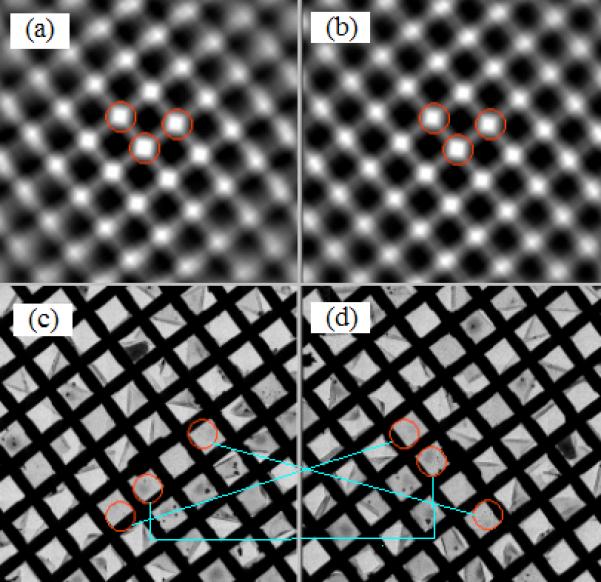
Correlative analysis of atlas maps constructed before and after specimen rotation to determine the rotational alignment parameters. Atlas maps were composed of 121 images of 1024 × 1024 pixels with 4x on-chip binning and 0.1s exposure acquired with a GATAN UltraCam CCD camera. The magnification was 480x on FEI TF30 Polara G2 electron microscope. (a) Auto-correlation image of the atlas map before specimen rotation. (b) Auto-correlation image of the atlas map after specimen rotation. (c) Atlas map before specimen rotation. (d) Atlas map after specimen rotation.

Three peaks in red circles and nearest to the image center are detected and shown in Fig. 4(a) and Fig. 4(b), giving rise to two vectors originated at the image center. These two vectors represent the grid orientation and unequal grid spacing. The specimen rotation can then be readily computed from the orientation change between these two pairs of vectors with the magnification change determined from the magnitude variation (note: we know that the rotation is ~90 degrees). One of the maps is then magnified and rotated accordingly prior to cross correlation with the other map to determine the translational displacement. With the complete determination of the alignment parameters, any coordinate in the map prior to rotation can be easily converted onto the post-rotation map based upon planar geometric rotation and translation. The target areas visited before specimen rotation and their counterparts are connected by the light blue lines in Figs. 4(a) and 4(b).

4.2. Hierarchical Refinement of Target Locations

With the determined alignment parameters and by performing combined rotational and translational coordinate transformation, target relocation as a result of specimen rotation can be calculated. Since the alignment parameters are drawn from the correlative analysis of two LM-mode atlas maps that cover about 1000μm × 1000μm grid area, the computed locations are not sufficiently precise for centering the targets at the data collection magnification. It is not difficult to anticipate that there will always exist some grid imperfection or microscope non-ideality that will give rise to alignment errors. Since a slight error in rotation angle can induce a significant error in finding targets that are far from the rotation center, further refinement of target locations is necessary. Therefore, a hierarchical refinement has been designed to bring targets to the CCD center at the final magnification where tomographic data sets are to be taken.

The first refinement is performed by correlating a pair of M-mode maps built at the lowest magnification in M mode. Fig. 5(b) shows one of M-mode maps after rotation while its counterpart map before rotation is given in Fig. 5(a). Again, rotational cross correlation is employed for each pair of the M-mode maps before and after specimen rotation, to measure the residual translational shift. Upon determination of the translational shift, all the targets shown in red circles in Fig. 5(a) are transformed on to the post-rotation map with their refined locations also represented by red circles (Fig. 5(b)). As an example, the light blue line drawn between a pair of circles in Figs. 5(a) and 5(b) illustrates the location of a target before and after rotation.

Fig. 5.

Rotational alignment of a pair of M-mode maps and relocation of target holes. (a) M-mode atlas map before specimen rotation. (b) M-mode atlas map after specimen rotation. (c) Target holes in a tile image before specimen rotation. (d) Target holes relocated after specimen rotation.

The final round of alignment is to refine where the specimen rotation relocates these target holes. This is performed by correlating each target tile with its counterpart after specimen rotation. Since the location of a target tile is represented by its center and can be relocated by specimen rotation to any arbitrary point that in general does not coincide with the center of a post-rotation tile image, a new image is taken at this location reached by driving the stage and then correlated against the pre-rotation target tile to refine the translational shift. Fig. 5(d) shows the newly acquired image corresponding to the target tile displayed in Fig. 5(c). While the target holes are manually picked by users in Fig. 5(c), the red circles in Fig. 5(d) are all computational results of the alignment. Upon successful alignment of the current target tile, each associated target image acquired at the intermediate magnification is also digitally rotated accordingly to generate a new target image with an updated stage coordinate. Therefore, there is no need to collect any new target images at the intermediate magnification. This procedure is automatically repeated until all target tiles and the associated target images have been processed.

The conclusion of the hierarchical alignment gives rise to a list of target images that are digitally rotated from those acquired before specimen rotation. The associated stage positions are mapped onto the post-rotation coordinate system. The sequential data collection can then be resumed and runs in the same fashion as the initial single axis data collection.

It should be noted that the setting up for sequential dual-axis tomographic data collection is quite straightforward and almost identical to that for nonsequential counterpart. Only one extra calibration is introduced that determines the image shift induced by switching from the lowest M-mode magnification to the intermediate magnification where the final targets are selected. It takes in general around 30 minutes to complete all necessary calibrations, most of which do not need to be recalibrated for each data collection.

5. Experimental Verification

In conjunction with our other ongoing projects, we chose to use 20S Proteasomes as our test specimen. Samples were vitrified in liquid ethane onto Cu 200 mesh Quantifoil 1/4 holey carbon films (Quantifoil, Jena, Germany) using FEI Mark I Vitrobot. The experiment was performed on our FEI Polara G2 TF30 electron microscope using GATAN “flip-flop” rotation stage at LN₂ temperature. The tomographic tilt data were collected at 86000x CCD magnification (60000x nominal reading). The energy filter slit was centered on the zero loss peak with 20eV slit width. Each data set was collected in the angular range of ±60° and at every 4°. It took about 17 minutes to take a data set that includes centering the target, running auto-eucentricity and auto-focus routines, and performing GIF zero loss alignment.

Since this experiment was intended to test the hierarchical alignment scheme, acquisition of a large number of data sets was not the goal. Only thirteen targets were selected allowing time to collect them all, rotate the specimen, and resume data collection for the second axis within the same day. It should be emphasized that there are no constraints on the number of targets that can be selected. Our sequential data collection scheme has been routinely used for overnight/multi-day data collections without any user intervention. Upon completion of acquiring the tomographic data on all thirteen targets, the specimen was rotated and the hierarchical alignment scheme was then invoked with all thirteen targets successfully found at the end. The sequential data collection for the second axis was thereafter invoked with twelve of thirteen data sets acquired without any problem. The only failed data set was not because of erroneous hierarchical alignment but a glitch in the zero loss alignment that failed to center the slit on the zero-loss peak. For the given tilting setup, each data acquisition took seventeen minutes including the overhead for automatic setting eucentricity, defocus, and zero-loss alignment. Fig. 6 presents one pair of dual-axis data sets where the top row displays three tilted images before the specimen rotation and the corresponding images after rotation are shown in the bottom row. The images acquired at α = −60°, 0°, and +60° before and after specimen rotation are displayed from left to right in Fig. 6. Given the small size of 20S Proteasomes (150 Å), the 300 keV acceleration voltage, and the low dose per image (2.44 e⁻/Ų) visualization in a single frame is difficult. As a result, we present this pair of dual-axis data because the presence of ice crystals shows how well the developed scheme relocates the original objects following specimen rotation. Clearly, the ice crystals are fully covered throughout the data collection performed before and after specimen rotation. The pre-rotation data set was collected at the stage xyz coordinate (−95.20, 152.96, 78.73) microns while the post-rotation data was at (−287.96, −82.90, 79.08). Therefore, the specimen rotation has horizontally relocated the target 304μm from its original location. Our scheme is still able to discover its location with sufficient precision to allow tomographic data collection at magnifications as high as 80000x.

Figure 6.

A pair of tomographic tilt data sets collected before and after specimen rotation. The top row displays three tilted images before specimen rotation and the bottom rows shows the counterparts at the same angles after specimen rotation. (a) α = –60°, (b) α = 0°, (c) α = +60°, (d) α = –60°, (e) α = 0°, (f) α = +60°

6. Dose Evaluation

Table 1 lists the auxiliary dose distributed at each step prior to sequential data collection for the setup at which the data displayed in Fig. 6 was taken. Column Dual-axis indicates whether or not the corresponding step is required after the specimen rotation. The amount of dose is unknown for zero loss alignment because it is internally performed by software DigitalMicrograph (GATAN). However, this amount of dose can be safely excluded for assessing the total auxiliary dose received by targets because zero loss alignment is conducted away from the targets. For single-axis EMT data collection the total auxiliary dose is calculated by adding up all the on-target doses distributed at each step. This gives rise to 0.404 e/Ų. For dual-axis EMT data collection the total auxiliary dose is equal to about double the single-axis auxiliary dose. It is unnecessary to collect reference images after rotation as they were generated by digital rotation of those acquired before rotation. Therefore, this amount of dose should be counted only once. As is shown in Table 1, this total auxiliary dose prior to EMT data collection along the second axis is 0.729 e/Ų.

Table 1.

Auxiliary dose distribution for the setup at which the data displayed in Fig. 6 was taken.

Step	Magnification and CCD Area	Dose (e/Å2)	On-target	Dual-axis
Build LM-mode Atlas Map	480× 89.1 × 89.1 μm2	5.95 × 10−5	Yes	Yes
Build M-mode Atlas Map	3000× 14.3 × 14.3 μm2	6.74 × 10−3	Yes	Yes
Acquire Reference Images	14000× 3.06 × 3.06 μm2	8.47 × 10−2	Yes	No
Auto-eucentricity & focus	14000× 3.06 × 3.06 μm2	0.312	No	Yes
Center Target	14000× 3.06 × 3.06 μm2	7.80 × 10−2	Yes	Yes
Auto-focus (Refinement)	14000× 3.06 × 3.06 μm2	0.234	Yes	Yes
Align Zero Loss	60000× 0.71 × 0.71 μm2	Unknown (off target)	No	Yes
Single-axis Total Auxiliary Dose (e/Å2)			0.404
Dual-axis Total Auxiliary Dose (e/Å2)			0.729

7. Summary

Although it is highly desirable to utilize dual-axis electron microscopic tomography for its capability to improve 3D resolution by integrating the two complementary data sets acquired before and after specimen rotation to reduce missing wedge, the lack of an efficient approach to precisely and automatically relocate the targets often limits its broad application. We have developed a montage based hierarchical alignment scheme that can pinpoint where targets are relocated with almost negligible extra dose and little user intervention. Once low resolution montage maps are created, dual-axis tomographic for an extensive list of user-specified targets can automatically be collected. Although the developed scheme was tested on a microscope equipped with a “flip-flop” 90° rotation cryo stage, our approach can work well with motorized room- or cryo-temperature side entry rotation stages allowing efficient collection of dual-axis tomography of embedded samples. Moreover the method is not premised on orthogonal rotations and therefore has the potential for locating targets being studied by correlative optical and electron microscopy. In such situations specimens are arbitrarily rotated and with significant magnification changes. To enhance versatility, we have integrated the hierarchical target selection and centering scheme with our predicative tomographic, random conical, and single particle data collection procedures within the frame of UCSF Tomography software system. Our streamlined EM data acquisition not only improves efficiency but should also result in enhanced resolution.