Quantification of Endothelial Cell-Targeted Anti Bcl-2 Therapy and its Suppression of Tumor Growth and Vascularization

Abstract

Pro- and anti- apoptotic proteins in the Bcl family are key regulators of programmed cell death. It is the interaction between these molecules that determine cellular response to apoptotic signals, making them attractive targets for therapeutic intervention. In recent experiments designed to study tumor angiogenesis, Bcl-2 up-regulation in endothelial cells was shown to be a critical mediator of vascular development. In this paper, we develop a mathematical model that explicitly incorporates the response of endothelial cells to variations in pro- and anti-apoptotic proteins in the Bcl family, as well as the administration of specific anti-angiogenic therapies targeted against Bcl-2. The model is validated by comparing its predictions to in vitro experimental data that reports microvessel density prior to, and following the administration of 0.05–5.0 µM BL193, a promising small molecule inhibitor of Bcl-2. Numerical simulations of in vivo treatment of tumors predict the existence of a threshold for the amount of therapy required for successful treatment and quantify how this threshold varies with the stage of tumor growth. Further, the model demonstrates how rapidly the least effective dosage of BL193 decreases if an even moderately better inhibitor of Bcl-2 is used and predicts that increasing cell wall permeability of endothelial cells to BL193 does not signicantly effect this threshold. A critical challenge of experimental therapeutics for cancer is to decide which drugs are the best candidates for clinical trials. These results underscore the potential of mathematical modeling to guide the development of novel anti-angiogenic therapies and to direct drug design.

Introduction

The Bcl family of proteins have been identified as crucial mediators of apoptosis, a form of cell death in which a programmed sequence of events leads to the disintegration of cells without releasing harmful substances into the surrounding tissue. There are anti-apoptotic Bcl proteins including Bcl-2 and Bcl-X_L, as well as their pro-apoptotic counterparts Bax, Bad, Bak, and Bid. These proteins are constitutively expressed within cells and it is the interaction between these molecules that determines cellular response to apoptotic signals such as intra-cellular damage and deprivation of or exposure to cytokines and growth factors [1, 2, 3]. Bcl proteins all differ slightly in size and intra-cellular location. Bcl-2 is a 26-kDa protein [4], while Bcl-X_L is reported to be slightly smaller [5]. They are located mainly in the nuclear envelope, parts of the endoplasmic reticulum, and outer mitochondrial membrane [4, 6]. Bax is a 21-kDa protein [7], and is localized to the outer mitochondrial membrane [6]. The 18.4-kDa protein Bad can be found on the mitochondrial outer membrane, as well as the cytoplasm¹, while the 23.4-kDa protein Bak is a single-pass membrane protein¹. Bid is a 22-kDa protein and resides in the cytoplasm¹.

The core component of cellular apoptotic machinery is a family of proteases called caspases [1]. Caspase activation can be initiated either extracellularly (extrinsic) or intracellularly (intrinsic). The extrinsic pathway triggers apoptosis in response to ligation of cell death receptors, which include Tumor Necrosis Factor Receptor 1 (TNFR1), Fas (CD95/Apo1), DR4, and DR5. Upon activation by their respective ligands, including TNF alpha, Fas-ligand (FasL), TRAIL/Apo2L, the intracellular domains of the death receptors, also known as death domains, bind to the adaptor protein Fas-associated death domain (FADD). This results in the recruitment and activation of caspase 8 and/or caspase 10 leading to the assembly of the death-inducing signaling complex (DISC), ultimately inducing cellular apoptosis [8, 9].

The intrinsic pathway triggers apoptosis in response to DNA damage, defective cell cycle, hypoxia, cellular damage induced by most chemotherapy agents or irradiation and other types of severe cell stress [8]. Cell death occurs due to the presence of cytochrome c in the cell cytoplasm, which together with Apaf1 activates caspase 9. This in turn activates downstream effector caspases like caspase 3, which induce apoptosis [10]. The Bcl family of proteins helps regulate this process by controlling the release of cytochrome c, typically from the mitochondrial outer membrane. Broadly speaking, the pro-apoptotic members of the Bcl family may be divided into two sub-families. Members of the Bax-like sub-family include Bax and Bak, and are very similar to Bcl-2 in sequence, while the BH3-only proteins including Bad and Bid bear no sequence similarity to the members of the Bcl family apart from containing a BH3 binding domain [10]. Members of the BH3-only sub-family bind to BH3 binding pockets that form on the anti-apoptotic proteins like Bcl-2 and Bcl-X_L, preventing them from inhibiting activation of members of the Bax-like sub-family. It is believed that this results in the release of cytochrome c into the cell cytoplasm [3, 10]. Thus, the anti-apoptotic function of Bcl-2 and Bcl-X_L is at least partly due to their ability to heterodimerize with Bax, Bad, Bak and Bid, inhibiting their pro-apoptotic function [3]. The various pathways that Bcl-2 and its family are involved in, are shown in Figure 1A.

Figure 1.

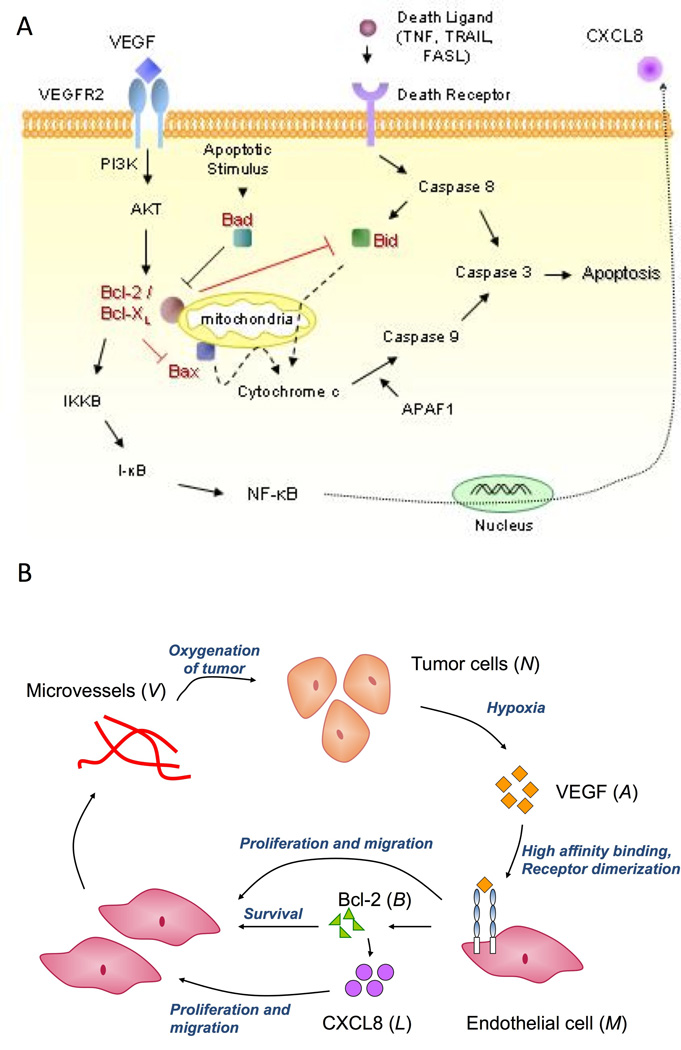
A, Schematic diagram showing intra-cellular functions of the Bcl family of proteins. VEGF induces Bcl-2 expression via the VEGFR-2, PI3K/Akt signalling pathway. Pro-apoptotic proteins such as Bad and Bid heterodimerize with Bcl-2/Bcl-X_L thus regulating their ability to inhibit activation of other pro-apoptotic proteins like Bax. Activation of Bax results in the release of cytochrome c from the mitochondrial outer membrane, which together with Apaf1, causes caspase activation. This induces cell apoptosis. Bcl-2 also acts as a pro-angiogenic signalling molecule, by activating the NF-κB signaling pathway, inducing expression of the pro-angiogenic chemokine, CXCL8. B, A partial model schematic diagram. Tumor cells produce VEGF under conditions of hypoxia, which binds to endothelial cells via cell surface receptors resulting in receptor dimerization and activation. This elicits a proliferative and chemotactic response from the endothelial cells. Further, this causes over-expression of the pro-survival protein Bcl-2, which in turn results in up-regulation of CXCL8 production by them. CXCL8 in turn induces cell proliferation and chemotaxis. The endothelial cells begin to aggregate and differentiate into microvessels, that eventually fuse with mouse vessels and become blood borne, resulting in oxygenation of the tumor.

The Bcl family proteins have been shown to play a key role in tumor development and progression. Tumor cells in several types of cancers such as prostrate, breast, colorectal, head and neck cancers, lymphomas, and melanoma are known to over-express either Bcl-2, or Bcl-X_L, or both [3]. In addition to promoting cell survival, this could provide cancer cells with some measure of protection from chemo-and radiotherapy, especially if these therapies directly or indirectly induce apoptosis [3]. Further, Nör et al have demonstrated that in the case of some head and neck cancers, cancer cells are able to extend this protective effect to the endothelial cells lining the blood vessels in the vicinity of the tumor by up-regulating levels of Bcl-2 within these cells, thus enhancing intra-tumoral angiogenesis [11, 12, 13]. This makes Bcl-2 and Bcl-X_L attractive targets for the development of anti-cancer drugs. In fact, several forms of therapy targeting Bcl-2/Bcl-X_L are under development. These include antisense bcl-2 and bcl-X_L oligonucleotides that work by inhibiting Bcl-2/Bcl-X_L expression levels, single chain antibodies and peptides that bind to the Bcl-2 molecule inhibiting it's functions, and an anti-bcl-2 ribozyme, that works by degrading bcl-2 mRNA [3]. However, Wang et al [3] propose that nonpeptidic, cell-permeable small molecule inhibitors of Bcl-2 and Bcl-X_L may have greater potential as anti-cancer drugs than the therapies mentioned above for a variety of reasons including better bio-availability, stability, low cost and the ability to penetrate the blood-brain barrier of the central nervous system. These inhibitor molecules act as antagonists of Bcl-2/Bcl-X_L by binding to their BH3 binding pocket, thus preventing pro-apoptotic members such as Bax, Bad, Bak from binding to Bcl-2/Bcl-X_L.

With all of these new possibilities, a critical challenge in experimental therapeutics for cancer is to decide which drugs are the best candidates for clinical trials. Mathematical modeling, such as that developed here can help to determine which anti-cancer drugs have the most potential for therapeutic benefit. In particular, we concentrate on the anti-angiogenic potential of therapies targeted at Bcl-2, in the form of small molecule inhibitors such as BL193 [14, 15] and TW37 [15]; both of which have been shown to cause a marked decrease in angiogenic potential of endothelial cells in vitro. Since BL193 has similar inhibition constants for both Bcl-2 and Bcl-X_L, we focus on this as our drug of choice. Our model is based on the experiments of Nör et al [11, 12, 13], wherein Human Dermal Microvascular Endothelial Cells (HDMECs) along with oral squamous carcinoma cells are transplanted into severe combined immuno-deficient (SCID) mice on biodegradable polymer scaffolds. These endothelial cells differentiate into functional human microvessels that anastomose with neighboring mouse vessels thus generating human tumors vascularized with human microvessels [13]. It is observed that the pro-angiogenic chemokine Vascular Endothelial Growth Factor (VEGF) is the main tumor secreted growth factor in these experimental systems. VEGF mediates a proliferative and migratory response from the HDMECs, and exerts a pro-survival inuence by up-regulating intra-cellular Bcl-2 levels [11, 12]. Bcl-2 in turn causes the endothelial cells to increase production of Interleukin-8 (CXCL8), which is a strong chemotactic agent and a potent inducer of endothelial cell mitosis [11]. We have already developed and presented a mathematical model describing these experiments [16], and it is our goal to extend this model to explicitly incorporate the pro-apoptotic as well as anti-apoptotic members of the Bcl family, so that we can better understand the implications and effects of therapy targeted against these proteins.

Our preliminary mathematical model [16] was the first to connect the molecular events associated with VEGFR2 dimerization and intra-cellular signaling with the temporal changes in endothelial cell proliferation, migration and survival. We were able to use this model to predict the effect of decreasing the bio-availability of VEGF, CXCL8 and Bcl-2 on tumor growth and vascular structure. Our preliminary results suggest that Bcl-2 is the most promising target for anti-angiogenic therapies along the VEGF pathway of interest. These results also led to the hypotheses that anti-Bcl-2 therapies applied at early and late stages of tumor growth will significantly affect, with a dose-dependent threshold, both the time course of tumor development as well as the maximum tumor cell and blood vessel densities. In this paper we will test this hypothesis by explicitly modeling the cellular response to variations in pro-and anti-apoptotic proteins in the Bcl family, as well as the administration of specific anti-angiogenic therapies targeted against the VEGF-Bcl-2-CXCL8 pathway at different stages of tumor development. A partial model schematic is shown in Figure 1B.

Due to the abundance of experimental data describing the interaction of Bcl-2 with its pro-apoptotic family members [1, 2, 4, 10, 17] and the increasing interest in the mechanism of action and therapeutic potential of the small molecule inhibitor BL193 [3, 14], it is important to develop a mathematical approach that includes the current understanding of the intra-cellular apoptotic signaling that is mediated by the Bcl family of proteins. While our preliminary model could not address the mechanism of action of BL193 and could not relate its binding efficiency to its therapeutic efficacy, the model presented here will be able to study both of these important issues as well as predict tumor response with increased accuracy.

Materials and Methods

Model Foundation

A biochemically motivated, ordinary differential equation model is developed to capture the essential intra-cellular dynamics of the Bcl family of proteins governing programmed cell death. The mathematical model has as its foundation specific biological assumptions that are based on the accepted knowledge of the function of and cellular response to various pro and anti-apoptotic proteins. Specifically, the intra-cellular concentration, in femtograms per cell, of a single anti-apoptotic protein Bcl-2, and a single pro-apoptotic representative of the Bcl family, Bad, will be tracked in time. Using one representative of the pro and anti apoptotic family members allows us to avoid involving a number of intra-cellular binding parameters for which there is no experimental data. The particular choice of the representative proteins was made for the following reasons: (1) BL193 has similar binding affinities to both of the anti-apoptotic proteins, Bcl-2 and Bcl-X_L, on which it has been shown to act [15], (2) it is intra-cellular levels of Bcl-2 that are up-regulated in response to a VEGF stimulus [12] and (3) Bad binds to Bcl-2 with a higher affinity than the other Bcl proteins [3]. It also acts upstream of the Bax-like members of the Bcl family, making it the protein of choice to represent the pro-apoptotic members of the Bcl family. The intra-cellular concentration of Bcl-2 will be represented by the letter B, while that of Bad will be represented by the letter X.

It is known that Bcl-2 and Bad interact with each other within the endothelial cell to form heterodimers. This balance between pro- and anti-apoptotic proteins regulates cell death rate. In an endothelial cell, unbound Bcl-2, unbound Bad and Bcl-2-Bad dimers will be present at their respective constitutive levels. We assume that the amount of unbound protein Bad determines the cell death rate, since it is the pro-apoptotic members of the Bcl family that are directly responsible for regulating caspase activation within the cells [10]. It has experimentally been shown that Bcl-2 induces the expression of CXCL8 in endothelial cells through its ability to activate the NF-κB signaling pathway [14]. Therefore, we assume that the amount of unbound Bcl-2 is responsible for CXCL8 production by the endothelial cells. The VEGF-Bcl-2-CXCL8 pathway discovered in the experiments of Nör et al [11, 12] is explicitly included in this model by allowing for the up-regulation of Bcl-2 in the presence of VEGF. In turn, this up-regulates production of CXCL8 by the endothelial cell, due to increase in free Bcl-2 levels within the cell. High levels of Bcl-2 would mean low levels of Bad in its unbound state since it would be taken up as Bcl-2-Bad dimers. This would result in a decrease in cell death rate. Thus, we are able to capture the essential principles of cell death regulation by the Bcl family proteins, as well as account for the pro-survival, and pro-angiogenic effect of Bcl-2 in particular. The complete derivation of equations is discussed in the sections that follow.

Bcl protein interactions within a single cell

We begin our model development at the single cell level, so that we may include the role of the Bcl family proteins in cell apoptosis explicitly. Once we are able to describe the relevant apoptotic pathways within a single cell, we can scale the model up to the population level, and thus obtain a better quantitative understanding of the role of these intra-cellular molecular pathways in determining vascular development in tumors.

Bcl-2 - Bad and Bcl-2- BL193

The law of mass action is used to translate the reaction diagram in Figure 2, which describes the hetero-dimerization of Bcl-2 and Bad as well as the inhibition of Bcl-2 by BL193, into a system of differential equation (1) – equation (5) that govern the temporal changes in the intra-cellular concentrations of these proteins [18]. Specifically, the upper case letters in equation (1) – equation (5) represent chemical concentrations, measured in femtograms per cell. Then, B is unbound Bcl-2 protein per cell, X is unbound Bad protein per cell, C_bx is the quantity per cell of the heterodimer formed when one molecule of Bcl-2 binds to one molecule of Bad, I is the amount of small molecule inhibitor or BL193 per cell, and C_bi is quantity per cell of the complex formed when one molecule of Bcl-2 binds to one molecule of BL193. Note that, while we could find no experimental data on constitutive intracellular levels of Bcl-2 and Bad in HDMECs, there is evidence that Bcl-2, Bcl-X−L, and Bax are expressed in femtogram levels in other cell types [19],[20]². To lend our model greater clinical applicability, the exact levels of intracellular Bcl-2 and Bad would need to be estimated experimentally. However, these numbers do not effect the qualitative predictions of our model.

Figure 2.

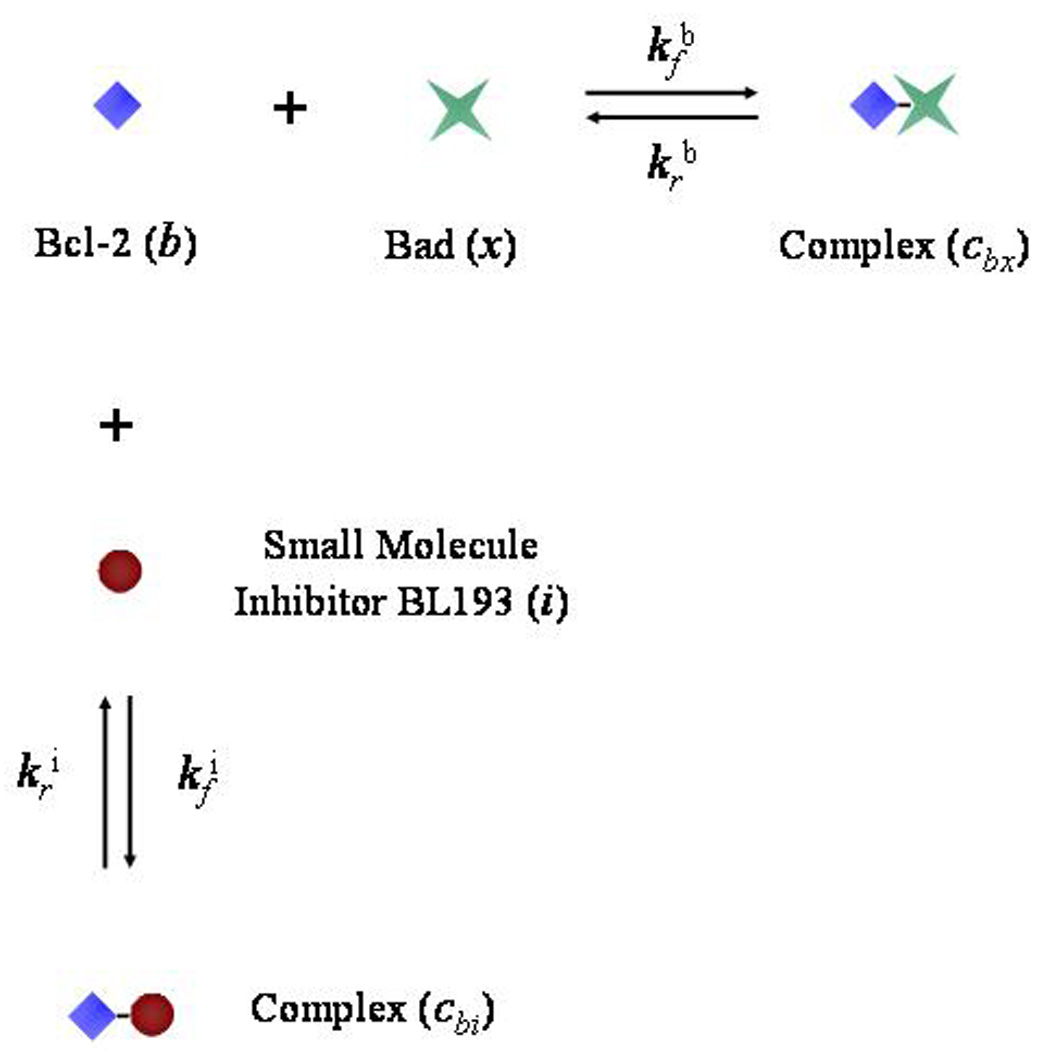
Reaction diagram showing the heterodimerization reaction between the Bcl-2 (b) and Bad (x) molecules, and the inhibition of Bcl-2 by a small molecule inhibitor, BL193 (i).

It is assumed that upon application of therapy, the inhibitor molecules diffuse into the endothelial cell across the cell membrane. This is consistent with the design strategy behind these small molecule inhibitors (BL193 has a molecular weight of only 0.5 kDa [15]). Thus, there is a source term in equation (4), where the rate of entry of the inhibitor molecules into an endothelial cell is proportional to the difference of extracellular and intra-cellular BL193 concentrations. The extracellular concentration, I₀, of BL193 in the local environment of a cell is a parameter that varies as the dosage level of therapy changes, and is fit to match such experiments. The constant D_i is a measure of cell wall permeability to BL193, and has units of 1/day. We can write the rate D_i as −(ln 1/2)/t_1/2, where t_1/2 is the amount of time it takes half the drug, external to a cell, to be internalized. The inhibition constant K_i of BL193, which is given by the ratio of $k_r^i$ to $k_f^i$, is 320 nM [15]. The effect on intra-cellular Bcl-2 and Bad concentrations of the addition of varying amounts of BL193 can be seen from Figure 3A. As BL193 level within a cell increases from 0 to 0.9 femtograms, free Bcl-2 concentration is seen to decrease by 79%, causing free Bad concentration to increase by 13%, over their respective constitutive levels.

$$\frac{\mathit{\text{dB}}}{\mathit{\text{dt}}}=-k_f^{b}BX+k_r^b{C}_{\mathit{\text{bx}}}-k_f^{i}BI+k_r^i{C}_{\mathit{\text{bi}}}$$ (1)

$$\frac{\mathit{\text{dX}}}{\mathit{\text{dt}}}=-k_f^{b}BX+k_r^b{C}_{\mathit{\text{bx}}}$$ (2)

$$\frac{{\mathit{\text{dC}}}_{\mathit{\text{bx}}}}{\mathit{\text{dt}}}=k_f^{b}BX-k_r^b{C}_{\mathit{\text{bx}}}$$ (3)

$$\frac{\mathit{\text{dI}}}{\mathit{\text{dt}}}=-k_f^{i}BI+k_r^i{C}_{\mathit{\text{bi}}}+D_i (I_0-I)$$ (4)

$$\frac{{\mathit{\text{dC}}}_{\mathit{\text{bi}}}}{\mathit{\text{dt}}}=k_f^{i}BI-k_r^i{C}_{\mathit{\text{bi}}}$$ (5)

Figure 3.

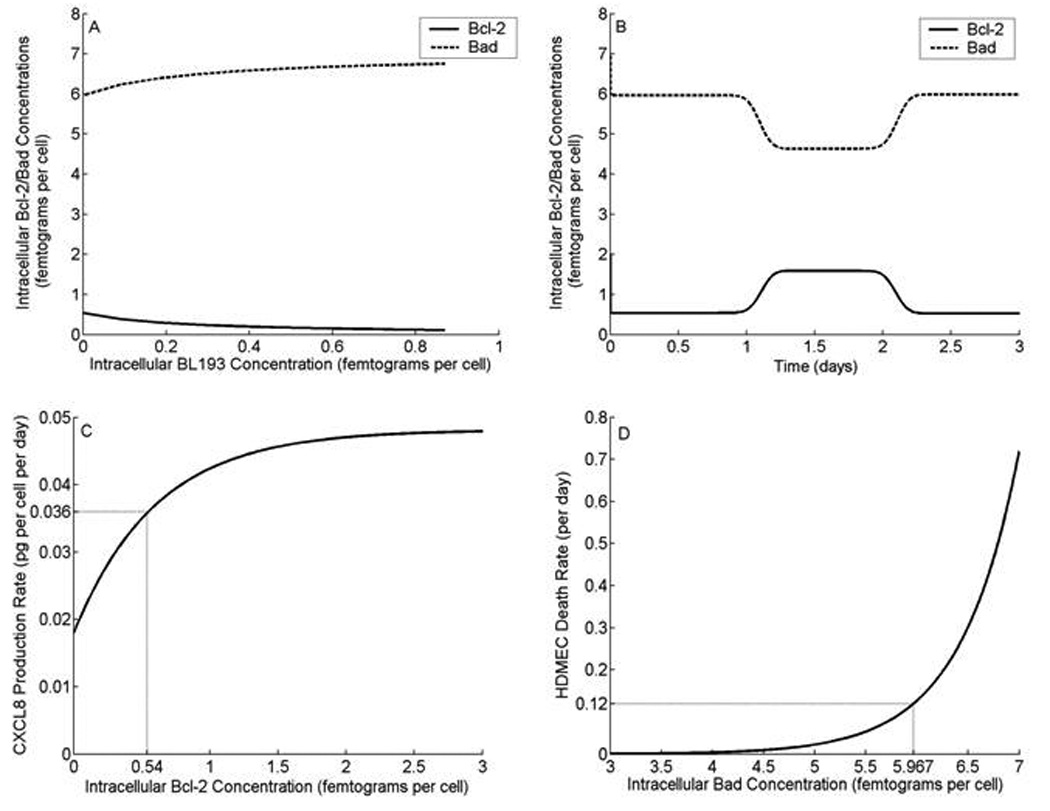
Intra-cellular Bcl-2 and Bad concentrations, and their effect on cell death rate and CXCL8 production rate. A, Bcl-2 levels within a single cell are seen to decline, as increasing amounts of BL193 therapy are administered, causing a corresponding increase in Bad levels. B, Upon application of 50 ng/ml VEGF, Bcl-2 level within a cell is seen to increase 3.1 fold, causing a 22% decrease in the level of Bad. As VEGF is consumed, Bcl-2 and Bad protein levels return to their constitutive state. C, CXCL8 production rate by HDMECs increases to a maximum, as intra-cellular Bcl-2 levels increase. At the constitutive level of Bcl-2, CXCL8 production rate is fixed at 0.0358 pg of CXCL8 per HDMEC per day [16]. The model allows for CXCL8 production independent of Bcl-2 up-regulation as well. D, HDMEC death rate is taken to increase exponentially with the amount of intra-cellular Bad protein. At the constitutive level of Bad, cell death rate is taken to be 0.12 per day [21].

The effect of VEGF on Bcl-2 Levels

Extracellular concentrations of cytokines and growth factors inuence intracellular concentrations of the Bcl family proteins. In order to capture the effect of VEGF on Bcl-2 and Bad levels within each cell, we postulate that the amount of Bcl-2 produced is directly proportional to the number of active VEGF-receptor dimer complexes per cell. A corresponding source term for Bcl-2 may be included in Equation (1), which changes to equation (6) given below.

$$\frac{\mathit{\text{dB}}}{\mathit{\text{dt}}}=-k_f^{b}BX+k_r^b{C}_{\mathit{\text{bx}}}-k_f^{i}BI+k_r^i{C}_{\mathit{\text{bi}}}+{\beta }_a\frac{d}{\mathit{\text{dt}}}({\varphi }_a)$$ (6)

Here, ϕ_a is the density of active VEGF-receptor dimer complexes in pg per cell. In the presence of 50 ng per ml VEGF, it is observed that Bcl-2 is up-regulated 3.1 fold [12]. This is used to fix the constant β_a, which determines the level of up-regulation of Bcl-2 by VEGF. In Figure 3B, levels of Bcl-2 and Bad within a single cell are plotted versus time. An external dose of 50 ng/ml VEGF is given after 1 day, and lasts for 1 day. It can be observed that unbound Bcl-2 concentration increases by 3.1-fold as VEGF is taken up by the cell. Corresponding to this, unbound Bad concentration decreases. As the VEGF is consumed, the amounts of Bcl-2 and Bad proteins eventually fall back to constitutive levels.

The CXCL8 production rate of HDMECs (see equation (14)), denoted by β_l, is taken to be dependent on intracellular Bcl-2 concentration, B. The functional form of β_l(B) is taken as follows:

$${\beta }_l(B)={\beta }_m+a_p(1-e^{-b_{p}B})$$ (7)

The CXCL8 production rate by HDMECs is assumed to increase to a maximum level, as intracellular Bcl-2 concentration increases, under the effect of VEGF. We also allow for the possibility that CXCL8 could be produced by endothelial cells independent of Bcl-2. Thus, if intra-cellular Bcl-2 level falls to zero, there is still a constant background rate of CXCL8 production, namely β_m. The remaining parameters are determined by fits in the least squares sense to experimental data presented in [11]. Figure 3C shows a graph of the CXCL8 production rate. We can see that as intra-cellular Bcl-2 levels increase, which may be in response to the presence of VEGF, the production rate of CXCL8 also increases.

Apoptotic regulation at the population level

Temporal changes in Bcl-2 concentration, within a single cell, will now be explicitly incorporated into the population level model of tumor growth and sustained angiogenesis described in [16]. To accomplish this, the death rate of HDMECs, denoted by λ_m, is taken to be dependent on intracellular Bad concentration, X (see equation (9)). In this way, the behavior predicted by the single cell model described in the previous section is used to determine the response of a population of cells to their microenviroment. The functional form of λ_m is taken as follows:

$${\mathrm{\lambda }}_m(X)=a_d{e}^{b_{d}X}$$ (8)

In the absence of experiments designed to determine the precise functional dependence of cell death on pro-apoptotic members of the Bcl family, we choose an exponential form of the death rate. This reflects the fact that cells are highly sensitive to pro-apoptotic signals such as intra-cellular Bad levels, which are normally tightly controlled and balanced by anti-apoptotic proteins like Bcl-2. There is some indirect experimental justification for this, which can be seen from a comparison of the model predictions to in vitro therapy results, presented in the next section. Figure 3D shows a graph of HDMEC death rate as a function of its intra-cellular environment. The graph also gives insight into the effect of extracellular events on the fate of the cell. For instance, if as a result of anti Bcl-2 therapy, 0.5 femtograms of BL193 are incorporated by an endothelial cell, then free Bcl-2 level within the cell falls by 66%, and free Bad level increases by 11 %, over their respective constitutive values (Figure 3A). This causes an increase of 208% in cell death rate.

The model described above cuts across multiple levels of biological organization, from intracellular signaling to tissue level tumor growth dynamics, providing greater insight into intra-tumoral vascular development. Specifically, in order to access the role of Bcl proteins on vascular tumor growth and treatment, the model described above (equation 1–equation 8) is combined with a set of delay differential equations (see Appendix A) that keep track of temporal changes in tumor and endothelial cell densities, VEGF and CXCL8 concentrations and microvessel density. Additionally, intracellular concentrations of Bcl-2, Bad and BL193 are also measured over time. These equations represent a mathematical translation of the model schematic presented in Figure 1B, and the Bcl-2-Bad-BL193 interactions and their effect on cellular apoptosis as described in the preceding sections. The parameters values used in our model, along with a brief note on their estimation are listed in Appendix C.

Results

A series of numerical experiments using the model described in the previous sections are carried out to simulate both, microvessel formation in vitro, as well as tumor induced angiogenesis in vivo. To date, the effect of the small molecule inhibitor BL193 of Bcl-2, on sprout formation, has only been tested experimentally in vitro [14, 15]. Therefore, we first validate our model by presenting a comparison of model simulations to these in vitro experiments. This is followed by in vivo simulations designed to predict the effects of the administration of BL193 on intra-tumoral angiogenesis. The dependence of drug efficacy on its 50% inhibition constant of Bcl-2, and on the permeability of the endothelial cell wall to the drug are studied in particular. These are both key factors in drug design strategy. Therefore the results of our simulations may be used to guide in vivo experimentation.

In vitro therapy

In a series of in vitro experiments described in [14], capillary sprouting assays were carried out on HDMECs. The endothelial cells were exposed to 50 ng per mL VEGF for 5 days and then to 50 ng/mL VEGF in the presence of 0 to 5 µmol per L BL193 thereafter, and the number of sprouts counted at daily intervals. To represent this experimental system, our model of intra-tumoral angiogenesis needs to be modified slightly by removing the tumor cell equation, and keeping free VEGF concentrations fixed at 50 ng/ml. The resulting system of equations is listed in Appendix B. The values of all parameters barring the amount of drug administered I₀, were estimated prior to simulation of treatment strategies, and these values were kept constant thereafter. This allows us to validate our model by direct comparison of model predictions of treatment by BL193, with experimental observations.

Numerical and experimental observations are compared in Figures 4A, B and C, where the dosage of BL193 administered starting from day 5 increases from 0.05 µM, to 0.5 µM, and finally to 5 µM. The model predictions of microvessel densities are seen to match the experimental observations well, thus validating our model. It should be noted that at this final concentration of BL193, the cells simply die from too much chemical within them, rather than from a disruption in the Bcl-2 regulated anti-apoptotic pathway. The model does not account for such a possibility, and the last data point in Figure 4C therefore does not match in vitro observations. The effect of therapy on intracellular protein levels can be seen in Figure 4D, which plots the amounts of anti-apoptotic protein B, pro-apoptotic protein X and BL193 per cell, corresponding to a therapy level of 0.05 µM of BL193.

Figure 4.

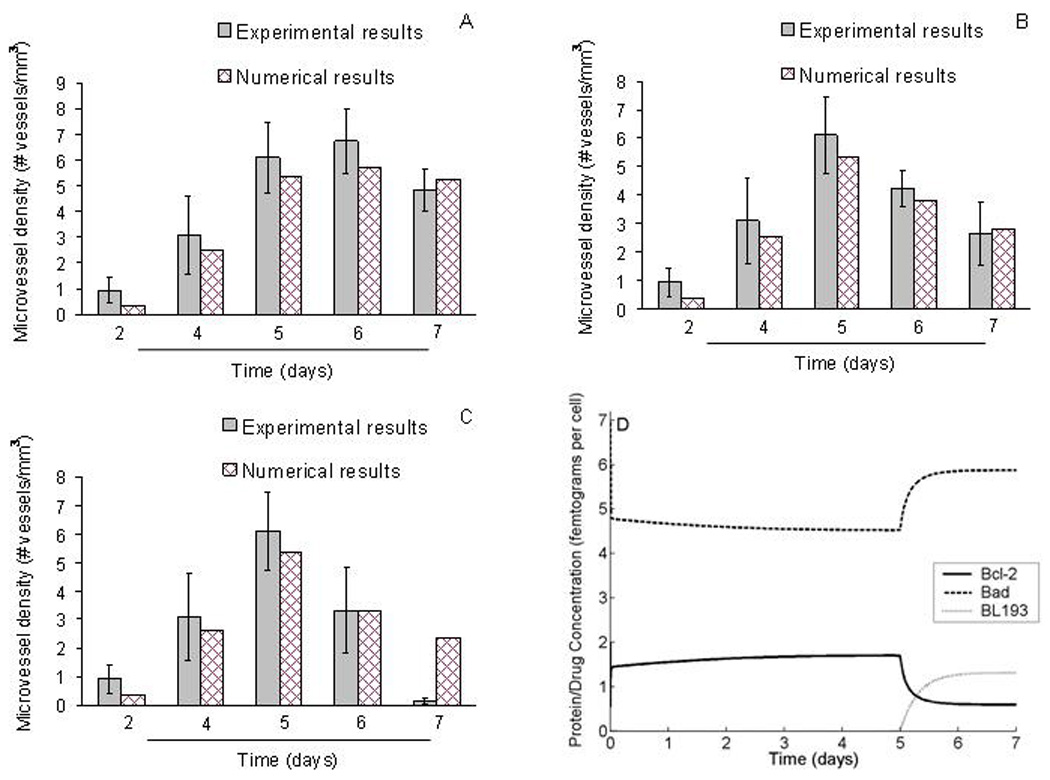
Comparison of model simulations to in vitrosimulations designed to study the effect of BL193 on capillary formation. A, B, C, In capillary sprouting assays described in [14], HDMECs were cultured on type I collagen in the presence of 50 ng per ml VEGF. Starting on day 5, BL193 was administered in increasing doses from 0.05 µM (A), 0.5 µM (B), and 5 µM (C), and the number of sprouts counted. Numerical simulations of our model are seen to be in good agreement with experimental data, thus providing a validation for it. D Intra-cellular Bcl-2, Bad and BL193 levels are tracked with time, as 0.05 µM BL193 therapy is administered. Starting on day 5, BL193 levels within a cell begin to increase, causing a decrease in amounts of unbound Bcl-2 protein, and a corresponding increase in unbound Bad protein.

In vivo therapy

Having validated our model by comparison to in vitro experimental results, we can now perform a series of numerical simulations to investigate the effect of BL193 therapy on in vivo tumor growth dynamics when applied at an early stage of tumor development.

First, a series of numerical simulations are performed to investigate the effect of therapy on tumor growth dynamics when applied at an early stage of tumor development. Prior to treatment, with parameters at their baseline values, the tumor cell density reaches it's maximum level (8:669 × 10³ cells per mm³) about 28 days after implantation (Figure 5A). The first blood-bearing vessels are seen 5 days after implantation, reaching their steady state of about 53 vessels per mm³, 19 days later (Figure 5B). When a dose of 0.05 µM of BL193 is administered, it takes about a week longer for the vasculature to fully develop, and the tumor cell density to reach its maximal value, when compared to the no therapy case. If the dosage is increased to 0.5 µM, the delay in vascular development increases by 16 days, while the tumor cells take 18 days longer to reach their steady state. A dosage level of 5 µM BL193 appears to be enough to cause the tumor to regress (Figure 5A,B). Thus, based on these numerical predictions, anti-angiogenic therapies directed at Bcl-2, such as the use of small molecule inhibitors of Bcl-2, appear to be highly efficacious, especially when administered to an early stage tumor.

Figure 5.

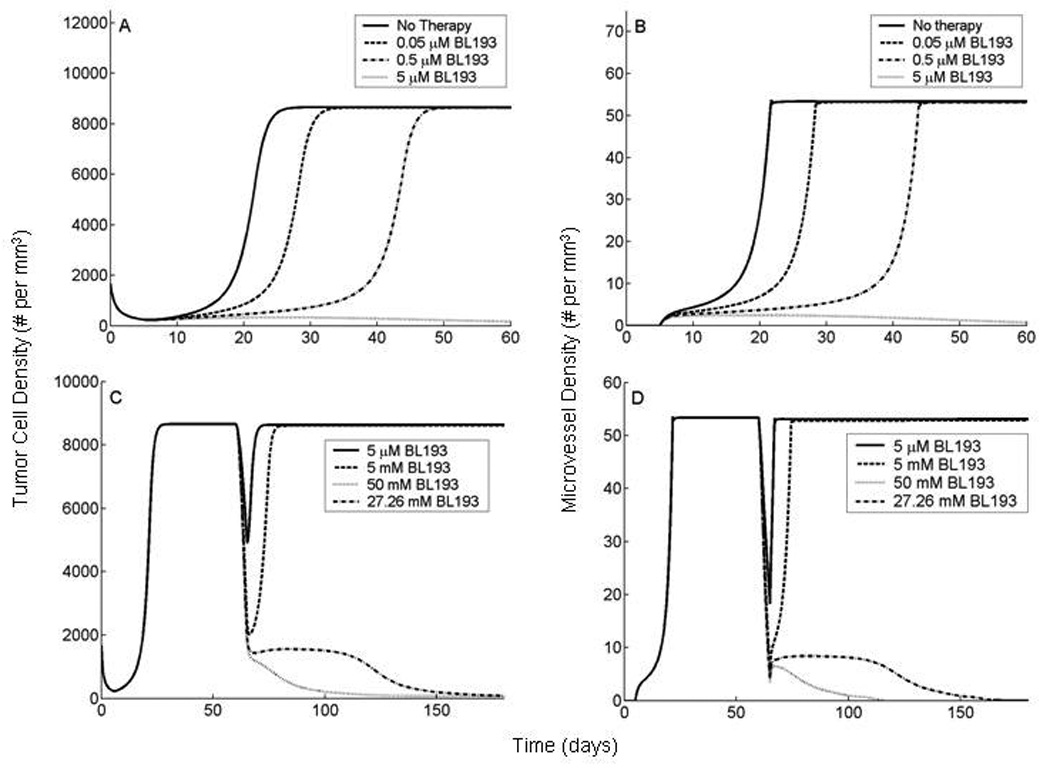
In vivo simulations of anti-Bcl-2 therapy applied to a tumor at early and late stages of development. Our model is based on experiments described in [11, 12, 13], wherein HDMECs along with oral squamous carcinoma cells are transplanted into SCID mice, on ploy-L lactic acid matrices. The HDMECs are observed to differentiate into functional microvessels, giving rise to a vascularized tumor. A,B, BL193 is administered in starting from the day of implantation and continuing thereafter. As therapy levels increase from 0 to 0.05 µM, and to 0.5 µM, time taken to reach maximal tumor cell density increases by 25% and 89% respectively (A). The corresponding increase in time taken to reach maximal vessel density is 37% and 121% respectively (B). 5 µM of BL193 appears to be enough to effect a cure. C,D, BL193 is administered to a fully developed tumor, starting from day 60 of implantation and continuing thereafter. 5 µM of BL193 is insufficient to effect a cure, and only a temporary reduction in tumor cell (C), and vessel densities (D) is observed. The minimum amount of therapy required in order to cause tumor regression is predicted to be 27.26 mM.

Next, we investigate the effect of application of BL193 to a tumor that has been allowed to reach maximal tumor cell and microvessel densities (Figure 5C,D). Therapy is applied continuously from day 60 of implantation. The model predicts that at a dosage level of 5 µM BL193, the vessel density is seen to decrease (Figure 5D), leading to a corresponding decrease in tumor cell density (Figure 5C). However, the tumor cells appear to compensate for this loss of blood supply by increasing VEGF production. The vessel density soon returns to its pre-treatment level, and the tumor recovers rapidly. In fact, we need to increase the dosage of BL193 to approximately 24.5 mM to induce tumor regression. In this case, the microvessel density is observed to fall to a level that is too low for the tumor to recover from as a result of anti-Bcl-2 therapy (Figure 5D).

Sensitivity to drug design parameters

There are two important considerations behind the design strategy of small molecule inhibitors of Bcl-2 such as BL193. Firstly, to maximize the inhibition of Bcl-2 by the molecule. Secondly, to maximize the cell-permeability of the molecule. We therefore carry out a sensitivity analysis on the inhibition constant K_Di of BL193, and the rate of diffusion D_i of BL193 across the cell wall. In all the simulations carried out here, the drug is administered to a late stage tumor, and the least amount of drug required to induce tumor regression is observed. Numerical simulations predict that decreasing K_Di, decreases exponentially the amount of drug required to effect a cure (Figure 6A). For instance, the required dosage of an inhibitor with a K_Di 25% lower than that of BL193 is 0.52 mM, while that of an inhibitor with a K_Di 50% lower than that of BL193 is 11.04 µM. The required dosage for BL193 is 27.26 mM. Likewise, increasing cell-permeability of BL193, i.e. increasing the rate of diffusion of BL193 across the cell wall reduces the level of therapy required (Figure 6B). A 10-fold increase in D_i reduces the minimum drug dosage needed for a cure by a factor of 53%, but any increase in D_i beyond this does not significantly affect this dosage further.

Figure 6.

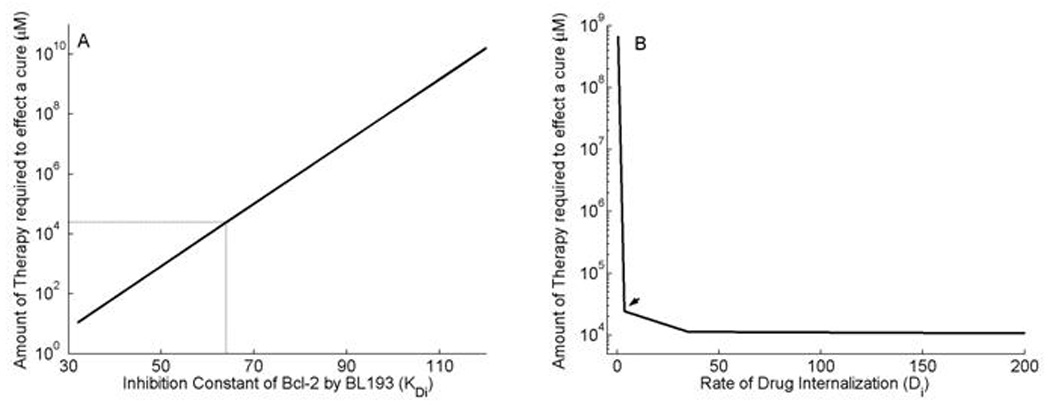
Simulations to guide drug design strategies for anti Bcl-2 therapy. A, Minimum amount of therapy required to induce tumor regression is observed to vary exponentially with the inhibition constant K_Di of BL193 for Bcl-2. Reducing K_Di from its baseline value by 25% decreases the least amount of therapy required from 27.26 mM to 0.52 mM. B, As the rate of diffusion D_i of BL193 into the cell is increased, the least amount of efficacious therapy reduces by a maximum amount of 56%, after which no significant change is observed, when compared to baseline values for D_i.

Discussion

A deeper understanding of the cellular and molecular events that govern tumor-induced blood vessel growth is crucial to the development of anti-cancer therapies targeted at angiogenesis. Therefore, it has been the focus of intensive research. Several experimental models have been developed to study it. One such experimental model investigated the importance of the up-regulation of Bcl-2 by VEGF in sustained intra-tumoral angiogenesis [11, 12], and the effect of blocking this by means of a small molecule inhibitor BL193 of Bcl-2 [14]. We previously published a mathematical model describing this experimental setup, at an extracellular and tissue level [16]. The main goal of this research was to incorporate the intra-cellular dynamics of the Bcl family of proteins in our existing model. This enabled us to quantify in a more definitive way, the role Bcl-2 plays in intra-tumoral angiogenesis, and to assess its potential as a target for anti-angiogenic therapy. By building a model specific to this experimental system, we were able to validate it by direct comparison with experimental results. The model was then used to simulate the application of therapy in vivo, thereby highlighting its usefulness as a guiding tool in the development of anti-angiogenic drugs designed to inhibit the function of Bcl-2.

Numerical simulations of the full model provide valuable insight into the growth dynamics of tumors and their response to the application of BL193 therapy. The model was first calibrated versus control in vitro capillary sprouting assays. It was found to be in good agreement with experimental observations taken after the application of BL193. The model was then used to predict the effect of therapy applied at various stages of tumor growth in vivo. Numerical results indicated that even low levels of BL193 administered to an early stage tumor, induced significant delays in tumor and vascular development. In fact, 5µM Bl193 was sufficient to cause the tumor to regress. This could be due to the fact that if the vasculature has not had a chance to develop in a tumor, then administering anti Bcl-2 therapy has the effect of preventing further vascular development, by inducing cell death. However, in a simulation carried out to test this drug on a fully developed tumor, we found that the amount of therapy required to effect a cure increased by 3–4 orders of magnitude. It was observed that below a certain threshold, anti Bcl-2 therapy elicited little response from the tumor, but as therapy was increased beyond this threshold, the tumor and vascular development were arrested at much lower levels. However, it is possible that this threshold corresponds to an amount of therapy that is toxic for the host, and thus not administrable in practice. These results accentuated the importance of timely detection and treatment of tumors, and indicated that a single point of attack at a fully developed tumor may be insufficient in order to effect a cure. Finally, numerical experiments were run to provide an insight into drug design strategies aimed at improving the effectiveness of the small molecule inhibitor therapy, especially in late stage tumors. A small molecule that was only 25% more efficient than BL193 in inhibiting Bcl-2, reduced the required therapy level by as much as 97%. Therefore, even a moderately better inhibitor of Bcl-2 may prove to be a much better target for the development of anti-angiogenic therapy. However, increasing the cell-wall permeability of the drug molecules could reduce the minimum effective therapy level by at most 56%. These numerical simulations suggest that improving drug design in terms of permeability across cell walls has limited potential as far as minimizing drug efficacy level is concerned. Continued quantitative modelling in this direction could have a profound impact on the development of anti-angiogenic drugs aimed at the intra-cellular regulators of cell death.

The research carried out in this paper transcends the boundaries between biomedicine and mathematics, and has the potential to aid efficient drug design and to optimize administration protocols. This type of modeling has proved useful to experimentalists by providing a quantitative rationale for anti-Bcl-2 therapy as the more effective target for the development of an anti-angiogenic drug. However, eventual clinical application of theoretical modeling such as that carried out here necessitates the accurate estimation of a number of parameters in a defined experimental setting. Building such a dataset is therefore of paramount importance. This underscores the need of a close collaboration between researchers from biomedicine, mathematics and physics in order to advance our understanding of diseases such as cancer and arrive at effective treatment strategies.

Table 1.

List of parameter values

Parameter	Value	Units	Source
r1	1.2924	per day	[16]
C1	0.1	Oxygen concentration	[16]
r2	0.001	per Tumor cell density per day	[16]
σ	1.0029	dimensionless	[16]
C2	0.054	Oxygen concentration	[16]
Cm	0.2	Oxygen concentration	[16]
k	16.0	# Microvessels per mm3	1
μa	12.8810	# HDMECs per pg of Da per day	[11]2
μl	806.9190	# HDMECs per pg of Cl per day	[11]2
ad	3.8780×10−6	per day	[11], [21]3
bd	1.7329	per Bad concentration	[11], [21]3
α1	30.0	# HDMECs per Microvessel	[16]
M0	17×103	# HDMECs per mm3	[16]
α2	0.2984	# Microvessels per pg of Da per day	[22]2
α3	6.5757	# Microvessels per pg of Cl per day	[22]2
${\eta }_1^a$	0.2250	pg VEGF per pg Ra	[16]
${\eta }_2^a$	0.1837	pg VEGF per pg Ca	[16]
${\eta }_3^a$	0.8163	pg Ra per pg Ca	[16]
${\eta }_4^a$	0.4494	pg Ra per pg Da	[16]
${\eta }_5^a$	1.2250	pg Ca per pg Ra	[16]
${\eta }_6^a$	0.5506	pg Ca per pg Da	[16]
${\eta }_7^a$	2.2250	pg Da per pg Ra	[16]
λa	15.5958	per day	[16]
r3	0.1507	pg VEGF per Tumor cell per day	[12]4
$k_{f1}^a$	1.6232	per VEGF concentration per day	[16]
$k_{r1}^a$	49.3025	per day	[16]
$k_{f2}^a$	162.32	per Ca concentration per day	[16]
$k_{r2}^a$	0.493025	per day	[16]
$k_p^a$	16.0	per day	[16]
Vchar	55.0	# Microvessels per mm3	[16]
V0	2.0	# Microvessels per mm3	[16]
∊	1.0	# Microvessels per mm3	[16]
$k_f^l$	6.7587	per CXCL8 concentration per day	[16]
$k_r^l$	43.2557	per day	[16]
$k_p^l$	24.0	per day	[16]
${\eta }_1^l$	0.1311	pg CXCL8 per pg Rl	[16]
${\eta }_2^l$	0.1159	pg CXCL8 per pg Cl	[16]
${\eta }_3^l$	0.8841	pg Rl per pg Cl	[16]
${\eta }_4^l$	1.1311	pg Cl per pg Rl	[16]
λl	15.5958	per day	[16]
βm	8.1139×10−4	pg of CXCL8 per HDMEC per day	[11] [16]2,5
ap	6.9620×10−4	pg of CXCL8 per HDMEC per day	[11] [16]2,5
bp	1.6185	per Bcl-2 concentration	[11] [16]2,5
α4	0.24845	# Microvessels per HDMEC	[16]
$k_f^b$	4	per Bad concentration per day	1
$k_r^b$	8.832	per day	[3]
$k_f^i$	40	per BL193 concentration per day	[3]6
$k_r^i$	2.56	per day	[3]6
βa	40	fg of Bcl-2 per pg Da	[12]
Di	3.4650	per day	1

¹In the absence of experimental data, biologically realistic values for these parameters were chosen so that the solution profiles best fit experimental observations.

²The parameters associated with CXCL8 production, and CXCL8 and VEGF effect on HDMEC proliferation, and microvessel formation were estimated using least squares fits of experimental data in [11, 22].

³We know that the normal death rate of HDMECs is 0.12 per day [21]. Further, in the presence of 50 ng per ml VEGF, Bcl-2 is up-regulated 3.1 fold, and consequently the level of Bad falls by a factor of 0.77. We assume a very low HDMEC death rate corresponding to this low level of Bad. From these two observations, the constants a_d and b_d may be determined.

⁴Keeping all other parameter values fixed, VEGF production rate by tumor cells was determined by fitting the microvessel density after 21 days with that observed experimentally in a (control) tumor that was allowed to grow without the application of any anti-cancer therapy [12].

⁵A relation between the constants β_m, a_p and b_p may be found by observing that at constitutive Bcl-2 levels, the production rate of CXCL8 is 0.0358 pg of CXCL8 per HDMEC per day [16]. Note that at constitutive levels of Bcl-2 and Bad, the cell death rate is taken to be 0.12 per day [21] and HDMEC CXCL8 production rate is fit to experiments in [12]

⁶It was assumed that rate of forward reaction of BL193 with Bcl-2 was higher than that of Bad binding to Bcl-2, due to the much smaller size of BL193.

Abbreviations Used

CXCL8

Interleukin-8

HDMEC

Human Dermal Microvascular Endothelial Cells

SCID

Severe Combined Immuno-deficient

VEGF

Vascular Endothelial Growth Factor

Appendix

A Full Model Equations

The full system of equations used to model sustained angiogenesis are given below. We adopt the following notation for the various species being modelled.

• M = Human dermal microvascular endothelial cell density

• A = Unbound VEGF concentration

• R_a = VEGFR-2 concentration

• C_a = VEGF - VEGFR-2 complex concentration

• D_a = VEGF- VEGFR-2 - VEGF complex concentration

• L = Unbound CXCL8 concentration

• R_l = CXCL8 receptor concentration

• C_l = CXCL8-receptor complex concentration

• V = Microvessel density

• B = Intracellular unbound Bcl-2 concentration

• X = Intracellular unbound Bad concentration

• C_bx = Intracellular Bcl-2 - Bad complex concentration

• I = Intracellular unbound BL193 concentration per cell

• C_bi = Intracellular Bcl-2 - BL193 complex concentration

• N = Tumor cell density

$$\begin{array}{cc}\frac{\mathit{\text{dM}}}{\mathit{\text{dt}}}=\hfill & ({\mu }_a{\varphi }_a+{\mu }_l{\varphi }_l-{\lambda }_m(X))M \left(1-\frac{M+{\alpha }_{1}V}{M_0}\right)\hfill \\ \hfill & -{\alpha }_1({\alpha }_2{\varphi }_a+{\alpha }_3{\varphi }_l)M_{\tau }\hfill \end{array}$$ (9)

$$\begin{array}{cc}\frac{\mathit{\text{dA}}}{\mathit{\text{dt}}}=\hfill & -2{\eta }_1^a{k}_{f1}^a{AR}_a+{\eta }_2^a{k}_{r1}^a{C}_a-{\lambda }_{a}A\hfill \\ \hfill & +r_{3}N (1+\mathrm{\text{tanh}}\left(\frac{V_{\mathit{\text{char}}}-(V+V_0)}{\epsilon }\right))\hfill \end{array}$$ (10)

$$\begin{array}{cc}\frac{{\mathit{\text{dR}}}_a}{\mathit{\text{dt}}}=\hfill & -2k_{f1}^a{AR}_a+{\eta }_3^a{k}_{r1}^a{C}_a-k_{f2}^a{C}_a{R}_a+2{\eta }_4^a{k}_{r2}^a{D}_a+2{\eta }_4^a{k}_p^a{D}_a\hfill \\ \hfill & +R_t^a\text{Prod}(M,V)-\frac{R_a}{R_a+{\eta }_3^a{C}_a+2{\eta }_4^a{D}_a}{R}_t^a\text{Death}(M,V)\hfill \end{array}$$ (11)

$$\begin{array}{cc}\frac{{\mathit{\text{dC}}}_a}{\mathit{\text{dt}}}=\hfill & 2{\eta }_5^a{k}_{f1}^a{AR}_a-k_{r1}^a{C}_a-{\eta }_5^a{k}_{f2}^a{C}_a{R}_a+2{\eta }_6^a{k}_{r2}^a{D}_a\hfill \\ \hfill & -\frac{C_a}{R_a+{\eta }_3^a{C}_a+2{\eta }_4^a{D}_a}{R}_t^a\text{Death}(M,V)\hfill \end{array}$$ (12)

$$\begin{array}{cc}\frac{{\mathit{\text{dD}}}_a}{\mathit{\text{dt}}}=\hfill & {\eta }_7^a{k}_{f2}^a{C}_a{R}_a-2k_{r2}^a{D}_a-k_p^a{D}_a\hfill \\ \hfill & -\frac{D_a}{R_a+{\eta }_3^a{C}_a+2{\eta }_4^a{D}_a}{R}_t^a\text{Death}(M,V)\hfill \end{array}$$ (13)

$$\frac{\mathit{\text{dL}}}{\mathit{\text{dt}}}=-{\eta }_1^l{k}_f^l{LR}_l+{\eta }_2^l{k}_r^l{C}_l-{\mathrm{\lambda }}_{l}L+{\beta }_l(B)M$$ (14)

$$\begin{array}{cc}\frac{{\mathit{\text{dR}}}_l}{\mathit{\text{dt}}}=\hfill & -k_f^l{LR}_l+{\eta }_3^l{k}_r^l{C}_l+{\eta }_3^l{k}_p^l{C}_l\hfill \\ \hfill & +R_t^l\text{Prod}(M,V)-\frac{R_l}{R_l+{\eta }_3^l{C}_l}{R}_t^l\text{Death}(M,V)\hfill \end{array}$$ (15)

$$\begin{array}{cc}\frac{{\mathit{\text{dC}}}_l}{\mathit{\text{dt}}}=\hfill & {\eta }_4^l{k}_f^l{LR}_l-k_r^l{C}_l-k_p^l{C}_l\hfill \\ \hfill & -\frac{C_l}{R_l+{\eta }_3^l{C}_l}{R}_t^l\text{Death}(M,V)\hfill \end{array}$$ (16)

$$\frac{\mathit{\text{dV}}}{\mathit{\text{dt}}}=({\alpha }_2{\varphi }_a+{\alpha }_3{\varphi }_l)M_{\tau }-{\alpha }_4{\mathrm{\lambda }}_m(X){\alpha }_{1}V$$ (17)

$$\frac{\mathit{\text{dN}}}{\mathit{\text{dt}}}=r_1\frac{C^2(V)}{C_1^2+C^2(V)}N-r_2\left(1-\sigma \frac{C^2(V)}{C_2^2+C^2(V)}\right)N^2$$ (18)

$$\frac{\mathit{\text{dB}}}{\mathit{\text{dt}}}=-k_f^{b}BX+{\eta }_1^b{k}_r^b{C}_{\mathit{\text{bx}}}-k_f^{i}BI+{\eta }_1^i{k}_r^i{C}_{\mathit{\text{bi}}}+{\beta }_a\frac{d}{\mathit{\text{dt}}}\left(\frac{D_a}{M+{\alpha }_{1}V}\right)$$ (19)

$$\frac{\mathit{\text{dX}}}{\mathit{\text{dt}}}=-{\eta }_2^b{k}_f^{b}BX+{\eta }_3^b{k}_r^b{C}_{\mathit{\text{bx}}}$$ (20)

$$\frac{{\mathit{\text{dC}}}_{\mathit{\text{bx}}}}{\mathit{\text{dt}}}={\eta }_4^b{k}_f^{b}BX-k_r^b{C}_{\mathit{\text{bx}}}$$ (21)

$$\frac{\mathit{\text{dI}}}{\mathit{\text{dt}}}=-{\eta }_2^i{k}_f^{i}BI+{\eta }_3^i{k}_r^i{C}_{\mathit{\text{bi}}}+D_i(I_0-I)$$ (22)

$$\frac{{\mathit{\text{dC}}}_{\mathit{\text{bi}}}}{\mathit{\text{dt}}}={\eta }_4^i{k}_f^{i}BI-k_r^i{C}_{\mathit{\text{bi}}}$$ (23)

$$C(V)=C_m\frac{V_0+V}{k+V_0+V}$$ (24)

$$\text{Prod}(M,V)=({\mu }_a{\varphi }_a+{\mu }_l{\varphi }_l)M\left(1-\frac{M+{\alpha }_{1}V}{M_0}\right)$$ (25)

$$\text{Death}(M,V)={\mathrm{\lambda }}_m(X)M\left(1-\frac{M+{\alpha }_{1}V}{M_0}\right)+{\alpha }_1{\alpha }_1{\alpha }_4{\mathrm{\lambda }}_m(X)V$$ (26)

$${\varphi }_a=\frac{D_a}{M+{\alpha }_{1}V}$$ (27)

$${\varphi }_l=\frac{C_l}{M+{\alpha }_{1}V}$$ (28)

$${\mathrm{\lambda }}_m(X)=a_d{e}^{b_{d}X}$$ (29)

$${\beta }_l(B)={\beta }_m+a_p(1-e^{-b_{p}B})$$ (30)

B In Vitro Model Equations

The system of equations used to model capillary formation in vitro are given below.

$$\begin{array}{cc}\frac{\mathit{\text{dM}}}{\mathit{\text{dt}}}=\hfill & ({\mu }_a{\varphi }_a+{\mu }_l{\varphi }_l-{\mathrm{\lambda }}_m(X))M\left(1-\frac{M+{\alpha }_{1}V}{M_0}\right)\hfill \\ \hfill & -{\alpha }_1({\alpha }_2{\varphi }_a+{\alpha }_3{\varphi }_l)M_{\tau }\hfill \end{array}$$ (31)

$$\frac{\mathit{\text{dA}}}{\mathit{\text{dt}}}=0$$ (32)

$$\begin{array}{cc}\frac{{\mathit{\text{dR}}}_a}{\mathit{\text{dt}}}=\hfill & -2k_{f1}^a{AR}_a+{\eta }_3^a{k}_{r1}^a{C}_a-k_{f2}^a{C}_a{R}_a+2{\eta }_4^a{k}_{r2}^a{D}_a+2{\eta }_4^a{k}_p^a{D}_a\hfill \\ \hfill & +R_t^a\text{Prod}(M,V)-\frac{R_a}{R_a+{\eta }_3^a{C}_a+2{\eta }_4^a{D}_a}{R}_t^a\text{Death}(M,V)\hfill \end{array}$$ (33)

$$\begin{array}{cc}\frac{{\mathit{\text{dC}}}_a}{\mathit{\text{dt}}}=\hfill & 2{\eta }_5^a{k}_{f1}^a{AR}_a-k_{r1}^a{C}_a-{\eta }_5^a{k}_{f2}^a{C}_a{R}_a+2{\eta }_6^a{k}_{r2}^a{D}_a\hfill \\ \hfill & -\frac{C_a}{R_a+{\eta }_3^a{C}_a+2{\eta }_4^a{D}_a}{R}_t^a\text{Death}(M,V)\hfill \end{array}$$ (34)

$$\begin{array}{cc}\frac{{\mathit{\text{dD}}}_a}{\mathit{\text{dt}}}=\hfill & {\eta }_7^a{k}_{f2}^a{C}_a{R}_a-2k_{r2}^a{D}_a-k_p^a{D}_a\hfill \\ \hfill & -\frac{D_a}{R_a+{\eta }_3^a{C}_a+2{\eta }_4^a{D}_a}{R}_t^a\text{Death}(M,V)\hfill \end{array}$$ (35)

$$\frac{\mathit{\text{dL}}}{\mathit{\text{dt}}}=-{\eta }_1^l{k}_f^l{LR}_l+{\eta }_2^l{k}_r^l{C}_l-{\mathrm{\lambda }}_{l}L+{\beta }_l(B)M$$ (36)

$$\begin{array}{cc}\frac{{\mathit{\text{dR}}}_l}{\mathit{\text{dt}}}{=}_{}\hfill & -k_f^l{LR}_l+{\eta }_3^l{k}_r^l{C}_l+{\eta }_3^l{k}_p^l{C}_l\hfill \\ \hfill & +R_t^l\text{Prod}(M,V)-\frac{R_l}{R_l+{\eta }_3^l{C}_l}{R}_t^l\text{Death}(M,V)\hfill \end{array}$$ (37)

$$\begin{array}{cc}\frac{{\mathit{\text{dC}}}_l}{\mathit{\text{dt}}}=\hfill & {\eta }_4^l{k}_f^l{LR}_l-k_r^l{C}_l-k_p^l{C}_l\hfill \\ \hfill & -\frac{C_l}{R_l+{\eta }_3^l{C}_l}{R}_t^l\text{Death}(M,V)\hfill \end{array}$$ (38)

$$\frac{\mathit{\text{dV}}}{\mathit{\text{dt}}}=({\alpha }_2{\varphi }_a+{\alpha }_3{\varphi }_l)M_{\tau }-{\alpha }_4{\mathrm{\lambda }}_m(X){\alpha }_{1}V$$ (39)

$$\frac{\mathit{\text{dB}}}{\mathit{\text{dt}}}=-k_f^{b}BX+{\eta }_1^b{k}_r^b{C}_{\mathit{\text{bx}}}-k_f^{i}BI+{\eta }_1^i{k}_r^i{C}_{\mathit{\text{bi}}}+{\beta }_a\frac{d}{\mathit{\text{dt}}}\left(\frac{D_a}{M+{\alpha }_{1}V}\right)$$ (40)

$$\frac{\mathit{\text{dX}}}{\mathit{\text{dt}}}=-{\eta }_2^b{k}_f^{b}BX+{\eta }_3^b{k}_r^b{C}_{\mathit{\text{bx}}}$$ (41)

$$\frac{{\mathit{\text{dC}}}_{\mathit{\text{bx}}}}{\mathit{\text{dt}}}={\eta }_4^b{k}_f^{b}BX-k_r^b{C}_{\mathit{\text{bx}}}$$ (42)

$$\frac{\mathit{\text{dI}}}{\mathit{\text{dt}}}=-{\eta }_2^i{k}_f^{i}BI+{\eta }_3^i{k}_r^i{C}_{\mathit{\text{bi}}}+D_i(I_0-I)$$ (43)

$$\frac{{\mathit{\text{dC}}}_{\mathit{\text{bi}}}}{\mathit{\text{dt}}}={\eta }_4^i{k}_f^{i}BI-k_r^i{C}_{\mathit{\text{bi}}}$$ (44)

where,

$$\text{Prod}(M,V)=({\mu }_a{\varphi }_a+{\mu }_l{\varphi }_l)M\left(1-\frac{M+{\alpha }_{1}V}{M_0}\right)$$ (45)

$$\text{Death}(M,V)={\mathrm{\lambda }}_m(X)M \left(1-\frac{M+{\alpha }_{1}V}{M_0}\right)+{\alpha }_1{\alpha }_1{\alpha }_4{\mathrm{\lambda }}_m(X)V$$ (46)

$${\varphi }_a=\frac{D_a}{M+{\alpha }_{1}V}$$ (47)

$${\varphi }_l=\frac{C_l}{M+{\alpha }_{1}V}$$ (48)

$${\lambda }_m(X)=a_d{e}^{b_{d}X}$$ (49)

$${\beta }_l(B)={\beta }_m+a_p(1-e^{-b_{p}B})$$ (50)

C Parameter Values

Where possible, the choice of parameters is based on values given in the literature. In cases where no data could be found, parameter values were chosen so that microvessel densities best fit pre-treatment experimental data taken from [14, 11, 12]. Briey, the model was first reduced to represent the in vitro experimental system, then a least squares fit of the modified model to the HDMEC or microvessel density vs time experimental data was performed. Care was taken to fit no more than 2–3 parameters to any given set of experimental data. Biologically realistic values were chosen for the parameters for which no experimental data was available. All of the parameter estimation was done prior to simulation of treatment strategies, and these values were kept constant thereafter.