Breakdown of Effective Connectivity During Slow Wave Sleep: Investigating the Mechanism Underlying a Cortical Gate Using Large-Scale Modeling

Abstract

Effective connectivity between cortical areas decreases during slow wave sleep. This decline can be observed in the reduced interareal propagation of activity evoked either directly in cortex by transcranial magnetic stimulation (TMS) or by sensory stimulation. We present here a large-scale model of the thalamocortical system that is capable of reproducing these experimental observations. This model was constructed according to a large number of physiological and anatomical constraints and includes over 30,000 spiking neurons interconnected by more than 5 million synaptic connections and organized into three cortical areas. By simulating the different effects of arousal promoting neuromodulators, the model can produce a waking or a slow wave sleep-like mode. In this work, we also seek to explain why intercortical signal transmission decreases in slow wave sleep. The traditional explanation for reduced brain responses during this state, a thalamic gate, cannot account for the reduced propagation between cortical areas. Therefore we propose that a cortical gate is responsible for this diminished intercortical propagation. We used our model to test three candidate mechanisms that might produce a cortical gate during slow wave sleep: a propensity to enter a local down state following perturbation, which blocks the propagation of activity to other areas, increases in potassium channel conductance that reduce neuronal responsiveness, and a shift in the balance of synaptic excitation and inhibition toward inhibition, which decreases network responses to perturbation. Of these mechanisms, we find that only a shift in the balance of synaptic excitation and inhibition can account for the observed in vivo response to direct cortical perturbation as well as many features of spontaneous sleep.

INTRODUCTION

On transition to slow wave sleep from wakefulness, spontaneous firing rates in cortex remain relatively unchanged (Steriade et al. 2001), but signal transmission changes dramatically. This change has been assessed by measuring effective connectivity in the brain, which refers to the ability of one brain region to make a difference to the activity in another brain region (Gerstein and Perkel 1969; Tononi and Sporns 2003). Effective connectivity can be measured by perturbing a specific brain site and measuring how evoked activity propagates to other sites. In humans, this has been done by using transcranial magnetic stimulation (TMS) combined with high-density electroencephalography (hd-EEG). TMS permits the direct perturbation of cortex, thereby bypassing thalamus and other subcortical structures to provide a clear indication of one cortical areas influence on another. During wakefulness, TMS-evoked activity rapidly propagates to specific cortical areas from the site of stimulation, whereas during slow wave sleep, such activity remains confined to the site of stimulation, indicating a reduction in effective connectivity in this state (Massimini et al. 2005).

Signs of decreased cortical effective connectivity in slow wave sleep can also be seen in brain responses to sensory stimuli. Such changes have traditionally been assessed by using EEG or magnetoencephalography to record the cortical response to sensory stimulation. Early components of sensory-evoked responses that reflect activations in the brain stem or primary sensory areas (Picton et al. 1974) are often the same in waking and slow wave sleep (Addy et al. 1989; Amadeo and Shagass 1973; Campbell and Bartoli 1986; Emerson et al. 1988; Erwin and Buchwald 1986). However, later components, reflecting activations in higher cortical areas (Picton et al. 1974), are often reduced in amplitude regardless of whether they are evoked by auditory stimulation (Deiber et al. 1989; Kakigi et al. 2003), somatosensory stimulation (Kakigi et al. 2003; Kitamura et al. 1996), or visual stimulation (Kakigi et al. 2003). Imaging work also provides further evidence for this decline in effective connectivity. The blood-oxygen-level-dependent response to auditory stimulation is the same in primary auditory cortex but reduced in higher order areas in slow wave sleep compared with waking (Portas et al. 2000). This work collectively suggests that effective connectivity from primary sensory areas to higher cortical areas is reduced in slow wave sleep.

The traditional view explaining reduced brain responsiveness during slow wave sleep is that a thalamic gate disrupts signal transmission from the periphery to cortex (Steriade et al. 1990). This gate is created by the hyperpolarization of thalamocortical neurons that occurs during slow wave sleep, which places these neurons further from threshold and reduces their firing in response to a prethalamic activation (Timofeev et al. 1996). However, while the thalamic gate can account for certain reductions in brain responsiveness to peripheral stimuli, it is unable to explain diminished direct propagation of activity between cortical areas.

Reduced cortical effective connectivity during slow wave sleep could be accounted for by the existence of a cortical gate. We envision that the decrease in levels of arousal promoting neuromodulators that occurs with the transition from wakefulness to slow wave sleep could produce a cortical gate through three potential mechanisms. It is known that during slow wave sleep cortex is bistable, undergoing alternations between active up states and silent, hyperpolarized down states (Steriade et al. 2001) and that the emergence of the down state is in part due to the increased conductance of a variety of potassium channels (Bazhenov et al. 2002; Compte et al. 2003; Hill and Tononi 2005). It is possible that stimulation of cortex triggers a local downstate, which prevents the propagation of activity to other cortical areas. A second possibility is that increased potassium channel conductance during slow wave sleep directly reduces neuronal responsiveness to an extent sufficient to reduce signal transmission. A third possibility is that a change in synaptic release probability, which occurs with decreased levels of arousal promoting neuromodulators (Gil et al. 1997; Salgado et al. 2007), alters the ratio of evoked excitatory to inhibitory synaptic responses, thereby reducing signal propagation between areas. Testing these potential mechanisms through traditional in vivo or in vitro experimental techniques is difficult due to the involvement of multiple synaptic and cellular systems. Therefore here we employ large-scale modeling of the thalamocortical system to reproduce EEG responses to TMS and sensory stimulation during different arousal states and to test the capacity of the above mechanisms to produce a cortical gate during slow wave sleep.

METHODS

Large-scale thalamocortical model

The large-scale model employed for this work embodies general anatomical and physiological features of the thalamocortical system. This model is a modified version of a previously presented model (Hill and Tononi 2005). In what follows, a description is presented of the principles used to construct and scale the simulated cortical and thalamic regions, the layout of the various connection pathways within and among these regions, and the implementation of cellular and synaptic properties within individual neurons. A description of the sources of spontaneous activity and procedures for the collection and analysis of data then follows.

Regional organization

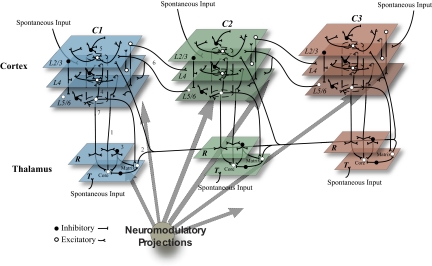
The model (Fig. 1) is organized in regions and pathways comprising three cortical areas, cortical area 1 (C1), cortical area 2 (C2), and cortical area 3 (C3), arranged in a hierarchical fashion. Cortical areas are divided into three layers with different patterns of afferent, efferent and local connectivity corresponding to cortical layers 2 and 3 (L2/3), layer 4 (L4), and layers 5 and 6 (L5/6). Each cortical area is associated with a section of the thalamus (T1–T3) and thalamic reticular nucleus (R1–R3).

Fig. 1.

Schematic of the thalamocortical model showing 3 hierarchically organized cortical areas (C1–C3) each with an associated thalamic sector (T) and corresponding section of the reticular nucleus (R). Excitatory (white) and inhibitory (black) cells receive spontaneous input in the waking mode from areas representing cortical and subcortical structures. (1) Thalamic core cell thalamocortical loops: excitatory core cells in T project to the associated cortical area L4 (corresponding to cortical layer 4), to L5/6 (corresponding to cortical layers 5 and 6), and, via collaterals, to R. (2) Matrix cell thalamocortical loops: excitatory matrix cells in T project to L2/3 (corresponding to cortical layers 2 and 3) and L5/6 of all cortical areas as well as R. (3) Reticular nucleus network: R neurons send inhibitory projections to the neurons in the associated T sector. (4) Cortical interlaminar (vertical) connections: columnar connections are made from L4 to L2/3, L2/3 to L5/6, and L5/6 to L4 and L2/3. (5) Cortical intralaminar (horizontal) connections: each layer contains excitatory and inhibitory projections to other cells within the same layer. (6) Interareal corticocortical loops: forward projections (C1 to C2 and C2 to C3) are from excitatory L2/3 cells to L4, whereas back projections (C3 to C2 and C2 to C1) are from excitatory L5/6 cells to L2/3 and L5/6. (7) Corticothalamic connections: excitatory cells in L5/6 project via slow connections to core cells in T, forming collaterals with R, and via fast projections to matrix cells in T. (8) Diffuse neuromodulatory (cholinergic, noradrenergic, histaminergic, etc) systems project throughout the entire thalamocortical network. Not drawn to scale.

Each model area corresponds to ∼1.5 mm² of cortical surface. Each area consists of cortical minicolumns (Mountcastle 1997), which we represent here with nine model neurons (2 excitatory and 1 inhibitory for each of the 3 layers). This represents a downsampling of neuronal number by approximately an order of magnitude from in vivo cortical columns (Mountcastle 1997), which we institute to reduce the computational burden of the model. Each cortical area is organized into a 30 × 30 grid of such minicolumns, thus assuming each minicolumn to have a diameter of ∼50 μm. To reproduce specifically projecting core cells and diffusely projecting matrix cells found in the primate thalamus (Jones 2002), the model thalamic nuclei contain core cells that project to the associated cortical area and matrix cells that project diffusely to all three cortical areas. In T1 and T2 core cells comprised 80% of thalamic cells while matrix cells made up the remaining 20% of thalamic neurons. In T3 10% of neurons were core cells with the remaining 90% of cells being matrix neurons. Thus T3 reflects the propensity of some thalamic nuclei, in particular certain nuclei associated with nonprimary cortical areas, to show a high degree of matrix cells (Jones and Hendry 1989). Thalamic nuclei are organized into 30 × 30 grids with each topographic location containing an excitatory thalamocortical neuron (core or matrix) and an inhibitory interneuron. The three sectors of the thalamic reticular nucleus are modeled as 30 × 30 grids of inhibitory neurons.

Connectivity

In constructing the model, special emphasis was placed on the incorporation of realistic network properties, such as the spread and relative proportions of the various sets of connections composing the intra- and interregional thalamocortical circuitry. Contacts from presynaptic neurons to postsynaptic cells in the target area are made probabilistically according to Gaussian spatial density profiles. The specific connection parameters are presented in Table 1.

Table 1.

Connections

Source Layer/Region	Source Cell Type	Targer Layer or Region	Target Cell Type	Receptor	Pmax	Radius	Strength	Mean Delay
Horizontal intralaminar connections
L2/3	Exc	L2/3	Exc,Inh	AMPA, NMDA	0.1	12	0.38	1 ± 0.25
L4	Exc	L4	Exc,Inh	AMPA,NMDA	0.05	7	0.38	1 ± 0.25
L5/6	Exc	L5/6	Exc,Inh	AMPA,NMDA	0.1	12	0.38	1 ± 0.25
Vertical interlaminar connections
L2/3	Exc	L5/6	Exc,Inh	AMPA,NMDA	1	2	1.88	1 ± 0.25
L4	Exc	L2/3	Exc,Inh	AMPA,NMDA	1	2	1.88	1 ± 0.25
L5/6	Exc	L2/3	Exc,Inh	AMPA,NMDA	1	2	0.47	1 ± 0.25
L5/6	Exc	L4	Exc,Inh	AMPA,NMDA	1	2	0.47	1 ± 0.25
Intracortical inhibitory connections
L2/3	Inh	L2/3	Exc,Inh	GABAA	0.25	7	0.95	0.75 ± 0.1
L4	Inh	L4	Exc,Inh	GABAA	0.25	7	0.95	0.75 ± 0.1
L5/6	Inh	L5/6	Exc,Inh	GABAA	0.25	7	0.88	0.75 ± 0.1
L2/3	Inh	L2/3,L4,L5/6	Exc,Inh	GABAA	1	2	1.19	4 ± 0.25
Forward interareal connections
L2/3	Exc	L4 (higher area)	Exc,Inh	AMPA,NMDA	0.2	12	0.94	12 ± 4.0
							0.00
							0.00
Feedback interareal connections
L5/6	Exc	L2/3,L5/6 (lower area)	Exc,Inh	AMPA,NMDA	0.15	12	0.45	12 ± 4.0
							0.00
							0.00
Corticothalamic connections
L5/6	Exc	T	Core,Inh	AMPA,NMDA	0.15	12	1.69	12 ± 2.0
L5/6	Exc	T	Matrix,Inh	AMPA,NMDA	1	2	2.18	5 ± 1
L5/6	Exc	NRT	Inh	AMPA,NMDA	0.15	12	4.50	12 ± 2.0
Thalamocortical connections
T	Core	L4	Exc,Inh	AMPA,NMDA	0.2	4	9.00	7 ± 0.5
T	Core	L5/6	Exc,Inh	AMPA,NMDA	0.2	4	2.25	7 ± 0.5
T	Matrix	L2/3,L5/6 (All areas)	Exc,Inh	AMPA,NMDA	0.1	12	1.50	7 ± 2.0
Thalamic connections
T	Exc	NRT	Inh	AMPA,NMDA	1	2	3.75	2 ± 0.25
T	Inh	T	Exc,Inh	GABAA	0.3	2	1.59	1 ± 0.25
NRT	Inh	T	Exc,Inh	GABAA	0.4	5	0.35	1.5 ± 0.25
NRT	Inh	T	Exc,Inh	GABAB	0.2	5	0.70	1.5 ± 0.25
Noise input
Cortical noise	Exc	L4	Exc,Inh	AMPA,NMDA	0.2	12	1.00	8 ± 4.0
Subcortical noise	Exc	T	Exc,Inh	AMPA,NMDA	0.2	12	1.00	3 ± 0.25

Parameters for the connectivity profiles used to construct the thalamocortical network. Connectivity patterns are specified as follows: source layer or region, source cell type (Exc, excitatory; Inh, inhibitory), layer or region of termination, target cell type, type(s) of synaptic receptor activated by the connection, maximum probability of connection (P_max), radius of the target to which the projections from a single source cell diverge (expressed in number of topographic elements along vertical and horizontal axis in target map), strength of the connections (expressed in average number of simultaneous postsynaptic potentials per connection) and mean±SD of the conduction delay from the source cell to the target cells. All connections are made to the origin cells same area unless otherwise specified. NMDA, N-methyl-d-aspartate.

Connections within each area are modeled as in Hill and Tononi (2005). Briefly, vertical interlaminar connections form a cortical loop from L4 to L2/3, from L2/3 to L5/6 and from L5/6 back to L4 and L2/3, whereas horizontal intralaminar connections project to other neurons within the same layer. Compared with Hill and Tononi (2005), the network employed here contains more areas and a greater use of N-methyl-d-aspartate (NMDA) channels. To maintain network balance in the increased presence NMDA channels, the connection strengths from Hill and Tononi (2005) were halved and then fine-tuned to produce spontaneous firing in the network comparable to values observed in vivo. Connections between areas have a laminar profile (Barbas and Rempel-Clower 1997). Feedforward interareal connections (C1 to C2 and C2 to C3) project from L2/3 of the lower order area to L4 of the higher-order area. Feedback interareal connections (C3 to C2 and C2 to C1) project from L5/6 of the higher-order area to L2/3 and L5/6 of the lower-order area. Connections between cortex and core cells in the thalamus follow the organization described in Hill and Tononi (2005), in which corticothalamic projections from L5/6 target the associated reticular nucleus and core cells of the associated thalamic nucleus (e.g., C1 to T1 and R1). Thalamocortical connections from the core cells target L4 and L5/6 in the associated cortical area. Following evidence that fast connections from layer 5 target matrix cells while bypassing the reticular nucleus (Swadlow 1994; Zikopoulos and Barbas 2007), model neurons in L5/6 sent a separate group of connections to matrix neurons in the associated thalamic nucleus but not to the reticular nucleus. Based on evidence that matrix cells project primarily to superficial and deep layers (Zikopoulos and Barbas 2007) and project diffusely to many cortical areas (Jones 1998), each model matrix cell targets L2/3 and L5/6 in all three modeled areas.

Transmission delays in the model reflect axonal conduction time and synaptic delays. Local excitatory connections typically have a latency of 0.6–1.5 ms (Thomson et al. 2002), while local inhibitory connection latency is ∼0.75 ms (Gonzalez-Burgos et al. 2005). Conduction time between nearby cortical areas is typically ∼4 ms (Godschalk et al. 1984; Tokuno and Nambu 2000). Corticothalamic conduction delays have been have been measured at about 12 ms for connections originating from layer 6 cells, while connections originating from layer 5 cells show considerably shorter conduction times (Swadlow 1994). Conduction times for thalamocortical connections range from 2 to 6 ms (Noda and Yamamoto 1984). These values were used to determine transmission delays in the model (detailed in Table 1).

Model neurons

Neurons are modeled as single-compartments incorporating Hodgkin-Huxley (Hodgkin and Huxley 1952) style currents with spiking dynamics simplified for computational reasons as in Hill and Tononi (2005). Model neurons thus behave like a hybrid between traditional integrate-and-fire neurons and full-fledged Hodgkin-Huxley neurons.

The change in subthreshold membrane potential V for each neuron is as follows

$$\frac{\text{d}V}{\text{d}t}=\left(-g_{\text{Na}L}\left(V-E_{\text{Na}}\right)-g_{\text{KL}}\left(V-E_{\text{K}}\right)-I_{\text{syn}}-I_{\mathrm{int}}\right)/{\tau }_{\text{m}}-g_{\text{spike}}\left(V-E_{\text{K}}\right)/{\tau }_{\text{spike}}$$

where τ_m is the membrane time constant (Table 2) as derived from experimental data for excitatory and inhibitory cells (Baranyi et al. 1993b). Resting membrane potential is primarily determined by the sodium and potassium leak conductances (g_NaL and g_KL; Table 3). Reversal potentials are E_Na = 30 mV and E_K = −90 mV. Two main categories of input contribute to the membrane potential: synaptic currents (I_syn) and intrinsic currents (I_int), which are described in the following text.

Table 2.

Neuron membrane parameters

Cell Type	τm, ms	θeq, mV	τθ, ms	τspike, ms	tspike, ms
Cortical excitatory	15	−51	1.0	1.3	1.4
Cortical inhibitory	7	−53	1.0	.55	.75
Thalamic	7	−53	1.0	.55	.75
Thalamic reticular	7	−53	1.0	.55	.75
Nucleus

Table 3.

Intrinsic channel g_peak values

Parameter	Region	Cell Type	Waking Value	Sleep Value
gKL	C	Exc	0.3	0.55
gKL	C	Inh	0.209	0.55
gKL	T	Exc	0.209	0.55
gKL	NRT	Inh	0.7315	0.4
gDK	C	Exc	0.25	0.75
gDK	C	Inh	0.143	0.75
gKS	C	Exc	3	6
gKS	C	Inh	2	6
gNaL	C, T, NRT	Exc,Inh	0.05	0.05
gNaP	C, T, NRT	Exc,Inh	1	2
gh	T	Exc	0.4	0.4
gh	C	IB	0.4	0.4
gt	T	Exc	6	12
gt	NRT	Inh	6	12
gKCa	NRT	Inh	12	48

Intrinsic channel g_peak values in the model's wake mode and sleep mode. Values are given for different regions and cell types (exctatory, Exc; inhibitory, Inh; and intrinsically bursting, IB). IB cells make up 30% of cortical L5/6 neurons and include the same channels as cortical excitatory cells with the addition of the l_hchannel.

When V exceeds a threshold (θ), a spike is generated by setting V and θ instantaneously to E_Na, modeling the contribution of the fast-spiking I_Na current. The activation of a fast potassium current during a spike is represented by a brief pulse (duration t_spike) with an amplitude g_spike = 1 and governed by the time constant τ_spike, thereby driving the membrane potential toward E_K, while continuing to integrate intrinsic and synaptic currents. Following a spike, θ decays according to

$$\frac{\mathrm{d}\theta }{\mathrm{d}t}=-(\theta -{\theta }_{\mathrm{eq}})/{\tau }_{\theta }$$

These four parameters, τ_θ, τ_spike, t_spike, and θ_eq (Table 2), allow the key characteristics of spike generation to be modeled, including action potential width, after hyperpolarization and relative refractory period (Baranyi et al. 1993a,b).

Synaptic channels

The synaptic input, I_syn, is the sum of all synaptic channel currents, I_syn=∑_ij g_j⁽ⁱ⁾(V−E_j). Simulated synaptic channels provide voltage-dependent (NMDA-like) and voltage independent (AMPA-like) excitation, as well as fast (GABA_A-like) and slow (GABA_B-like) inhibition. The conductance g, for each afferent i, on each channel j, specifies the amplitude and time course of the postsynaptic potentials (PSPs). The reversal potential for each channel E_j, determines whether a current is inhibitory or excitatory.

Synaptic activation is expressed as a change in channel conductance, g(t), according to a dual-exponential response to single spike events, given by

$$g\left(t\right)=g_{\text{peak}}\frac{e^{-t/{\tau }_1}-e^{-t/{\tau }_2}}{e^{-t_{\text{peak}}/{\tau }_1}-e^{-t_{peak}/{\tau }_2}}$$

where g_peak is the peak conductance for each channel, and τ₁ and τ₂ are the rise and decay time constants, respectively. Parameterization for the synaptic types, AMPA (τ₁ = 0.5 ms, τ₂ = 2.4 ms, E_rev = 0 mV), NMDA (τ₁ = 4.0 ms, τ₂ = 40.0 ms, E_rev = 0 mV) GABA_A (τ₁ = 1.0 ms, τ₂ = 7.0 ms, E_rev = −70 mV in cortex and −80 mV in thalamic cells), and GABA_B (E_rev = −90 mV, activation described in the following text) is as in Hill and Tononi (2005). The g_peak values for all synapse types are provided in Table 4. These values were set based on observations that single excitatory postsynaptic potentials have an amplitude of ∼1 mV (Crochet et al. 2005; Feldmeyer et al. 2002), that AMPA and unblocked NMDA channels have approximately the same conductance (Myme et al. 2003), and that single inhibitory postsynaptic potentials have an amplitude of 1–1.5 mV (Thomson et al. 1996). The time to peak, t_peak, is

$$t_{\text{peak}}=\frac{{\tau }_2{\tau }_1}{{\tau }_2-{\tau }_1}\text{In}\left(\frac{{\tau }_{\text{2}}}{{\tau }_{\text{1}}}\right)$$

NMDA-like channels are modeled with an additional factor to account for the voltage dependence of NMDA, according to the equation

$${\mathrm{g̃}}_{\text{NMDA}}=m\left(V\right){\text{g}}_{\text{NMDA}}\left(t\right)$$

where g_NMDA(t) is a dual-exponential impulse response and m(V) is a sum of two exponential functions with fast and slow time constants that modulates the change in NMDA conductance. Although the blocking of NMDA channels by Mg²⁺ occurs instantaneously (<0.06 μs) the unblocking occurs with a slower dynamic, at two times scales (Vargas-Caballero and Robinson 2003). Therefore we model unblocking as a two-stage process with one component unblocking quickly (∼1 ms) and second slow component that unblocks in ∼20 ms.

Table 4.

Synaptic channel g_peak, δ_P, and τ_P given for the model's wake mode and sleep mode

Synapse Type	gwake	gsleep	δwake	δsleep	τP, ms
AMPA	0.1	0.133	0.0564	0.075	200
NMDA	0.1	0.133	0.0564	0.075	200
GABAA	0.33	0.33	0.0375	0.0375	200
GABAB	1	1	0.0375	0.0375	200

GABA_B-like channels are simulated to take into account the nonlinear change in conductance in response to increasing activation based on a previously developed model (Destexhe and Sejnowski 1995). Channel conductance is given by

$$\frac{\mathrm{d}\left[R\right]}{\mathrm{d}t}=K_1\left[S\right](1-[R\left]\right)-K_2\left[R\right]$$

$$\frac{\mathrm{d}\left[G\right]}{\mathrm{d}t}=K_3\left[R\right]-K_4\left[G\right]$$

$$g_{{\text{GABAB}}_{\text{B}}}={ḡ}_{{\text{GABA}}_{\text{B}}}\frac{{\left[G\right]}^4}{{\left[G\right]}^4+K_{\text{d}}}$$

where [S] represents the strength of each synaptic event, [R] represents the fraction of activated receptor, [G] is the concentration of activated G protein, ḡGABA_B is GABA_B peak conductance (Table 4). For thalamic GABA_B channels, K₁ = 0.66, K₂ = 0.02, K₃ = 0.083, K₄ = 0.0079, and K_d = 100 (Destexhe and Sejnowski 1995). Cortical GABA_B channels use K₁ = 0.18, K₂ = 0.0096, K₃ = 0.19, K₄ = 0.060, and K_D = 17.83 (Thomson and Destexhe 1999).

Synaptic depression is simulated to reflect short-term changes in synaptic efficacy that are caused by the depletion of presynaptic pools of readily releasable neurotransmitter vesicles (Zucker and Regehr 2002). In the model, short-term synaptic depression is simulated using a simple vesicle pool model (Abbott et al. 1997). Peak conductance of a given synaptic channel is scaled by the size of the corresponding presynaptic pool of synaptic “vesicles.” The dynamics of this pool are governed by the equation dP/dt = −spike·δ_P·P + (P_peak − P)/τ_P. The pool P decreases by the fraction δ_P for each spike. The pool recovers its peak value P_peak according to the time constant τ_p. Parameter values governing vesicle pool dynamics are given in Table 4.

Intrinsic ion channel properties

Ion channel currents are modeled as in (Hill and Tononi 2005) according to the Hodgkin-Huxley formalism I_int=g_peakm^Nh(V − E_int), where g_peak is the maximal conductance for the channel, m and h determine activation and inactivation respectively, and E_int is the reversal potential for the given channel. The factor N, which is one unless otherwise noted, allows the activation to occur at a different time course than inactivation. The gating of activation and inactivation follows the equation: dx/dt = [x_∞(V) − x]/τ_x(V) where x_∞ is the steady-state activation/inactivation value for the channel. The g_peak values for all intrinsic channel types are provided in Table 3. Values were tuned so as to maintain an ∼0.75 ratio between total excitatory synaptic conductance and total intrinsic conductance, in accordance with in vivo observations (Destexhe et al. 2003).

The pacemaker current, I_h, is a noninactivating hyperpolarization-activated cation current. The activation variable for I_h is modeled by m_h = 1/{1 + exp[(V − V_threshold)/5.5]} with V_threshold = − 75.0 mV, while the rate τ_m of activation is τ_m = 1/[exp(−14.59 − 0.086 V) + exp(−1.87 + 0.0701V)] (Huguenard and McCormick 1992).

Persistent sodium current, I_Na(p), activates rapidly near spike threshold and inactivates very slowly (on the order of seconds). We borrowed the formulation for I_Na(p) from previous work (Compte et al. 2003; Fleidervish et al. 1996). The steady-state activation is m_∞(V) = 1/[1 + exp(−V + 55.7)/7.7], with n = 3. We did not model the inactivation of this current given its very slow time course.

The noninactivating potassium current, I_KS, is a slow potassium current. It is modeled based on previous work (Wang 1999), using an activation variable m_∞ = 1/[1 + exp(−V + 34.0)/6.5] with the voltage-dependent time constant τ_m = 8/{exp[−(V + 55)/30] + exp[(V + 55)/30]}.

The depolarization activated potassium current, I_DK, is modeled as an approximate combination of sodium- and calcium-dependent potassium currents. A factor D accumulates with depolarization and decays according to dD/dt = D_influx −D·(1 − D_eq)/τ_D where D_influx = 1/{1 + exp[−(V − D_θ)/σ_D]}. The voltage-dependent influx D_influx is determined by a sigmoid function with a threshold D_θ = −10 mV and slope σ_D = 5.0. The equilibrium level for the depolarization-dependent value is D_eq = 0.001, and τ_D = 800 ms is the time constant that determines the return to D_eq. Depolarization-dependent activation is determined by m_∞ = 1/[1 + (0.25D)^3.5].

The low-threshold calcium current, I_T, is a low-threshold fast-activating calcium current. I_T is modeled based on previous work (Destexhe et al. 1996; Huguenard and McCormick 1992) using an activation variable m_∞(V) = 1/{1 + exp[−(V + 52.0)/7.4]} with the voltage-dependent time constant τ_m = 0.15/{exp[(V + 27.0)/10.0] + exp[−(V + 102.0)/15.0]}+ 0.44. Inactivation of I_T is modeled as h_∞ = 1/{1 + exp[(V + 80.0)/5.0]} with the inactivation time constant τ_h = 22.7 + 0.27/{exp[(V + 48.0)/4.0] + exp[−(V + 407.0)/50.0]}.

A calcium-activated potassium channel, I_KCa is present on NRT cells. I_KCa is modeled based on previous work (Destexhe et al. 1996; Huguenard and McCormick 1992). Intracellular calcium levels are determined according to dCa/dt = −5.18·10⁻⁶·I_T + (Ca_eq − Ca)/τ_Ca where the calcium equilibrium level Ca_eq = 0.00024 and τ_Ca = 160 ms is the time constant that determines the return to Ca_eq. The activation variable for I_KCa is modeled as dm/dt = 48·Ca²(1 − m) − 0.03m with n = 2. We do not model the inactivation of this current due to its slow time course.

Influence of diffuse neuromodulatory systems

Under physiological conditions, ascending neuromodulatory projections from several brain stem nuclei and the basal forebrain activate cholinergic, noradrenergic, serotoninergic, histaminergic, and glutamate metabotropic receptors. These receptors modulate various cellular conductances and synaptic release properties that influence the overall level of depolarization on which the sleep-wake cycle critically depends.

The model's sleep mode is designed to reflect slow wave sleep (N3). The transition from the waking mode to the sleep mode reflects the reduction of the levels of arousal promoting neuromodulators listed in the preceding text and is simulated by simultaneous changes of the conductances of various intrinsic channels and an increase in neurotransmitter release (values detailed in Tables 3 and 4). The majority of these changes have been instantiated in previous versions of this model (Hill and Tononi 2005) and, in brief, were based on the following in vitro observations. The reduced action of acetylcholine unblocks potassium leak channels (McCormick 1992) and the noninactivating potassium current (Madison et al. 1987). Furthermore, deactivation of muscarinic acetylcholine receptors increases persistent sodium conductance (Mittmann and Alzheimer 1998) and low-threshold calcium conductance (McCormick 1992). Decreasing acetylcholine and norepinephrine unblocks slow potassium currents (McCormick 1992). Decreasing acetylcholine levels reduces glutamate release from excitatory cells (Gil et al. 1997). Changes in neuromodulation are simulated as having a greater influence on inhibitory neurons than excitatory neurons based on observations that inhibitory neurons show a greater relative presence of cholinergic receptors compared with excitatory neurons (Disney et al. 2006) and thus presumably show a greater response to changes in this neuromodulator. The final intrinsic conductance values used in the sleep mode were fine tuned so as to produce a slow-wave-sleep-like state characterized by slow wave downstates separated by long upstates as is commonly observed in light sleep. This allowed us to easily test responses to TMS during stable upstates or during downstates.

Modified inhibition parameter set

We named the parameters for the sleep mode described in the preceding text (Tables 1–4) the base sleep parameter set. For a number of the simulations presented in this paper, we tested the combined effect of two changes in the model's sleep mode that were not considered in the version of this model presented in Hill and Tononi (2005). Reduced levels of acetylcholine produce an increase in the per spike release of GABA from inhibitory cells (Metherate and Ashe 1995; Salgado et al. 2007). In addition, under in vitro conditions with low levels of arousal promoting neuromodulators, inhibitory cells have greater potassium channel conductance than excitatory cells (Hamill et al. 1991). Based on these observations, we created the modified inhibition parameter set. This parameter set includes values identical to those in the base sleep parameter set with the following changes. We increase per spike GABA release from cortical inhibitory neurons by setting GABA_A g_peak to 0.66, GABA_B g_Peak to 2.0 and the GABA vesicle pool depletion parameter, δ_P, to 0.075 in this sleep mode of the model. For this sleep mode, the increased sensitivity of inhibitory neurons to changes in neuromodulation is enhanced by increasing the conductance of inhibitory cell potassium channels (inhibitory cell g_KL = 0.7315, g_KS = 8, g_DK = 1.0).

Spontaneous activity

L4 of each cortical area receives input via interareal feedforward projections (see Table 1) from an associated cortical noise area. The cortical noise area is modeled as 900 separate Poisson processes firing at 1 Hz in waking, which helped to produce spontaneous firing rates in the network comparable to values observed in vivo (Steriade et al. 2001). The specific thalamic nucleus of each cortical area receives input from a subcortical noise area, which is modeled as 900 separate Poisson processes with firing at 25 Hz during waking so as to produce thalamic firing rates in the 10- to 20-Hz range that has been observed experimentally (Farley 1997; Raeva et al. 1999). The firing rate of all noise areas was set to 0 Hz in model's sleep mode.

In addition, we model “minis,” the spontaneous release of neurotransmitter quanta (Vautrin and Barker 2003), as low-amplitude PSPs (mean = 0.5 ± 0.25 mV) consistent with experimental observations (Timofeev et al. 2000). The mean frequency of these Poisson distributed synaptic minis is set to 1 Hz (total for an individual cell).

Data recording and analysis

Membrane potentials and synaptic currents are recorded for all units at 1 kHz. The EEG is believed to primarily reflect excitatory postsynaptic potentials in cortex (Mitzdorf 1985). Therefore the simulated EEG is derived based on the equations for extracellular voltage described in (Nunez and Srinivasan 2006) according to the following

$$V_{\mathrm{ext}}=\frac{R_{\mathrm{e}}}{4\pi }\sum _j\frac{I_j}{r_j}$$

where V_ext is the extracellular potential, R_e (230 Ωcm) is the extracellular resistivity, I_j are current sources produced by excitatory synapses, and r_j is the distance from synaptic activity I_j to the recording site. Effects of volume conduction are not modeled and the number of neurons in the model is not comparable to a real brain, therefore voltage levels in the EEG are not meant to be compared with those observed in vivo. Analysis of the simulation data were carried out using standard toolboxes in MATLAB (The MathWorks, Natick, MA).

For certain analyses, the we identified the transition from cortical up state to down state as the time when the average firing rate of cortical excitatory cells, sorted into 1-ms bins, fell <5% of the average firing rate observed over the recorded period.

Simulating a TMS pulse

The cortical response to TMS during waking has been simulated in a previous iteration of this model (Esser et al. 2005). In brief, TMS activation is of limited range, likely having its primary direct effect on a small number of cortical areas (Thielscher and Kammer 2002). Furthermore, synaptic terminations of vertically oriented fibers appear to be the most sensitive site to stimulation (Fox et al. 2004; Maccabee et al. 1993). Therefore TMS is simulated as an instantaneous activation (1 time step) of all vertically oriented synapses (interlaminar, interareal and thalamocortical) impinging on the targeted cortical area. The strength of a simulated TMS pulse is defined as the percentage of these fibers activated.

Simulation techniques

All simulations were performed using a general-purpose object-oriented interactive neural simulator called Synthesis written by Sean Hill (www.synthesis-simulator.com). The model files can be found at: http://www.synthesis-simulator.com/Downloads/3AreaModel.zip. Differential equations were numerically integrated using the Runge-Kutta fourth-order method [Press and Numerical Recipes Software (Firm) 1992] with a step size of 0.1 ms. The model was tested at smaller time steps with no significant differences observed. Simulations were performed on a quad-core 2.5-GHz Power Macintosh G5 machine running Mac OS 10.4 and equipped with 4.0 GB RAM (Apple, Cupertino, CA). One second of simulation required ∼1 h to compute.

RESULTS

Potential mechanisms for producing a cortical gate during slow wave sleep

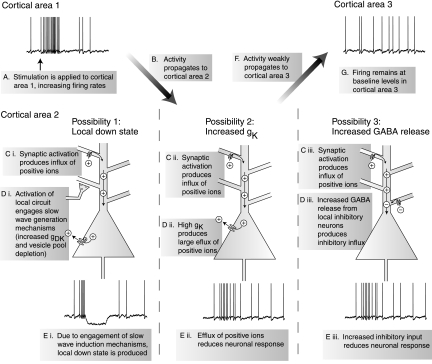
We investigated three mechanisms that might be responsible for producing a cortical gate during slow wave sleep. All three mechanisms involve stimulation producing an activation in a cortical area (Fig. 2 A), which propagates to a second cortical area (B). The first mechanism we investigated involves the generation of a local down state. During spontaneous slow wave sleep, cortex is bistable, alternating between active depolarized periods and silent hyperpolarized phases (Steriade et al. 2001). During the active phase, network activity leads to the gradual depletion of synaptic vesicle pools, resulting in synaptic depression, and a progressive increase of an activity-dependent potassium current, producing a hyperpolarizing drive on neurons (Bazhenov et al. 2002; Compte et al. 2003; Hill and Tononi 2005). Eventually, these two factors build up sufficiently to drive the network into a hyperpolarized down state, which is a reflection of cortical bistability during slow wave sleep. It is possible that an activation in cortex (Fig. 2Ci) will increase local firing, engaging the same mechanisms that produce a spontaneous slow wave (Di) to produce a local down state (Ei). This down state would be associated with hyperpolarization of the membrane potential, reducing responses to input and thus diminishing signal propagation (Fig. 2, F and G).

FIG. 2.

Schematic showing 3 possible mechanisms that could produce a cortical gate. In each of these scenarios, transcranial magnetic stimulation (TMS) is envisioned as producing an activation in 1 cortical area (A and B). One of 3 possible mechanisms (C–E) then greatly diminishes the propagation of the evoked activity to other cortical areas (F and G). The mechanisms illustrated here are tested in our thalamocortical network.

A second mechanism we investigated involves changes to intrinsic channel conductances in slow wave sleep. During slow wave sleep, due to the reduction in the levels of arousal promoting neuromodulators, the conductance of a variety of potassium channels increases (Madison et al. 1987; McCormick 1992). Therefore although a synaptic activation would be produced in the second cortical area (Fig. 2Cii), the influence of this activation would be reduced by the large hyperpolarizing drive produced by the increased potassium channel conductance (Dii). This in turn would reduce the excitability of cortical neurons (Fig. 2Eii) and could possibly reduce the propagation of activity to further cortical areas (F and G).

A third mechanism is mediated by changes to excitatory and inhibitory synaptic efficacy during sleep. It has recently been shown that a decrease of acetylcholine levels, as happens during slow wave sleep, produces an increase of per spike glutamate release by ∼33% (Gil et al. 1997) while more than doubling GABA release (Salgado et al. 2007). It is possible that when activation reaches the second cortical area (Fig. 2Ciii), the firing of local inhibitory neurons produces a strong inhibitory influence on the network due to this increase in the ratio of synaptic inhibition to excitation (Diii). This would then diminish local neuronal responses (Fig. 2Eiii) and decrease the further propagation of activity (F and G).

Testing the capacity of candidate mechanisms to produce a cortical gate

The most direct evidence to date of a cortical gate in humans is provided by EEG data indicating that a cortical perturbation produced by TMS will propagate to different cortical areas in waking but not in sleep (Massimini et al. 2005). In our model, we reproduced such measurements by simulating TMS delivery to cortical area C1 and examining the responses in simulated EEG traces from each cortical area. We employed this basic technique to test the capacity of the three mechanisms discussed in the preceding text to limit the propagation of activity evoked in C1 to other areas in the model.

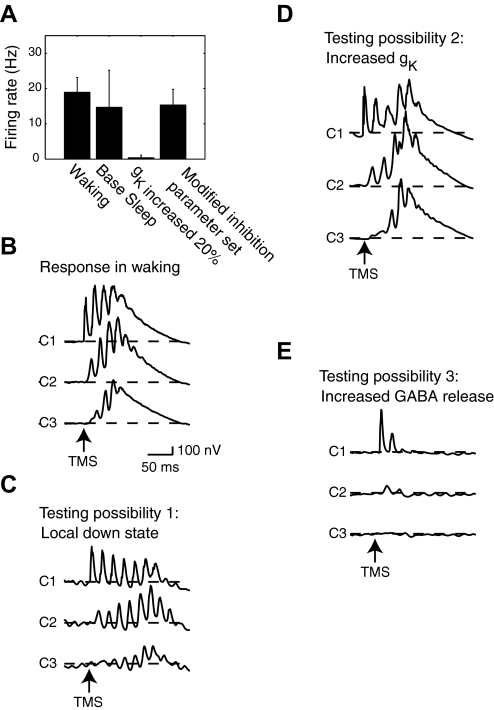
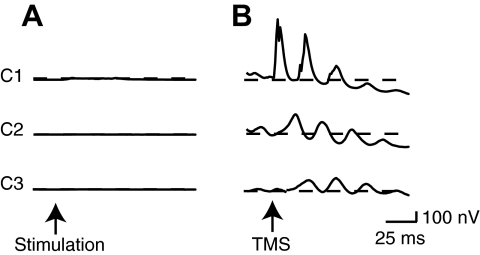
We first examined the model's waking mode, which showed robust spontaneous activity and firing rates of 18.9 ± 4.2 (SD) Hz in all cortical neurons (Fig. 3 A). When we simulated the delivery of moderate intensity TMS, which activated 30% of all vertically oriented fibers in C1 (defined as strength 30%, see methods) in this mode, an activation was initially produced in C1 (Fig. 3B). The evoked activity from C1 propagated between all cortical areas with initial peaks in the EEG response occurring at 15.4, 28.7, and 43.4 ms and with an amplitude increase of 506.6, 271.1, and 145.6 nV over baseline in areas C1–C3, respectively. EEG activity in cortex returned to baseline levels with a latency of 241.7, 241.8, and 246.2 ms in areas C1–C3, respectively. Stronger TMS pulses produced similar responses that showed propagation through all three cortical areas (not shown).

FIG. 3.

A: firing rates from all cortical neurons. B: TMS (strength, 30%) delivered during the model's waking mode produces activity that propagates and reverberates among all 3 cortical areas. C: TMS (strength, 30%) delivered to C1 does not produce a local down state prior to the propagation of activity through all 3 cortical areas. D: when cortical potassium channel conductance was increased by 20% in the model's sleep mode, TMS delivered to C1 (strength, 30%) produced activation that propagated through all 3 cortical areas (middle). E: an increase in GABA release (using the modified inhibition parameter set) disrupts the propagation of activity through the network.

During the model's sleep mode, using the base sleep parameter set, we next examined the possibility that a local down state might block interareal signal transmission. In this sleep mode, the model produced robust firing in all cortical neurons (14.7 ± 10.5 Hz; Fig. 3A). When we then simulated a moderate strength TMS pulse (30% strength), we did not observe the generation of a local down state (Fig. 3C). Following this stimulation, the maximum EEG increase from baseline for areas C1–C3 was 405.3, 367.4, and 241.1 nV, respectively, and the first peak in the EEG had a latency of 10.2, 23.2, and 33.3 ms in C1–C3, respectively. These peaks occurred on the same approximate time scale as the propagation of TMS-evoked activity between nearby cortical areas in the human brain (Massimini et al. 2005) and indicate a propagation of activity that is fast compared with the time required for the development of a cortical downstate. Specifically, slow waves evoked in vivo by sensory stimulation, called K-complexes, typically require several hundred milliseconds to develop (Colrain 2005) as do global slow waves evoked by specific types of TMS stimulation (Massimini et al. 2007). We also found that TMS delivered at higher intensities (≤100% strength) did not produce a local downstate (not shown). Thus it seems unlikely that a TMS-evoked local down state would occur rapidly enough to diminish initial waves of propagation in cortex.

Next we examined the capacity of increased potassium channel conductance to reduce effective connectivity in cortex. We simulated the response to TMS (strength, 30%) under multiple conditions, using the base sleep parameter set but with progressively greater cortical potassium channel conductances. We found that increasing potassium channel conductances by 20% from normal sleep levels had the effect of greatly disrupting normal cortical firing, reducing excitatory cell firing rates to 0.4 ± 0.7 Hz (Fig. 3A). When TMS was simulated under these conditions, activity still propagated between cortical areas, with peak EEG activations of 694.0, 912.3, and 735.6 nV in C1–C3, respectively (Fig. 3D). We found that increasing potassium channel conductances to 25% of normal sleep levels was able to reduce the propagation of activity between areas although this also eliminated spontaneous firing in cortex. Thus it appears that an increase in intrinsic channel conductance is not able to produce a cortical gate without also drastically reducing spontaneous activity in the network.

Finally, we tested whether a change to inhibitory and excitatory synaptic efficacy was capable of producing a cortical gate. For this, we increased cortical GABA release and increased the conductance of potassium channels on inhibitory neurons, using the modified inhibition parameter set described in methods. Increasing the conductance of inhibitory cell potassium channels in the model's sleep mode decreased inhibitory cell firing so that even though each inhibitory spike was more powerful, the total inhibition affecting the network remained at normal levels and allowed for robust spontaneous activity (as described in detail in the following text). When we simulated TMS (strength, 30%) under these conditions, activation was produced in area C1, while propagation to C2 was markedly reduced, and there was almost no propagation to C3 (Fig. 3D). The maximum EEG response compared with baseline for areas C1–C3 was 498.4, 91.3, and 2.9 nV. The initial peak activations in these areas had latencies of 12.6, 23., and 35.7 ms, respectively. Spontaneous activity in this sleep mode also showed robust firing of all cortical neurons (15.3 ± 4.4 Hz; Fig. 3E). These simulations suggest that an increased per spike release of GABA is capable of producing a cortical gate. We observed a similar response when multiple stimuli were delivered with a period of 2–2.3 s as in Massmini (2005) (data not shown). We investigate this mechanism in detail in the following text.

High levels of spontaneous activity are maintained in the presence of increased GABA release in the model's sleep mode

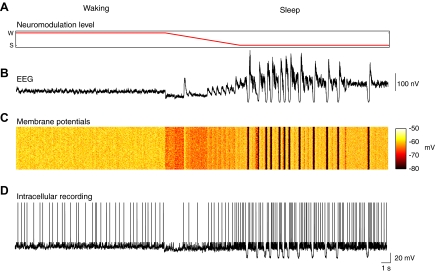
Unless otherwise noted, for the remainder of simulations of the sleep mode in this paper, the modified inhibition parameter set was used. We examined spontaneous activity in the model by allowing it to run freely without stimulation. We ran the model in its waking mode for 16 s (Fig. 4 A), during which time we observed low-voltage fast activity in the simulated EEG (Fig. 4B) and robust activity in individual neurons (Fig. 4, C and D). We then decreased the levels of arousal promoting neuromodulators in the system over the course of 8 s (Fig. 4A) until the sleep mode was reached as marked by the appearance of high-amplitude slow waves and then allowed it to run freely for an additional 16 s. The sleep mode showed sporadic slow waves in the simulated EEG (Fig. 4B), which occurred in conjunction with oscillations between hyperpolarized and depolarized states in single cells (Fig. 4, C and D). These EEG and single-cell activity patterns are comparable to those observed in vivo during wakefulness and natural sleep (Steriade et al. 2001). The average neuronal membrane potential in cortex was −60.0 ± 0.3 mV in waking and −63.9 ± 6.2 mV in sleep. These values are comparable to what has been observed in previous versions of this model (Esser et al. 2005; Hill and Tononi 2005) and to those observed in vivo (Steriade et al. 2001).

FIG. 4.

Signals recorded from area C1 of the thalamocortical model while the simulated levels of arousal promoting neuromodulators are decreased, producing a transition from waking to sleep. A: the level of arousal promoting neuromodulation, which is gradually decreased from waking to sleep levels during the simulation. B: an electroencephalographic (EEG)-like recording showing the transition from low-voltage fast activity to slow wave like behavior. C: the membrane potential of 100 excitatory cells in L2/3. D: an intracellular-like recording of the membrane potential from a typical L2/3 excitatory cell.

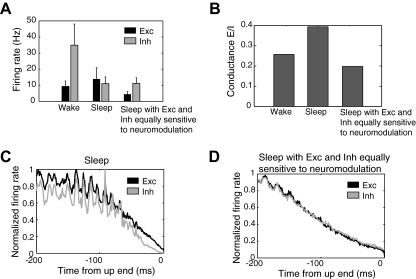
To better understand spontaneous activity in the model, we examined firing rates of all cortical neurons during the 16-s periods of spontaneous waking and sleep from the above simulation. Average spontaneous firing of cortical excitatory cells increased on transition from the waking to the sleep mode, from 9.3 ± 3.6 to 16.3 ± 11.1 Hz, while there was a decrease in the spontaneous firing of cortical inhibitory cells from 34.9 ± 7.7 to 15.1 ± 11.5 Hz (Fig. 5 A). Similar firing rate values have been observed in previous versions of this model (Esser et al. 2005; Hill and Tononi 2005) and in vivo (Rudolph et al. 2007; Steriade et al. 2001). Thus even though GABA release is increased in the model's sleep mode, the decrease in spontaneous inhibitory neuronal firing rates kept overall levels of GABA conductance comparable to those observed in waking, thus allowing for robust cortical activity. Indeed when we measured synaptic conductance in all cortical neurons, we found that the ratio of excitatory to inhibitory synaptic conductance changed minimally during the sleep mode (Fig. 5B). A similar preservation of the ratio of excitatory and inhibitory synaptic conductance between waking and sleep has been observed in vivo (Rudolph et al. 2007).

FIG. 5.

A: spontaneous firing rates of excitatory and inhibitory cortical neurons during waking, sleep, and sleep with inhibitory cells showing the same sensitivity to arousal promoting neuromodulation as excitatory cells. B: the excitatory to inhibitory conductance ratio during spontaneous waking for all cortical excitatory cells in the wake mode, sleep mode, and sleep with equal sensitivity of excitatory and inhibitory cells to arousal promoting neuromodulation. The firing rates of excitatory and inhibitory neurons during sleep relative to the end of the up state are depicted for the sleep mode (C) and sleep with inhibitory cells showing the same sensitivity to arousal promoting neuromodulation as excitatory cells (D).

Inhibitory cells were last active during spontaneous activity in the model's sleep mode because inhibitory neurons were simulated as having greater sensitivity to changes in acetycholine levels than excitatory neurons and as having higher potassium channel conductances than excitatory cells in the sleep mode (see methods). To investigate the importance of the resulting increased hyperpolarizing drive on inhibitory cells compared with excitatory cells, we tested what would happen if inhibitory cells were instead stimulated as having the same sensitivity to changes in neuromodulation as excitatory cells (with g_KLeak = 0.383, g_KS = 4, and g_DK = 0.429 for cortical inhibitory cells). We found that this produced a substantial decrease in the firing of excitatory neurons and a decrease in the ratio of excitatory to inhibitory conductance compared with waking (Fig. 5, A and B).

We next examined how the differences in acetylcholine sensitivity between excitatory and inhibitory cells affected firing rates over the course of the up state. When we examined firing rates during the up states of all slow waves during a 16-s period, we observed that inhibitory neurons left the upstate more rapidly than excitatory cells during normal sleep, decreasing to 10% of wave maximum firing rates 21.0 ms more rapidly than excitatory cells (Fig. 5C). When inhibitory neurons experienced the same sensitivity to acetylcholine as excitatory cells, excitatory cells reached 10% of wave maximum firing rates 2.6 ms before inhibitory cells (Fig. 5D). This suggests that the greater hyperpolarizing drive of potassium channels on inhibitory neurons during the sleep mode causes them to exit the up state more rapidly than excitatory cells. Intriguingly, this difference in excitatory and inhibitory neuronal firing over the course of the up state has been noted in vivo (Haider et al. 2006).

Cortical gate produced by increased GABA release is effective regardless of slow wave phase

Figure 3D shows the response to TMS delivered in a period between slow waves. We observed similar responses if TMS was delivered during a slow wave. If TMS (strength, 30%) was delivered immediately prior to a down state, the first peak in the EEG response had an amplitude relative to baseline in C1 and C2 of 513.1 and 97.7 nV and a latency in these areas of 10.7 and 22.1 ms, respectively (Fig. 6 A). If TMS (strength, 30%) was delivered during a down state, the initial EEG responses in C1 and C2, respectively, had amplitudes of 352.0 and 136.1 nV and latencies of 8.1 and 19.9 ms (Fig. 6B). If TMS (strength, 30%) was delivered immediately following a downstate, the initial response in C1 and C2, respectively, had amplitudes of 608.1 and 114.4 nV and showed latencies of 9.8 and 20.4 ms (Fig. 6C). No discernible peaks were observed in C3 following any of these stimulations. Thus the model predicts that interareal signal transmission should be reduced during slow wave sleep whether during the downstate of a slow wave or during an upstate (Fig. 6D).

FIG. 6.

A simulated TMS pulse was delivered to C1 on entry into a downstate (A), during the middle of the downstate (B), or on exit from the downstate (C). For comparison purposes, the response to TMS delivered to C1 during an upstate is also depicted (D). The EEG from all 3 cortical areas is depicted to show the response evoked by this stimulation.

Cortical gate produced by increased GABA release is effective following high-intensity stimulation

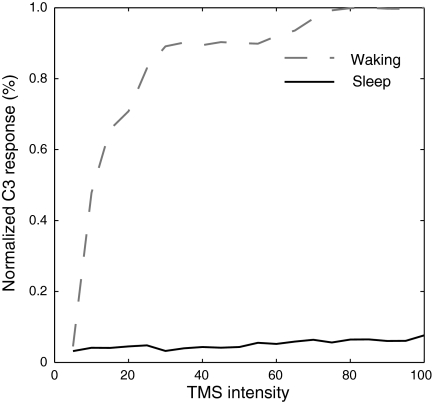
To investigate how the response to TMS changes with stimulus intensity, we simulated TMS at intensities from 5 to 100% in intervals of 5% in the model's waking and sleep mode. We then summed across time the rectified EEG in C3 from 25 to 100 ms after TMS was delivered to C1 and normalized this response to the maximum observed across conditions, thus allowing us to determine the extent activity propagated through the network (Fig. 7). During wakefulness, this response showed distinct dose dependence, growing rapidly and saturating near 75% stimulus strength. During sleep, the response in C3 changed minimally with increasing stimulus strength. Thus the model predicts that the cortical gate is effective at reducing the propagation of activity evoked at a variety of stimulus intensities, including very strong stimulation.

FIG. 7.

Dose response curve of the EEG response evoked in area C3 following simulated TMS delivery to C1 in waking and in sleep. The curve shows summed rectified EEG activity in C3 in the time period of 25–100 ms following TMS, normalized to the maximum response observed.

Cortical gate produced by increased GABA release is effective at a variety of increased GABA levels

We also investigated how the response to TMS changed if the levels of per spike GABA release were varied from those used in the modified inhibition parameter set. Specifically, we simulated the response to TMS delivered to C1 with per spike GABA release set in increments of 10% between 50 and 150% of levels in the modified inhibition parameter set. We found that activity was able to propagate between cortical areas with GABA release at 70% of levels in the modified inhibition parameter set (initial peaks following TMS occurring in the simulated EEG with amplitude of 1398.1, 772.2, and 640.3 nV in C1–C3, respectively). For per spike GABA release levels at 80% of those in the modified inhibition parameter set or greater, interareal activity propagation was greatly reduced (with GABA release at 80% levels, initial peaks in the simulated EEG occurred with latency of 965.1, 370.5, and 45.8 nV in C1–C3, respectively).

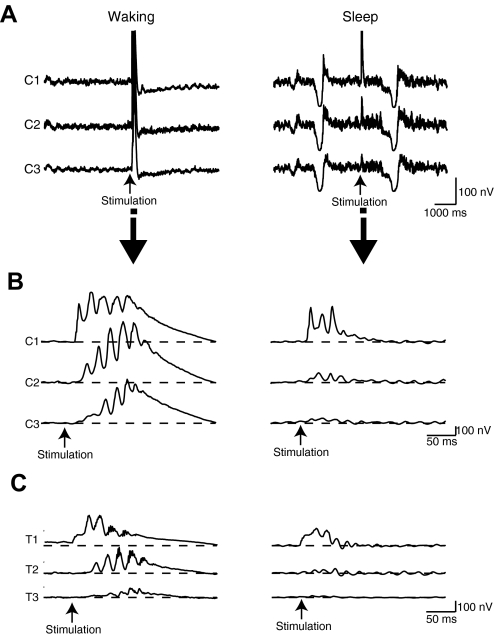
Increased GABA release reduces propagation between cortical areas of sensory-evoked activity

In addition to examining how the model's response to direct cortical stimulation changes during slow wave sleep, we were also interested in how the model's response to peripheral stimulation changes. While our model was not designed to specifically represent a particular sensory system, each thalamic area receives subcortical input, which can be used to approximate brain stem or optic nerve activity. Therefore we simulated the application of a peripheral stimulus by setting the firing rates of the area providing subcortical input to T1 to 150 Hz for 50 ms. In the waking mode, this stimulation produced an initial activation in the thalamus with a first peak occurring in T1 at 2.1 ms after stimulus onset, followed by a peak in the C1 EEG with a latency of 19.2 ms and amplitude of 439.0 nV, a peak in the C2 EEG with a latency of 31.8 ms and amplitude of 216.8 nV and a peak in the C3 EEG with a latency of 40.0 ms and amplitude of 107.3 nV as activity reached cortex and propagated among the cortical areas (Fig. 8, A–C, left). During the sleep mode, the stimulation produced an initial activation in the thalamus at 8.6 ms, with a subsequent activation in the C1 EEG occurring at 21.1 ms with an amplitude of 384.4 nV, followed by a small peak occurring in C2 at 35.9 ms with amplitude 93.5 nV, then a peak in C3 at 43.2 ms with amplitude 39.9 nV, which was barely above baseline EEG levels (Fig. 8, A–C, right). Thus an increased release of GABA with each spike during slow wave sleep can account for reduced propagation of activity between cortical areas, regardless of whether that activity is initially evoked through direct cortical perturbation or sensory stimulation.

FIG. 8.

EEG-like response in all cortical areas to peripheral stimulation delivered to C1. In the model's waking mode, activity propagates through all three cortical areas and reverberates for tens of milliseconds (A and B, left). During sleep, the propagation of activity from C1 to C2 and C3 is greatly diminished (A and B, right). Thalamic activation can be observed in the wake mode (C, left) and sleep mode (C, right).

Thalamic gate alone is insufficient to reduce interareal signal transmission

We also sought to investigate whether a thalamic gate alone is sufficient to prevent the direct transfer of activity between cortical areas in our model. In the model's sleep mode, we simulated a thalamic gate strong enough to completely block the transfer of an activation produced by a peripheral, sensory-like stimulus into cortex by increasing the depolarization of the thalamic reticular nucleus (NRT g_Na = 3.0, g_K = 0.2) and increasing the hyperpolarization of thalamic cells (T g_t = 0.0, g_K = 2.5). It should be noted that such a strong thalamic gate is an extreme case we used for this demonstration and is not intended to reflect the thalamic gate present during normal sleep. In the presence of this strong thalamic gate, we simulated the application of a peripheral stimulus by setting the firing rates of the area providing subcortical input to T1 to 150 Hz for 50 ms. We found that this completely prevented activity from reaching cortex (Fig. 9 A). When we simulated delivery of a moderate strength TMS pulse (strength, 30%), we found that this produced an activation that was able to propagate between the three cortical areas, producing initial peaks in the simulated EEG with latencies of 4.6, 19.2, and 31.3 ms and amplitudes of 743.7, 229.6, and 155.7 nV in C1–C3, respectively (Fig. 9B). Thus a thalamic gate strong enough to completely isolate our simulated cortex from sensory stimulation still allowed signal transmission between cortical areas.

FIG. 9.

EEG-like traces are depicted for all cortical model areas during simulation of a strong thalamic gate. Under these conditions, a peripheral stimulation is unable to reach cortex (A) while TMS delivered to C1 produces an activation that propagates to C2 and C3 (B).

DISCUSSION

Model reproduces in vivo results that demonstrate a breakdown of effective connectivity during slow wave sleep

In this work, we employed a large-scale model of the thalamocortical system that was built based on previous work (Esser et al. 2005; Hill and Tononi 2005) and incorporates basic principles of thalamocortical architecture, cellular and synaptic physiology, and the influence of various arousal promoting neuromodulators. By reducing the levels of these neuromodulators, the model can reproduce sleep patterns from the network to single cell level, as reflected in simulated EEG and membrane potential traces. Due to our focus on evoked responses during slow wave sleep, provisions were not made for simulating other phenomena of spontaneous sleep, such as sleep spindles.

Using this model, we were able to reproduce experiments conducted in vivo demonstrating reduced effective connectivity during slow wave sleep. Specifically, it has been shown that for many brain areas in vivo, a TMS pulse will produce a local activation that propagates rapidly through a functionally connected network of brain areas during waking, showing initial EEG peaks, corresponding to activations of different cortical regions, at 10, 23, and 51 ms (Massimini et al. 2005). During slow wave sleep in vivo, such activations briefly reverberate in a local circuit, showing initial peaks occurring at 10 and 36 ms (Massimini et al. 2005). In the model, simulated TMS produces an activation in the targeted that propagates among all three areas in the model's waking mode but not in its sleep mode with peak's in the simulated EEG occurring with latencies comparable to those observed in vivo (see results).

It has also been shown in vivo that the propagation of sensory-evoked activity from primary to higher-order areas is reduced in slow wave sleep (Deiber et al. 1989; Kakigi et al. 2003; Kitamura et al. 1996; Portas et al. 2000). In our model, a peripheral stimulation that propagates to cortex via the specific thalamic pathway produces an initial activation in that cortical area, which propagates to the other two simulated areas in the model's waking mode but not in its sleep mode.

Cortical gate can explain the reduced propagation of evoked activity during slow wave sleep

We postulate here the existence of a cortical gate that reduces the intercortical propagation of activity during slow wave sleep. This builds on the classic notion of a thalamic gate, which is believed to partially reduce the propagation of sensory-evoked activity through thalamus to cortex (Steriade et al. 1990). We believe that by attenuating the propagation of activity through cortex, this cortical gate is able to account for the dramatically different responses the brain shows to stimulation in slow wave sleep compared with wakefulness. The thalamic gate and the cortical gate may serve complementary roles during slow wave sleep. While the thalamic gate is capable of reducing sensory input to cortex, it is unable to reduce the direct propagation of activity between cortical areas. The cortical gate might serve a role in reducing such direct interareal signal transmission, thereby disrupting activity that reaches cortex through the thalamic gate or that arises intrinsically during sleep.

We further wish to note that the cortical gate we propose here is different from cortical gating that has been suggested to occur as a result of the down state during the sleep slow wave (Rosanova and Timofeev 2005). While the slow wave down state certainly is likely to reduce propagation of evoked activity through the network due to the high degree of neuronal hyperpolarization present during this state, the cortical gate we propose involves a distinct mechanism that is effective regardless of whether the network is in an up state or a down state.

Mechanism underlying the cortical gate

Using our model, we tested three mechanisms that might be capable of producing a cortical gate. The first possibility we examined was that TMS produces a local down state that blocks the propagation of activity to other areas. However, we found that the propagation of activity between cortical areas occurs on a faster time scale than the development of a cortical down state. We next examined the possibility that increased conductance of potassium channels during slow wave sleep (Madison et al. 1987; McCormick 1992) reduces neuronal responsiveness. We found that high potassium channel conductances indeed were capable of blocking the propagation of activity between cortical areas, but in doing so they reduced spontaneous firing rates in cortex to levels much lower than those observed in vivo. The final possibility we examined was that increased per spike GABA release during slow wave sleep (Salgado et al. 2007) decreases the ratio of synaptic excitation to inhibition during an evoked response. We found that such a mechanism did reduce signal propagation between cortical areas in a fashion that left normal spontaneous activity intact.

Thus we propose that a cortical gate is formed during slow wave sleep due to the increased per spike release of GABA. When acetylcholine levels decline in cortex, as happens during slow wave sleep, glutamate release increases by about a third (Gil et al. 1997) while per spike GABA release can more than double (Salgado et al. 2007). This increases the ratio of synaptic inhibition to excitation evoked by activity propagation to a given area. This will limit firing in the cortical area in question, diminishing signal transmission through cortical circuits. We showed that this cortical gate is able to disrupt signal transmission whether the initial perturbation arises from direct perturbation of cortex or through transthalamic sensory-like pathways.

During spontaneous slow wave sleep, increased per spike GABA release on its own would be expected to increase inhibition and to produce a substantial decline in activity. However, in slow wave sleep in our model, as well as in vivo, it has been demonstrated that excitatory firing rates are comparable to those during waking, but that spontaneous inhibitory firing rates decline (Rudolph et al. 2007; Steriade et al. 2001). The total synaptic inhibitory influence on a network corresponds to per spike GABA release levels multiplied by firing rates, so this decrease of inhibitory cell firing likely allows a similar ratio of excitatory and inhibitory synaptic conductance, as suggested by our model and work in vivo (Rudolph et al. 2007). This in turn allows the network to generate robust spontaneous activity during slow wave sleep. The decreased firing of inhibitory neurons during slow wave sleep arose in the model due to greater sensitivity to the influence of arousal promoting neuromodulators of inhibitory cells compared with excitatory cells, leading to higher levels of potassium channel conductance in inhibitory cells in the sleep mode. Such a mechanism was implemented in the model based on the greater frequency of acetylcholine receptors on inhibitory neurons, making them more susceptible to decreases in this neuromodulator during sleep (Disney et al. 2006). Furthermore, it has been observed that the conductance of potassium channels is higher in inhibitory neurons than excitatory neurons in the absence of various neuromodulators such as acetylcholine (Hamill et al. 1991). We observed in the model that the increased neuromodulation sensitivity in inhibitory cells resulted in these neurons leaving the up state prior to excitatory cells. Such a difference in excitatory and inhibitory firing patterns has been observed in vivo (Haider et al. 2006). In general, we thus observed that increased potassium channel conductance, while not directly reducing signal transmission in slow wave sleep, may play an important role in maintaining balanced spontaneous activity in this state.

Mechanisms other than those examined here may also be capable of producing a cortical gate during slow wave sleep, although they seem less likely than the possibilities tested here. For example, it has been shown that neuronal input resistance is lower in the up state of slow wave sleep compared with wakefulness (Rudolph et al. 2007), which would produce a reduction in postsynaptic potential amplitude. However, the change in input resistance shown by Rudolph et al. (2007) is relatively small and its effect on post synaptic potential amplitude is likely offset largely by the increased release of glutamate expected in slow wave sleep (Gil et al. 1997).

It is of course not feasible to perform a comprehensive analysis of the parameter space involved in determining our results due to the large number of parameters used in our simulation. However, in the course of performing our simulations, we found that small changes to parameter values did not substantially affect our primary result, the reduction of interareal signal transmission during slow wave sleep. In particular, we found that reductions to a key parameter value in the model, the level of per spike GABA release, did not substantially affect interareal signal transmission until levels were reduced <80% of those used in the modified inhibition parameter set. Increasing GABA release levels produced no change in interareal signal transmission for ≤150% of levels used in the modified inhibition parameter set.

Limitations of the cortical gate

There are clear limitations to the types of activity affected by such a cortical gate. Sleep slow waves have been shown to synchronize and travel across cortical areas (Massimini et al. 2004; Murphy et al. 2009). Thus the cortical gate may work somewhat like a low-pass filter, allowing slow, widespread activity to propagate through the brain, while blocking the propagation of focal fast perturbations. Widespread activation across the brain can also of course be produced if many cortical areas simultaneously receive input. For example, slow wave activity can be increased across the brain through constant application of a slowly oscillating electric field (Marshall et al. 2006). Also strong peripheral stimuli, which are believed to activate subcortical structures that project diffusely throughout the brain, are able to elicit large responses throughout much of cortex known as K-complexes (Colrain 2005). Furthermore, TMS delivered to centro-parietal brain areas has been shown to evoke a global, slow wave like response (Massimini et al. 2007), which may also occur through some form of synchronous global activation. It is our intention to investigate the specific mechanisms by which such global responses can be evoked in a subsequent paper.

In addition to direct corticocortical signal transmission, interareal communication may be mediated partially through a cortico-thalamocortical route that involves thalamic cells receiving input from one cortical area and projecting to a higher-order cortical area, as proposed by Guillery and Sherman (Sherman and Guillery 1996; Sherman et al. 2006). The existence of such cortico-thalamocortical pathways is still being debated, and their contribution to overall communication between cortical regions is unknown. Due to this uncertainty, we did not include such a pathway in the model. However, it is possible that if this pathway does contribute substantially to interareal communication, then changes to the thalamus during slow wave sleep could disrupt interareal signal transmission in addition to the cortical gate proposed here.

Implications of the cortical gate

What functional role might the cortical gate serve? The cortical gate produces disconnection from the environment and blocks strong internal signaling. By reducing cortical responsiveness to peripheral stimuli, such a gate may work in conjunction with a thalamic gate to help to maintain sleep by preventing arousal to certain stimuli.

Recent work has suggested that sleep may be important for learning and memory. One body of research has suggested that sleep plays a role in memory consolidation through a reactivation of memory traces learned during wakefulness (Born et al. 2006; Buzsaki 1998; Sejnowski and Destexhe 2000; Walker and Stickgold 2006). Reactivation, if left unchecked, could lead to a hyperactive and possibly seizure like state in the brain. The cortical gate may play a role in keeping reactivations contained to the most relevant cortical circuits. Sleep has also been proposed to play a role in homeostatic regulation of synaptic strength, which requires testing the strength of all synapses impinging on a given neuron to effect appropriate adjustments (Tononi and Cirelli 2003, 2006). This might be achieved by random firing in cortical circuits during the slow wave up state that would produce an activation of a random selection of each neuron's inputs. A cortical gate may contribute to this mechanism in two ways. First, testing synaptic efficacy through random neuronal firing may carry the risk of producing seizure like activity. A cortical gate would reduce the spread of such activity to other areas and could help to diminish it if it begins. Second, as demonstrated, the mechanism proposed here to underlie a cortical gate does not disrupt normal spontaneous activity but does prevent the propagation of strong waves of firing. The cortical gate would thus prevent large networks of correlated, highly active neurons from developing and so help to maintain random spontaneous firing in the network.

The cortical gate may be involved in the fading of consciousness observed during early slow wave sleep. A recent theory has proposed that the capacity to integrate information is crucial to consciousness and that such integration requires a high degree of effective connectivity among disparate thalamocortical areas (Tononi 2004). By reducing effective connectivity, the cortical gate produces a clear reduction of integration and therefore may be directly responsible for the loss of consciousness that occurs during early slow wave sleep and, presumably, in the loss of consciousness that occurs during anesthesia (Alkire et al. 2008).

Future directions

It is clear that further research is needed to validate the role of increased GABA release in producing a cortical gate during sleep. At the moment, the sensitivity of GABA release to acetylcholine has only been measured in auditory cortex (Salgado et al. 2007), although other groups have observed that activation of muscarinic receptors can decrease the amplitude of inhibitory postsynaptic potentials in neostriatum (Koos and Tepper 2002) and hippocampus (Haas 1982; Valentino and Dingledine 1981). Furthermore, acetylcholine may have different effects in different cortical areas, raising the possibility that different brain regions show different levels of gating. Measurements of an increase in GABA release in response to a decrease in acetylcholine levels in other cortical areas would support the possibility a cortical gate is a cortex wide phenomenon during sleep. If this is indeed the case, the model predicts that local applications of cholinergic agents during sleep should increase the propagation of evoked activity through the targeted areas. Furthermore, while a per spike decrease of GABA release has been observed following a decrease of acetylcholine (Salgado et al. 2007), and acetylcholine levels are known to decrease on transition to slow-wave sleep, changes in per spike release of GABA have not been directly measured in slow wave sleep. We suggest that improving techniques in microdialysis and fixed-potential amperometry might make this possible.

GRANTS

This work was supported by National Research Service Award F31 NS555533 to S. K. Esser.