Weighted Feature Significance: A Simple, Interpretable Model of Compound Toxicity Based on the Statistical Enrichment of Structural Features

Abstract

In support of the U.S. Tox21 program, we have developed a simple and chemically intuitive model we call weighted feature significance (WFS) to predict the toxicological activity of compounds, based on the statistical enrichment of structural features in toxic compounds. We trained and tested the model on the following: (1) data from quantitative high–throughput screening cytotoxicity and caspase activation assays conducted at the National Institutes of Health Chemical Genomics Center, (2) data from Salmonella typhimurium reverse mutagenicity assays conducted by the U.S. National Toxicology Program, and (3) hepatotoxicity data published in the Registry of Toxic Effects of Chemical Substances. Enrichments of structural features in toxic compounds are evaluated for their statistical significance and compiled into a simple additive model of toxicity and then used to score new compounds for potential toxicity. The predictive power of the model for cytotoxicity was validated using an independent set of compounds from the U.S. Environmental Protection Agency tested also at the National Institutes of Health Chemical Genomics Center. We compared the performance of our WFS approach with classical classification methods such as Naive Bayesian clustering and support vector machines. In most test cases, WFS showed similar or slightly better predictive power, especially in the prediction of hepatotoxic compounds, where WFS appeared to have the best performance among the three methods. The new algorithm has the important advantages of simplicity, power, interpretability, and ease of implementation.

Accurate and efficient assessment of the potential toxicity of drugs in development and environmental chemicals remains a significant scientific challenge (Collins et al., 2008; Kola and Landis, 2004). Predictive computational models can complement experimental approaches for prioritizing and focusing toxicity testing and may therefore decrease the time and cost associated with testing as well as reducing or replacing the need for animal-based studies (Pritchard et al., 2003). Descriptor-based quantitative structure-activity relationship (QSAR) models (Hansch and Fujita, 1964) have been commonly used for toxicity prediction (Mohan et al., 2007). The quality of these models depends on the mathematical approach, the molecular descriptors for the particular toxicity end point, and the quality of the data used to develop the model (Pohjala et al., 2007). The predictive value of a QSAR model is often limited by the nature of the compounds used in model development, and such models frequently work well only on small sets of structurally related compounds and a single defined toxicity target. Toxicological data from more diverse noncongeneric compound series are required to develop models with more general predictive value (Schultz et al., 2001).

Chemical toxicity often originates from interactions between certain functional groups and physiologically important biological targets. Some functional groups have been demonstrated to react chemically with biopolymers and serve as structural alerts for potential toxicity (Evans et al., 2004; Guengerich, 2005; Guengerich and MacDonald, 2007; Kalgutkar et al., 2005; Nelson, 1994). In this context, fragment-based QSAR models have been developed in an effort to identify biologically active substructures (toxicophores) responsible for toxicity (Casalegno et al., 2006; Perez Gonzalez et al., 2003; Toropov and Benfenati, 2006). Unlike descriptor-based QSAR models, which are holistic approaches, fragment-based toxicophore methods investigate structure-activity relationships at the substructural level, allowing more precise relationships between structures and toxic effects to be defined. The toxicophores are then used to predict potential toxicity in other compounds, on the assumption that substances containing the same toxicophore are likely to cause similar toxic effects. These models have been used to predict pesticide toxicity for small sets of compounds and have shown reasonable predictive values (Casalegno et al., 2006). Some commercial efforts have also been made to generalize this approach to other problems in toxicity (Enslein et al., 1994; Klopman, 1984; Klopman, 1992; Klopman et al., 2004; Sanderson and Earnshaw, 1991; Smithing and Darvas, 1992; Woo et al., 1995), although these systems have been shown to have limited prognostic utility (Guengerich and MacDonald, 2007).

Two of the biggest challenges faced by computational modeling for toxicity prediction are the diversity of compound structural space and the multiplicity of structures that can produce the same toxicological outcome. Traditional modeling methods rely heavily on structural similarity for activity prediction and have difficulty with structurally diverse compounds (i.e., these models often cannot be extended to structurally unrelated compound sets). At the same time, chemical similarity is not very predictive of biological responses, particularly in the area of toxicology (Martin et al., 2002). There are usually multiple groups of molecules that can affect the same target or generate the same toxicity, and structurally unrelated compounds may produce the same toxicity via different mechanisms (Guengerich and MacDonald, 2007). It is therefore difficult for similarity-based models to recognize structurally distinct compounds as toxic without compromising model specificity.

We have developed a new fragment-based approach to modeling toxicity that was designed to alleviate the problem of having to rely on whole molecule similarity for toxicity prediction, allowing our model to achieve good performance with structurally diverse sets of compounds. Models were developed for four different toxicity end points including in vitro cytotoxicity measured by cell viability (Xia et al., 2008) and caspase-3,7 induction (Huang et al., 2008) in different cell types, Salmonella typhimurium mutagenicity (Ashby and Tennant, 1991) as well as hepatotoxicity (Collins et al., 2008). The performances of all models were rigorously assessed using receiver operating characteristic (ROC) curves (Schoonjans, 2005). In addition, to evaluate the external validity of the cytotoxicity model, we used it to predict the cytotoxicity of an independent set of compounds from the U.S. Environmental Protection Agency (EPA), which included structures that were distinct from those in the training set provided by the National Toxicology Program (NTP). Following computational prediction, the EPA compounds were tested experimentally to assess predictive accuracy. Model performance was also compared with two standard classification algorithms: Naive Bayesian and sequential minimal optimization (SMO) (Duda et al., 2000; Platt, 1999). The latter is a high-performance kernel-based classification method (Schölkopf et al., 1999).

MATERIALS AND METHODS

Data Sets

A brief description of each data set is shown in Table 1. Cytotoxicity (Xia et al., 2008) and caspase-3,7 activation (Huang et al., 2008) data used in the training/test sets were generated on 1408 chemicals (1353 unique) supplied by the NTP (PubChem, 2007c) and tested in 13 different cell types representing different human and rodent tissue origins (Xia et al., 2008). The cell types included human embryonic kidney cells (HEK293), human hepatocellular carcinoma cells (HepG2), human neuroblastoma cells (SH-SY5Y and SK-N-SH), human leukemia T cells (Jurkat), human normal foreskin fibroblasts (BJ), human normal lung fibroblasts (MRC-5), human normal vascular endothelial cells (HUVEC), human renal mesangial cells, rat hepatoma cells (H4-II-E), rat primary renal proximal tubule cells, mouse neuroblastoma cells (N2a), and mouse fibroblasts (NIH 3T3). Cytotoxicity data used in the validation test set were generated on an independent set of 1408 compounds (1351 unique) from the EPA (PubChem, 2009). Validation data for the EPA compounds were generated on three kidney cell types: human HEK293 cells, human renal mesangial cells, and rat primary renal proximal tubule cells. For replicated compounds in a collection, the replicate values were averaged such that each unique compound only has one data value. All the normalized cytotoxicity (PubChem, 2007b) and caspase-3,7 (PubChem, 2007a) data obtained for the 13 cell types have been deposited into PubChem (http://www.ncbi.nlm.nih.gov/sites/entrez?db=pcassay, search term “NCGC[sourcename] AND viability AND NIEHS”, or search term “NCGC[sourcename] AND caspase AND NIEHS”).

TABLE 1.

Toxicity Data Sets

Data set	Source	Sample no.	% Toxic	Unique structural feature no.
Cell viability	NCGC/NTP	1408	6.3	2949
Cell viability	NCGC/EPA	1408	7.2	3596
Caspase activation	NCGC/NTP	1408	5.6	2949
Salmonella	NTP	1105	33	2545
Hepatotoxicity	RTECS	1755	6.6	4757

Note. NCGC: National Institutes of Health Chemical Genomic Center.

Based on each chemical's activity in terms of cytotoxicity or caspase-3,7 activation across the 13 cell types, a score was generated for each end point. Briefly, all compounds were tested at 14 different concentrations ranging from 0.23 to 100μM and then designated as classes 1–4 according to the type of concentration-response curve observed (Inglese et al., 2006). Curve classes are heuristic measures of data confidence, classifying concentration responses on the basis of efficacy, number of data points showing above background activity, and the quality of fit. Compounds with concentration-response curve classes of 1, 2, or 3 in these assays were designated as being active with decreasing degree of confidence, and compounds with class 4 curves were considered inactive over the concentration range tested (see Inglese et al., [2006] for a more detailed description of curve classification). Table 2 shows the curve class scoring scheme, where compounds are assigned a score of 0–10 on the basis of curve quality. Using this approach, each compound was assigned a score in each of the 13 cell viability and 13 caspase-3,7 activator screens across the training/test compound sets. For the purposes of this study, a compound was classified as “pan-cytotoxic” or as a “pan-caspase-3/7 activator” if it had an average score of ≥ 5 in the cell viability assays or ≥ 1 in the caspase-3,7 assays. Generally, compounds with class 1 or 2 curves are considered active or cytotoxic and class 3 curves inconclusive because of lower data quality. However, many compounds had bell-shaped curves in the caspase-3,7 activation assays due to cell death at high concentrations, and concentrations greater than the concentration of maximal response were masked for regression purposes (Huang et al., 2008). As a result, these compounds were classified as class 3 but were still reliable actives. Since compounds with class 1 or 2 curves were assigned a score of 5 or above and class 3 compounds were scored between 1 and 4, we chose the score of 5 as the cutoff for activity in the cell viability assays and 1 as the cutoff for activity in the caspase-3,7 assays. The score was averaged across all 13 cell types for the NTP compound collection for which measurements were available from all cell types, and the average scores from the three renal cell types were used for the EPA collection, which was only tested in these three cell types. Of the 1353 unique compounds tested in these two assays, 82 (6%) and 73 (5%) were classified as pan-cytotoxic or pan-caspase-3/7 activation, respectively, using this criteria.

TABLE 2.

Cytotoxicity Scoring Scheme Based on Curve Class

Curve class	Score
1.1	10
2.1	8
1.2	7
2.2	5
Other non-4	2
4	0

Salmonella mutagenicity data on 1105 compounds generated by the NTP were obtained from the Leadscope toxicity databases (Anonymous, 2009; Zeiger, 1996). In this data set, compounds are assigned a score of either 1 or 0, one being positive and zero negative. Of the 1105 compounds tested in this battery, 352 (32%) were defined as mutagenic with a positive score of 1.

Hepatotoxicity data on 1755 compounds extracted from the Registry of Toxic Effects of Chemical Substances (RTECS) database were also obtained from Leadscope (RTECS, 2007). In this database, hepatotoxicity is scored on a categorical scale from 0 to 5. For our modeling exercises, we classified compounds with a score of 4 or 5 as hepatotoxic; this accounted for 105 (6.6%) of the compounds. The purpose of applying relatively stringent criteria for defining toxicity is to ensure data confidence and limit interference from noise in order to build meaningful models.

Modeling Algorithms

Weighted feature significance.

Weighted feature significance (WFS) is a two-step scoring algorithm. In the first step, a Fisher's exact test is used to determine the significance of enrichment for each structural feature in the active compounds compared to the inactive compounds, and a p value is calculated for all the structural features present in the data set. Structural features for each compound set were exported from Leadscope; these fingerprints are used here only as an illustrative example and could be substituted by any other nonproprietary structural fingerprints. If a feature is less frequent in the active compound set than the inactive compound set, then its p value is set to 1. These p values form what we call a “comprehensive” feature fingerprint, which is then used to score each compound for its toxicity potential according to Equation 1, where p_i is the p value for feature i; C is the set of all features present in a compound; M is the set of features encoded in the comprehensive feature fingerprint (i.e., features present in at least one cytotoxic compound); N is the number of features; and α is the weighting factor, which is a constant between 0 and 1. α is normally set to 1 unless otherwise indicated. Cytotoxic compounds are expected to have a high frequency of toxic features and therefore a high WFS score:

(1)

Naive Bayesian and SMO.

These two classical modeling algorithms were applied to the same data sets to compare to the performance of the WFS algorithm. We selected these two algorithms for comparison because they are among the most widely used and successful methods for classification and toxicity prediction (Bahler et al., 2000; Cronin, 2004; von Korff and Sander, 2006). We used the Weka implementation (Witten and Frank, 2000) of these algorithms to perform modeling exercises.

Model Training and Testing

Models were built for each type of response measured in the four different data sets: pan-cytotoxicity using cell viability data from 13 cell types, pan-caspase-3,7 activation using the caspase-3,7 data from the same 13 cell types, Salmonella mutagenicity data, and hepatotoxicity. For each data set, compounds were evenly divided after random shuffling into two groups of approximately equal size, with one designated as training and the other as testing. Models were built using only data generated from compounds in each training set. The model was then applied to predict the response of compounds in the corresponding testing set. In the case of the WFS algorithm, active feature frequencies were computed using data from the training set and WFS scores were calculated using these p values for compounds in both the training and the testing sets. For the validation of the pan-cytotoxicity prediction model, the model was trained on data from the NTP compound collection and applied not only to the NTP test set but also to the EPA collection. The number of compounds identified as true or false positive (TP, active and predicted as active and FP, not active but predicted as active) and true or false negative (TN, not active and not predicted as active and FN, active but not predicted as active) was counted. To assess the overall performance of a model, ROC curves were generated by plotting sensitivity (defined as TP/[TP + FN]) against 1-specificity (defined as TN/[FP + TN]). The area under the ROC curve (AUC) is a rigorous measure of the predictive power of the model. A maximum AUC is 1, which occurs when a model is 100% accurate. A model with an AUC of 0.5 indicates that applying the model is no different than picking compounds at random. A model with an AUC of 0.7 is generally considered as reasonably predictive.

RESULTS

Modeling Cytotoxicity Data to Predict Pan-cytotoxicity

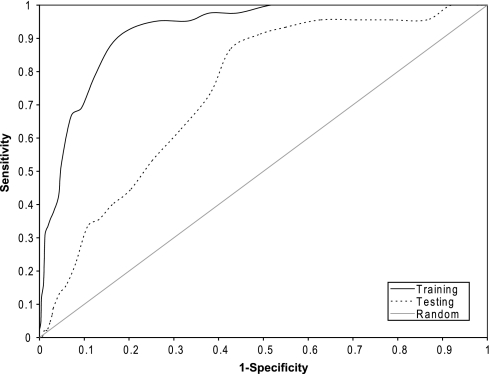
The 1353 compounds in the NTP collection were randomly divided into two sets of approximately equal size, using one set for training and the other one for testing. WFS scores were calculated for compounds in both the training and the testing sets. When the WFS scores were applied to predict compound pan-cytotoxicity in the training set, an AUC of 0.92 was obtained (Fig. 1). Using the optimal WFS score cutoff (i.e., when both specificity and sensitivity are maximized), the model can achieve 83% sensitivity and 86% specificity. This means that the model can correctly identify 83% of the toxic compounds and 86% of the nontoxic compounds in the training compound set. If sensitivity is maximized to 95% (i.e., 95% of the toxic compounds are identified), the specificity of the model decreases to 74%. Conversely, when specificity is maximized to 95% (i.e., 95% of the nontoxic compounds are correctly identified), the sensitivity of the model drops significantly to 52%. When the WFS scores were applied to predict pan-cytotoxic compounds in the testing set, the AUC decreased to 0.74 (Fig. 1). Decreases in model performance for the test set versus the training set are quite common and are expected because the testing set of compounds may contain structure features not captured by the training compound set from which the model was derived. Nonetheless, an AUC of 0.74 on the test set indicates that this is a good predictive model.

FIG. 1.

ROC curves for the prediction of cytotoxic compounds in the training and testing compound sets using cell viability data generated on the NTP collection. WFS scores were calculated using feature p values generated from the training compound set. The predictive power of the model decreased, but is still significantly better than random, when applied to the testing compound set as indicated by the reduction in the AUC.

Validation of the Pan-cytotoxicity Prediction Model

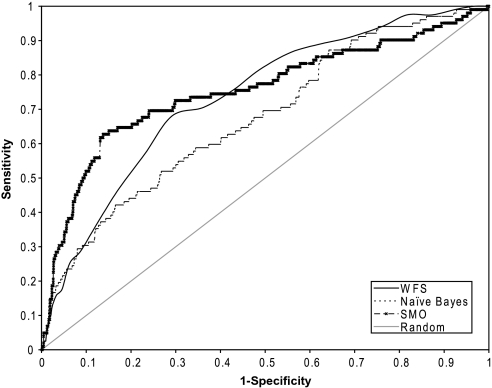
Though the WFS model performed well in predicting the pan-cytotoxicity of the Tox21 NTP test compounds, we wished to further examine the general applicability of the model in predicting pan-cytotoxicity among an independent set of chemicals. For this analysis, we generated cell viability data on a collection of 1408 Tox21 compounds (1351 unique) nominated by the EPA and excluded in the model testing the 253 compounds which were also in the NTP set, for a final number of 1098 compounds. First, each EPA compound was predicted to be pan-cytotoxic or “not cytotoxic” using the WFS model. Experimental cell viability data were then generated using the same concentration-response quantitative high–throughput screening (qHTS) paradigm used for the NTP chemicals (Xia et al., 2008); three kidney-derived cell types, HEK293, human mesangial cells, and rat proximal tubule cells, were assayed. Using these data, a cytotoxicity score of 0–10 was calculated for each compound in each of the three cell types (Table 2). As stated earlier, compounds with a mean score of ≥ 5 were designated as experimentally pan-cytotoxic, whereas compounds with a mean score of < 5 were designated as “noncytotoxic”. Comparing predicted versus experimental designations, the WFS model yielded an ROC with an AUC of 0.72 (Fig. 2), demonstrating a high degree of predictability, comparable to the AUC (0.74) obtained from the NTP testing set. If only data generated from the three kidney cell types were used to build the model, the AUC obtained from predicting the EPA collection dropped slightly to 0.70, indicating that data from only three cell types are probably not as robust as data from all 13 cell types in predicting pan-cytotoxicity.

FIG. 2.

ROC curves for the prediction of cytotoxic compounds in the EPA collection using three different modeling approaches: WFS, Naive Bayesian, and SMO. Models are trained on data generated from compounds in the NTP collection.

The number of unique structure features in the EPA compound set was 3596, only 2341 (65%) of which were also present in the NTP compound set. Of the 190 features that were significantly enriched in the EPA compounds found to be experimentally pan-cytotoxic, 179 (94%) were present in the NTP collection but only 96 (50%) were evaluated as significantly toxic. This shows that, as expected, not all cytotoxic structural features could be covered by a relatively small, though diverse, compound collection such as the NTP collection; accordingly, the current WFS model has good, but imperfect, predictive power. The slightly lower AUC for the EPA compound toxicity prediction may also reflect the use of only three cell types to test the model on the EPA compounds compared to data on 13 cell types used to predict cytotoxicity of the NTP compounds. The accuracy of the model is expected to improve as data on more compounds become available from the Tox21 collaboration (Collins et al., 2008), more compound features responsible for toxicity are captured, and more experimental cytotoxicity data are generated.

Comparison of WFS with Other Classification Algorithms

Table 3 lists the AUCs from other classification algorithms, Naive Bayesian and support vector machines (SVM) (SMO with and without logistic model), for four different toxicity data sets. For the prediction of EPA compound cytotoxicity based on the NTP compound collection, the WFS algorithm outperformed Naive Bayesian and had predictive power comparable to SMO without a logistic model but the logistic SMO had the best performance of the four algorithms by a slight margin, with an AUC of 0.75. The ROC plots of the three different modeling results are shown in Figure 2 (only the logistic SMO is shown for SVM). Comparing the ROC curves of WFS and SVM, SVM outperformed WFS in the first half of the ROC plot, where SVM achieved its optimal predictive power with 86% specificity and 63% sensitivity, whereas WFS outperformed SVM slightly in the later half of the ROC plot, where it had better sensitivities at the same specificity levels as SVM. These results may be due to the difference in the basis of the two algorithms. The WFS algorithm is fragment based, whereas SVM relies more on whole molecule similarity; therefore, nontoxic compounds with toxic features could have high WFS scores but low SMO scores, whereas toxic compounds that do not a whole structurally similar counterpart in the training set will have low SMO scores but could still have high WFS scores. Consequently, the WFS is likely to have a higher false-positive rate at higher WFS score ranges (earlier half of the ROC plot); in contrast, SVM tends to have higher false-negative rates at lower SMO score ranges (later half of the ROC plot).

TABLE 3.

Comparison of Model Performance in Terms of AUCs of ROCs on Four Different Data Sets

Modeling algorithm	Cell viability (NTP training/test)	Cell viability (EPA test)	Caspase activation (training/test)	Salmonella (training/test)	Hepatotoxicity (training/test)
WFS	0.92/0.74	0.72	0.88/0.71	0.81/0.77	0.83/0.67
Naive Bayesian	0.89/0.72	0.67	0.90/0.75	0.82/0.76	0.86/0.62
SMO	0.99/0.69	0.74	0.99/0.68	0.95/0.69	0.96/0.61
SMO (logistic model)	1/0.78	0.75	0.99/0.66	0.99/0.78	0.99/0.64

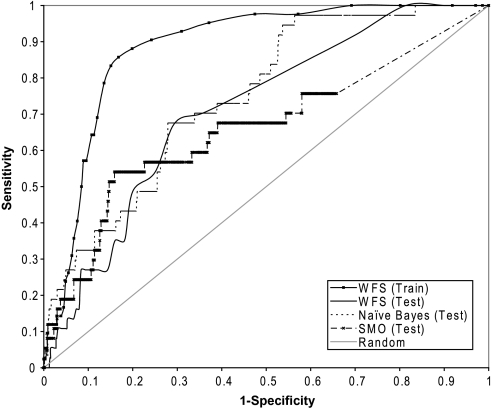
A compound's ability to activate caspases (caspase-3,7 in this particular study) and cause apoptosis is another measure of cytotoxicity. When modeling caspase activation data on the NTP compound collection using the four classification algorithms, the Naive Bayesian approach achieved the best performance with an AUC of 0.75 for the test set; WFS came in second, with a reasonably good testing AUC of 0.71; and neither of the SVM methods performed as well as the other methods with AUCs less than 0.7. The large decrement (> 30% difference in AUC) in the predictive power of the SVM models when applied to the test sets indicates that the models fit the training data nearly perfectly but did not extrapolate well to new sets of compounds, suggesting overfitting during model building, leading the algorithm to interpret noise in the training data as true signals. In contrast, the other two algorithms, WFS and Naive Bayesian, only had a 15–17% difference between their training and testing AUCs, suggesting a better applicability of these methods to new compounds. Figure 3 shows the ROC plots of the different modeling approaches. The figure shows that Naive Bayesian outperformed WFS mainly in the later portion of the ROC curve, where Naive Bayesian had better sensitivities than WFS at the same specificity levels. However, at this part of the curve, both the WFS scores and the Bayesian scores are in their lower ends and the false-negative rates are low for both algorithms. Only a few compounds are identified as false negatives, and the differences between the two algorithms are statistically insignificant (Fisher's exact test: p > 0.05).

FIG. 3.

ROC curves for the prediction of compounds that activated caspase-3,7 in the testing compound set of the NTP collection using three different modeling approaches: WFS, Naive Bayesian, and SMO. Models are built using data generated from the training compound set. The predictive power of the model decreased, but is still significantly better than random, when applied to the testing compound set as indicated by the reduction in the AUC.

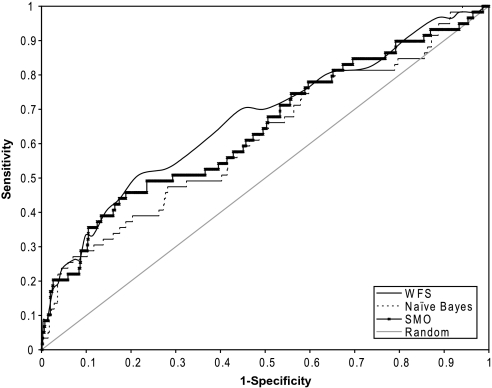
All three methods, WFS, Naive Bayesian and SVM (SMO with logistic model), had very similar performances on indentifying compounds that are mutagens (NTP's Salmonella assay), with testing AUCs of 0.76–0.78; the only exception being nonlogistic SMO, which had an AUC of 0.69 only. WFS appeared to have the best performance of all three methods on the prediction of hepatotoxic compounds, with an AUC of 0.67, whereas the other methods had AUCs ranging from 0.61 to 0.64. Furthermore, WFS also had the smallest drop in predictive power when applied to a new set of compounds, with only a 16% difference between its training and testing AUCs. In contrast, the nonlogistic SVM method had the worst performance, and both SVM methods again showed signs of overfitting with nearly perfect training AUCs but huge loss (35%) in predictive power when applied to the testing set. The ROC plots of the results from the three modeling approaches are shown in Figure 4. At the optimal WFS score cutoff, the model had a sensitivity of 63% and a specificity of 61%.

FIG. 4.

ROC curves for the prediction of hepatotoxic compounds using three different modeling approaches: WFS, Naive Bayesian, and SMO (logistic model). WFS is as shown the superior method of the three.

Structural Features Responsible for Toxicity

One of the advantages of the WFS algorithm is that it identifies structural features that might be responsible for toxicity. The structural features found most significantly enriched in the toxic compounds in the NTP collection are listed in Supplementary Table 1a. Many of these features are substituted/activated benzenes, 1,3-dienes, imines, quinones, nitrogen containing heterocycles (e.g., piperidines, pyridines, pyrans, pyrrolidines), and halogenated groups, most of which are known reactive groups susceptible to bioactivation (Guengerich and MacDonald, 2007); others are new structural features identified to contribute to compound toxicity. Not surprisingly, heavy metals showed up as one of the most significant toxic features. In the NTP collection, compounds containing metals include mercury, chromium, and cobalt compounds, which are well-known toxic compounds.

Cytotoxic compounds were identifiable by the presence of certain structural features. However, very few features were found significantly enriched in the “inactive”, or noncytotoxic compounds (Supplementary Table 1b). The most prominent feature among the few identified as significant was carboxylic acid, which is a functional group very common in biological chemicals, including all amino acids. It thus appears that the presence of this feature in a compound mitigates against toxicity. However, correlation with cytotoxicity or its absence currently does not allow firm prediction of cytotoxic properties of compounds containing them; these effects are likely to be context dependent and will be defined further as the Tox21 data set grows. As a general rule, compounds that are not cytotoxic have very few features in common, and the reason for their lack of cytotoxicity is more likely due to the absence of toxic features than the presence of specific nontoxic or toxicity-protective features.

A set of significant features was also identified for compounds that activated caspase activity (Supplementary Table 2) in the NTP collection. There were 235 features with p < 0.05, 173 (74%) of which overlap with significant toxic features (Supplementary Table 1a) identified based on cell viability data. This was not surprising since the compounds that activated caspase activity were roughly a subset of the compounds that reduced cell viability as caspase activation is one of the mechanisms that cause cell death. However, the order of significance for those features for caspase activation is different than reducing cell viability or cytotoxicity in general. Cyclic alkyl ketones and alkyl halides became the most dominant features in the caspase-activating compounds, suggesting that these features may be responsible for the caspase activation of the compounds. Unlike the features that could be used to identify cytotoxic compounds, the features significant in compounds activating caspase could be used to predict or identify compounds that kill cells through one particular mechanism (i.e., caspase activation). Organohalogen compounds (e.g., polychlorinated biphenyls, dichlorodiphenyltrichloroethane, and polybrominated diphenyl ethers) are known to cause hepatotoxicity (Sonne et al., 2005). Organohalides were also identified by our model as the most predominant features among the structural features significantly enriched in the hepatotoxic compounds (Supplementary Table 3). The fact that these features are also predictive of caspase activation suggests that cell death through caspase activation might be one of the mechanisms for hepatotoxicity caused by these compounds. In addition to the organohalides, other features significant for hepatotoxicity were also found to overlap with features significant in caspase-activating compounds and features that caused reduction in cell viability. The overlaps between the hepatotoxic features and the other two sets of toxic features were roughly 30 and 40%, respectively, indicating that certain features that can cause cytotoxicity will also cause toxicity in vivo. As the compound set used for the Salmonella mutagenicity model may include compounds that require metabolic activation, the structural features predicted by the model that contribute to the mutagenicity of a compound may be affected (Kalgutkar et al., 2005). A more careful analysis will be conducted in a follow-up study that takes into consideration the metabolic potential of compounds.

DISCUSSION

Data Quality and Model Performance

The cytotoxicity prediction model was built using cell viability data from 13 cell types for the prediction of pan-cytotoxic compounds. To test if a model can be built using data from a single cell type to predict cytotoxicity of a new compound in that cell type, we built a model for each of the three kidney-derived cell types, HEK293, human mesangial, and rat renal proximal tubule. We trained the models on data from the NTP collection and tested the models on the EPA collection. Table 4 lists the AUCs for each of the three kidney cell types. The performance of the cell type–specific cytotoxicity prediction is good but not as accurate as the prediction of pan-cytotoxic compounds. This is not surprising since the data used for defining and testing pan-cytotoxic compounds are based on multiple cell lines and thus are statistically more robust than data generated from a single cell line. Comparing the prediction results for the three kidney cell types, the predictive power of the rat proximal tubule cell toxicity model, with an AUC of 0.60, is notably lower than the ones for HEK293 and human mesangial cells, with AUCs of 0.70 and 0.68, respectively.

TABLE 4.

AUCs of Model ROCs for the Prediction of EPA Compounds Toxic to Specific Cell Types Using Significant Features Generated from Training Data Sets (NTP Collection)

Cell type	Reproducibility (%)	AUC
HEK293	93	0.70
Mesangial cell	90	0.68
Rat renal proximal tubule	85	0.60

To investigate the cause for the lower performance of the proximal tubule cytotoxicity prediction model, we examined the data reproducibility within the three kidney cell types using the 253 compounds present in both the EPA and the NTP collections and thus tested in replicates. The activity of a compound was designated as “reproduced” if both the NTP and the EPA copy produced a class 4 curve or both produced a nonclass 4 curve (i.e., 1, 2, or 3) in a given cell type. The percentage of the 253 compounds that reproduced for each cell type is listed in Table 3, which shows that data generated from the HEK293 cells were the most reproducible with 93% of the 253 compounds reproducing; data generated using the human mesangial cells were slightly less reproducible with 90% reproducibility; and data generated using the rat renal proximal tubule cells were the least reproducible yielding 85% reproducibility. Note all three values are within the expected range of reproducibility of high-throughput screening data, and the lower reproducibility of the rat proximal tubule cell data may be that these are primary cells, and thus more susceptible to variations in batch to batch preparations than the HEK293 or human mesangial cells. Regardless of the reason, the reproducibility of the data in the three cell types is directly proportional to the accuracy (i.e., AUC) of their respective cytotoxicity prediction models. These results clearly illustrate the point that data quality is critical to deriving high-quality models for toxicity prediction. When the rat proximal tubule data were excluded from the analysis, the predictive power of the pan-toxicity model improved to an AUC of 0.74.

Structural Diversity and Model Performance

The compound structures in each of the four-modeled data sets are quite diverse, as indicated by the average pairwise Tanimoto coefficient (Randic, 1997) (Daylight fingerprints) calculated for each compound collection (Table 5), ranging from 0.13 to 0.16, very small compared to the cutoff of Tanimoto ≥ 0.7 commonly used to define structurally similar compounds. When building structure-based models, similarity between compounds, or specifically toxic compounds in the case of toxicity prediction, in the training and testing sets always helps. To evaluate the effect of structural similarity/diversity on the performance of our models, we calculated another metric, Tmax, defined as the Tanimoto score (Leadscope fingerprints are used in this case because these are the structural data used for our model building) between a compound in the testing set and its most structurally similar toxic compound in the training set. The average Tmax score for toxic compounds in each data set is listed in Table 5. The hepatotoxicity compound set is the most diverse structurally having the lowest average intrapopulation Tanimoto score (0.13) and with its toxic compounds in the testing set least similar to those in the training set, as indicated by it having the smallest average Tmax (0.32). At the other end of the spectrum, the Salmonella compound set is the least diverse and have both the largest intrapopulation Tanimoto score (0.16) and Tmax (0.53). Consistent with the structural characteristics of these data sets, the performance of the best model built for a data set is found directly proportional to the structural similarity level between the compounds within the data set (Table 5). However, it is interesting to note the relationship between the structural diversity of a data set and the best-performing algorithm found for that data set. Table 5 shows that our WFS algorithm is the best-performing algorithm for the structurally most diverse data set (hepatotoxicity) and one of the best-performing algorithms for a structurally similar data set (Salmonella). On the other hand, the SVM algorithm (SMO) only performed well on the structurally most similar data sets (Salmonella and cell viability). These results suggest that because SVM-based algorithms rely on whole molecule similarity (as measured by Tanimoto scores), their application to unrelated compounds is limited, whereas the WFS approach can succeed even when compound structures are highly diverse.

TABLE 5.

Structural Diversity and Model Performance

Data set	Average tanimoto	Average Tmaxa	Best model	Best model ROC
Cell viability (EPA test)	0.15	0.38	SMO (logistic)	0.75
Caspase activation	0.15	0.33	Naive Bayesian	0.75
Salmonella	0.16	0.53	SMO (logistic)/WFS	0.78/0.77
Hepatotoxicity	0.13	0.32	WFS	0.67

^aTanimoto score (Leadscope fingerprints) between a compound in the testing set and its most structurally similar toxic compound in the training set.

A fragment-based approach appears more suitable for accurate toxicity predictions instead of whole molecule similarity. We calculated the Tmax scores for all the compounds in the EPA collection (the testing set) against the NTP collection (the training set). Of the correctly predicted cytotoxic EPA compounds, 77% had a Tmax < 0.7 and 26% had a Tmax < 0.3. The correctly predicted cytotoxic EPA compound that was the most dissimilar to any of the cytotoxic NTP compounds only had a Tmax of 0.125. The fact that the model was able to correctly identify toxic compounds in the testing set that were not structurally similar (in terms of whole molecule similarity) to any of the toxic compounds in the training set clearly shows that our WFS model is not driven by whole molecule similarity. These compounds were scored as toxic because they consist of features that were identified as toxic in some (as opposed to just one) compounds in the training set. Cytotoxic EPA compounds not identified by the model (FN) were structurally more dissimilar to the cytotoxic NTP compounds than the correctly predicted compounds, with a median Tmax of 0.23. The structural features that were responsible for their toxicity were either not significantly enriched or not present in the toxic NTP compounds. Interestingly, some toxic EPA compounds were more similar to the nontoxic NTP compounds than the toxic NTP compounds if judged by whole molecule similarity.

Data generated from a diverse set of chemicals are essential for the development of robust structural predictors of various toxicity end points. A learning curve analysis on the current Tox21 compound collection (EPA and NTP) showed that it has not reached a plateau in terms of structural diversity and number of chemicals and that additional chemicals are required to increase the diversity of this collection (Supplementary Fig. 1). To meet this goal, the Tox21 collaboration is currently in the process of acquiring more chemicals to expand the collection to about 10,000 chemicals.

Interpretability of the WFS Model

In this modeling work, we have tested whether the overrepresentation of certain structural features is indicative of a compound's overall cytotoxicity and how this can be used to predict the potential of compounds to induce cytotoxicity. The end result is a simple and interpretable model for cytotoxicity prediction based on compound structural features. The model is heuristically attractive because it has a simple chemical basis (i.e., compound activity can be directly linked to structure components and functional groups). The modeling results show that structural features enriched in toxic compounds and the level of enrichment, as measured by a p value, are predictive of compound toxicity. That is, compounds that contain features overrepresented in many known toxic compounds are also likely to be toxic. The level of enrichment (i.e., the statistical significance of this enrichment) is also important as compounds with more significantly enriched toxic features are more likely to be toxic. This is the reason why we choose to weigh the features by their significance of enrichment and score compounds for their toxic potential using p values. The predictive power of the model decreased when simple presence or absence of toxic features was used to score compounds instead of p values (data not shown). The size of a compound is taken into consideration in the scoring scheme as well such that the final score is adjusted by the total number of structure features the compound has. The reason for this treatment is that a large molecule with many insignificant features could have a large sum of p values but is not necessarily toxic or more likely to be toxic than a small molecule with a few significant toxic features. This adjustment has improved the performance of the model. Unlike most classical modeling algorithms, the algorithm behind the WFS model is simple and transparent, which allows easy implementation and interpretation of results.

We have developed a simple modeling algorithm, WFS, to predict compound toxicological effects using statistical enrichment of structural features. The models were trained and tested on a series of cell viability and caspase activation qHTS data as well as on Salmonella reverse mutagenicity data from the NTP and hepatotoxicity data from the RTECS database. The predictive power of the model for cytotoxicity prediction was further validated on a completely orthogonal compound collection independent of the collection used to train and test the model. The performance of the WFS algorithm was compared with traditional classification methods such as Naive Bayesian clustering and SMO, a support vector machine approach. Our WFS algorithm showed comparable or better predictive power in most test cases. For hepatotoxicity prediction, the WFS model, while of modest predictive power, seemed to outperform the other classification algorithms. We have shown that this comprehensive cytotoxic fingerprint approach has advantages over whole molecule similarity methods, is simple to implement, and produces results that are straightforward to interpret. With further refinement, the WFS model may serve as a basis for structural alerts of potentially cytotoxic compounds.

SUPPLEMENTARY DATA

Supplementary Tables 1–3 and Figure 1 are available online at http://toxsci.oxfordjournals.org/.

FUNDING

Intramural Research Programs (NIH Interagency agreement #Y2-ES-7020-01) of the National Toxicology Program; National Institute of Environmental Health Sciences and the National Human Genome Research Institute; National Institutes of Health (NIH); and the NIH Roadmap for Medical Research Molecular Libraries Program (U54MH084681).