Skip to main content
PMC home page
BMC Bioinformatics logoLink to BMC Bioinformatics
. 2009 Oct 29;10:361. doi: 10.1186/1471-2105-10-361

Predicting sulfotyrosine sites using the random forest algorithm with significantly improved prediction accuracy

Zheng Rong Yang 1,✉
PMCID: PMC2777180  PMID: 19874585

Abstract

Background

Tyrosine sulfation is one of the most important posttranslational modifications. Due to its relevance to various disease developments, tyrosine sulfation has become the target for drug design. In order to facilitate efficient drug design, accurate prediction of sulfotyrosine sites is desirable. A predictor published seven years ago has been very successful with claimed prediction accuracy of 98%. However, it has a particularly low sensitivity when predicting sulfotyrosine sites in some newly sequenced proteins.

Results

A new approach has been developed for predicting sulfotyrosine sites using the random forest algorithm after a careful evaluation of seven machine learning algorithms. Peptides are formed by consecutive residues symmetrically flanking tyrosine sites. They are then encoded using an amino acid hydrophobicity scale. This new approach has increased the sensitivity by 22%, the specificity by 3%, and the total prediction accuracy by 10% compared with the previous predictor using the same blind data. Meanwhile, both negative and positive predictive powers have been increased by 9%. In addition, the random forest model has an excellent feature for ranking the residues flanking tyrosine sites, hence providing more information for further investigating the tyrosine sulfation mechanism. A web tool has been implemented at http://ecsb.ex.ac.uk/sulfotyrosine for public use.

Conclusion

The random forest algorithm is able to deliver a better model compared with the Hidden Markov Model, the support vector machine, artificial neural networks, and others for predicting sulfotyrosine sites. The success shows that the random forest algorithm together with an amino acid hydrophobicity scale encoding can be a good candidate for peptide classification.

Background

Tyrosine sulfation is a posttranslational modification (PTM), which introduces a sulfate group to a tyrosine residue in a protein [1-3]. During the modification process, sulfation is catalysed by tyrosylprotein sulfotransferase [4]. A targeted tyrosine for sulfation is normally required to be exposed on a protein surface [5]. Previous studies have indicated that Sulfation is an important anticipator for extracellular protein-protein interactions [6,7]. Studies have shown that sulfation is related to various diseases when a malfunction of a cellular activity occurs. For instance, sulfotyrosine can alter the affinity in some chemokine receptors leading to a downstream signalling cascade which affects the cells involved in acute and chronic events of cellular immunity [8]. Disease-related alterations at the non-reducing termini of chondroitin and dermatan sulfate have been found useful for monitoring proteoglycan metabolism [9]. In biochemistry, sulfation has been recognised as an important contributor to detoxication for endogenous compounds [10]. Sulfation activity has been investigated in various cancer studies such as breast cancer [11-13], lung cancer [14], prostate cancer [15,16], and pancreatic cancer [17-19]. Because of the relevance to various disease, tyrosine sulfation has been the target for drug design for over a decade [20-25].

In silico prediction of posttranslational modification sites is a significant activity in bioinformatics. For instance, in ExPASy http://www.expasy.ch/tools various PTM site predictors have been implemented. Specifically, a predictor named as Sulfinator http://www.expasy.ch/tools/sulfinator for sulfotyrosine site prediction has been successfully implemented using Hidden Markov Models (HMM) [26]. The predictor was able to obtain a sensitivity (the accuracy of predicting true sulfotyrosine sites) of 98% and total prediction accuracy of 98%. When the predictor is used on newly sequenced proteins, it is found that the predictor has a particularly low sensitivity although the specificity (the accuracy of predicting unconfirmed sulfotyrosine sites) is high. In this study, a new approach is therefore developed aiming to improve the sensitivity while maintaining the specificity. There is another predictor developed only for tyrosine sulfation sites in animal viruses using Position-Specific-Scoring-Matrix (PSSM) [27]. This approach is very similar to the so-called h-function proposed by Poorman [28] 18 years ago. Because only positive peptides are used for scoring, such an approach suffers low specificity when used for making prediction on unseen data [29]. 69 Jackknife simulations were conducted for only positive data. Although it claimed prediction accuracy of 96.43%, the model was actually trained with a carefully selected threshold. The claimed accuracy was observed after tuning the threshold, which is therefore likely over-estimated. Meanwhile, there is no public available tool for the comparison.

In a review paper, some most common features describing the patterns of the residues flanking a tyrosine sulfation site were given [30]. The patterns are found from the residues which flank the experimentally verified tyrosine sulfation sites using a regular expression pattern match approach. This is commonly used in various posttranslational modification pattern analysis projects. The web tool called WebLogos (or sequence logos) is such an application [31]. The reviewer discussed some motif patterns summarised from an earlier study, for instance, Glu and Asp commonly occur between -2 and 2 of a tyrosine sulfation site. However, the regular expression approach suffers two theoretical limitations. First, such an approach assumes that motif positions are mutually independent with a uniform background distribution which may not be true in most applications [32]. Second, the motifs generated this way are sensitive to experimental errors [33]. Machine learning models, on the other had, are more error-tolerate and have been recognised being capable of generalising well on unseen data.

In the common practice of peptide classification, the input for site prediction is normally a symmetrical peptide of consecutive amino acid resides that flank the potentially modified tyrosine. In this study three peptide sizes have been evaluated and the amino acids have been encoded using a hydrophobicity scale [34]. The encoded numerical data of peptides are then treated as inputs for building prediction models using various machine learning algorithms.

The reason of using a hydrophobicity scale is due to its traditional role in analysing the impact of amino acid hydrophobicity on protein structure and potential sites for protein-protein interactions [35]. Hydrophobic amino acids are generally located in the protein interior whereas hydrophilic amino acids are generally located on the protein surface as targets for binding with other molecules. A protein whose surface is composed of mainly negatively charged amino acids such as glutamate and aspartate will bind to a protein with mainly positively-charged molecules such as lysine and arginine [36-40]. This means that the hydrophobicity scale can be one candidate for encoding amino acids for constructing a predictive model. This study has used the Cornette scale [34].

Results

There are 18 experimentally verified sulfotyrosine sites and 33 unconfirmed sulfotyrosine sites in 15 blind test sequences. Two inferred sulfotyrosine sites were not used for the evaluation. Table 1 shows the prediction result for these sequences using the Sulfinator. In the table, "Actual" means the experimentally verified sulfotyrosine sites while "Predicted" means the predicted sulfotyrosine sites. "Accession" is the accession number from NCBI database. Numbers in bold face are the sulfotyrosine sites missed from the Sulfinator. Numbers in italic are the false sulfotyrosine sites. The total prediction accuracy is 82% with a specificity of 94% and a sensitivity of 61%. The sensitivity is 33% lower than the specificity.

Table 1.

The prediction result for the 15 blind test sequences using the Sulfinator.

Accession Actual sites Predicted sites
Q9PU41 112 112
P61073 21 21
Q9NZ53 97 118 97
A2ZBG5 110 112
A2YFB4 80 82 80
Q7 M3V5 114 114 102 131
P84900 62
Q0VTT9 62
P0C1V8 16 16
P0C1V7 16 16
Q800F1 62
P68116 5 5
P68124 4 4
P68121 3 3
P68119 6 6
Open in a new tab

Table 2 shows the prediction performances of all machine learning models constructed in this study. In the Table, the figures in bold face represent the models that outperform the Sulfinator. 10, 20, and 30 represent the peptide sizes. "n.a." represents "not available" because the kNN models have no AUR. The models built using the LDA, QDA, CART, 1NN and ANN5 approaches are not compatible with the Sulfinator. Other approaches generate at least one model as accurate as the Sulfinator depending on peptide sizes. All three RF models outperform the Sulfinator, so do all three 5NN models. Four models have achieved >90% total prediction accuracy with improved specificity and sensitivity. The RF models increase the sensitivity by 22%, the specificity by 3%, and the total prediction accuracy by 10% compared with the Sulfinator. The 20-mer SVM model increases the specificity by 6%, the sensitivity by 11%, and the total prediction accuracy by 8%.

Table 2.

The prediction performances of all machine learning models.

10 20 30
Spe Sen Tot AUR Spe Sen Tot AUR Spe Sen Tot AUR
LDA 70 78 73 0.80 76 89 80 0.87 82 83 82 0.88
QDA 85 50 73 0.82 88 44 73 0.80 91 72 84 0.84
CART 91 72 84 n.a. 76 83 78 n.a. 88 83 86 n.a.
1NN 91 72 84 n.a. 88 72 82 n.a. 85 72 80 n.a.
3NN 85 78 82 n.a. 94 72 86 n.a. 94 72 86 n.a.
5NN 94 72 86 n.a. 97 72 88 n.a. 97 72 88 n.a.
7NN 88 67 78 n.a. 88 78 84 n.a. 94 78 88 n.a.
9NN 94 50 78 n.a. 88 78 86 n.a. 94 78 88 n.a.
RF 97 83 92 0.93 97 83 92 0.95 97 83 92 0.94
ANN5 94 28 71 0.81 88 67 80 0.86 88 78 84 0.92
ANN10 100 33 76 0.82 94 78 88 0.94 91 72 84 0.92
ANN15 91 56 78 0.86 97 67 86 0.89 94 78 88 0.93
ANN20 91 56 78 0.88 94 72 86 0.96 94 78 88 0.93
SVM 87 78 83 0.89 100 72 90 0.94 94 78 88 0.92
Open in a new tab

The Chi-square test which has been used in bioinformatics [41] is used to evaluate the significance of the improvement of the sensitivity. The test value is 7.93 (p < 0.01). This represents that the new predictor is able to increase the sensitivity significantly compared with the previous one.

Figures 1 and 2 show the ROC curves of the RF and SVM models, respectively. It can be seen that three RF models are consistent while the SVM model built on the 20-mer peptide outperforms the other two SVM models, i.e. the curve is more close to the top-left corner.

Figure 1.

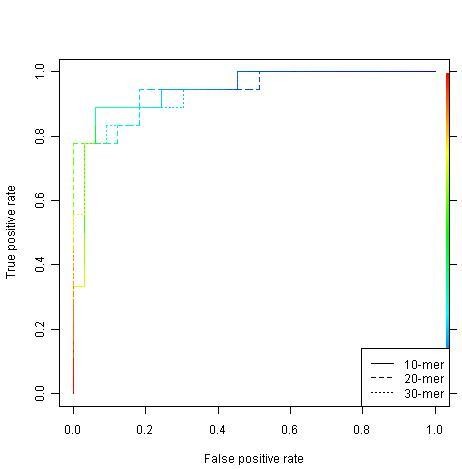
Figure 1

Open in a new tab

RF ROC curves for the 10-mer, 20-mer and 30-mer data sets. The horizontal axes are the false alarm rates (1 - specificity) and vertical axes are the sensitivity. For specific threshold for discriminating between positive (true sulfotyrosine sites) and negative (unconfirmed sulfotyrosine sites) data points, there will be a pair of these two values, i.e., 1 - specificity and sensitivity. A pair of values is then represented by a point in this two-dimensional space. Each curve is made by connecting all these points. A model is said to be robust whether its ROC curve is close to the top left corner. The area under a ROC curve is a quantitative indicator of this robustness.

Figure 2.

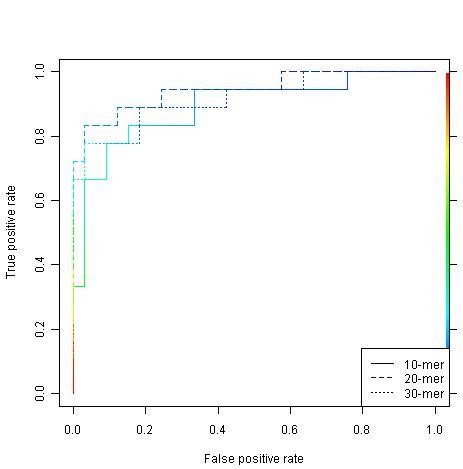
Figure 2

Open in a new tab

SVM ROC curves for the 10-mer, 20-mer and 30-mer data sets. The horizontal axes are the false alarm rates (1 - specificity) and vertical axes are the sensitivity. For specific threshold for discriminating between positive (true sulfotyrosine sites) and negative (unconfirmed sulfotyrosine sites) data points, there will be a pair of these two values, i.e., 1 - specificity and sensitivity. A pair of values is then represented by a point in this two-dimensional space. Each curve is made by connecting all these points. A model is said to be robust whether its ROC curve is close to the top left corner. The area under a ROC curve is a quantitative indicator of this robustness.

Discussion

In order to investigate the consistency among the RF models, correlation analysis is conducted. Figure 3 shows the correlation analysis of the predictions generated from the 10-mer RF model and 20-mer RF model. The correlation is 0.97. Figure 4 shows the correlation analysis of the predictions generated from the 10-mer RF model and 30-mer RF model. The correlation is 0.95. Figure 5 shows the correlation analysis of the predictions generated from the 20-mer RF model and 30-mer RF model. The correlation is 0.98. The high correlation indicates that three RF models are very consistent in prediction demonstrating a high robustness of the algorithm.

Figure 3.

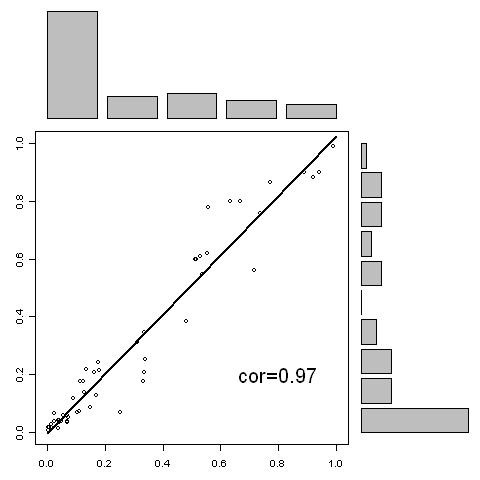
Figure 3

Open in a new tab

The correlation of the predictions between 10-mer model predictions (horizontal axis) and the 20-mer model predictions (vertical axis) for the blind data set.

Figure 4.

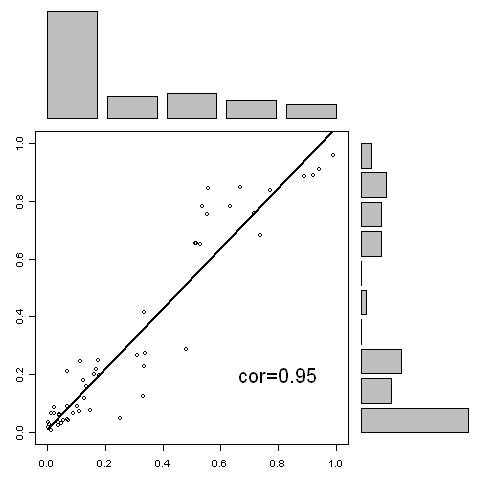
Figure 4

Open in a new tab

The correlation of the predictions between 10-mer model predictions (horizontal axis) and the 30-mer model predictions (vertical axis) for the blind data set.

Figure 5.

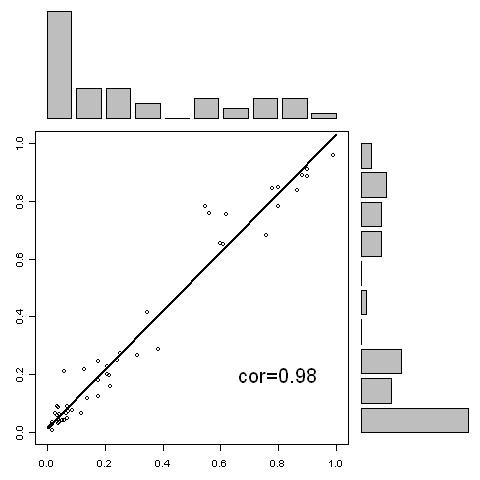
Figure 5

Open in a new tab

The correlation of the predictions between 20-mer model predictions (horizontal axis) and the 30-mer model predictions (vertical axis) for the blind data set.

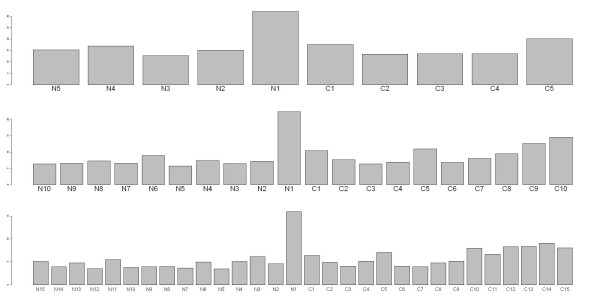
Figure 6 shows the ranking results from three RF models (mean decrease Gini gain [42,43]). It can be seen that residue N1 has been consistently highly ranked. Other residues with higher rank values are C5, C10, and C14. Based on the conditional density functions of N1and C1 shown in Figure 7, it can be seen that residue N1does contribute more to the classification of the two classes of peptides compared with C1. Because tyrosine sulfation plays a role in protein-protein interaction, several laboratorial works have found that N-terminal residues contribute to sulfotyrosines, i.e., the N-terminal domain of sulfotyrosines involve direct protein-protein interaction through a P-selection [44-48].

Figure 6.

Figure 6

Open in a new tab

The ranking results of residues in three RF models. The horizontal axis represents residue positions in peptides. The upper panel is for the 10-mer data, hence having residue positions ranging from N5 to C5. The middle panel is for the 20-mer data, hence 20 bars. The lower panel is for the 30-mer data, hence 30 bars. The vertical axis indicates the mean decrease Gini measures.

Figure 7.

Figure 7

Open in a new tab

The conditional density functions drawn at N1 and C1 residues, respectively. The horizontal axes represent the Cornette scale values while the vertical axes represent the density values. The density functions are estimated using the kernel approach using the R stats package with default parameter setting. The graph shows that the density functions drawn at N1 demonstrate a larger separation between two classes while this difference is getting smaller for the residue C1, which does not have a high rank value from RF models. Note that negative means unconfirmed sulfotyrosine whilst positive means experimentally verified sulfotyrosine.

The major differences between the Sulfinator and the predictors constructed in this paper are the use of different algorithms as well as the different presentation approaches of amino acids to a machine learning model. HMM does not need an encoding process while the predictors constructed in this study use a hydrophobicity scale to encode the amino acids. It is known that the random forest algorithm and the support vector machine algorithm have been well-known in improving the generalisation capability of a model. The significant improvement in the prediction accuracy in blind data these models can result from the use of RF and SVM algorithms and the use of hydrophobicity scale.

Finally, a single RF predictor is built using whole training data coded using 20-mer peptides (excluding any blind sequences). The RF predictor, a C program which is used to extract 20-mer peptides from a query sequence and encoding peptides using the Cornette scale, the whole training sequences and the blind sequences are available in the web site http://ecsb.ex.ac.uk/sulfotyrosine for free use, where a web tool is also available.

The RF predictor is then used to make prediction on the 15 blind sequences. Its performance is the same as that obtained from cross-validation models. For instance, protein Q9PU41 is a Cholecystokinin with 130 residues. It is related to the release of pancreatic enzymes in the gut [49]. A high degree of identity was found between the sequence from chicken and chinchilla which inferred a homologous function [50]. The sulfotyrosine is the first residue of the peptide Cholecystokinin-7 (112-118). The residue has been accurately predicted by both cross-validation RF predictions and the single RF predictor, as well as using Sulfinator. Protein A2ZBG5 is a Phytosulfokines 2. Two sulfotyrosine sites have been found in the peptide Phytosulfokine-beta (110-113). This protein is associated with plant cell differentiation, organogenesis, somatic embryogenesis and cell proliferation. The sulfated tyrosine is for binding to a putative membrane receptor [51]. In this case both sites have been accurately predicted using the RF model. However, Sulfinator failed to predict both. The RF predictor failed to predict three sulfotyrosine sites in extracellular proteins (Y21 in P61073 as well as Y97 and Y118 in Q9NZ53) while Sulfinator failed to predict one of these three sites (Y118 in Q9NZ53). Details of the analysis of all the predictions can be seen in Table 3. In the Table, "Site" represents the experimentally verified sulfotyrosine sites as well as those tyrosine residues which are not experimentally verified sulfotyrosine sites. If the value in the "TURE" column is 1, it represents that the site is an experimentally verified one. Sulfinator represents the predictions of the Sulfinator tool, where "Y" represents predicted sulfotyrosine sites including false positives. The sites 102 and 131 of Q7 M3V5 are missed experimentally verified sulfotyrosine sites. Blanks represent predicted non- sulfotyrosine sites. "RF1" represents the prediction (posterior probabilities) of cross-validation predictions while "RF2" represents the predictions (posterior probabilities) made by a single RF predictor. "Peptide" represents the segments in which the sulfotyrosine sites sit. "Region" represents the protein in which the sulfotyrosine sites are.

Table 3.

The prediction details of 15 blind testing proteins.

Protein Site TRUE Sulfinator RF1 RF2 Peptide Region
Q9PU41 112 1 Y 0.9884 0.988 Cholecystokinin-7
Q9PU41 2 0 0.1384 0.122
Q9PU41 79 0 0.0588 0.036
P61073 21 1 Y 0.2528 0.158 Extracellular
P61073 7 0 0.176 0.092
P61073 12 0 0.128 0.264
P61073 45 0 0.0188 0.006
P61073 65 0 0.086 0.074
P61073 76 0 0.1776 0.164
P61073 103 0 0.0084 0.008
P61073 116 0 0.04 0.036
P61073 121 0 0.034 0.03
P61073 135 0 0.0284 0.022
P61073 157 0 0.0404 0.034
P61073 184 0 0.0408 0.026
P61073 190 0 0.0688 0.062
P61073 219 0 0.016 0.02
P61073 255 0 0.0152 0.02
P61073 256 0 0.0388 0.04
P61073 302 0 0.0176 0.02
Q9NZ53 97 1 Y 0.0692 0.076 Extracellular
Q9NZ53 118 1 0.2072 0.236
Q9NZ53 391 0 0.0672 0.06
Q9NZ53 481 0 0.1168 0.112
Q9NZ53 498 0 0.1776 0.152
Q9NZ53 522 0 0.0384 0.052
A2ZBG5 110 1 0.618 0.606 Phytosulfokine-beta
A2ZBG5 112 1 0.7988 0.814
A2YFB4 80 1 Y 0.5476 0.596 Phytosulfokine-beta
A2YFB4 82 1 0.7788 0.796
Q7 M3V5 114 1 Y 0.2064 0.226 Callisulfakinin-1
Q7 M3V5 2 0 0.3116 0.358
Q7 M3V5 12 0 0.0608 0.064
Q7 M3V5 56 0 0.0528 0.044
Q7 M3V5 64 0 0.2184 0.232
Q7 M3V5 65 0 0.0348 0.038
Q7 M3V5 81 0 0.3856 0.378
Q7 M3V5 102 0 Y 0.072 0.054
Q7 M3V5 131 0 Y 0.5604 0.592
P84900 62 1 0.608 0.582 Phyllokinin
Q0VTT9 62 1 0.598 0.57 [Thr6, Val10]-phyllokinin
P0C1V8 16 1 Y 0.8816 0.92 Alpha-conotoxin AnIC
P0C1V7 16 1 Y 0.8988 0.93 Alpha-conotoxin AnIA
Q800F1 62 1 0.5984 0.57 [Thr6]-phyllokinin
P68116 5 1 Y 0.7984 0.816 Fibrinopeptide B
P68116 2 0 0.3464 0.338
P68124 4 1 Y 0.8984 0.902 Fibrinopeptide B
P68121 3 1 Y 0.7584 0.742 Fibrinopeptide B
P68119 6 1 Y 0.8648 0.864 Fibrinopeptide B
Open in a new tab

It is also important to see how confident we trust the predictions made by a model and whether this new approach is making a significant contribution to prediction accuracy compared with old models. For this we investigate the properties of the negative and positive predictive powers [52-55]. The negative predictive power measures how likely a negative prediction is true. In other words, it measures the probability that a prediction of unconfirmed sulfotyrosine is a true unconfirmed sulfotyrosine. It is calculated by the fraction of correctly identified unconfirmed sulfotyrosine sites over the total predicted unconfirmed sulfotyrosine sites. The positive predictive power then measures the probability that a sultyrosine prediction is a true sulfotyrosine. This is calculated by the fraction of correctly identified true sulfotyrosine sites over the total predicted sulfotyrosine sites. Given the confusion matrix made by testing the blind sequences as in Table 4, we can work out these two measurements. In the Table, "Negative" represents unconfirmed sulfotyrosine and "Positive" represents experimentally verified sulfotyrosine. The left panel is the result obtained when using Sulfinator while the right panel is the result generated by the RF model based on the 20-mer data. When using Sulfinator, the negative and the positive predictive powers are 82% and 85%, respectively. However they are 91% and 94%, respectively, when using the RF models. It can be seen that the confidence of trusting an unconfirmed sulfotyrosine site has increased by 9% using the RF models and the confidence of trusting a sulfotyrosine site has improved by 9% as well.

Table 4.

Confusion matrices for Sulfinator and the RF models in this study.

Sulfinator RF model
Negative Positive Negative Positive
Negative 31 2 94% 32 1 97%
Positive 7 11 61% 3 15 83%
82% 85% 82% 91% 94% 92%
Open in a new tab

Conclusion

This paper has presented a new predictor for sulfotyrosine sites in protein sequences. The sequences annotated after 2002 are used as the blind test data for comparing the models constructed using various other machine learning algorithms in this study and Sulfinator, a prediction tool established in 2002. Through evaluation, it has been found that the predictors constructed using the random forest algorithm and the support vector machine algorithm show significantly improved prediction accuracy compared with Sulfinator. The random forest models demonstrate consistently better performance. Using the RF models, the sensitivity is increased by 22%, the specificity is increased by 3%, and the total prediction accuracy is increased by 10% compared with the sulfinator. Both negative and positive predictive powers have been increased by 9% using the RF models. The 20-mer RF model is the method of choice for implementing a predictor because it has the highest AUR.

Methods

Data

363 proteins with experimentally verified sulfotyrosine sites were collected from NCBI [56]. Two rules were used for pre-processing the data. First, any sequence without an experimentally verified sulfotyrosine was removed. Second, the CD-HIT algorithm [57-59] was used to remove sequences with ≥ 90% similarity. Applying these two rules gave 94 sequences for the study. Among them, 79 were annotated before 2002 (inclusive) while the rest 15 were annotated after 2002. 79 early annotated sequences were used to train and select a predictor while 15 later annotated sequences were used as blind test data set for the comparison with the Sulfinator. The separation of data in 2002 was because the Sulfinator was developed in 2002. All the sequences annotated after 2002 should therefore be blind to the predictor.

Peptide formation and coding

All the tyrosines were extracted from the 79 test sequences. Following a common procedure in constructing a PTM site predictor, a peptide was formed symmetrically using both N-terminal and C-terminal consecutive residues flanking a tyrosine. It was denoted by Nm-Nm-1-...N1- C1-...Cm-1-Cm. Here, 2 m was the number of flanking residues in a peptide with N-k as an N-terminal residue and C-k as a C-terminal residue of a tyrosine. Note that the tyrosine in the middle was not used because it was identical in all peptides. Three peptide sizes were used, i.e. 2 m = 10, 20, and 30. A peptide generated from an experimentally verified sulfotyrosine was labelled as positive while a peptide generated from an unconfirmed sulfated tyrosine (has not yet been declared as a sulfated tyrosine) was labelled as negative. 132 positive and 626 negative non-repeated peptides were found in 79 sequences. Here, "non-repeated" indicated that any repeated peptide was removed. Each peptide was encoded to a numeric vector using the Cornette hydrophobicity scale.

Model construction

The machine learning algorithms used in this study were linear discriminant analysis (LDA) [43,60], quadratic discriminant analysis (QDA) [43,60], k-nearest neighbour (kNN) [43,60], classification and regression tree (CART) [61], the random forest algorithm (RF) [62], the support vector machine (SVM) [63] and artificial neural network (ANN) [64]. Because RF is a newly developed machine learning algorithm, a brief description of it is placed below. All these algorithms were available in the R programming environment (built by the R project, http://www.r-project.org/). The hidden neurons of ANN were 5, 10, 15, and 20. The numbers of nearest neighbours were 1, 3, 5, 7, and 9. The distance used in kNN was the Euclidean distance. The radial basis kernel function of the SVM was used with the smoothing parameter as 0.2. The cost parameter of the SVM was 100. The default parameters of LDA, QDA, CART, and RF were used.

Model evaluation

Models were evaluated by the sensitivity (Sen, the prediction accuracy of true sulfotyrosine sites), the specificity (Spe, the prediction accuracy of unconfirmed sulfotyrosine sites), the total accuracy (Tot), and receiver operating characteristics (ROC) analysis [65]. ROC was used to measure whether a model was robust. The areas under ROC curves (AURs) were used as a quantitative indicator of model robustness. The five-fold cross-validation approach [66] was used for model evaluation. ROC curves were drawn using the ROCR R package [67] and the area under ROC curves was calculated using the caTools R package http://cran.r-project.org/web/packages/caTools/index.html.

The random forest algorithm

The random forest algorithm is a newly developed machine learning algorithm [62]. The basic idea is to construct many trees using random vectors sampled from a data set. For the kth tree, a random vector is generated independently from the random vectors generated for the past k-1 trees. The remaining data are used for prediction. The approach of sampling random vectors is similar to bootstrap, i.e. the replacement sampling approach, which has also been applied to analysing biological data [68]. For each node in a tree, a small fraction of variables is randomly selected. The best split for the node is based on the prediction error. Each tree is fully grown without pruning. RF is able to provide a number of excellent features, for instance, the capability of handling a large number of variables, ranking the variables, and detecting the interaction among the variables. The algorithm has been recently applied to various biological data mining projects, for example, the prediction of the interactions between HIV-1 and human proteins using gene expression data [69], the analysis of differential gene expression [70], the diagnosis of ulcerative colitis based on gene expression data [71], the detection of cancers [72], the prediction of childhood leukaemia using gene expression data [73], and the prediction of protein-protein interactions [74]. All these applications show that the random forest algorithm outperforms some other algorithms.

Authors' contributions

ZRY collected the data, wrote and debugged C and R scripts for model construction and evaluation as well as the presentation of the work, implemented the web tool using JavaScript and Perl, and completed the manuscript preparation.

Acknowledgments

Acknowledgements

ZRY thanks Mathew Turnbull and Robin Batten for providing technique support during the implementation of the web tool and Andrew Dalby for critical discussions of the work. The UK high education funded this work.

References

  1. Hille A, Rosa P, Huttner WB. Tyrosine sulfation: a post-translational modification of proteins destined for secretion? FEBS Lett. 1984;177:129–134. doi: 10.1016/0014-5793(84)80996-5. [DOI] [PubMed] [Google Scholar]
  2. Andersen BN. Species variation in the tyrosine sulfation of mammalian gastrins. Gen Comp Endocrinol. 1985;58:44–50. doi: 10.1016/0016-6480(85)90134-0. [DOI] [PubMed] [Google Scholar]
  3. Danielsen EM. Tyrosine sulfation, a post-translational modification of microvillar enzymes in the small intestinal enterocyte. EMBO J. 1987;6:2891–2896. doi: 10.1002/j.1460-2075.1987.tb02592.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Negishi M, Pedersen LG, Petrotchenko E, Shevtsov S, Gorokhov A, Kakuta Y, Pedersen LC. Structure and function of sulfotransferases. Arch Biochem Biophys. 2001;390:149–157. doi: 10.1006/abbi.2001.2368. [DOI] [PubMed] [Google Scholar]
  5. Leitinger B, Brown JL, Spies M. Tagging secretory and membrane proteins witha tyrosine sulfation site. The Journal of Biological Chemistry. 1984;269:8115–8121. [PubMed] [Google Scholar]
  6. Kehoe JW, Bertozzi CR. Tyrosine sulfation: a modulator of extracellular protein-protein interactions. Chem Biol. 2000;7:R57–61. doi: 10.1016/s1074-5521(00)00093-4. [DOI] [PubMed] [Google Scholar]
  7. Seibert C, Sakmar TP. Toward a framework for sulfoproteomics: Synthesis and characterization of sulfotyrosine-containing peptides. Biopolymers. 2008;90:459–477. doi: 10.1002/bip.20821. [DOI] [PubMed] [Google Scholar]
  8. Liu J, Louie S, Hsu W, Yu KM, Nicholas HB, Jr, Rosenquist GL. Tyrosine sulfation is prevalent in human chemokine receptors important in lung disease. Am J Respir Cell Mol Biol. 2008;38:738–743. doi: 10.1165/rcmb.2007-0118OC. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Plaas AH, West LA, Wong-Palms S, Nelson FR. Glycosaminoglycan sulfation in human osteoarthritis. Disease-related alterations at the non-reducing termini of chondroitin and dermatan sulfate. J Biol Chem. 1998;273:12642–12649. doi: 10.1074/jbc.273.20.12642. [DOI] [PubMed] [Google Scholar]
  10. Coughtrie MW, Bamforth KJ, Sharp S, Jones AL, Borthwick EB, Barker EV, Roberts RC, Hume R, Burchell A. Sulfation of endogenous compounds and xenobiotics--interactions and function in health and disease. Chem Biol Interact. 1994;92:247–256. doi: 10.1016/0009-2797(94)90067-1. [DOI] [PubMed] [Google Scholar]
  11. Koo CY, Sen YP, Bay BH, Yip GW. Targeting heparan sulfate proteoglycans in breast cancer treatment. Recent Pat Anticancer Drug Discov. 2008;3:151–158. doi: 10.2174/157489208786242278. [DOI] [PubMed] [Google Scholar]
  12. Dumas NA, He D, Frost AR, Falany CN. Sulfotransferase 2B1b in human breast: differences in subcellular localization in African American and Caucasian women. J Steroid Biochem Mol Biol. 2008;111:171–177. doi: 10.1016/j.jsbmb.2008.05.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Hui Y, Yasuda S, Liu MY, Wu YY, Liu MC. On the sulfation and methylation of catecholestrogens in human mammary epithelial cells and breast cancer cells. Biol Pharm Bull. 2008;31:769–773. doi: 10.1248/bpb.31.769. [DOI] [PubMed] [Google Scholar]
  14. Wang Y, Spitz MR, Tsou AM, Zhang K, Makan N, Wu X. Sulfotransferase (SULT) 1A1 polymorphism as a predisposition factor for lung cancer: a case-control analysis. Lung Cancer. 2002;35:137–142. doi: 10.1016/s0169-5002(01)00406-8. [DOI] [PubMed] [Google Scholar]
  15. Sakko AJ, Butler MS, Byers S, Reinboth BJ, Stahl J, Kench JG, Horvath LG, Sutherland RL, Stricker PD, Henshall SM, Marshall VR, Tilley WD, Horsfall DJ, Ricciardelli C. Immunohistochemical level of unsulfated chondroitin disaccharides in the cancer stroma is an independent predictor of prostate cancer relapse. Cancer Epidemiol Biomarkers Prev. 2008;17:2488–97. doi: 10.1158/1055-9965.EPI-08-0204. [DOI] [PubMed] [Google Scholar]
  16. Teng YH, Tan PH, Chia SJ, Zam NA, Lau WK, Cheng CW, Bay BH, Yip GW. Increased expression of non-sulfated chondroitin correlates with adverse clinicopathological parameters in prostate cancer. Mod Pathol. 2008;21:893–901. doi: 10.1038/modpathol.2008.70. [DOI] [PubMed] [Google Scholar]
  17. Skandalis SS, Kletsas D, Kyriakopoulou D, Stavropoulos M, Theocharis DA. The greatly increased amounts of accumulated versican and decorin with specific post-translational modifications may be closely associated with the malignant phenotype of pancreatic cancer. Biochim Biophys Acta. 2008;1760:1217–1225. doi: 10.1016/j.bbagen.2006.03.021. [DOI] [PubMed] [Google Scholar]
  18. Li J, Kleeff J, Abiatari I, Kayed H, Giese NA, Felix K, Giese T, Büchler MW, Friess H. Enhanced levels of Hsulf-1 interfere with heparin-binding growth factor signaling in pancreatic cancer. Mol Cancer Res. 2005;4:14. doi: 10.1186/1476-4598-4-14. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Bloushtain N, Qimron U, Bar-Ilan A, Hershkovitz O, Gazit R, Fima E, Korc M, Vlodavsky I, Bovin NV, Porgador A. Membrane-associated heparan sulfate proteoglycans are involved in the recognition of cellular targets by NKp30 and NKp46. J Immunol. 2004;173:2392–2401. doi: 10.4049/jimmunol.173.4.2392. [DOI] [PubMed] [Google Scholar]
  20. Otvos LJ, Cappelletto B, Varga I, Wade JD, Xiang ZQ, Kaiser K, Stephens LJ, Ertl HC. The effects of post-translational side-chain modifications on the stimulatory activity, serum stability and conformation of synthetic peptides carrying T helper cell epitopes. Biochim Biophys Acta. 1996;1313:11–19. doi: 10.1016/0167-4889(96)00046-8. [DOI] [PubMed] [Google Scholar]
  21. Wolfender J, Chu F, Ball H, Wolfender F, Fainzilber M, Baldwin M, Burlingame A. Identification of tyrosine sulfation in conus pennaceus conotoxins a-PnIA and a-PnIB: further Investigation of aabile sulfo- and phosphopeptides by electrospray, matrix-assisted laser desorption/Ionization (MALDI) and atmospheric pressure MALDI mass spectrometry. J Mass Spectrom. 1999;34:447–454. doi: 10.1002/(SICI)1096-9888(199904)34:4<447::AID-JMS801>3.0.CO;2-1. [DOI] [PubMed] [Google Scholar]
  22. Coughtrie MW. Sulfation through the looking glass--recent advances in sulfotransferase research for the curious. Pharmacogenomics J. 2002;2:297–308. doi: 10.1038/sj.tpj.6500117. [DOI] [PubMed] [Google Scholar]
  23. Buxbaum JD, Geoghagen NS, Friedhoff LT. Cholesterol depletion with physiological concentrations of a statin decreases the formation of the Alzheimer amyloid Abeta peptide. J Alzheimers Dis. 2001;3:221–229. doi: 10.3233/jad-2001-3207. [DOI] [PubMed] [Google Scholar]
  24. Hasegawa M, Crowther RA, Jakes R, Goedert M. Alzheimer-like changes in microtubule-associated protein Tau induced by sulfated glycosaminoglycans. Inhibition of microtubule binding, stimulation of phosphorylation, and filament assembly depend on the degree of sulfation. J Biol Chem. 1997;272:33118–33124. doi: 10.1074/jbc.272.52.33118. [DOI] [PubMed] [Google Scholar]
  25. Caporaso GL, Gandy SE, Buxbaum JD, Greengard P. Chloroquine inhibits intracellular degradation but not secretion of Alzheimer beta/A4 amyloid precursor protein. Proc Natl Acad Sci USA. 1992;89:2252–2256. doi: 10.1073/pnas.89.6.2252. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Monigatti F, Gasteiger E, Bairoch A, Jung E. The Sulfinator: predicting tyrosine sulfation sites in protein sequences. Bioinformatics. 2002;18:769–770. doi: 10.1093/bioinformatics/18.5.769. [DOI] [PubMed] [Google Scholar]
  27. Lin HC, Tsai K, Chang BL, Liu J, Young M, Hsu W, Louie S, Nicholas HB, Jr, Rosenquist GL. Prediction of tyrosine sulfation sites in animal viruses. Biochem Biophys Res Comm. 2003;312:1154–1158. doi: 10.1016/j.bbrc.2003.11.047. [DOI] [PubMed] [Google Scholar]
  28. Poorman RA, Tomasselli AG, Heinrikson RL, Kezdy FJ. A cumulative specificity model for protease from human immunodeficiency virus types 1 and 2, inferred from statistical analysis of an extended substrate data base. J Biol Chem. 1991;22:14554–14561. [PubMed] [Google Scholar]
  29. Yang ZR. Peptide bioinformatics: peptide classification using peptide machines. Methods Mol Biol. 2008;458:159–183. doi: 10.1007/978-1-60327-101-1_9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Monigatti F, Hekking B, Steen H. Protein sulfation analysis - a primer. Biochimica Biophysica Acta. 2006;1764:1904–1913. doi: 10.1016/j.bbapap.2006.07.002. [DOI] [PubMed] [Google Scholar]
  31. Schneider TD, Stephens RM. Sequence logos: a new way to display consensus sequences. Nucleic Acids Res. 1990;18:6097–6100. doi: 10.1093/nar/18.20.6097. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Vacic V, Iakoucheva LM, Radivojac P. Two Sample Logo: a graphical representation of the differences between two sets of sequence alignments. Bioinformatics. 2006;22:1536–1537. doi: 10.1093/bioinformatics/btl151. [DOI] [PubMed] [Google Scholar]
  33. Freyhult E, Moulton V, Ardell DH. Visualizing bacterial tRNA identity determinants and antideterminants using function logos and inverse function logos. NAR. 2006;34:905–916. doi: 10.1093/nar/gkj478. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Cornette JL, Cease KB, Margalit H, Spouge JL, Berzofsky JA, DeLisi C. Hydrophobicity scales and computational techniques for detecting amphipathic structures in proteins. J Mol Biol. 1987;195:687–693. doi: 10.1016/0022-2836(87)90189-6. [DOI] [PubMed] [Google Scholar]
  35. Creighton TE. Proteins: structures and molecular properties. San Francisco: W. H. Freeman; 1993. [Google Scholar]
  36. Urry DW. The change in Gibbs free energy for hydrophobic association - Derivation and evaluation by means of inverse temperature transitions. Chem Phy Lett. 2004;399:177–181. [Google Scholar]
  37. Georges E. The P-glycoprotein (ABCB1) linker domain encodes high-affinity binding sequences to alpha- and beta-tubulins. Biochemistry. 2007;46:7337–7342. doi: 10.1021/bi7006228. [DOI] [PubMed] [Google Scholar]
  38. Neuwirth M, Flicker K, Strohmeier M, Tews I, Macheroux P. Thermodynamic characterization of the protein-protein interaction in the heteromeric Bacillus subtilis pyridoxalphosphate synthase. Biochemistry. 2007;46:5131–5139. doi: 10.1021/bi602602x. [DOI] [PubMed] [Google Scholar]
  39. Nomura T, Sokabe M, Yoshimura K. Lipid-Protein Interaction of the MscS Mechanosensitive Channel Examined by Scanning Mutagenesis. Biophys J. 2006;91:2874–2881. doi: 10.1529/biophysj.106.084541. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Sohn J, Rudolph J. Temperature dependence of binding and catalysis for the Cdc25B phosphatase. Biophys Chem. 2006;125:549–555. doi: 10.1016/j.bpc.2006.11.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Pevsner J. Bioinformatics and Functional Genomics. 2. NY: Wiley-Blackwell; 2003. [Google Scholar]
  42. Archer KJ, Kimes RV. Empirical characterization of random forest variable importance measures. Computational Stat & Data analysis. 2007;52:2249–2260. [Google Scholar]
  43. Ripley BD. Pattern Recognition and Neural Networks. Cambridge: Cambridge University Press; 1996. [Google Scholar]
  44. Wilkins PP, Moore KL, McEver RP, Cummings RD. Tyrosine sulfation of P-selectin glycoprotein ligand-1 is required for high affinity binding to P-selectin. J Biol Chem. 1995;270:22677–22680. doi: 10.1074/jbc.270.39.22677. [DOI] [PubMed] [Google Scholar]
  45. Pouyani T, Seed B. PSGL-1 recognition of P-selectin is controlled by a tyrosine sulfation consensus at the PSGL-1 amino terminus. Cell. 1995;83:333–343. doi: 10.1016/0092-8674(95)90174-4. [DOI] [PubMed] [Google Scholar]
  46. Sako D, Comess KM, Barone KM, Camphausen RT, Cumming DA, Shaw GD. A sulfated peptide segment at the amino terminus of PSGL-1 is critical for P-selectin binding. Cell. 1995;83:323–331. doi: 10.1016/0092-8674(95)90173-6. [DOI] [PubMed] [Google Scholar]
  47. Somers WS, Tang J, Shaw GD, Camphausen RT. Insights into the molecular basis of leukocyte tethering and rolling revealed by structures of P- and E-selectin bound to SLe(X) and PSGL-1. Cell. 2000;103:467–479. doi: 10.1016/s0092-8674(00)00138-0. [DOI] [PubMed] [Google Scholar]
  48. Hoffhines AJ, Damoc E, Bridges KG, Leary JA, Moore KL. Detection and purification of tyrosine-sulfated proteins using a novel anti-sulfotyrosine monoclonal antibody. J Biol Chem. 2006;281:37877–37887. doi: 10.1074/jbc.M609398200. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Furuse M. Release and endogenous actions of the gastrin/cholecystokinin (CCK) family in the chicken. J Exp Zool. 1999;283:448–454. [PubMed] [Google Scholar]
  50. Fan ZW, Eng J, Miedel M, Hulmes JD, Pan YC, Yalow RS. Cholecystokinin octapeptides purified from chinchilla and chicken brains. Brain Res Bull. 1987;18:757–760. doi: 10.1016/0361-9230(87)90211-5. [DOI] [PubMed] [Google Scholar]
  51. Matsubayashi Y, Takagi L, Sakagami Y. Phytosulfokine-alpha, a sulfated pentapeptide, stimulates the proliferation of rice cells by means of specific high- and low-affinity binding sites. PNAS. 1997;94:13357–13362. doi: 10.1073/pnas.94.24.13357. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Barkley RA, Grodzinksi GM. Are tests of frontal lobe functions useful in the diagnosis of Attention Deficit Disorders? The Clinical Neurologist. 1994;8:121–139. [Google Scholar]
  53. Ellwood RW. Clinical discriminations and neuropsychological tests: An appeal to Bayes' theorem. The Clinical Neuropsychologist. 1993;7:224–233. doi: 10.1080/13854049308401527. [DOI] [PubMed] [Google Scholar]
  54. Matier-Sharma K, Perachio N, Newcorn JH, Sharma V, Halperin JM. Differential diagnosis of ADHD: Are objective measures of attention, impulsivity, and activity level helpful? Child Neuropsychology. 1995;1:118–127. [Google Scholar]
  55. Wherry JN, Paal N, Jolly JB, Balkozar A, Holloway C, Everett B, Vaught L. Concurrent and discriminant validity of the Gordon Diagnostic System: A preliminary study. Psychology in the Schools. 1993;1:29–36. [Google Scholar]
  56. Ostell JM, Kans JA. The NCBI data model. Methods Biochem Anal. 1998;39:121–144. doi: 10.1002/9780470110607.ch6. [DOI] [PubMed] [Google Scholar]
  57. Li W, Jaroszewski L, Godzik A. Clustering of highly homologous sequences to reduce the size of large protein databases. Bioinformatics. 2001;17:282–293. doi: 10.1093/bioinformatics/17.3.282. [DOI] [PubMed] [Google Scholar]
  58. Li W, Jaroszewski L, Godzik A. Tolerating some redundancy significantly speeds up clustering of large protein databases. Bioinformatics. 2002;18:77–82. doi: 10.1093/bioinformatics/18.1.77. [DOI] [PubMed] [Google Scholar]
  59. Li W, Godzik A. Cd-hit: a fast program for clustering and comparing large sets of protein or nucleotide sequences. Bioinformatics. 2006;22:1658–1660. doi: 10.1093/bioinformatics/btl158. [DOI] [PubMed] [Google Scholar]
  60. Venables WN, Ripley BD. Modern Applied Statistics with S. 4. NewYork: Springer; 2002. [Google Scholar]
  61. Breiman L, Friedman JH, Olshen RA, Stone CJ. Classification and Regression Trees. Wadsworth. 1984.
  62. Breiman L. Random forests. Machine Learning. 2001;45:5–32. [Google Scholar]
  63. Vapnik V. The Nature of Statistical Learning Theory. New York: Springer-Verlag; 1995. [Google Scholar]
  64. Rumelhart DE, McClelland JL. Parallel Distributed Processing: Foundations. Vol. 1. Cambridge, MA, USA: The MIT Press; 1987. [Google Scholar]
  65. Metz CE. Basic principles of ROC analysis. Seminars in Nuclear Medicine. 1978;8:283–288. doi: 10.1016/s0001-2998(78)80014-2. [DOI] [PubMed] [Google Scholar]
  66. Efron B. Nonparametric estimates of standard error: The jackknife, the bootstrap and other methods. Biometrika. 1981;68:589–599. [Google Scholar]
  67. Sing T, Sander O, Beerenwinkel N, Lengauer T. ROCR: visualizing classifier performance in R. Bioinformatics. 2005;21:3940–3941. doi: 10.1093/bioinformatics/bti623. [DOI] [PubMed] [Google Scholar]
  68. Efron B, Halloran‡ E, Holmes S. Bootstrap confidence levels for phylogenetic trees. PNAS. 1996;93:13429–13434. doi: 10.1073/pnas.93.23.13429. [DOI] [PMC free article] [PubMed] [Google Scholar]
  69. Tastan O, Qi Y, Carbonell JG, Klein-Seetharaman J. Prediction of interactions between HIV-1 and human proteins by information integration. Pac Symp Biocomput. 2009:516–527. [PMC free article] [PubMed] [Google Scholar]
  70. Wu XY, Wu ZY, Li K. Identification of differential gene expression for microarray data using recursive random forest. Chin Med J. 2008;121:2492–2496. [PubMed] [Google Scholar]
  71. Olsen J, Gerds TA, Seidelin JB, Csillag C, Bjerrum JT, Troelsen JT, Nielsen OH. Diagnosis of ulcerative colitis before onset of inflammation by multivariate modeling of genome-wide gene expression data. Inflamm Bowel Dis. 2009;15:1032–1038. doi: 10.1002/ibd.20879. [DOI] [PubMed] [Google Scholar]
  72. Abba MC, Sun H, Hawkins KA, Drake JA, Hu Y, Nunez MI, Gaddis S, Shi T, Horvath S, Sahin A, Aldaz CM. Breast cancer molecular signatures as determined by SAGE: correlation with lymph node status. Mol Cancer Res. 2007;5:881–890. doi: 10.1158/1541-7786.MCR-07-0055. [DOI] [PMC free article] [PubMed] [Google Scholar]
  73. Hoffmann K, Firth MJ, Beesley AH, de Klerk NH, Kees UR. Translating microarray data for diagnostic testing in childhood leukaemia. BMC Cancer. 2006;6:229. doi: 10.1186/1471-2407-6-229. [DOI] [PMC free article] [PubMed] [Google Scholar]
  74. Qi Y, Bar-Joseph Z, Klein-Seetharaman J. Evaluation of different biological data and computational classification methods for use in protein interaction prediction. Proteins. 2006;63:490–500. doi: 10.1002/prot.20865. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from BMC Bioinformatics are provided here courtesy of BMC

RESOURCES