Abstract
It has been claimed that connectionist (artificial neural network) models of language processing, which do not appear to employ “rules”, are doing something different in kind from classical symbol processing models, which treat “rules” as atoms (e.g., McClelland and Patterson in Trends Cogn Sci 6(11):465–472, 2002). This claim is hard to assess in the absence of careful, formal comparisons between the two approaches. This paper formally investigates the symbol-processing properties of simple dynamical systems called affine dynamical automata, which are close relatives of several recurrent connectionist models of language processing (e.g., Elman in Cogn Sci 14:179–211, 1990). In line with related work (Moore in Theor Comput Sci 201:99–136, 1998; Siegelmann in Neural networks and analog computation: beyond the Turing limit. Birkhäuser, Boston, 1999), the analysis shows that affine dynamical automata exhibit a range of symbol processing behaviors, some of which can be mirrored by various Turing machine devices, and others of which cannot be. On the assumption that the Turing machine framework is a good way to formalize the “computation” part of our understanding of classical symbol processing, this finding supports the view that there is a fundamental “incompatibility” between connectionist and classical models (see Fodor and Pylyshyn 1988; Smolensky in Behav Brain Sci 11(1):1–74, 1988; beim Graben in Mind Matter 2(2):29--51,2004b). Given the empirical successes of connectionist models, the more general, super-Turing framework is a preferable vantage point from which to consider cognitive phenomena. This vantage may give us insight into ill-formed as well as well-formed language behavior and shed light on important structural properties of learning processes.
Keywords: Connectionism, Artificial neural networks, Chomsky hierarchy, Turing computation, Super-Turing computation, Dynamical automata, Dynamical recognizers, Grammar
Introduction
In the 1980s and 1990s, Jerry Fodor and Zenon Pylyshyn, on the one hand, and Paul Smolensky, on the other, had a debate about the relationship between symbolic and connectionist (artificial neural network) approaches to cognition. Part of the discussion centered on a notion of “compatibility”. Fodor and Pylyshyn (1988) and Fodor and McLaughlin (1995) argued that the symbolic approach is right about the nature of cognition, and thus that, if connectionism is incompatible with the symbolic approach, it must be rejected. In fact, they argued that there is only one sense in which the connectionist approach might be compatible with the symbolic approach and that is as an “implementation” (see Smolensky 1995a): it might, for example, describe how the primitive symbols of symbol systems are instantiated in physical brains. Crucially, on this “implementation” view, there is a clean division between the “lower” implementation level and the “higher” symbolic level of description such that all the causal relations at the symbolic level can be described without reference to properties at the implementation level. This claim has important implications for cognitive science: it suggests that cognitive scientists concerned with “high level” phenomena (presumably language, memory, conceptual structure, etc.) need to pay no attention to connectionism or any other implementation mechanism in order to successfully construct a theory of the phenomena. Fodor and Pylyshyn’s description of what goes on in symbolic cognition is also in line with the view that the computational processes of high level cognition fall within the domain of “effective computation” as identified by the Church-Turing thesis: high level cognitive computation can be fully formulated within the framework of so-called “Turing Computation”.
Smolensky (1988, 1995a,b) took a contrary position, arguing for “incompatibility” between connectionism and the symbolic approach. He distinguished between “implementation” and “refinement”, arguing that there is a way of doing connectionist modeling of cognition in which the models are not implementations but refinements of the symbolic models. He argued that the sense of implementation that Fodor and Pylyshyn must mean (in order to push the point about the irrelevance of connectionism to high level cognition) is the sense used in computer science, where a low-level description (e.g., an assembly language description like MIPS or SPARC) is an implementation of a high-level description (e.g., BASIC or JAVA). In this case, the high-level description and the low-level description contain the same algorithmic information: a programmer employing the high level language will perceive no difference in functionality whether the high level language is implemented, for example, in MIPS or SPARC. A low-level refinement, by contrast, contains additional algorithmic information that is lacking in a high-level description. He says, “Far from the conclusion that ‘nothing can be gained by going to the lower-level account’, there is plenty to be gained: completeness, precision, and algorithmic accounts of processing, none of which is generally available at the high level” (Smolensky 1995a, p. 168).
This claim of novelty and relevance for connectionist models would be vindicated if it could be shown that connectionist models do something systematically different from symbolic models and that empirical evidence favors the connectionist approach. In fact, connectionist networks have had unusual empirical success in several domains where classical approaches have not made much headway. Among these are the learning of syntactic structure from word sequence data (Elman 1990, 1991; Rohde 2002; Rohde and Plaut 1999), the modeling of quasi-regular behavior in phonology and morphology (Harm and Seidenberg 2004; Plaut et al. 1996; Seidenberg and Gonnerman 2000; Seidenberg and McClelland 1989), and the derivation of overregularization as a consequence of the learning process in language acquisition (Elman et al. 1996; Plunkett and Marchman 1991; Rumelhart and McClelland 1986). In each of these cases, the models exhibit surprising, empirically justified behaviors and this makes them interesting to the field of cognition. However, without formal insight into the relation of the connectionist models to symbolic models, it is not clear what fundamental conclusions these results imply for the field. It might be that the connectionist models are simply an alternative form of symbolic model, perhaps one in which the symbols refer to more fine-grained features of mental computation than those in classical cognitivist theories. It is noteworthy that some researchers participating in the debate put a large amount of weight on subtle verbal contrasts which are not obviously clarifying: e.g., the contrast between whether the language system “uses mechanisms that are combinatorial and sensitive to grammatical structure and categories” (Pinker and Ullman 2002) or whether rules are “approximate descriptions of patterns of language use; no actual rules operate in the processing of language” (McClelland and Patterson 2002). In this paper, in order to make headway on the issue, I adopt a particular, formal approach, examining a simple type of dynamical system that is closely related to the Elman network (Elman 1990). I make the assumption that classical symbolic computation can be appropriately understood as computation by some type of Turing device (a review of Turing devices is provided below). I then argue, following Moore (1998) and Siegelmann (1999), that the dynamical models include this kind of computation as one possibility but also include additional, super-Turing behaviors. I further argue that understanding these additional behaviors and their relationship to classical behaviors may be helpful for making new headway in the cognitive sciences.
In a recent development of the connectionist/symbolist debate, beim Graben (2004b) suggests that we take advantage of insights from dynamical systems theory, especially the method of symbolic dynamics (Devaney 1989), to clarify the discussion. In particular, it is helpful to note that the state space of a connectionist model is generally a real vector space so there is a continuum of possible states. Focusing on discrete update (iterated map) dynamics, the method of symbolic dynamics adopts a finite partition of such a state space and treats the partition indices as symbols. Thus, the iterating dynamical system on the vector space is associated with an iterating dynamical system on the symbol space. This correspondence gives rise to two ways of describing the system, which beim Graben and Atmanspracher (2006) refer to as the “ontic” (vector space) and “epistemic” (symbolic alphabet) levels. Beim Graben (2004b) suggests that the ontic/epistemic distinction provides a good model for the subsymbolic/symbolic (low/high) distinction discussed in cognitive science. He goes on to suggest that the dynamical notion of topological equivalence (or topological conjugacy) can help formalize the concept of compatibility between descriptions. Two dynamical systems, f: X →X and g: Y→Y are topologically conjugate if there is a homeomorphism h: X →Y satisfying 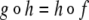 . A homeomorphism is a continuous, one-to-one function.Topological conjugacy is a kind of structural correspondence: the states of two conjugate systems are in complete, point-to-point correspondence, and the patterns of transitions between states also correspond perfectly across the systems. A particularly strong kind of topological conjugacy occurs when the partition is a generating partition. A partition is generating if the future of the boundaries of the partition subdivides the space arbitrarily finely. In this case, almost all the information about the details of the continuous dynamics can be reconstructed from the information about how the symbols are sequenced. For many dynamical systems, however, there is no generating partition and it is not possible to choose a single partition for which the symbolic dynamics reveals (almost) all the detail about the subsymbolic (continuous) dynamics. Such cases, beim Graben maintains (beim Graben 2004b), should count as cases of incompatibility between symbolic and subsymbolic dynamics. The fact that they exist among connectionist networks reveals, against Fodor and Pylyshyn’s position, a fundamental incompatibility between the symbolic and connectionist approaches.
. A homeomorphism is a continuous, one-to-one function.Topological conjugacy is a kind of structural correspondence: the states of two conjugate systems are in complete, point-to-point correspondence, and the patterns of transitions between states also correspond perfectly across the systems. A particularly strong kind of topological conjugacy occurs when the partition is a generating partition. A partition is generating if the future of the boundaries of the partition subdivides the space arbitrarily finely. In this case, almost all the information about the details of the continuous dynamics can be reconstructed from the information about how the symbols are sequenced. For many dynamical systems, however, there is no generating partition and it is not possible to choose a single partition for which the symbolic dynamics reveals (almost) all the detail about the subsymbolic (continuous) dynamics. Such cases, beim Graben maintains (beim Graben 2004b), should count as cases of incompatibility between symbolic and subsymbolic dynamics. The fact that they exist among connectionist networks reveals, against Fodor and Pylyshyn’s position, a fundamental incompatibility between the symbolic and connectionist approaches.
In this paper, I side with Smolensky and beim Graben in arguing for incompatibility between connectionist and symbolic systems. I also endorse beim Graben’s emphasis on the value of a dynamical systems perspective. However, I’ll suggest that beim Graben’s formalization of the notion of incompatibility is not the most useful one, and if we adopt a formulation more suitable to the central questions facing cognitive science, then the incompatibility is deeper than has been demonstrated in the aforementioned papers. Likewise, the lack of completeness and precision that Smolensky mentions is certainly valid, but it does not seem to argue for a strong change in our approach to cognitive science. After all, the high-level algorithms that run on digital computers do not completely and precisely describe the physical actions of the computer chips; yet this lack does not, in any significant sense except for the remote possibility of hardware errors, require that we pay attention to chip physics when describing the information processing behavior of digital computers. Beim Graben’s (2004b) examples of dynamical systems with incompatible epistemic and ontic dynamics are generally cases in which one partition induces symbolic dynamics corresponding to some familiar or simple algorithm (e.g., parsing a sentence, categorizing objects based on features, or a simple finite-state process). None of the examples have generating partitions (at least under the parameterizations considered), so none exhibit strong informational equivalence across the levels. I will argue, however, that such cases should not interest us very much. They are all situations in which a vector space dynamical system can be used to generate a familiar algorithmic process via symbolic dynamics and there is nothing unexpected in the behavior at the symbolic level. In particular, Fodor and Pylyshyn’s claim of separability seems to hold: if our interest is in the higher level description (i.e., the symbolic dynamics), then we don’t need the vector space description to characterize these dynamics.
Smolensky (1995a) also states that “algorithmic accounts of processing” are not available at the higher level for the connectionist systems he has in mind (p. 168). This is news if it means that no algorithm at all will suffice to describe the high-level behaviors of some of the systems. However, Smolensky does not provide evidence that such cases exist. A main purpose of this paper is to show, in keeping with (Siegelmann 1999), that such cases do exist, and to suggest that they have implications for the type of phenomena we expect to observe in high level cognition. In making this point, I’ll note that beim Graben’s focus on the difference between systems with generating partitions and those which lack them is very helpful. However, I’ll argue that it is actually the caseswith generating partitions that exhibit the kind of incompatibility we should be interested in. I reach this conclusion by a simple argument: the case of greatest interest is the case in which a connectionist model does something that a classical symbol system cannot do; under certain conditions,connectionist models with real-valued weights compute non-Turing computable functions (Siegelmann 1999; Turing 1939). In fact, they can only do this when there is a generating partition. Assuming that Turing computability is a good formalization of classical symbolic computation, I argue that “incompatibility” of classical and symbolic computation should be associated with the availability, not the lack, of a generating partition.
Overview
The essence of the present work is an analysis of the computational properties of affine dynamical automata. The next section reviews basic distinctions between types of formal languages. The following section defines affine dynamical automata and their associated formal languages. Section “Range of phenomena within the class” presents several theorems which support a structural classification of all parameter settings of an interesting subset of affine dynamical automata. Section “Parameter space map” presents a parameter space map based on this classification. I suggest that such maps offer a useful new perspective on cognitive processes like development and learning. Section “Conclusion”, considers the implications of these findings for cognitive science, returning to the question about the compatibility or incompatibility of the connectionist and symbolic views.
Affine dynamical automata are a type of dynamical system with feedback. The present work is thus closely related to other work that asks how complex computation can be accomplished by feedback dynamical systems. Many efforts in this regard have been directed at defending the claim that recurrent connectionist models, a type of feedback dynamical system, can handle the recursive computations that appear to underlie natural language syntax (Elman 1991; Pollack 1987; Smolensky 1990; Tabor 2000). Recently several projects have adopted some of these dynamical recursion mechanisms to model neural data on real time language processing (beim Graben 2004a, b, 2008a, b; beim Graben and Potthast 2009) [Gerth and beim Graben, this issue (Gerth and beim Graben 2009)]. In all of these projects, the focus is on getting the dynamical system to exhibit a complex behavior that the classical paradigm already handles. The current work takes a more general perspective, noting that that feedback dynamical systems can handle complex recursive computations and also handle processes that are not computable by Turing machines. The focus is on clarifying the relationships between these different behaviors within the general framework of super Turing computation and on highlighting the possible usefulness of the more general perspective to the field of cognition.
Relevant formal language classes
This section describes the classes of formal languages that are important in the discussion below.
A formal language is standardly defined as a set of finite-length strings drawn from a finite alphabet (Hopcroft and Ullman 1979). Here, I extend the definition to include one-sided infinite length strings over a finite alphabet. Many of the same classificational principles apply to this more general case. The Chomsky hierarchy (Chomsky 1956) classifies finite-sentence formal languages on the basis of the type of computing mechanism required to generate (or recognize) all and only the strings of the language. For example, the language L1, consisting of the strings {ab, abab, ababab, ...}, can be generated/recognized by a computing device with a finite number of distinct states. Such a device is called a “Finite State Automaton” (FSA) and its language is called a “Finite State Language”. A more powerful type of device, the “Pushdown Automaton” (PDA) consists of a finite state automaton combined with an unbounded stack (first-in, last-out) memory. The top (last-in) symbol of the stack and the current state of the FSA jointly generate/predict the next symbol at each point in time. Each PDA language can be generated by a “Context Free Grammar” (CFG) and vice versa, so PDAs and Context Free Grammars are equivalent formalisms. A CFG is a finite list of constituency rules of the form, A →A1A2…An where n is a finite positive integer (possibly different for each rule in the list). The language L2 = {ab, aabb, aaabbb, ...} (also called “anbn”), consisting of the strings with a positive whole number of “a”’s followed by the same number of “b”s, can be processed by a PDA (or CFG), but not by a FSA. Arguments have several times been advanced on linguistic grounds that human language processing employs something similar in computational capability to a Context Free Grammar (or PDA) (Gazdar 1981), though the current consensus is that a slightly more powerful device called a Tree Adjoining Grammar (Joshi and Schabes 1996) provides the best characterization of the formal patterning of the syntax of natural languages (Savitch 1987). An even more powerful device than those so far mentioned is the “Turing Machine” (TM). A TM consists of a FSA that controls an infinite tape memory (unbounded number of slots, the FSA controller can move step-by-step along the tape, either backwards or forwards, reading symbols and then either leaving them untouched or overwriting them as it goes). Chomsky (1956) noted that the devices on this hierarchy define successively more inclusive sets of formal languages: every FSA language can be generated by a PDA; every PDA language can be generated by a TM; but the reverse implications do not hold.1
Consider the set of all one-sided infinite strings formed by right-concatenation of strings drawn (with replacement) from a countable source set. If the source set is the language of a Chomsky Hierarchy device, we say that the device generates/recognizes the set of one-sided infinite strings. If, on the other hand, a set of one-sided infinite strings has no such source set, then we say that that set of one-sided infinite strings is not Turing machine computable.
Although they are not conventionally treated as a level on the Chomsky Hierarchy, there is a proper subset of the set of FSA languages that will be of relevance later in the present discussion: the Finite Languages. These can be specified with a finite list of finite-length strings. There are also sets of strings that are not generated by any Turing Machine, the most powerful device on the Chomsky Hierarchy. These string-sets are sometimes called “super-Turing” languages (Siegelmann 1999). These will also be relevant in the discussion below.
Formal paradigm: affine dynamical automata
Pollack (1991) defined dynamical recognizers: suppose fi:X →X for i = 1, …, K are functions on the continuous space, X. Given a string of integers, σ, drawn from the set {1,…, K}, we start the recognizer in a specified initial state in X and apply the functions corresponding to the integers of σ in order. If, at the end of applying the functions, the system is in a specified subset of the space (sometimes called the “accepting region”), then the string σ is said to be accepted by the dynamical recognizer. The set of strings accepted by the recognizer is a formal language. Moore (1998) explores conditions under which dynamical recognizers produce languages in various computational classes related to the Chomsky Hierarchy. One notable result is that, by choosing functions and regions judiciously, one can make dynamical recognizers for all Chomsky Hierarchy classes as well as for all super-Turing languages (Moore 1998).
Here, I focus on a class of devices called “affine dynamical automata”. These are a subclass of the “dynamical automata” defined in Tabor (2000) which have similar computational properties to dynamical recognizers. Unlike dynamical recognizers, which can execute any function at any time, the functions of dynamical automata have restricted domains, so they are useful for modeling organisms (like language producers) whose history restricts the set of possible (or probable) behaviors at each point in time. A few preliminary definitions support the main definitions.
Definition An affine function
 is a function of the form f(h) = ah + b, where a and b are real numbers. If b = 0, then f is linear. If b ≠ 0, then f is strictly affine.
is a function of the form f(h) = ah + b, where a and b are real numbers. If b = 0, then f is linear. If b ≠ 0, then f is strictly affine.Definition The length of a string σ is denoted |σ| and is equal to the number of characters in σ if σ has a finite number of characters and is called “infinite” if σ does not have a finite number of characters.
-
Definition If an infinite string has an initial character, it is called a right sided infinite string. If it has a final character, it is called a left-sided infinite string.
We will not be concerned here with the difference between left-sided and right-sided infinite strings, so, for convenience, we assume that all infinite strings are right-sided infinite (they have an initial character but no final character).
Definition The length n initial substring of a string σ of length ≥ n is denoted σ[n] and consists of the first n characters of σ in order.
Definition A finite string σ is a proper initial substring of a string σ′ either finite or one-sided infinite, if σ′[|σ|] = σ and |σ′| > |σ|.
- Definition An affine dynamical automaton is a device
where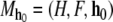
1 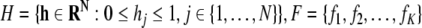 is a set of affine functions that map H into itself, and
is a set of affine functions that map H into itself, and 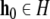 is the initial state. The domain, di, of each function, fi, is {
is the initial state. The domain, di, of each function, fi, is {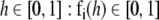 , where fi has the same functional form as fi but unrestricted domain}. For a string, σ, of integers drawn from
, where fi has the same functional form as fi but unrestricted domain}. For a string, σ, of integers drawn from 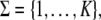 the system starts at
the system starts at  and, if possible, invokes the functions corresponding to the integers of σ in order. A string is said to be traceable under
and, if possible, invokes the functions corresponding to the integers of σ in order. A string is said to be traceable under 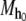 if every function corresponding to its integers can be invoked, in order, from left to right, starting from
if every function corresponding to its integers can be invoked, in order, from left to right, starting from  A string is maximal under
A string is maximal under 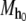 if it is traceable and it is not an initial substring of any longer, traceable string. The set of maximal strings under
if it is traceable and it is not an initial substring of any longer, traceable string. The set of maximal strings under 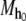 is the language of
is the language of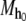 and is denoted
and is denoted 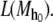
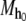 is said to generate and recognize its language and each string of its language.
is said to generate and recognize its language and each string of its language.
For 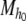 an affine dynamical automaton, I will use the notation M to refer to the set of affine dynamical automata
an affine dynamical automaton, I will use the notation M to refer to the set of affine dynamical automata 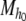 with h0 ∈ [0, 1].
with h0 ∈ [0, 1].
Affine dynamical automata are closely related to connectionist networks with sigmoidal activation functions. For example, Simple Recurrent Networks (Elman 1990, 1991) can approximately process infinite-state formal languages by using the contraction and expansion of the so-called “linear” (or central) section of the sigmoid to traverse fractal sets (Rodriguez 1995, 2001; Rodriguez et al. 1999; Wiles and Elman 1995). Closely related devices called “Fractal Grammars” employ affine dynamical automata as their core computational mechanism and exactly process infinite state languages in a manner similar to that of Simple Recurrent Networks (Tabor 2000, 2003). In particular, the affine maps of affine dynamical automata play an analogous role to the linear sections of the sigmoids. Thus, the study of affine dynamical automata may be informative about how connectionist networks can process complex languages.
Affine dynamical automata can generate both finite and infinite length strings:
Definition Let
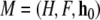 be an affine dynamical automaton. Let σ be a maximal string of
be an affine dynamical automaton. Let σ be a maximal string of 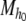 . If the length of σ is finite, then σ is a finite sentence of
. If the length of σ is finite, then σ is a finite sentence of 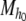 . If the length of σ is not finite, then σ is an infinite sentence of
. If the length of σ is not finite, then σ is an infinite sentence of 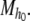
Definition An affine dynamical automaton is proper if
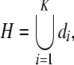 i.e., if at least one of the automaton’s functions can be applied at every point in H.
i.e., if at least one of the automaton’s functions can be applied at every point in H.
In a proper affine dynamical automaton all the sentences have infinite length. Although standard formal language theory focuses on finite sentence languages, the theory extends naturally to infinite sentence languages. I focus on proper affine dynamical automata here.
Even two function affine dynamical automata generate a rich variety of formal languages. The next section supports this claim by providing examples of affine dynamical automata that generate finite languages, finite state (non finite) languages, context free (non finite state) languages, and super-Turing languages. In fact each of these cases exists among both linear and and strictly affine dynamical automata.
Range of phenomena within the class
Finite languages
A cobweb diagram illustrating one trajectory of the affine system
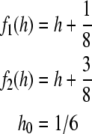 |
2 |
is shown in Fig. 1. This trajectory corresponds to the sentence, “1 2 1 1”. Only sentences satisfying
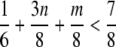 |
3 |
where m ≥ 0 is the number of 1s and n ≥ 0 is the number of 2s can be generated under this system. Since there are only a finite number of such cases, this automaton generates a finite language.
Fig. 1.
A sample trajectory of f1(h) = h + 1/8, f2(h) = h + 3/8, h0 = 1/6. The state space is the interval [0, 1]. The line segment labeled “i”, for i ∈ {1, 2}, is a plot of fi(h). The zig-zag line indicates the sample trajectory
The linear system
 |
4 |
generates the finite language {“1 1 1′′, “1 2′′, “2 1 1′′, “2 2′′}.
Every linear system with a1 > 1 and a2 > 1 and h0 > 0 generates a finite language.
Finite state languages
If the initial state in the previous example is replaced with h0 = 0, then the system generates a finite-state language that is not a finite language. Figure 2 depicts a FSA that generates/recognizes this language. I call this FSA BA for “Bernoulli Automaton” because one can think of it as a nonprobabilistic version of the Bernoulli Process. The circle corresponds to the single state of the machine. The system always starts in the state labelled “S”. It moves between states by following arcs. The label on each arc indicates the symbol that is generated when the system traverses the arc. The Bernoulli Automaton generates all infinite sentences on the two-symbol alphabet Σ = {1, 2}. In fact, every linear system with h0 = 0 generates L(BA) and every linear system with a1 ≤ 1 and a2 ≤ 1 generates L(BA) for all initial states.
Fig. 2.

The Bernoulli automaton
Figure 3a shows trajectories of the affine system
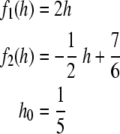 |
5 |
Fig. 3.
Trajectories (a) and finite state diagram (b) for the system, f1(h) = 2h, f2(h) = − 1/2h + 7/6, h0 = 1/5
This system is generated by the non-deterministic finite-state machine shown in Fig. 3b.
Context free languages
Context free languages (i.e., languages generated/recognized by PDAs or CFGs) arise when contraction and expansion are precisely matched (Tabor 2000). In particular, the following theorem states conditions under which linear dynamical automata generate context free languages:
Theorem 1 Let DA = ([0, 1], {f1(h) = a1h, f2(h) = a2h}, h0 > 0) be a linear dynamical automaton. If
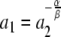 |
6 |
where α and β are positive integers and a1 and a2 are not both 1, then L(DA) is a context free language that is not a finite state language.
Appendix 1 provides a proof.
Figure 4 illustrates a trajectory and provides a context free grammar for a linear dynamical automaton that generates context free languages. A corresponding affine case is:
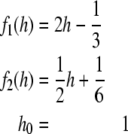 |
7 |
Fig. 4.
Trajectories (a) and context free grammar (b) for the system, 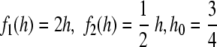
Super-Turing processes
Super Turing behavior occurs in the linear regime when the system has both expansion and contraction, but the two are not related by a rational power. To show this, some background is needed.
Definition Let
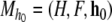 be a dynamical automaton with fi(h) = aih + bi. If ai ≠ 0 for i ∈ {1, ..., |F|}, then let
be a dynamical automaton with fi(h) = aih + bi. If ai ≠ 0 for i ∈ {1, ..., |F|}, then let 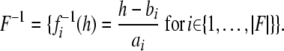 Then
Then 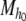 is said to be invertible with inverse
is said to be invertible with inverse 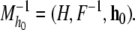
Consider the set of linear dynamical automata, 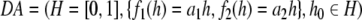 with a1 > 1 and 0 < a2 < 1. Note that d1, the domain of f1 is [0, 1/a1]. Thus, b = 1/a1 is the boundary between the subset of H on which f1 can apply and the subset of H on which it cannot. b is called an internal partition boundary of the state space. Consider DA−1, the inverse of DA:
with a1 > 1 and 0 < a2 < 1. Note that d1, the domain of f1 is [0, 1/a1]. Thus, b = 1/a1 is the boundary between the subset of H on which f1 can apply and the subset of H on which it cannot. b is called an internal partition boundary of the state space. Consider DA−1, the inverse of DA:
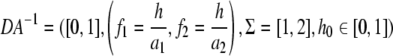 |
8 |
DA−1 computes the inverse of the history of DA for each h.
Definition The future of a state, h ∈ H, is the set {x ∈ H: x = Φσ(h) for some σ ∈ Σ*}.
That is, the future of a state h is the set of all states that the system can visit when started at h, including h itself.
Lemma Let DA be a set of invertible affine dynamical automata with inverses DA−1. Consider an internal partition boundary, b of DA. If some subset of DA−1bis dense in an uncountable set in H, then for uncountably many initial states h0, DAh0 generates a super Turing language.
A proof of the Lemma is provided in Appendix 2. The Lemma provides a way of showing that some linear dynamical automata exhibit super Turing behavior.
Theorem 2 Let DA = (H = [0, 1], {f1(h) = a1h, f2(h) = a2h}) be a linear dynamical automaton. If
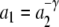 |
9 |
where γ is a positive irrational number, then there are statesh ∈ Hfor whichL(DAh)is not generable/recognizable by any Turing device.
Theorem 2 is proved in Appendix 2.
Figure 5 shows a linear dynamical automaton that generates super-Turing languages. The illustration shows a single trajectory starting from the initial state, 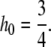 I do not know if this particular initial state generates a super-Turing language. But, by Theorem 2, there is bound to be a state very close to this initial state that generates a super-Turing language. Thus, the figure is illustrating an approximation of a super-Turing case. Even this approximation appears to be less regular than the trajectories in the finite, finite-state, and context-free examples discussed above.
I do not know if this particular initial state generates a super-Turing language. But, by Theorem 2, there is bound to be a state very close to this initial state that generates a super-Turing language. Thus, the figure is illustrating an approximation of a super-Turing case. Even this approximation appears to be less regular than the trajectories in the finite, finite-state, and context-free examples discussed above.
Fig. 5.
A single trajectory of the system 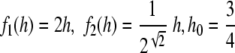
It is a little easier to show the existence of super Turing behaviors in the affine case. The chaotic Baker Map (Devaney 1989) is equivalent to the affine dynamical automaton,
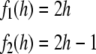 |
10 |
The inverse of the Baker Map (BM−1) is
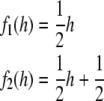 |
11 |
The Baker Map has one internal partition boundary at h = 1/2. The union of the zero’th through the n’th iterates of 1/2 under BM−1 consists of the points {k/2n} for k = 1…2n-1. Therefore any point in H can be arbitrarily well approximated by a finite iterate of BM−1 and the future of 1/2 is dense in H. Thus, by the Lemma, there are uncountably many initial states h, for which L(BMh) is not generable by a Turing Machine. A similar argument applies to the Tent Map (Devaney 1989).
Parameter space map
The results of the preceding section justify the construction of the parameter space map shown in Fig. 6. The slope of the first function is encoded along the horizontal dimension and the slope of the second is encoded along the vertical.2 The map indicates the type of language associated with most initial states under the parameter setting. The blocks with shaded bands contain settings that generate context-free languages and settings that generate super-Turing languages. Within the blocks, when the exponent, γ, is rational, then all initial states except h0 = 0 are associated with context free languages that are not finite state languages. The grey scale indicates, for rational values of γ, the number of symbols required to write a grammar of the language, with lighter shading corresponding to languages requiring fewer symbols. The super-Turing languages occur when γ is irrational, but only for a proper subset (uncountably infinite) of the initial states.
Fig. 6.
Deployment of language types in the parameter space of two-function linear dynamical automata
Conclusion
The paper has provided evidence that a rich variety of computational structures occur in even very simple dynamical computing devices. All two-function linear dynamical automata were considered, supporting the presentation of a parameter space map for this subclass.
I return now to the issues raised in the introductory argument about the compatibility of connectionist and classical symbolic computation, arguing that the present, super-Turing perspective offers some valuable new tools for approaching challenging problems in the study of cognition.
Relation between affine dynamical automata and connectionist models
In the Introduction, I suggested that the rich repertoire of these affine devices extends to other connectionist devices, including those that have been shown to exhibit appealing empirical properties, like induction of syntactic structure, sensitivity to quasi-regularity in morphology, and transient overgeneralization. The plausibility of this claim is suggested by related work which shows that a gradient-based learning model with affine recurrent processors at its core exhibits learning behaviors similar to that of other connectionist models (Tabor 2003). Nevertheless, there is a need for further formal development to clarify this relationship. One important goal is to extend the approach to higher-dimensional networks. Another is to consider nonlinear/non affine functions. I leave these as goals for future work.
Turing machine computation as a formalization of “computation” in the classical sense
The argument of the Introduction was also based on the assumption that the Turing machine framework is a good formalization of the “computation part” of the symbolic paradigm of cognitive science. This assumption is worth reviewing here in order to lay some groundwork for assessing the merits of the super-Turing framework. Fodor and Pylyshyn (1988) argue that the core computational feature of symbolic theories is “combinatorial symbol combination”. This property is plausibly a foundational element in four empirically defensible properties that Fodor and Pylyshyn cite as evidence for the symbolic approach: productivity (unbounded combination ability), systematicity (understanding “John loves Mary” implies understanding “Mary loves John”), compositionality (the parts—e.g., words—make essentially the same contribution to the meaning of the whole in all contexts), and inferential coherence (there is an isomorphism between human logic and actual logic).
Something like a context free grammar seems to have the right properties to support a model of at least most of these phenomena. If a context free grammar has recursive rules, it exhibits unbounded combination ability (productivity); if it is combined with a Montagovian semantics (Montague 1970), in which syntactic combination rules are parallel to semantic combination rules, and the categorical equivalence of “John” and “Mary” as syntactic elements can be justified, then the context freeness implies the interchangeability of their roles (systematicity). Likewise, the context freeness implies a context independent interpretation of all constituents (compositionality). Although the grammatical nature of actual logic is an open question, the evidence that Fodor and Pylyshyn bring to bear in favor of inferential coherence is based on the compositional structure of certain particular logical relationships: it would be bizarre, they say, to have a logic in which 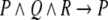 but
but 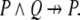 Again, a context free grammar is suitable for generating the well-formed formulas of the non-bizarre logical subsystem alluded to here. All of this suggests that some kind of Turing mechanism, perhaps a context free grammar or something akin to it, is a good mechanism for specifying the computations of thought, as conceived under the symbolic paradigm.
Again, a context free grammar is suitable for generating the well-formed formulas of the non-bizarre logical subsystem alluded to here. All of this suggests that some kind of Turing mechanism, perhaps a context free grammar or something akin to it, is a good mechanism for specifying the computations of thought, as conceived under the symbolic paradigm.
Benefits of the super-Turing perspective
What benefit, then, does the super-Turing framework offer cognitive science? I suggested at the beginning, that the empirical credentials of connectionist networks are strong enough that pursuit of a formal understanding of their computational properties is warranted. Now that the formal analysis is in view, a few other observations can be made in support of the usefulness of the super-Turing perspective.
Gradual metamorphosis is a hallmark property of grammar change (Hopper and Traugott 2003) and grammar development in children (Hyams 1995; Snyder 2007). I have argued elsewhere that, under the classical paradigm, there is no satisfactory way to model the phenomenon of gradual grammar change (Tabor 1994, 1995). The essential problem is that grammatical structures seem to come and go from languages via gradual accretion/loss of similar structures. But the classical paradigm offers no systematic way of measuring similarity relationships among grammars. The super-Turing framework offers a natural insight into this problem by revealing real-valued metric relations among grammars in neurally motivated computing mechanisms.
-
One may note that to distinguish between Turing and super-Turing mechanisms among the linear dynamical automata, one must refer to infinite-precision encodings of the parameter values. Since the real world is noisy, infinite precision is not realistic, so perhaps there is no need to consider the super-Turing devices (considering only Turing devices will get us “close enough” to everything we need to know). This argument is reminiscent of the argument that there is no need to consider infinite state computation in the study of language because one can only ever observe finite-length sentences. This argument can be countered by noting that consideration of infinite state computing devices allows us to discover principles of linguistic and logical organization like compositionality which would be out of reach if only finite state computation or finite computation were employed. This provides at least a cautionary note: we should not reject formal frameworks out of hand just because they refer to ideal systems.
However, there is also a reason that we may, from a practical standpoint, want to include super-Turing computation in the purview of cognitive science. There appear to be regions of the affine parameter space where the systems exhibit a behavior akin to robust chaos. In particular, when both a1 and a2 are greater than 1, the system vigorously explores the structure in the initial state, producing exponentially diverging trajectories for an uncountable number of initial states. This results in traditional chaos (e.g., Devaney 1989) in the deterministic Baker Map and Tent Map mentioned above. A natural extension of the traditional chaos to nondeterministic affine dynamical automata (Tabor and Terhesiu 2004) suggests that the nondeterministic cases may have similar properties. There appear to be regions of positive measure in the parameter space of two function affine dynamical automata where this generalized chaos is pervasive; in this sense the chaos is robust. We know from studies in other sciences that chaos is a practically relevant phenomenon that can be detected empirically (Abarbanel et al. 1996). Therefore, these chaotic regions of the parameter space may be relevant in a measurable way to the science of mind—perhaps, for example, they will offer a way of modeling ill-formed behavior, an area about which classical cognitive theory, with its emphasis on well-formedness, has relatively little to say (Thomas and Karmiloff-Smith 2005). Now, the question is: What is the relationship between chaos and super-Turing behaviors? Although the two are not coextensive, it is at least clear that super-Turing behaviors are pervasive in regions where there is chaos. Moreover, the mathematics of chaos requires infinite precision. Therefore it seems wise to adopt the more general computational framework.
The super-Turing framework suggests a way of understanding neural learning from a new perspective. In addition to considering generic local properties of a cost function as is done in the derivation of low-level learning procedures (Rumelhart et al. 1995) or the stability structure of the cost-function dynamics (Wei et al. 2008), we may consider the computational landscape that the learning process traverses via parameter-space maps like Fig. 6. This approach may shed light on the structural stages of the learning processes and the relationship between the emergentist perspective of many connectionist modelers and the structural perspective of linguistic theory.
Return to “compatibility”
Returning to the compatibility issue raised in the Introduction, the current line of argument suggests that dynamical models with real parameters, like recurrent connectionist networks, are, indeed, incompatible with classical symbolic approaches in that their behaviors form a strict superset of the behaviors exhibited by Turing devices.While the case at hand only shows partial overlap between the two classes of mechanisms, the results of (Moore 1998) suggest that sufficiently large parameterizable connectionist devices include all Turing computation as a proper subset. On the other hand, it is noteworthy that the Turing devices among linear dynamical automata are dense in the parameter space (see Fig. 6), so, in this subregion of the affine domain, the behavior of any super-Turing computation can well approximated by a Turing mechanism. Perhaps this is why it has seemed sufficient, from the standpoint of classical (structuralist) approaches to cognition, to use Turing computation models: they can approximate observed structures quite well. But the present work suggests that we ought to adopt a super Turing framework for the same reason that one does well to consider the real continuum when formalizing an understanding of concepts like differentiation and integration: the theory of processes is much simplified by working in complete metric spaces—viz. spaces which don’t have any points “missing”.
Finally, it is also interesting to note that the non-finite state behaviors of the linear dynamical automata come about through a complementarity between the two parameters: they arise when one is expansive and the other is contractive. Furthermore, if we take the complexity of a positive rational number, γ, to be the sum of its numerator and denominator when it is expressed in lowest terms, then, for a linear dynamical automaton satisfying a1 = a−γ2, the complexity of γ gives essentially the number of rules required to write a context free grammar of the automaton. One can thus say that the simplest exponent corresponds to the simplest context free grammar. Whereas the Turing computation framework does not give us any particular insight into why context free computation, among all Turing machine types, seems to be a kind of backbone of cognitive computation, the neurally grounded super-Turing framework considered here suggests an insight: it stems from a fundamental symmetry (multiplicative inversion) of real numbers.
In sum, the super-Turing framework is appealing because it is more general than the Turing machine framework and it allows us to consider relationships between devices that have been invisible in prior work on the structure of cognitive computation.
Acknowledgments
The foundation for this work was accomplished in collaboration with Dalia Terhesiu. Thanks to the attendees at the Workshop on Dynamical Systems in Language at the University of Reading in September, 2008, and to the University of Connecticut Group in Philosophical and Mathematical Logic for helpful comments.
Appendix 1
Theorem 1 Let DA = ([0, 1], {f1(h) = a1h, f2(h) = a2h}, h0 > 0) be a linear dynamical automaton. If
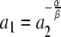 |
12 |
forα, β positive integers and a1, a2 ≠ 1. ThenL(DA)is a context free language that is not a finite state language.
Proof Without loss of generality, we can assume a1 > 1 and a2 < 1. Choose two real numbers, m and n satisfying
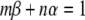 |
13 |
For example, we could take m = 0 and 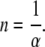 Let
Let
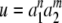 |
14 |
Therefore
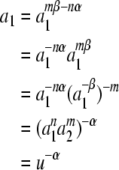 |
15 |
Similarly
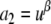 |
16 |
Note that 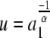 where α is a positive integer and a1 > 1, so u < 1.
where α is a positive integer and a1 > 1, so u < 1.
Let PDA be a pushdown automaton with a one-symbol stack alphabet. Whenever PDA reads a 2, it pushes β symbols onto its stack. Whenever PDA reads a 1, it pops α symbols off its stack. For x ∈ [0, 1], let
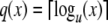 |
17 |
where 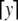 denotes the least integer greater than or equal to y. At the start of processing, the stack of PDA has q(h0) symbols on it. For σ ∈ Σ∞, if PDA makes a possible move at every symbol of σ in sequence (i.e., it never encounters a 1 with fewer than α symbols on its stack), then PDA is said to recognize σ. Let L(PDA) be the set of strings recognized by PDA.
denotes the least integer greater than or equal to y. At the start of processing, the stack of PDA has q(h0) symbols on it. For σ ∈ Σ∞, if PDA makes a possible move at every symbol of σ in sequence (i.e., it never encounters a 1 with fewer than α symbols on its stack), then PDA is said to recognize σ. Let L(PDA) be the set of strings recognized by PDA.
Let σ ∈ Σ∞ be a sentence of L(DA). Consider σ[n] the length n prefix of σ for n ∈ N. Suppose that, upon processing the prefix σ[n], PDA has j symbols on its stack and M is at a point x ∈ [0, 1] where q(x) = j. Then, if the next symbol is a 2, PDA will add β symbols to its stack. Similarly, the new state of M will be x2′ = f2(x) = a2x = uβx. Therefore, 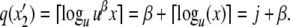 Likewise, if the next symbol is a 1, then PDA will remove α symbols from its stack. Similarly, the new state of M will be x′1 = f1(x) = a1x = u−αx. Therefore,
Likewise, if the next symbol is a 1, then PDA will remove α symbols from its stack. Similarly, the new state of M will be x′1 = f1(x) = a1x = u−αx. Therefore, 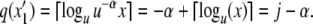 Therefore, since q(h0) was the number of symbols on the stack at the start of processing, q(x) equals the number of symbols on the stack at every step, provided that every legal move of M is a legal move of PDA and vice versa. In other words, it only remains to be shown that PDA and DA always generate/accept the same next symbol.
Therefore, since q(h0) was the number of symbols on the stack at the start of processing, q(x) equals the number of symbols on the stack at every step, provided that every legal move of M is a legal move of PDA and vice versa. In other words, it only remains to be shown that PDA and DA always generate/accept the same next symbol.
When the stack has α or more symbols on it, both 1 and 2 are possible next inputs. But when the stack has fewer than α symbols on it, only 2 is a possible next input. Likewise, if q(x) ≥ α then the state of M is in the domains of both f1 and f2, but when q(x) < α then
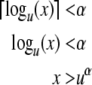 |
18 |
since u < 1 and α > 0. Thus
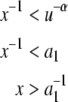 |
19 |
Since a−11 is the upper bound of the domain of f1, only f2 can be applied. Thus L(M) = L(PDA). By a well-known theorem (Hopcroft and Ullman 1979), L(PDA) is a context free language. Since PDA can have an unbounded number of symbols on its stack during the processing of legal strings from its language, L(PDA) is not a finite state language. Thus L(M) is a context free language that is not a finite state language. 
Appendix 2
Lemma Let DA be a set of invertible affine dynamical automata with inverses DA−1. Consider an internal partition boundary, b of DA. If some subset of 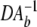 is dense in an uncountable set in H, then for uncountably many initial states
is dense in an uncountable set in H, then for uncountably many initial states 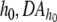 generates a super Turing language.
generates a super Turing language.
Proof Consider the future, Fb, of the internal partition boundary, b = 1/a1 under DA−1. Suppose that some part of this future is dense in an uncountable set. There must be an uncountable number of points that are pairwise separated from one another by points in Fb. Consider any pair of such points, x and y and the separating point, B ∈ Fb. Consider iterating DA, the forward map, simultaneously from the initial points x, y, and B. Since B lies strictly between x and y and the functions of DA are linear, if the same symbol is chosen for each of the three trajectories at every step, then each iterate of the future of B will always lie strictly between each iterate of x and y. Therefore, foor some σ, Φσ(B) = b. Thus the futures of x and y eventually lie on opposite sides of the internal partition boundary. Therefore the futures of x and y are nonidentical. Consequently L(DAx) ≠ L(DAy). Since this is true of uncountably many pairs of points, there must be an uncountable number of distinct languages generated by DA. Since the Turing processes are countable, uncountably many of these languages must be Super Turing languages. 
Theorem 2 Let DA = (H = [0, 1], {f1(h) = a1h, f2(h) = a2h}) be a linear dynamical automaton. If
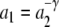 |
20 |
where γ is a positive irrational number, then there are states h ∈ H for which L(DAh) is not generable/recognizable by any Turing device.
Proof Without loss of generality, assume a1 > 1. By the Lemma, it will suffice to show that the future, F, of the point, 1/a1, under DA−1 is dense in an interval of positive length. In fact, F is dense in H itself. Let α1 = 1/a1 and α2 = 1/a2. Note that 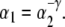 Consider
Consider 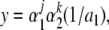 for j and k nonnegative integers and k ≤ γ(j + 1), a point in the future of 1/a1 under DA−1. I will show that for every x ∈ H and every ε, there exists y satisfying the conditions just mentioned, with |y − x| < ε. Note that
for j and k nonnegative integers and k ≤ γ(j + 1), a point in the future of 1/a1 under DA−1. I will show that for every x ∈ H and every ε, there exists y satisfying the conditions just mentioned, with |y − x| < ε. Note that
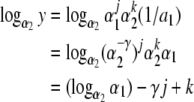 |
21 |
f(z) = z − γ(mod 1) is an irrational rotation on [0, 1]. Therefore the set {z − γj (mod 1): j = 0, 1, 2, ...} is dense in [0, 1]. Thus there is a nonnegative integer j such that 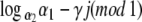 is within ε of
is within ε of 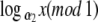 . It follows that there is a nonnegative integer k (k ≤ γ(j + 1)) such that
. It follows that there is a nonnegative integer k (k ≤ γ(j + 1)) such that 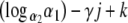 is within ε of
is within ε of 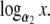 Since
Since 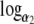 is expansive on (0, 1), it also follows that
is expansive on (0, 1), it also follows that 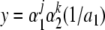 is within ε of x. Thus F is dense in [0, 1].
is within ε of x. Thus F is dense in [0, 1]. 
Footnotes
Chomsky (1956) also identified the set of Linear Bounded Automata which define a class of languages (“Context Sensitive Languages”) that have the PDA languages as a proper subset, and are themselves a proper subset of the TM languages. Context Sensitive Languages are not of central concern in the present study.
Maps with one or both slopes negative generate only finite or finite state languages and are not shown.
References
- Abarbanel HDI, Gilpin ME, Rotenberg M (1996) Analysis of observed chaotic data. Springer, New York
- beim Graben P (2004a) Language processing by dynamical systems. Int J Bifurcat Chaos 14(2):599–621 [DOI]
- beim Graben P (2004b) Incompatible implementations of physical symbol systems. Mind Matter 2(2):29–51
- beim Graben P, Atmanspracher H (2006) Complementarity in classical dynamical systems. Found Phys 36(2):291–306 [DOI]
- beim Graben P, Potthast R (2009) Inverse problems in dynamical cognitive modeling. Chaos 19:015103-1--015103-21 [DOI] [PubMed]
- beim Graben P, Gerth S, Vasishth S (2008) Towards dynamical systems models of language-related brain potentials. Cogn Neurodyn 2:229–255 [DOI] [PMC free article] [PubMed]
- beim Graben P, Pinotsis D, Saddy D, Potthast R (2008) Language processing with dynamical fields. Cogn Neurodyn 2:79–88 [DOI] [PMC free article] [PubMed]
- Chomsky N (1956) Three models for the description of language. IRE Trans Inf Theory 2(3):113–124. A corrected version appears in Luce, Bush, Galanter (eds) (1965) Readings in mathematical psychology, vol 2
- Devaney RL (1989) An introduction to chaotic dynamical systems, 2nd edn. Addison-Wesley, Redwood City
- Elman JL (1990) Finding structure in time. Cogn Sci 14:179–211 [DOI]
- Elman JL (1991) Distributed representations, simple recurrent networks, and grammatical structure. Mach Learn 7:195–225
- Elman JL, Bates EA, Johnson MH, Karmiloff-Smith A, Parisi D, Plunkett K (1996) Rethinking innateness: a connectionist perspective on development. MIT Press, Cambridge
- Fodor JA, McLaughlin BP (1995) Connectionism and the problem of constituency: why smolenksy’s solution doesn't work. In: MacDonald C, MacDonald G (eds) Connectionism. Debates on Psychological Explanation, pp 199--222. Blackwell, Oxford
- Foder JA, Pylyshyn ZW (1988) Connectionistm and cognitive architecture: a critical analysis. Cognition 28:3--71 [DOI] [PubMed]
- Gazdar G (1981) On syntactic categories. Phil Trans (Ser B) R Soc 295: 267–283 [DOI]
- Gerth S, beim Graben P (2009) Unifying syntactic theory and sentence processing difficulty through a connectionist minimalist parser. Cogn Neurodyn. doi:10.1007/s11571-009-9093-1 [DOI] [PMC free article] [PubMed]
- Harm MW, Seidenberg MS (2004) Computing the meanings of words in reading: cooperative division of labor between visual and phonological processes. Psychol Rev 111(3):662–720 [DOI] [PubMed]
- Hopcroft JE, Ullman JD (1979) Introduction to automata theory, languages, and computation. Addison-Wesley, Menlo Park
- Hopper PJ, Traugott EC (2003) Grammaticalization, 2nd edn. Cambridge University Press, Cambridge
- Hyams N (1995) Nondiscreteness and variation in child language: Implications for principle and parameter models of language development. In: Levy Y (ed) Other children, other languages. Lawrence Erlbaum, LK, pp 11–40
- Joshi AK, Schabes Y (1996) Tree-adjoining grammars. In: Rozenberg G, Salomaa A (eds) Handbook of formal languages, vol 3. Springer, New York, pp 69–123
- McClelland JL, Patterson K (2002) Rules or connections in past tense inflection: what does the evidence rule out? Trends Cogn Sci 6(11):465–472 [DOI] [PubMed]
- Montague R (1970) English as a formal language. In: BV et al (eds) Linguaggi nella e nella Tecnica. Edizioni di Comunità, pp 189–224. Reprinted in Formal philosophy: selected papers of Richard Montague, pp 108–221, ed. by Thomason RH, Yale University Press, New Haven, 1974
- Moore C (1998) Dynamical recognizers: real-time language recognition by analog computers. Theor Comput Sci 201:99–136 [DOI]
- Pinker S, Ullman MT (2002) Combination and structure, not gradedness, is the issue. Trends Cogn Sci 6(11):472–474 [DOI] [PubMed]
- Plaut DC, McClelland JL, Seidenberg MS, Patterson KE (1996) Understanding normal and impaired word reading: computational principles in quasi-regular domains. Psychol Rev 103:56–115 [DOI] [PubMed]
- Plunkett K, Marchman V (1991) U-shaped learning and frequency effects in a multi-layer perceptron: implications for child language acquisition. Cognition 38:43–102 [DOI] [PubMed]
- Pollack J (1987) On connectionist models of natural language processing (1987). Unpublished doctoral dissertation, University of Illinois
- Pollack JB (1991) The induction of dynamical recognizers. Mach Learn 7:227–252
- Rodriguez P (1995) Representing the structure of a simple context-free language in a recurrent neural network: A dynamical systems approach. On-line Newsletter of the Center for Research on Language, University of California, San Diego
- Rodriguez P (2001) Simple recurrent networks learn context-free and context-sensitive languages by counting. Neural Comput 13(9):2093–2118 [DOI] [PubMed]
- Rodriguez P, Wiles J, Elman J (1999) A recurrent neural network that learns to count. Connect Sci 11(1):5–40 [DOI]
- Rohde D (2002) A connectionist model of sentence comprehension and production. Unpublished PhD Dissertation, Carnegie Mellon University
- Rohde D, Plaut D (1999) Language acquisition in the absence of explicit negative evidence: how important is starting small? J Mem Lang 72:67–109 [DOI] [PubMed]
- Rumelhart DE, McClelland JL (1986) On learning the past tenses of english verbs. In: Rumelhart DE, McClelland JL (eds) Parallel distributed processing: explorations in the microstructure of cognition, vol 1. MIT Press, Cambridge
- Rumelhart D, Durbin R, Golden R, Chauvin Y (1995) Backpropagation: the basic theory. In: Backpropagation: theory, architectures, and applications. Lawrence Erlbaum
- Savitch WJ (ed) (1987) The formal complexity of natural language. Kluwer, Norwell
- Seidenberg MS, Gonnerman LM (2000) Explaining derivational morphology as the convergence of codes. Trends Cogn Sci 4(9):353–361 [DOI] [PubMed]
- Seidenberg MS, McClelland JL (1989) A distributed, developmental model of word recognition and naming. Psychol Rev 96:447–452 [DOI] [PubMed]
- Siegelmann HT (1999) Neural networks and analog computation: beyond the Turing limit. Birkhäuser, Boston
- Smolensky P (1988) On the proper treatment of connectionism. Behav Brain Sci 11(1):1–74
- Smolensky P (1990) Tensor product variable binding and the representation of symbolic structures in connectionist systems. Artificial Intelligence 46. Special issue on Connectionist symbol processing edited by G. E. Hinton
- Smolensky P (1995a) Connectionism, constituency, and the language of thought. In: MacDonald C, MacDonald G (eds) Connectionism. Debates on Psychological Explanation. Blackwell, Oxford
- Smolensky P (1995b) Reply: constituent structure and explanation in an integrated connectionist/symbolic architecture. In: MacDonald C, MacDonald G (eds) Connectionism. Debates on Psychological Explanation. Blackwell, Oxford
- Snyder W (2007) Child language: the parametric approach. Oxford University Press, London
- Tabor W (1994) Syntactic innovation: A connectionist model. Ph.D. dissertation, Stanford University
- Tabor W (1995) Lexical change as nonlinear interpolation. In: Moore JD, Lehman JF (eds) Proceedings of the 17th annual cognitive science conference. Lawrence Erlbaum
- Tabor W (2000) Fractal encoding of context-free grammars in connectionist networks. Expert Syst Int J Knowl Eng Neural Netw 17(1):41–56
- Tabor W (2003) Learning exponential state growth languages by hill climbing. IEEE Trans Neural Netw 14(2):444–446 [DOI] [PubMed]
- Tabor W, Terhesiu D (2004) On the relationship between symbolic and neural computation. AAAI Technical Report FS-04-03. ISBN 1-57735-214-9
- Thomas M, Karmiloff-Smith A (2005) Can developmental disorders reveal the component parts of the human language faculty? Lang Learn Dev 1(1):65–92 [DOI]
- Turing A (1939) Systems of logic based on ordinals. In: Proceedings of the London Mathematical Society. Series 2, vol 45, pp 161--228
- Wei H, Zhang J, Cousseau F, Ozeki T, Amari S (2008) Dynamics of learning near singularities in layered networks. Neural Comput 20:813–843 [DOI] [PubMed]
- Wiles J, Elman J (1995) Landscapes in recurrent networks. In: Moore JD, Lehman JF (eds) Proceedings of the 17th annual cognitive science conference. Lawrence Erlbaum







