C-terminal deletion of leucine-rich repeats from YopM reveals a heterogeneous distribution of stability in a cooperatively folded protein

Abstract

Terminal deletions of units from α-helical repeat proteins have provided insight into the physical origins of their cooperativity. To test if the same principles governing cooperativity apply to β-sheet-containing repeat proteins, we have created a series of C-terminal deletion constructs from a large leucine-rich repeat (LRR) protein, YopM. We have examined the structure and stability of the resulting deletion constructs by a combination of solution spectroscopy, equilibrium denaturation studies, and limited proteolysis. Surprisingly, a high degree of nonuniformity was found in the stability distribution of YopM. Unlike previously studied repeat proteins, we identified several key LRR that on deletion disrupt nearby structure, at distances as far away as up to three repeats, in YopM. This partial unfolding model is supported by limited proteolysis studies and by point substitution in repeats predicted to be disordered as a result of deletion of adjacent repeats. We show that key internal- and terminal-caps must be present to maintain the structural integrity in adjacent regions (roughly four LRRs long) of decreased stability. The finding that full-length YopM maintains a high level of cooperativity in equilibrium unfolding underscores the importance of interfacial interactions in stabilizing locally unstable regions of structure.

Introduction

The distribution of energy within the substructures of globular proteins is difficult to assess experimentally. Globular proteins have many contacts between residues that are distant in primary structure. This network of interactions has hindered the determination of energetic contributions by individual units to the overall stability.^1,2 Linear repeat proteins, which are made up of tandem modular units, are devoid of contacts between residues distant in primary structure, providing a system by which energetic contributions of small structural segments can be studied.

The network of interactions found in globular proteins has been thought of as a potential origin of two-state folding mechanisms (all folded or unfolded).¹ The interactions between residues distant in primary structure would limit the ability of individual segments of the protein to remain folded while others are unfolded, promoting cooperative equilibrium folding. However, a number of repeat proteins with elongated architectures have also been shown to fold and unfold by equilibrium two-state transitions. The origin of this cooperative behavior has been described for several α-helical repeat proteins.^3–5 In the Notch ankyrin domain, coupling between the stabilizing interfaces and the intrinsically unstable individual repeat units³ and a uniform stability distribution over medium length scales^6,7 give rise to cooperative unfolding transitions. A similar distribution of stability between intrinsic units and their interfaces has been found for α-helical consensus repeat proteins.^4,5

In naturally occurring β-sheet-containing repeat proteins, both two-state and multistate reactions have been shown to occur.^8,9 For internalin B (7.5 leucine-rich repeats (LRRs) and an N-terminal α-helical cap) and Yersinia outer protein M (YopM, 15.5 LRRs and an N-terminal α-helical cap) equilibrium two-state folding has been shown.^10–12 In contrast, for a consensus LRR protein, which is expected to have a rather uniform distribution of stability (by design), equilibrium-unfolding transitions are consistent with a high population of intermediates.¹³

To examine the distribution of stability and to gain insight into the interactions that underlie the highly folding cooperativity of YopM, we studied a nested set of fragments from YopM bearing C-terminal deletions of whole repeats. Solution structure of C-terminal deletion constructs was examined by circular dichroism (CD) and fluorescence, global stability was examined by urea-induced unfolding, and local stability was probed by limited proteolysis. This C-terminal deletion series can in principle resolve the stability contribution of single LRRs along with an N-terminal interfacial contribution. However, we find that a limited number of specific segments act as caps, without which multirepeat segments become disordered up to the next (N-terminal) cap, preventing resolution of folding energies to the level of single-repeats.

Results

The full-length protein contains an N-terminal α-helical cap, followed by 15 tandem LRR units, each composed of 20 or 22 residues in length, and a six amino acid long C-terminal β-strand cap [Fig. 1(A)]. To map the distribution of stability across the LRRs of YopM and to gain insight into the origin of cooperativity, we removed individual LRRs from the C-terminus. Boundaries between repeats, which correspond to breakpoints in the terminal deletion series, are shown in Figure 1. The smallest deletion removes the C-terminal nuclear localization signal (NLS,¹⁶ which is disordered in the crystal structure¹⁴), resulting in the construct referred to as N-β-cap. Further removal of the C-terminal β-strand cap results in the construct referred to as N-15. Subsequent truncations remove full LRRs, resulting in constructs that span from the N-terminus through the end of each LRR [N-14 through N-3, Fig. 1(C)].

Figure 1.

Ribbon representation and sequence of YopM. (A) On the left side of the molecule the N-terminal α-helical cap (transparent gray), followed by 15 LRRs and a C-terminal β-strand cap (black). (B) Sequence of YopM divided by LRRs and terminal caps, using the same color scheme as panel A. Residues in lower case are not shown in the crystal structure in panel A. Residues in italics are positions of sequence substitutions. Residues in bold represent possible trypsin cleavage sites. (C) Deletion constructs are named for the C-terminal LRR, and are colored as in (A). Panel A was generated using the structure 1JL5.pdb,¹⁴ and was prepared using PyMOL (http://www.pymol.org).¹⁵

Solution spectroscopy of C-terminal deletion constructs

To determine whether the C-terminal deletion constructs maintain native secondary and tertiary structural features, far- and near-UV CD spectra were obtained. The constructs N-β-cap, N-15, N-14, N-13, N-12, N-11, and N-10 show a negative ellipticity maximum at 217 nm, a characteristic feature of β-strand secondary structure¹⁷ [Fig. 2(A)]. These spectra suggest some loss of signal that is most pronounced on a per-residue basis for N-15, N-14, N-13, and N-12. When these spectra are scaled to match the N-β-cap signal at 217 nm, spectra for N-15 through N-11 all have similar shape (not shown), whereas N-10 is broader, suggesting a loss of secondary structure formation in N-10.

Figure 2.

Circular dichroism spectroscopy of YopM C-terminal deletion constructs. (A) Far- (B) and near-UV CD spectra of C-terminal deletion constructs: N-3 (light purple), N-4 (light pink), N-5 (tan), N-6 (brown), N-7 (gray), N-8 (pink), N-9 (red), N-10 (orange), N-11 (yellow), N-12 (green), N-13 (teal), N-14 (blue), N-15 (purple), and N-β-cap (black). Near-UV ellipticities are reported per mole of protein and are not normalized to chain length. Conditions: 200 mM NaCl, 20 mM Tris-HCl (pH 7.6), and 0.01 mM TCEP.

The far-UV spectra of constructs N-9, N-8, N-7, and N-6 differ significantly in shape from longer constructs, suggesting that LRR 10 is important for secondary structure integrity. The spectra for these constructs show a minimum at 208 nm, which is characteristic of proteins containing partial α-helical structure.¹⁷ The shape of the far-UV spectrum changes again for N-5, which appears to retain some secondary structure, yet shows a minimum at 204 nm, which is characteristic of disordered polypeptide. Removal of LRRs 5 and 4 (N-4 and N-3) result in spectra more closely resembling disordered polypeptide.

The near-UV spectra of constructs containing five or more LRRs show multiple minima, similar to the full-length construct. Much of the intensity and features in the full-length YopM spectrum arise from the two tryptophans in the N-terminal α-helical cap.¹² Thus, these constructs likely retain rigid, native-like tertiary structure at the N-terminus. The removal of LRR 5 results in a loss of ellipticity in the near-UV, suggesting that only a small fraction of the population of N-4 maintains a well-structured α-helical cap; on this basis N-3 appears to be even less structured. This loss of structure is in agreement with that from the far-UV CD spectra, which suggest substantial disorder in constructs lacking LRR 5.

Urea-induced unfolding transitions of C-terminal deletion constructs

To determine the contribution of individual LRRs to the stability of YopM, urea-induced unfolding transitions were monitored by far-UV CD as a probe of overall secondary structure. In addition, tryptophan fluorescence was used as a probe for the unfolding of the N-terminal α-helical cap.¹² For constructs longer than N-5, full baseline-resolved unfolding transitions were observed, and could be well-fitted by a two-state (all-or-none) model for unfolding (see Fig. 3).

Figure 3.

Equilibrium unfolding of YopM C-terminal deletion constructs. Normalized urea-induced unfolding transitions, monitored by far-UV CD (filled symbols, solid lines) and tryptophan fluorescence (open symbols, dashed lines) of C-terminal deletion constructs: N-4 (light pink), N-5 (tan), N-6 (brown), N-7 (gray), N-8 (pink), N-9 (red), N-10 (orange), N-11 (yellow), N-12 (green), N-13 (teal), N-14 (blue), N-15 (purple), N-β-cap (black), and full-length (black, diamonds). Line for constructs N-6 through full-length are the result of fitting a two-state unfolding model to individual transitions. Lines for N-5 and N-4 are not the result of fitting, but connecting lines intended to guide the eye. Conditions: 200 mM NaCl, 20 mM Tris-HCl (pH 7.6), and 0.01 mM TCEP.

Rather than decreasing evenly on deletion of each repeat, the midpoints of the unfolding transitions (C_m) decrease abruptly on deletion of the β-cap and again on deletion of LRR 11 (Fig. 3, Table I). Deletions of LRR 6 and LRR 5 also decrease C_m, and result in incomplete unfolding transitions in which the native baseline is not observed. Deletions of LRR 12 and LRR 7 result in more modest decreases in C_m. In contrast, removal of LRRs 13–15 and 8–10 have very small effects on C_m.

Table I.

Thermodynamic Parameters of YopM C-Terminal Deletion Series from Urea-Induced Unfolding Transition

	(kcal mol−1)		m (kcal mol−1 M−1)		Cm (M)
	CD	Fluorescence	CD	Fluorescence	CD	Fluorescence
Full-length	−10.7 ± 0.2	−11.0 ± 0.2	6.2 ± 0.03	6.3 ± 0.1	1.73 ± 0.02	1.74 ± 0.03
N-β-cap	−10.7 ± 0.1	−11.2 ± 0.3	6.5 ± 0.1	6.8 ± 0.2	1.66 ± 0.02	1.66 ± 0.03
N-15	−7.3 ± 0.1	−7.5 ± 0.2	5.2 ± 0.1	5.4 ± 0.2	1.39 ± 0.02	1.39 ± 0.02
N-14	−6.7 ± 0.1	−7.1 ± 0.5	4.9 ± 0.1	5.1 ± 0.4	1.38 ± 0.01	1.38 ± 0.01
N-13	−7.1 ± 0.1	−7.3 ± 0.1	5.1 ± 0.04	5.3 ± 0.1	1.38 ± 0.01	1.36 ± 0.03
N-12	−7.5 ± 0.1	−7.5 ± 0.03	5.5 ± 0.1	5.5 ± 0.1	1.35 ± 0.02	1.36 ± 0.02
N-11	−6.5 ± 0.1	−6.7 ± 0.1	5.2 ± 0.2	5.3 ± 0.04	1.25 ± 0.03	1.26 ± 0.03
N-10	−2.5 ± 0.2	−2.8 ± 0.1	3.1 ± 0.2	3.2 ± 0.2	0.81 ± 0.03	0.89 ± 0.04
N-9	−2.6 ± 0.1	−2.5 ± 0.2	3.1 ± 0.1	3.1 ± 0.2	0.84 ± 0.04	0.80 ± 0.01
N-8	−2.5 ± 0.01	−2.5 ± 0.1	3.0 ± 0.04	3.0 ± 0.04	0.84 ± 0.01	0.85 ± 0.02
N-7	−2.3 ± 0.1	−2.3 ± 0.1	2.8 ± 0.1	2.8 ± 0.03	0.80 ± 0.02	0.82 ± 0.05
N-6	−1.7 ± 0.1	−1.7 ± 0.1	2.4 ± 0.1	2.6 ± 0.03	0.70 ± 0.03	0.68 ± 0.01

Parameters are averages of three or more independent urea-induced unfolding transitions. Uncertainties represent the standard error on the mean. Parameters for N-5 and N-4 are not shown because only partial unfolding transitions were observed. Conditions: 200 mM NaCl, 20 mM Tris-HCl (pH 7.6), and 0.01 mM TCEP.

Changes in the steepness of the unfolding transitions (and fitted m-values, Figure S1) follow the same trend, with substantial decreases resulting from deleting the β-cap and LRR 11, and little or no change from deletion of the other repeats. If the removal of the β-cap and LRRs from the C-terminus leaves all of the remaining LRRs folded and coupled in an equilibrium two-state unfolding reaction, the m-value for each C-terminal deletion construct should be roughly proportional to the number of repeats.^18,19 The abrupt decreases in the steepness of the unfolding transitions indicate either that some of the remaining repeats become unstructured under native conditions or that intermediates are populated in the unfolding transition.

For C-terminal deletion constructs N-6 through N-β-cap the urea-induced unfolding transitions monitored by CD and fluorescence are coincident (see Fig. 3), and fitted thermodynamic parameters using a two-state model are almost identical (Table I).^* These results suggest that the structure formed in each of these constructs, which includes the N-terminal α-helical cap, is lost in a concerted unfolding transition. Thus, the abrupt decreases in m-value suggest that some repeats near the site of deletion do not participate in the main structural transition. These LRRs may be disordered or may possess residual secondary structure that is disrupted by the addition of small amounts of urea. This conclusion is supported by point substitution and limited proteolysis studies presented below.

Analysis of these unfolding transitions with a two-state model provides estimates for stabilities of the cooperatively folded LRRs, together with the N-terminal α-helical cap. Removal of the β-strand cap (construct N-15) is substantially destabilizing, increasing the free energy of folding by ∼3.6 kcal mol⁻¹, compared with N-β-cap (Table I). Removal of LRRs 15, 14, and 13 (constructs N-14, N-13, and N-12) do not change stability further. In contrast, removal of LRR 12 (construct N-11) is modestly destabilizing, increasing the free energy of folding by ∼0.9 kcal mol⁻¹ (Table I). As with removal of the β-strand cap, removal of LRR 11 (construct N-10) is substantially destabilizing, increasing the free energy of folding by ∼3.9 kcal mol⁻¹, compared with N-11 (Table I).

Similar to the removal of LRRs 13–15, removal of LRRs 10, 9, and 8 (constructs N-9, N-8, and N-7) do not change stability further (Table I). Similar to the removal of LRR 12, removal of LRR 7 (construct N-6) is modestly destabilizing, increasing the free energy of folding by ∼0.55 kcal mol⁻¹ (Table I). Removal of LRR 6 eliminates the folded baseline, indicating that a significant population of N-5 is unfolded under “native” conditions used here. A more dramatic decrease in stability occurs with removal of LRR 5 (construct N-4), for which the transition is dominated by an unfolded baseline. This result is consistent with the far- and near-UV CD spectra of N-4, in which the construct appears to be mostly disordered (see Fig. 2).

Overall, the abrupt pattern of changes in folding free energies as repeats are deleted mirrors changes in both the C_m and m-values. This stepwise behavior indicates that different LRRs are not thermodynamically equivalent. Two regions (LRRs 12–15 and 7–10) appear to be comparatively unstable; folding of these segments requires interfacial interactions with three key caps: the C-terminal β-strand cap, and the “internal” caps of LRR 11 and LRR 6. This interpretation, which is supported by results described later, is depicted as a partial unfolding model in Figure 4.

Figure 4.

Partial unfolding model. Segments of YopM unfold when key caps (the C-terminal β-strand cap, and the internal caps LRRs 11 and 6) are removed. For N-5, N-7, and N-12, it appears that part (but not all) of the C-terminal LRR remains folded.

Point substitutions support loss of structure of C-terminal LRRs without the β-strand cap

To probe the extent to which LRRs 13, 14, and 15 are unfolded when the C-terminal β-strand cap is removed, we replaced a leucine in the hydrophobic core in each of these repeats (at positions 329, 349, and 369) with a destabilizing phenylalanine [Fig. 1(B), italics]. Based on decreases in C_m values, these substitutions destabilize the full-length construct (Supporting Information Table SI). In contrast, when the β-strand cap is missing, the C_m remains constant (see Fig. 5). This observation is consistent with a partial unfolding model (see Fig. 4) for C-terminal deletion. Because m-values decrease substantially for constructs containing these point substitutions (Supporting Information Table SI), we restrict analysis to C_m values, because the two-state model is unlikely to be adequate to describe these unfolding transitions.

Figure 5.

Midpoints from urea-induced unfolding of C-terminal sequence variants. Substitutions of leucine to phenylalanine in the hydrophobic core in the background of full-length (left) and deletion construct N-15 (right), in LRR 15, in LRR 14, and in LRR 13. Conditions: 200 mM NaCl, 20 mM Tris-HCl (pH 7.6), and 0.01 mM TCEP.

Limited proteolysis to probe structure formation in C-terminal deletion constructs

Resistance to mild proteolytic cleavage has been correlated to formation of local structure and stability.^20,21 To further investigate the distribution of structure, and test the partial unfolding model, C-terminal deletion constructs of YopM were subjected to a time course of limited proteolysis with trypsin, as monitored by SDS-PAGE [Fig. 6(A–C)]. Masses of proteolytic fragments were identified by matrix assisted laser desorption ionization time-of-flight mass spectrometry (MALDI-TOF MS). The masses of the fragments were mapped to specific segments of YopM by comparison to masses of potential cleavage products of constructs by trypsin [Fig. 6(D) and Supporting Information Table SII]. There are 24 potential trypsin cleavage sites, within the structured region of YopM. Although these cleavage sites are not distributed evenly, 10 of the 15 LRRs of YopM have at least one potential site. Thus, even though we cannot probe proteolytic susceptibility within each LRR, the distribution of sites allows us to probe the structural integrity of each of the segments that are proposed to become unstructured in the partial unfolding model (see Fig. 4).

Figure 6.

Limited tryptic digests identifies locally unfolded regions. (A) SDS-PAGE of untreated constructs. (B) SDS-PAGE of constructs digested with trypsin for 30 s. (C) SDS-PAGE of constructs digested with trypsin for 180 s. (D) Fragments identified by MALDI-TOF MS from C-terminal deletion constructs digested with trypsin for 180 s. The full-length YopM construct is shown with repeats colored as in Figure 1(B). Fragments identified by MALDI-TOF MS (filled rectangles) are colored the same as the C-terminal most LRR of the C-terminal deletion construct (open rectangles) from which the fragments originated. Potential trypsin cleavage sites are indicated along the C-terminal deletion constructs (red). Measured and predicted masses are in Supporting Information Table SII. In panel D, the red asterisks show fragments with masses between 32.6 and 34.7 kDa and the black crosses show fragments with masses around 21 kDa. The corresponding bands in panels B and C are indicated with the same symbols.

Constructs show different levels of resistance to proteolytic cleavage over the time course of digestion [Fig. 6(A–C)]. The two constructs containing the β-strand cap (full-length and N-β-cap) modestly decrease in mass, especially at short digestion times. The major cleavage product for N-β-cap, at ∼41 kDa, retains all C-terminal residues through the β-strand cap, but is lacking disordered residues at the N-terminus, as identified by MALDI-TOF MS (Fig. 6, Supporting Information Table SII). The major cleavage product for full-length YopM is of similar size that of N-β-cap. These results suggest that the β-cap protects sites in repeats 15, 14, and 13 from proteolysis. In contrast, the N-terminal histidine tag, the leader sequence, and the C-terminal NLS are not well protected from proteolysis, and are thus likely to be unstructured.

On removal of the β-strand cap (constructs N-12 through N-15), the extent of proteolysis increases, resulting in a persistent band around 34 kDa. This band corresponds to a combination of fragments with various C-termini in LRR 15, 14, 13, and part of 12 [Fig. 6(D), Supporting Information Table SII]. This increased susceptibility suggests that the β-cap is required to protect LRRs 13–15 from proteolysis, consistent with the partial unfolding model (see Fig. 4). In contrast, the trypsin site in LRR 10 remains protected, indicating that this more central region of the molecule can remain folded in the absence of the β-cap.

Although further deletion of LRRs 15 through 12 results in the appearance of some smaller proteolytic products, all of these intermediate constructs retain protection at LRR 10, suggesting that the trypsin site in LRR 10 retains at least some protection from proteolysis. In contrast, on removal of LRR 11, protection at LRR 10 is lost, as is protection at a trypsin site in LRR 9. Constructs lacking LRR 11 (constructs N-6 through N-10) show proteolytic susceptibility in LRR 7 (giving rise to a band around 21 kDa), but show protection from proteolysis at a site in LRR 5, again consistent with the partial unfolding model. In summary, the abrupt change in proteolytic susceptibility on removal of the β-strand cap and LRR 11 is consistent with the stepwise behavior seen in CD spectra and urea-induced unfolding transitions.

Discussion

Numerous studies have revealed and explored the origins of a high level of cooperativity in α-helical repeat-protein folding.^{2,3,5,6,22–25} Two factors have been shown to contribute to this cooperativity: strongly stabilizing interfaces between intrinsically unstable repeats,^3,5 and an even distribution of stability on a medium length scale.^6,7,24,25 For β-sheet-containing repeat proteins, although studies are limited, there are examples of both two-state and multistate equilibrium folding, with the latter being more common than for α-helical repeat proteins.

Unlike α-helical repeat proteins, the origins of cooperative versus multistate folding in β-sheet-containing repeat proteins are not known. For internalin B and YopM (the two LRR proteins for which two-state folding has been demonstrated^10–12), N-terminal α-helical caps are important for folding kinetics¹³ and regular secondary structure formation (unpublished observation), respectively. However, systematic studies examining structural and thermodynamic consequences of removal of C-terminal β-strand caps and repeats of these proteins have not been reported. Here, we have shown that not only is the C-terminal β-strand cap critical for maintaining structural integrity, but also that internal caps are necessary for maintaining secondary structure over the length of YopM. Unlike comparable terminal deletion studies in ankyrin repeat proteins,^3,26,27 partial unfolding as a result of LRR removal appears to be the norm in YopM rather than the exception.

C-terminal and internal caps maintain structural integrity of YopM

Despite their similarity in sequence and structure,¹⁴ we have shown that individual LRRs contribute unevenly to the overall thermodynamic stability of YopM. Even for LRRs 6 and 8, which have 86.4% sequence identity, the consequences of C-terminal deletion differ significantly. We have identified three separate regions where structural integrity is lost when a C-terminal flanking repeat is removed. These regions are: N-5, LRRs 7–10, and LRRs 12–15. The folding of each of these regions is highly coupled to the folding of adjacent key caps: LRR 6 for N-5, LRR 11 for LRRs 7–10, and the β-cap for LRRs 12–15.

This heterogeneous distribution of stability is depicted in a partial unfolding model (see Fig. 4). The C-terminal β-strand cap acts as a buttress, forming a direct interface with LRR 15, which maintains the folding of LRRs 14, 13 and at least part of 12. This conditional folding is supported by CD spectroscopy [Fig. 2(A)], thermodynamics (Table I and Fig. 3), thermodynamic response to point substitutions (see Fig. 5), and proteolytic susceptibility (see Fig. 6). The removal of LRR 12 is slightly destabilizing (Table I), suggesting that it remains partially folded. From MALDI-TOF MS, N-12 is cleaved in the middle of the LRR 12. From these data, it appears that LRRs 13–15 unfold, as does at least part of LRR 12, with removal of the β-cap (see Fig. 4). Partial unfolding does not appear to propagate past LRR 11, which remains folded based on the far-UV CD spectrum of N-11 [Fig. 2(A)], its contribution to stability (Table I and Fig. 3), and the protection it provides to the cleavage site in LRR 10 from proteolysis [Fig. 6(A–D)].

Without LRR 11, structure in LRR 7 through LRR 10 is disrupted. Although the far-UV CD spectrum of N-10 has more characteristic β-strand secondary structure than N-6, it is no more stable based on urea-induced unfolding transitions (Table I). In addition, unlike N-11, N-10 is readily proteolysed to the same 21 kDa fragment as N-7 [Fig. 6(B–D)]. C-terminal deletion constructs ending in LRRs 7, 8, and 9 all have similar far-UV CD spectra [Fig. 2(A)] and stabilities (Table I). In addition, constructs N-7 through N-10 all form a protease resistant fragment ending in the middle of LRR 7 [Fig. 6(D)], indicating a loss of structure at least to this point. Thus, like the β-cap, LRR 11 forms an internal cap through its interface with LRR 10, and maintains the structural integrity of LRRs 7–10.

Similar to LRR 12, LRR 7 shows some contribution to stability [Table I; Fig. 6(A–D)]. On deletion of LRR 7, LRR 6 does not unfold, but instead appears to contribute to stability and proteolytic resistance. Similar to deletion of LRR 11, on deletion of LRR 6, the secondary structure appears to contain a large portion of unfolded polypeptide [Fig. 2(A)], and urea-induced unfolding transitions reveal a further decrease in stability. From near-UV CD, most of the rigid tertiary structure around the two N-terminal tryptophans is maintained [Fig. 2(B)]. However, N-5 demonstrates some resistance to proteolysis [Fig. 6(B–D)]. A protected proteolytic fragment of N-5 includes nine residues of the N-terminal α-helical cap through the first residue of LRR 5 [Fig. 5(D)], suggesting a significant population is folded (see Fig. 4). On deletion of LRR 5 the folded population is significantly decreased, based on far- and near-UV CD spectra (see Fig. 2) and urea-induced unfolding transitions (see Fig. 3). A further decrease in the folded population occurs on the removal of LRR 4 based on far- and near-UV spectra (see Fig. 2). The partial unfolding model (see Fig. 4) depicts the most populated configuration as interpreted from our results.

Three-segment model and cooperativity

Given the high level of cooperativity in full-length YopM,¹² partial unfolding of LRRs on removal of key terminal and internal caps is rather surprising. Our studies here define a stability profile of YopM containing at least three relatively unstable segments, approximately four LRRs long. These results suggest that two interfaces located between the segments are not stabilizing enough to drive the folding of the C-terminal LRRs in deletion constructs. To explore how cooperativity can be maintained despite this apparent internal instability, we developed a three-segment statistical thermodynamic model. This model incorporates stability constraints from the C-terminal deletion studies, but the distribution within locally unstable segments to vary, allowing us to determine which (if any) distributions can support two-state folding. From this analysis, we find that cooperativity is maintained over the length of YopM when the two interfaces are stabilizing and the intervening segments are relatively unstable.

Although our deletion series does not contain enough independent stability measurements to uniquely determine stability parameters for each repeat, the three fully structured constructs (N-6, N-11, and N-β-cap; Fig. 4) provide reasonable stability estimates for the corresponding segments, and by subtraction, provide stability estimates for LRRs 7–11 and 12-β-cap, along with their adjoining interfaces. Moreover, the partly unfolded segments indicate that these two interfaces (between LRRs 6 and 7, and between LRRs 11 and 12) are relatively unstable (black boundaries, Fig. 7).

Figure 7.

Three-segment model to account for the cooperativity of YopM. (A) YopM is divided into three segments (N-6, LRRs 7–11, and LRR 12-β-cap; gray), which are coupled to each other through two interfaces (int 6/7 and int 11/12; black). The parameter j is used as a counting index for configurations in Eq. (2). The weight (w_j) for each configuration is a product of the equilibrium constants (defined in the text) for the folded segments and formed interfaces.

To investigate stability distributions for which cooperative behavior breaks down (i.e., when the three segments are no longer tightly coupled), we used parameters constrained by additivity (Table II) in the three-segment partition function [Eq. (A1)]. We simulated CD- and fluorescence-observed urea-induced unfolding transitions using Eq. (A2) [Fig. 8(A)]. Additivity of the free energies of folding was maintained, while progressively shifting the stability from the interfaces to the LRRs 7–11 and LRR 12-β-cap (Table II). Cooperativity decreases as stability is shifted away from these interfaces, as evidenced by deviation of CD and fluorescence curves, and fitted parameters (apparent and m-value) derived from the simulated curves. For example, when the free energy of folding is equally distributed between the interfaces and segment to the C-terminus (Table II), fitting a two-state model yields thermodynamic parameters of −6.28 kcal mol⁻¹ and −6.57 kcal mol⁻¹_, and m-values of 3.92 and 4.30 kcal mol⁻¹M⁻¹ for CD and fluorescence, respectively [Fig. 8(A)]. These simulated values significantly differ, both from each other and from experimental values (Table I), and the partially folded LRR 7-β-cap and LRR 12-β-cap configurations are significantly populated in the transition region [Fig. 8(B)].

Table II.

Thermodynamic Parameters Used as Input for the Three-Segment Model of YopM

	(kcal mol−1)
	Constraineda	Distributedb	m (kcal mol−1 M−1)
N-6	−1.68	−1.68	2.4
Interface 6/7	−5.78	−2.42	0
LRRs 7–11	0.95	−2.42	2.84
Interface 11/12	−4.95	−2.1	0
12-β-cap	0.75	−2.1	1.22

^aFree energies based on constraints described in text.

^bFree energies distributed equally between the interfaces and C-terminal segments.

Figure 8.

Simulated urea-induced unfolding transitions using a three-segment model. (A) Simulated urea-induced unfolding transitions monitored by CD (open circles, solid line) and fluorescence (x, dashed line) with constrained parameters for two-state unfolding (Table II) are coincident. Predicted urea-induced unfolding transitions monitored by CD (filled circles, solid line, gray) and fluorescence (filled diamonds, dashed line, gray), with the free energy of folding equally partitioned between interfaces and segments (Table II) are not coincident. Experimentally determined urea-induced unfolding transitions monitored by CD (filled squares, solid line) and fluorescence (open diamonds, dashed line). (B) Population plots with the free energy of folding equally partitioned between interfaces and segments. (C) Population plots for constrained parameters. For panels B and C, the j = 1–13 configurations (see Fig. 7) are represented as: filled circle, open circle, cross, x, vertical line, dash, open cross, open triangle pointed right, filled square, open upside down triangle, filled triangle, open triangle and filled diamond.

Additional constraints were obtained based on the assumption that unfolded segments have positive free energies (see Fig. 4). The details of these constraints are described in the Appendix section; limiting values are given in Table II. Using these constrained parameters (Table II) in the three-segment partition function [Eq. (1)], we simulated CD- and fluorescence-observed urea-induced unfolding transitions using Eq. (2) [Fig. 8(A)]. These curves are well-fitted by a two-state model and yield thermodynamic parameters of −10.52 kcal mol⁻¹ and m-values of 6.37 kcal mol⁻¹M⁻¹ for both CD and fluorescence, similar to those obtained experimentally (Table I). Populations through the transition region are dominated by fully folded and unfolded species [Fig. 8(C)].

In summary, these simulations show that although the interfaces between LRRs 6 and 7, and LRRs 11 and 12 are not stable enough to promote folding in C-terminal deletion constructs, they must indeed be stabilizing. Thus, the local instability of LRRs 7–11 and 12-β-cap in this format must be internal to these segments. This local instability is likely to result from a combination stabilizing interfaces and intrinsically unstable free energies of folding for individual LRRs. As seen with the Notch ankyrin domain,³ the LRRs of YopM maintain cooperativity when interfaces are more stable than the structural segments. The constraints described here capture the two-state behavior observed experimentally for YopM, and demonstrate that relatively unstable segments of YopM lacking direct physical contact can be tightly coupled through highly stabilizing interfaces, even though substantial segments become disordered on C-terminal deletion.

Biological relevance of partial unfolding

YopM is a bacterial virulence factor that enters a host cell through a type III secretion system, which has an inner diameter of 25 Å wide.^28–30 In its native state, YopM is ∼35 Å wide, and thus would be expected to be sterically incapable of translocation through the type III system. Instead, the Yersinia outer proteins have been speculated to be unfolded or partially unfolded to undergo translocation.²⁹ If YopM is translocated C-terminus to N-terminus, the unfolding of the terminal or internal caps may be sufficient to unfold large segments of YopM and may contribute to its ability to both be unfolded to enter the secretion system. If instead YopM is translocated N-terminus to C-terminus, the ability of parts of the protein to fold at the N-terminus when the C-terminal segments are unfolded may allow it to fold as it is translocated into the cytosol of the host cell.

Materials and Methods

Subcloning, protein expression, and purification

YopM was inserted into pET15b expression vector (Novagen, Madison, WI) from the pMal-C2 vector (New England Biolabs, Bevelery, MA). YopM primers with NdeI and BamHI restriction sites were added at the N- and C-terminus. The PCR product was gel purified, double digested with NdeI and BamHI and ligated into pET15b, resulting in the expression of the full length YopM polypeptide sequence in Figure 1(B). C-terminal deletion constructs and sequence point substitutions were made using Quikchange (Stratagene, La Jolla, CA) to introduce stop and phenylalanine codons, respectively.

All polypeptides were expressed in Escherichia coli (BL21 [DE3]) overnight at 20°C in TB,³¹ and were purified using a nickel-NTA (Qiagen, Valencia, CA) or HisTrap HP column on an AKTA purifier (GE Healthcare Bio-Sciences Corp., Piscataway, NJ). Fractions containing YopM were dialyzed to 20 mM NaCl, 20 mM Tris-HCl pH 7.6, 2 mM EDTA, 0.1 mM DTT, and were run on a HiTrap Q ion exchange column. YopM-containing fractions of greater than 95% purity, as judged by SDS-PAGE, were dialyzed into storage buffer (200 mM NaCl, 20 mM Tris-HCl pH 7.6, 0.1 mM Tris(2-carboxyethyl)-phosphine (TCEP)), concentrated using a VivaSpin 500 microconcentrator (Sartorius; Aubagne, France), passed through an 0.22 μm filter, flash frozen, and stored at −80°C. Protein concentrations were determined as described by Edelhoch.³²

CD spectroscopy and urea-induced unfolding transitions

CD spectra were collected on an Aviv 62A DS spectropolarimeter (Lakewood, NJ) and a Jasco J-810 spectropolarimeter (Easton, MD). Far- and near-UV CD spectra were collected in 0.1 and 1.0 cm cuvettes with protein concentrations of 10–24 and 20–30 μM, respectively, in storage buffer at 25°C. Spectra were obtained by signal averaging for 20 s every 1.0 nm.

Urea-induced unfolding transitions

Urea-induced unfolding transitions were monitored by CD at 217 nm on an Aviv 62A DS or 410 CD spectrometer. Tryptophan fluorescence was monitored using an excitation wavelength of 280 nm with an emission filter at 320 nm on an Aviv 62A DS or 410 CD spectrometer, or by selecting 320 nm emission with an 6.40 nm bandwidth on an Aviv ATF 105 spectropolarimeter. Urea purchased from Amresco (Solon, OH) was stirred with mixed-bed resin (Bio-Rad; Hercules, CA) as described in Street et al.³³ Urea concentration was determined by refractometry.³⁴ Urea titrations were carried out automatically using a computer controlled Microlab syringe titrator (Hamilton Company, Reno, NV) to deliver buffered urea solutions (containing protein) into a buffered protein sample. At each urea concentration, samples were equilibrated for 5 min at 25°C, and CD and fluorescence signals were averaged for 30 s. For each titration, protein stocks were diluted with fresh storage buffer to a concentration of 1–3.2 μM.

Two-state analysis of equilibrium urea-induced unfolding transitions

Equilibrium urea-induced unfolding transitions were related to the equilibrium constant for unfolding assuming a population-weighted average of the signal of the native (Y_N) and denatured (Y_D) signals:

(1)

where f_N and f_D are the fraction of native and denatured protein, and K_u represents the equilibrium constant for folding. Y_N and Y_D are assumed to have linear dependence on urea are represented as: Y_N = a_N + b_N[urea] and Y_D = a_D + b_D[urea]. The equilibrium constant for folding is related to the reaction free energy by the standard formula:

(2)

The two-state model was fit to data from CD and fluorescence signals were expressed by combining Eqs. (1) and (2):

(3)

Thermodynamic parameters were estimated using the linear extrapolation method,^34,35 in which the free energy of folding varies linearly with urea concentration^34–36:

(4)

Equation (4) was inserted into Eq. (3), which was then fitted to unfolding transitions using the nonlinear least-squares tool of Kaleidagraph 3.4 (Synergy Software, Reading, PA).

Limited tryptic digests

YopM full-length and C-terminal deletion constructs were diluted with storage buffer to 10–27 μM, depending on the size of the construct. Trypsin (Sigma-Aldrich, St. Louis, MO) was diluted to a final concentration of 0.96 μM as determined gravimetrically. Digests were incubated at room temperature in storage buffer. Aliquots of samples were removed at various time points and quenched with a final concentration of 25 mM PMSF in 25% isopropanol. All samples were immediately flash frozen and stored at −80°C. Precast Tris-HCl gels (10–20% acrylamide) were purchased from Bio-Rad to run undigested and digested samples.

Identification of tryptic fragments by MALDI-TOF mass spectrometry

To identify fragments produced from trypsin digests, samples were analyzed using MALDI-TOF mass spectrometry. An Applied Biosystems MALDI 100 plate was spotted with 1 μL of sinapinic acid matrix (Sigma-Aldrich) and air dried. Samples were rapidly thawed, were mixed at a 1:1 ratio of 50% acetonitrile and 0.1% TFA, were spotted on the matrix, and were air dried. An additional 1 μL of matrix was spotted on top of the sample and allowed to dry. Calibration mixture 3, containing insulin (5734.5 Da), thioredoxin (E. coli) (11,674.48 Da), and apomyoglobin (16,952.56 Da), was used to calibrate a Voyager DE-STR MALDI-TOF (Applied Biosystems, Foster City, CA). The average mass of peaks matched to predicted peptide masses from MS-DIGEST (Baker, P.R. and Clauser, K.R. http://prospector.ucsf.edu).

Appendix

Three-Segment Model

Treating the three segments (N-6, N-11, and N-β-cap; Fig. 4) and two interfaces (between LRRs 6 and 7, and between LRRs 11 and 12) as separate folding (and association) reactions gives 13 conformations, which can be represented by a configurational partition function:

(A1)

where K_N-6, K_7–11, and K_12-β-cap are intrinsic equilibrium constants for folding of the three segments, and K_int6/7 and K_int11/12 are equilibrium constants for the interfacial interactions between folded segments.

Equilibrium constants for each of the three segments are assumed to vary exponentially with urea concentration, imparting the usual linear denaturant dependence on corresponding folding free energies. As an example, the free energy of folding of the N-6 segment is represented by:

where is the value for folding of N-6 in the absence of urea, and m_N-6 is the urea sensitivity of this change in free energy. To simplify the model, the interfacial equilibrium constants and associated free energies are assumed to be independent of urea.³,⁶,³⁷

The free energy of folding and m-values for N-6, N-11, and N-β-cap are taken directly from fitted transitions for each corresponding construct (Table I). If we assume the m-values to be additive, the urea dependences are determined by simple subtraction and are listed in Table II. The free energy of folding for each segment and interface is constrained by the additivity relationship defined in the model (see Fig. 7), and the measured free energies of C-terminal deletion constructs (Table I).

To simulate folding transitions with the three-segment model, the observed spectroscopic signals (CD and fluorescence) are represented as the population-weighted sum of the signals of the individual conformational states (j, Fig. 7):

(A2)

where w_j and Y_j are the statistical weight and spectroscopic signal, respectively, of the jth conformational state and q is the partition function [Eq. (1)]. The CD signal is assumed to be uniformly distributed on a per-residue basis. The fluorescence is assumed to monitor the folding of the N-6 segment, which contains the only two tryptophans in YopM [Figs. 1(B) and 7].

Constraints for the three-segment model were defined using experimentally determined free energies of folding and m-values. In addition, some assumptions were made based on experimental observations. The free energy of folding and m-values for N-6, N-11, and N-β-cap are taken directly from fitted transitions for each corresponding construct (Table I). Assuming the m-values to be additive, the urea dependence of LRR 7–11 and LRR 12-β-cap are:

and

Assuming the free energy of folding to be additive, the difference between folding free energies of N-6 and N-11 is equal to the free energies of folding for LRR 7–11 and the 6/7 interface:

(A3)

Likewise, the difference between folding free energies of N-11 and N-β-cap is equal to the folding free energies of LRR 12-β-cap and the interface 11/12 is:

(A4)

Based on the observation that LRR 1-β-cap does not fold without an N-terminal α-helical cap ( > 0; unpublished), free energies of the smaller fragments lacking the α-helical cap are expected to be positive. Constraining and 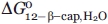to values greater than or equal to zero in Eqs. (A3) and (A4), provides upper limits for and of less than or equal to −4.83 and −4.20 kcal mol⁻¹, respectively.

Additional free energy constraints come from the observation that the segment LRR 7–10 unfold on removal of LRR 11, and that the segment LRR 12–15 unfolds on the removal of the β-cap (see Fig. 4). The interface between LRRs 6 and 7 is not stabilizing enough drive folding of LRRs 7–10, constraining the sum of the interface and the segment to be:

(A5)

Introducing the upper limit that ≤ −4.83 to Eq. (A3) gives ≥ 4.83. Adding the value for and :

sets a lower bound for the segment free energy of folding of the segment LRR 7–11:

This value is inserted into Eq. (A2), limiting to less than or equal to −5.78 kcal mol⁻¹.

Similarly, the interface between LRRs 11 and 12 is not stabilizing enough drive folding of LRRs 12–15, constraining the sum of the interface and the segment to be:

(A6)

Introducing the upper limit that ≤ −4.2 kcal mol⁻¹ to Eq. (A6) gives ≥ 4.2 kcal mol⁻¹. Adding the value for and :

sets the lower bound for the segment free energy of folding of LRR 12-β-cap:

This value is inserted into Eq. (A5), limiting to less than or equal to −4.95 kcal mol⁻¹.