Ultrasound Simulation of Real-Time Temperature Estimation during Radiofrequency Ablation using Finite Element Models

Abstract

Radiofrequency ablation is the most common minimally invasive therapy used in the United States to treat hepatocellular carcinoma and liver metastases. The ability to perform real-time temperature imaging while a patient is undergoing ablation therapy may help reduce the high recurrence rates following ablation therapy. Ultrasound echo signals undergo time shifts with increasing temperature due to sound speed and thermal expansion, which are tracked using both 1D cross correlation and 2D block matching based speckle tracking methods. In this paper, we present a quantitative evaluation of the accuracy and precision of temperature estimation using the above algorithms on both simulated and experimental data.

A finite element analysis simulation of radiofrequency ablation of hepatic tissue was developed. Finite element analysis provides a method to obtain the exact temperature distribution along with a mapping of the tissue displacement due to thermal expansion. These local displacement maps were combined with the displacement due to speed of sound changes and utilized to generate ultrasound radiofrequency frames at specified time increments over the entire ablation procedure. These echo signals provide an ideal test-bed to evaluate the performance of both speckle tracking methods, since the estimated temperature results can be compared directly to the exact finite element solution. Our results indicate that the 1D cross-correlation (CC) method underestimates the cumulative displacement by 0.20 mm, while the underestimation with 2D block matching (BM) is about 0.14 mm after 360 seconds of ablation. The 1D method also overestimates the size of the ablated region by 5.4% when compared to 2.4% with the 2D method after 720 seconds of ablation. Hence 2D block matching provides better tracking of temperature variations when compared to the 1D cross-correlation method over the entire duration of the ablation procedure. In addition, results obtained using 1D cross-correlation diverge from the ideal finite element results after 7 minutes of ablation and for temperatures greater than 65°C.

In a similar manner, experimental results presented using a tissue-mimicking phantom also demonstrate that the maximum percent difference with 2D block matching was 5%, when compared to 31% with the 1D method over the 700 second heating duration on the phantom.

INTRODUCTION

Hepatocellular Carcinoma (HCC) is the fifth most common cancer in men and the eighth most common cancer in women worldwide with more than 500,000 new cases of HCC reported each year [1]. HCC is currently the fastest growing cancer type in the United States and is expected to increase over the next 15 years due to Hepatitis C infections [2, 3]. In addition, most patients who do not receive treatment, do not survive longer than a year after being diagnosed with HCC [1].

The two primary treatments for HCC are surgical resection and liver transplantation. Surgical resection is not performed for large tumors, presence of multiple tumors or if the patient is not amenable or a candidate for surgery. Since differentiating between benign liver nodules and malignant tumors during early HCC is difficult, surgical resection may not be a viable option in many cases. Liver transplants are limited by availability of liver tissue for transplant procedures when compared to large number of candidates for this surgery. The above problems with the two primary treatment options have led the medical community to develop alternative minimally invasive procedures for treating HCC and other liver metastases.

Minimally invasive procedures destroy HCC tumors without damaging surrounding healthy liver tissue. The six main types of minimally invasive procedures used to treat HCC include microwave ablation [4-12] laser-induced thermotherapy (LITT) [4, 5, 13-15], cryoablation [4, 16], percutaneous ethanol injection therapy (PEIT) [17, 18], high-intensity focused ultrasound (HIFU) [19-22] and radio-frequency (RF) ablation [4, 17, 18, 23, 24]. RF ablation is the most commonly used minimally invasive therapy in the United States for treatment of HCC. RF and cyroablation are also the only minimally invasive therapy procedures currently approved by the FDA for treating HCC.

Initial insertion of the RF probe is usually conducted under ultrasound guidance, since it offers a fast and effective method of monitoring the insertion of the probe into the tumor in real-time. CT guidance of RF ablation has been used in many centers, however, the number of scans that can be performed under CT guidance is limited by the amount of contrast agent that can be injected (due to possible renal failure) and concerns regarding the radiation dose to both patient and physician. Following insertion, MRI has been utilized to perform temperature imaging for RF ablation, however it is expensive and currently limited by availability of FDA approved MRI compatible RF probes [25, 26]. On the other hand, no effective methods for determining the ablated region using ultrasound exist. For instance, ablated areas after the procedure have been described to be hypo-echogenic, hyper-echogenic or to have the same echogenicity before and after the RF ablation procedure [24].

Several methods for measuring temperature-dependent ultrasonic parameters have also been proposed in the literature for temperature imaging [27-36]. These methods range from tracking attenuation changes [27-29], tracking frequency shifts in the harmonics of the center frequency [31], measuring changes in backscattered energy [32] and tracking echo-shifts in the ultrasound echo signal due to thermal expansion and speed of sound (SOS) changes [33-36]. From in vitro experimentation, Arthur et al. [32] show that variations in backscattered energy are proportional to temperature ranges from 40°C to 50°C. To overcome echo shifts due to SOS change and thermal expansion, manual motion compensation was performed to align the echoes during their study. It has also been reported that, frequency shift methods fails for temperature changes greater than 20°C (for ablation monitoring we frequently encounter temperature elevations of approximately 60°C, i.e. 37°C to ~100°C) [31].

Feasibility of ultrasound-based temperature imaging was previously demonstrated by Varghese et. al. [33] using accumulated echo shifts along with a single valued displacement gradient-temperature calibration curve [34]. This calibration curve provides a conversion between displacement gradients due to SOS and thermal expansion changes to a temperature measurement. Prior knowledge of the thermal expansion coefficient for tissue and SOS changes with temperature are required for this method of temperature tracking. Utilizing the calibration curve they were able to use speckle tracking algorithms such as 1D cross-correlation (CC) [33, 34, 37] to track local displacements and finally obtain temperature distributions. In this paper, we demonstrate the accuracy of temperature estimated using 1D CC [38] and 2D block matching using sum squared differences (SSD) [39] algorithms by comparing estimated temperature values to exact temperature distribution simulated by Finite Element Analysis (FEA) for RF ablation procedures. We also show that these methods can non-invasively estimate a broader range of temperatures (i.e. 37°C to ~100°C) accurately over the entire 12 minute ablation duration than has been previously demonstrated.

Prior ultrasound based experimental work on temperature imaging [33, 36] has been performed in vivo and in vitro in liver tissue. In this paper we utilize an FEA model of RF ablation to generate both temperature and tissue displacement maps induced by thermal expansion and SOS changes. Displacement maps due to both thermal expansion and SOS changes are then fed into an ultrasound simulation program to generate raw radiofrequency data. Both 1D CC and 2D block matching methods are then applied to the radiofrequency echo data to estimate the composite or cumulative displacement. Following displacement estimation a linear least squares approach is used to estimate the gradient of the axial displacement. The calibration curve is then used to convert these gradients into temperatures maps that are compared to the ideal FEA generated temperature maps. In this paper we present the accuracy and precision of using displacement gradients to track temperature distributions obtained using FEA, from ultrasound simulations. It should be noted that ‘ideal’ for the purposes of this paper refers to the exact FEA solution for the RF ablation geometry presented in the paper. The 1D CC and 2D block matching based speckle tracking methods strive to replicate the exact or ‘ideal’ solution by tracking and accumulating the displacements over the entire duration of the ablation procedure and estimating the temperature distribution that is compared to the ‘ideal’ FEA solution. Both the 1D CC and 2D block matching temperature estimation methods are also evaluated on experimental radiofrequency data acquired during an ablation procedure on a tissue-mimicking (TM) phantom.

FINITE ELEMENT ANALYSIS OF RF ABLATION

Method

The RITA 1500 probe was modeled using commercially-available FEA software ANSYS (ANSYS Inc., Pittsburgh, PA). The RITA 1500 is a multi-tine single needle electrode, where the single needle is inserted into the tumor, and multiple NiTi tines are deployed from the end of the needle into the tumor volume. The tines can be deployed to ablate volumes ranging in diameter from 2 cm to 6 cm. Upon successful ablation the tines are withdrawn into the needle, and the exit track is cauterized as the needle exits the patient.

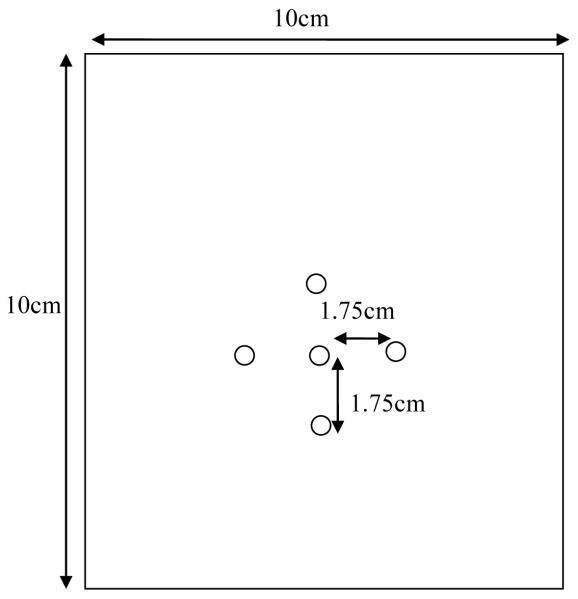
In this simulation, a 10×10 cm 2D model of normal liver was created. Thermal and electrical properties of normal liver can be found in Table 1 below [40]. A fine mesh (2×2 mm maximum grid spacing) grid was selected in ANSYS to ensure sufficient grid points to adequately sample the 10 ×10cm liver section modeled. The two-dimensional 4-node thermal-electrical element (PLANE 67 in ANSYS) was chosen for the liver tissue. Five Nickel Titanium (NiTi) RF electrode tines with diameters of 0.5334 cm were placed in the modeled liver tissue. The electrode tines were attached to the surrounding liver tissue in ANSYS to ensure that thermal, electrical and structural contact between the tines and the liver was made. The same element type PLANE 67 was also utilized to model the tines. The tines were assigned the material properties found in Table 1 [40] for NiTi. All boundary conditions and simplifications described below were designed to mimic heating of a 2D slice in a 3D cube of hepatic tissue (10cm ×10cm × 10cm). The fine mesh setting was used in ANSYS to ensure that there were enough nodes connecting the tines and liver tissue. In the general model, one electrode tine was placed at the center of the liver tissue with the other four electrode tines being placed 1.75 cm above, below and to the right and left of the central electrode, as illustrated in Figure 1. This represents the maximum spacing of the tines for the RITA 1500 system.

Table 1.

Thermal and Electrical Properties of the Materials in the FEA Model

FEA Region	Material	ρ(kg/m3)	c (J/kg·K)	k(W/m·K)	σ (S/m)
Electrode	Ni-Ti	6450	840	18	1×108
Tissue	Liver	1060	3600	0.512	0.333
Blood	Blood	1000	4180	0.0543	0.667

Figure 1.

Schematic diagram of FEA simulated liver tissue and RF electrode tines.

The outer boundaries of the FEA liver model was set to zero volts using the Dirichlet boundary conditions, i.e. the voltage function must be zero at all four edges of 2D model of the liver [40]. An initial temperature of 37°C was applied to the entire model, to mimic baseline body temperature. A voltage was then applied to the tines and FEA software used to solve the bioheat equation, using the thermal-electrical model in ANSYS. The bio-heat equation can be written as:

$$\rho c\frac{\partial T}{\partial t}=\nabla •k\nabla T+\stackrel{‒}{J}•\stackrel{‒}{E}-h_{\mathit{bl}}(T-T_{\mathit{bl}}),$$ (1)

where $\stackrel{‒}{J}•\stackrel{‒}{E}=\sigma {(\nabla V)}^2$ is evaluated at six second time steps, V represents the voltage distribution of the FEA model, T denotes the temperature, while the term $\stackrel{‒}{J}•\stackrel{‒}{E}$ represents a distributed heat source, where J is the current density, E is the electric field [41], T is the temperature of the hepatic tissue, and T_bl is the temperature of blood. The term h_bl denotes the convective heat transfer coefficient for blood perfusion given by h_bl = ρ_blc_blw_bl, where ρ_bl is the density of blood, c_blis the specific heat of blood and w_bl is the blood perfusion of hepatic tissue. The blood perfusion term is on the order of -1.7 × 10^-3W / mm³. Literature values shown in Table 1 were used for the density (ρ), specific heat (c), thermal conductivity (k), and electrical conductivity (σ) for liver, blood and Ni-Ti, in addition to the blood perfusion (w_bl) term of 6.4 × 10³1/ s . Equation (1) relates changes in tissue temperature with ablation duration, due to tissue heating generated from an oscillating electric field. The six second time step was chosen to demonstrate feasibility of monitoring the RF ablation procedure using larger time steps when compared to previous work where a 0.5 second time step with 1D CC was utilized [33, 36]. Use of the larger time-step, significantly reduces processing time thereby enabling real-time temperature estimation and display.

The ablation model described in this paper is similar to the RF ablation FEA models developed by Jain [42], and Tungjitkusolmun et al. [43], but simplified since the term dealing with heat loss due to blood perfusion is ignored. This model is an accurate representation of RF ablation of the liver with blood flow occluded. The average voltage applied to the tines was 28.37 volts which agrees with the voltage level of 30 V used by Tungjitkusolmun et al. [43] for a similar FEA simulation. Note that effects of carbonization, which occurs when liver tissue reaches temperatures of 100°C and higher are not taken into consideration. This is due to the fact that the impact of carbonization or vaporization changes on liver material properties is not currently known. Moreover, most RF ablation electrodes (including the RITA 1500) have onboard temperature controllers that inhibit temperature increases > 100°C, as carbonization significantly reduces thermal lesion size and therefore effectiveness of the ablation procedure.

The FEA model is switched from a thermal-electrical model to a thermal-structural model. In ANSYS this was performed by changing the element type from the PLANE 67 thermal-electrical element to the two-dimensional 4-node thermal-structural element (PLANE 42). The structural and thermal parameters used for both the NiTi tines and the normal liver can be found in Table 2 below [34, 44]. Temperature distributions obtained at each time step are then applied to the model and used to calculate displacements due to the thermal expansion using the boundary conditions described below. The plane stress condition was used to calculate thermal expansion, allowing the simulated 2D object to expand in the third dimension with no constraints. The plane stress condition fully satisfies the equilibrium equations in solid mechanics and is often used for simplification. All tissue thermal properties were obtained from Techavipoo et. al. [45] experimental data on canine livers.

Table 2.

Thermal and Structural Properties of the Materials in the FEA Model

FEA Region	Material	Young’s Modulus (kPa)	Poisson’s Ratio	Thermal Expansion (/K)
Electrode	Ni-Ti	7.14×107	0.33	1.00×10-6
Tissue	Liver (37°C)	4.52	0.4995	N/A
	Liver (70°C)	18.0	0.4995	5.46×10-4
	Liver (80°C)	13.2	0.4995	1.97×10-3
	Liver (90°C)	29.3	0.4995	1.75×10-3

For the ANSYS FEA simulations, the specified boundary conditions are described below. For this model, the center of the model was assumed to be fixed and tissue allowed to expand out from the center of the heat source. Hence tissue above this point expands towards the transducer, and tissue below this point expands away from the transducer. This leads to a positive gradient of the displacement from the transducers reference frame. Material parameters from the peer-reviewed literature for the Young’s modulus, Poisson’s ratio, thermal expansion coefficient, and thin film coefficient values shown in Table 2 [34, 44], are utilized in this part of the simulation. Mechanically, the tines are perfectly bound to the treated tissue, due to protein denaturation. Hence, a linearly elastic model listed in Table 2, as first approximation, is appropriate to investigate the interaction between the tines and tissue. Displacements due to thermal expansion are then saved for each 6 second time step of the FEA simulation. The apparent displacement due to changes in the SOS with temperature are obtained from a 2^nd order polynomial fit of the experimental data relating the SOS changes to temperature data shown in Table 3 [28]. The FEA was performed only once, since the FEA temperature and displacement results are deterministic and do not change for given boundary conditions and thermal loading.

Table 3.

Speed of sound vs. temperature values for normal canine liver tissue

Liver
Temperature (°C )	Speed of sound in Liver (m/s)
37	1597.77
50	1600.64
60	1601.84
70	1599.93
80	1593.88
90	1585.35

Cumulative displacement estimates or maps that incorporate both the apparent displacement due to SOS changes and local displacements from thermal expansion obtained from the FEA simulation are generated. The resulting composite displacement estimates are then fed into an ultrasound simulation program as described below.

Ultrasound Simulation

A simulation phantom containing scatterers significantly smaller than the wavelength and dense enough to ensure Rayleigh scattering was used [46, 47]. The density of scatterers was 9900×10⁶ scatterers/m³. Scatterers were randomly distributed throughout the phantom. For each time step, the composite displacement estimate was applied to the computer-simulated phantom and the scatterer positions displaced accordingly. Scatterer position information that has been altered based on the cumulative displacement, was then fed into the 2D frequency domain ultrasound simulation program developed by Li and Zagzebski [46]. The transducer modeled was a linear array transducer with a center frequency of 5 MHz, and a 90% bandwidth. The linear array transducer was placed on the top surface of the phantom, and consists of 475 rectangular elements, with each element having a 2mm width and a 10 mm height. The (elevation) slice thickness in the ultrasound simulation was set at 1.5-cm. The transducer was focused at a depth of 90mm in tissue. Radiofrequency echo signal frames were digitized using a sampling frequency of 26 MHz. The ultrasound imaging parameters used are typical of modern real-time clinical ultrasound scanners. Attenuation was simulated to be 0.5dB/cm/MHz and a SOS of 1597.8 m/s (SOS in liver tissue at 37°C) [28] was used. The size of the resulting ultrasound simulation field was 120 by 105 mm. The diameter of the tines in the RF ablation electrode was 0.5334 mm which is close to the point spread function (0.7-mm (axial) 2.2-mm (lateral) at -6 dB) of the ultrasound system used in this study and is therefore not resolved in the B-mode images. Our imaging experience using the RF ablation probe on TM phantoms and liver tissue, indicates the tines are readily observed only when they are moved, corroborates this result. The ultrasound simulation was repeated five times to study its repeatability and to perform statistical analysis of the results.

After obtaining raw radiofrequency echo signal data loops over the entire ablation duration, for the specified time step, both 1D CC and 2D block matching algorithms were applied to estimate and accumulate local displacements over the entire data set. The 1D CC method uses a two-step 1D CC algorithm to estimate local displacements [48]. The first step uses a larger window size (15 wavelengths) in order to determine gross displacements. These gross displacements are then used to guide the second displacement estimation step that uses a significantly smaller window size (4 wavelengths) for better resolution and sensitivity. The 2D block matching [49] method relies on a modified tracking algorithm developed for real-time strain imaging. It uses a predictive search algorithm that limits the search area of the tracking kernel based on the result of the previous displacement estimate. It also checks for consistency between displacement estimates before moving from one search row to the next. The input parameters to the 2D block matching algorithm were the length of the gated A-line (axial length of the kernel), kernel width and correlation technique namely block-matching. For the results shown in this paper, a window length of 4 wavelengths and lateral kernel width of 7 wavelengths was chosen.

Echo shifts in the RF data over consecutive frames of radiofrequency echo data were calculated sequentially (using both the speckle tracking methods mentioned above), e.g. the echo shift between 0 and 6 seconds of ablation was computed, then the echo shift between 6 and 12 seconds of ablation etc. The total or cumulative displacement for a spatial location from the start (0 seconds) of the ablation procedure to the current frame was obtained by accumulating these frame-to-frame echo shifts and tracking the motion trajectory. This is done until all the echo shifts over the entire 720 seconds of the ablation procedure were accumulated. This method of using successive frames allows the accumulation of large displacements over time effectively, while maintaining accuracy in the displacement estimation. After every 6 second time steps, the gradient of the cumulative displacement was computed and the displacement gradient versus temperature calibration curve [34] was used to convert the gradient value to a temperature estimate [33]. The displacement gradient versus temperature calibration curve was calculated based on experimental ex vivo measurements of the thermal expansion and SOS changes with temperature of liver tissue. These parameters are required apriori and have to be determined for each tissue type undergoing ablation. The change in temperature to the gradient of the displacement are related from the expression $G=(c_0∕c)(\delta d+1)-1$, where δd represents the normalized tissue expansion given by $\delta d=\frac{d_0-d}{d_0}$, c denotes the SOS of liver tissue at the elevated temperature, c_o is the speed of sound of the liver at 37°C, d₀ is the initial distance between two points in tissue, and d is the distance between two points in tissue at the elevated temperature. This creates a single-valued curve that relates the displacement gradient (G) to the change in temperature [34]. The curve is valid for a temperature range of 37°C-90°C. A lookup table is utilized to transform the gradient of the displacement to a temperature estimate. The same parameters were used to obtain displacement-gradient for both the 1D CC and 2D block matching algorithms.

FEA SIMULATION RESULTS

FEA Solution for RF ablation

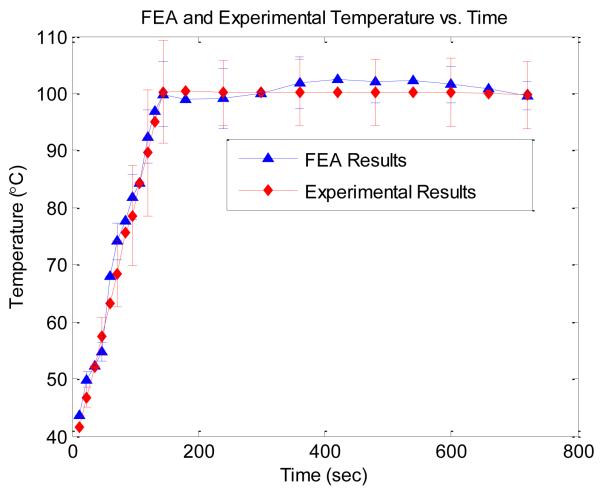
Figure 2, presents the average temperature of the five tines in the FEA simulation which matches well with experimental results acquired during an in-vitro experiment on canine hepatic tissue using an actual RITA 1500 RF ablation electrode. Use of the average or mean temperature at the tines represents one of the operating modes on the RITA 1500. This temperature is measured by the temperature sensors located at the tips of each of the tines of the RITA 1500 electrode providing real-time temperatures that were recorded. The average of these tines over an ablation procedure is the basis for the experimental data shown in Fig. 2. For the simulation data in Fig. 2, the average of the temperature of the tines was calculated at each respective time step. For a 12 minute ablation (representative of a standard ablation procedure) the 6 second time step results in 120 temperature maps. Note that the average temperature at the tines of the FEA simulation in Fig. 2, drops after 400 seconds, reflecting the lowering of the voltage applied at the tines. This process mimics the operation of the RITA 1500, which lowers the voltage to the tines to maintain tine temperatures at ~100°C.

Figure 2.

Comparison of the average tine temperature versus time for an actual experimental results and an FEA simulation.

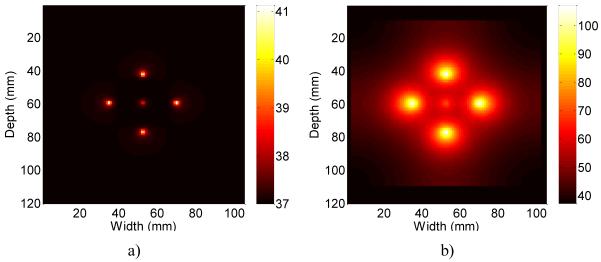
Two representative temperature maps at 6 (Fig. 3, a)) and 360 seconds (Fig. 3, b)) after the start of the ablation procedure are shown in Fig. 3. The middle tine in these images is at a lower temperature than the outer tines, due to the geometry of the simulated liver phantom. The electrical fields of the outer tines serve to limit the flow of current from the middle tine to the edges of the liver tissue block. This limited current flow in turn reduces the effectiveness of the middle tine when compared to the outer tines, in terms of the ability to heat up the surrounding liver tissue. The central tine therefore remains at a lower temperature. This is common in ablation procedures, where some tines have a more direct path to the grounding pads than other tines and therefore heat up to a higher temperature.

Figure 3.

Comparison of the ideal temperature map of the liver after a) 6 seconds and b) after 360 seconds of ablation. The errorbars are shown only for limited estimates to reduce the clutter in the graph.

Note that the size of the temperature maps were scaled to fit within the size of the ultrasound simulation field resulting in the black border around the sides of the temperature images (this becomes more noticeable after 360 seconds of ablation). In addition, the temperature scale for the two images were not the same, with Fig. 3 (a) depicting a maximum temperature of 41.5°C after 6 seconds, and Fig. 3 (b) utilizing a maximum temperature value of 100°C after 360 seconds of ablation

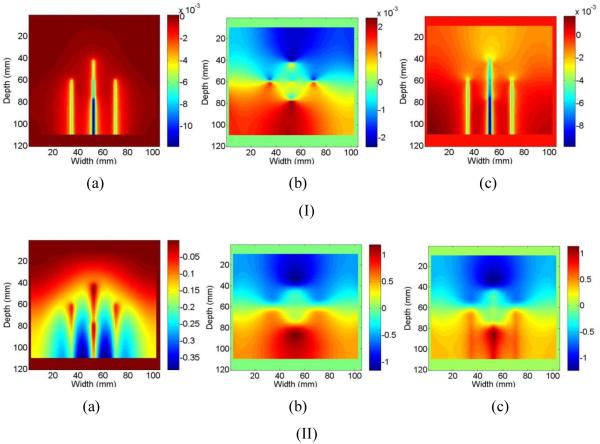
Representative images of the ideal (calculated) SOS displacement (Fig. 4, a)), ideal (FEA simulation results) thermal expansion displacement (Fig. 4, b)), and the ideal composite displacement (sum) (Fig. 4, c)) are shown in Fig. 4 at 6 seconds of heating (Fig. 4, Row I), and 360 seconds of heating (Fig. 4, Row II). Note that the units on the displacement images after 6 seconds of heating are 10^-3 mm. A negative displacement indicates tissue movement towards the top of the scanning plane, while a positive displacement indicates tissue movement towards the bottom of the image. The tines are not directly visualized in these images as we observe the spatially-varying echo shifts due to the difference between the SOS assumed by the beam-former (i.e. 1540 m/s) and the actual spatial and temporally-varying SOS in tissue due to temperature elevation.

Figure 4.

Ideal displacement images due to a) SOS changes, b) thermal expansion and c) cumulative displacements after I) 6 seconds and II) 360 seconds after ablation.

Observe the presence of streak artifacts in the ideal (calculated) SOS displacement image (Fig. 4, a)). These streaks are due to the temperature along the A-line being non-uniform, i.e. higher around the tines than the surrounding liver. The resulting displacement from the changes in the SOS is due to the average SOS encountered by the sound pulse at a given depth in the liver and not just the SOS at that depth. These artifacts obscure the three middle tines, leading to the long streak seen. This is an important distinction when compared to the results reported in Techavipoo et al [45], where each A-line was assumed to be at a uniform temperature (RF ablation tines were not modeled) and therefore no streak artifacts were generated. However, this artifact will occur during experimental ultrasound-based temperature estimation for monitoring RF ablation as demonstrated by this model.

In addition, after 6 seconds the apparent displacements due to SOS changes are significantly larger than displacements due to thermal expansion (Fig. 4, Row I). Therefore, when non-uniform temperatures elevations exist along an A-line the total or cumulative ideal (FEA simulation result) displacement image is more heavily weighted towards the SOS displacement than the displacement due to thermal expansion after 6 seconds of heating. However, after 360 seconds of heating, this situation is reversed, with the displacement due to thermal expansion being approximately three times the apparent displacement from changes in the SOS (Fig. 4, Row II). Therefore, the ideal cumulative displacement image is almost the same as that obtained from thermal expansion alone and only incrementally modified by the apparent displacement due to SOS variations. The reason for this is at higher temperatures, thermal expansion of liver tissue contributes significantly more toward the overall echo shift than SOS changes, and this is consistent with experimental results described by Techavipoo et al. [45].

Ultrasound Simulation

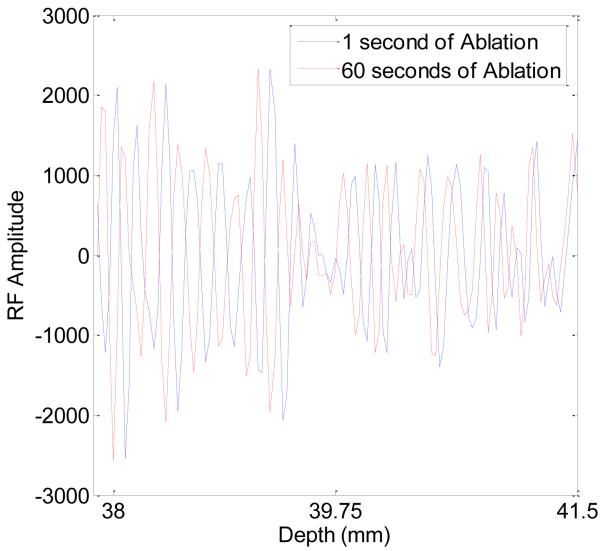
Simulated ultrasound radiofrequency echo data were computed after each 6 second time step as described in the Methods section. Figure 5 shows a segment of the radiofrequency echo signal near the upper tine after 1 second and 60 seconds of ablation respectively. Note the displacement in the radiofrequency echo signal with time, which are tracked and accumulated using our signal-processing methods. Composite displacement images are computed from the radiofrequency echo data using 1D CC and 2D block matching analysis between consecutive radiofrequency frames. Local displacements between frames were summed or accumulated to estimate the total displacement from 0 seconds of ablation to the time instant of the current frame. A comparison of the ideal FEA displacement (Fig. 6 (a)), along with those estimated using both 1D (Fig. 6 (b)) and 2D block matching analysis (Fig. 6 (c)) is shown in Figure 6. Note that the computational domains for 1D CC and 2D block matching differ from the FEA image. The reason is that 1D CC and 2D block matching require different numbers of points outside the search region in order to effectively and accurately estimate the local displacements. In turn, this leads to the different computational domains as illustrated in Figure 5.

Figure 5.

Radiofrequency echo data segment near the upper tine after 1 second (blue) and 60 seconds (red) of ablation.

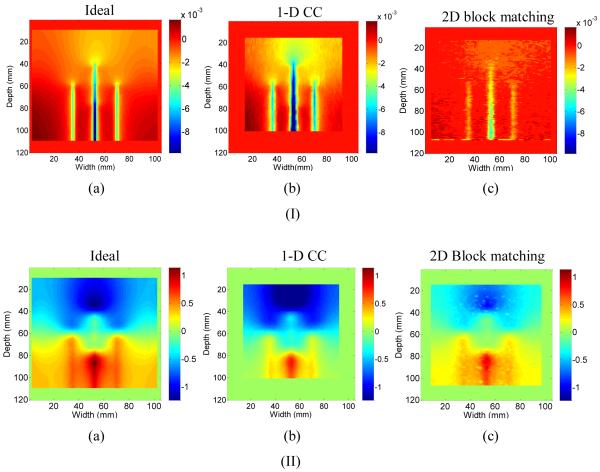
Figure 6.

Comparison of the a) ideal total displacement obtained using FEA to the b) 1D and c)2D BM accumulated displacement, after I) 6 seconds and II) 360 seconds after ablation.

Note that 6 seconds into the ablation procedure, the 2D block matching displacement image (Fig. 6, Row I, a)) is fairly noisy but the displacement scale shows similar magnitudes for both 2D block matching displacement and the ideal displacement image (Fig. 6, Row I, c)). Two ROI’s were chosen around the upper and lower tine in order to determine the accuracy and precision of the two methods used for tracking displacements. These specific ROI were chosen since they represent areas of maximum negative and positive displacement respectively. Therefore, these are areas where increased errors in displacement estimation are likely to occur. Around the upper tine ROI (see Figure 8a) 2D block matching has an average displacement of -0.0046 mm compared to -0.0057 mm around the upper tine ROI with the FEA result. Around the lower tine ROI (Fig. 8a), 2D block matching also underestimates the displacement (-0.0064 mm) when compared to the FEA result (-0.008 mm). However, 360 seconds following ablation, noise artifacts are reduced and the 2D block matching displacement image (Fig. 6, Row II, a)) matches the ideal displacement image (Fig. 6, Row II, c)). 2D block matching underestimates the displacement around the upper tine ROI (-0.701 mm) when compared to the FEA result (-0.843 mm) and overestimates the displacement around the lower tine ROI (0.897 mm) when compared to 0.754 mm obtained using FEA. Note that, the 2D block matching colorbar scale is identical to the ideal FEA image colorbar scale, enabling a direct comparison of these images.

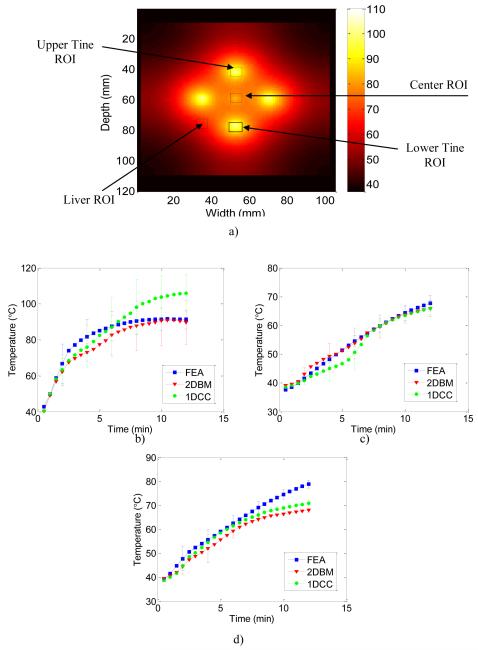
Figure 8.

FEA temperature images illustrating the regions of interest (ROI) over which the temperature estimates obtained using FEA and US simulations based on 1D CC and 2D BM algorithms were compared in Figure 8 a). Quantitative comparisons of the temperature estimated from ultrasound simulation using the 1D CC and 2D BM based temperature estimation algorithms using the calibration curve. The blue curve denotes the FEA computation, the red curve 2D BM and the green curve 1D CC results. Displacement data was accumulated from radiofrequency echo data acquired every 6 seconds for ROI’s at the b) tine (left side), c) simulated liver (right side) and at the d) center. The errorbars are shown only for limited estimates to reduce the clutter in the graph.

This result demonstrates that 2D block matching accurately tracks displacements between frames and the cumulative displacement over the large time durations of an ablation procedure. 1D CC underestimates displacements in the ROI around the upper (-0.0046 mm) and lower tine (-0.007 mm) at 6 seconds (Fig. 6, Row I, b) when compared to the FEA results on the upper (-0.0057 mm) and lower (-0.007 mm) ROI respectively. 1D CC also underestimates the displacement around the upper (-0.804 mm) and lower (.542 mm) ROI when compared to the FEA upper (-0.843 mm) and lower (0.754 mm) tine ROI after 360 seconds (Fig. 6, Row II, b) of ablation.

Interestingly, 2D block matching overestimates the displacement around the lower tine by the same amount that it underestimates the displacement around the lower tine (.143 mm). Hence the displacement for 2D block matching accurately tracks the displacement compared to FEA with a shift, while 1D CC consistently underestimates the displacement regardless of the time step or ROI. Since the temperature maps depend on the gradient of the displacement and not the displacement itself, 2D block matching should provide more accurate temperature results than 1D CC. From the accumulated composite displacement images, images of the displacement gradient were formed by calculating the slope of the displacement vector using least squares estimation [50]. The displacement-gradient or unscaled temperature distribution was then converted into an actual temperature using the displacement gradient-to-temperature calibration curve previously discussed [34].

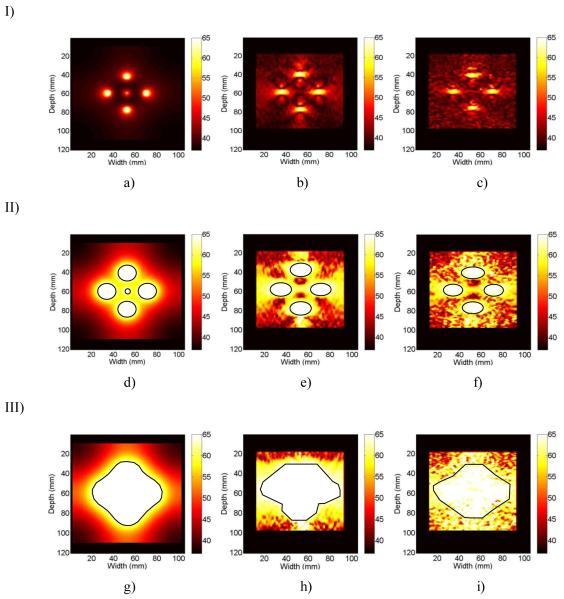
In the temperature images shown in Figure 7, observe the similarity in temperature maps generated from the ultrasound simulation, where the accumulated frame to frame displacements obtained using 1D CC and 2D block matching are compared to the ideal FEA temperature maps. Figure 7, Row I, shows the ideal FEA temperature map (Fig. 7 (a)), along with the ultrasound based temperature images obtained using 1D CC (Fig. 7 (b)), and 2D block matching tracking (Fig. 7 (c)) 90 seconds into the ablation procedure. Observe that 90 seconds into the ablation procedure, the temperature map obtained from the ultrasound simulation is fairly noisy when compared to the ideal FEA temperature map, but the four outer tines are clearly visible. In these temperature images, a fixed temperature scale of 37-65°C was utilized. This fixed scale ensures that regions of liver tissue that have attained temperature elevations where possible cell death has been induced can be clearly visualized. The 65°C limit was chosen, because when a temperature of 65°C is reached in tumor cells, “there is sufficient tissue coagulation to cause cell death” [51]. The axial aspect (depth in tissue) of the ablated region is slightly underestimated, and the width (lateral aspect) is slightly overestimated using both 1D and 2D block matching when compared to FEA results. No statistical comparison of the size of the ablated region was done at 90 seconds of ablation, since the size of the ablated regions are quite small for FEA, 1D CC, and 2D block matching, and a small difference in the relative size could lead to large errors.

Figure 7.

Comparison of the a) FEA simulated ideal images to those estimated using, b) 1D CC and c) 2D BM processing from ultrasound simulations. The images shown in row I was obtained after 90 seconds, row II after 360 seconds and row III after 720 seconds of ablation. The temperature scale in all the images was scaled to be in the 0-65°C temperature range. ROI outlined in black represent manual segmentation of the ablated area.

The next set of temperature images, Row II, compares FEA (Fig. 7 (a)), 1D (Fig. 7 (b)) and 2D block matching (Fig. 7 (c)), maps 360 seconds into the ablation procedure using the same fixed temperature range of 37-65°C. Manual segmentation of the ablated region was used to compare the size of the respective ablated regions. Manual segmentation was used in order to eliminate errors in size estimates of the ablated region due to noise and artifacts that may arise from temperature discontinuities. The areas that were above the 65°C threshold are outlined in black in Fig. 7 below. After 360 seconds, FEA indicates that 6.9% of the total simulated hepatic area was ablated, while 1D CC was found to have 7.9%, and 2D block matching 6.6% of the total area ablated. In comparing the images with a fixed temperature range, after 360 seconds of ablation the FEA and ultrasound temperature maps correlate reasonably, however 2D block matching estimates the size of the ablated region better than that obtained with1D CC. The final set of temperature images, Row III, compares FEA (Fig. 7 (a)), 1D (Fig. 7 (b)) and 2D block matching (Fig. 7 (c)), maps 720 seconds into the ablation procedure. In these images, the size of the ablated region obtained using FEA was 19.6% of the total simulated liver area, while 2D block matching had 22% and 1D CC 25% of the total area being successfully ablated.

For both the temperature estimation algorithms there is an overall underestimation of the temperature in the ablated region at 90 and 360 seconds mainly between the middle tine and the upper and lower outer tines. This underestimation of the temperature is likely due to the underestimation of the displacements discussed above (see Figure 6). These results show that displacement accumulation using 2D block matching or 1D CC and then creating temperature maps from those displacements using the calibration curve or lookup table can accurately predict the zone of ablation or necrosis in a liver tissue model. However, 2D block matching suffers from fewer errors than 1D CC in estimating the size of the ablated region after both 360 and 720 seconds of ablation.

Figure 8a), presents a FEA image of the temperature map showing regions-of —interest (ROI) over which a quantitative analysis of the temperature estimation is performed. The ROI’s selected included a region around a tine, a region at the center and a third region in simulated liver. Figure 8b)-8d), presents results on the accuracy of the 1D and 2D block matching temperature estimation algorithms at the three different ROI’s. The ROI around the tine contain the largest temperature gradients, so the temperature values in this region would exhibit the largest variations. Figure 8 (b-d) presents plots of the average temperature in the respective ROI’s obtained from the ideal FEA, 1D CC and 2D block matching respectively. An extrapolated calibration curve was used to determine the temperature for high temperatures. The calibration curve was extrapolated by extending the last part of the calibration curve from 90°C to 110°C.

A high level of correspondence between ultrasound-based temperature maps and FEA was found as shown in Figs. 8 (b-d). For the ROI around a tine, 2D block matching underestimated the temperature by a mean value of 5%, while 1D CC overestimated temperature by a mean value of 8% (Fig. 8, b)). It should be noted that 1D CC would have overestimated the temperature more if the maximum temperature was not limited to 110°C. The gradient of the 1D CC calculated displacement was much higher than the maximum gradient allowed by the calibration curve. Since these higher temperatures were truncated at 110°C, the overestimation of the temperature by 1D CC is artificially low. Note that temperature estimated using the 1D CC method gradually diverges from the ideal FEA estimates after time duration of 8 minutes for temperatures larger than 80°C. The large temperature range around the upper tine ROI is the reason for the large error bars found in Figure 8b.

In the other areas in the simulated liver however, both 1D CC and 2D block matching do a good job in estimating temperature when compared to the ideal FEA temperature. For the ROI in the simulated liver with lower temperature gradients, 1D CC underestimated the temperature by a mean value of 3.2%, while 2D block matching overestimated temperature by a mean value of 1.8% (Fig. 8, b)). In the ROI around the center tine, however, both 1D CC and 2D block matching underestimate the temperature by 5% and 7% respectively (Fig. 8, d)). Overall, 2D block matching does a better job of estimating temperatures, no matter the location in the image, but does suffer from underestimation around the center tine after 8 minutes of ablation as described above.

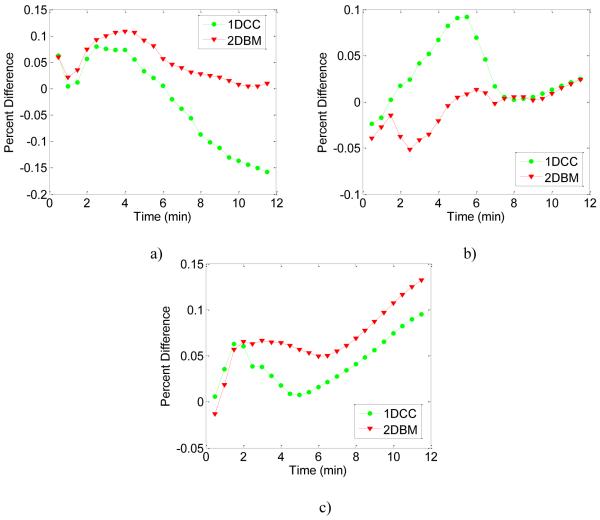
Figure 9 presents the percent difference in the temperature estimated between 1D CC and 2D block matching with the ideal FEA result for the three ROI’s described above. Figure 9a) demonstrates that for ROI around the upper tine, the percent difference is smaller for 2D block matching than 1D CC over the entire duration of the ablation. For the ROI around the center tine in Fig. 9b), the percent difference is approximately the same for 1D CC and 2D block matching for the first two minutes of ablation. Between two and seven minutes of ablation 2D block matching has a smaller percent difference than 1D CC. During the final five minutes of ablation, the percent difference is approximately the same for both the methods. Finally, Fig. 9c depicts the percent difference in the liver ROI. For the first two minutes of ablation the percent difference is similar for both methods. After two minutes of ablation, 1D CC has a smaller percent difference than 2D block matching. However, over all the three ROI’s and over the entire ablation duration, 2D block matching has a smaller percent difference or error in the temperature estimated than 1D CC.

Figure 9.

Comparison of the percent difference or error between temperature estimates calculated using 1D CC and 2D BM based temperature algorithms using the calibration curve versus the “ideal” FEA temperature. The red curve denotes 2D BM and the green curve 1D CC results. The percent difference in temperature was computed for the three ROI shown in Figure 8, at the a) tine (left side), b) simulated liver (right side) and at the d) center.

EXPERIMENTAL EVALUATION OF RF ABLATION

Tissue-Mimicking Phantom for Temperature Measurement

Experimental evaluation of the two speckle tracking algorithms was performed using a thermal and acoustic TM phantom. The TM phantom was constructed using material consisting of 1-2 mm diameter talc-in-agar spheres surrounded by a 10% n-propanol solution [52]. The thermal and acoustical properties of the TM material have been previously characterized [53]. The electrical impedance of the TM material was titrated using Salt (NaCl) (0.6 grams/liter) to mimic that of the human body. The TM phantom and the experimental apparatus have been previously described by Daniels et al. [52]. The TM phantom consists of two containers, where the inner container holds the TM material, and the outer container contains the 10% n-propanol solution. A RITA 1500 RF ablation electrode was attached to the wall of the larger enclosure, with the tines of the RF probe extended into the middle of the TM phantom to lie within the ultrasound scanning plane. Three IPITEK (IPITEK, Carlsbad, CA) invasive fiber optic temperature probes were placed near the ends of the extended electrode tines at the center. The RF ground is placed below the container of TM material.

Ultrasound Data Acquisition

Ultrasound data acquisition was performed using an Ultrasonix 500RP clinical ultrasound system equipped with a research interface (Ultrasonix Medical Systems, Redmond WA). A 1D linear array ultrasound transducer with a 6.6 MHz center frequency and 40 mm width was placed in contact with the TM material directly above the fiber optic temperature probes and electrode tines. The ultrasound transducer has an approximate 60% bandwidth and the echo signals were digitized using a 40 MHz sampling frequency. The research interface on the ultrasound system provided radiofrequency echo signal frames as the phantom underwent an 8 minute RF heating procedure. The maximum temperature generated in the TM phantom was approximately 65°C, which is lower than the 100°C temperature typically used for RF ablation of the liver. This was necessary to keep the phantom temperature lower than the 78°C melting point of the talc-in-agar spheres. Invasive temperature values obtained using the fiber-optic probes were also recorded simultaneously during the heating procedure using a laptop computer connected to the fiber optic temperature controller. The transducer on the top surface of the phantom was held in place by a Lucite block to ensure that it remained stationary during the heating procedure. Radiofrequency echo data was recorded at a frame rate of approximately 1.25 frames per second, providing echo signals over an area of 6 cm (depth) by 5 cm (width) in the TM phantom.

Data Processing

Displacements were tracked using both the 1D CC and 2D block matching speckle tracking methods previously described for the FEA simulations. The echo shifts were accumulated over the entire duration (480 seconds) of the heating procedure. A 3×3 moving average filter was applied to the displacement field to reduce noise artifacts. The gradient of the cumulative displacement was then computed using the linear least squares approach, and a displacement gradient versus temperature calibration curve applied to convert the gradient value into a temperature estimate. The calibration curve for the TM phantom material was obtained as discussed in Daniels et al. [52].

TM Phantom Results

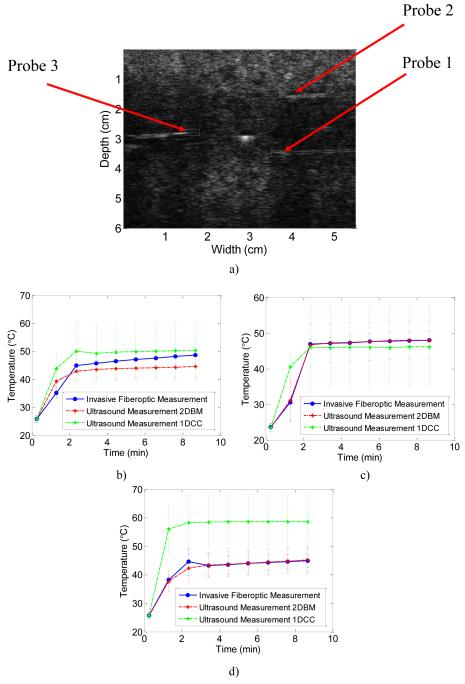
In Figure 10a) a B-mode image of the TM phantom is presented. Three ROI around the three invasive fiber optic temperature probes are outlined in white. The ultrasound B-mode image was acquired at the center of the TM phantom. The center tine is visible in the image, as the outer tines were not observed on the B-mode image unless they are moved. The reason for this is that the size of the tines (0.534 mm) is on the order of the PSF of the Ultrasonix transducer at 6.6 MHz.

Figure 10.

B-mode image illustrating the regions of interest (ROI) over which the average temperature was obtained using both 1D CC and 2D BM methods 10a). Quantitative comparisons of the temperature are shown in Figures 10 (b-d). The red curve denotes the 2D block matching temperature estimate, the green curve denotes the 1D CC temperature estimate, and the blue curve denotes the invasive temperature obtained using the fiber-optic probe. The temperature was calculated from radiofrequency echo data accumulated every 2.5 seconds for ROI’s at b) Probe 1 (lower right side), c) Probe 2 (upper right side) and at the d) Probe 3 (lower left side).

Figure 10 (b-d), presents the average temperature for the three ROI’s calculated using both 1D CC and 2D block matching over 10 independent data sets. In Fig. 10b) the average temperature is shown for the ROI around Probe 1 over the entire 700 seconds of the heating procedure. The average percent difference for 2D block matching was 5%, and that for 1D CC was 7.5% when compared to the invasive fiber-optic temperature measurement. In a similar manner, Figure 10c) presents both 1D CC and 2D block matching based temperature estimates in the ROI around Probe 2, where 1D CC has a higher average percent difference (0.77%) than 2D block matching (0.18%). This trend is repeated for the final ROI around Probe 3 as shown in Fig. 10d), where 2D block matching had an average percent difference of 0.44%, when compared to 31% for the 1D CC method.

For all three ROI’s the largest percent difference for both 1D CC and 2D block matching occurred between 1 and 3 minutes. This is most likely due to the fact that although the temperature of the tines has heated up to 65°C, the surrounding TM phantom material has not reached this temperature. Hence a large temperature gradient exists between the RF electrode tines and the TM material. This in turn, leads to a large amount of heat transfer to the TM material, whereby the TM material undergoes the most expansion and displacement. For all the three ROI’s both 2D block matching and 1D CC incur the largest percent difference during this time period.

DISCUSSION & CONCLUSION

RF ablation is the most commonly used minimally invasive therapy in the United States to treat HCC and liver metastases. However, the effectiveness of the therapy is limited by the fact that currently cost-effective and FDA approved methods to obtain real-time temperature maps during the ablation procedure are not available. This has led to the high recurrence rate of HCC in the liver and consequently repeat ablation procedures on the patient. In this paper, we demonstrate using FEA and ultrasound simulations that real-time temperature imaging is feasible using 2D block matching analysis with the use of larger frame intervals for improved processing speeds. In addition, temperature values obtained were, within 1.8% between the ideal and ultrasound derived temperature maps over a large temperature range and during the entire 12 minute duration of an RF ablation procedure. Temperature variations estimated were based on thermal expansion and SOS changes that occur during the ablation procedure. 2D block matching was also shown to provide consistently more accurate temperature estimates (5% difference in temperature) than 1D CC (31% difference in temperature) over three ROI during heating of a TM phantom. This processing would enable the use of ultrasound (the most commonly used method of monitoring RF probe placement) to provide real-time feedback to the clinician enabling them to visualize and ascertain if the entire tumor has been successfully ablated. In turn, this could help lower recurrence rates of RF ablation on HCC tumors and liver metastases, and thereby the number of repeat procedures for patients. Note that this method of temperature imaging can also be utilized for other thermal ablation methods. Future work will examine the effectiveness of this method of temperature imaging for other ablation modalities.

Future work will also examine the effect of blood perfusion in the ablated region and our ability to track temperature under these conditions. It should be noted, that including uniform blood perfusion would only affect the size of the resulting ablated region and would not affect our ability to track temperature changes in real-time. On the other hand, non-inclusion of uniform blood perfusion incorporates the estimation of increased temperature variations during the ablation procedure which is tracked using the algorithms described in this paper. However, local blood perfusion (e.g. presence of an artery within the ablated region) could result in complex temperature patterns due to local heat transfer over the ablated region and this aspect requires further investigation. The simulation presented here is appropriate for the lower liver where no major vessels are present and when blood flow to the liver has been occluded.

The cumulative displacement magnitude was underestimated by 1D CC by -0.04mm in the ROI around the upper tine and by -0.21 mm around the lower tine ROI after 360 seconds of ablation. 2D block matching underestimated the displacement around the upper tine ROI and overestimated the displacement around the lower tine ROI by 0.14mm as shown in Fig. 6. The underestimation of the displacement by 1D CC leads to a subsequent overestimation of the temperature after 360 seconds of ablation. This is an interesting result since even though the displacement is underestimated the temperature is overestimated.

It should be noted that the under / over estimation by 2D block matching does not significantly affect the size of the ablated region that reaches 65°C and thereby the region where cell death would be induced if the temperature were held at this level for the specified time duration. Although ways of correcting for this under/over estimation (such as the use of smaller time steps, or changing the input parameters of the 2D block matching algorithm) will be examined, the under/over estimation of the displacement, at this time would not impact the clinician’s ability to determine if the tumor has been completely ablated.

It should also be noted that temperature tracking with 2D block matching performs better than 1D CC temperature tracking. For instance, 2D block matching overestimates the percent of the liver that has been successfully ablated by 2.38%, while 1D CC overestimates the size of the ablated region by 5.38% after 720 seconds.

For the TM phantom experiment 2D block matching had a maximum percent difference of 5%, while 1D CC had a maximum percent difference of 31%. In addition, 1D CC suffers from much larger standard deviations (at least a factor of two larger) than 2D block matching in all the three ROI. Therefore, 2D block matching tracks the temperature with more precision and accuracy than 1D CC. This is true for both the FEA-based simulation results and the experimental results presented.

The ability of 2D block matching to track better than 1DCC is primarily because thermal expansion in our FEA model occurs in 2D. However, given sufficiently high frame rates (> 30 frame/second for high end systems); the out-of-plane motion due to thermal expansion, would not be as severe as that which occurs during breast elastography. In breast elastography, breast tissue is manually compressed up to 20% [49] against the chest wall, thereby inducing much larger out-of-plane motions and has been successfully tracked by a high frame rate system. On the other hand, in temperature imaging for liver ablation, the frame-to-frame signal decorrelation due to thermal expansion would be minimal. However, respiratory and cardiac motion artifacts are generally present during in-vivo imaging. Simulating realistic 3-D respiratory and cardiac motion patterns and compensating of these motion artifacts during temperature imaging is fairly complex and is an ongoing area of research. The results of this FEA / ultrasound simulation and TM phantom are promising and support prior work [36, 37].

Our method for calibrating ultrasound based temperature images to read out actual temperature values requires apriori knowledge of thermal expansion coefficient and changes in the SOS with temperature. This is a limitation of this method, since the necessary SOS and thermal expansion measurements have not been measured in many tissue types. However, these measurements can be performed in a similar manner as described in Techavipoo et al. [54] for the measurement in canine liver tissue. As RF ablation is used more extensively for ablative therapies, such as nephron sparing surgery in the kidney to treat renal cell carcinoma, SOS changes and thermal expansion experiments have to be performed in order to extend the echo-shift method for ultrasound based thermal imaging to these procedures. FEA simulations can similarly benefit from knowledge of the material properties of fatty and cirrhotic liver, as well as carbonized liver tissue. This would allow us to develop more realistic FEA simulations which in conjunction with the inclusion of local perfusion would provide better estimation of the size of the ablated region.