Determination of the Surface pK of Carboxylic- and Amine-Terminated Alkanethiols Using Surface Plasmon Resonance Spectroscopy

Abstract

When using self-assembled monolayers (SAMs) with ionizable functional groups, such as COOH and NH₂, the dissociation constant (pK_d) of the surface is an important property to know, since it defines the charge density of the surface for a given bulk solution pH. In this study, we developed a method using surface plasmon resonance (SPR) spectroscopy for the direct measurement of the pK_d of a SAM surface by combining the ability of SPR to detect the change in mass concentration close to a surface and the shift in ion concentration over the surface as a function of surface charge density. This method was then applied to measure the pK_d values of both COOH- and NH₂-functionalized SAM surfaces using solutions of CsCl and NaBr salts, respectively, which provided pK_d values of 7.4 and 6.5, respectively, based on the bulk solution pH. An analytical study was also performed to theoretically predict the shape of the SPR plots by calculating the excess mass of salt ions over a surface as a function of the difference between the solution pH and surface pK_d. The analytical relationships show that the state of surface charge also influences the local hydrogen ion concentration, thus resulting in a substantial local shift in pH at the surface compared to the bulk solution as a function of the difference between the bulk solution pH and the pK_d of the surface.

Introduction

Surface plasmon resonance (SPR) spectroscopy is a valuable analytical tool that provides real-time, label-free surface interaction analysis with high sensitivity.^1–3 The interactions of a wide range of molecules can be analyzed using SPR spectroscopy from small biomolecules, such as lipids and peptides, to macromolecules, such as DNA and even whole cells and bacteria.^4–9 Another advantage of SPR spectroscopy is its ability to monitor interactions on surfaces with varying degrees of complexity that can be built on gold sensor chips, such as simple model functionalized surfaces,⁴ biosensors constructed by bio-molecule immobilization,⁵ and even multilayered assemblies.⁶

Alkanethiol self-assembled monolayers (SAMs) are commonly used as model surfaces for SPR spectroscopy because they form stable, well-ordered monolayers on gold.^7–9 Alkanethiols (HS-(CH₂)_n-R) have a thiol group on one end, which spontaneously bonds to a gold substrate, a relatively long alkyl midchain segment, which orders the chains on the surface in a well-defined structure, and a variable headgroup (R), which forms the surface of the monolayer. By this design, alkanethiols with different terminal R-groups are thus very useful to change the functionality and properties of the monolayer for the investigation of how surface chemistry influences the adsorption behavior of molecular species in solution.

For SAM surfaces with ionizable terminal groups, the surface dissociation constant (pK_d) is an important property because it defines the charge density of the surface when in equilibrium with a bulk solution of a designated pH value. Several different techniques have been developed to measure the pK_d of SAM surfaces using methods such as contact angle titration,^10–13 quartz crystal microbalance (QCM),^14,15 chemical force microscopy,^16,17 electrochemical titration,^18,19 the laser-induced temperature jump technique (ILIT),²⁰ double-layer-capacitance titration,^21,22 amperometry,²³ voltammetry,²⁴ and Raman spectroscopy.²⁵ These different methods, however, have resulted in reported values of pK_d for COOH-SAM surfaces formed from 11-mercaptoundecanoic acid (HS-(CH₂)₁₁-COOH) ranging from 5.2 to 10.3, thus suggesting that the measured values are technique-dependent. In particular, double-layer-capacitance titration has been shown to be very sensitive to the length of the alkanethiol and produce pK_d values much greater than those of the other methods when the chain is longer than 10 carbon atoms.²⁰ Reports have also shown that pK_d measurements can be influenced by surface topography²⁶ as well as by the electrolyte used in the analysis.²⁷

The objective of this work was to develop a method of measuring the pK_d of SAM surfaces using SPR combined with theoretical analyses both to support our ongoing adsorption studies with various SAM surfaces using SPR and as an attempt to understand possible reasons for the wide range of reported values of pK_d of these surfaces as measured by other methods. Our method involves running salt solutions of CsCl and NaBr with a wide range of bulk solution pH values over COOH-SAM and NH₂-SAM surfaces, respectively, while recording the SPR response at the surface. As the surface charge of the SAM changes as a function of pH, the heavier counterions are attracted to the surface while the lighter co-ions are repelled, resulting in an increase in mass at the surface compared to bulk solution, which is readily detected by the SPR signal as a change in solution refractive index. Calculations were then performed for the experimental conditions based on the Poisson—Boltzmann equation to theoretically determine ion concentration profiles over each surface as a function of the difference between solution pH and the measured pK_d of the surface. The analytical results serve to both support the experimental measurements and provide greater insight into the physical behavior of these types of systems.

Our results demonstrate that SPR spectroscopy can be used to measure the surface pK_d of COOH- and NH₂-terminated alkanethiol SAMs using these simple salt solutions and that the experimental data are well-supported by the analytical model. The analytical results also predict that the pH at the SAM surface will be shifted several pH units from that of the bulk solution due to the shift in hydrogen ion concentration as a function of the state of surface charge. These results may thus at least partially explain the wide range of reported pK_d values in the literature for these types of surfaces, with the measured pK_d value substantially varying depending on whether it is based on the bulk solution pH or the pH of the solution immediately adjacent to the SAM surface.

Experimental Methods

Alkanethiol SAMs

Bare gold sensor chips for SPR were purchased from Biacore AB (BR-1004–05). Prior to SAM formation, all chips were sonicated at 25°C for 1 min in each of the following solutions in order: “piranha” wash (7:3 H₂SO₄/H₂O₂), a basic solution (1:1:5 NH₄OH/H₂O₂/H₂O), and an acidic solution (1:1:5 HCl/H₂O₂/H₂O). After each cleaning solution, the slides were thoroughly rinsed with nanopure water. The cleaned slides were rinsed with ethanol and incubated into the appropriate 1 mM alkanethiol solution (alkanethiols purchased from Aldrich, Prochimia, or Asemblon) in 200-proof ethanol for a minimum of 16 h. All alkanethiols used in these experiments had a structure of HS-(CH₂)₁₁-R with the following terminal R groups: OH, NH₂, or COOH. After incubation, the slides were rinsed with ethanol, dried with nitrogen gas, and characterized by ellipsometry and contact angle goniometry before mounting onto the SPR sensor chip holders.

Ellipsometry

Ellipsometry measurements were taken on a Sopra GES 5 variable-angle spectroscopic ellipsometer prior to surface modification and after surface treatment at six different spots to establish the bare-substrate optical constants and to calculate the thickness of the monolayer on each surface, respectively. The spectra were collected at an incidence of 70° in the wavelength range of 250–800 nm at 10 nm intervals. The layer thickness was calculated using the regression method in Sopra’s Winelli (version 4.07) software.

Contact Angle Goniometry

The surface energies of the gold and SAM surfaces were characterized by contact angle goniometry using a CAM 200 optical contact-angle goniometer from KSV Instruments, Ltd. The advancing contact angles, using nanopure water (pH 7), from six separate drops were measured on each of the sensor chips before and after surface modification.

Surface Dissociation Constant

A Biacore X SPR spectrometer was used to measure the local change in refractive index caused by the change in the cation and anion concentration distributions of CsCl and NaBr salts above COOH- and NH₂-SAMs, respectively, as a function of pH. Titrations (pH 4.0–10.0) of 150 mM CsCl and 150 mM NaBr solutions, with 1 mM NaH₂PO₄ added as buffer, were made by adjusting the pH with small amounts of NaOH and HCl. Preliminary studies confirmed that the contribution to the SPR signal, measured in response units (RUs), from the addition of 1 mM NaH₂-PO₄ to the salt solutions over this pH range resulted in a negligible shift compared to the response of the 150 mM CsCl and NaBr salts alone (<20 RUs). Using nanopure H₂O as the running buffer, the response unit shift (RU, 1 RU = 10⁻⁶ refractive index units ∞ 1 pg/mm²) from flowing the various pH solutions over the SAMs was recorded. The bulk shift response for these solutions was determined by conducting similar titrations over an OH-SAM to correct for small shifts in refractive indices (typically < 20 RU). This uncharged, hydrophilic surface was selected for this purpose based on previous studies in our laboratory that demonstrated that the SPR response to salt solutions flowing over an OH-SAM is entirely due to bulk-shift effects within the detection limits of our instrument.²⁸ Based on these measurements, the excess mass per unit area over the COOH- and NH₂-SAM surfaces was determined by subtracting the bulk-shift response from the RU shift of each titration. This was then plotted vs bulk solution pH, from which the pK_d of the surface was defined as the middle inflection point of the sigmoidally shaped SPR response curve. Measurements were conducted on four separate SPR sensor chips for each surface type, with a set of six independent titrations conducted on each chip for the determination of its pK_d value. The four independent measurements of pK_d for each type of surface were then statistically combined to calculate the mean and 95% confidence interval (CI) about the mean for each type of SAM surface.

Analytical Model

In this section, we develop the analytical equations that serve to support and provide theoretical insights for the experimental measurements made by SPR. The SPR response as a function of solution pH reflects how the refractive index of the solution changes in response to the changes in the excess mass concentration of ions over the surface as a function of the charge density of the SAM surface. The surface charge density, in turn, is a function of the difference between the solution pH and the dissociation constant (pK_d) of the ionizable groups on the surface.

The average excess mass of ions per unit area over the SAM surface (M̄_ex) can be expressed as

$${\overline{\mathrm{M}}}_{\text{ex}}={\displaystyle \sum _i}\{{\int }_0^{Sh}[{(C_i)}_x{M}_i-{(C_i)}_{\mathrm{b}}{M}_i]\mathrm{d}V\}/{\int }_0^S\mathrm{d}S$$ (1)

where (C_i)_x and (C_i)_b are the molar concentrations of ion type i at distance x from the surface (x = 0 is located at the outer Helmholtz plane²⁹) and in the bulk solution (subscript b), respectively, M_i is the molecular weight of ion type i, and V is the volume of solution over the surface with unit area S (1.0 mm²) within a distance of x = h from the surface.

The expression for the molar concentration of each ion type i as a function of x, (C_i)_x, can be derived based on the thermodynamic principle that at equilibrium the chemical potential of each ion type at a distance x from the surface must be constant.^29,30 This can be expressed as

$${({\mu }_i)}_x={\mu }_i^{\mathrm{o}}+z_{i}e{\mathrm{\Psi }}_x+k_{\mathrm{B}}T\text{ln}{(a_i)}_x=\text{constant}$$

thus,

$${\mu }_i^{\mathrm{o}}+z_{i}e{\mathrm{\Psi }}_x+k_{\mathrm{B}}T\text{ln}(a_i{)}_x={\mu }_i^{\mathrm{o}}+k_{\mathrm{B}}T\text{ln}(a_i{)}_{\mathrm{b}}$$

With

$$a_i={\gamma }_i{C}_i/C_i^{\mathrm{o}},{({\gamma }_i)}_{\mathrm{b}}/{({\gamma }_i)}_x\equiv {({\gamma }_{i\mathrm{r}})}_x,\text{and}{C}_i^{\mathrm{o}}\equiv 1.0M$$

this results in the relationship:

$${(C_i)}_x={({\gamma }_{i\mathrm{r}})}_x{(C_i)}_{\mathrm{b}}\text{exp}(-z_{i}e{\mathrm{\Psi }}_x/k_{\mathrm{B}}T)$$ (2)

where (µ_i)_x, ${\mu }_i^o$, and (a_i)_x are the chemical potential, the standard state chemical potential, and the activity of ion species “i” at position x, respectively, z_i is the valance of ion i, e is the absolute value of the charge of an electron (1.602 × 10⁻¹⁹ C), ψ_x is the electrostatic potential over the surface at position x, k_B is Boltzmann’s constant, T is absolute temperature, ψ_b and (a_i)_b are the electrostatic potential and activity of ion species i in bulk solution, respectively, far away from the surface where ψ_b approaches 0 mV, γ_i is the activity coefficient of ion species i, and (γ_ir)_x is defined here as the activity coefficient ratio of ion species i in the bulk solution compared to its activity coefficient at position x. To simplify the analytical expression, it is assumed that the activity coefficient of the ions in solution is not a function of concentration, thus making the ratio of the activity coefficients (γ_ir)_x equal to 1.0. This same simplifying assumption is made in eqs 3 and 4 below. The effects of a departure from this assumption are addressed in the discussion section. Accordingly, by eq 2, the concentration of an ion at position “x” above a charged surface is shown to be exponentially related to the electrostatic potential at that position above the surface.²⁹

The electrostatic potential at x (ψ_x) is a function of the surface charge density (σ), which in turn is a function of the fraction of the total number of SAM chains that are charged (f). The parameter f can be expressed by the following relationships.³⁰

For the COOH SAM:

$$\text{COOH}\leftrightarrow {\text{COO}}^{-}{+\mathrm{H}}^{+},K_{\mathrm{d}}{=\{(a}_{{\text{COO}}^{-}}{)(a}_{{\mathrm{H}}^{+}}{)/(a}_{\text{COOH}}{)\}}_{\text{eq}}$$

Again, with

$$\begin{array}{c}{C}_i^{\mathrm{o}}=1.0M\text{and}{\gamma }_{\mathrm{r}\text{COOH}}\equiv ({\gamma }_{{\text{COO}}^{-}})({\gamma }_{{\mathrm{H}}^{+}})/({\gamma }_{\text{COOH}})=\hfill \\ \hfill 1.0,K_{\mathrm{d}}=\{(C_{{\text{COO}}^{-}})(C_{{\mathrm{H}}^{+}})/(C_{\text{COOH}})\}\end{array}$$

and thus

$$\begin{array}{c}\mathrm{p}{K}_{\mathrm{d}}=\text{pH}-\text{log}\left(\frac{C_{{\text{COO}}^{-}}}{C_{\text{COOH}}}\right),\text{pH}-\mathrm{p}{\mathrm{K}}_{\mathrm{d}}=\hfill \\ \hfill \text{log}\left(\frac{C_{{\text{CO}O}^{-}}}{C_{\text{COOH}}}\right),\text{and}\left(\frac{C_{{\text{COO}}^{-}}}{C_{\text{COOH}}}\right)={10}^{(\text{pH}-\mathrm{p}{K}_{\mathrm{d}})}\end{array}$$

With

$$f=\left(\frac{C_{{\text{COO}}^{-}}}{C_{\text{COOH}}+C_{{\text{COO}}^{-}}}\right)=\frac{C_{{\text{COO}}^{-}}/C_{\text{COOH}}}{1+C_{{\text{COO}}^{-}}/C_{\text{COOH}}},f=\frac{{10}^{(\text{pH}-\mathrm{p}{\mathrm{K}}_{\mathrm{d}})}}{1+{10}^{(\text{pH}-\mathrm{p}{\mathrm{K}}_{\mathrm{d}})}}$$ (3)

For the NH₂ SAM:

$${{\text{NH}}_3}^{+}\leftrightarrow {\text{NH}}_2{+\mathrm{H}}^{+}{,K}_{\mathrm{d}}{=\{(a}_{\text{NH}2}{)(a}_{{\mathrm{H}}^{+}}{)/(a}_{{\text{NH}3}^{+}}{)\}}_{\text{eq}}$$

Again, with

$$\begin{array}{c}{C}_i^{\mathrm{o}}=1.0M\text{and}{\gamma }_{\mathrm{r}{\text{NH}}_2}\equiv ({\gamma }_{{{\text{NH}}_2}^{-}})({\gamma }_{{\mathrm{H}}^{+}})/({\gamma }_{{{\text{NH}}_3}^{+}})=\hfill \\ \hfill 1.0,K_{\mathrm{d}}=\{(C_{{\text{NH}}_2})(C_{{\mathrm{H}}^{+}})/(C_{{{\text{NH}}_3}^{+}})\}\end{array}$$

and thus

$$\begin{array}{c}\mathrm{p}{K}_{\mathrm{d}}=\text{pH}-\text{log}\left(\frac{C_{{\text{NH}}_2}}{C_{{{\text{NH}}_3}^{+}}}\right),\text{pH}-\mathrm{p}{K}_{\mathrm{d}}=\hfill \\ \hfill \text{log}\left(\frac{C_{{\text{NH}}_2}}{C_{{{\text{NH}}_3}^{+}}}\right),\text{and}\left(\frac{C_{{{\text{NH}}_3}^{+}}}{C_{{\text{NH}}_2}}\right)={10}^{(\mathrm{p}{K}_{\mathrm{d}}-\text{pH})}\end{array}$$

With

$$f=\left(\frac{C_{{{\text{NH}}_3}^{+}}}{C_{{\text{NH}}_2}+C_{{{\text{NH}}_{\mathit{3}}}^{+}}}\right)=\frac{C_{{{\text{NH}}_3}^{+}}/C_{{\text{NH}}_2}}{1+C_{{{\text{NH}}_3}^{+}}/C_{{\text{NH}}_2}},f=\frac{{10}^{(\mathrm{p}{K}_{\mathrm{d}}-\text{pH})}}{1+{10}^{(\mathrm{p}{K}_{\mathrm{d}}-\text{pH})}}$$ (4)

For alkanethiol-SAM chains formed on a gold (111) surface, which have a surface area of 21.4 Ų/alkanethiol chain,³¹ the surface charge density (σ) is related to f by

$$\begin{array}{c}{\sigma =z}_{i}f\frac{\text{SAM}\text{chain}}{21.4{\AA }^2}\frac{{10}^{20}{\AA }^2}{{\mathrm{m}}^2}\frac{1.602\times {10}^{-19}C}{\text{charged}\text{chain}}=0.749z_{i}f\hfill \\ \hfill (\text{units}:{\mathrm{C}/\mathrm{m}}^2)\end{array}$$ (5)

where z_i = −1 and +1 for the COOH- and NH₂-SAM surfaces, respectively.

The relationship between the electrostatic potential at the surface (ψ₀) and the surface charge density (σ) is expressed by the Grahame equation as (see the Supporting Information, section S-I)²⁹

$${\mathrm{\Psi }}_0=\frac{2k_{\mathrm{B}}T}{e}{\text{sinh}}^{-1}\left\{\frac{\sigma }{\sqrt{8\epsilon {\epsilon }_{\mathrm{o}}{k}_{\mathrm{B}}T{(C_{\text{salt}})}_{\mathrm{b}}}}\right\}$$ (6)

where ɛ and ɛ_o are the relative permittivity of water (78.5 at 298 K) and the permittivity of free space (8.854 × 10⁻¹²C²/J/m), respectively, and (C_salt)_b is the concentration of the salt in the bulk solution.

Based on the above equations, the Poisson—Boltzmann equation can be solved to express ψ_x as (for details, see the Supporting Information, section S-II)²⁹

$$\begin{array}{c}{\mathrm{\Psi }}_x=\left(\frac{2k_{\mathrm{B}}T}{e}\right)\text{ln}\left(\frac{1+\phi \text{exp}(-\kappa x)}{1-\phi \text{exp}(-\kappa x)}\right),\hfill \\ \hfill \text{with}\phi =\text{tanh}\left(\frac{e{\mathrm{\Psi }}_0}{4k_{\mathrm{B}}T}\right)\text{and}\kappa ={[2{(C_{\text{salt}})}_{\mathrm{b}}{e}^2/\epsilon {\epsilon }_{\mathrm{o}}{k}_{\mathrm{B}}T]}^{1/2}\end{array}$$ (7)

where κ is the inverse Debye length. Note that, in eq 7, the sign of ψ₀ determines the sign of ψ_x.

The relationship for ψ_x expressed in eq 7 can now be used in eq 2 to express the concentration profiles of the cations and anions in solution as a function of x by the following relationships:

$$\begin{array}{c}{(C_i)}_x={(C_i)}_{\mathrm{b}}\text{exp}(-z_{i}e{\mathrm{\Psi }}_x/k_{\mathrm{B}}T)=\hfill \\ \hfill {(C_i)}_{\mathrm{b}}\text{exp}\left\{-2z_i\text{ln}\left(\frac{1+\phi \text{exp}(-\kappa x)}{1-\phi \text{exp}(-\kappa x)}\right)\right\}=\\ \hfill {(C_i)}_{\mathrm{b}}{\left(\frac{1+\phi \text{exp}(-\kappa x)}{1-\phi \text{exp}(-\kappa x)}\right)}^{-2z_{\mathrm{i}}}\end{array}$$ (8)

The resulting concentration profiles can now be inserted in eq 1 to calculate the average excess mass of ions over the surface as a function of bulk solution pH relative to the pK_d of the SAM surface.

Accordingly, eqs 1–8 were applied to the conditions used in the SPR experiments, and the values of the parameters, ψ_x, (C_a)_x, and (C_c)_x, were then calculated and plotted as a function of x for bulk solution pH = 7.4 and for the measured pK_d values of each type of SAM surface. In addition, the values of the excess mass per unit area (M̄_ex) were also calculated and plotted as a function of the difference between pH and pK_d for comparison with the experimental results. The differences between the local pH at each surface and the bulk solution pH were then also calculated and plotted vs the bulk solution pH for each type of surface.

Results and Discussion

Surface Characterization

Table 1 presents the surface characterization data for each of the SAM surfaces in terms of their water contact angle and the thickness of the SAM layers as measured by ellipsometry. The thickness values show that there is only a single alkanethiol monolayer on each of the SAM surfaces and the contact angles are in good agreement with previously published values.^32,33

Table 1.

Advancing Water Contact Angle (pH 7) and Thickness of the OH-, COOH-, and NH₂-SAMs (N = 6, Mean ± 95% CI)

	OH	COOH	NH2
contact angle (°)	17.6 ± 1.9	17.9 ± 1.3	37.6 ± 1.8
thickness (Å)	12.1 ± 1.4	15.8 ± 1.9	14.7 ± 2.5

SPR Data

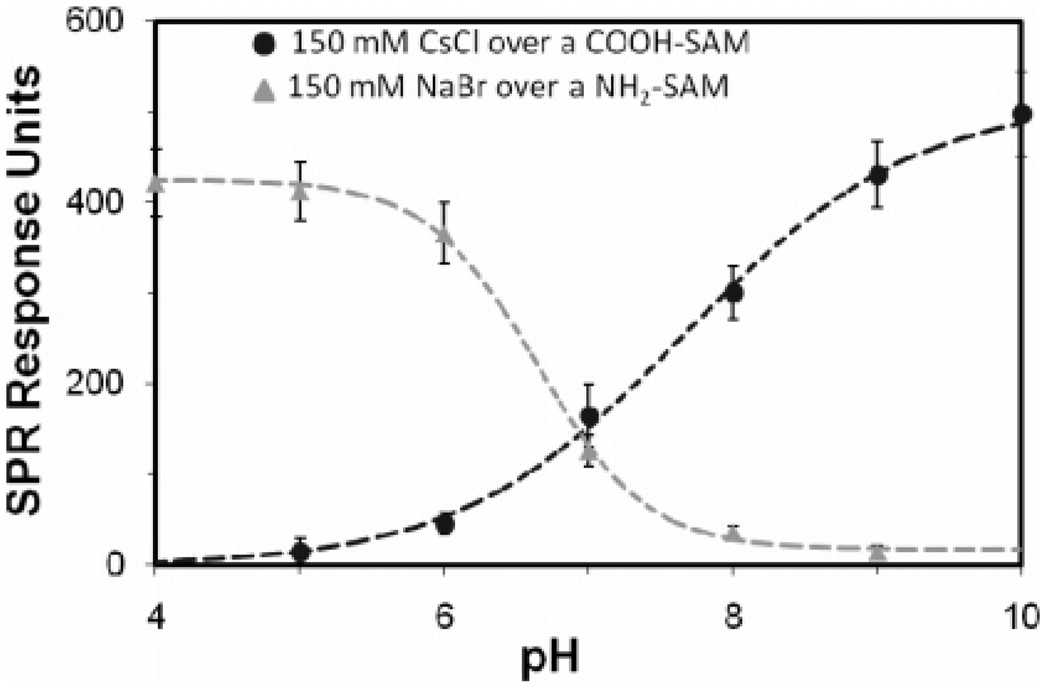
The SPR data in the form of the RU shift vs pH for one of the COOH-SAM sensor chips is plotted in Figure 1. This shows a clear sigmoidally shaped SPR response for this SAM surface (see the Supporting Information, Section S-III, Table S1 for the detailed experimental results for the COOH-SAMs). The pK_d point was determined by fitting the following equation, which is a modification of eqs 3 and 4, to the SPR data and minimizing the sum of the squared errors:

$$\text{RU}=A\left[\frac{{10}^{B(\mathrm{p}{K}_{\mathrm{d}}-\text{pH})}}{{1+10}^{B(\mathrm{p}{K}_{\mathrm{d}}-\text{pH})}}\right]+C$$ (9)

where A and B are scaling factors and C is the offset. The mean pK_d value for the COOH-SAM sensor chips was calculated as 7.4 ± 0.2 (95% CI). When the solution pH is well below the pK_d of the surface, a low fraction of the COOH groups are in their deprotonated, negatively charged state, resulting in little excess mass over the surface. As the solution pH is increased, the fraction of charged groups on the surface rapidly increases, resulting in an increase in excess mass at the surface due to the charged groups preferentially attracting the heavier cations toward the surface while repelling the lighter anions away from the surface. As the pH continues to increase, the fraction of deprotonated COOH groups begins to approach unity, which subsequently leads to the minimal change in the fractional charge state with the further increase of solution pH, and the excess mass concentration over the surface stabilizes, as reflected in the SPR signal.

Figure 1.

SPR plot of the corrected RU shift of the salt solutions vs pH for a COOH-SAM and a NH₂-SAM (1 RU = 1 pg/mm²). Points represent mean ± 95% CI, N = 6.

The SPR data for an NH₂-SAM sensor chip is also shown in Figure 1 (see the Supporting Information, Section S-III, Table S2 for the detailed experimental results for the NH₂-SAMs). The mean pK_d value for the NH₂-SAMs was 6.5 ± 0.3 (95% CI). When exposed to basic solutions, there is a low fraction of NH₂ groups that are protonated and positively charged, resulting in a minimal buildup of excess ions at the surface. As the bulk pH above the surface shifts toward neutral, the response begins to increase, indicating that a larger number of NH₂ groups are becoming charged. As the pH drops below 5, there is little change in the response, since the fraction of positively charged groups approaches 1.0.

The experimental results show that the pK_d value for the COOH-SAMs is more basic than that of the NH₂-SAMs, which at first glance seems to be an odd result given that acetic acid (CH₃-COOH) and methylamine (CH₃NH₂) in dilute solutions have pK_d values around 4.7 and 10.5, respectively.³⁴ It is important to note, however, that the measured pK_d values for the COOH- and NH₂-SAMs are the “effective” pK_d values, since they are based on the pH of the bulk solutions and not on the pH at the surface. The results from the analytical model provide an estimate of the shift in the “effective” pK_d value due to surface charge induced differences in the pH at the SAM surface compared to the bulk solution.

Analytical Results

Based on the experimental results, eqs 1–8 were applied to theoretically analyze the behavior of these systems under two conditions: when the bulk solution pH is at the measured pK_d value and when bulk pH is 7.4 (physiological conditions). As shown by the experimental results based on the pH of the bulk solution, the pK_d for the COOH-SAM surface was determined to actually be equal to the physiological pH (7.4), while the measured pK_d value for the NH₂-SAM was 6.5.

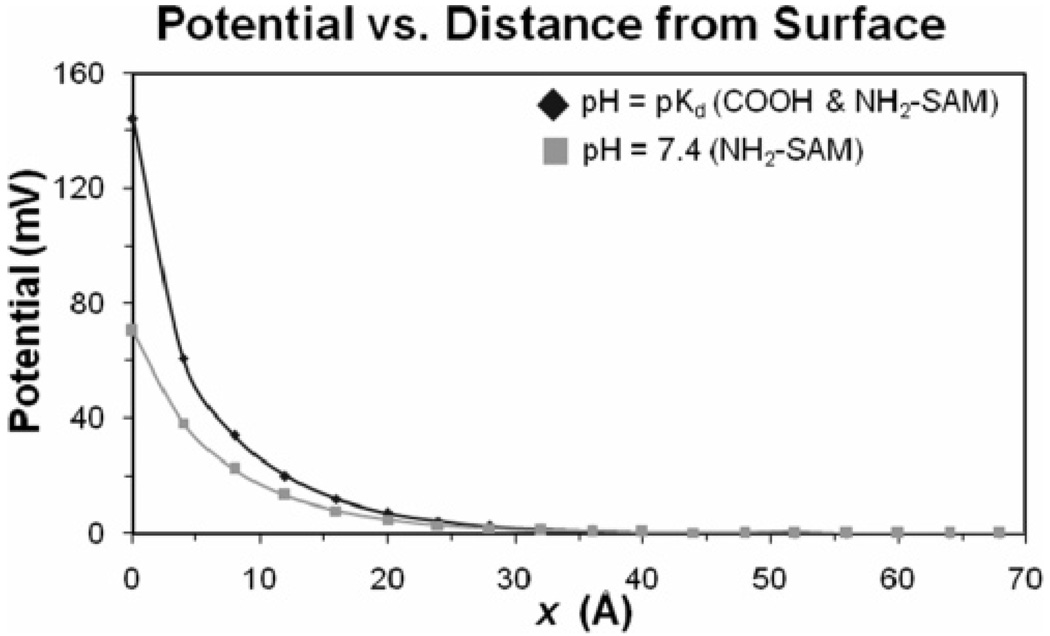
The electrical potential created by each of the charged SAM surfaces as a function of distance from the surface (ψ_x), as expressed in eq 7, is presented in Figure 2 for the case when the pH equals the measured pK_d value and for the physiological pH of 7.4. As shown, the potential is highest at the surface and exponentially decays toward zero as a function of the distance from the surface. The surface charge profiles are the same in magnitude for each surface (but opposite in sign) when the pH is equal to the pK_d of the surface. For the NH₂-SAM at pH = 7.4, which is 0.9 pH units above the measured pK_d value, the potential at the surface drops from 144 to 70 mV, with the potentials under both conditions decaying to about zero within the first 50 Å from the surface.

Figure 2.

Absolute magnitude of electrical potential (ψ_x) vs distance from the SAM surface. For the COOH-SAM and NH₂-SAM surfaces, the electrostatic potential is negative and positive, respectively.

The presence of a surface charge density results in a change in ion concentration as a function of distance from the surface as expressed by eq 8. The calculated concentrations of the Cs⁺ and Cl⁻ ions over the COOH-SAM surface at pH = 7.4 are presented in the Supporting Information, Section S-IV, Figure S1. As expected, it was determined from these analyses that the counterion concentration is greatly increased as the surface is approached, while the concentration of co-ions is reduced, with the concentrations of both types of ions transitioning to bulk conditions (0.150 M) within the first 50 Å from the surface. The calculated concentrations of the Na⁺ and Br⁻ ions over the NH₂-SAM surface at both pH = 7.4 and 6.5 (pK_d) are presented in the Supporting Information, Figure S2. In this case, the Br⁻ anions are preferentially attracted to the positively charged surface, while the Na⁺ cations are repelled.

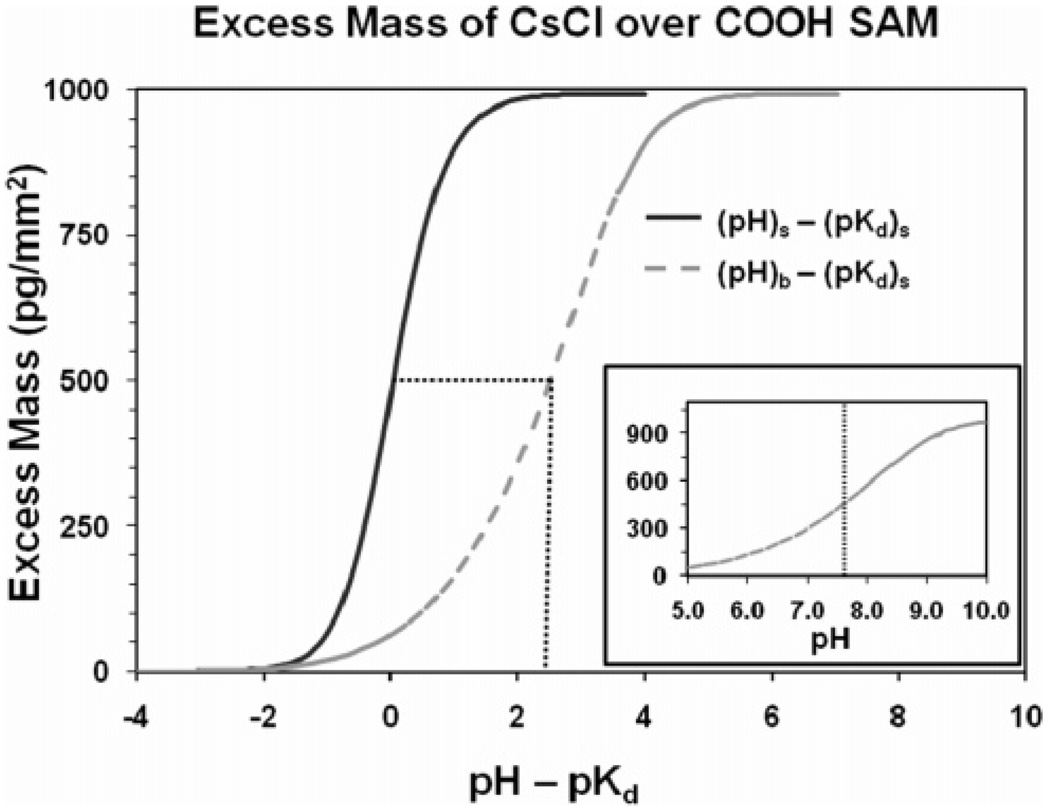
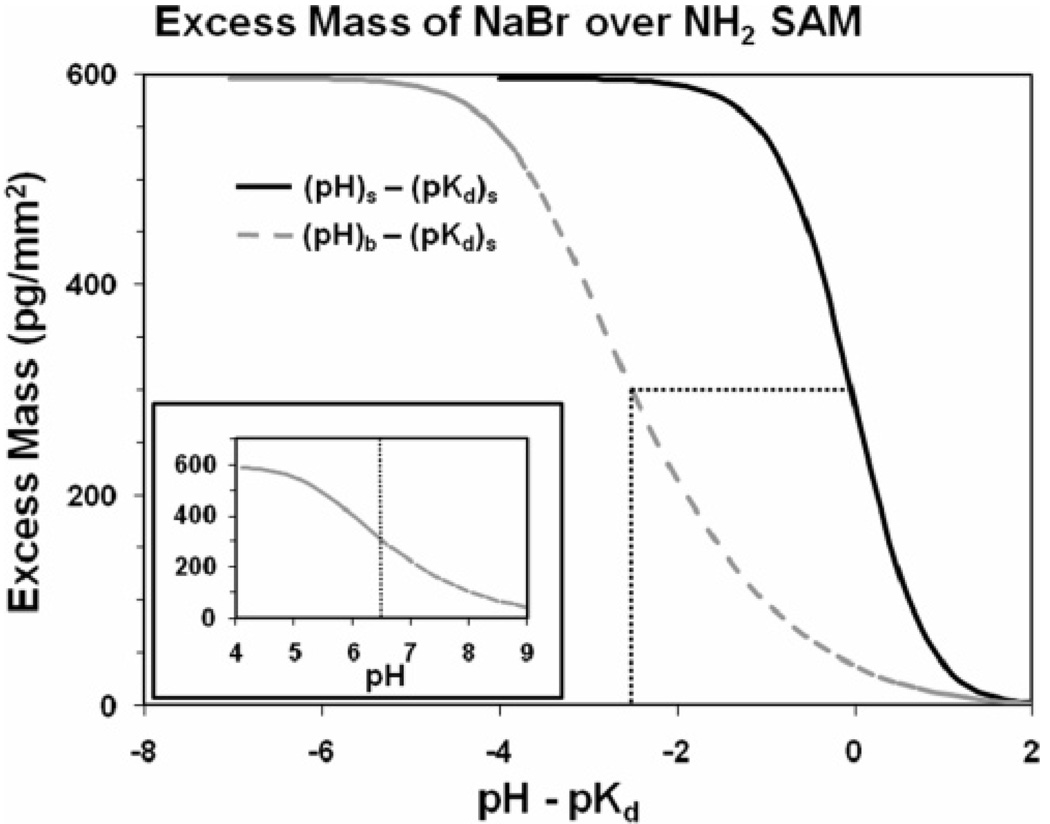
As expressed by eqs 4–8, the ion concentration profiles are a function of the surface charge density, which is in turn a function of the difference between the pH and the pK_d of the solution for conditions at the SAM surface (i.e., at x = 0). By integrating the concentration profiles over 1.0 mm² of surface area fromx = 0 to 100 Å and subtracting the bulk concentration, as shown in eq 1, the total excess mass of the ions per square millimeter over the surface can be calculated for a given (pH − pK_d) value. Plots of these relationships are shown by the solid curves in the main plots presented in Figure 3 and Figure 4 for the COOH-SAM and NH₂-SAM surfaces, respectively.

Figure 3.

Calculated excess mass per square millimeter vs the difference between pH and pK_d for the COOH-SAM surface. Solid curve in the main plot represents excess mass based on conditions at the SAM surface, i.e., pH at x = 0 (pH_s) and pK_d at x = 0 ((pK_d)_s). Dashed curve in the main plot represents conditions in the bulk solution over the surface relative to conditions at the surface, i.e., pH in bulk solution (pH_b) relative to the pK_d at x = 0 ((pK_d)_s). Curve shown in the inset plot represents the portion of the dashed curve of the main plot with its pK_d value and the pH range set to match the experimentally determined values shown in Figure 1 for direct comparison with the experimental results.

Figure 4.

Calculated excess mass per square millimeter vs the difference between pH and pK_d for the NH₂-SAM surface. Solid curve in the main plot represents excess mass based on conditions at the SAM surface, i.e., pH at x = 0 (pH_s) and pK_d at x = 0 ((pK_d)_s). Dashed curve in the main plot represents conditions in the bulk solution over the surface relative to conditions at the surface, i.e., pH in bulk solution (pH_b) relative to the pK_d at x = 0 ((pK_d)_s). Curve shown in the inset plot represents the portion of the dashed curve of the main plot with its pK_d value and the pH range set to match the experimentally determined values shown in Figure 1 for direct comparison with the experimental results.

The excess mass vs (pH − pK_d) plots show the characteristic sigmoidal curve shape, which reflects the response of the ion concentration profiles over the surface as a function of the protonation state of the surface. As noted above, the solid curves in the main plots shown in Figure 3 and Figure 4 represent the excess mass over the SAM surfaces based on the conditions at the surface (i.e., at x = 0), which differ from the bulk solution. These plots thus cannot be directly compared with the experimentally measured plots shown in Figure 1 and Figure 2, because, as expressed in eq 2, the hydrogen ion concentration in the solution is influenced by the state of surface charge in the same manner as the salt ions. Accordingly, as the charge density of the COOH-SAM surface becomes increasingly more negative with increasing pH, it attracts hydrogen ions toward the surface, thus resulting in the pH of the bulk solution being higher than the pH at the surface. Likewise, as the charge density of the NH₂-SAM surface becomes increasingly more positive, it tends to repel hydrogen ions away from the surface, thus resulting in a lower pH in the bulk solution than at the SAM surface. This behavior results in a broadening of the pH range over which the characteristic S-curves develop when based on the pH of the bulk solution compared to the condition at the surface. These pH shift effects, which were calculated based on eq 2, are shown in the dashed curves presented in the main plots in Figure 3 and Figure 4 for the COOH- and NH₂-SAM surfaces, respectively.

The curves shown in the inset plots in Figure 3 and Figure 4 present the results from the dashed curves of the main plots of Figure 3 and Figure 4, but with the curves shifted such to place the pK_d values of the plots at the experimentally measured values for the data sets that are presented in Figure 1. The ranges of pH about the pK_d values shown in these plots have also been set to correspond to the range of experimentally measured pH values for each of these SAM surfaces to most directly compare the shape of these plots to the shape of the experimentally determined plots shown in Figure 1. As indicated, the shapes of the calculated curves for the COOH- and NH₂-SAM surfaces correspond fairly closely to the shapes of the experimental curves, with the exception that the range of excess mass is substantially higher than the experimentally measured values for both surfaces and with the calculated curve for the NH₂-SAM shown to be slightly broader than the experimentally measured curve.

The higher magnitude of excess mass calculated for both surfaces compared to the experimental results can be partially explained by the fact that the SPR signal dissipates in a nonlinear manner as a function of distance from the surface,³⁵ while the theoretical calculation considers the entire amount of excess mass over the surface without dissipation. In addition, the analytical model assumes a perfect SAM surface while the surfaces used in the experiments will always contain some degree of defects in the SAM surface (e.g., grain boundaries and vacancies in the SAM lattice). The presence of such surface defects will tend to reduce the average charge density of the surface for the same degree of functional group deprotonation, which will in turn result in a lower excess mass over the surface. The discrepancy in excess mass may also be a result of the initial simplifying assumption in eq 2 that the activity coefficient ratio (γ_ir)_x is equal to 1.0 for all concentrations of the salt in solution. The activity coefficients of CsCl and NaBr in the bulk solution (0.150 M) are reported as being about 0.72 and 0.76, respectively,³⁴ with activity coefficients of monovalent salts tending to initially decrease and then steadily increase with increasing concentration to values exceeding 1.0.^36–38 As indicated by eq 2, these complex shifts in the activity coefficients of the salt ions as a function of concentration can be expected to result in a subsequent shift in the ion concentration profiles over the SAM surfaces. This, in turn, can be expected to influence the magnitude of the resulting SPR signal for a given state of surface charge.

The calculated broadening of the S-curve for the NH₂-SAM compared to the experimental results may be explained by similar arguments. As shown in eq 4, the activity coefficient ratio (γ_rNH2) for the protonation of the NH₂-SAM surface was assumed to be 1.0. A shift away from this assumption will have the effect of influencing the degree of protonation of the amine groups on the surface as a function of solution pH, resulting in either a broadening or tightening of the pH range over which full protonation of the surface occurs.

To further explore the relationship between the pH conditions at the SAM surfaces compared to the bulk solution, the magnitude of this shift, as calculated from eq 8, is shown in Figure 5 for both the COOH-SAM and NH₂-SAM surfaces.

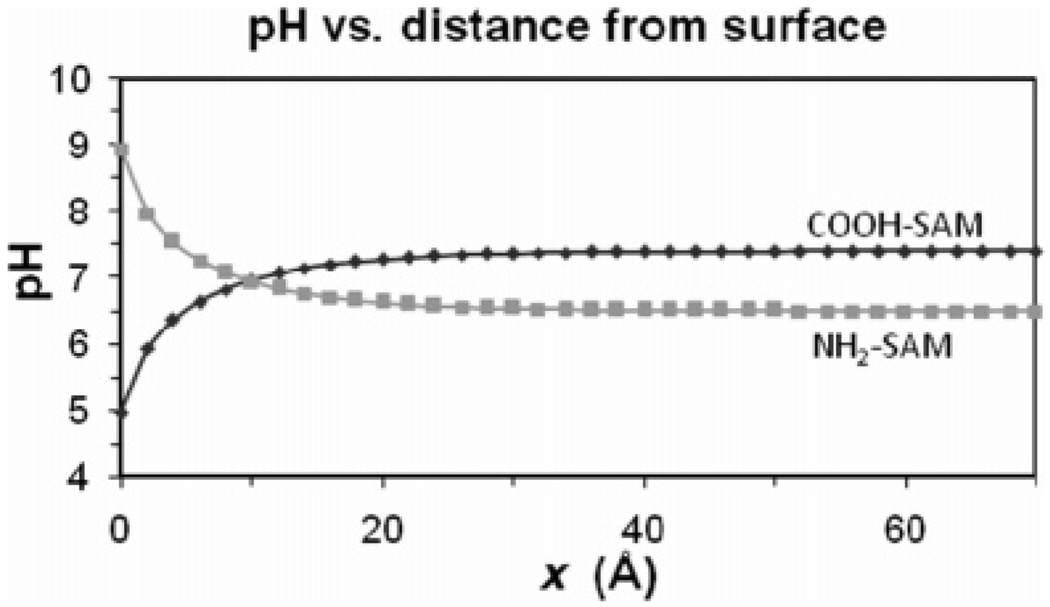
Figure 5.

Local pH as a function of distance from the charged surface for the COOH-SAM for a bulk solution pH = 7.4 (measured pK_d) and for the NH₂-SAM for a bulk solution pH = 6.5 (measured pK_d).

As shown in this figure, the measured value of the pK_d of the surface based on the pH of the bulk solution does not actually reflect the pH conditions at the surface. For the case of the COOH-SAM, the negative charge on the surface preferentially concentrates hydrogen ions near the surface, resulting in a substantial decrease of the local pH value. For the NH₂-SAM, the positively charged surface repels the hydrogen ions, thus resulting in an increase in pH at the surface. Therefore, when a COOH-SAM is exposed to a bulk solution pH of 7.4, which is at the experimentally determined pK_d, the calculated pH at the surface is 5.0 (a difference of 2.4 pH units) due to the concentrating effect that the surface charge has on the hydrogen ions in solution. This corrected value more appropriately represents the local pH that is influencing the protonation state of the COOH groups on the surface. Likewise, for the NH₂-SAM, while the measured pK_d value based on the bulk solution pH is 6.5, the calculated pH at the surface is actually 8.9 (a difference of 2.4 pH units), with this pH again being the factor that actually determines the protonation state of the NH₂ groups on the surface. Thus, when based on the bulk solution conditions, the pK_d value of the COOH-SAM surface occurs, somewhat surprisingly, under more basic conditions than the pK_d value of the NH₂-SAM surface. However, when based on conditions at the SAM surfaces, the pK_d value for the COOH-SAM surface occurs under more basic conditions than the pK_d value for the NH₂-SAM surface, as intuitively expected.

These effects may explain the apparent discrepancies in the literature regarding the pK_d values of these types of SAM surfaces that are measured using different experimental methods. Based on these calculations, if the experimental method reflects a pK_dmeasurement based on the pH value that is localized at the surface, the reported values can be expected to be shifted about 2.4 pH units compared to a measurement that is based on the pH of the bulk solution over the surface. To further describe these relationships, plots of the calculated shift between the pH of the bulk solution and that at the SAM surface for bulk solution pH values ranging from 2 to 12 are provided in the Supporting Information, Section S-V, Figures S3 and S4.

Conclusions

These methods have shown that SPR spectroscopy responds to the change in concentration of CsCl and NaBr salt solutions over COOH- and NH₂-SAM surfaces, respectively, as a function of their protonation state in a manner that is reasonably close to the analytical solution for these types of systems. This provides a relatively simple and straightforward method to determine the pK_d for charged SAM surfaces that is nondisruptive and minimally interactive with the surface.

The analytical solutions of the ion concentration profiles corresponding to the conditions used in the experimental studies emphasize the fact that not only do the cation and anion concentration profiles of the selected salts shift as a function of the protonation state of the surface, but also the hydrogen ion concentrations should shift as well. This leads to a substantial shift of the pH at the surface compared to the bulk solution relatively far from the surface. Based on the combined experimental and analytical results from these studies, it is concluded that the pK_d values of the COOH- and NH₂-SAM surfaces are 7.4 and 6.5, respectively, based on the bulk solution pH, and approximately 5.0 and 8.9, respectively, based on the theoretical analyses of the local pH at the SAM surfaces.

The differences in the pK_d values of these surfaces depending on the basis for measurement (i.e., based on conditions in the bulk solution or locally at the actual surface) may partially explain the relatively large range of pK_d values reported in the literature for these types of SAM surfaces. These results emphasize the importance of clearly stating the basis of measurement (i.e., bulk or local surface) when reporting the pK_d value of a functionalized surface.