Automatic particle selection from electron micrographs using machine learning techniques

Abstract

The 3D reconstruction of biological specimens using Electron Microscopy is currently capable of achieving subnanometer resolution. Unfortunately, this goal requires gathering tens of thousands of projection images that are frequently selected manually from micrographs. In this paper we introduce a new automatic particle selection that learns from the user which particles are of interest. The training phase is semi-supervised so that the user can correct the algorithm during picking and specifically identify incorrectly picked particles. By treating such errors specially, the algorithm attempts to minimize the number of false positives. We show that our algorithm is able to produce datasets with fewer wrongly selected particles than previously reported methods. Another advantage is that we avoid the need for an initial reference volume from which to generate picking projections by instead learning which particles to pick from the user. This package has been made publicly available in the open-source package Xmipp.

1 Introduction

There is at present a strong investment in achieving high-throughput elucidation of large biological complexes using 3D Electron Microscopy (3DEM). The goal is to automate as much as possible all the steps from data acquisition to 3D reconstruction. In this line, several projects aim at automating the image acquisition within the microscope (Lei and Frank, 2005; Suloway et al., 2005; Stagg et al., 2006), the CTF detection (Sorzano et al., 2007), and the particle picking (see Zhu et al. (2004) and references therein). In this article we address this latter problem. Particle picking aims to locate the bidimensional projections of the structure under study in an electron micrograph. In the modality of single particles, the macromolecule under study is imaged in such a way that each particle is most often isolated from the rest, as opposed to the formation of large molecular arrays or regular crystals. Currently, in most structural biology studies employing the single particle approach, the projections are manually identified by the scientist. The goal of automatic particle picking (APP) is to reduce the particle picking time with the aim of being able to select a large number of particles from a set of micrographs. At the same time, using APP algorithms improves the objectivity of the picking process so that it is more reproducible.

APP algorithms can be divided into three categories depending on the features being sought within the image. A large group of algorithms uses a reference volume from which projections are generated in all directions. The different particle views are matched in the micrographs (Huang and Penczek, 2004; Rath and Frank, 2004; Roseman, 2004; Wong et al., 2004). Another group of algorithms is completely reference free and the particles are automatically detected based on some measure of “saliency” of the images (Kumar et al., 2004; Ogura and Sato, 2005; Plaisier et al., 2004; Singh et al., 2004; Umesh Adiga et al., 2004). Between these two extremes there is another group of algorithms that learn the kind of images to be picked by a training dataset provided by the user (Hall and Patwardhan, 2004; Mallick et al., 2004; Ogura and Sato, 2004; Plaisier et al., 2004; Short, 2004; Volkmann, 2004). Still, some other algorithms rely on a simplified geometric description of the overall shape of the particles being sought (Yu and Bajaj, 2004). The algorithms based on a 3D reference volume are useful for an advanced stage of the image processing in which such a reference already exists and it is used to collect more images. However, they are not useful in early stages in which the reconstructed volume is not yet available. On the other hand, those algorithms relying solely on image saliencies disregard completely the user preferences and assume that all particles and orientations in the micrographs are desired. This may not always be the case, as for some projects it is required to select only a particular set of orientations or of particle type (see, for example, Zhu et al. (2003, 2004)).

Our algorithm belongs to the family of algorithms that learn from the user which is the kind of images of interest. A number of features is learned from each training image and the new projections are picked according to the statistical distribution of the learned features. Our method differs from other APP approaches (Hall and Patwardhan, 2004; Mallick et al., 2004; Short, 2004; Volkmann, 2004) in the features calculated for each training image, the classifier used, and our emphasis on a continuous learning process so that the user can always “teach” the algorithm about wrongly selected particles (false positives) as more and more micrographs are being processed. Our image features are rotationally invariant (inspired by those of Short (2004)), speeding up the particle selection process by avoiding having to learn rotated training images or rerunning the algorithm on the same micrograph at different orientations. Our classifier is an ensemble classifier (Polikar, 2007), using a modified Naive Bayes classifier at its base. The classifier has been designed to reduce as much as possible the false positive rate (i.e., selected objects that do not correspond to true particles). This is important to reduce the number of junk particles selected. We applied our algorithm to the standard KLH dataset used in Zhu et al. (2003, 2004) as well as to the in-house datasets of the SV40 Large T antigen in complex with Replication Protein A (LTAg+RPA, Alcorlo et al., manuscript in preparation) and adenovirus.

2 Methods

In this section we present the details of our APP algorithm. First we explain our approach to micrograph preprocessing and our choice of image features that will be used to identify the particles; then we introduce our basic classifier, and finally we present our three-stage ensemble classifier.

2.1 Micrograph preprocessing

Before computing the image features, it is important to remove as much noise as possible so that the computed features are stable. We propose to high-pass filter the image, then to apply a Bayesian wavelet denoising algorithm (Sorzano et al., 2006), downsampling the image by a factor two by removing all high frequency wavelet components, outlier rejection clipping all extremely small and high values, and histogram partitioning into a fixed (user supplied) number of bins. Fig. 1 shows an example of this preprocessing. We suggest to perform the high-pass filter with a cutoff frequency of 0.02 (the maximum digital frequency is 0.5). The outlier rejection is performed by removing 2.5% of the smallest values and 2.5% of the largest values. Note that this outlier rejection is performed in real space and not in wavelet space since it is aimed at getting rid of bright or dark pixels usually related to hot/cold pixels in a CCD camera or dust particles. For the histogram partitioning we used 8 bins.

Fig. 1.

Original piece of a micrograph with KLH particles and its preprocessed counterpart. Note that the size of the preprocessed image is half the size of the original image. However, it has been rescaled for better visualization.

2.2 Image features

In order to identify particles disregarding their in-plane orientation, for each image we compute a vector of rotational invariant features. These vectors will be used by the classifier to distinguish between particles, non-particles and errors (this concept will be introduced later).

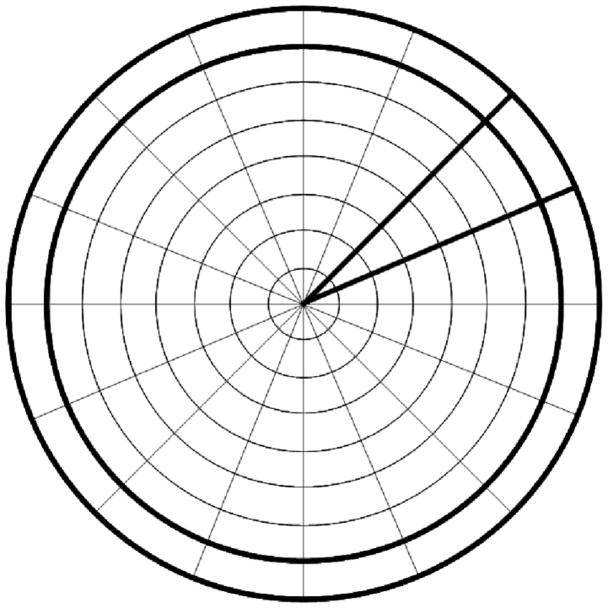
For achieving rotational invariance, we compute a coarse polar representation of our image formed by N_r equally thick rings, and N_s sectors (see Fig. 2). The polar conversion is performed by simply adding all pixel values falling in a polar bin. The diameter of the circle should be a little bit larger than the expected diameter of the particle. The rotational invariant feature vector is formed by the histogram of all the rings, the correlation function between the rings i and i–j where j ∈ {1, 2}, the average of the vector Φ_δ (to be defined later) and the autocorrelation of Φ_δ.

Fig. 2.

Coarse polar representation of an image with N_r = 8 rings and N_s = 16 sectors. The outer ring and one of the sectors have been highlighted.

Given a ring as a vector of size N_r, the correlation between two such rings r_i1 and r_i2 is computed as

$${\phi }_{r_{i_1},r_{i_2}}[k]=\sum _{m=0}^{N_s-1}{r}_{i_1}[(k+m)mod{N}_s]r_{i_2}[m],$$ (1)

where r[m] denotes the m-th component of vector r.

The correlation between two sectors s_i1 and s_i2 is computed as

$${\phi }_s(i_1,i_2)=\frac{{\displaystyle \sum _{m=0}^{N_r-1}}(s_{i_1}[m]-{\overline{s}}_{i_1})(s_{i_2}[m]-{\overline{s}}_{i_2})}{\sqrt{\left({\displaystyle \sum _{m=0}^{N_r-1}}{(s_{i_1}[m]-{\overline{s}}_{i_1})}^2\right)\left({\displaystyle \sum _{m=0}^{N_r-1}}{(s_{i_2}[m]-{\overline{s}}_{i_2})}^2\right)}}.$$ (2)

With this correlation index between sectors, for each δ ∈ {1, 2, …, N_s − 1}, we construct the vector Φ_δ as

$${\mathrm{\Phi }}_{\delta }=({\phi }_s(0,(0+\delta )mod{N}_s),{\phi }_s(1,(1+\delta )mod{N}_s),\cdots ,{\phi }_s(N_s-1,(N_s-1+\delta )mod{N}_s)),$$ (3)

whose average and autocorrelation (defined as in Eq. (1)) are rotation invariants.

The total number of features in our feature vector is

$$\begin{array}{l}N=\sum _{r=0}^{N_r-1}(N_g-1)+\sum _{\delta =1}^2\sum _{r=r_0}^{N_r-1-\delta }{N}_s+\sum _{\delta =1}^{N_s-1}(1+N_s)\\ =N_r(N_g-1)+(2N_r-2r_0-3)N_s+(N_s-1)(1+N_s).\end{array}$$ (4)

The first term accounts for the ring histograms (N_g is the number of gray values used in the histogram partitioning described in the previous section; the last value of the histogram is not stored since the fact that the sum of the histogram values must add up to 1 reduces 1 degree of freedom). The second term considers the correlation between rings (r₀ makes sure that the rings are not too small to have reliable estimates of their values). The last term accounts for the correlation between sectors (φ_s(i₁, i₂)). In our experiments we used N_g = 8, N_r = 16, r₀ = 8 and N_s = 16, so the total length of the feature vector was 575.

This feature vector is computed on a regular grid of points within the micrograph. It is recommended that the distance between grid points is much smaller than the expected particle diameter. In our experiments we made it 10%, meaning that within the area of an expected particle, 100 (=10×10) grid points are explored as possible particle candidates.

2.3 Basic classifier

We use an ensemble classifier formed by many individual classifiers. As each member of the ensemble behaves similarly, we present here the most basic classifier.

Let us consider the problem of classifying a dataset into K classes with N_k (k ∈ {0, 1, …, K −1} training vectors for each class. The training vectors in each class are called ${\mathbf{v}}_i^k$ with i ∈ {0, 1, …, N_K − 1}. Let $v_{i,j}^k$ be the j-th component of this vector (i.e., the value of the j-th feature for this image). Let us also assume that there are up to J features in each vector.

We discretize each feature independently into N_j bins so as to have maximum separation between classes. To perform this partition, let us consider the absolute range of the feature observed in all classes [v_f,min, v_{f max}]. We first find a value T within this range such that the entropy of the partition is maximized, i.e.,

$$T^{\ast }=arg\underset{T}{max}\sum _{k=0}^{K-1}\left(Pr\left\{v_{i,j}^k<T\right\}log\frac{1}{Pr\left\{v_{i,j}^k<T\right\}}+Pr\left\{v_{i,j}^k\ge T\right\}log\frac{1}{Pr\left\{v_{i,j}^k\ge T\right\}}\right).$$ (5)

Once we have splitted the interval [v_j,min, v_j,max] into two halves, we repeat the same procedure with each one of the halves. This process is iterated until the desired amount of bins is achieved. In our experiments we used N_j = 8.

Let us call $L(v_{i,j}^k)$ a label between 0, 1, …, N_j −1 corresponding to the bin containing the value $v_{i,j}^k$. If a feature is good for classification, the probability density function (PDF) of labels under class k must be very different from the PDF under class k′. Differences between two PDFs can be measured through the Kullback-Leibler divergence

$$D_{KL}(k||k^{\prime };j)=\sum _{l=0}^{N_j-1}Pr\left\{L(v_{i,j}^k)=l\right\}log\frac{Pr\left\{L(v_{i,j}^k)=l\right\}}{Pr\left\{L(v_{i,j}^{k^{\prime }})=l\right\}}.$$ (6)

We define the classification power of feature j as

$$w_j=\frac{1}{K(K-1)}\sum _{k=0}^{K-1}\sum _{k^{\prime }=0}^{K-1}{D}_{KL}(k||k^{\prime };j).$$ (7)

This number is close to 0 if the feature j cannot discriminate between the K classes and increases as the discriminative power of the feature increases.

Given a feature vector v that we want to classify, a discrete Naive Bayes classifier (NBC) assigns the class that maximizes the probability that this vector comes from the distribution of vectors in class k assuming that each feature is independent from the rest:

$$k^{\ast }=arg\underset{k}{max}Pr\{k\}\prod _{j=0}^{J-1}Pr\left\{L(v_{i,j}^k)=L(v_j^k)\right\},$$ (8)

where Pr {k} is the a priori probability of class k. It is directly estimated from the training set as the number of cases in class k over the total number of cases in the training set.

Although features are seldom independent, NBCs usually yield powerful classifiers whose performance is not far from the classifier using the true dependence structure (Hand and Yu, 2001; Zhang, 2004). The performance of the NBC can be improved if the different features are weighted according to their classification power

$$k^{\ast }=arg\underset{k}{max}Pr\{k\}\prod _{j=0}^{J-1}{\left(Pr\left\{L(v_{i,j}^k)=L(v_j^k)\right\}\right)}^{w_j}.$$ (9)

In this scheme, features with low classification powers (they are distributed similarly for any of the classes) have an exponent (w_j) close to 0 and, therefore, the corresponding probability ${\left(Pr\left\{L(v_{i,j}^k)=L(v_j^k)\right\}\right)}^{w_j}$ is close to 1. In this way we avoid introducing noise in the classification process due to features that cannot distinguish between different classes.

The classification rule in Eq. (9) assumes that the cost of committing a classification error is the same for all classes. However, in this work we have made the choice of preferring to miss a true particle than picking up a non-particle image. Therefore, we assign different costs to different classification errors. Let C(k, k′) be the cost matrix, i.e., the cost of classifying an object as of class k when actually it is of class k′ (in our setting C(k, k) = 0). Instead of looking for the class that maximizes the probability of observing the feature vector v, we look for the class that minimizes the expected cost

$$k^{\ast }=arg\underset{k}{min}\sum _{k^{\prime }}\left(C(k,k^{\prime })Pr\{k^{\prime }\}\prod _{j=0}^{J-1}{\left(Pr\left\{L(v_{i,j}^{k^{\prime }})=L(v_j^{k^{\prime }})\right\}\right)}^{w_j}\right)$$ (10)

We will refer to this classifier as cost-aware, weighted Naive Bayes classifier (CWNBC). In our experiments we set the cost of missing a particle to 1, and the cost of picking a non-particle to 10. Of course, different families of classifiers could be designed using these weights.

As will be seen in the two subsequent sections, the CWNBC is the most basic unit of the ensemble classifier, i.e., each member of the ensemble is a CWNBC. In the overall structure, three ensemble classifiers are gathered in a three-stage classifier, which is our proposed schema to classify candidate particle centers as really being particles or not.

2.4 Ensemble classifier

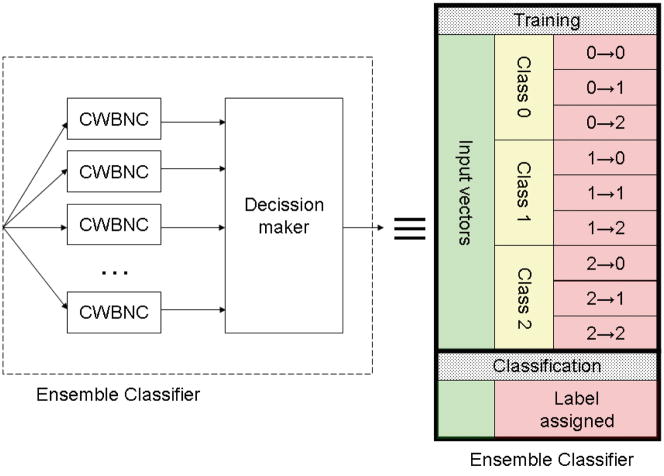
An ensemble classifier is a classifier formed by many potentially weak classifiers (Polikar, 2007). In our case we chose the CWNBC as the basic unit of the ensemble classifier. Each individual classifier assigns a label to the input vector, then a decision is made based upon the labeling of the individual classifiers (see Fig. 3). The particularities of the decision making process in our case will be described in the next section. The advantage of using ensemble classifiers resides in the fact that even if each individual classifier has bad classification error rates, collectively they have a much better performance (Polikar, 2007).

Fig. 3.

Left: Internal structure of the ensemble classifier. Several weak classifiers (CWNBC) assign a label to a given input vector. Based on these labels, a final decision is made and a label is assigned to the input vector. Right: From an operational point of view, the ensemble classifier can be seen, like any other classifier, as a black box that is trained on input vectors with known class labels and applied to input vectors with unknown class labels. The training vectors are used to learn the classification rules. The application of these rules to the training data yields correctly classified vectors (like a vector of class 0 classified as class 0, 0 → 0) and incorrectly classified vectors (like a vector of class 0 classified as class 1, 0 → 1).

For this schema to work, each classifier in the ensemble must be trained differently from the rest of the elements. For achieving this goal, randomness is usually introduced at the training level so that none of the individual classifiers is identical to any other. In our case, we chose to train each CWNBC on a bootstrap sample of the training vectors and features (Efron and Tibshirani, 1993; Zoubir and Iskander, 2007), i.e., each CWNBC sees a different subset of training vectors and a different subset of features randomly chosen from the original set of training vectors and features by sampling with replacement following a uniform distribution.

From an operational point of view, the ensemble classifier can be seen as a black box that is trained on a given set of input vectors whose label is known, and that operates on input vectors with unknown labels to assign them. The training vectors are used to learn the classification rules. Application of these rules to the training vectors produces correctly assigned vectors as well as incorrectly assigned ones. For instance, a vector of class 0 that is classified as class 0 (0 → 0) is correctly classified, while a vector of class 0 that is classified as class 1 (0 → 1) is incorrectly classified. This notion and notation will be important in the next section when defining the particle classifier.

As described in the next section, our particle classifier is a three-stage classifier. At each stage, there is an ensemble classifier which has to classify in either two (particles vs. errors) or three classes (particles vs. non-particles and errors).

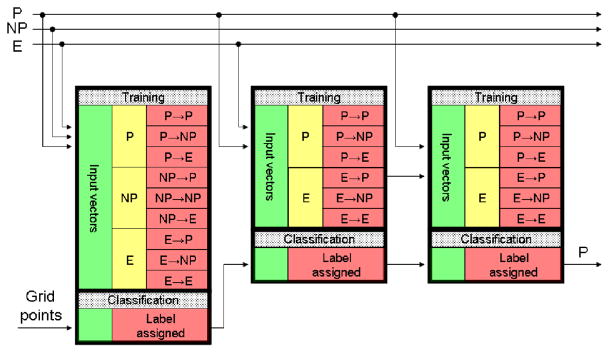
2.5 Three-stage classifier

Our classification algorithm has been designed either to continuously learn from the user if they decide to do so, or to learn from just a few micrographs at the beginning of the process, and then work independently. The algorithm works as follows. For the first micrograph, the user must manually pick all particles, typically obtaining a dataset of between 50–100 particles. If this amount is not achieved in one micrograph, several micrographs can be used. For the sake of simplicity, let us assume that the first micrograph already contains enough particles. These particles will be used to train the algorithm. The algorithm assumes that anything in the first micrograph that was not picked up is not a particle, and uses this information to learn how to distinguish between particles and non-particles. In the second micrograph, the algorithm is trained with the particle and non-particle vectors determined for the first micrograph, and then it tries to predict which are particles and which are not. After taking a decision for each point of a fine grid in the micrograph, the results are presented to the user. The user can then correct the algorithm results by adding new particles and by removing those wrongly picked particles. These errors are treated differently in our algorithm from non-particles, since they are probably more similar to particles and, therefore, more difficult to distinguish. They form a new class, and the classifier for the third micrograph will have to distinguish between particles, non-particles and errors (i.e., non-particles particularly similar to particles). Therefore, the classifier for the third micrograph is trained on the set of all particles picked up in micrographs 1 and 2, the set of all non-particles identified in micrographs 1 and 2, and the set of errors committed in micrograph 2. Then, the classifier tries to assign a label to each grid point. Only those points identified as particles are presented to the user, who can again correct the algorithm and increase the population of errors. To successfully perform this three-class classification, our algorithm makes use of three classification stages. Each stage is formed by an ensemble classifier with a different task. The structure of this classifier is presented in Fig. 4 while a detailed explanation is given in the following paragraphs.

Fig. 4.

Structure of the multistage ensemble classifier. Stages are cascaded to refine the previous classification. Each stage is formed by several classifiers in parallel. In the figure P stands for the particle class, NP for the non-particles, and E for the errors (see text for a detailed explanation). Particles, non-particles and errors of the present micrograph engross the training population for the next micrograph.

The first stage of classifiers must distinguish among the three different classes. If a certain percentage of the classifiers decides that the vector to be classified corresponds to a particle, the vector progresses to the next stage. Otherwise, the vector is discarded as not corresponding to a particle. In our experiments we used 10 classifiers in each ensemble, and in this stage it sufficed that 1 of them classified the vector as particle.

The task of the first stage is a difficult one since it has to draw decision boundaries between three classes, two of them (particles and errors) being rather similar. The second stage takes the alleged particles produced by the first stage and classifies them between particles and errors. Since it has only to distinguish between two classes, the task is easier (although still the separation between particles and errors is a difficult one). If a certain percentage of the classifiers classifies the vector as error, then the vector does not progress any more through the cascade (in our experiments we used 10 classifiers and it sufficed that 1 of them classified the vector as error). Those vectors marked as particles progress to the next stage.

The second stage still makes many classification errors (in the order of 30% of the errors used for training in the training phase are wrongly classified as particles). The errors of the second stage are those really difficult errors that cannot be well distinguished from true particles using the computed rotational invariant features. The third classifier focuses in these very difficult particles and is trained to distinguish between particles and the classification errors of stage 2. Again, it suffices that a certain percentage of the classifiers in the ensemble classifies the vector as error so as to be considered as an error (in our experiment we used 10 classifiers in the ensemble and the particle was removed from the list of particle candidates if at least one of the basic classifiers classified it as error). This idea of concentrating on the errors of a previous classifier is the one also exploited in Adaboost (Freund and Schapire, 1996) which was already used in (Mallick et al., 2004). Adaboost is a rather general Machine Learning technique. However, we have tuned this method for our algorithm by disregarding classification errors caused by non-particles and instead concentrating only on the errors between particles and false particles.

2.6 Post-processing

The list of particle candidates is sorted by ascending average cost (Eq. 10). Candidates at the top of the list are finally returned as valid candidates, while candidates lower in the list are removed if they have another close-by (determined by a distance threshold) candidate above in the list. In our implementation we give the user the possibility of further choosing high-quality particles by removing particles of this sorted list through a slider that permits to drop the most costly particles in the remaining list.

3 Results

To test the experimental validity of our APP algorithm, we applied it to the standard dataset of KLH (Keyhole Limpet Haemocyanin) (Zhu et al., 2003, 2004) on which many other papers have reported their results (Mallick et al., 2004; Roseman, 2004; Volkmann, 2004; Wong et al., 2004; Yu and Bajaj, 2004), and where, therefore, comparison is possible. We also applied it to two in-house produced datasets to test its performance on images and specimens with different characteristics.

KLH Dataset

82 micrographs at a magnification of 66000x were collected in a Phillips CM200 transmission electron microscope. Images were recorded in a Tietz CCD camera of size 2048×2048. The pixel size is approximately 2.2 Å/pixel. Our results will be presented on the far from focus subset as it was done in previous works (Mallick et al., 2004; Roseman, 2004; Volkmann, 2004; Wong et al., 2004; Yu and Bajaj, 2004). The defocus used for these images was −3μm.

We chose the particle diameter to be 256 pixels, the minimum distance between particle candidates 64, and the distance between grid points 26. The high-pass filter for preprocessing was 0.02, the preprocessed image gray levels were binned into 8 bins (see Fig. 1), and the polar transformation (see Fig. 2) was calculated with 8 rings and 16 sectors.

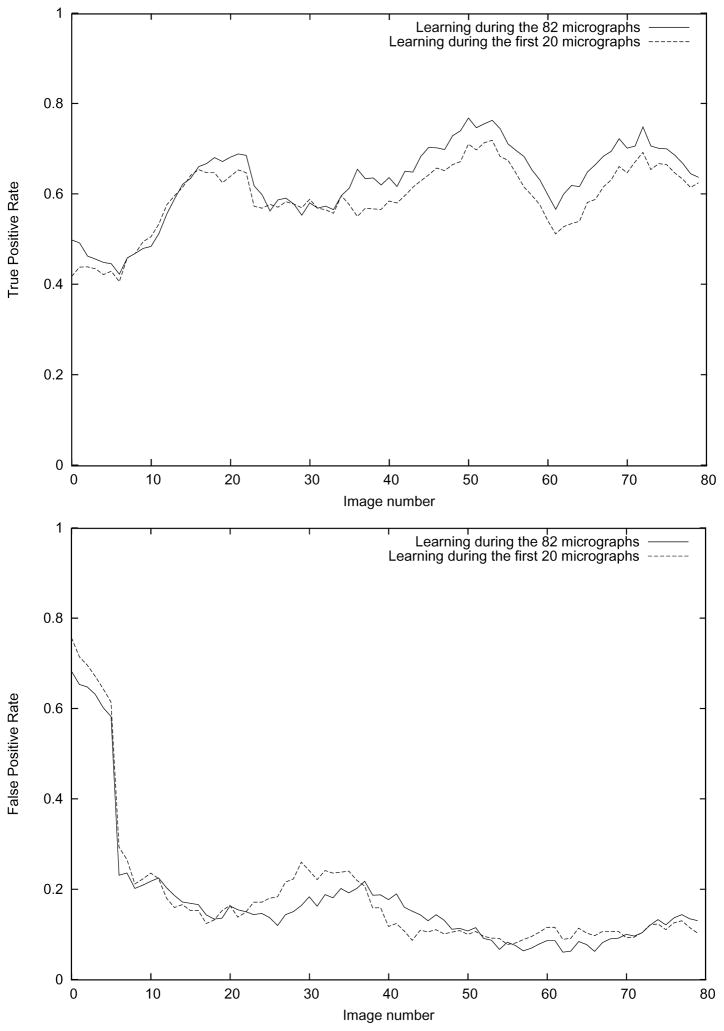
We used the particles picked by Fabrice Mouche (Zhu et al., 2004) in the first three micrographs to initially train the algorithm. This first training set had 44 vectors corresponding to particles (learned from Fabrice Mouche), and 202 vectors of non-particles (learned from regions far from the picked particles). The algorithm tried to automatically pick up particles from the 4th micrograph. It picked 74 particles out of which 10 corresponded to true particles (there were 11 of them, therefore, we have a True Positive Rate (TPR) at this micrograph of 10/11=91%) and 64 corresponded to errors (i.e., a False Positive Rate (FPR) of 64/74=86%). We labeled the 64 wrongly picked particles as errors, picked the missed particle, and built a new model now with 55 particles, 273 non-particles, and 64 errors. We repeated this procedure with all the 82 micrographs, Fig. 5 shows the TPR and FPR results for the whole process.

Fig. 5.

True Positive Rate and False Positive Rate for the APP algorithm proposed in this article. The True Positive Rate is defined as the number of true particles automatically picked over the number of true particles manually picked by Fabrice Mouche in Zhu et al. (2004). The False Positive Rate is defined as the ratio between the wrongly picked particles (a particle is wrong if it does not belong to the Fabrice Mouche set) and the total number of particles picked.

As can be seen in Fig. 5, the algorithm learns a reasonably good model after 20 micrographs. In the following micrographs (between 21 and 50), the TPR is 62.9% and the FPR is 16.0%. However, if we keep training, the TPR increases to 69.1% and the FPR decreases to 9.3% (measured over the last 30 micrographs). Fig. 6 shows an example of particles picked up in the last micrograph after learning from the 82 micrographs.

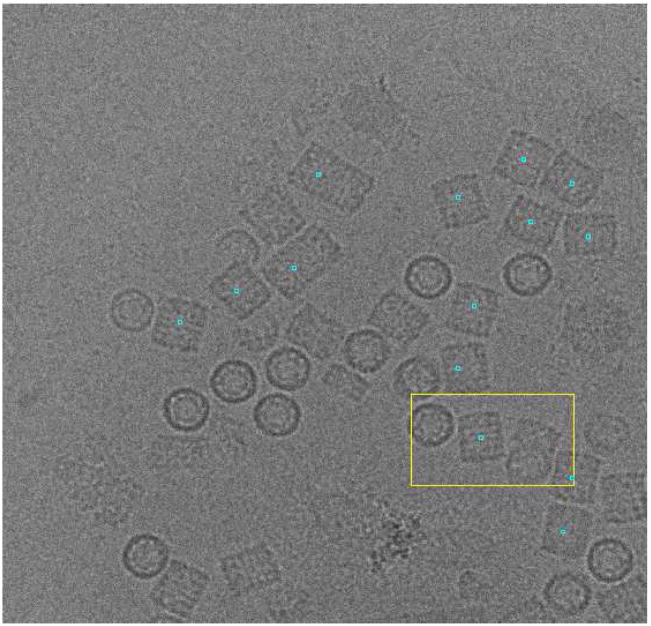
Fig. 6.

Sample micrograph with the particles picked in the KLH dataset after learning for 82 micrographs. Note that in this case, the user is not interested in top views (circularly shaped projections).

In an experimental setting it is more convenient to train the algorithm on a few micrographs and let it run without any more training for the rest of the micrographs. We chose to train the algorithm for 20 micrographs and then pick up the rest of the micrographs using this model. Note that this training on the first 20 micrographs was run independently from our previous experiments and, therefore, the two models need not be the same up to the 20-th micrograph. The model after 20 micrographs had 282 true particles, 1839 non-particles, and 94 errors. When this model was evaluated on the set of the 60 remaining micrographs, the TPR was 61.5% and the FPR 13.6%. For a fair comparison with the previous experiment (described in the previous paragraph), we evaluated this model in the last 30 micrographs, the TPR was then 63.4% and the FPR 10.7%.

In this particular case in which the particles being sought are all side views (rectangularly shaped), quite similar to each other, the set of automatically picked particles can be further refined by aligning the automatically picked particles (we used a Maximum Likelihood alignment with only one class (Scheres et al., 2005)). Then, the cross-correlation between the picked particles and the average of the aligned particles was computed. Knowing that a typical FPR is somewhere between 10% and 20%, we removed 15% of the images with the smallest correlation coefficients (this idea was already introduced by Zhu et al. (2004)). The resulting dataset had only 1.6% false positives, and the TPR dropped from 61.5% to 60.0%.

In any of the two experiments described above, the processing time per micrograph was 41 seconds in a single core of a Intel Core Duo, 64 bits, 2 Ghz. The following table shows the FPR and TPR, principle of learning (projections learned from user, projections learned from an initial 3D reference model, or KLH geometry specifically exploited) for our algorithm as well as for those reported in Zhu et al. (2004). The table has been sorted by ascending FPR.

Algorithm	FPR (%)	TPR (%)	Principle	Time/Micrograph
Proposed partially trained and filtered	1.6	60.0	Projections	47s
Sigworth (2004)	4.5	76.8	Initial 3D	NA
Proposed fully trained	9.3	69.1	Projections	41s
Proposed partially trained	10.7	63.4	Projections	41s
Mallick et al. (2004)	11.7	85.8	Projections	120s
Volkmann (2004)	12.2	72.6	Projections	60s
Zhu et al. (2003)	13.7	90.3	KLH Geometry	NA
Wong et al. (2004)	16.2	76.2	Initial 3D	NA
Roseman (2004)	16.6	97.6	Projections	42s
Hall and Patwardhan (2004)	22.0	72.6	Projections	NA
Ludtke et al. (1999)	23.7	56.6	Projections	10s
Yu and Bajaj (2004)	24.7	92.7	KLH Geometry	20s
Huang and Penczek (2004)	30.7	53.2	Initial 3D	NA

LTAg+RPA Datataset

To further explore the capabilities of our algorithm, we applied it to a dataset of much more contrasted images. As expected, in this case we found that we can train our algorithm with fewer micrographs than in the previous experiment since the images are well contrasted.

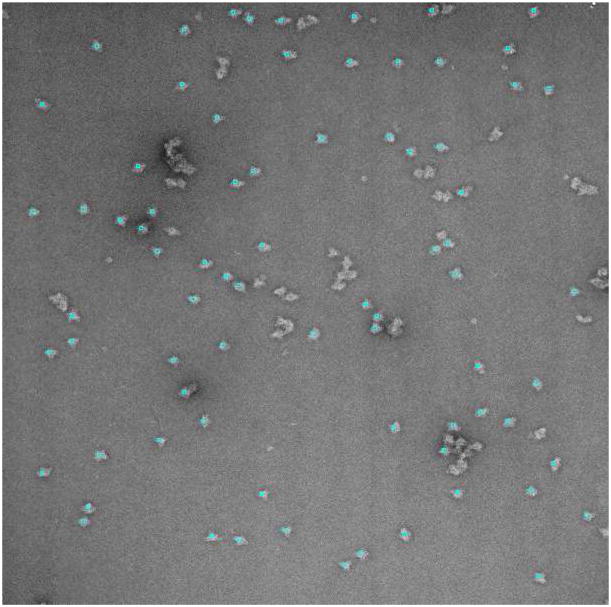
LTAg-RPA complexes were adsorbed to glow-discharged, carbon-coated grids, negatively stained with 2% uranyl acetate and observed in a JEOL 1230 transmission electron microscope at 120 kV accelerating voltage and a magnification of 50000x. Twenty-two micrographs were obtained under minimum-dose conditions, on Kodak SO-163 plates and scanned in a Zeiss/Imaging scanner. The sampling rate was 4.2 Å/pixel. Note that although this dataset has much better contrast due to the negative staining (see Fig. 7), not all bright objects in the micrograph are considered to be particles, but only those that are sufficiently separated and within an appropriate size range.

Fig. 7.

Sample micrograph with the particles picked after learning for 4 micrographs in the Large T antigen+RPA dataset.

For our algorithm we set the particle diameter to 100 pixels, and the distance between grid points to 10. The minimum distance between two adjacent particles was set to 25 pixels. The rest of parameters remained as in the previous dataset.

We manually picked 39 particles in the first two micrographs (see Fig. 7 for examples of particles). The particle selection of the algorithm was corrected in the third and fourth micrographs, and these were the only micrographs on which the algorithm was trained. After these, the algorithm was used to automatically pick up particles in the 18 remaining micrographs. A total of 1440 particles were automatically detected. The TPR was 97.4% and the FPR 5%. These figures mean that only 5% of the 1440 automatically selected particles were wrong, and that most (97.4%) of the particles that a person would have picked, were actually picked.

The processing time per micrograph was 12 minutes in a single core of a Intel Core Duo, 64 bits, 2 Ghz. This is much larger than the processing time for the KLH, however it must be noted that the number of grid points in the LTAg+RPA case was 18 times larger (since the micrographs are larger and the particle is smaller). In our implementation, several micrographs can be processed in parallel as long as they all use the same image model for the particles to be picked (which is the case of all micrographs processed after the training stage). Therefore, the processing time for a single micrograph should be divided by the number of processors available.

Adenovirus dataset

Finally, we explored the applicability of our algorithm to pick up large objects in cryomicroscopy conditions. This is a much more challenging technique since the specimen is not stained. This dataset consisted of 206 micrographs of human adenovirus type 5, an icosahedral virus producing mild cold symptoms that has the potential of being used as a therapeutic tool (San Martín et al., 2008). Virus samples were flash-frozen in liquid ethane and observed at −175°C and 200kV in a FEI Tecnai G2 transmission electron microscope. Images were recorded on Kodak SO-163 film using a radiation dose of 10 electrons/Ų, a magnification of 50000x and defocus values in a range between −0.8 and −6μm. Micrographs were digitized in a Zeiss Photoscan TD scanner with a 7μm pixel size (1.4Åin the sample).

We kept all parameters of our algorithm the same as in the previous two examples except the diameter of the particle, that was set to 380, the distance between grid points to 38, and the minimum distance between two particles to 95.

We manually picked the first micrograph in which 148 viruses were available. We trained the algorithm on other nine micrographs, correcting the picking up errors committed by the algorithm after the first micrograph. This process finished the training stage with 401 particles, 2368 non-particles and 71 errors. After training for 10 micrographs we let the algorithm pick up viruses in the 196 remaining micrographs. The particle picking process took 5 minutes per micrograph in an Intel Core Duo, 64 bits, 2 Ghz. The algorithm automatically detected 6646 particles, the TPR was 98.75%, and the FPR was 21.75% corresponding mostly to adenoviruses falling outside the support holes. The automatically picked particles were aligned using Maximum Likelihood (Scheres et al., 2005) into a single class. After removing the 25% particles with smallest likelihood to avoid the particles in the border as well as the errors, the FPR was reduced to 3.6% and the TPR to 93.6%.

4 Discussion

In this article we have introduced a new automatic particle picking algorithm for electron microscopy images of biological specimens. Its main advantages are its generality and speed. Moreover, it does not depend upon knowing a low resolution model of the particle being picked, but it learns directly from the user what kind of particles she is interested in. This learning capability is maintained during the whole application of the algorithm and, at any moment, the user can teach more particles or errors in order to refine the model. This learning capability is an advantage over algorithms fully relying on a previous 3D model, or on algorithms using no specific information of the kind of particles looked for.

The algorithm has been tested with a range of experimental datasets, from “test” datasets (the KLH one), to images of negatively stained samples and, finally, images of unstained cryospecimens.

For the KLH dataset there are two manually picked sets of coordinates used as gold standards in the field (Zhu et al., 2004), the reported FPR between the two datasets oscillated between 2.3% and 11.7%. Interestingly, our FPR is about 10%, although as can be seen in Fig. 6, our wrongly picked particles usually correspond to long particles in which two or more KLH aggregate.

The LTAg+RPA dataset has much better TPR (97.4%) and FPR (5%) figures because particles present better contrast due to the staining. However, it must be noted that the presence of highly contrasted particles does not make the algorithm pick all of these salient objects. Rather, our algorithm is able to distinguish between good particles and aggregated, broken or small particles.

One of the important steps of our APP algorithm is image preprocessing. Algorithms based on image saliencies (Kumar et al., 2004; Ogura and Sato, 2005; Plaisier et al., 2004; Singh et al., 2004; Umesh Adiga et al., 2004) certainly stress this aspect. However, this does not seem to be the case of the algorithms based on template matching with the projections of a 3D model, or based on image features, where simple image preprocessing (mostly, normalization and masking) is employed. In our case, a careful image preprocessing is important in order to reduce noise and highlight the projections of the particle with respect to their background. The wavelet denoising is crucial in this task (Sorzano et al., 2006), and the posterior histogram partitioning also helps to highlight the structure being picked.

The other important key points of our algorithm is the definition of the rotationally invariant description vector. Due to the extremely noisy nature of the Electron Microscopy images (Signal-to-Noise Ratios below 0.3), traditional rotation invariant moments (Chong et al., 2003; Kotoulas and Andreadis, 2007) did not work in our hands. Our invariants are based on histograms, averages and correlations that due to their summation construction tend to reduce the noise level. One of the critical points in the algorithm is the construction of the low resolution image in polar coordinates (defined by the number of rings and sectors). We used 16 rings and 16 sectors as a compromise between the desired summation properties just referred to (for this it would be desirable to have as few sectors and rings as possible) and the desired good polar representation of the original image (for this it would be desirable to have as many sectors and rings as possible). The description vector we construct is based on three basic features: the histogram of annular rings, the correlation function between nearby rings, and the second order characterization (mean and autocorrelation) of the correlation vector between sectors at all distances. Depending on the number of sectors and rings, the size of the description vector will be larger or smaller. In our experiments, the description vector had 575 components. Depending on the particle to pick some of them will be relevant for the classification and some of them will not. For instance, when telling the difference between round and square particles, the peaks of the cross-correlation between nearby rings will be much more strongly pronounced for the square particles than the round. In some cases a particular location of the correlation profile will be a more suitable feature on which to classify (as determined explicitly by the classification power) and in other cases will be unimportant. Therefore having a large pool of features allows the classification algorithm to better adapt to the particles at hand by selecting which ones are important.

Our algorithm is based on a multistage ensemble classifier. Multistage classification is the basis of the Adaboost algorithm in which each stage concentrates on the classification errors of the previous classifers until no further improvement of the classification error is observed. In our experiments we observed that no further improvement was achieved after three stages. Moreover, we tuned the standard Adaboost algorithm to our needs by focusing only on the separation of particles from errors since the first stage already does a reasonable job of separating particles from non-particles. The number of classifiers in each ensemble (in our experiments 10) must be a tradeoff between the complexity of the classifier (aiming at a low number of classifiers) and the classification accuracy (aiming at a high number of classifiers).

As shown in the Results Section, our algorithm is able to produce particle datasets with FPR a little bit lower than those already reported in the literature with similar rationale (Hall and Patwardhan, 2004; Mallick et al., 2004; Ogura and Sato, 2004; Plaisier et al., 2004; Short, 2004; Volkmann, 2004). In Mallick et al. (2004) the Receiver-Operating-Curve (ROC) is presented for their algorithm (see Fig. 7 in their article), and many other algorithms are plotted within this curve. Our algorithm is over the curve with a False Positive Rate of about 10% and a TPR between 60% and 70%. Our FPR could be further reduced to 1.6% by removing the worse images considering their correlation with the average of all particles automatically picked.

This performance is achieved at a cost of about 40 seconds per micrograph (in the case of the KLH), thus allowing nearly picking particles in real-time. The processing time of our algorithm has been further reduced in our implementation in two different ways. First, the algorithm has been internally threaded so that it can benefit from the existence of several cores in order to process a single micrograph. Moreover, it has been integrated in the image processing protocols published in Scheres et al. (2008) from which, after the training phase, several micrographs can be processed in parallel in a computer cluster further dividing the processing time. In particular, with 32 cores we were able to automatically select all particles in the adenovirus dataset in only 30 minutes.

5 Conclusions

In this paper we have presented a new algorithm for automatic particle picking. The algorithm learns from the user the kind of particles of interest, and after some training the algorithm is able to pick up the same type of particles. The algorithm does not need a previous 3D reference model for picking the particle in different orientations. Moreover, it takes only a few seconds in processing a whole micrograph of size 2048×2048 (with a particle diameter of 256) and, therefore, can be used to pick particles in real-time in conjunction with an automatic micrograph acquisition program. The algorithm described in this paper is freely available in the software package for image processing of electron micrographs Xmipp (Sorzano et al. (2004), http://xmipp.cnb.csic.es) and is accessible from the image processing protocols described in Scheres et al. (2008).

Fig. 8.

Sample micrograph with the particles picked after learning for 10 micrographs in the Adenovirus dataset. The curved structure in the top-right corner corresponds to the edge of the hole in the carbon grid on which the particles are suspended.