Abstract
Clustering analysis is one of the most widely used statistical tools in many emerging areas such as microarray data analysis. For microarray and other high-dimensional data, the presence of many noise variables may mask underlying clustering structures. Hence removing noise variables via variable selection is necessary. For simultaneous variable selection and parameter estimation, existing penalized likelihood approaches in model-based clustering analysis all assume a common diagonal covariance matrix across clusters, which however may not hold in practice. To analyze high-dimensional data, particularly those with relatively low sample sizes, this article introduces a novel approach that shrinks the variances together with means, in a more general situation with cluster-specific (diagonal) covariance matrices. Furthermore, selection of grouped variables via inclusion or exclusion of a group of variables altogether is permitted by a specific form of penalty, which facilitates incorporating subject-matter knowledge, such as gene functions in clustering microarray samples for disease subtype discovery. For implementation, EM algorithms are derived for parameter estimation, in which the M-steps clearly demonstrate the effects of shrinkage and thresholding. Numerical examples, including an application to acute leukemia subtype discovery with microarray gene expression data, are provided to demonstrate the utility and advantage of the proposed method.
Keywords and phrases: BIC, EM algorithm, High-dimension but low-sample size, L1 penalization, Microarray gene expression, Mixture model, Penalized likelihood
1. Introduction
Clustering analysis is perhaps the most widely used analysis method for microarray data: it has been used for gene function discovery (Eisen et al. 1998 [10]) and cancer subtype discovery (Golub et al. 1999 [15]). In such an application involving a large number of genes arrayed, it is necessary but challenging to choose a set of informative genes for clustering. If some informative ones are excluded because fewer genes are used, then it becomes difficult or impossible to discriminate some phenotypes of interest such as cancer subtypes. On the other hand, using redundant genes introduces noise, leading to the failure to uncover the underlying clustering structure. For example, Alaiya et al. (2002) [1] considered borderline ovarian tumor classification via clustering protein expression profiles: using all 1584 protein spots on an array failed to achieve an accurate classification, while an appropriate selection of spots (based on discriminating between benign and malignant tumors) did give biologically more meaningful results.
In spite of its importance, it is not always clear how to select genes for clustering. In particular, as demonstrated by Pan and Shen (2007) [39] and Pan et al. (2006) [37], unlike in the context of supervised learning, including regression, best subset selection, one of the most widely used model selection methods for supervised learning, fails for clustering and semi-supervised learning, in addition to its prohibitive computing cost for high-dimensional data; the reason is the existence of many correct models, most of which are not of interest. In a review of the earlier literature on this problem, Gnanadesikan et al. (1995) [14] commented that “One of the thorniest aspects of cluster analysis continue to be the weighting and selection of variables”. More recently, Raftery and Dean (2006) [41] pointed out that “Less work has been done on variable selection for clustering than for classification (also called discrimination or supervised learning), perhaps reflecting the fact that the former is a harder problem. In particular, variable selection and dimension reduction in the context of model-based clustering have not received much attention”. For variable selection in model-based clustering, most of the recent researches fall into two lines: one is Bayesian (Liu et al. 2003 [30]; Hoff 2006 [18]; Tadesse et al. 2005 [43]; Kim et al. 2006 [25]), while the other is penalized likelihood (Pan and Shen 2007 [39]; Xie et al. 2008 [52]; Wang and Zhu 2008 [50]). The basic statistical models of these approaches are all the same: informative variables are assumed to come from a mixture of Normals, corresponding to clusters, while noise variables coming from a single Normal distribution; they differ in how they are implemented. In particular, the Bayesian approaches are more flexible than the penalized methods (because the latter all require a common diagonal covariance matrix, though our main goal here is to relax this assumption), but they are also computationally more demanding because of their use of MCMC for stochastic search; furthermore, penalized methods enjoy the flexibility of the use of penalty functions, such as to accommodate grouped parameters or variables as to be discussed later. Other recent efforts include the following: Raftery and Dean (2006) [41] considered a sequential, stepwise approach to variable selection in model-based clustering; however, as acknowledged by the authors, “when the number of variables is vast (e.g., in microarray data analysis when thousands of genes may be the variables being used), the method is too slow to be practical as it stands”. Friedman and Meulman (2004) [11] dealt with a more general problem: selecting possibly different subsets of variables and their associated weights for different clusters for non-model-based clustering; Hoff (2004) [17] pointed out that the method might only “pick up the change in variance but not the mean”, and advocated the use of his model-based approach (Hoff 2006 [18]). Mangasarian and Wild (2004) [32] proposed the use of L1 penalty for K-median clustering; the idea with the use of L1 penalty is similar to ours, but we consider a more general case with cluster-specific variance parameters.
The penalized methods proposed so far for simultaneous variable selection and model fitting in model-based clustering all assume a common diagonal covariance matrix. For high-dimensional data, it may be necessary to utilize a diagonal covariance matrix for model-based clustering; even for supervised learning, it has been shown that using a diagonal covariance matrix in naive Bayes discriminant analysis or its variants is more effective than that of a more general covariance matrix (Bickel and Levina 2004 [5]; Dudoit et al. 2002 [7]; Tibshirani et al. 2003 [47]). Hence we will restrict our discussion to a diagonal covariance matrix in what follows. On the other hand, the common (diagonal) covariance matrix assumption implies that the clusters all have the same size, as in the K-means method (which further assumes that all the clusters are sphere-shaped with a scaled identity matrix as the covariance). Of course, this assumption may be violated in practice. A general argument is the following: it is well known that the variance of gene expression levels is in general a function of the mean expression levels, suggesting possibly varying variances of a gene’s expression levels across clusters with different mean expression levels; this point is going to be verified for our real data example. Here we extend the method to allow for cluster-dependent (diagonal) covariance matrices, which is nontrivial and requires a suitable construction of penalty function.
In some applications, there is prior knowledge about grouping variables: some variables function as a group; either all of them or none of them is informative. Yuan and Lin (2006) [54] discussed this issue in the context of penalized regression; they demonstrated convincingly the efficiency gain from incorporating such prior knowledge. On the other hand, in genomic studies of clustering samples through gene expression profiles, it is known that genes function in groups as in biological pathways. Hence, rather than treating genes individually, it seems natural to apply biological knowledge on gene functions to group the genes accordingly in clustering microarray samples, which has not been considered in previous applications of model-based clustering of expression profiles (e.g. Ghosh and Chinnaiyan 2002 [13]; Li and Hong 2001 [27]; McLachlan et al. 2002 [33]; Yeung et al. 2001 [53]). Note that, a few existing works clustered genes by incorporating gene function annotations in a weaker form that did not require either all or none of a group of genes to appear in a final model: Pan (2006b) [38] treated the genes within the same functional group as sharing the same prior probability of being in a cluster, while genes from different groups might not have the same prior probability, in model-based clustering of genes; others took account of gene groups in the definition of a distance metric in other clustering methods (Huang and Pan 2006 [20]). In addition, the aforementioned clustering methods did not allow for variable selection directly, while it is our main aim to consider variable selection, possibly assisted with biological knowledge. This is in line with the currently increasing interest in incorporating biological information on gene functional groups into analysis of detecting differential gene expression (e.g. Pan 2006 [37]; Efron and Tibshirani 2007 [8]; Newton et al. 2007 [36]).
The rest of this article is organized as follows. Section 2 briefly reviews the penalized model-based clustering method with a common diagonal covariance, followed by our proposed methods that allow for cluster-specific diagonal covariance matrices and for grouped variables. The EM algorithms for implementing the proposed methods are also detailed, in which the M-steps characterize the penalized mean and variance estimators with clear effects of shrinkage and thresholding. Simulation results in section 3 and an application to real microarray data in section 4 illustrate the utility of the new methods and their advantages over other methods. Section 5 presents a summary and a short discussion on future work.
2. Methods
2.1. Mixture model and its penalized likelihood
We have K-dimensional observations xj, j = 1, …, n. It is assumed that the data have been standardized to have sample mean 0 and sample variance 1 across the n observations for each variable. The observations are assumed to be (marginally) iid from a mixture distribution with g components: , where θi is an unknown parameter vector of the distribution for component i while πi is a prior probability for component i. To obtain the maximum penalized likelihood estimator (MPLE), we maximize the penalized log-likelihood
where Θ represents all unknown parameters and pλ (Θ) is a penalty with regularization parameter λ. The specific form of pλ (Θ) depends on the aim of analysis. For variable selection, the L1 penalty is adopted as in the Lasso (Tibshirani 1996 [46]).
Denote by zij the indicator of whether xj is from component i; that is, zij = 1 if xj is indeed from component i, and zij = 0 otherwise. Because we do not observe which component an observation comes from, zij’s are regarded as missing data. If zij’s could be observed, then the log-penalized-likelihood for complete data is:
| (1) |
Let X = {xj: j = 1, …, n} represent the observed data. To maximize log LP, the EM algorithm is often used (Dempster et al. 1977 [6]). The E-step of the EM calculates
| (2) |
while the M-step maximizes QP to update estimated Θ. In the sequel, because τij’s always depend on r, for simplicity we may suppress the explicit dependence from the notation.
2.2. Penalized clustering with a common covariance matrix
Pan and Shen (2007) [39] specified each component fi as a Normal distribution with a common diagonal covariance structure V:
where , and . They proposed a penalty function pλ(Θ) with an L1 norm involving the mean parameters alone:
| (3) |
where μik’s are the components of μi, the mean of cluster i. Note that, because the data have been standardized to have sample mean 0 and variance 1 for each variable k, if μ1k = ··· = μgk = 0, then variable k is noninformative in terms of clustering and can be considered as a noise variable and excluded from the clustering analysis. The L1 penalty function used in (3) can effectively shrink a small μik to be exactly 0.
For completeness and to compare with the proposed methods, we list the EM updates to maximize the above penalized likelihood (Pan and Shen 2007 [39]). We use a generic notation Θ(r) to represent the parameter estimate at iteration r. For the posterior probability of xj’s coming from component i, we have
| (4) |
for the prior probability of an observation from the ith component fi,
| (5) |
for the variance for variable k,
| (6) |
and for the mean for variable k in cluster i,
| (7) |
with i = 1, 2, …, g and k = 1, 2, …, K. Evidently, we have μ̂ik = 0 if λ1 is large enough. As discussed earlier, if μ̂1k = μ̂2k = ··· = μ̂gk = 0 for variable k, variable k is a noise variable that does not contribute to clustering.
2.3. Penalized clustering with unequal covariance matrices
To allow varying cluster sizes, we consider a more general model with cluster-dependent diagonal covariance matrices:
| (8) |
where , and .
As discussed earlier, to realize variable selection, we require that a noise variable have a common mean and a common variance across clusters. Hence, the penalty has to involve both the mean and variance parameters. We shall penalize the mean parameters in the same way as before, while the variance parameters can be regularized in two ways: shrink towards 1, or shrink towards 0.
2.3.1. Regularization of variance parameters: scheme one
First, we will use the following penalty for both mean and variance parameters:
| (9) |
Again the L1 norm is used to coerce a small estimate of μik to be exactly 0, while forcing an estimate of that is close to 1 to be exactly 1. Therefore, if a variable has common mean 0 and common variance 1 across clusters, this variable is effectively treated as a noise variable; this aspect is evidenced from (4), where a noise variable does not contribute to the posterior probability and thus clustering.
Note that penalty (9) differs from the so-called double penalization in non-parametric mixed-effect models for longitudinal and other correlated data (Lin and Zhang 1999 [29]; Gu and Ma 2005 [16]): aside from the obvious differences in the choice of the L1-norm here versus the L2-norm there and in clustering here versus regression there, they penalized fixed- and random-effect parameters, both mean parameters, whereas we regularize variance parameters in addition to mean parameters. Ma et al. (2006) [31] applied such a mixed-effect model to cluster genes with time course (and thus correlated) expression profiles; in addition to the aforementioned differences, a key difference is that their use of penalization was for parameter estimation, not for variable selection as aimed here.
An EM algorithm is derived as follows. The E-step gives QP as shown in (2). The M-step maximizes QP with respect to the unknown parameters, resulting in the same updating formulas for τij and πi as given in (4) and (5). In Appendix B, we derive the following theorem:
Theorem 1
The sufficient and necessary conditions for μ̂ik to be a (global) maximizer of QP are
| (10) |
and
| (11) |
resulting in a slightly changed formula for the mean parameters
| (12) |
For the variance parameters, some algebra yields the following theorem:
Theorem 2
The necessary conditions for to be a local maximizer of QP are
| (13) |
and
| (14) |
Although a sufficient condition for can be derived as a special case of Theorem 5, we do not have any sufficient condition for . Hence, we do not have a simple formula to update . Below we characterize the solution , suggesting a computational algorithm as well as illustrating the effects of shrinkage.
Let , and , then (13) reduces to , while (14) becomes |bi − cik| ≤ λ2. Note that is the usual MLE when λ2 = 0. It is easy to verify that if , then . Below we consider cases with λ2 > 0 and . It is shown in Appendix B that
-
if |bi − cik| > λ2,
(15) is the unique maximizer of QP and is between 1 and ;
-
if |bi − cik| ≤ λ2,
if , then is the unique maximizer;
if , i) if bi − cik < λ2, then is a local maximizer; there may exist another local maximizer between and 1; between the two, the one maximizing QP is chosen; ii) if bi − cik = λ2, then either or is the unique maximizer.
Naturally the above formulas suggest an updating algorithm for . Clearly, has been shrunk towards 1, and can be exactly 1 if, for example, λ2 is sufficiently large.
2.3.2. Regularization of variance parameters: scheme two
The following penalty is adopted for both mean and variance parameters:
| (16) |
Note that the only difference between (9) and (16) is the penalty of the variance parameters, where is replaced by , which is used to shrink to 0 (i.e. to 1) if is close to 0. Therefore, variable selection can be realized as before.
An EM algorithm for the variance parameters is derived as follows.
Theorem 3
The sufficient and necessary conditions for to be a local maximizer of QP are
| (17) |
and
| (18) |
If we denote and , then (17) reduces to , while (18) becomes |bi − cik| ≤ λ2, where is the usual MLE for λ2 = 0. Derivations in Appendix B imply that . Combining the two cases, we obtain
| (19) |
The above formula suggests an updating algorithm for . When λ2 is small, sign(|bi − cik| − λ2)+ = 1, has been shrunk from towards 1; when λ2 is sufficiently large, sign(|bi − cik| − λ2)+ = 0, then is exactly 1.
2.4. Using adaptive penalization to reduce bias
We can adopt the idea of adaptive penalization, as proposed by Zou (2006) [57] for regression, in the present context. Following Pan et al. (2006) [40], we use a weighted L1 penalty function
| (20) |
where wik = 1/|μ̂ik|w and with w ≥ 0, and μ̂ik and are the MPLE obtained in section 2.3.1; we also tried the usual MLE in wik and vik, but it did not work well in simulations, hence we skip its discussion; we only consider w = 1. The EM updates are slightly modified for the purpose: we only need to replace λ1 and λ2 by λ1wik and λ2vik respectively, while keeping other updates unchanged.
The main idea of adaptive penalization is to reduce the bias of the MPLE associated with the standard L1 penalty: as can be seen clearly, if an initial estimate |μ̂ik| is larger, then the resulting estimate is shrunk less towards 0; similarly for the variance parameter.
2.5. Penalized clustering with grouped variables
Now we consider a situation where candidate variables can be grouped based on the prior belief that either all the variables in the same group or none of them are informative to clustering. Following the same idea of the grouped Lasso of Yuan and Lin (2006) [54], we construct a penalty for this purpose here.
Suppose that the variables are partitioned into M groups with the corresponding mean parameters , and . Accordingly, we decompose and with Vim as a km × km diagonal matrix, and is the column vector containing the diagonal elements of matrix Vim.
For grouping mean parameters, we will use a penalty pλ (Θ) containing
for the mean parameters, where ||v|| is the L2 norm of vector v. Accordingly, we use
as a penalty for grouped variance parameters. Note that we do not have to group both means and variances at the same time. For instance, we may group only means but not variances: we will thus use the second term in (9) as the penalty for variance parameters while retaining the above penalty for grouped mean parameters.
The E-step of the EM yields QP with the same form as (2). Next we derive the updating formulas for the mean and variance parameters in the M-step.
2.5.1. Grouping mean parameters
If the penalty for grouped means is used, we have the following result.
Theorem 4
The sufficient and necessary conditions for , i = 1, 2, …, g and m = 1, 2, …, M to be a unique maximizer of QP are
| (21) |
and
| (22) |
yielding
| (23) |
where , and is the usual MLE.
It is clear that, due to thresholding, when, for example, λ1 is sufficiently large. Noting that depends on , we use (23) iteratively to update .
2.5.2. Grouping variance parameters
If the penalty for grouped variances is used, we have the following theorem:
Theorem 5
The sufficient and necessary conditions for , i = 1, 2, …, g and m = 1, 2, …, M, to be a local maximizer of QP are
| (24) |
The necessary condition for to be a local maximizer of QP is
| (25) |
It is clear that when, for example, λ2 is large enough. It is also easy to verify that (24) and (25) reduce to the same ones for non-grouped variables when km = 1. To solve (24) and (25), we develop the following algorithm. Let and . Consider any k′th component of ; correspondingly, bik′ and cimk′ are the k′th components of bi and cim, respectively. In Appendix B, treating aim as a constant (i.e. by plugging-in a current estimate of ), we show the following cases. i) If , then is a maximizer of QP as other ’s for ∀k ≠ k′ are fixed. ii) If , there exists only one real root satisfying ; a bisection search can be used to find the root. iii) If , the real roots must be inside ( , 1), hence a bisection search can be used to find a root; once a root is obtained, the other two real roots, if exist, can be obtained through a closed-form expression; we choose the real root that maximizes QP (while other for k ≠ k′ are fixed at their current estimates) as the new estimate of . After cycling through all k′, we update aim with the new estimate. Then the above process is iterated.
2.5.3. Other grouping schemes
To save space, we briefly discuss grouping variables under a common diagonal covariance matrix, for which only mean parameters need to be regularized. The EM updating formula for the mean parameters remains the same as in (23) except that the cluster-specific covariance Vim there is replaced by a common Vm; updating formulas for the other parameters remain unchanged. Simulation results (see Xie et al. (2008) [52]) demonstrated its improved performance over its counterpart without grouping. In addition, we can also group the mean parameters for the same variable (or gene) across clusters (Wang and Zhu 2008 [50]), and combine it with grouping variables (Xie et al. 2008 [52]).
The grouping scheme discussed so far follows the grouped Lasso of Yuan and Lin (2006) [54], which is a special case of the Composite Absolute Penalties (CAP) of Zhao et al. (2006) [56]. In Appendix A, we derive the results with the CAP, including using both schemes on regularizing the variance parameters.
2.6. Model selection
To introduce penalization, following Pan and Shen (2007) [39] and Pan et al. (2006) [40], we propose a modified BIC as the model selection criterion:
where de = g + K + gK − 1 − q is the effective number of parameters with q = #{(i, k): μik = 0, }. The definition of de follows from that in L1-penalized regression (Efron et al. 2004 [9]; Zou et al. 2004 [59]). This modified BIC is used to select the number of clusters g and the penalization parameters (λ1, λ2) jointly. We propose using a grid search to estimate the optimal (g, λ̂1, λ̂2) as the one with the minimum BIC.
For any given (g, λ1, λ2), because of possibly many local maxima for the mixture model, we run an EM algorithm multiple times with random starts. For our numerical examples, we randomly started the K-means and used the K-means’ results as an initialization for the EM. From the multiple runs, we selected the one giving the maximal penalized log-likelihood as the final result for the given (g, λ1, λ2).
3. Simulations
3.1. A common covariance versus unequal covariances
3.1.1. Case I
We first considered four simple set-ups: the first was a null case with g = 1; for the other three, g = 2, corresponding to only mean, only variance, and both mean and variance differences between the two clusters. Specifically, we generated 100 simulated datasets for each set-up. In each dataset, there were n = 100 observations, each of which contained K = 300 variables. Set-up 1) is a null case: all the variables had a standard normal distribution N(0, 1), thus there was only a single cluster. For each of the other three set-ups, there were two clusters. One cluster contained 80 observations while the other contained 20; while 279 variables were noises distributed as N(0, 1), the other 21 variables were informative: each of the 21 variables were distributed as 2) N(0, 1) in cluster 1 versus N(1.5, 1) in cluster 2; 3) N(0, 1) versus N(0, 2); 4) N(0, 1) versus N(1.5, 2) for the three set-ups respectively.
For each simulated dataset, we fitted a series of models with the three numbers of components g = 1, 2, 3 and various values of penalization parameter(s). For comparison, we considered both the equal covariance and unequal covariance mixture models (8); for the former, we considered the unpenalized method (λ1 = 0) corresponding to no variable selection and penalized method using BIC to select λ; similarly, for the latter we considered five cases corresponding to fixing or selecting one or two of (λ1, λ2): no variable selection with (λ1, λ2) = (0, 0), penalizing only mean parameters with (λ1, λ2) = (λ̂1, 0), penalizing only variance parameters with (λ1, λ2) = (0, λ̂2), and our proposed two methods of penalizing both mean and variance parameters with (λ1, λ2) = (λ̂1, λ̂2). We also compared the numbers of predicted noise variables among the true 21 informative (z1) and 279 noise variables (z2).
The frequencies of selecting g = 1 to 3 based on 100 simulated datasets are shown in Table 1. First, our proposed methods performed best, in general, in terms of selecting both the correct number of clusters and relevant variables. For example, it selected fewest noise variables and most informative variables. Second, no variable selection (i.e. no penalization) led to incorrectly selecting g = 1 for the three non-null set-ups. Third, penalizing only the mean parameters could not distinguish the two clusters differing only in variance as in set-up 3. Fourth, between the two regularization schemes for the variance parameters, based on both cluster detection and sample assignment (Table 2), the two gave comparable results, though scheme two with log-variance performed slightly better.
Table 1.
Simulation case I: frequencies of the selected numbers (g) of clusters, and mean numbers of predicted noise variables among the true informative (z1) and noise variables (z2). Here N1 and N2 were the frequencies of selecting UnequalCov(λ̂1, λ̂2) (with variance regularization scheme one) and EqualCov(λ̂1) by BIC, respectively. UnequalCov(λ̂1, λ̂2) (logvar) used variance regularization scheme two. For set-up 1, the truth was g = 1, z1 = 21 and z2 = 279; for others, g = 2, z1 = 0 and z2 = 279
| UnequalCov(λ1, λ2) |
EqualCov(λ1) |
BIC |
||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (0, 0) |
(λ̂1, 0) |
(0, λ̂2) |
(λ̂1, λ̂2) |
(λ̂1, λ̂2)(logvar) |
(0) |
(λ̂1) |
||||||||||
| Set-up | g | N | N | N | N | z1 | z2 | N | z1 | z2 | N | N | z1 | z2 | N1 | N2 |
| 1 | 99 | 83 | 99 | 100 | 21.0 | 279.0 | 100 | 21.0 | 279.0 | 100 | 100 | 21.0 | 279.0 | 0 | 100 | |
| 1 | 2 | 0 | 3 | 0 | 0 | - | - | 0 | - | - | 0 | 0 | - | - | 0 | 0 |
| 3 | 1 | 14 | 1 | 0 | - | - | 0 | - | - | 0 | 0 | - | - | 0 | 0 | |
| 1 | 99 | 89 | 99 | - | - | - | - | - | - | 100 | 0 | - | - | 0 | 0 | |
| 2 | 2 | 0 | 1 | 0 | 100 | 0.03 | 276.0 | 100 | 0.03 | 276.0 | 0 | 87 | 0.03 | 275.1 | 0 | 87 |
| 3 | 1 | 10 | 1 | - | - | - | - | - | - | 0 | 13 | 9.8 | 0.0 | 0 | 13 | |
| 1 | 97 | 74 | 97 | 52 | 21.0 | 279.0 | 43 | 21.0 | 279.0 | 100 | 100 | 21.0 | 279.0 | 48 | 4 | |
| 3 | 2 | 0 | 3 | 0 | 42 | 5.4 | 276.8 | 48 | 3.4 | 275.1 | 0 | 0 | - | - | 42 | 0 |
| 3 | 3 | 23 | 3 | 6 | 6.8 | 277.8 | 9 | 3.6 | 276.3 | 0 | 0 | - | - | 6 | 0 | |
| 1 | 97 | 74 | 97 | 0 | - | - | 0 | - | - | 100 | 4 | 21.0 | 279.0 | 0 | 0 | |
| 4 | 2 | 0 | 3 | 0 | 98 | 0.2 | 275.9 | 97 | 0.1 | 275.2 | 0 | 88 | 2.9 | 276.2 | 90 | 2 |
| 3 | 3 | 23 | 3 | 2 | 0.5 | 276.5 | 3 | 0.3 | 274.0 | 0 | 8 | 6.0 | 276.8 | 8 | 0 | |
| 1 | 100 | 100 | 100 | 52 | 21.0 | 279.0 | 51 | 21.0 | 279.0 | 100 | 100 | 21.0 | 279.0 | 0 | 63 | |
| 3 | 2 | 0 | 0 | 0 | 38 | 2.5 | 277.4 | 40 | 2.1 | 275.0 | 0 | 0 | - | - | 34 | 0 |
| (adapt) | 3 | 0 | 0 | 0 | 10 | 3.5 | 277.6 | 9 | 3.4 | 275.4 | 0 | 0 | - | - | 3 | 0 |
Table 2.
Sample assignments for ĝ = 2 and (adjusted) Rand index (RI/aRI) values for the two regularization schemes for the variance parameters for simulation set-ups 2–4. #Corr represents the average number of the samples from a true cluster correctly assigned to an estimated cluster
| Sample assignments, ĝ = 2 |
Rand Index |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Cluster 1 (n = 80) | Cluster 2 (n = 20) | ĝ = 1 | ĝ = 2 | ĝ = 3 | Overall | ||||||
| Set-up | Methods | #Corr | #Corr | RI | aRI | RI | aRI | RI | aRI | RI | aRI |
| 2 | L1(var-1) | 78.8 | 19.0 | - | - | 1.00 | 0.99 | - | - | 1.00 | 0.99 |
| L1(logvar) | 78.8 | 19.0 | - | - | 1.00 | 0.99 | - | - | 1.00 | 0.99 | |
| 3 | L1(var-1) | 74.6 | 15.1 | 0.68 | 0.0 | 0.89 | 0.75 | 0.87 | 0.70 | 0.78 | 0.36 |
| L1(logvar) | 76.9 | 16.6 | 0.68 | 0.0 | 0.94 | 0.85 | 0.95 | 0.88 | 0.83 | 0.49 | |
| 4 | L1(var-1) | 78.4 | 19.0 | - | - | 0.99 | 0.98 | 0.97 | 0.93 | 0.99 | 0.98 |
| L1(logvar) | 78.8 | 19.0 | - | - | 1.00 | 0.99 | 0.99 | 0.98 | 1.00 | 0.99 | |
The results for adaptive penalty for set-up 3 are detailed in row 3(adapt) of Table 1, which are similar to that of using the L1-norm penalty in terms of both variable and cluster number selection. Since the performance of adaptive penalty might heavily depend on the choice of weights (or initial estimates), we expect improved performance if better weights can be used.
3.1.2. Case II
We considered a more practical scenario that combined clusters’ differences in means or variances or both for informative variables. As before, for each dataset, n = 100 observations were divided into two clusters with 80 and 20 observations respectively; among the K = 300 variables, only 3K1 were informative while the remaining K − 3K1 were noises; The first, second and third K1 informative variables were distributed as i) N(0, 1) for cluster 1 versus N(1.5, 1) for cluster 2, ii) N(0, 1) versus N(0, 2), iii) N(0, 1) versus N(1.5, 2), respectively; any noise variable was distributed N(0, 1). We considered K1 = 5, 7, and 10.
The results are shown in Table 3. Again it is clear that our proposed method worked best: it most frequently selected the correct number of clusters (g = 2), and used most informative variables while being able to weed out most noise variables. As expected, using noise variables, as in non-penalized methods without variable selection, tended to mask out the existence of the two clusters.
Table 3.
Simulation case II. The mean numbers of the predicted noise variables as in each of the first three groups of true informative and the other group of noise variables were given by z1–z4; the truth was that g = 2, z1 = z2 = z3 = 0 and z4 = 300 − 3K1
| UnequalCov(λ1, λ2) |
EqualCov(λ1) |
||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (0, 0) |
(λ̂1, 0) |
(0, λ̂2) |
(λ̂1, λ̂2) |
(0) |
(λ̂1) |
||||||||||
| K1 | g | N | N | N | N | z1 | z2 | z3 | z4 | N | N | z1 | z2 | z3 | z4 |
| 1 | 96 | 76 | 96 | 48 | 5.0 | 5.0 | 5.0 | 285.0 | 100 | 74 | 5.0 | 5.0 | 5.0 | 285 | |
| 5 | 2 | 0 | 1 | 0 | 42 | 2.0 | 1.8 | 1.5 | 283.5 | 0 | 15 | 0.0 | 4.5 | 0.5 | 279.7 |
| 3 | 4 | 23 | 4 | 10 | 0.2 | 0.4 | 0.0 | 283.9 | 0 | 11 | 0.0 | 4.2 | 0.3 | 279.5 | |
| 1 | 96 | 81 | 96 | 11 | 7.0 | 7.0 | 7.0 | 279.0 | 100 | 26 | 7.0 | 7.0 | 7.0 | 279 | |
| 7 | 2 | 2 | 4 | 2 | 81 | 0.8 | 1.0 | 0.5 | 276.5 | 0 | 54 | 0.0 | 6.3 | 0.7 | 274.7 |
| 3 | 2 | 15 | 2 | 8 | 0.0 | 0.6 | 0.0 | 277.0 | 0 | 20 | 0.0 | 6.6 | 0.6 | 275.3 | |
| 1 | 99 | 86 | 99 | 0 | - | - | - | - | 100 | 1 | 10.0 | 10.0 | 10.0 | 270.0 | |
| 10 | 2 | 0 | 2 | 0 | 94 | 0.2 | 0.9 | 0.1 | 266.3 | 0 | 81 | 0.01 | 9.0 | 0.8 | 266.6 |
| 3 | 1 | 12 | 1 | 6 | 0.0 | 0.3 | 0.0 | 266.8 | 0 | 18 | 0.0 | 9.1 | 0.7 | 267.6 | |
3.2. Grouping variables
We grouped variables for each simulated data under case II. We used correct groupings: the informative variables were grouped together, and so were the noise variables; the group sizes were 5, 7 and 5 for K1 = 5, 7 and 10 respectively. Table 4 displays the results for grouped variables. Compared to Table 1, it is clear that grouping variables improved the performance over non-grouped one in terms of more frequently selecting the correct number g = 2 of the clusters as well as better selecting relevant variables. Furthermore, grouping both means and variances performed better than grouping means alone.
Table 4.
Simulation case II for grouped variables
| K1 | g | Grouping means only |
Means and variances |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| N | z1 | z2 | z3 | z4 | N | z1 | z2 | z3 | z4 | ||
| 5 | 1 | 21 | 5.0 | 5.0 | 5.0 | 285.0 | 14 | 5.0 | 5.0 | 5.0 | 285.0 |
| 2 | 62 | 0.2 | 0.5 | 0.2 | 283.4 | 71 | 0.0 | 0.0 | 0.0 | 284.6 | |
| 3 | 17 | 0.0 | 0.7 | 0.0 | 283.2 | 15 | 0.0 | 0.0 | 0.0 | 284.7 | |
| 7 | 1 | 2 | 7.0 | 7.0 | 7.0 | 279.0 | 1 | 7.0 | 7.0 | 7.0 | 279.0 |
| 2 | 90 | 0.0 | 0.6 | 0.0 | 277.4 | 92 | 0.0 | 0.0 | 0.0 | 278.9 | |
| 3 | 8 | 0.0 | 0.8 | 0.0 | 277.4 | 7 | 0.0 | 0.0 | 0.0 | 279.0 | |
| 10 | 1 | 0 | - | - | - | - | 0 | - | - | - | - |
| 2 | 96 | 0.0 | 0.7 | 0.0 | 268.3 | 98 | 0.0 | 0.0 | 0.0 | 269.8 | |
| 3 | 4 | 0.0 | 0.8 | 0.0 | 266.8 | 2 | 0.0 | 0.0 | 0.0 | 270.0 | |
4. Example
4.1. Data
A leukemia gene expression dataset (Golub et al. 1999 [15]) was used to demonstrate the utility of our proposed method and to compare with other methods. The (training) data contained 38 patients, among which 11 were AML (acute myeloid leukemia) while the remaining were ALL (acute lymphoblastic leukemia) samples; ALL samples consisted of two subtypes: 8 T-cell and 19 B-cell samples. For each sample, the expression levels of 7129 genes were measured by an A3ymetrix microarray. Following Dudoit et al. (2002) [7], we pre-processed the data in the following steps: 1) truncation: any expression level xjk was truncated below at 1 if xjk < 1, and above at 16,000 if xjk > 16, 000; 2) filtering: any gene was excluded if its max/min ≤ 5 and max − min ≤ 500, where max and min were the maximum and minimum expression levels of the gene across all the samples. Finally, as a preliminary gene screening, we selected the top 2000 genes with the largest sample variances across the 38 samples.
4.2. No grouping
4.2.1. Model-based clustering methods
Table 5 displays the clustering results: the two penalized methods selected 4 and 11 clusters, respectively, while the two standard methods chose 2 and 3 clusters, respectively. For the new penalized method, we show the results for scheme one of regularizing the variance parameters; the other scheme and the adaptive penalization both gave similar results, and hence are skipped. In terms of discriminating between the luekemia subtypes, obviously the new penalized method performed best: only one ALL B-cell sample was mixed into the AML group, while others formed homogeneous groups. In contrast, with a large number of clusters, the L1 method with an equal covariance still misclassified 4 ALL B-cell samples as AML. The two standard methods perhaps under-selected the number of clusters, resulting in 11 and 10 mis-classified samples, respectively. Unsurprisingly, based on the Rand index (Rand 1971 [42]) (or adjusted Rand index (Hubert and Arabie 1985 [22])), the new method was a winner with the largest value at 0.85 (0.65), compared to 0.73 (0.46), 0.70 (0.37) and 0.70 (0.25) of the other three methods. In addition, judged by BIC, the new penalized method also outperformed the other methods with the smallest BIC value of 52198. Finally, the new penalized method used only 1728 genes, while penalizing only means with a common covariance matrix used 1821 genes; the other two standard methods used all 2000 genes.
Table 5.
Clustering results for Golub’s data with the number of components (g) selected by BIC
| Methods |
UnequalCov(λ1, λ2) |
EqualCov(λ1) |
||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (0, 0) |
(λ̂1, λ̂2) |
(0) |
(λ̂1) |
|||||||||||||||||
| RI/aRI |
0.73/0.46 |
0.85/0.65 |
0.70/0.37 |
0.70/0.25 |
||||||||||||||||
| BIC |
71225 |
52198 |
75411 |
63756 |
||||||||||||||||
| Clusters | 1 | 2 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| Samples(#) |
||||||||||||||||||||
| ALL-T(8) | 8 | 0 | 0 | 0 | 8 | 0 | 8 | 0 | 0 | 7 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| ALL-B(19) | 17 | 2 | 11 | 1 | 0 | 7 | 0 | 8 | 11 | 0 | 4 | 5 | 2 | 4 | 0 | 0 | 1 | 1 | 1 | 1 |
| AML(11) | 0 | 11 | 0 | 11 | 0 | 0 | 0 | 0 | 11 | 0 | 0 | 0 | 0 | 7 | 4 | 0 | 0 | 0 | 0 | 0 |
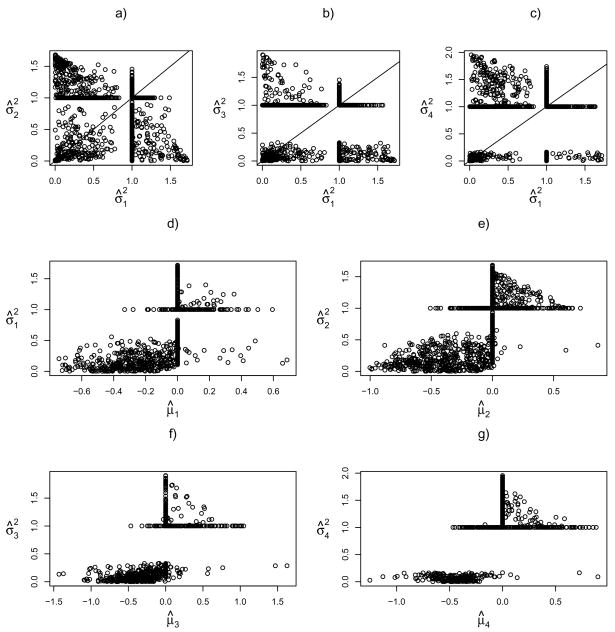
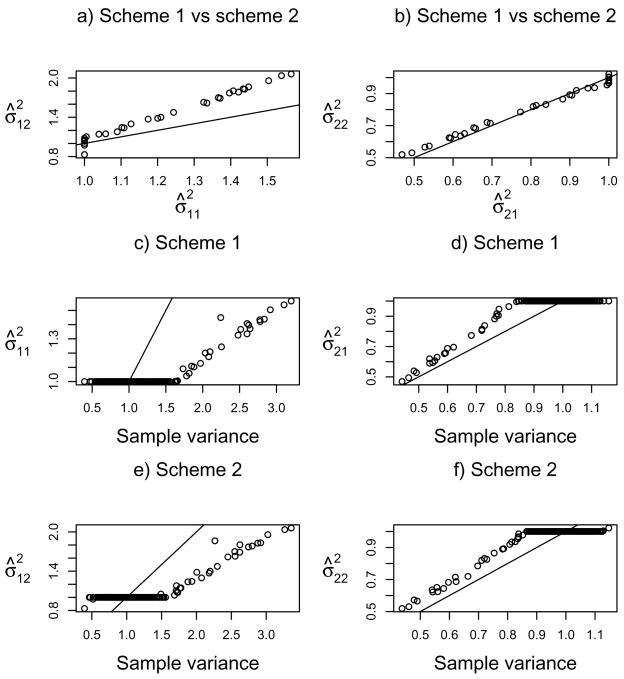
Figure 1 displays the estimated means and variances of the genes in different clusters. Panels a)–c) clearly show that the genes may have different variance estimates across the clusters, though many of them were shrunk to be exactly to be one, as expected. Note that, due to the standardization of the data yielding an overall sample variance one for each gene, we do not observe any gene with the variance estimates more than one in two or more clusters. Panels d)–f) confirmed that there appears a monotonic relationship between the mean and variance, as well-known in the microarray literature (e.g. Huang and Pan 2002 [19]); the Pearson correlation coefficients were estimated to be 0.64, 0.69, 0.65 and 0.63 for the four clusters respectively. Hence, it lends an indirect support for the use of cluster-specific covariance matrices: if it is accepted that the genes have varying mean parameters across clusters, then their variance parameters are expected to change too.
Fig 1.
Scatter plots of the estimated means and variances by the new penalized method. Panels a)–c) are scatter plots of the estimated variances in cluster 1 versus those in cluster 2, 3 and 4, respectively; panels d)–g) are the scatter plots of the estimated means versus estimated variances for the four clusters respectively.
Next we examine a few genes in more details. CST3 (cystatin c, M23197) and ZYX (zyxin, X95735) were in the top 50 genes ranked by Golub et al. (1999) [15], and two of the 17 genes selected by Antonov et al. (2004) [2] to discriminate between the AML/ALL subtypes. In addition, the two genes, together with MAL (X76223), were also identified among the top 20 genes used in the classifier by Liao et al. (2007) [28] to predict leukemia subtypes. Bardi et al. (2004) [4] used CST3 to assess glomerular function among children with leukemia and solid tumors and found that CST3 was a suitable marker. Koo et al. (2006) [26] reviewed the literature showing the relevance of MAL to T-cell ALL and concluded that it might play an important role in T-cell activations. Baker et al. (2006) [3] and Wang et al. (2005) [49] identified ZYX as the most significant gene for classifying AML/ALL subtypes. Tycko et al. (1991) [48] found that LCK (M26692) was related to activated T cells and thus it might contribute to the formation of human cancer. Wright et al. (1994) [51] studied the mutation of LCK and concluded that it probably played a role in some human T-cell leukemia.
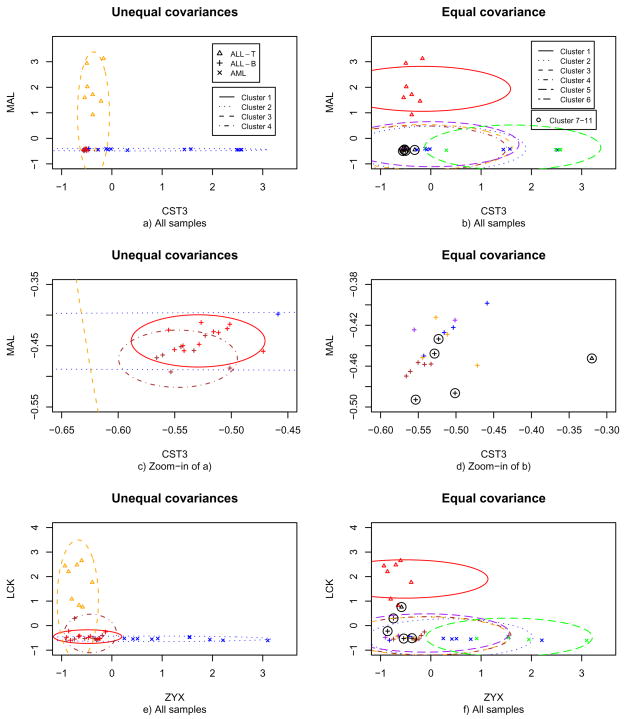
In Figure 2, panels c)–d) are the zoom-in versions of the left bottom of a)–b), the plots of gene pair CST3 and MAL for all samples for the two penalized methods respectively, while e)–f) are for gene pair LCK and ZYX with all samples. Given two genes, their observed expression levels, along with the 95% confidence region of the center for each cluster, were plotted. The penalized method with an equal covariance found 11 clusters, among which 5 clusters had only one sample, and the remaining 6 clusters had more than 2 samples; for clarity, we only plotted the confidence regions of the centers of the six largest clusters. Panels a) and e) clearly show evidence of varying variances, and thus cluster-specific covariance matrices: for example, MAL was highly expressed with a large dispersion for ALL-T samples, so was CST3 for AML samples, in contrast to the low expression of both genes for ALL-B samples, suggesting varying cluster sizes. It also clearly illustrates why there were so many clusters if an equal covariance model was used: the large number of the equally-sized clusters were used to approximate the three or four size-varying true clusters. Panel c) also suggests an explanation to the use of two clusters for ALL-B samples by the new penalized method: the expression levels of MAL and CST3 were positively correlated, giving a cluster not parallel with either coordinate; on the other hand, use of a diagonal covariance matrix in the penalized method implied a cluster parallel to one of the two coordinates. Hence, two coordinate-parallel clusters were needed to approximate the non-coordinate-parallel true cluster; a non-diagonal covariance matrix might give a more parsimonious model (i.e. with fewer clusters).
Fig 2.
Observed expression levels of two pairs of genes and the corresponding clusters found by the two penalized methods.
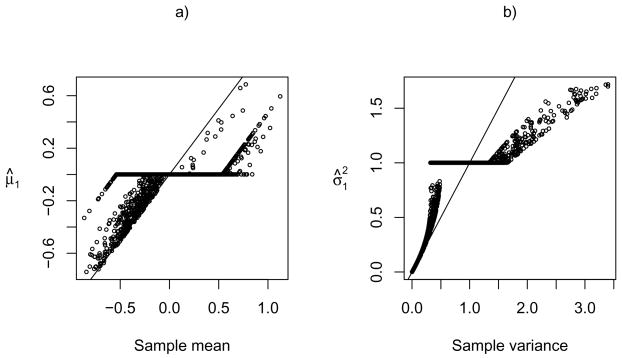
Finally, we show the effects of shrinkage and thresholding for the parameter estimates by the new penalized method. Figure 3 depicts the penalized mean estimates (panel a) and variance estimates (panel b) versus the sample means and variances respectively for cluster one. It is confirmed that the penalized mean estimates were shrunk towards 0, some of which were exactly 0, while the penalized variance estimates were shrunk towards 1, and can be exactly 1.
Fig 3.
Penalized mean and variance estimates for cluster one containing the 11 ALL B-cell samples by the new penalized method.
4.2.2. Other clustering methods
Previous studies (e.g. Thalamuthu et al. 2006 [44]) have established model-based clustering as one of the best performers for gene expression data. Although it is not our main goal here, as a comparison in passing, we show the results of other three widely used methods as applied to the same data with the top 2000 genes: hierarchical clustering, partitioning around medoids (PAM) and K-means clustering.
It is challenging to determine the number of clusters for PAM and K-means. Here we consider two proposals. First, we used the silhouette width (Kaufman and Rousseeuw 1990 [24]) to select the number of clusters. Two and six clusters were chosen for PAM and K-means respectively; neither gave a good separation among the three leukemia subtypes (Table 6). Second, to sidestep the issue, we applied the two methods with three and four clusters because those numbers seemed to work best for model-based clustering. Nevertheless, PAM worked poorly, while K-means with 4 clusters gave a reasonable result, albeit not as good as that of the new penalized model-based clustering, as judged by an eye-ball examination or the (adjusted) Rand index.
Table 6.
Clustering results for Golub’s data by PAM and K-means methods. The number of clusters selected by the silhouette width are masked by *
| Methods |
PAM |
K-means |
||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RI/aRI |
0.46/0 |
0.65/0.24 |
0.64/0.22 |
0.67/0.27 |
0.80/0.53 |
0.75/0.42 |
||||||||||||||||
| Clusters | 1 | 2* | 1 | 2 | 3 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | 5 | 6* |
| Samples (#) |
||||||||||||||||||||||
| ALL-T (8) | 7 | 1 | 1 | 7 | 0 | 1 | 7 | 0 | 0 | 5 | 3 | 0 | 0 | 0 | 8 | 0 | 0 | 0 | 0 | 0 | 8 | 0 |
| ALL-B (19) | 11 | 8 | 8 | 3 | 8 | 8 | 3 | 7 | 1 | 10 | 7 | 2 | 10 | 2 | 0 | 7 | 1 | 9 | 0 | 8 | 0 | 1 |
| AML (11) | 11 | 0 | 11 | 0 | 0 | 11 | 0 | 9 | 0 | 0 | 1 | 10 | 0 | 10 | 0 | 1 | 0 | 4 | 7 | 0 | 0 | 0 |
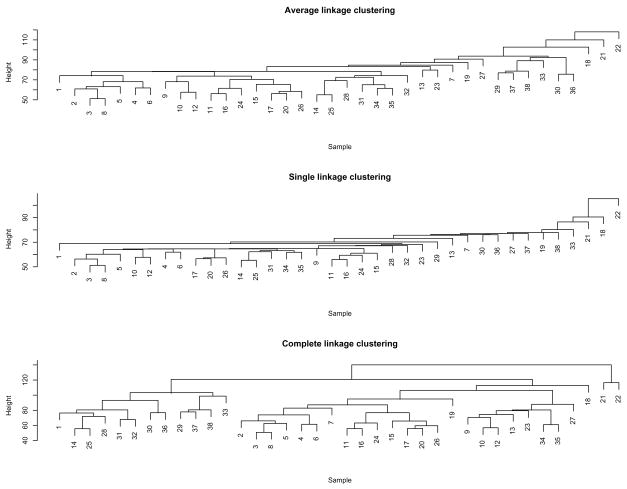
Figure 4 gives the results of hierarchical clustering with all three ways of defining a cluster-to-cluster distance: average linkage, single linkage and complete linkage. The average linkage clustering gave the best separation among the three leukemia subtypes: all 8 T-cell samples, except sample 7, were grouped together; there were 10 B-cell samples in a group; all other ALL samples seemed to appear in the AML group. On the other hand, the average linkage clustering identified about six outlying samples, which were samples 7, 18, 19, 21, 22 and 27 respectively; this finding was consistent with that of the penalized model-based clustering with an equal covariance matrix, which detected the same five outliers except sample 19.
Fig 4.
Agglomerative hierarchical clustering results for the 38 leukemia samples: the first 8 samples were T-cell ALL; samples 9–27 were B-cell ALL; the remaining ones were AML.
4.2.3. Other comparisons
Although mainly studied in the context of supervised learning, with several existing studies, Golub’s data may serve as a test bed to compare various clustering methods. Golub et al. (1999) [15] applied self-organizing maps (SOM): first, with two clusters, SOM mis-classified one AML and 3 ALL samples; second, with four clusters, similar to the result of our new penalized method, AML and ALL-T each formed a cluster while ALL-B formed two clusters, in which one ALL-B and one AML samples were mis-classified. They did not discuss why or how g = 2 or g = 4 clusters were chosen. In Bayesian model-based clustering by Liu et al. (2003) [30], two clusters were chosen with one AML and one ALL mis-assigned; they did not discuss classification with ALL subtypes.
In a very recent study by Kim et al. (2006) [25], with two clustering algorithms and two choices of a prior parameter, they presented four sets of clustering results. In general, ALL samples formed one cluster while AML samples formed 5 to 6 clusters, giving 0–3 mis-assigned ALL samples; although not discuss explicitly, because either all or almost all the ALL samples fell into one cluster, their method obviously could not distinguish the two subtypes of ALL. Furthermore, their result on the multiple clusters of AML was in contrast to ours and Golub’s on the homogeneity of AML samples. Because Kim et al. used different data pre-processing with 3571 genes as input to their method, for a fair comparison, we applied the same dataset to our new penalized method, yielding five clusters: only one ALL-B was mis-assigned to a cluster containing 10 AML samples, one cluster was consisted of one ALL-B and AML samples, while the other three clusters contained 8 ALL-T, 10 ALL-B and 7 ALL-B respectively. For this dataset, our method seemed to work better.
It was somewhat surprising that there were about 1800 genes remaining for the penalized methods, though previous studies showed that there were a large number of the genes differentially expressed between ALL and AML; in particular, Golub et al. (1999) [15] stated that “roughly 1100 genes were more highly correlated with the AML-ALL class distinction than would be expected by chance”; see also Pan and Shen (2007) [39] and references therein. For a simple evaluation, we applied the elastic net (Zou and Hastie 2005 [58]) to the same data with top 2000 genes; the elastic net is a state-of-the-art supervised learning method specifically designed for variable selection for high-dimensional data and is implemented in R package elasticnet. Five-fold cross-validation was used for tuning parameter selection. As usual, we decomposed the three-class problem into two binary classifiers, ALL-T vs AML, and ALL-B vs ALL, respectively. The two classifiers eliminated 395 and 870 noise genes, respectively, with a common set of 227 genes. Hence the elastic net used 1773 genes, a number comparable to those selected by the penalized clustering methods.
4.3. Grouping genes
The 2000 genes were grouped according to the Kyoto Encyclopedia of Genes and Genomes (KEGG) Pathway database (Kanehisa and Goto 2000 [23]). About 43 percent of the 2000 genes belonged to at least one of 126 KEGG pathways. If a gene was in more than one pathway, it was randomly assigned to one of the pathways to which it belonged. Each genes un-annotated in any pathway was treated as an individual group with size 1. Among the 126 KEGG pathways, the largest pathway size was 44, the smallest one was 1 and the median size was 4; about three quarters of the pathways had sizes less than 8.
The clustering results with the grouped mean and variance penalization were exactly the same as that of UnequalCov and kept 1795 genes. Among the 205 identified noise genes, 23 genes were from 17 KEGG pathways: all contained only one genes except only three pathways, each containing 2, 3 and 4 genes respectively.
To further evaluate the above gene selection results, we searched a Leukemia Gene Database containing about 70 genes that were previously identified in the literature as leukemia-related (www.bioinformatics.org/legend/leuk_db.htm). Among these informative genes, 58 were related to 21 leukemia subtypes, among which only 47 and 36 genes appeared in the whole Golub’s data and the 3337 genes after preprocessing respectively. Among the top 2000 genes being used for clustering, there were only 30 genes in the Leukemia Gene Database, most of which were not in any KEGG pathways; only 7 genes appeared in KEGG pathways: GMPS, ETS1, NOTCH3, MLL3, MYC, NFKB2 and KIT. Table 7 lists the genes that were selected in and deleted from the final model. Among the 205 noise genes selected by our group penalized method, five of them were annotated in the Leukemia Gene Database, among which one was related to AML.
Table 7.
The genes in the Leukemia Gene Database that were retained in or removed from the final model for the grouped method. The six genes in italic font were annotated in KEGG pathways
| Leukemia Subtype | Gene Name | |
|---|---|---|
| Retained | Acute Lymphoblastic Leukemia | MYC, ZNFN1A1 |
| Acute Myelogenous Leukemia | IRF1, GMPS | |
| Acute Myeloid Leukemia | CBFB, NUP214, HOXA9, FUS, RUNX1 | |
| Acute Promyelocytic Leukemia | PML | |
| Acute Undifferentiated Leukemia | SET | |
| B-cell Chronic Lymphocytic Leukemia | BCL3, BTG1 | |
| Myeloid Leukemia | CLC | |
| pre B-cell Leukemia | PBX1, PBX3 | |
| T-cell Leukemia | TCL6 | |
| T-cell Acute Lymphoblastic Leukemia | NOTCH3, LYL1, LMO2, TAL2 | |
| Cutaneous T-cell Leukemia | NFKB2 | |
| Human Monocytic Leukemia | ETS1 | |
| Mast cell Leukemia | KIT | |
| Mixed Linkage Leukemia | MLL3 | |
| Removed | Acute Myeloid Leukemia | LCP1 |
| Acute Myelogenous Leukemia | RGS2 | |
| Murine Myeloid Leukemia | EVI2B | |
| pre B-cell Leukemia | PBX2 | |
| T-cell Leukemia | TRA@ | |
Because most of the known leukemia genes were not in any KEGG pathways, reflecting perhaps the current lack of prior knowledge, the grouped method could not be established as a clear winner over the none-grouped method in terms of leukemia gene selection in the above example. To confirm the potential gain with a better use of prior knowledge, we did two additional experiments. First, in addition to the KEGG pathways, we grouped all the 19 leukemia genes not in any KEGG pathways into a separate group: the samples were clustered as before; among the 200 genes removed from the final model, there were only two leukemia gene, ETS1, which was related to human monocytic leukemia, neither AML nor ALL, and NOTCH3, related to T-cell ALL. Second, in addition to the KEGG pathways, we grouped the AML (“acute myeloid leukemia” in Table 7) or ALL (“acute lymphoblastic leukemia” and “T-cell acute lymphoblastic leukemia”) genes into two corresponding groups while treating the other leukemia genes individually: again the samples were clustered as before; among the 216 genes removed from the final model, ETS1, RGS2, EVI2B, PBX2, TRA@ were the four leukemia genes and there was no single gene related to AML or ALL. These two experiments demonstrated the effectiveness of grouping genes based on biological knowledge, and that, as expected, the quality of the prior knowledge would influence performance. Nevertheless, our work here is just a first step, and more research is necessary to establish the practical use of grouping genes for microarray data.
5. Discussion
We have proposed a new penalized likelihood method for variable selection in model-based clustering, permitting cluster-dependent diagonal covariance matrices. A major novelty is the development of a new L1 penalty involving both mean and variance parameters. The penalized mixture model can be fitted easily using an EM algorithm. Our numerical studies demonstrate the utility of the proposed method and its superior performance over other methods. In particular, it is confirmed that for high-dimensional data such as arising from microarray experiments, variable selection is necessary: without variable selection, the presence of a large number of noise variables can mask the clustering structure underlying the data. Furthermore, we have also studied penalties for grouped variables to incorporate prior knowledge into clustering analysis, which, as expected, improves performance if the prior knowledge being used is indeed informative.
The present approach involves only diagonal covariance matrices. It is argued that for “high dimension but small sample size” settings as arising in genomic studies, the working independence assumption is effective, as suggested by Fraley and Raftery (2006) [12], as well as demonstrated by the popular use of a diagonal covariance matrix in the naive Bayes and other discriminant analyses due to its good performance (Bickel and Levina 2004 [5]; Dudoit et al. 2002 [7]; Tibshirani et al. 2003 [47]). Nevertheless, it is worthwhile to generalize the proposed approach to other non-diagonal covariance matrices, possibly built on the novel idea of shrinking variance components as proposed here. However, this task is much more challenging; a main difficulty is how to guarantee a shrunk covariance matrix to be positive definite, as evidenced by the challenge in a simpler context of penalized estimation of a single covariance matrix (Huang et al. 2006 [21]; Yuan and Lin 2007 [55]). An alternative approach is to have a model intermediate between the independent and unrestricted models. For example, in a mixture of factor analyzers (McLachlan et al. 2003 [35]), local dimension reduction within each component is realized through some latent factors, which are also used to explain the correlations among the variables. Nevertheless, because the latent factors are assumed to be shared by all the variables while in fact they may only be related to a small subset of informative variables, variable selection may still be necessary; however, how to do so is an open question. Finally, although our proposed penalty for grouped variables provides a general framework to consider a group of genes, e.g. in a relevant biological pathway or functional group, for their either “all in” or “all out” property in clustering, there remain some practical questions, such as how to choose pathways and how to handle genes in multiple pathways. These interesting topics remain to be studied.
Acknowledgments
We thank the editor for an extremely timely and helpful review. This research was partially supported by NIH grant GM081535; in addition, BX and WP by NIH grant HL65462 and a UM AHC Faculty Research Development grant, and XS by NSF grants IIS-0328802 and DMS-0604394.
Appendix A: Composite Absolute Penalties (CAP)
We generalize our proposed group penalization, including the two regularization schemes on variance parameters, to the Composite Absolute Penalties (CAP) of Zhao et al. (2006) [56], which covers the group penalty of Yuan and Lin (2006) [54] as a special case.
For grouping mean parameters, the following penalty function is used for the mean parameters:
| (26) |
where , γm > 1 and ||v||γm is the Lγm norm of vector v. Accordingly, we adopt
| (27) |
or
| (28) |
as a penalty for grouped variance parameters. To achieve sparcity, as usual, we use γ0 = 1.
The E-step of the EM yields QP with the same form as (2). Next we derive the updating formulas for the mean and variance parameters in the M-step.
A.1. Grouping mean parameters
If the CAP penalty function (26) for grouped means is used, we can derive the following Theorem:
Theorem 6
The sufficient and necessary conditions for , i = 1, 2, …, g and m = 1, 2, …, M, to be a unique maximizer of QP are
| (29) |
and
| (30) |
yielding
| (31) |
where , and is the usual MLE.
Proof
Consider two cases
-
. First, by definition and using the Hölder’s inequality, we can prove that the Lγm norm is convex, thus the penalty function for grouped means is convex in . Second, treating QP as the Lagrange multiplier for a constrained optimization problem with the penalty as the inequality constraint, and considering that both minus the objective function and the penalty function are convex, by the Karush-Kuhn-Tucker (KKT) condition, we have the following sufficient and necessary condition
from which we can easily get (29).
-
. By definition, we have
Notice as . By the Hölder’s inequality, we have , and the ” = ” can be attained. Thus the above inequality is equivalent to (30).
It is clear that, if λ1 is large enough, will be exactly 0 due to thresholding. Since depends on , we use (31) iteratively to update .
A.2. Grouping variance parameters
A.2.1. Scheme 1
If the penalty function (27) for grouped variances is used, we have the following theorem:
Theorem 7
The sufficient and necessary conditions for , i = 1, 2, …, g, and m = 1, 2, …, M, to be a local maximizer of QP are
| (32) |
The necessary condition for to be a local maximizer of QP is
| (33) |
Proof
If is a local maximum, by definition, we have the following sufficient and necessary condition
Thus,
Using Taylor’s expansion, we have
for some constant vector c. After dividing both sides by and using the same argument as before, we obtain (32) as the sufficient and necessary condition for to be a local maximizer of QP.
Setting the first-order derivative of QP equal to 0, we have (33), the necessary condition for to be a local maximizer of QP.
It is clear that we have when, for example, λ2 is large enough. It is also easy to verify that the above conditions reduce to the same ones for for non-grouped variables when km = 1 and reduce to (24) and (25) for grouped variables when .
A.2.2. Scheme 2
If we use the CAP penalty function (28) for grouped variances, then the following theorem can be obtained by a similar argument as before:
Theorem 8
The sufficient and necessary conditions for , i = 1, 2, …, g and m = 1, 2, …, M, to be a local maximizer of QP are
| (34) |
The necessary condition for to be a local maximizer of QP is
| (35) |
Appendix B: Proofs
B.1. Derivation of Theorem 1
Since QP is differentiable with respect to μik when μik ≠ 0, while non-differentiable at μik = 0, we consider the following two cases:
-
If μik ≠ 0 is a maximum, given that QP is concave and differentiable, then the sufficient and necessary condition for μik to be the global maximum of QP is
from which we have (10).
If μik = 0 is a maximum, we compare QP (0,.) with QP (Δμik,.), values of QP at μik = 0 μik = Delta;μik respectively (while other components of μi are fixed at its maximum). By definition, we have
It is obvious that from (10) we have , thus
B.2. Derivation of Theorem 2
Since QP is differentiable with respect to when , we know a local maximum must satisfy the following conditions
| (36) |
where. in QP (1,.) represents all parameters in QP except .
Notice that , where C1, C2 and C3 are constants with respect to . Therefore the first equation of (36) becomes
from which we can easily get (13).
Starting from the second equation of (36), we have
and thus
Using Taylor’s expansion, we have
leading to
letting , we obtain (14).
B.3. Derivation of in section 2.3.1
Note that from (13) we have . Define f(x) = aikx2 + bix − cik = 0.
First, we consider the case with |bi − cik| ≤ λ2.
When , and if . On the other hand, limx→1+ f(x) = λ2 + bi − cik ≥ 0, since |bi − cik| ≤ λ2; and f(x) = − λ2x2 + bix − cik < − λ2x2 + bi − cik < 0 if x < 1. Thus, based on the signs of f(x), QP has a unique local maximum at .
-
When , we have , and if ; limx→1− f(x) = −λ2 + bi − cik ≤; and f(x) = λ2x2 + bix − ci > λ2 + bi − ci > 0 if x > 1. However, for , f(x) =− λ2x2 + bix − cik is a continuous and quadratic function, which may have two roots
If bi − cik <λ2, then limx→1− f(x) < 0, implying that, according to the signs of f(x) around x = 1, x = 1 is a local maximum of QP, and the smaller of x1,2 is also a local maximum (if it exists); on the other hand, if bi − cik = λ2, then limx→1− f(x) = 0, implying that either x = 1, the smaller root of x1,2 if , or x = cik/λ2, the larger root of x1,2 if , is the unique maximum.
Second, we claim that, if |bi − cik| > λ2, there exists a unique local maximizer for QP and it must lie between 1 and , the usual MLE without penalty. This can be shown in the following way.
When , and if . On the other hand, limx→1+ f(x) = λ2 + bi − cik < 0, since bi − cik < − λ2; and f(x) = − λ2x2 + bix − cik < − λ2x2 + bi − cik < 0 if x < 1. Thus f(x) has a unique root .
When , similarly we have , and if ; limx→1 − f(x) = −λ2 + bi − cik > 0; and f(x) = λ2x2 + bix − ci > bi − ci > 0 if x > 1. Thus f(x) has a unique root .
Based on the signs of f(x) around , it is easy to see that is indeed a local maximizer.
Third, (13) can be expressed as
| (37) |
From the first equation of (37), we get . Since and that bi − cik > λ2 implies while must be between and 1, we only have one solution . From the second equation, similarly we get . Combining the two cases, we obtain (15).
Note that the expression inside the square root of (15) is non-negative. To prove it, we only need to show that for . Consider two cases:
-
When cik − bi > λ2 ≥ 0,
-
When cik − bi < −λ2 ≤0,
B.4. Derivation of Theorem 3
We prove the necessary conditions below, while the sufficiency is proved as a side-product in Appendix B.5.
Since QP is differentiable with respect to when , we know a local maximum must satisfy the following conditions
| (38) |
where. in QP (1,.) represents all parameters in QP except .
Notice that , where C1, C2 and C3 are constants with respect to . Therefore the first equation of (38) becomes
from which we can easily get (17).
Starting from the second equation of (38), we have
and thus
Using Taylor’s expansion, we have
leading to
letting , we obtain (18).
B.5. Derivation of in section 2.3.2
Let , where f(x) is defined as . Thus (17) is equivalent to . First, we consider the case with |bi − cik| ≤ λ2, the necessary condition of .
When if x > 1. On the other hand, if . Thus, based on the signs of f(x), QP has a unique local maximum at .
When , we have cik/bi < 1, thus 0 < bi − cik < λ2. if x > 1. On the other hand, if 0 < x < 1. Thus, based on the signs of f(x), QP has a unique local maximum at .
i) and ii) indicates that |bi − cik| ≤ λ2 is also the sufficient condition of
Second, we claim that, if |bi − cik| > λ2, there exists a unique local maximizer for QP and it must lie between 1 and , the usual MLE without penalty. This can be shown in the following way.
When , we have bi < cik, and further cik − bi > λ2. Notice if 0< x <1. Thus the possible root of f(x) = 0 should be larger than 1. For x > 1, is a linear function of x. , and . Thus f(x) = 0 has a unique root .
When , we have bi > cik, and further bi − cik > λ2. Notice if x >1. Thus the possible root of f(x) = 0 should be smaller than 1. For x < 1, is a linear function of x. and . Thus f(x) = 0 has a unique root .
Based on the signs of f(x) around , it is easy to see that is indeed a local maximizer. And
B.6. Derivation of Theorem 4
Consider two cases:
-
. First, by definition and using the Cauchy-Schwarz inequality, we can prove that the L2 norm is convex, thus the penalty function for grouped means is convex in . Second, treating QP as the Lagrange multiplier for a constrained optimization problem with the penalty as the inequality constraint, and considering that both minus the objective function and the penalty function are convex, by the Karush-Kuhn-Tucker (KKT) condition, we have the following sufficient and necessary condition
from which we can easily get (21).
-
. By definition, we have
Plugging-in and letting α → 0, we obtain (22) from the above inequality. On the other hand, by the Cauchy-Schwarz inequality, we have , and because is positive definite, we obtain the above inequality from (22).
B.7. Derivation of Theorem 5
If is a local maximum, by definition, we have the following sufficient and necessary condition
Thus,
Using Taylor’s expansion, we have
for some constant vector c. After dividing both sides by and using the same argument as before, we obtain (24) as the sufficient and necessary condition for to be a local maximizer of QP.
B.8. Characterization of solutions to (25)
Consider any component k′, , of . Equation (25) corresponds to
where , and bik′ and cimk′ are the k′th components of bi and cim respectively. If λ2 = 0, then , the usual MLE without penalization; if λ2 ≠= 0 and we treat aim as a constant (i.e. by plugging-in a current estimate of ), the above equation becomes a cubic equation of ,
where a = −1, b = bik′/aim, c = − cimk′/aim.
Now we consider the following two cases:
When , we have , f(x) < 0 for ∀x < 1, and f(x) > 0 for . Therefore, the real roots of this equation must be between 1 and . Recall the fact that an odd-order equation has at least one real root, and the sum of all three roots of this equation equals −a = 1, the equation must have only one real root . Because , based on the signs of f(x) near , we know that is a local maximizer.
-
When , we have , f(x) > 0 for ∀x > 1, and f(x) < 0 for . Therefore, the real roots of this equation must be between and 1. By factorization, we have
where x1 is a root of f(x) = 0. Thus, if we use a bisection search to find the first root x1, the other two (real or complex) roots of f(x) = 0 are
If there is more than one real root, we choose the one maximizing QP as the new estimate .
Appendix C: Simulation
C.1. Comparison of the two regularization schemes
We investigated the performance of the two regularization schemes for the variance parameters for set-up 3 in simulation case I. There were 36 (or 5) out of 100 datsets which were identified with 2 (or 3) clusters by both (var-1) and log(var) methods. Table 8 summarizes the numbers of the genes with their penalized variance estimates as exactly one by either regularization scheme. For ĝ = 3, the two schemes gave exactly the same number of the genes for each cluster and discovered the same genes with their variances estimated as one across all 3 clusters. For ĝ = 2, the results of the two schemes were also similar, though scheme one (i.e. penalizing var-1) identified slightly more genes with their variances estimated to be one for each cluster and more genes across both the clusters than did scheme two.
Table 8.
The mean numbers of the genes (or variables) whose penalized variance parameters were exactly one by the two regularization schemes, averaged over the datasets with ĝ = 2 and ĝ = 3 respectively. “Overlap” gives the common genes between the two regularization schemes or between/among the two/three clusters
|
ĝ = 2 |
ĝ = 3 |
|||||||
|---|---|---|---|---|---|---|---|---|
| Cluster 1 | Cluster 2 | Overlap | Cluster 1 | Cluster 2 | Cluster 3 | Overlap | ||
| 3 | L1(var-1) | 281.0 | 283.2 | 278.0 | 288.0 | 290.0 | 286.0 | 286.0 |
| L1(logvar) | 277.3 | 279.2 | 272.5 | 288.0 | 290.0 | 286.0 | 286.0 | |
| Overlap | 276.8 | 278.9 | 271.9 | 288.0 | 290.0 | 286.0 | 286.0 | |
Figure 5 compares the variance parameter estimates by the two regularization schemes and the sample variance estimates based on the estimated sample assignments for the estimated ĝ = 2 clusters for one simulated dataset in set-up 3. Due to the construction of the simulation data and standardization, the true cluster with 80 samples always had sample variances smaller than 1 for informative variables, while the other cluster with 20 samples always had sample variances larger than 1 for those informative variables. Compared to the sample variance estimates, the penalized estimates from both schemes were clearly shrunken towards 1, and could be exactly 1. Between the two schemes, they gave similar estimates for cluster 2, but scheme 1 in general shrank many variance parameters more than scheme 2, which was in agreement with and explained the results in Table 8.
Fig 5.
Comparison of the two regularization schemes on the variance parameters for one dataset of set-up 3. σ̂is is MPLE for cluster i by scheme s.
Appendix D: Golub’s data
D.1. Comparison of the two regularization schemes
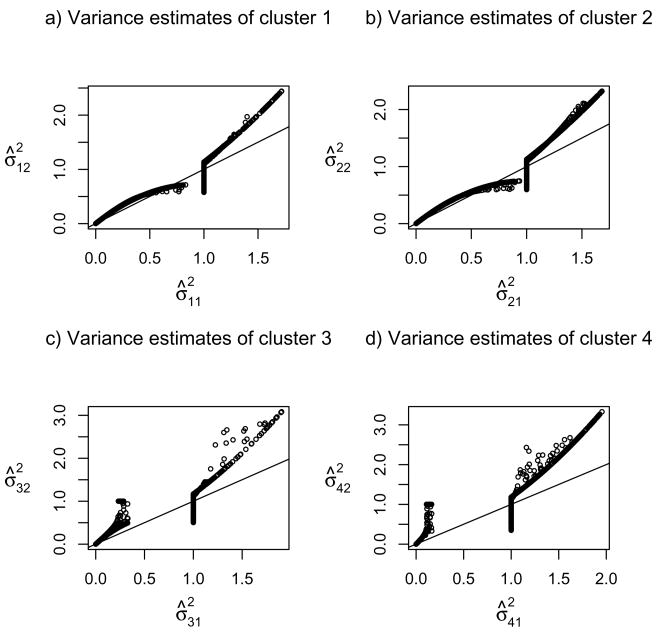
Figure 6 compares the MPLEs of the variance parameters given by the two regularization schemes for Golub’s data with the top 2000 genes. Although the two schemes in general gave similar MPLEs, scheme 1 seemed to shrink more than did scheme 2, especially if σ̂2 > 1.
Fig 6.
Comparison of the two regularization schemes on the variance parameters for Golub’s data with the top 2000 genes. X-axis and y-axis give the MPLEs by scheme 1 and scheme 2 respectively.
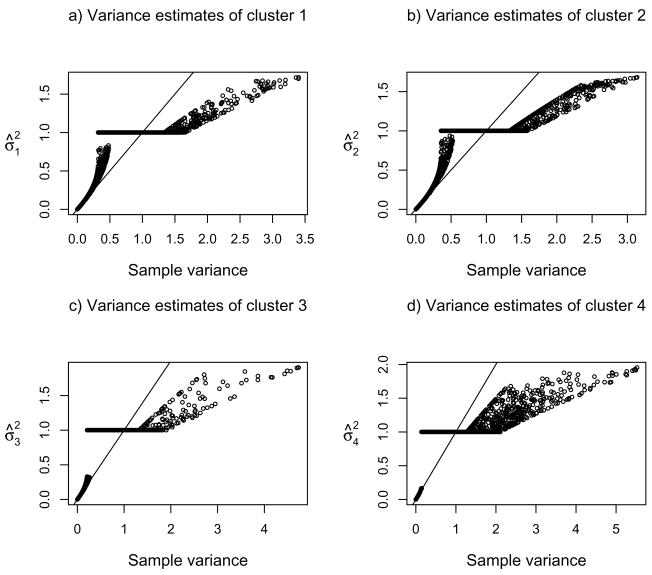
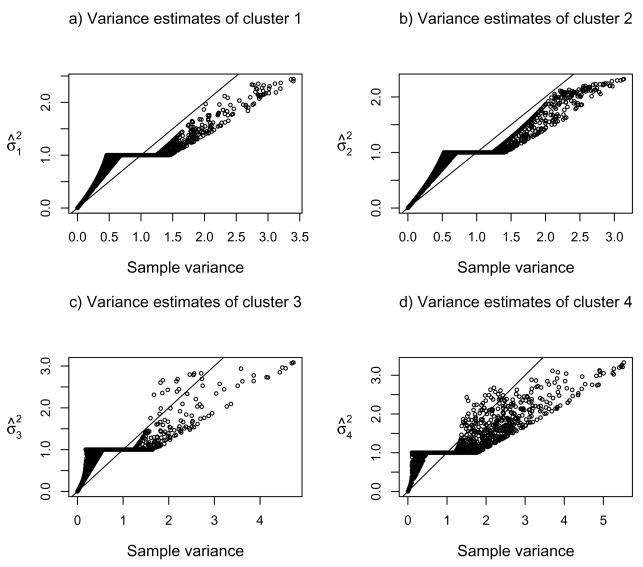
Figures 7–8 compare the MPLEs from the two schemes with the sample variances based on the final clusters. The effects of shrinkage to and thresholding at 1 by the two regularization schemes were striking. In particular, there was a clear thresholding in MPLE when the sample variances were less than and close to 1 for scheme 1 (Figure 7). To provide an explanation, we examined expression (15) given in the paper. We notice that if (in the form of the usual MLE) is less than 1, and λ2 is large enough, then the MPLE . Therefore, did have a ceiling at 2(1 − λ2/bi).
Fig 7.
Comparison of the penalized variance estimates by regularization scheme 1 and the sample variances for Golub’s data with the top 2000 genes.
Fig 8.
Comparison of the penalized variance estimates by regularization scheme 2 and the sample variances for Golub’s data with the top 2000 genes.
D.2. Comparison with Kim et al. (2006)’s method
We applied our penalized clustering methods to the Golub’s data that were pre-processed as in Kim et al. (2006) [25], resulting in 3571 genes; see Table 9. The standard methods without variable selection under-selected the number of clusters at 2, failing to distinguish between ALL-T and ALL-B, even between ALL and AML (for the equal covariance model), in agreement with our simulation results. Our proposed new penalized method could largely separate the AML samples and the two ALL subtypes; only two samples were mis-assigned. In contrast, Kim et al’s method could not separate the two subtypes of ALL samples.
Table 9.
Clustering results for Golub’s data with 3571 genes. The number of components (g) was selected by BIC
| UnequalCov(λ1, λ2) |
EqualCov(λ1) |
||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Methods |
(0, 0) |
(λ̂1, λ̂2) |
(0) |
(λ̂1) |
|||||||||
| BIC |
148898 |
116040 |
134660 |
124766 |
|||||||||
| Clusters | 1 | 2 | 1 | 2 | 3 | 4 | 5 | 1 | 2 | 1 | 2 | 3 | 4 |
| Samples(#) |
|||||||||||||
| ALL-T(8) | 0 | 8 | 0 | 0 | 8 | 0 | 0 | 5 | 3 | 0 | 0 | 8 | 0 |
| ALL-B(19) | 5 | 14 | 10 | 1 | 0 | 7 | 1 | 11 | 8 | 11 | 1 | 0 | 7 |
| AML(11) | 11 | 0 | 0 | 10 | 0 | 0 | 1 | 1 | 10 | 0 | 11 | 0 | 0 |
Contributor Information
Benhuai Xie, Division of Biostatistics, School of Public Health, University of Minnesota, benhuaix@biostat.umn.edu.
Wei Pan, Division of Biostatistics, School of Public Health, University of Minnesota, weip@biostat.umn.edu, url: www.biostat.umn.edu/~weip.
Xiaotong Shen, School of Statistics, University of Minnesota, xshen@stat.umn.edu.
References
- 1.Alaiya AA, et al. Molecular classification of borderline ovarian tumors using hierarchical cluster analysis of protein expression profiles. Int J Cancer. 2002;98:895–899. doi: 10.1002/ijc.10288. [DOI] [PubMed] [Google Scholar]
- 2.Antonov AV, Tetko IV, Mader MT, Budczies J, Mewes HW. Optimization models for cancer classification: extracting gene interaction information from microarray expression data. Bioinformatics. 2004;20:644–652. doi: 10.1093/bioinformatics/btg462. [DOI] [PubMed] [Google Scholar]
- 3.Baker Stuart G, Kramer Barnett S. Identifying genes that contribute most to good classification in microarrays. BMC Bioinformatics. 2006 Sep 7;7:407. doi: 10.1186/1471-2105-7-407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Bardi E, Bobok I, Olah AV, Olah E, Kappelmayer J, Kiss C. Cystatin C is a suitable marker of glomerular function in children with cancer. Pediatric Nephrology. 2004;19:1145–1147. doi: 10.1007/s00467-004-1548-3. [DOI] [PubMed] [Google Scholar]
- 5.Bickel PJ, Levina E. Some theory for Fisher’s linear discriminant function, “naive Bayes”, and some alternatives when there are many more variables than observations. Bernoulli. 2004;10:989–1010. MR2108040. [Google Scholar]
- 6.Dempster AP, Laird NM, Rubin DB. Maximum likelihood from incomplete data via the EM algorithm (with discussion) JRSS-B. 1977;39:1–38. MR0501537. [Google Scholar]
- 7.Dudoit S, Fridlyand J, Speed T. Comparison of discrimination methods for the classification of tumors using gene expression data. J Am Stat Assoc. 2002;97:77–87. MR1963389. [Google Scholar]
- 8.Efron B, Tibshirani R. On testing the significance of sets of genes. Annals of Applied Statistics. 2007;1:107–129. [Google Scholar]
- 9.Efron B, Hastie T, Johnstone I, Tibshirani R. Least angle regression. Annals of Statistics. 2004;32:407–499. MR2060166. [Google Scholar]
- 10.Eisen M, Spellman P, Brown P, Botstein D. Cluster analysis and display of genome-wide expression patterns. PNAS. 1998;95:14863–14868. doi: 10.1073/pnas.95.25.14863. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Friedman JH, Meulman JJ. Clustering objects on subsets of attributes (with discussion) J Royal Statist Soc B. 2004;66:1–25. MR2102467. [Google Scholar]
- 12.Fraley C, Raftery AE. MCLUST Version 3 for R: Normal Mixture Modeling and Model-Based Clustering. Technical Report no. 504. Department of Statistics, University of Washington; 2006. [Google Scholar]
- 13.Ghosh D, Chinnaiyan AM. Mixture modeling of gene expression data from microarray experiments. Bioinformatics. 2002;18:275–286. doi: 10.1093/bioinformatics/18.2.275. [DOI] [PubMed] [Google Scholar]
- 14.Gnanadesikan R, Kettenring JR, Tsao SL. Weighting and selection of variables for cluster analysis. Journal of Classification. 1995;12:113–136. [Google Scholar]
- 15.Golub T, et al. Molecular classification of cancer: class discovery and class prediction by gene expression monitoring. Science. 1999;286:531–537. doi: 10.1126/science.286.5439.531. [DOI] [PubMed] [Google Scholar]
- 16.Gu C, Ma P. Optimal smoothing in nonparametric mixed-effect models. Ann Statist. 2005;33:377–403. MR2195638. [Google Scholar]
- 17.Hoff PD. Discussion of ‘Clustering objects on subsets of attributes’. In: Friedman J, Meulman J, editors. Journal of the Royal Statistical Society, Series B. Vol. 66. 2004. p. 845. MR2102467. [Google Scholar]
- 18.Hoff PD. Model-based subspace clustering. Bayesian Analysis. 2006;1:321–344. MR2221267. [Google Scholar]
- 19.Huang X, Pan W. Comparing three methods for variance estimation with duplicated high density oligonucleotide arrays. Functional & Integrative Genomics. 2002;2:126–133. doi: 10.1007/s10142-002-0066-2. [DOI] [PubMed] [Google Scholar]
- 20.Huang D, Pan W. Incorporating biological knowledge into distance-based clustering analysis of microarray gene expression data. Bioinformatics. 2006;22:1259–1268. doi: 10.1093/bioinformatics/btl065. [DOI] [PubMed] [Google Scholar]
- 21.Huang JZ, Liu N, Pourahmadi M, Liu L. Covariance selection and estimation via penalised normal likelihood. Biometrika. 2006;93:85–98. MR2277742. [Google Scholar]
- 22.Hubert L, Arabie P. Comparing partitions. Journal of Classification. 1985;2:1993–218. [Google Scholar]
- 23.Kanehisa M, Goto S. KEGG: Kyoto Encyclopedia of Genes and Genomes. Nucleic Acids Res. 2000;28:27–30. doi: 10.1093/nar/28.1.27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Kaufman L, Rousseeuw PJ. Finding Groups in Data: An Introduction to Cluster Analysis. Wiley; New York: 1990. MR1044997. [Google Scholar]
- 25.Kim S, Tadesse MG, Vannucci M. Variable selection in clustering via Dirichlet process mixture models. Biometrika. 2006;93:877–893. MR2285077. [Google Scholar]
- 26.Koo JY, Sohn I, Kim S, Lee J. Structured polychotomous machine diagnosis of multiple cancer types using gene expression. Bioinformatics. 2006;22:950–958. doi: 10.1093/bioinformatics/btl029. [DOI] [PubMed] [Google Scholar]
- 27.Li H, Hong F. Cluster-Rasch models for microarray gene expression data. Genome Biology. 2001;2:research0031.1-0031.13. doi: 10.1186/gb-2001-2-8-research0031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Liao JG, Chin KV. Logistic regression for disease classification using microarray data: model selection in a large p and small n case. Bioinformatics. 2007;23:1945–1951. doi: 10.1093/bioinformatics/btm287. [DOI] [PubMed] [Google Scholar]
- 29.Lin X, Zhang D. Inference in generalized additive mixed models by using smoothing splines. JRSS-B. 1999;61:381–400. MR1680318. [Google Scholar]
- 30.Liu JS, Zhang JL, Palumbo MJ, Lawrence CE. Bayesian clustering with variable and transformation selection (with discussion) Bayesian Statistics. 2003;7:249–275. MR2003177. [Google Scholar]
- 31.Ma P, Castillo-Davis CI, Zhong W, Liu JS. A data-driven clustering method for time course gene expression data. Nucleic Acids Research. 2006;34:1261–1269. doi: 10.1093/nar/gkl013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Mangasarian OL, Wild EW. Feature selection in k-median clustering. Proceedings of SIAM International Conference on Data Mining, Workshop on Clustering High Dimensional Data and its Applications; April 24, 2004; La Buena Vista, FL. 2004. pp. 23–28. [Google Scholar]
- 33.McLachlan GJ, Bean RW, Peel D. A mixture model-based approach to the clustering of microarray expression data. Bioinformatics. 2002;18:413–422. doi: 10.1093/bioinformatics/18.3.413. [DOI] [PubMed] [Google Scholar]
- 34.McLachlan GJ, Peel D. Finite Mixture Model. New York: John Wiley & Sons, Inc; 2002. MR1789474. [Google Scholar]
- 35.McLachlan GJ, Peel D, Bean RW. Modeling high-dimensional data by mixtures of factor analyzers. Computational Statistics and Data Analysis. 2003;41:379–388. MR1973720. [Google Scholar]
- 36.Newton MA, Quintana FA, den Boon JA, Sengupta S, Ahlquist P. Random-set methods identify distinct aspects of the enrichment signal in gene-set analysis. Annals of Applied Statistics. 2007;1:85–106. [Google Scholar]
- 37.Pan W. Incorporating gene functional annotations in detecting differential gene expression. Applied Statistics. 2006;55:301–316. MR2224227. [Google Scholar]
- 38.Pan W. Incorporating gene functions as priors in model-based clustering of microarray gene expression data. Bioinformatics. 2006b;22:795–801. doi: 10.1093/bioinformatics/btl011. [DOI] [PubMed] [Google Scholar]
- 39.Pan W, Shen X. Penalized model-based clustering with application to variable selection. Journal of Machine Learning Research. 2007;8:1145–1164. [Google Scholar]
- 40.Pan W, Shen X, Jiang A, Hebbel RP. Semi-supervised learning via penalized mixture model with application to microarray sample classification. Bioinformatics. 2006;22:2388–2395. doi: 10.1093/bioinformatics/btl393. [DOI] [PubMed] [Google Scholar]
- 41.Raftery AE, Dean N. Variable selection for model-based clustering. Journal of the American Statistical Association. 2006;101:168–178. MR2268036. [Google Scholar]
- 42.Rand WM. Objective criteria for the evaluation of clustering methods. JASA. 1971;66:846–850. [Google Scholar]
- 43.Tadesse MG, Sha N, Vannucci M. Bayesian variable selection in clustering high-dimensional data. Journal of the American Statistical Association. 2005;100:602–617. MR2160563. [Google Scholar]
- 44.Thalamuthu A, Mukhopadhyay I, Zheng X, Tseng GC. Evaluation and comparison of gene clustering methods in microarray analysis. Bioinformatics. 2006;22:2405–2412. doi: 10.1093/bioinformatics/btl406. [DOI] [PubMed] [Google Scholar]
- 45.Tian L, Greenberg SA, Kong SW, Altschuler J, Kohane IS, Park PJ. Discovering statistically significant pathways in expression profiling studies. PNAS. 2005;102:13544–13549. doi: 10.1073/pnas.0506577102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Tibshirani R. Regression shrinkage and selection via the lasso. JRSS-B. 1996;58:267–288. MR1379242. [Google Scholar]
- 47.Tibshirani R, Hastie T, Narasimhan B, Chu G. Class prediction by nearest shrunken centroids, with application to DNA microarrays. Statistical Science. 2003;18:104–117. MR1997067. [Google Scholar]
- 48.Tycko B, Smith SD, Sklar J. Chromosomal translocations joining LCK and TCRB loci in human T cell leukemia. Journal of Experimental Medicine. 1991;174:867–873. doi: 10.1084/jem.174.4.867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Wang Y, Tetko IV, Hall MA, Frank E, Facius A, Mayer KFX, Mewes HW. Gene selection from microarray data for cancer classification -a machine learning approach. Comput Biol Chem. 2005;29:37–46. doi: 10.1016/j.compbiolchem.2004.11.001. [DOI] [PubMed] [Google Scholar]
- 50.Wang S, Zhu J. Variable Selection for Model-Based High-Dimensional Clustering and Its Application to Microarray Data. 2008 doi: 10.1111/j.1541-0420.2007.00922.x. To appear in Biometrics. [DOI] [PubMed] [Google Scholar]
- 51.Wright DD, Sefton BM, Kamps MP. Oncogenic activation of the Lck protein accompanies translocation of the LCK gene in the human HSB2 T-cell leukemia. Mol Cell Biol. 1994;14:2429–2437. doi: 10.1128/mcb.14.4.2429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Xie B, Pan W, Shen X. Division of Biostatistics, University of Minnesota; 2008. Variable selection in penalized model-based clustering via regularization on grouped parameters. To appear in BiometricsAvailable at http://www.biostat.umn.edu./rrs.php as Research Report 2007–018. [DOI] [PubMed] [Google Scholar]
- 53.Yeung KY, Fraley C, Murua A, Raftery AE, Ruzzo WL. Model-based clustering and data transformations for gene expression data. Bioinformatics. 2001;17:977–987. doi: 10.1093/bioinformatics/17.10.977. [DOI] [PubMed] [Google Scholar]
- 54.Yuan M, Lin Y. Model selection and estimation in regression with grouped variables. JRSS-B. 2006;68:49–67. MR2212574. [Google Scholar]
- 55.Yuan M, Lin Y. Model selection and estimation in the Gaussian graphical model. Biometrika. 2007;94:19–35. [Google Scholar]
- 56.Zhao P, Rocha G, Yu B. Grouped and hierarchical model selection through composite absolute penalties. Technical Report. Dept of Statistics, UC-Berkeley; 2006. [Google Scholar]
- 57.Zou H. The Adaptive Lasso and Its Oracle Properties. JASA. 2006;101:1418–1429. MR2279469. [Google Scholar]
- 58.Zou H, Hastie T. Regularization and variable selection via the elastic net. Journal of the Royal Statistical Society B. 2005;67:301–320. MR2137327. [Google Scholar]
- 59.Zou H, Hastie T, Tibshirani R. On the “Degrees of Freedom” of the Lasso. 2004 To appear Ann StatisticsAvailable at http://stat.stanford.edu/~hastie/pub.htmMR2363967.