Site-renormalised molecular fluid theory: on the utility of a two-site model of water

Abstract

We propose a simple, two-site model of water, using the familiar three-site Simple Point Charge (SPC) model as a guide. We briefly examine the resulting dielectric and solvation properties of the bulk fluid, both pure and in a three component mixture of apolar or ionic simple fluid solutes, using integral equation methods. The results confirm a practical utility of this simplified model, and the essential predictive properties of the site-renormalised molecular fluid theory.

1. Introduction

The work of J.J. Weis has played an important role in the development of the theory of polar liquids, such as the Verlet–Weis cluster expansion for systems with dipolar symmetry [1]. We celebrate Weis's long and successful involvement in polar liquids theory with this note on the dielectric properties and general utility of a two-site model of water.

Many of the model systems that Weis and co-workers have used to great effect in their work have been based on a fundamental picture of the pair interactions of molecular fluids. In particular, the models of interest have usually been constructed from embedding a small number of terms from the multipole expansion of the Coulomb potential within a spherical shell. This approach has a significant practical outcome, in that the fundamental orientational contributions introduced by molecules are maintained, while allowing the researchers to use integral equation methods, based on the molecular Ornstein–Zernike equation, which are well developed for the systems of interest. Our own interest in this area has been concentrated on the related family of models that are constructed from the atomic picture of molecular systems based on site–site models [2–7].

Our recent work has focused on developing the quantitative theory of site–site model liquids [5,7]. Using the necessary equivalence between the diagrammatically proper Interaction Site Model (PISM) theory of Chandler et al. [8] and the molecular Ornstein–Zernike theory of Blum and Torruella [9]. we have developed a molecularly-complete theoretical description that is essentially quantitatively predictive of the structure and thermodynamics of pure polar and apolar diatomic liquids [5]. In particular, we have, for the first time, shown that one can reliably predict the dielectric constant of site–site model liquids [7]. This encouraging result leads us here to examine the practical utility of a two-site model system of water in comparison to the similar work of Levesque et al. [10].

We construct here a basic two-site model of water, using the familiar three site family of water models as a guide. In particular, we will maintain the size, dipole moment, and charge separation of the familiar SPC model of water [11]. We have two main goals for constructing this simple system. First, familiar problems in the general theory of site–site model systems necessitate a methodical approach, and this simple water model, together with a mixture of simple apolar or ionic solutes, allows us to examine some basic properties of the theory. Second, one of the principle models which Weis and company have used to great effect is a dipole embedded in a sphere [10]. A two-site model of water is then an obvious basis for comparison against their well-known electrolyte results [10].

2. Method

Here we outline the equations used. We recall first, for a pure, diatomic fluid, the basic equations [5,7]. Typically, for most work to date, site–site model systems have been investigated using the Interaction Site Model (ISM) integral equation theories which can be derived from the Reference Interaction Site Model (RISM) theory of Chandler and Andersen [12]. The chief advantage of these methods is that the equations are written only in terms of radially symmetric functions. This also proves to be their chief weakness; namely, that the intramolecular correlations are not consistently angle-averaged with the intermolecular correlations. Our recent work has focused on the fact that the diagrammatically proper interaction site model (PISM) variant of these equations [8] should be fundamentally equivalent to a Mayer [13] expansion of the complete molecular system of equations [14]. This expansion can be performed in full angular generality, prior to angular averaging. That is, we use a diatomic molecular system with a site–site model potential defined [15] by

$$U(\mathit{r},{\Omega }_1,{\Omega }_2)=\sum _{ij}u\left(\mid {\mathit{r}}_{ij}\mid \right),$$ (1)

where r is the displacement between molecules 1 and 2, Ω₁ and Ω₂ are the orientations of molecules 1 and 2, respectively, and the i, j are the sums over the i sites in molecule 1 and j sites in molecule 2. In the form written, the intramolecular geometry is implicit in the distance between sites i and j.

The four distinct terms in the molecular potential between diatomic molecules may be written as either site–site terms as above or as angular dependent proper terms given by

$$\begin{array}{cc}\hfill U({\mathit{r}}_{ij},{\Omega }_1,{\Omega }_2)=& u^o\left(r_{ij}\right)+u^l({\mathit{r}}_{ij},{\Omega }_1)+u^r({\mathit{r}}_{ij},{\Omega }_2)\hfill \\ \hfill & +u^b({\mathit{r}}_{ij},{\Omega }_1,{\Omega }_2),\hfill \end{array}$$ (2)

where r_ij is the displacement vector between site i on molecule 1 and site j on molecule 2 and the none, left, right and both proper convention is a superscript.

For this system, the exponential form of the molecular closure [16] can also be readily separated into four distinct none, left, right, and both terms [8]. Then, by recalling that the expansion in rotational invariants necessary to the molecular OZ equation is simply a set of weighted angular averages [9], the full molecular expansions on site origins can be readily generated [5].

This labelling convention is explained in detail in the previous work [5,7]. To this point, we have found that, if the diagrammatic terms are resummed carefully, then the first, spherical term in the general basis set expansion, defined for each site–site pair by

$$\begin{array}{cc}\hfill & {\stackrel{‒}{c}}_{ij}^o\left(r\right)=g_{ij}^o\left(r\right)-{\tau }_{ij}^o\left(r\right)-1,\hfill \\ \hfill & {\stackrel{‒}{c}}_{ij}^l\left(r\right)=g_{ij}^o\left(r\right)(g_{ij}^l\left(r\right)-1)-{\tau }_{ij}^l\left(r\right),\hfill \\ \hfill & {\stackrel{‒}{c}}_{ij}^r\left(r\right)=g_{ij}^o\left(r\right)(g_{ij}^r\left(r\right)-1)-{\tau }_{ij}^r\left(r\right),\hfill \\ \hfill & {\stackrel{‒}{c}}_{ij}^b\left(r\right)=g_{ij}^o\left(r\right)(g_{ij}^b\left(r\right)-g_{ij}^l\left(r\right)-g_{ij}^r\left(r\right)+1)-{\tau }_{ij}^b\left(r\right),\hfill \end{array}$$ (3)

is a dramatic improvement over the basic ISM results. Here, the ${\stackrel{‒}{c}}_{\mathit{ij}}\left(r\right)$ functions are topologically resummed forms of the familiar site–site direct correlation functions, the g functions are defined in the molecular hypernetted chain (HNC) approximation as

$$\begin{array}{cc}\hfill g_{ij}^o\left(r\right)=& \exp (-\beta u_{ij}\left(r\right)+{\tau }_{ij}^o\left(r\right)),\hfill \\ \hfill g_{ij}^l\left(r\right)=& \frac{1}{2}{\int }_{-1}^1\exp (-\beta {\stackrel{‒}{u}}_{ij}^l\left(\mid {\mathit{r}}_{ij}-{\mathit{l}}_1\mid \right)+{\tau }_{ij}^l\left(r\right))d\cos {\theta }_1,\hfill \\ \hfill g_{ij}^r\left(r\right)=& \frac{1}{2}{\int }_{-1}^1\exp (-\beta {\stackrel{‒}{u}}_{ij}^r\left(\mid {\mathit{r}}_{ij}+{\mathit{l}}_2\mid \right)+{\tau }_{ij}^l\left(r\right))d\cos {\theta }_2,\hfill \\ \hfill g_{ij}^b\left(r\right)=& \frac{1}{8\pi }{\int }_{-1}^1{\int }_{-1}^1{\int }_0^{2\pi }\exp (-\beta {\stackrel{‒}{u}}_{ij}^b\left(\mid \mathit{ij}-{\mathit{l}}_1+{\mathit{l}}_2\mid \right)\hfill \\ \hfill & -\beta {\stackrel{‒}{u}}_{ij}^l\left(\mid {\mathit{r}}_{ij}-{\mathit{l}}_1\mid \right)-\beta {\stackrel{‒}{u}}_{ij}^r\left(\mid {\mathit{r}}_{ij}+{\mathit{l}}_2\mid \right)+{\tau }_{ij}^b\left(r\right)\hfill \\ \hfill & +{\tau }_{ij}^l\left(r\right)+{\tau }_{ij}^r\left(r\right))d\cos {\theta }_{1}d\cos {\theta }_{2}d{\varphi }_{12},\hfill \end{array}$$ (4)

where β⁻¹ = k_BT, k_B is Boltzmann's constant, T is the absolute temperature and the u functions are the diagrammatically resummed effective potentials

$$\begin{array}{cc}\hfill {\stackrel{‒}{u}}_{ij}^l({\mathit{r}}_{ij},{\Omega }_1)=& u_{jj}\left(\mid {\mathit{r}}_{ij}-{\mathit{l}}_1\mid \right)-{\tau }_{jj}^o\left(\mid {\mathit{r}}_{ij}-{\mathit{l}}_1\mid \right),\hfill \\ \hfill {\stackrel{‒}{u}}_{ij}^r({\mathit{r}}_{ij},{\Omega }_1)=& u_{ii}\left(\mid {\mathit{r}}_{ij}+{\mathit{l}}_2\mid \right)-{\tau }_{ii}^o\left(\mid {\mathit{r}}_{ij}+{\mathit{l}}_2\mid \right),\hfill \\ \hfill {\stackrel{‒}{u}}_{ij}^b({\mathit{r}}_{ij},{\Omega }_1,{\Omega }_2)=& u_{ji}\left(\mid {\mathit{r}}_{ij}-{\mathit{l}}_1+{\mathit{l}}_2\mid \right)-{\tau }_{ji}^o\left(\mid {\mathit{r}}_{ij}-{\mathit{l}}_1+{\mathit{l}}_2\mid \right)\hfill \\ \hfill & -{\tau }_{ii}^l\left(\mid {\mathit{r}}_{ij}-{\mathit{l}}_1\mid \right)-{\tau }_{jj}^r\left(\mid {\mathit{r}}_{ij}+{\mathit{l}}_2\mid \right).\hfill \end{array}$$ (5)

Finally, we use an OZ equation, with a familiar algebraic form in Fourier space,

$$\begin{array}{cc}\hfill \mathbf{H}& =\chi +\mathbf{S}+(\chi +\mathbf{S})\rho \mathbf{H},\hfill \\ \hfill \tau & =\mathbf{H}-\mathbf{S}-\stackrel{‒}{\mathbf{c}},\hfill \end{array}$$ (6)

where the S matrix is the intramolecular distribution function, with the rigid distribution $S_{\mathit{ij}}^b=\sin \left(kl\right)∕kl\rho$ if i ≠ j, and 0 in every other term. The χ matrix is here the first, spherical, term in a set of general angular convolutions,

$$\chi =\stackrel{‒}{\mathbf{c}}-\Phi +(\stackrel{‒}{\mathbf{c}}-\Phi )\rho \prime \chi .$$ (7)

The Φ(_ij matrix elements are the self-consistent topological renormalisation functions, necessary to insure the proper diagrammatic construction, defined in r-space as

$$\begin{array}{cc}\hfill {\varphi }_{ij}^o\left(r\right)=& 0,\hfill \\ \hfill {\varphi }_{ij}^l\left(r\right)=& g_{ij}^l\left(r\right)-1,\hfill \\ \hfill {\varphi }_{ij}^r\left(r\right)=& g_{ij}^r\left(r\right)-1,\hfill \\ \hfill {\varphi }_{ij}^b\left(r\right)=& g_{ij}^b\left(r\right)-g_{ij}^l\left(r\right)\times g_{ij}^r\left(r\right)\hfill \\ \hfill & -\langle (\exp (-\beta {\stackrel{‒}{u}}_{ij}^b\left(\mid {\mathit{r}}_{ij}-{\mathit{l}}_1+{\mathit{l}}_2\mid \right))-1)\phantom{\rangle }\hfill \\ \hfill & \times (\exp (-\beta {\stackrel{‒}{u}}_{ij}^l\left(\mid {\mathit{r}}_{ij}-{\mathit{l}}_1\mid \right))-1)\hfill \\ \hfill & {\phantom{\langle }\times (\exp (-\beta {\stackrel{‒}{u}}_{ij}^r\left(\mid {\mathit{r}}_{ij}+{\mathit{l}}_2\mid \right))-1)\rangle }_{{\Omega }_1,{\Omega }_2},\hfill \end{array}$$ (8)

where the brackets 〈 〉_{Ω1; Ω2} represent the angular average. The $\stackrel{‒}{\mathbf{c}}$ and ρ matrices have the familiar PISM form, while ρ′ involves the molecular convolutions, such that

$$\begin{array}{cc}\hfill \stackrel{‒}{\mathbf{c}}& =\left(\begin{array}{cc}\hfill {\stackrel{‒}{c}}_{ij}^o\left(k\right)\hfill & \hfill {\stackrel{‒}{c}}_{ij}^r\left(k\right)\hfill \\ \hfill {\stackrel{‒}{c}}_{ij}^l\left(k\right)\hfill & \hfill {\stackrel{‒}{c}}_{ij}^b\left(k\right)\hfill \end{array}\right),\hfill \\ \hfill \rho & =\left(\begin{array}{cc}\hfill \rho \hfill & \hfill \rho \hfill \\ \hfill \rho \hfill & \hfill 0\hfill \end{array}\right)(\mathrm{if}i=j),\hfill \\ \hfill \rho & =\left(\begin{array}{cc}\hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill \end{array}\right)\text{otherwise},\hfill \\ \hfill \rho \prime & =\left(\begin{array}{cc}\hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \rho ∕2\hfill \end{array}\right)(\mathrm{if}i=j),\hfill \\ \hfill \rho \prime & =\left(\begin{array}{cc}\hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill \end{array}\right)\text{otherwise},\hfill \end{array}$$ (9)

where the ${\stackrel{‒}{c}}_{\mathit{ij}}\left(k\right)$ are the familiar Fourier–Hankel transforms,

$${\stackrel{‒}{c}}_{ij}\left(k\right)=\int {\stackrel{‒}{c}}_{ij}\left(r\right)\frac{\sin \left(kr\right)}{kr}\mathrm{d}\mathit{r},$$ (10)

ρ is the molecular number density, and the factor 1/2 in ρ′ is the topological symmetry number appropriate to diatomic systems. The equations to this point have been given for a pure diatomic fluid. The extension to a mixture is straightforward.

We consider a three component mixture, where the first component is the diatomic fluid, and the second and third components are simple, spherical solutes. This makes the solute–solute distribution functions equivalent to none functions in the diatomic fluid formalism, with the solvent–solute functions having only none and left terms. The resulting closure equations are

$$\begin{array}{cc}\hfill {\stackrel{‒}{c}}_{ij}^o\left(r\right)& =g_{ij}^o\left(r\right)-{\tau }_{ij}^o\left(r\right),\hfill \\ \hfill {\stackrel{‒}{c}}_{ij}^l\left(r\right)& =g_{ij}^o\left(r\right)(g_{ij}^l\left(r\right)-1)-{\tau }_{ij}^l\left(r\right)\hfill \end{array}$$ (11)

for the solvent–solute functions. The solute–solvent functions have the equivalent right form, while the solute–solute functions are the simple fluid form,

$${\stackrel{‒}{c}}_{ij}^o\left(r\right)=g_{ij}^o\left(r\right)-{\tau }_{ij}^o\left(r\right).$$ (12)

The resulting matrices, including the Coulomb potential renormalisation discussed immediately below, are written out in detail in the accompanying appendix. The equations here are written for general potential models of the site–site form. Introducing point charges requires more formal considerations [7].

We have previously shown that, for pure fluids, the Coulomb potential in a polar diatomic model system can be renormalised after cancellation in a straightforward manner. The chief result of our previous work [7] was that the total Coulomb potential can be formally constrained to only the g^b function in the closure equations above. This results from the well-known cancellations in the Legendre expansion of the full potential. Similarly here, the charge–charge terms will be confined to the g^b functions in the solvent–solvent terms, the g^r functions in the solvent–solute terms, and the g^o functions in the solute–solute terms, such that

$$\begin{array}{cc}\hfill g_{ij}^b\left(r\right)=& \frac{1}{8\pi }{\int }_{-1}^1{\int }_{-1}^1{\int }_0^{2\pi }\exp (-\beta U^c\left(\mid {\mathit{r}}_{ij}-{\mathit{l}}_1+{\mathit{l}}_2\mid \right)\hfill \\ \hfill & -\beta {\stackrel{‒}{u}}_{ij}^b\left(\mid {\mathit{r}}_{ij}-{\mathit{l}}_1+{\mathit{l}}_2\mid \right)-\beta {\stackrel{‒}{u}}_{ij}^l\left(\mid {\mathit{r}}_{ij}-{\mathit{l}}_1\mid \right)\hfill \\ \hfill & -\beta {\stackrel{‒}{u}}_{ij}^r\left(\mid {\mathit{r}}_{ij}+{\mathit{l}}_2\mid \right)+{\tau }_{ij}^b\left(r\right)+{\tau }_{ij}^l\left(r\right)\hfill \\ \hfill & +{\tau }_{ij}^r\left(r\right))d\cos {\theta }_{1}d\cos {\theta }_{2}d{\varphi }_{12}\hfill \end{array}$$ (13)

for the solvent–solvent

$$\begin{array}{cc}\hfill g_{ij}^l\left(r\right)=& \frac{1}{2}{\int }_{-1}^1\exp (-\beta U^c\left(\mid {\mathit{r}}_{ij}-{\mathit{l}}_1\mid \right)-\beta {\stackrel{‒}{u}}_{ij}^l\left(\mid {\mathit{r}}_{ij}-{\mathit{l}}_1\mid \right)\hfill \\ \hfill & +{\tau }_{ij}^l\left(r\right))d\cos {\theta }_1\hfill \end{array}$$ (14)

similarly for the solvent–solute terms, g^r terms and

$$g_{ij}^o\left(r\right)=\exp (-\beta U^c\left(r\right)-\beta {\stackrel{‒}{u}}_{ij}\left(r\right)+{\tau }_{ij}^o\left(r\right))$$ (15)

for the solute–solute terms. As previously, we use the error function method of Ng to resum the Coulomb potential, such that

$$\beta U^c\left(\mid {\mathit{r}}_{ij}-{\mathit{l}}_1+{\mathit{l}}_2\mid \right)=\sum _{ij}\frac{\beta q_i{q}_j(1-\mathrm{erf}\left(\alpha r\right))}{\mid {\mathit{r}}_{ij}-{\mathit{l}}_1+{\mathit{l}}_2\mid }$$ (16)

for the solvent, and similarly for the solvent–solute and solute–solute terms. This leads to one final matrix, defined in Fourier space as

$${\psi }_{\mathit{ij}}^b\left(k\right)=\frac{4\pi \beta q_i{q}_j\exp (-{(k∕\alpha )}^2){(1-[\sin \left(kl\right)∕kl])}^2}{k^2},$$ (17)

for the solvent–solvent terms, and

$$\begin{array}{cc}\hfill {\psi }_{\mathit{ij}}^l\left(k\right)& =\frac{4\pi \beta q_i{q}_j\exp (-{(k∕\alpha )}^2)(1-[\sin \left(kl\right)∕kl])}{k^2},\hfill \\ \hfill {\psi }_{\mathit{ij}}& =\frac{4\pi \beta q_i{q}_j\exp (-{(k∕\alpha )}^2)}{k^2}\hfill \end{array}$$ (18)

for the solute–solvent and solute–solute terms, respectively, and the solute–solvent ψ^r terms similar to the solvent–solute ψ^l terms. All other elements of the resulting ψ matrix are 0. Finally, the charge-renormalisation matrix ψ is included in the OZ formalism via the chain sum in Fourier space,

$$\chi =\stackrel{‒}{\mathbf{c}}-\Phi -\psi +(\stackrel{‒}{\mathbf{c}}-\Phi -\psi )\rho \prime \chi .$$ (19)

We investigate some basic predictions of these equations for a simplified two-site model of water below.

3. Results

As stated above, our goal here is to generate a basic model of aqueous mixtures using a simplified, two-site model of water. We use the SPC model as our starting point. The familiar three-site models of water share certain characteristics. The SPC model in particular is defined by placing the oxygen site at the center of a Lennard-Jones sphere. The hydrogen sites are then displaced from the oxygen center, with the HOH angle defined by the l_HH distance. The hydrogen sites do not carry a Lennard-Jones sphere. In order to generate a two-site model from these definitions, we keep the oxygen site at the center with σ_OO = 3.16Å, ∊/k_B = 78 K, q_O = −0.38e, and use one hydrogen-like site displaced by l_OH = 1 Å with q_H = +0.38e. The units of charge are the absolute value of the fundamental charge, e. This maintains the Lennard-Jones size and energy, and the fixed dipole moment and charge separation of the original model. We note that, as previously [7] we have no need to carry a Lennard-Jones sphere on the hydrogen-like site, since the theory is molecularly consistent by construction.

The basic fluid state features of the resulting model, as the pure solvent, are illustrated in Figures 1 and 2. In Figure 1, the radial distribution functions for T = 300 K and ρ_i = 0.03346 molecules Å^–3 are plotted. We note that the basic features are somewhat similar to the familiar three-site SPC results. In Figure 2, the dielectric constant is plotted as a function of temperature for the same density. As in the previous work [7]. we use the Kirkwood formula,

$$\begin{array}{cc}\hfill \frac{(∊-1)(2∊+1)}{9∊}& =g_{K}Y,\hfill \\ \hfill g_K& =1+\frac{4\pi {\rho }_i}{3}{\int }_0^{\infty }{h}_{\mathit{ij}}^{110}\left(r\right)r^2\mathrm{d}r,\hfill \\ \hfill Y& =\frac{4\pi {\mu }^2{\rho }_i}{6k_{\mathrm{B}}T},\hfill \end{array}$$ (20)

where the calculation of the $h_{\mathit{ij}}^{110}$ functions are the cos θ₁₂-weighted angular averages detailed previously [5,7]. We note that, subject to numerical error, the dielectric behaviour of the model is a quite satisfactory quantitative model of the high dielectric properties of water in the liquid state.

Figure 1.

The site–site radial distribution functions for the pure fluid two-site water model, at 300 K and ρ_i = 0.03346 molecules Å⁻³.

Figure 2.

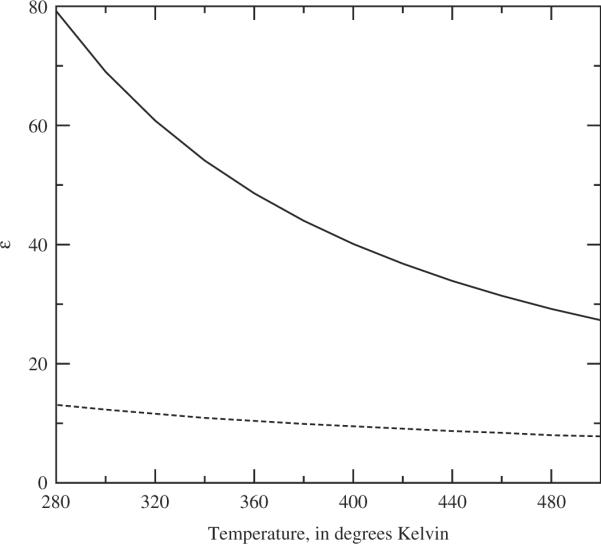
The predicted dielectric constant, ∊, of the pure two-site water model as a function of temperature at ρ_i = 0.03346 molecules Å⁻³. The solid line is the integral equation result, the dashed line is the ideal dipole gas result, ∊ = 1 + 3Y.

In order to establish basic solution properties for this model system, we examine here a three component mixture of the two-site water model with two distinct, simple fluid species. The two solute sites are apolar without charge but can be made to represent ions with charge and stoichiometric constraints. The model definitions are σ₁₁ = 2.94 Å, ∊₁₁/k_B = 13.052K, σ₂₂ = 3.671 Å, and ∊₂₂/k_B = 130.5 K. We use the standard Lorenz–Berthelot mixing rules [16] and keep the solute densities equivalent to each other, ρ₁ = ρ₂, throughout.

There are, in principle, many different measures of the solvation properties of the resulting system. Recent work by many groups has focused on the Kirkwood G integrals, defined for each site–site pair as

$$G_{\mathit{ij}}=\int h_{\mathit{ij}}\left(r\right)\mathrm{d}\mathit{r}.$$ (21)

We recall that these integrals are fundamental to the Kirkwood–Buff theory of solutions [17] and that the different algebraic combinations of the G_ij's are used as measures of the thermodynamic properties of the system. As such, we use the G integrals here as proxies for the general properties of the model system. We note that thermodynamic consistency requires that the different site–site integrals all be equivalent. That is, G_HH = G_OH = G_OO. In our previous work [5,7], we found that this condition was reasonably satisfied in the present theory for most phase points investigated. Here, we find a similar result, though the numerical deviations between the site–site pairs increases as the temperature is lowered. Overall, the deviation between site–site pairs differs in degree, but not in kind, meaning that the trends are identical for all site pairs measured. As a result, we use G_OH as our default calculation of the solvent–solvent G's in this work, and average over the G_Oj and G_Hj terms for the solute–solvent pairs. We are investigating different formal and numerical methods for dealing with this deviation in ongoing work.

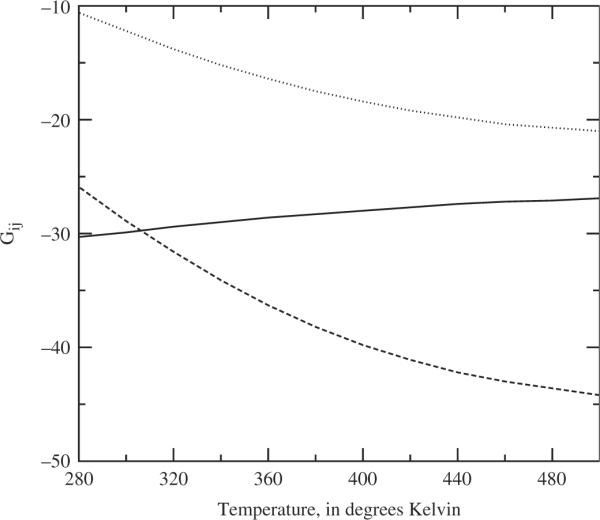
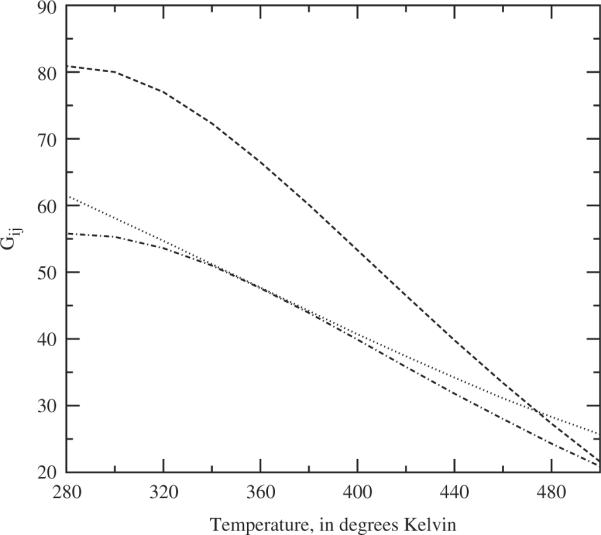
The Kirkwood G results for the apolar solutes are summarised in Figures 3 and 4 as a function of temperature. The G's indicate solvation by the fact that the solute–solute terms remain positive throughout. The most interesting results are for the solute–solvent G_ij results. There are at least three implications. First, it is clear that the presumed onset of a phase change is clearly reflected in the trends plotted. Second, recalling that it is the combinations of the G_ij factors which lead to measures of the phase behaviour of the system, it is clear that, in this case, the G_ij integrals should be convenient structural order parameters for studying the phase behaviour of the system [17]. Finally, there is a distinct difference in the self terms, and difference in magnitude in the solute–solvent terms, between the smaller solute 1 and larger solute 2. That these size differences are clearly measured indicates that, at least for apolar solutes, this simplified water model might prove useful in studying various solvation theories, including simple molecular recognition and general mechanisms of solvation.

Figure 3.

The predicted solute–solvent Kirkwood G_ij values for the apolar solutes, as a function of temperature, at solvent density ρ_i = 0.03346 molecules Å⁻³ and solute densities ρ₁ = ρ₂ = 0.0006 Atoms Å⁻³. The solid line is the solvent–solvent G_ij, the dotted line is the solute–solvent G_ij for solute 1, and the dashed line is the solute–solvent G_ij for solute 2.

Figure 4.

The predicted solute–solute Kirkwood G_ij values for the apolar solutes, as a function of temperature, at solvent density ρ_i = 0.03346 molecules;⁻³ and solute densities ρ₁ = ρ₂ = 0.0006 Atoms Å⁻³. The dotted line is the self G_ij for solute 1, the dashed line is the self G_ij for solute 2, and the dot-dashed line is the cross-term G_ij between solute 1 and solute 2.

As with the related hard spheres results of Levesque et al. [10] we found that solutes with full ionic charges, q = 1.0e, are insoluble in the liquid regime investigated here. Thus we would have only a model of ionic solutions for the super critical regime. Therefore, we use reduced charges at more reasonable temperatures for the next systems investigated here. This limits the general utility of the two-site water model, but the specific goals here are unaffected. In Figure 5, we show the predicted dielectric constant as a function of ionic density at T = 500 K and T = 350 K for the ionic charges q₊ = 0.5e and solvent density of ρ_i = 0.03346 molecules Å⁻³. Though we investigated several different solute size combinations, following Levesque et al. [10] the dielectric results plotted here are for the particular solute system with σ₁₁ = σ₂₂ = 4.671 Å and ∊₁₁/k_B = ∊₂₂/k_B = 130.5K.

Figure 5.

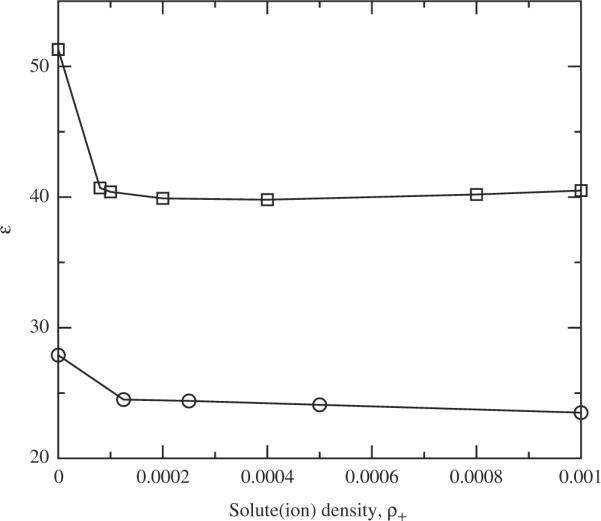
The predicted dielectric constant for the ionic mixtures as a function of the positive ion density, ρ₁. The line with square symbols is at 350K, the line with circle symbols is at 500 K.

Of the various possible routes to measure the dielectric constant [10,18], we use here the familiar site–site result [2,4], $∊=1+3Y+{\rho }_i^2{\Sigma }_{\mathit{ij}}{h}_{\mathit{ij}}^{\left(2\right)}$, where the $h_{\mathit{ij}}^{\left(2\right)}$'s are the charge-weighted solvent–solvent second moments,

$$h_{\mathit{ij}}^{\left(2\right)}=-\frac{q_i{q}_j{\left(4\pi \right)}^2}{6}{\int }_0^{\infty }{r}^4{h}_{\mathit{ij}}\left(r\right)\mathrm{d}r.$$ (22)

In the very low salt concentrations, below ρ₁ ≈ 1 × 10⁻³, for this set of charges, the numerical results for the dielectric constant were found to be numerically indeterminate. By this we mean that, though the distribution functions were generally numerically stable, the various routes to measure the dielectric constant were such that none of them could be reliably judged to actually measure the functional behaviour of ∊ as the salt concentration goes to infinite dilution. This leads to the discontinuities in the plot between the pure solvent and low concentration salt results. Given the history of bridge function-like corrections required in this concentration regime (below tenth molar) this is not surprising. By contrast, the numerical behaviour of the higher salt concentration solutions were generally found to be robust in comparison to the hard spheres results [10]. However, for our purposes here, Figure 5 confirms that the theory as constructed appears to be fundamentally sound, in principle, and in reasonable qualitative agreement with the results for the dielectric constant for similar systems using the molecular OZ methods [10]. The utility of the two-site `water' for general solutions is more restricted.

Overall, this result points to the general nature of the problem. Since direct dipole–dipole screening does not occur, and so long as the approximation for the charge–charge potential model is self-consistently treated, we can reliably measure the resulting system, including the dielectric constant, and related properties. However, following the work of Levesque et al. [10], it seems clear that certain chemically and biologically interesting regimes of low concentration salt in room temperature liquids are non-trivially dependent on higher order terms at any given level of approximation.

4. Conclusions

In this paper, we have generated a simplified, two-site model of water. We used our recent site–site molecular integral equation theory to briefly investigate the resulting bulk fluid and solvation properties of the model, for simple apolar and ionic solute species. Overall, the results indicate that the model itself captures reasonably well the bulk dielectric and solvation properties of liquid state water for apolar solutes and the bulk fluid. For ionic solutes, the results were reasonably encouraging in the dense salt regime, while the low salt concentration results were inconclusive overall. This last result is, however, in line with those predicted by Levesque et al. [10], in that the basic model system is not particularly good at solvating arbitrary ionic constituents.

This result leaves us with several areas to study in the future. In particular, we will further investigate, in comparison to simulation results for the same model system, the particular nature of the failure to reliably predict the dielectric constant for the system in the low salt regime. It is possible that the problem is physical and that a phase transition intervenes. Given the particular results here, we suspect that, while the overall theory is properly constructed, there may be particular formal limiting cases which may be used to constrain the numerical behaviour of the system.

Appendix 1 Details of the matrix constructions

Here we write, in full dimensionality, the matrices involved in solving the matrix equations

$$\begin{array}{cc}\hfill \chi & =\stackrel{‒}{\mathbf{c}}-\Phi -\psi +(\stackrel{‒}{\mathbf{c}}-\Phi -\psi )\rho \prime \chi ,\hfill \\ \hfill \mathbf{H}& =\chi +\mathbf{S}+(\chi +\mathbf{S})\rho \mathbf{H},\hfill \\ \hfill \tau & =\mathbf{H}-\mathbf{S}-\stackrel{‒}{\mathbf{c}}\hfill \end{array}$$ (23)

for a three component mixture, where the first component, the solvent, is a polar diatomic molecule, and the second and third components are spherical ionic fluids. We use l as the bond length for the molecular solvent, subscript i to denote the first, arbitrarily chosen site of molecule 1 or 2, and subscript j to denote the second site of molecule 1 or 2. We use subscript 1 and subscript 2 to denote solute 1 and solute 2, respectively. The number densities are then ρ_i = ρ_j = molecules Å⁻³ for the solvent density, and ρ₁ and ρ₂ for the atomic solute densities, though for the calculations here ρ₁ = ρ₂ throughout.

We have first the 6 × 6 matrices whose elements are constant throughout,

$$\begin{array}{cc}\hfill \rho & =\left(\begin{array}{cccccc}\hfill {\rho }_i\hfill & \hfill {\rho }_i\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill {\rho }_i\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill {\rho }_j\hfill & \hfill {\rho }_j\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill {\rho }_j\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\rho }_1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill {\rho }_2\hfill \end{array}\right),\hfill \\ \hfill \rho \prime & =\left(\begin{array}{cccccc}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \frac{{\rho }_i}{2}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \frac{{\rho }_j}{2}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right),\hfill \\ \hfill \mathbf{S}& =\left(\begin{array}{cccccc}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \frac{\sin \left(kl\right)}{kl{\rho }_j}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \frac{\sin \left(kl\right)}{kl{\rho }_i}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right).\hfill \end{array}$$ (24)

The variable functions, whose individual elements are defined by the closure equations in Section 2, are

$$\begin{array}{cc}\hfill \stackrel{‒}{\mathbf{c}}& =\left(\begin{array}{cccccc}\hfill {\stackrel{‒}{c}}_{ii}^0\left(k\right)\hfill & \hfill {\stackrel{‒}{c}}_{ii}^r\left(k\right)\hfill & \hfill {\stackrel{‒}{c}}_{ij}^0\left(k\right)\hfill & \hfill {\stackrel{‒}{c}}_{ij}^r\left(k\right)\hfill & \hfill {\stackrel{‒}{c}}_{i1}^0\left(k\right)\hfill & \hfill {\stackrel{‒}{c}}_{i2}^0\left(k\right)\hfill \\ \hfill {\stackrel{‒}{c}}_{ii}^l\left(k\right)\hfill & \hfill {\stackrel{‒}{c}}_{ii}^b\left(k\right)\hfill & \hfill {\stackrel{‒}{c}}_{ij}^l\left(k\right)\hfill & \hfill {\stackrel{‒}{c}}_{ij}^b\left(k\right)\hfill & \hfill {\stackrel{‒}{c}}_{i1}^l\left(k\right)\hfill & \hfill {\stackrel{‒}{c}}_{i2}^l\left(k\right)\hfill \\ \hfill {\stackrel{‒}{c}}_{ji}^0\left(k\right)\hfill & \hfill {\stackrel{‒}{c}}_{ji}^r\left(k\right)\hfill & \hfill {\stackrel{‒}{c}}_{jj}^0\left(k\right)\hfill & \hfill {\stackrel{‒}{c}}_{jj}^r\left(k\right)\hfill & \hfill {\stackrel{‒}{c}}_{j1}^0\left(k\right)\hfill & \hfill {\stackrel{‒}{c}}_{j2}^0\left(k\right)\hfill \\ \hfill {\stackrel{‒}{c}}_{ji}^l\left(k\right)\hfill & \hfill {\stackrel{‒}{c}}_{ji}^b\left(k\right)\hfill & \hfill {\stackrel{‒}{c}}_{jj}^l\left(k\right)\hfill & \hfill {\stackrel{‒}{c}}_{jj}^b\left(k\right)\hfill & \hfill {\stackrel{‒}{c}}_{j1}^l\left(k\right)\hfill & \hfill {\stackrel{‒}{c}}_{j2}^l\left(k\right)\hfill \\ \hfill {\stackrel{‒}{c}}_{1i}^0\left(k\right)\hfill & \hfill {\stackrel{‒}{c}}_{1i}^r\left(k\right)\hfill & \hfill {\stackrel{‒}{c}}_{1j}^0\left(k\right)\hfill & \hfill {\stackrel{‒}{c}}_{1j}^r\left(k\right)\hfill & \hfill {\stackrel{‒}{c}}_{11}^0\left(k\right)\hfill & \hfill {\stackrel{‒}{c}}_{12}^0\left(k\right)\hfill \\ \hfill {\stackrel{‒}{c}}_{2i}^0\left(k\right)\hfill & \hfill {\stackrel{‒}{c}}_{2i}^r\left(k\right)\hfill & \hfill {\stackrel{‒}{c}}_{2j}^0\left(k\right)\hfill & \hfill {\stackrel{‒}{c}}_{2j}^r\left(k\right)\hfill & \hfill {\stackrel{‒}{c}}_{21}^0\left(k\right)\hfill & \hfill {\stackrel{‒}{c}}_{22}^0\left(k\right)\hfill \end{array}\right),\hfill \\ \hfill \Phi & =\left(\begin{array}{cccccc}\hfill 0\hfill & \hfill {\varphi }_{ii}^r\left(k\right)\hfill & \hfill 0\hfill & \hfill {\varphi }_{ij}^r\left(k\right)\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill {\varphi }_{ii}^l\left(k\right)\hfill & \hfill {\varphi }_{ii}^b\left(k\right)\hfill & \hfill {\varphi }_{ij}^l\left(k\right)\hfill & \hfill {\varphi }_{ij}^b\left(k\right)\hfill & \hfill {\varphi }_{i1}^l\left(k\right)\hfill & \hfill {\varphi }_{i2}^l\left(k\right)\hfill \\ \hfill 0\hfill & \hfill {\varphi }_{ji}^r\left(k\right)\hfill & \hfill 0\hfill & \hfill {\varphi }_{jj}^r\left(k\right)\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill {\varphi }_{ji}^l\left(k\right)\hfill & \hfill {\varphi }_{ji}^b\left(k\right)\hfill & \hfill {\varphi }_{jj}^l\left(k\right)\hfill & \hfill {\varphi }_{jj}^b\left(k\right)\hfill & \hfill {\varphi }_{j1}^l\left(k\right)\hfill & \hfill {\varphi }_{j2}^l\left(k\right)\hfill \\ \hfill 0\hfill & \hfill {\varphi }_{1i}^r\left(k\right)\hfill & \hfill 0\hfill & \hfill {\varphi }_{1j}^r\left(k\right)\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\varphi }_{2i}^r\left(k\right)\hfill & \hfill 0\hfill & \hfill {\varphi }_{2j}^r\left(k\right)\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right),\hfill \\ \hfill \psi & =\left(\begin{array}{cccccc}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\psi }_{ii}^b\left(k\right)\hfill & \hfill 0\hfill & \hfill {\psi }_{ij}^b\left(k\right)\hfill & \hfill {\psi }_{i1}^l\left(k\right)\hfill & \hfill {\psi }_{i2}^l\left(k\right)\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\psi }_{ji}^b\left(k\right)\hfill & \hfill 0\hfill & \hfill {\psi }_{jj}^b\left(k\right)\hfill & \hfill {\psi }_{j1}^l\left(k\right)\hfill & \hfill {\psi }_{j2}^l\left(k\right)\hfill \\ \hfill 0\hfill & \hfill {\psi }_{1i}^r\left(k\right)\hfill & \hfill 0\hfill & \hfill {\psi }_{1j}^r\left(k\right)\hfill & \hfill {\psi }_{11}^o\left(k\right)\hfill & \hfill {\psi }_{12}^o\left(k\right)\hfill \\ \hfill 0\hfill & \hfill {\psi }_{2i}^r\left(k\right)\hfill & \hfill 0\hfill & \hfill {\psi }_{2j}^r\left(k\right)\hfill & \hfill {\psi }_{21}^o\left(k\right)\hfill & \hfill {\psi }_{22}^o\left(k\right)\hfill \end{array}\right).\hfill \end{array}$$ (25)