Dependence of the Roll Angular Vestibuloocular Reflex (aVOR) on Gravity

Abstract

Little is known about the dependence of the roll angular vestibuloocular reflex (aVOR) on gravity or its gravity-dependent adaptive properties. To study gravity-dependent characteristics of the roll aVOR, monkeys were oscillated about a naso-occipital axis in darkness while upright or tilted. Roll aVOR gains were largest in the upright position and decreased by 7–15% as animals were tilted from the upright. Thus the unadapted roll aVOR gain has substantial gravitational dependence. Roll gains were also decreased or increased by 0.25 Hz, in- or out-of-phase rotation of the head and the visual surround while animals were prone, supine, upright, or in side-down positions. Gain changes, determined as a function of head tilt, were fit with a sinusoid; the amplitudes represented the amount of the gravity-dependent gain change, and the bias, the gravity-independent gain change. Gravity-dependent gain changes were absent or substantially smaller in roll (≈5%) than in yaw (25%) or pitch (17%), whereas gravity-independent gain changes were similar for roll, pitch, and yaw (≈20%). Thus the high-frequency roll aVOR gain has an inherent dependence on head orientation re gravity in the unadapted state, which is different from the yaw/pitch aVORs. This inherent gravitational dependence may explain why the adaptive circuits are not active when the head is tilted re gravity during roll aVOR adaptation. These behavioral differences support the idea that there is a fundamental difference in the central organization of canal-otolith convergence of the roll and yaw/pitch aVORs.

INTRODUCTION

The angular vestibuloocular reflex (aVOR) stabilizes images on the retina by inducing compensatory counter-rotation of the eyes when the head is rotated. To stabilize the visual environment when the axis of eye movement is aligned with that of head movement, the gain (eye velocity)/(head velocity) should be close to unity. In darkness, the gains of the horizontal (yaw) and vertical (pitch) aVOR's range to ∼0.9 in monkeys; vision augments the yaw and pitch aVOR gains to unity for frequencies ≤1 Hz (Fender and Nye 1961; Wyatt and Pola 1983). The gain of the torsional (roll) aVOR in darkness, however, is only ∼0.6, which represents an important difference among the yaw, pitch, and roll components (Crawford and Vilis 1991; Henn et al. 1992). Furthermore, visual enhancement of the roll aVOR is limited. Although substantial roll optokinetic nystagmus (OKN) velocities can be produced in the monkey when animals were supine and/or prone through activation of velocity storage (Raphan et al. 1992), there is no roll pursuit, and the frequency response of visually induced torsional eye movements is low (Misslisch et al. 1996; Raphan and Cohen 1988). Theoretically, therefore adequate compensation cannot be accomplished for torsional head movements by the aVOR, which are generally in the mid to high-frequency band.

Vision plays a critical role in adaptive modification of the yaw and pitch aVORs. If the eyes do not counter-rotate appropriately in light, continuous image slip is produced on the retina, and aVOR gains are altered (Cohen et al. 1992b; Gonshor and Melvill Jones 1973, 1976; Ito and Miyashita 1975; Lisberger et al. 1983; Melvill Jones and Davies 1976; Miles and Fuller 1974; Yakushin et al. 2000b). Horizontal and vertical aVOR components can be adaptively modified by introducing visual-vestibular mismatch with magnifying or minifying goggles (Bello et al. 1991; Cohen et al. 1992b; Miles and Eighmy 1980; Miles and Fuller 1974; Partsalis et al. 1995) with reversing prisms (Berthoz et al. 1981; Gonshor and Melvill Jones 1973, 1976; Haddad et al. 1980; Melvill Jones and Davies 1976; Miles and Eighmy 1980) or by rotating the visual surround in-phase or out-of-phase with the subject (Collewijn and Grootendorst 1978; Hirata and Highstein 2001; Miles and Eighmy 1980; Yakushin et al. 2000b). In these altered visual conditions, the normal counter-rotation of the eye relative to the head is not in consonance with the visual surround motion and the gain of the horizontal or vertical aVOR is increased or decreased.

The exact visual signals that effect adaptation are, however, still not known. There is general agreement that retinal slip is a major driver for aVOR gain adaptation, but visual fixation of a single or imaginary target (Melvill Jones et al. 1984) or fixation of a visual afterimage (Yasui and Young 1975) can also induce gain changes in the horizontal or vertical aVOR. Much less is known of the response of the roll aVOR to visual-vestibular mismatch. Because there is no torsional pursuit, only full-field retinal slip can be used to drive adaptation of torsional gain (Cheung and Howard 1991). Roll aVOR gain adaptation has been produced in squirrel monkeys (Bello et al. 1991) and in humans (Berthoz et al. 1981; Leigh et al. 1989). No essential differences were found between the adaptive properties of the roll aVOR and those of the horizontal and vertical aVOR except when gain changes were simultaneously induced in roll and pitch. Under these circumstances, the gain changes in roll were almost twice as small as those in pitch (Takagi et al. 2001). Thus the roll aVOR gain has normal and adaptive properties that are substantially different from those of yaw and pitch. Whether the roll aVOR also has gravity dependence that impacts its adaptive properties is not known.

In previous experiments, the roll aVOR gain has only been tested in the position of adaptation, and the frequencies that are effective in altering roll eye velocity have not been explored. Pitch aVOR gains were larger in the upright at low frequencies (<0.15 Hz), when the amplitude of oscillation exceeded 50° (Brettler et al. 2000; Tomko et al. 1987, 1988). At higher frequencies of oscillation (0.25 Hz), however, there were no changes in gain for tilts relative to gravity (Tomko et al. 1987). Findings were similar for yaw aVOR gains. Cats did not have significant changes in gain in different head orientations although the phase was affected at low frequencies (Brettler et al. 2000; Quinn et al. 1998).

The purpose of this research was to study the roll aVOR gain as a function of head orientation relative to gravity. We also wished to test whether there was a significant effect of the position of adaptation as well as the range of frequencies that are effective in altering roll eye velocity. Based on the inherent differences among the yaw, pitch, and the roll aVORs, we postulated that the gravity-dependent adaptive properties of the roll aVOR would be substantially different from that of the horizontal and vertical aVORs in the range of frequencies that produced adaptation.

METHODS

Four cynomolgus monkeys (Macaca fascicularis, M0102, M0091, M17115, and M17088) and one rhesus monkey (M. mulatta, M98064) were utilized in this study. The experiments conformed to the Guide for the Care and Use of Laboratory Animals and were approved by the Institutional Animal Care and Use Committee. Surgical procedures were performed under anesthesia and in sterile conditions. Procedures were performed in two stages. First, a head mount was implanted on the skull to provide painless head fixation in stereotaxic coordinates during testing (Sirota et al. 1988; Yakushin et al. 2000b). At a second surgery, two three-turn coils were implanted on the left eye. One coil measured the horizontal and vertical components of eye position (Judge et al. 1980; Robinson 1963). Another coil, placed approximately orthogonal to the frontal coil (Cohen et al. 1992a), was used to measure the torsional component of eye position.

Recording of eye movements with search coils

During testing, the monkey's head was fixed to a plastic frame, which held two sets of field coils that generated orthogonal oscillating magnetic fields at the same frequency (NeuroData Instruments). Eye movement were measured in head coordinates, composed of the naso-occipital (x axis, positive forward), the interaural (y axis, positive toward left ear), and the dorso-ventral (z axis, positive upward) axes. The axes of the field coils were along the y (pitch) and z (yaw) axes of the head, establishing a head-fixed reference frame for measuring the orientation of the frontal and top search coils. Monkeys were positioned so that the eye with the search coils was at the center of the magnetic fields. To calibrate eye movement, the animals were rotated in light at 30°/s about a spatial vertical axis while upright for yaw, left-side down for pitch, and prone for roll. It was assumed that the horizontal and vertical visual-vestibular gains were close to unity when upright or side-down (Raphan et al. 1979; Robinson 1963) and that torsional gains were 0.6 for rotation around a naso-occipital axis (Crawford and Vilis 1991; Henn et al. 1992; Yakushin et al. 1995).

Data processing

Voltages related to eye position, the velocity of chair oscillation, and the position of the tilt axes were recorded with amplifiers having a band-pass of DC to 40 Hz. Voltages were digitized at 1 kHz/channel with 16-bit resolution. Voltages related to eye position were digitally differentiated by finding the slope of the least squares linear fit to 25 data points. This corresponds to a filter, which has a 3-dB cutoff >40 Hz, the cutoff frequency of the filters used for data acquisition. Saccades were eliminated using a maximum likelihood ratio criterion (Singh et al. 1981). Accuracy of saccade detection was visually verified and inaccurately-detected saccades (<5%) were manually corrected.

Experimental protocol

The primate chair was positioned in a four-axis vestibular stimulator surrounded by an optokinetic drum. Each axis went through the center of rotation of the head. The stimulator has been described in detail in previous publications (Yakushin et al. 1995, 2000a). Briefly, the optokinetic drum had a diameter of 91 cm and contained vertical 10° black and white stripes. The axes of rotation of the animals and optokinetic drum were collinear, and when the optokinetic drum rotated around the animal in light, it produced full-field visual stimulation.

The roll aVOR was tested by oscillating animals about their naso-ocipital (x) axes at 0.5 Hz (60°/s) for 10 cycles either upright or tilted in 10° increments ≤90° in four planes: forward-backward (Fig. 1), left-right side down (LSD-RSD), left anterior-right posterior canal plane (LA-RP), and right anterior-left posterior canal planes (RA-LP). Desaccaded eye velocities and stimulus velocity were fit with a cosine function at the stimulus frequency to compute torsional gains and phases. Preadapted gains obtained in each head orientation were averaged, and three-dimensional (3-D) gain surfaces were constructed using a spline interpolation (Yakushin et al. 2005b). Each test started in the upright position, and the order of head tilt LSD versus RSD, prone versus supine, etc., was chosen randomly.

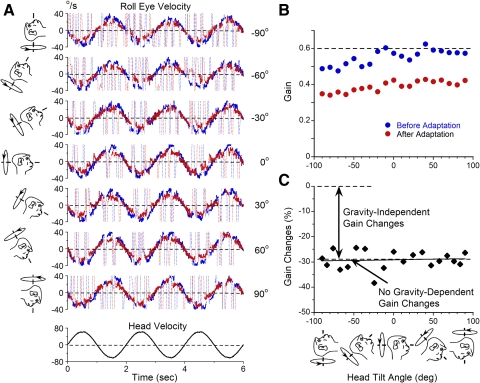
Fig. 1.

A: roll eye velocities evoked by sinusoidal oscillation of animal M0091 about naso-occipital axis while upright or tilted forward and backward before (blue traces) and after (red traces) torsional angular vestibuloocular reflex (aVOR) gain was decreased in the prone position. Slow phase eye velocities are shown by solid lines while velocities during saccades are shown as thin dashed lines. Insets: head orientation relative to gravity in which corresponding traces were obtained. Numbers on the right represent the angle between the axis of oscillation and spatial horizontal where positive values – tilt forward. Positive eye velocities represent clockwise rotation relative to the subject. B and C: torsional aVOR gains (B) and gain changes (C) plotted as a function of head tilt. Note: no gravity-dependent gain changes were produced in this experiment.

To induce adaptation of the roll aVOR, it was first necessary to determine the frequencies and velocities of oscillation of the visual surround at which there was significant suppression or enhancement of the torsional aVOR gain. An animal was rotated in- and out-of-phase with the full-field visual surround at various frequencies with a fixed stimulus velocity and at various velocities with a fixed frequency. The animal was face-down in a prone position during these tests. Similar oscillation was also given in yaw and pitch with the animal upright to provide a basis for comparison. Perfect compensation for in-phase rotation would have a gain of zero, while the ideal gain for the out-of-phase rotation would be 2.0.

The gain of the roll aVOR was decreased or increased by sinusoidal in- or out-of-phase rotation of the animal and visual surround about the animal's x axis for 4 h. In some experiments, the aVOR gain was decreased by rotating the animal and OKN drum in light in the same or in opposite directions with 20-s steps of velocity of 5–60°/s (Yakushin et al. 2000a). aVOR gains were adapted with animals upright or tilted 90° LSD, RSD, prone, or supine. The persistence and rate of loss of the effects of torsional aVOR gain adaptation were monitored in some animals for several days after adaptation. Based on these and earlier results (Yakushin et al. 2003a,b), at least a week elapsed between adaptation experiments to allow effects of gravity-dependent adaptation to dissipate.

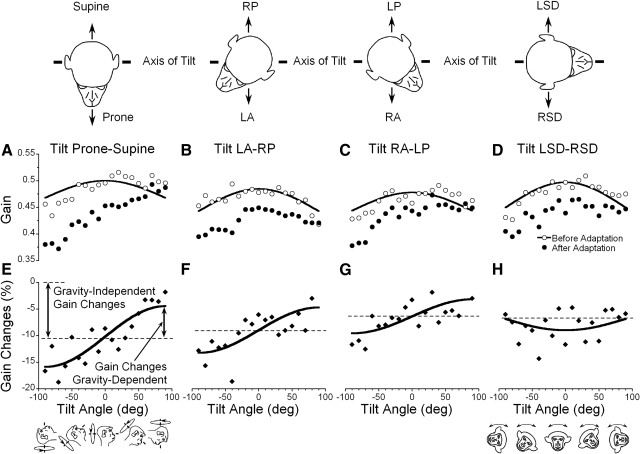
We previously demonstrated that adaptation of the yaw and pitch aVOR gain is composed of gravity-dependent and -independent components. The gravity-dependent component is maximal in the position of gain adaptation and decreases along a cosine function as the head orientation deviated from the position of adaptation. Gains, obtained before and after adaptation, were computed (Fig. 1B), and percent gain changes relative to preadapted values were determined at each head orientation (C). Changes were plotted as a function of head orientation for each plane and fit with sinusoidal function and bias

$$y=A\ast \cos \left(x+B\right)+C$$ (1)

to determine the gravity-dependent (Fig. 1A) and gravity-independent gain changes (Figs. 1C and 2E). Our previous experiments on yaw and pitch aVOR gain adaptation indicate that the spatial phase B, or the head orientation in which maximal gain changes were observed, is close to the position of adaptation (Yakushin et al. 2005a,b). Torsional aVOR gains were smaller than yaw or pitch gains and similar fluctuation in the gain values had a larger effect on spatial phase B (Fig. 2). Because a major purpose of this study was to determine the amount of gravity-dependent and -independent gain changes of the torsional aVOR and compare them to those of yaw and pitch components, it was assumed that the peak gain changes occurred in the position of adaptation. Therefore the spatial phase B was 90° for adaptation in prone and RSD and −90° for adaptation in supine and LSD. Data on yaw and pitch aVOR gain adaptation in the same head orientations in the same animals were processed based on the assumption that B is an angle corresponding to the position of adaptation. Data on gravity-dependent adaptation of the yaw aVOR components in M0102 and M17115 utilized in this study were previously reported (Yakushin et al. 2005b).

Fig. 2.

A–D: torsional aVOR gains obtained before (○) and after (●) decrease in supine (nose up) position in animal M0102. E–H: gain changes expressed in percent and plotted as a function of the head orientation in four tested planes. Gain changes were fitted with a cosine function (see text for details). Changes in bias were significant in every instance (E–H), indicating changes in the gravity-independent component. Changes in the gravity-dependent component were not significant. Insets: head orientation to the axis of tilt utilized for 4 planes of head tilt.

Statistical analysis

Statistical significance of sinusoidal fits to the data was determined using a F-statistic as follows: The mean square error obtained for a constant fit to the data and the mean square error of a sinusoidal fit to the data were determined. The ratio of these two mean squared errors was used as a F-statistic, and the F-test was used to determine whether the ratio exceeded a critical value (P < 0.05) and therefore that the sinusoidal fit to the data was significant. Significant gravity-dependent gain changes relative to a constant (F-statistic, P < 0.05) were determined, as described in the preceding text and in Yakushin et al. (1995). If the sinusoidal fit was not significant, i.e., there was no gravity-dependent variation, then a t-test was performed on the two data sets to determine whether the gravity-independent gain changes were significantly different from zero.

To minimize individual variation, the data obtained in three animals were averaged for each plane and a 3D surfaces were constructed using a spline-interpolation for the missing data points (Sandwell 1987) (see Fig. 6). Depending on the type of the experiment, standard t-test and ANOVA were used to analyze pairs or sets of data, respectively.

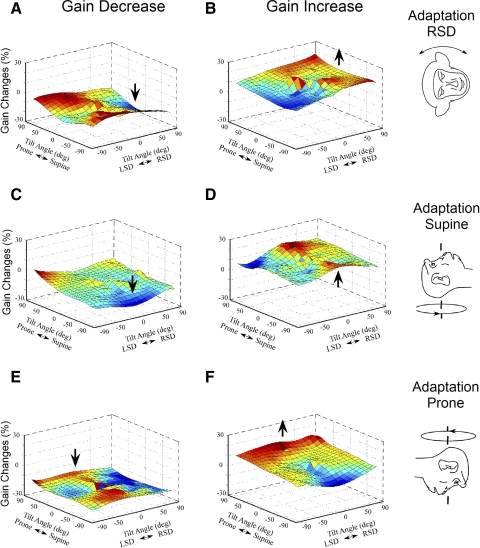
Fig. 6.

Three-dimensional surface of torsional aVOR gain changes obtained after the gain was decreased (A, C, and E) or increased (B, D, and F) in RSD (A and B), supine (C and D), and prone (E and F) head orientations. Maximal values are coded as a gradient of the red color, while minimal values are coded as a gradient of blue color.

RESULTS

Dependence of unadapted torsional aVOR gain on head orientation re gravity

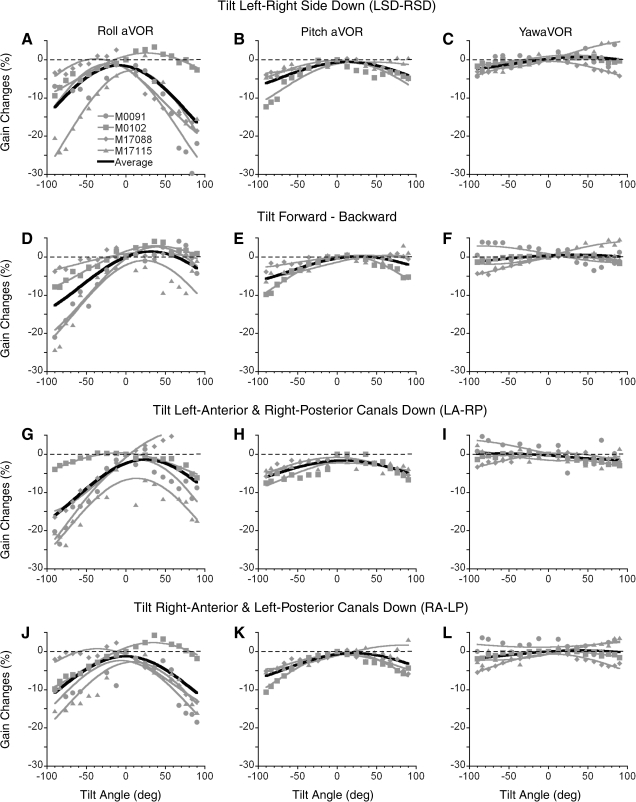
Roll aVOR gains were maximal when the head was close to the upright and gradually decreased as head was tilted in either direction (○, Fig. 2, A–D, M0102). There was variation between animals, but in every animal, the gains were maximal in the upright position, and decreased as animals were tilted in any direction from the upright. The changes were expressed in percent relative to the aVOR gain in the upright position to determine the extent of variation. Gain variations for each plane of tilt were fit with Eq. 1 to determine the amplitude of variation (A) based on data obtained in the four test planes. In each animal, roll gains decreased significantly as a function of head tilt away from the upright position (Fig. 3 A, D, G, and J, gray symbols and gray curves; F-statistic, P < 0.05). The average changes in gain were about the same when animals were tilted LSD-RSD (Fig. 3A black curve), prone-supine (Fig. 3D, black curve), and in two intermediate planes (Fig. 3, G and J, black curves). The percent changes in gain were the same for individual animals regardless of the direction of head tilt (ANOVA, P = 0.523, M0091; P = 0.272, M17115; P = 0.153, M0102; P = 0.106, M17088). Therefore the data were averaged for all directions of tilt. Two of the four tested animal had variations of the torsional aVOR gains of ≈14% (14.4 ± 3.2%, M0091; 13.7 ± 4.2%, M17115), whereas two other animal had smaller but still significant variations (8.2 ± 1.8%, M17088 and 7.2 ± 1.1%, M0102). Thus roll aVOR gains depended on head orientation relative to gravity, with changes in gain varying ≤14% in these four typical animals. Animals M0091 and M17115 were naïve before their roll aVOR gains were tested, while animals M0102 and M17088 had been utilized in experiments for horizontal and vertical aVOR gain adaptation for ∼2 yr before their roll aVORs were tested. All four animals were studied for roll aVOR gain adaptation for more than a year, and there was no apparent learning on the variation in the roll gains re gravity.

Fig. 3.

Change in gains of the torsional (A, D, G, and J), pitch (B, E, H, and K), and yaw (C, F, I, and L) aVOR of the four animals tested in different head orientations in left-right side down (LSD-RSD, A–C) and forward-backward (D–F), and in the left anterior-right posterior canal (LA-RP, G–I), and right anterior-left posterior canal planes (RA-LP, J–L). Individual values for each of the animals in each position are shown by the gray symbols, and the sinusoidal fits to the average values across all animals are shown by the heavy black line.

The spatial distribution of the nonadapted pitch (vertical) aVOR gains were determined in three of the four animals (1 was unavailable for testing) to establish whether there was a similar dependence of the pitch aVOR on gravity. Gain changes in pitch varied by 7.1 ± 1.4% for tilts in all four tested planes in one animal (M0102, F-statistic, P < 0.05) and by 3.7 ± 1.2% (P < 0.05) in two of the four planes in a second monkey (M17088), but did not vary in the other two planes (P > 0.05). Gain changes were not significantly altered by head position relative to gravity in the third animal (M17115). On average there was some modulation of the pitch aVOR in each plane of head tilt (Fig. 3, B, E, H, and K, black curves). Thus on average there was a weak tendency for the pitch aVOR to have gravity dependence in some animals, although it was considerably less than the dependence on gravity of the torsional aVOR, which was present in all animals.

Yaw gain changes for tilts in four tested planes were 1.7 ± 0.3% in M0102, 3.4 ± 0.6% in M17088 and M17115, and were not significant in the fourth animal, M0091. When the changes in the yaw aVOR gains of the four tested animal were averaged, they were negligible for each plane of tilt (Fig. 3, C–L, black curves). Thus dependence of the aVOR in the unadapted state on gravity was greatest in roll, less in pitch, and there was little or no dependence on gravity in yaw.

Determining optimal parameters for roll aVOR gain adaptation

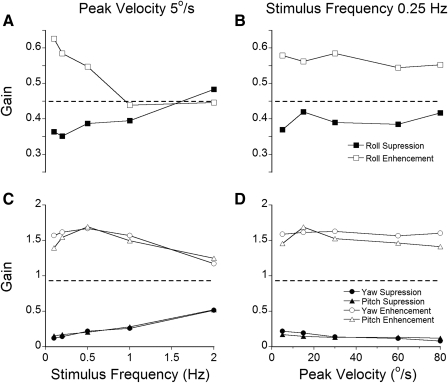
Peak roll aVOR gains during full field visual suppression and enhancement in monkey M0102 were 0.35 and ≈0.6, respectively at a velocity of 5°/s at the lowest frequencies of oscillation (0.1–0.25 Hz; Fig. 4A). For frequencies >0.25 Hz, roll gains fell toward the average gain of the roll aVOR in darkness (≈0.45, horizontal dashed line). Effects of increases in gain (□) were larger than for gain decreases (■). Thus full field retinal slip induced by visual-vestibular conflict about the naso-occipital axis could modify the gain of the roll aVOR only for stimulus frequencies below ≈0.5 Hz. Based on these results, 0.25 Hz was chosen as the representative frequency to test enhancement and reduction of the roll aVOR gain by visual-vestibular mismatch.

Fig. 4.

A and B: gains of roll component of the eye counter-rotation evoked by in-phase (suppression, ■) or out-of-phase (enhancement, □) rotation of the monkey and the visual surround, tested at different frequencies (A) and different peak velocities (B). C and D: gains of the yaw (●, ○), and pitch (▲, ▵) eye counter-rotation evoked by in-phase (suppression, ●, ▲) or out-of-phase (enhancement, ○, □) rotation of the monkey and the visual surround tested at different frequencies (C) and peak velocities (D).

Using oscillation at 0.25 Hz and peak velocities from 5 to 80°/s, we next determined how stimulus velocity affected the roll aVOR in M0102. The enhanced (□) and suppressed (■) gains of the torsional aVOR were ∼0.55 and 0.4, respectively, across the entire range of tested velocities (Fig. 4B). Thus within limits, the animal could modify eye velocities induced by torsional rotation independent of stimulus velocity. The other animals also had significant enhancement and suppression of the roll response when tested at 0.25 Hz. The response gains varied, however. Gains were ∼0.3 during visual suppression, but were as high as 0.88 in M17115 during visual enhancement.

The characteristics of the torsional aVOR were contrasted to those of the yaw and pitch components using the same in-phase and out-of-phase conditions (Fig. 4, C and D). Yaw and pitch aVOR gain changes were independent of stimulus velocity over the entire frequency range tested in the in-dark condition (Fig. 4, C and D, - - -). The enhanced and suppressed gains of yaw and pitch components in this animal were ∼1.5 and 0.2, respectively (○ and □ and ● and ▲, note difference in gains in A and B vs. C and D). Changes in yaw and pitch gains were largest at the lowest frequencies, similar to the roll aVOR, however.

To determine whether lower frequencies of the head oscillation in light were more effective in modifying the roll response gain, the head and the visual surround were rotated out-of-phase with constant velocities of 10 and 15°/s in two monkeys. The resultant response gain was always comparable to that obtained by sinusoidal oscillation at 0.25 Hz. This showed that similar to the yaw and pitch components, in-phase and out-of-phase oscillation at 0.25 Hz was an effective stimulus for adapting the torsional aVOR gain. The data in Fig. 4 were from a single animal (M0102) but were similar to those in the other animals. Thus eye velocities of all components of the aVOR could be modified by a broad range of stimulus velocities, but the changes were substantially less for torsion than for yaw and pitch. Moreover, there was not perfect reduction or enhancement of roll eye velocities by vision at any frequency. A frequency of 0.25 Hz was utilized to adapt the torsional aVOR gains in the present study. Similar results on the capability to enhance or suppress the roll aVOR gain at 0.5 Hz have been reported in humans (Leigh et al. 1989).

Gravity-dependent and -independent adaptation

We have previously shown that there is significant gravity-dependent and -independent adaptation of the yaw and pitch aVOR in normal monkeys and humans (Yakushin et al. 2000a, 2003a–c, 2005a,b). When aVOR gains have been increased or decreased, the changes in gain were largest when subjects were tested in the position of adaptation. There were a number of differences and similarities between the gravity-dependent and -independent changes in roll when compared with those in yaw and pitch. First, the gravity-dependent adaptation was not consistently produced in roll as in yaw and pitch. In 16 experiments that were done in four monkeys to reduce the gain of the torsional aVOR, a significant gravity-dependent gain decrease occurred in only six experiments (38%). In these experiments, the gravity-dependent gain changes occurred in the position of adaptation as in yaw and pitch.

There were significant gravity-independent changes in roll in 88% of these experiments, however. When the roll aVOR gain was increased, the gravity-dependent changes in gain were significant in only 50% of the experiments, and the gravity-independent gain changes were present in only 44%. Thus gravity-dependent gain changes of the roll aVOR gain were not consistently present either for gain increases or for gain decreases. Both gravity-dependent and -independent gain changes were produced in all experiments for yaw or pitch aVOR adaptation. Average gravity-independent gain changes in roll evoked in the upright position were 9% for gain decrease and 17.3% for gain increase. Changes obtained in the other head orientations are summarized in Table 1.

Table 1.

Average gravity-independent gain changes across animals

	Roll	Pitch	Yaw
Gain decrease
RSD	17.0	22.7	15.5
Supine	7.9	8.0	16.6
Prone	13.5	–	20.5
Gain increase
RSD	16.5	–	19.9
Supine	16.8	17.0	23.5
Prone	17.0	–	32.5
Average	14.8±3.6	15.9±7.4	21.4±6.1

Values are means ± SD. Average gravity-independent gain changes across animals. Each gain value is an average across all tested animals. Individual values were significant using ANOVA (P<0.05). There were increases in the gravity-independent gain when the aVOR gain was increased and decreases in gain when the aVOR gain was decreased. The dashes correspond to experiments that were not performed.

Comparative changes in yaw, pitch, and roll

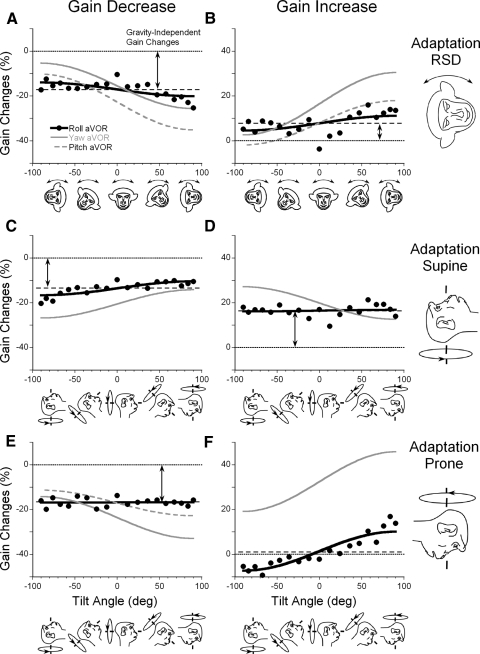
Experiments on roll aVOR gains following adaptation RSD (Fig. 5, A and B), supine (C and D), and prone (E and F) were averaged (filled circles) and compared with corresponding aVOR gain changes in yaw (solid gray line) and pitch (dashed gray line). When the aVOR gain was decreased in a side-down position (Fig. 5A), there was a significant gravity-dependent change in the gains of yaw and pitch but not in roll. In contrast, the gravity-independent gain changes were comparable between the experiments. The same was true for gain increases in RSD (Table 1), i.e., there was no significant gravity-dependent gain change in the roll aVOR, but the gravity-independent changes were the same in yaw, pitch, and roll (Fig. 5B).

Fig. 5.

Decrease (A, C, and E) and increase (B, D, and F) of the torsional aVOR gain in side-down (A and B), supine (C and D), and prone (E and F) head orientations. Filled symbols represent data averaged for three animals. Data were fitted with a cosine (Eq. 1, black solid line) and compared with the fits made through the average changes obtained after yaw (gray solid line) and pitch (gray dashed line) aVOR adaptation in the same animals.

Similar results were obtained when the aVOR was decreased and increased with the animals supine (Fig. 5, C and D) or when gains were decreased with animals prone (Fig. 5E). For gain increases in prone, there was an anomaly in that there was insignificant gravity independent gain changes (Fig. 5F), while the gravity-dependent change was significant (8.7%). This caused a decrease in gain when the animal was placed supine although the gain had been increased in prone.

In sum, the average gravity-independent aVOR gain changes induced during roll aVOR gain adaptation in all monkeys were comparable to those in yaw and pitch (Table 1, ANOVA, P = 0.177, Bonferroni's approach), regardless of whether the gains were increased or decreased except when the adaptation increased the gain with the animal in the prone position. When all experiments on roll were considered, the gravity-dependent aVOR gain changes were smaller compared with those in yaw and pitch (Table 1, P = 0.048, ANOVA with Bonferroni's approach; 3.0 ± 3.2, roll; 9.3 ± 3.4, pitch; and 10.0 ± 3.1, yaw).

Spatial distribution of the roll aVOR gain changes

To determine the spatial distribution of the gain changes of the roll aVOR in three dimensions, the gain was tested before and after adaptation while the head was tilted in four planes. When the torsional aVOR gain was decreased (Fig. 6A) or increased (B) in the RSD position, peak gain changes were close to the position of adaptation (vertical arrow). The same was true when the aVOR gain was decreased (C) or increased (D) in the supine position (vertical arrow). When the aVOR gain was decreased (E) or increased (F) in a prone position; however, there was no peak in the position of adaptation. Overall, therefore the surface describing the gain changes was generally below zero when the aVOR gain was decreased in all head orientation and was above zero when the aVOR gain was increased in the RSD and supine positions.

Duration of the gain changes

To determine how well the gain changes were maintained, the aVOR gain was tested over two additional days in five experiments after the torsional aVOR gain had been adaptively decreased in various head orientations. The gravity-dependent and -independent gain changes were determined each day, and then data from all experiments were averaged. There were small (≈5%) gravity-dependent gain changes just after adaptation, which persisted over the next 2 days. The gravity-independent gain changes were ≈20% just after adaptation, and fell to ≈12% on the next day and to ≈5% 2 days after adaptation. Thus there were still gravity-independent gain changes induced by 4 h of adaptation the next day.

DISCUSSION

This study shows that the gain of the roll aVOR has a dependence on head position relative to gravity, which is different from yaw and pitch. We also show that this gravitational dependence is inversely related to the degree of gravity-dependent adaptation that can be implemented. This gravity dependence may explain why the adaptive circuits are not active when the head is tilted re gravity during roll aVOR adaptation. These behavioral differences suggest that there is a fundamental difference in the central organization of canal-otolith convergence between the roll and yaw/pitch aVORs.

Gravitational dependence of the unadapted roll gain of the aVOR

In each of the three monkeys, roll aVOR gains were reduced significantly by 7–15% when the head was tilted from the upright. This was in contrast to the lack of change in the gain of the aVOR in pitch and yaw as the head was moved from the upright. Although there was a weak tendency for the aVOR to have gravity dependence for head positions in pitch, this was neither similar nor equal to the magnitude of the gravity dependence of the roll aVOR. Furthermore, the gain of the yaw aVOR was insensitive to tilts in any plane in any of the monkeys.

The functional significance of the reduced gain of the roll aVOR is that perturbations of the head in roll would not compensate as well in tilted head positions as when the head was upright. This may be due to the fact that the roll aVOR functions to compensate for head tilts and maintain the stability of the retina relative to the horizon. In lateral-eyed animals (Maruta et al. 2001; Oommen and Stahl 2007), there is approximately ±30° of ocular compensation for head tilt, whereas in frontal-eyed animals such as the monkey, stability is much less because the range of ocular counter-roll is only approximately equal to ±4° (Krejcová et al. 1971; Kushiro et al. 2002). There is likely to be a profound positive interaction between the orientation response due to the otoliths and the compensatory roll response due to the canals. That is, the compensatory response in lateral-eyed animals should increase to maintain stability of the retina due to perturbations of the visual streak, which is well maintained relative to the horizon over a large angle of head roll. The aVOR roll gains should be more uniform as a function of head tilt in these animals. Conversely, as the orientation response becomes more limited, the compensatory response also becomes less effective.

There are also structural differences between yaw/pitch and roll that may underlie the differences between the roll and yaw/pitch aVOR gains. Thus while our studies were based on passive rotations of the head and body, the fact that there are both natural gain differences between yaw/pitch and roll and adaptive properties has implications for their function during natural head movements. Yaw and pitch head movements that activate the semicircular canals are most commonly produced by movement of the head on joints at the base of the skull; rotation of the skull about the dens for yaw and by rotation of the skull on C₁ about the occipital condyles for pitch. These single joint movements would facilitate the high-frequency head movements in yaw and pitch, which would necessitate high gain compensation from the eyes. There is no similar single joint or set of joints that generates roll head movements. Rather head movements in roll are produced by progressive narrowing of spacing between cervical vertebrae (see Kunin et al. 2007 for review). The fact that more joints are involved in making head movements in roll than in yaw and pitch may impact the frequency capability of head movements, thereby affecting the gain.

Furthermore, the organization of yaw and pitch in a head/body coordinate frame reflects their close dependence on input from the semicircular canals. In contrast, the spatial coordinate frame of the roll aVOR appears to depend on input from both the canals and the otolith organs. The same appears to be true for the angular vestibulocollic reflex (aVCR). Thus the yaw and pitch aVCRs depend heavily on input from the semicircular canals, and the gains and phases of the aVCR are significantly altered by canal plugging, which eliminates the low-frequency input from the canals (Xiang et al. 2008). In contrast, the roll aVCR is unaffected by canal plugging (Xiang et al. 2008), making it likely that the roll aVCR has strong dependence on input from the otolith organs.

There are also striking differences between the central organization of yaw and pitch versus roll. There is a disproportionate number of cells in the vestibular nuclei, which project to the cervical spinal cord, that are responsive to head roll (Schor et al. 1984). It has been recently demonstrated (Xiang et al. 2008) that head stabilization in the monkey is more complete in roll than in yaw or pitch. Thus there appears to be a match between the insufficient compensatory characteristics of the roll aVOR and the enhanced capability of head stabilization in roll in space, which would obviate the necessity for unity gain in roll.

Of the two components of the visual system, the subcortical visual system has a three-dimensional representation of space, similar to that of the semicircular canals, with adequate representation of roll. The cortical visual system, on the other hand, is predominantly organized in yaw, pitch, and depth, with little representation of roll. Perhaps reflecting this, it is possible to make saccadic eye movements in yaw and pitch and to verge the eyes voluntarily, whereas most subjects cannot easily move their eyes voluntarily in roll (Balliet and Nakayama 1978). Listing's Plane also reflects these differences in that voluntary saccades and pursuit are driven by two-dimensional (pitch/yaw) control signals, while roll component is an outgrowth of the two-dimensional control of a three-dimensional plant and pulleys (Raphan 1998). Associated with this, there is no representation of roll in the superior colliculus or frontal eye fields, which have extensive representation of saccades in yaw and pitch (Van Opstal et al. 1991). The fact that there is active ocular pursuit for both yaw and pitch, but not for roll, is supported by the presence of direct visual pathways only for yaw and pitch, not for roll (Raphan and Cohen 1988). As a result, there is active suppression of the aVOR in yaw and pitch up to the limits of ocular pursuit, whereas suppression of the roll aVOR should be substantially weaker or absent (Fig. 4).

The yaw aVOR gain was found to have no dependence on head orientation re gravity in human subjects (Bockisch et al. 2005) or in monkeys (Angelaki and Hess 1996). This is consistent with our findings. Two monkeys, however, did have a slight dependence of the pitch aVOR gain on head orientation relative to gravity, but this was not consistently present in every plane of head reorientation. This is in general agreement with the data obtained in cats (Brettler et al. 2000; Tomko et al. 1987, 1988), monkeys (Angelaki and Hess 1996), and humans (Bockisch et al. 2005) at 0.5 Hz. Dependence of roll aVOR gain on head orientation relative to gravity was previously demonstrated in humans (Bockisch et al. 2005; Schmid-Priscoveanu et al. 2000; Groen et al. 1999), but not in rhesus monkeys (Angelaki and Hess 1996). The reason for the lack of gravity dependence in the previous study is not clear.

Context-specific gravity-dependent adaptation

A second major finding was that the roll aVOR has a diminished capability for adaptation, which is specific for the head orientation in which the changes were induced, i.e., gravity-dependent gain adaptation. This diminished adaptive capability is different from the aVOR in yaw and pitch (Yakushin et al. 2000a, 2003a–c, 2005a,b). Thus there was a reciprocal relationship between the inherent gravity dependence of the gain as a function of gravity and its gravity-dependent adaptive capability. Although there was little or no context specific gravity-dependent adaptation of the roll aVOR, the bias, i.e., the gravity-independent component was the same as the gravity-independent component in yaw and pitch in our experiments.

Gravity-dependent gain changes of the roll aVOR were significant in some experiments, but this did not occur in every animal or in each experiment, and on average, gravity-dependent adaptive changes were only ≈5% in roll. This is in contrast to pitch and yaw aVOR gain adaptation, in which gravity-dependent gain changes were 10–15% and gravity-independent changes were 20–30% in all experiments. Thus our findings demonstrate that gravity-dependent features of adaptation in roll are characteristically different from those of pitch and yaw, supporting the conclusion that there is a basic difference between the organization of the aVOR in roll and in pitch and yaw.

There are a number of reasons that could explain why there was little gravity-dependent adaptation in roll compared with pitch and yaw. The unadapted roll aVOR gain already has gravity dependence in the monkey, whereas the pitch and yaw aVOR's have little or no gravity dependence (Fig. 3). There were trials using the same animal, however, in which there was substantial gravity-dependent gain adaptation of the roll aVOR (Fig. 2). This indicates that there must be other contextual factors in the gravity-dependent adaptive process that make roll adaptation different from pitch and yaw. Regardless, on average the inherent gravity dependence of the roll aVOR gain must be an inhibiting factor in the adaptive process.

Another factor that might contribute to the lack of gravity-dependent roll aVOR gain adaptation is the nature of the visual signals that are utilized in the adaptive process. Activation of the roll aVOR in the presence of visual-vestibular mismatch induces full-field retinal slip that could activate only a low-frequency, velocity storage component because there is little or no direct roll pathway (Raphan and Cohen 1988). On the other hand, both the direct pathway and a velocity storage component would be activated during pitch or yaw rotation during visual-vestibular mismatch (Cohen et al. 1977; Raphan et al. 1979), and both could utilize ocular pursuit (Zee et al. 1987). There is evidence that pursuit mechanisms could at least partially be responsible for yaw and pitch aVOR gain adaptation (Fukushima et al. 1996; Miles and Lisberger 1981) and the central representation of the retinal slip, which drives the direct pathway may be a necessary component for gravity-dependent adaptation, whereas the central representation of the retinal slip that activates velocity storage may be important for the gravity-independent component.

In summary, we have presented evidence that the yaw and pitch aVORs, which have context-specific gravitational dependence after adaptation, are closely linked to activity generated in head/body coordinates from the semicircular canals, whereas the roll aVOR, which has an inherent spatial organization that depends heavily on input from the otolith organs (and body tilt receptors) as well as the canals, has little or no adaptive context-specific gravitational dependence. Interaction of the roll aVOR with the visual system and structural anatomical constraints may be at the root of these differences. Data from behavioral, single-unit, and anatomic studies support this conclusion.

GRANTS

This work was supported by National Institutes of Health Grants DC-04996, DC-03284, EY-04148, EY-11812, DC-005204, and EY-01867.