Abstract
Functional magnetic resonance imaging (fMRI) has revolutionized the study of human brain activity, in both basic and clinical research. The commonly used blood oxygen level dependent (BOLD) signal in fMRI derives from changes in oxygen saturation of cerebral blood flow as a result of brain activity. Beyond the traditional spatial mapping of stimulus–activation correspondences, the detailed waveforms of BOLD responses are of high interest. Especially intriguing are the transient overshoots and undershoots, often, although inconclusively, attributed to the interplay between changes in cerebral blood flow and volume after neuronal activation. While physically simulating the BOLD response in fMRI phantoms, we encountered prominent transient deflections, although the magnetic field inside the phantom varied in a square-wave manner. Detailed analysis and modeling indicated that the transients arise from activation-related partial misalignment of the imaging slices and depend heavily on measurement parameters, such as the time between successive excitations. The results suggest that some transients encountered in normal fMRI recordings may be spurious, potentially compromising the physiological interpretation of BOLD signal overshoots and undershoots.
Keywords: fMRI phantom, overshoot, undershoot, BOLD, fMRI
Since the advent of the blood oxygen level dependent (BOLD) imaging method (1–4), functional magnetic resonance imaging (fMRI) of human brain function has spread so rapidly that currently as many as eight new fMRI papers appear each day. The proper analysis of fMRI data (5) and the relationship between the fMRI signal and the underlying brain activity (6) continues to receive much attention, whereas the basic physics of the signal acquisition is considered to be sufficiently understood. Accordingly, computer simulations are used to successfully model the effects of different imaging parameters on the measured signals (7–9).
Such computational methods can, however, oversimplify factors affecting the signal acquisition and the MR signal. To scrutinize the behavior of the BOLD response in more detail, we recently introduced physical “fMRI phantoms” (10, 11) in which the BOLD signals can be physically simulated by accurately controlling current flow within a conducting medium.
The MRI signals of the brain arise from protons that are excited with radio frequency pulses applied at the protons' Larmor frequency in a static magnetic field (B0). With brief gradient fields, a slice of protons (e.g., perpendicular to the magnet's main axis z) can be selected. In a typical fMRI experiment, several (up to 50) slices are repeatedly excited while a subject performs a task or perceives stimuli. Soon after an excitation, the protons start to precess at slightly different frequencies because of local magnetic field inhomogeneities that arise from tissue properties, especially from a blood oxygenation level that varies according to neuronal activity. The field inhomogeneities result in dephasing, or transverse relaxation, of the originally synchronously precessing protons and thereby in a decay of the magnetic resonance signal (T2* effect); this effect eventually gives rise to the BOLD contrast. Another simultaneous phenomenon is the longitudinal relaxation. After each excitation, the protons start to return toward thermal equilibrium through energy exchange with the surroundings, and the characteristic time of return (T1) depends on the sample (for a review of fMRI methods, see e.g., ref. 12). During an fMRI experiment, the excitations are repeated so fast (e.g., once every 0.5–5 s) that the spin population reaches a pseudo steady state (different from the thermal equilibrium), such that the remaining nuclear magnetization is the same before each excitation. It is assumed that this pseudo steady state is not disrupted by small changes in the magnetic field caused by neuronal activity. Models connecting the fMRI signal, hemodynamics, and neural signaling have been developed to better understand the underlying brain function (13). However, a universally applicable model for short-lived transient deflections, most prominently the overshoot after stimulus onset and the poststimulus undershoot, remains to be found (14). Here, we demonstrate that some BOLD signal transients can be spurious, emerging by a nonphysiological mechanism that has not been previously proposed to our knowledge.
Results
We studied fMRI signals in a well-controlled setting, devoid of confounding factors such as movement, using two fMRI phantoms modified from our previous design (10). The experimental setup is explained in Methods and illustrated in Fig. 1A.
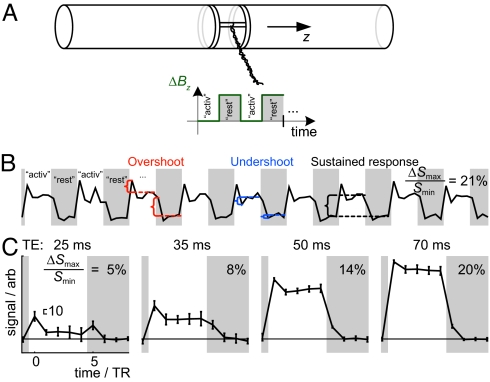
Fig. 1.
Set-up and fMRI time course of the gradient phantom. (A) An optical control signal was transformed into magnetic field by modulating Bz using a pair of coils. Mimicking fMRI activations, the times when the field is most homogeneous, i.e., additional Bz is off, is labeled activation. The gray areas denote the rest condition (i.e., additional Bz is turned on). (B) Mean signal from a 12-voxel ROI shows overshoots and undershoots between the sustained responses, after the changes of Bz. (C) Mean ± SD signal (n = 9) from the ROI as a function of TE. TR = 2,000 ms. The maximum range of the signal variation (ΔSmax) in relation to the lowest signal level at rest (Smin) are provided (B and C) along with a scale bar indicating an equal signal change (10) in arbitrary signal units in each plot (C). The rest and activation conditions both lasted 5 TRs, i.e., 10 s.
Fig. 1B shows the mean signal intensity from a 12-voxel region of interest (ROI) in the middle of the gradient phantom. The plot shows clearly that changing ΔBz between the “activation” and “rest” levels introduced, in addition to the sustained responses, overshoots and undershoots closely resembling similar phenomena in real fMRI recordings, although the current driving the phantom and thereby producing the ΔBz was devoid of any transient overshoots or undershoots (settling time 0.1 ms; see SI Text). The plots in Fig. 1C show that the shape of the response depended on the echo time (TE), so that increasing TE from 25 to 70 ms increased the sustained contrast and decreased the relative contributions of the onset transients.
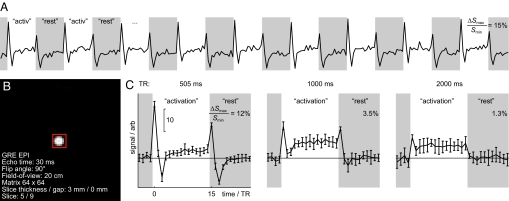
To scrutinize the possibility that prominent fMRI transients could arise from the field changes per se, we imaged the uniform phantom that generated a locally constant field change. Fig. 2 illustrates that biphasic transient signals occurred both after ΔBz changed from the rest period to active, and vice versa. The initial positive transients were stronger and shorter than the following undershoot deflections of opposite polarity. The sustained signal component was slightly higher at activation than in rest, which can be attributed to a minor field inhomogeneity produced even in this Maxwell coil configuration. The amplitudes of the transient signals decayed with increasing times between excitations [repetition times (TRs) of 505, 1,000, and 2,000 ms], as expected, because the spin population had more time to relax toward thermal equilibrium.
Fig. 2.
Transient signal components from the uniform phantom. (A) Mean signal from an ROI as a function of time. (B) The transverse section of the phantom, showing the 49-voxel ROI (red box); the imaging particulars are indicated. (C) The plots show the mean ± SD signal (n = 9) from the ROI. For all three TRs, step changes of Bz produced periods of transient deflections, the amplitudes of which decreased as TR was increased. Percentage signal changes and scale bars are as in Fig. 1. Each block of activation or rest lasted 15 TRs, i.e., 7.5, 15, or 30 s at TRs of 500 ms, 1 s, and 2 s, respectively.
Fig. 3 shows simulations of transverse magnetization after excitations at the applied three TRs and with different slice profiles (red and blue lines; see SI Text and Fig. S1). The results are strikingly similar to the experimental data (Fig. 2C), giving strong indication that a change in the position of a slice after a change in Bz, either because of current or susceptibility modulation, can create transient changes in the fMRI signal whenever the activation level changes even without any overshoots or undershoots.
Fig. 3.
Simulations. The fMRI signal was simulated for the TRs applied in Fig. 2C. The subplots demonstrate the simulation results for parameters indicated in the leftmost box. The apparent displacement of the whole volume was Δz, except for the subplots marked edge, where Bz remained constant at slices below the one observed. T1 values of the simulations are shown. Transition width as a percentage of full-width at half-maximum (key: bottom right) indicates the steepness of the slice profile. Both measurements and simulations show that the signal, after step changes of Bz, is modulated to a new level through periods of similar transient deflections.
A number of miscellaneous results are worth pointing out for discussion. In phantom measurements, slice thickness was positively correlated with the transient amplitude. In simulations, prolonged transition times between activation and rest states yielded prolonged transients of more complex shapes. Prolonging the transition to physiologically valid slew rates equalized measurements with different TRs. For example, when the ramp width was 3 s, the amplitudes of the transients at TR = 500, 1,000, and 2,000 ms were nearly the same; thus in human BOLD signal recordings the transients might not differ considerably at different TRs. With longer TRs (e.g., TR = 2,000 ms), the strongest transient was, depending on other simulation parameters, often associated with transition durations in the neighborhood of TR. Additionally, while the above examinations considered imaging of a stack of adjacent slices, strong transients were also obtained by repeatedly imaging just one slice; importantly, this experimental result was also predicted by simulation.
Discussion
Our measurements on fMRI phantoms, and corresponding computer simulations, demonstrate that step transitions of Bz are followed by a BOLD response that contains transients in addition to a sustained component. The sustained part of the response is caused by field homogeneity (11), whereas the clear decoupling of the transient and sustained responses implies a different generation mechanism for the transients. Importantly, the phantom was void of alterations of flow, volume, or any other transient (physiological) events commonly attributed to the signal transients, and thus the observed overshoots and undershoots had to emerge solely as consequences of the changing Bz. Very similar characteristics appeared in the simulations, where all experimental imperfections were absent, letting us to conclude that the experimental evidence convincingly supports the theory. The next paragraph discusses the emergence of the transients (Fig. S2).
During slice selection, the z-direction gradient field determines the proton spins capable of receiving energy from the excitation pulse. If any additional field with a z-component is superimposed on the gradient, the site of the excited protons is determined by the resultant field, instead of just the gradient.
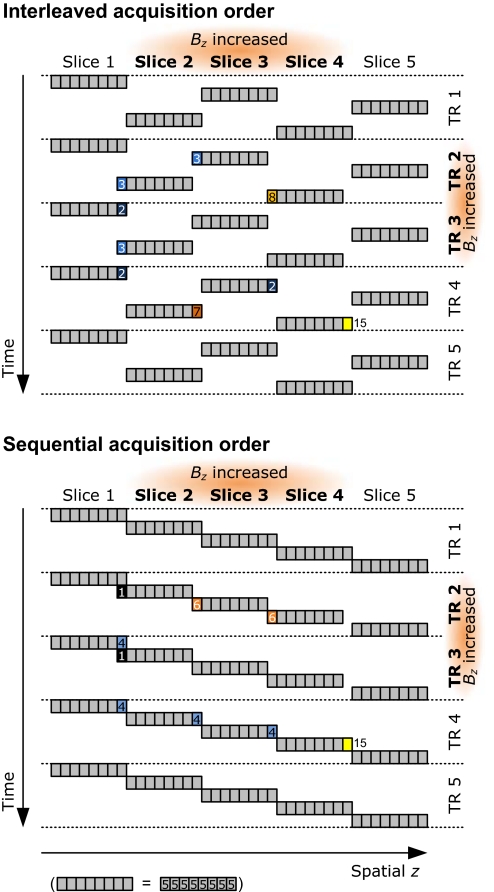
In vivo, the difference in magnetic susceptibility between oxygenated and completely oxygen-depleted red blood cells is 4π × 0.264 × 10−6 (15), which modulates Bz by 10-μT in a 3-T external field. Because the slice selection gradient applied during the excitation of our 3-mm thick slice was 5 mT·m−1 (15 μT across the slice), the field related to the susceptibility change would represent, at the exact location of the red cell, a ≈70% shift in the position of the slice, whereas for whole blood, with activation-induced oxygenation change, the shift would be 5% (see SI Text). As a result, without actual movement, protons in a given slice could be excited along with those of a spatially neighboring slice, a different slice than before the BOLD response; or they could receive excitations belonging to both slices, if they reside near the slice border. As is schematically illustrated in Fig. 4(for phantom), essentially, the temporal consistency of the excitations would break down, hence transient overshoots or undershoots could occur before a new pseudo steady state, even after completely flat on—off-type changes in the underlying physiology. As shown in Fig. 4, the transients can be quite different for different slices and slice acquisition orders. Although the signal in Fig. 4 stabilizes immediately after an excitation, in reality, because of finitely steep and overlapping excitation profiles, the undershoots last longer, as can be seen in Figs. 1–3.
Fig. 4.
Emergence of transients. Transient signal components arise when Bz takes on a new value. This schematic shows the emergence of transients in the uniform phantom, for interleaved (Upper) and sequential (Lower) slice acquisition order. Bz is temporally increased during the second and third TR, in the three central slices of a stack of five slices; each slice has been divided into eight fractions (gray squares). The signal changes are color- and number-coded: light to dark blue colors illustrate signal losses, orange to yellow represent signal gains. Numbers indicate magnetization values (baseline = 5 units). Gray areas remain unchanged. The schematic ignores most details, such as a realistic excitation profile. It assumes that the available longitudinal magnetization is completely excited and linear, and the maximum excitable magnetization is considered to be at least 15 units. It shows clearly that even when Bz changes in several adjacent slices (slice 3 is surrounded by equally affected slices), transients, which depend on the acquisition order, occur. The horizontal axis is labeled spatial z to emphasize that the apparent position generally differs (slightly) from the actual z because of Bz changes. The shifted slice positions indicate the apparent slice positions caused by the increase in ΔBz. Because the excitation profile is infinitely steep and all available magnetization is always excited, the transients in the schematic last for only one time point.
The shapes of the transients depend on several imaging parameters, dynamics of the field change, and physical factors, all of which will be briefly discussed next. Additional discussion on the bipolar nature of the transient is provided in SI Text.
The clear effects of the imaging parameters on the size of the transients are informative in designing methodologically clean measurements. For example, one can radically decrease the transients by increasing the strength of the slice selection gradient and adjusting the excitation pulse so that the slice thickness remains stable; this suppression of transients occurs because the susceptibility-related field change decreases in relation to the thickness of the slice. Technically, the scanner software in use modulated slice thickness by scaling the slice select gradient while keeping the bandwidth of the excitation pulse unchanged. Therefore, a thicker slice was selected just by using lower gradient amplitude, whereby the ΔBz caused by the phantom misplaced the slices further than with stronger gradient. In control experiments an approximately linear relationship between transient amplitude and slice thickness was observed.
In principle, more pronounced transients will occur at higher fields because susceptibility-related field augmentation increases linearly with the main field, and T1 is longer in higher magnetic fields. In practice, high-field scanners usually have stronger gradients, and thus the effect on transients depends on the details of how slice selection is implemented.
Further, reducing the flip angle decreased the transient amplitude (see Fig. S3).
The transients are also sensitive to the details of the excitation profile: abrupt slice profiles maximize independence of signals from the neighboring slices, but, as shown by the simulations, they amplify the transient amplitudes in case of step responses. However, the optimal slice profile depended on the transition time between rest and active conditions, which might be unknown beforehand in human BOLD signal recordings.
Long TE reduced the proportional amplitude of the transients with respect to the sustained amplitudes.
Increasing TR reduced transients unequivocally in the phantoms. However, in vivo this effect depends on the slew rate of the BOLD response and the rate of longitudinal relaxation. For example, if the BOLD signal changes slowly, the apparent slice position would not be too different at a short TR (e.g., 500 ms). At a longer TR, however, the difference would increase, but the longitudinal magnetization would have more time to relax and thereby reduce the transients. If, however, the BOLD signal change would mostly occur within one TR, the discrepancy between the apparent and actual slice positions would produce distinct transients, even though longitudinal relaxation would damp the amplitudes of the transients especially at long TRs. Further, in the brain, BOLD transients last longer than in our measurements (where the Bz changes were instantaneous). Because the hemodynamic response, during which magnetic susceptibility changes, builds up gradually, changes of Bz are similar during several successive TRs. Thus, individual transients line up and produce the long-lasting resultant transient. These observations were supported by simulation. Additionally, because with short TR the amplitude and width of the overshoot transient correlate with the abruptness of the hemodynamic change, it is possible that the amplitudes of the transients would carry useful information on the rate of the hemodynamic response. Because of the impact of T1 on the transient amplitudes, we predict particularly strong transients in brain regions neighboring compartments of cerebrospinal fluid.
Transient BOLD responses occurring, e.g., after the onset of a stimulus block or a task, are quite common in human brain imaging. Some of them have been considered as artifacts arising from subject movement (16, 17), but for transients that cannot be attributed to motion, the generation mechanisms have remained elusive. For example, the spatial distribution of the transients is unexpected: after sustained visual stimulation, the transients can be bilateral while the conventional sustained BOLD response is contralateral (18), or the transients at block transitions can be broadly distributed and sometimes occur independently of the type of the task (14). Dampened onset transients have been found in schizophrenic subjects, with variability according to the region and task (19). Consequently, the transients have been explained by nonlinearities in both neuronal firing and hemodynamics (including blood flow, blood volume, and blood oxygenation level) (18).
The simulations and the phantom experiments are, of course, simplifications, and the slice misplacement mechanism described here is likely to generate quite different transients in BOLD fMRI. The susceptibility effect from blood (and red cells) extends to the surrounding tissue, where the most static water should behave in a manner similar to the phantom. Intravascular water is, however, prone to cause poorly predictable transients because water molecules near hemoglobin may be in a drastically different field than the molecules further away, implying transients of different sizes. Moreover, changes in blood flow and water diffusion affect the site where the molecules reside during excitations (thus changing the effective pseudo steady state), etc. Nevertheless, all of these cases can be simulated in a principally identical manner by only taking into account where the water molecule is located at the moment of each radio frequency excitation.
Much remains to be explored: How large are the described transients in comparison with the main component of BOLD response and transients of vascular origin? How closely do the transients relate to neuronal events? Do these transients cause (some of) the apparent deviation from linearity of the BOLD responses with respect to stimulus duration or contrast (20)? Are the brain-related changes of appropriate magnitude and temporal nature to induce the onset overshoot and poststimulus undershoot by the explained mechanism? How much of the BOLD responses can really be explained by these “intrinsic motion artefacts” (near tissue boundaries the internal adjustment of Bz also changes the constant signal level) and what is the eventual contribution of dephasing? Some answers might arise from experiments with spin-echo pulse sequences that are insensitive to dephasing caused by Bz.
Our investigation prompts caution for explaining the BOLD signal transients purely with dynamical BOLD models because, as we demonstrated, the responses can be accompanied by nonphysiological signal transients. Importantly, the described physical mechanism and the physiological events are intertwined; for example, the more abrupt the hemodynamic change, the stronger the transient. Understanding the generation of these transients may provide additional means for extracting from fMRI data valuable information on brain function, thereby increasing understanding of the relationship between local neuronal activity and the BOLD response.
Methods
Measurements.
Physically simulated fMRI data were acquired from two phantoms with a 3-T MRI scanner using standard pulse sequences (details above and in SI Text) while ΔBz was periodically adjusted between two distinct levels as indicated in the figures. Each phantom (Fig. 1A) consisted of a water-filled (T1 ≈ 2,600 ms) acrylic cylinder around which pairs of coils were wound in Maxwell configuration. Current was lead to the coils to induce an additional magnetic field (ΔBz) parallel to the main 3-T Bz field in the magnet. In the uniform phantom, ΔBz was largely homogeneous between the coils, whereas in the gradient phantom, ΔBz was a radially homogeneous z-gradient field. The homogeneous field does not dephase the spins, thus the uniform phantom was devoid of major T2* effects, whereas the gradient field in the gradient phantom dephased the spins with a spatially varying magnitude. Thus, the T1 effect should remain apart from the T2* effect in the uniform phantom, whereas the T2* effect should be present in the gradient phantom.
Simulations.
Excitations with in-between step modulations of Bz were simulated [on Matlab version 7.1.0.246 (R14) Service Pack 3] to investigate how step modulations of Bz change for different T1, TR, and ΔBz values between active and rest conditions. A number of slice profiles of similar shapes but different steepnesses were simulated in each case (shown as the individual curves in the figures), starting from an extremely steep profile, where the transition from stop-band to pass-band took 2% of the slice thickness (red in Fig. 3), to a gently ramping one (38%; shown in blue in Fig. 3). See SI Text and Fig. S1 for details of the simulations.
Supplementary Material
Acknowledgments.
We thank Prof. Raimo Sepponen for discussions and advice during the previous stages of phantom development and Dr. Cathy Nangini for language check and discussions. This work was supported by the Academy of Finland (National Centres of Excellence Programme 2006–2011), Instrumentariumin Tiedesäätiö (to V.R.), the Signe and Ane Gyllenberg Foundation (to V.R.), and ERC Advanced Grant (to R.H.).
Footnotes
The authors declare no conflict of interest.
This article contains supporting information online at www.pnas.org/cgi/content/full/0911265106/DCSupplemental.
References
- 1.Bandettini PA, Wong EC, Hinks RS, Tikofsky RS, Hyde JS. Time course EPI of human brain function during task activation. Magn Reson Med. 1992;25:390–397. doi: 10.1002/mrm.1910250220. [DOI] [PubMed] [Google Scholar]
- 2.Kwong KK, et al. Dynamic magnetic resonance imaging of human brain activity during primary sensory stimulation. Proc Natl Acad Sci USA. 1992;89:5675–5679. doi: 10.1073/pnas.89.12.5675. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Ogawa S, Lee TM, Kay AR, Tank DW. Brain magnetic resonance imaging with contrast dependent on blood oxygenation. Proc Natl Acad Sci USA. 1990;87:9868–9872. doi: 10.1073/pnas.87.24.9868. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Ogawa S, et al. Intrinsic signal changes accompanying sesory stimulation: Functional brain mapping with magnetic resonance imaging. Proc Natl Acad Sci USA. 1992;89:5951–5955. doi: 10.1073/pnas.89.13.5951. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Kriegeskorte N, Simmons WK, Bellgowan PSF, Baker CI. Circular analysis in systems neuroscience: The dangers of double dipping. Nat Neurosci. 2009;12:535–540. doi: 10.1038/nn.2303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Logothetis NK. What we can do and what we cannot do with fMRI. Nature. 2008;453:869–878. doi: 10.1038/nature06976. [DOI] [PubMed] [Google Scholar]
- 7.Benoit-Cattin H, Collewet G, Belaroussi B, Saint-Jalmes H, Odet C. The SIMRI project: A versatile and interactive MRI simulator. J Magn Reson. 2005;173:97–115. doi: 10.1016/j.jmr.2004.09.027. [DOI] [PubMed] [Google Scholar]
- 8.Drobnjak I, Gavaghan D, Süli E, Pitt-Francis J, Jenkinson M. Development of a functional magnetic resonance imaging simulator for modeling realistic rigid-body motion artifacts. Magn Reson Med. 2006;56:364–380. doi: 10.1002/mrm.20939. [DOI] [PubMed] [Google Scholar]
- 9.Jochimsen TH, von Mengershausen M. ODIN: Object-oriented development interface for NMR. J Magn Reson. 2004;170:67–78. doi: 10.1016/j.jmr.2004.05.021. [DOI] [PubMed] [Google Scholar]
- 10.Renvall V. Functional magnetic resonance imaging reference phantom. Magn Reson Imaging. 2009;27:701–708. doi: 10.1016/j.mri.2008.11.007. [DOI] [PubMed] [Google Scholar]
- 11.Renvall V, Joensuu R, Hari R. Functional phantom for fMRI: A feasibility study. Magn Reson Imaging. 2006;24:315–320. doi: 10.1016/j.mri.2005.07.012. [DOI] [PubMed] [Google Scholar]
- 12.Huettel SA, Song AW, McCarthy G. Functional Magnetic Resonance Imaging. Sunderland, MA: Sinauer; 2004. [Google Scholar]
- 13.Buxton RB, Wong EC, Frank LR. Dynamics of blood flow and oxygenation changes during brain activation: The balloon model. Magn Reson Med. 1998;39:855–864. doi: 10.1002/mrm.1910390602. [DOI] [PubMed] [Google Scholar]
- 14.Fox MD, Snyder AZ, Barch DM, Gusnard DA, Raichle ME. Transient BOLD responses at block transitions. NeuroImage. 2005;28:956–966. doi: 10.1016/j.neuroimage.2005.06.025. [DOI] [PubMed] [Google Scholar]
- 15.Spees WM, Yablonskiy DA, Oswood MC, Ackerman JJH. Water proton MR properties of human blood at 1.5 Tesla: Magnetic susceptibility, T1, T2, T*2, and non-Lorentzian signal behavior. Magn Reson Med. 2001;45:533–542. doi: 10.1002/mrm.1072. [DOI] [PubMed] [Google Scholar]
- 16.Friston KJ, Williams S, Howard R, Frackowiak RS, Turner R. Movement-related effects in fMRI time-series. Magn Reson Med. 1996;35:346–355. doi: 10.1002/mrm.1910350312. [DOI] [PubMed] [Google Scholar]
- 17.Muresan L, Renken R, Roerdink JBTM, Duifhuis H. Automated correction of spin-history related motion artefacts in fMRI: Simulated and phantom data. IEEE Trans Biomed Eng. 2005;52:1450–1460. doi: 10.1109/TBME.2005.851484. [DOI] [PubMed] [Google Scholar]
- 18.Uludag K. Transient and sustained BOLD responses to sustained visual stimulation. Magn Reson Imaging. 2008;26:863–869. doi: 10.1016/j.mri.2008.01.049. [DOI] [PubMed] [Google Scholar]
- 19.Fox MD, Snyder AZ, McAvoy MP, Barch DM, Raichle ME. The BOLD onset transient: Identification of novel functional differences in schizophrenia. NeuroImage. 2005;25:771–782. doi: 10.1016/j.neuroimage.2004.12.025. [DOI] [PubMed] [Google Scholar]
- 20.Vazquez AL, Noll DC. Nonlinear aspects of the BOLD response in functional MRI. NeuroImage. 1998;7:108–118. doi: 10.1006/nimg.1997.0316. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.