Skip to main content
NCBI home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2010 Aug 7.
Published in final edited form as: J Biomech. 2009 May 28;42(11):1604–1609. doi: 10.1016/j.jbiomech.2009.04.041

Modeling of the Mechanical Function of the Human Gastroesophageal Junction Using an Anatomically-Realistic Three-Dimensional Model

R Yassi 1, L K Cheng 1, V Rajagopal 1, M P Nash 1,2, J A Windsor 3, A J Pullan 1,2,4
PMCID: PMC2778051  NIHMSID: NIHMS128781  PMID: 19481212

Abstract

The aim of this study was to combine the anatomy and physiology of the human gastroesophageal junction (the junction between the esophagus and the stomach) into a unified computer model. A three-dimensional computer model of the gastroesophageal junction was created using cross-sectional images from a human cadaver. The governing equations of finite deformation elasticity were incorporated into the three-dimensional model. The model was used to predict the intraluminal pressure values (pressure inside the junction) due to the muscle contraction of the gastroesophageal junction and the effects of the surrounding structures. The intraluminal pressure results obtained from the three-dimensional model were consistent with experimental values available in the literature. The model was also used to examine the independent roles of each muscle layer (circular and longitudinal) of the gastroesophageal junction by contracting them separately. Results showed that the intraluminal pressure values predicted by the model were primarily due to the contraction of the circular muscle layer. If the circular muscle layer was quiescent, the contraction of the longitudinal muscle layer resulted in an expansion of the junction.

In conclusion, the model provided reliable predictions of the intraluminal pressure values during the contraction of a normal gastroesophageal junction. The model also provided a framework to examine the role of each muscle layer during the contraction of the gastroesophageal junction.

Keywords: GEJ, mechanical behavior, muscle contraction, finite elasticity

1 Introduction

The gastroesophageal junction (GEJ) is a sophisticated region of the gastrointestinal tract where the narrow esophageal tube adjoins the stomach. In normal situations, the GEJ controls the entry of food into the stomach, but does not allow the passive return of food due to the presence of a high-pressure zone at the GEJ. There is a lack of accord between the anatomical and functional descriptions of the GEJ by anatomists, physiologists, gastroenterologists, radiologists and surgeons (Castell, 1995; Christensen, 1987; Gray et al., 1979; Liebermann-Meffert and Brauer, 1995). While physiologists refer to the GEJ as a sphincter due to the presence of a high-pressure zone, anatomists dispute the use of the word sphincter due to the lack of thickening in the muscle layer (Bombeck et al., 1966; Castell, 1975; Castell, 1995; Christensen, 1987; Gray et al., 1979; Liebermann-Meffert and Brauer, 1995). Some studies, however, have shown a slight increase in the circular muscle layer around the GEJ (Bombeck et al., 1966; Liebermann-Meffert and Brauer, 1995; Mosher, 1930). This lack of understanding of the microstructure of the GEJ has limited the understanding of the correlation between the anatomy and physiology of the GEJ.

During esophageal manometry, a catheter is inserted transnasally into the patient to provide measurements of the intraluminal pressure of the GEJ during swallowing (Castell and Richter, 2004; Gregersen, 2003; Tytgat, 1991). This is the standard method for evaluating GEJ function. The recorded intraluminal pressure profile of the GEJ is typically divided into three main stages. The first is known as the resting or basal pressure, which is recorded during the resting state of the GEJ and has been found to vary between 10–40 mmHg (1.33–5.33 kPa) (Christensen, 1987; Kahrilas, 1997; Patti et al., 1997; Richter et al., 1987; Shafik et al., 2006; Stein et al., 1995). When a swallow commences, the GEJ relaxes and the pressure drops to the relaxation pressure, which ranges between 0–12 mmHg (0–1.6 kPa) (Shi et al., 1998). The peak pressure is the maximum pressure caused by the contraction of the GEJ to empty the food into the stomach and can range between 50–80 mmHg (6.67–10.67 kPa) (Christensen, 1987; Mittal and Balaban, 1997; Sugarbaker et al., 1993; Tytgat, 1991). As the esophagus passes through the diaphragm, the GEJ is encircled by muscular portions of the diaphragm known as the crural pillars, which contribute to the total measured intraluminal pressure of the GEJ (Delattre et al., 2000). If the GEJ fails to relax or contract, the pressure recorded during manometry can detect such abnormalities. However, the contributions of the surrounding anatomical structures and the physiological functions related to the GEJ are difficult to assess using the current diagnostic methods.

The purpose of this study was to construct an anatomically- and physiologically-realistic computer model of the GEJ to aid in the understanding of how the anatomy and physiology of the GEJ are integrated in health and disease states, and to investigate the contribution of surrounding structures towards the functionality of this region. To this end, an anatomically-realistic three-dimensional (3D) model of the GEJ was constructed from cross-sectional images of the region. The governing equations of finite deformation elasticity were incorporated into the model and solved using the finite element method to investigate normal physiological behavior of human GEJ. The model was then used to investigate the contribution of the different muscle layers of the GEJ (longitudinal and circular), and the contribution of the crura to the behavior of the GEJ.

2 Materials and Methods

2.1 Constructing a three-dimensional model of the GEJ

To obtain a realistic geometric representation of the GEJ, a 3D model was constructed using the two-dimensional (2D) cross-sectional photographic images obtained from the Visible Human Project1 (Spitzer et al., 1996). The inner and outer boundaries of the esophageal wall and the crura were manually segmented from the images (spaced 2 mm apart). These segmented data were aligned, assembled and then used to construct 3D meshes of the esophagus and the crura using the methods outlined by Bradley et al. (1997). The surfaces of the meshes were represented using smoothly continuous cubic Hermite basis functions. The wall of the esophageal model was divided into two layers of equal thickness (Castell, 1995; Christensen, 1987; Liebermann-Meffert and Brauer, 1995) to represent the outer longitudinal muscle (LM) layer and the inner circular muscle (CM) layer (Castell and Richter, 2004) with appropriate fiber orientations.

In a healthy human, the GEJ is closed at rest, at the onset of swallowing the GEJ relaxes and opens to allow the passage of food to the stomach. The diameter of the GEJ was visually examined on the images obtained from the Visible Human Project and it was found that the lumen of the GEJ was in an open state. Therefore, the visible human data presented in this study was assumed to provide the relaxed or the stress- free reference state. The pressure of the GEJ in the relaxed state was assumed to be 0 mmHg.

2.2 Constitutive relations

A number of experiments have been carried out to obtain the stress-strain relationship of the esophagus at the zero-stress state in animals (Fan et al., 2004; Gregersen et al., 2000; Gregersen et al., 1999; Lu and Gregersen, 2001; Zhao et al., 2007) and in humans (Takeda et al., 2002). In addition, recent work has been carried out to describe the mechanical properties of the esophageal wall (Egorov et al., 2002; Takeda et al., 2004; Vanags et al., 2003) using different loading conditions and methods. However, to the best of our knowledge, a constitutive relation has not yet been developed to describe the mechanical behavior of the human GEJ.

Initial work on modeling the passive mechanical behavior of the esophagus in 2D has been carried out using animal data (Liao et al., 2003; Yang et al., 2004; Yang et al., 2006). The constitutive relations developed in these studies neglected the variations of stress and strain throughout the wall, as well as the muscle’s resistance to shear. To model the 3D physiological behavior of the muscular layers of the GEJ, we used the transversely isotropic constitutive relation proposed by Guccione, et al. (1991) to model cardiac ventricular muscle. The Guccione relation is capable of modeling the mechanical behavior of a tissue in 3D and also includes the resistance to shear. The strain-energy density function of this constitutive relation takes an exponential form as follows:

W¯=C2(eQ−1) (1)
whereQ=2c1(E11+E22+E33)+c2E112+c3(E222+E332+2E232)+2c4(E122+E132) (2)

The properties of the smooth muscle (longitudinal and circular) in the GEJ were described by the five material parameters, C, c1..c4, given in Equations (1) and (2). Trial simulations were carried out to examine the effect each material parameter had on the intraluminal pressure during muscle contraction of the GEJ. Using the conclusions drawn from these simulations, and by fitting the intraluminal pressure values predicted by the model to pressure values available from literature, the values of the parameters C, c1, c2, c3, and c4 were set to 1, 5, 195, 185, and 0.1 respectively.

2.3 Modeling active contraction of the esophagus

To model the active contraction of the muscle fibers in the GEJ, a technique previously developed to model the active contractile behavior of cardiac cells was used (Hunter et al., 1997; Malvern, 1969; Nash, 1998; Nash and Hunter, 2000). In this study, we assumed that the muscle fibers only generated active force in the direction of the fibers’ main axis and that the transverse and shear strains had no effect on the active tension generated by the fibers. To model the active contraction in the muscle fibers, an extra term was added to the 3D passive stress tensor in Equation (3):

TMN=12(∂W¯∂EMN+∂W¯∂ENM)−pCMN+TJ∂XM∂x1∂XN∂x1 (3)

where J = det F. The extra term altered the T11 component of the Cauchy stress tensor to include the active tension generated by the fiber, T. Further details can be obtained in Appendix A or from Hunter et al. (1998).

2.4 Modeling the intraluminal pressure

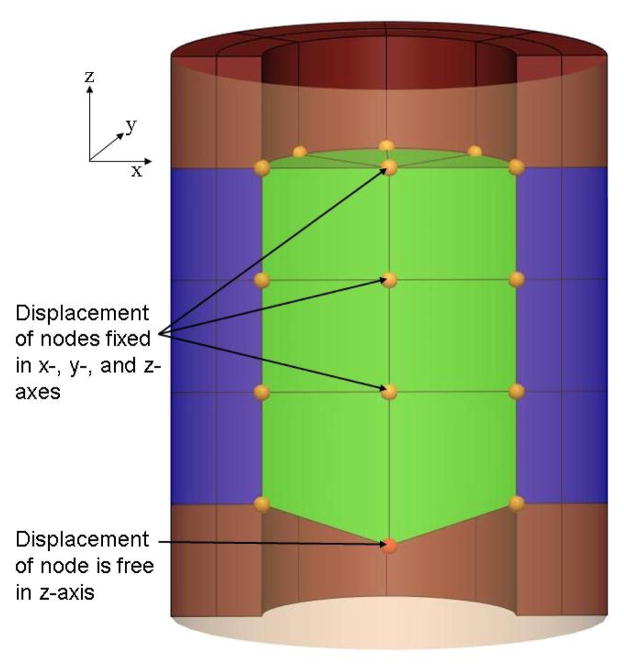
The intraluminal pressure recorded during manometry is due to the contraction of the GEJ against the manometer. A second mesh, referred to as the ‘cavity’ mesh, was created inside the GEJ lumen to calculate the intraluminal pressure values. Geometrically, the nodes of the outer wall of the cavity were identical to the nodes of the internal wall of the GEJ as illustrated with a cylindrical model in Figure 1. This method has previously been used to represent the blood in a model of cardiac mechanics (Nash, 1998). The cavity was assumed to be incompressible and all the elements of the cavity mesh have the same hydrostatic pressure value. This pressure was an additional solution degree of freedom (DOF), which was calculated using a single global constraint that equated the current volume of the cavity to the initial volume prior to contraction (Appendix B). As the mesh of the GEJ actively contracted, the size of the cavity mesh was expected to reduce in size. However, the cavity mesh was restricted to be of constant volume and therefore this leads to an increase in the cavity pressure, which was applied to the inner GEJ surface. To allow some movement in the radial direction of the GEJ mesh, one node of the cavity mesh (not shared with the GEJ mesh) was constrained to move approximately along the long axis of the GEJ. This additional constraint permitted contraction of the GEJ lumen while obeying the volume constraint of the cavity mesh. The displacement of the ‘free node’ in the axial direction was an additional solution DOF. The displacement of the free node was regulated to control the degree of cavity contraction, and hence the magnitude of the cavity pressure. To ensure the correct physiological movement of the GEJ towards the mouth (Winans, 1972), the displacements of the distal nodes connected to the stomach were fixed in all directions.

Figure 1.

Figure 1

Open in a new tab

A longitudinal cross-sectional view of a cylindrical model and a cavity mesh (lighter shade). The cavity mesh is visible through a transparent section of the cylindrical model. The displacements of the nodes of the cavity mesh were fixed in all directions with the exception of one node on the axis, which was constrained to move along the axial direction.

2.5 Mesh refinement and solution convergence

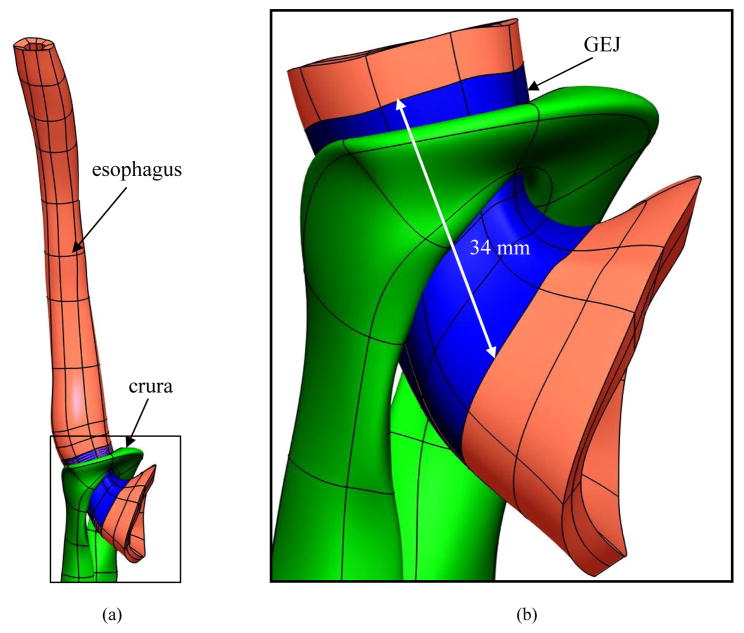
A portion of the 3D model of the esophagus was selected and used to model muscle contraction of the GEJ. The length of the GEJ has been found experimentally to range between 20–50 mm (Christensen, 1987; Kahrilas, 1997; Patti et al., 1997; Weinstock and Clouse, 1987; Winans, 1972). Some studies have shown that the proximal 20 mm of the GEJ is wrapped by the crura (Castell and Richter, 2004; Mittal and Balaban, 1997). The location of the crura in relation to the GEJ found in the literature was used to identify the GEJ in the 3D model. Therefore, the first mesh considered for simulations consisted of 80 tri-cubic Hermite elements, surrounded by the crura, representing a 34 mm long GEJ (blue region in Figure 2), 16 elements representing the lower esophagus and 32 elements representing the top part of the stomach (6305 total geometric degrees of freedom). The intraluminal pressure of the GEJ mesh was calculated as the global h-refinement was increased by sequentially dividing each element in half in each direction while maintaining regular element geometry. At each step a convergence analysis of the intraluminal pressure was performed.

Figure 2.

Figure 2

Open in a new tab

Identifying the external length of the GEJ using the location of the crura. (a) The crural mesh with respect to the 3D esophageal mesh. (b) Enlarged view illustrating the location of the crura in relation to the GEJ. The location of the crura was used to identify the GEJ.

An increased level of contraction was obtained with incremental increases of the Caactn parameter, which is a spatially constant non-dimensional parameter used to represent the level of activation. The peak pressure was obtained when the Caactn parameter reached the value of 1. At each loading step, convergence was achieved using 5–10 full Newton-Raphson iterations. Convergence was reached when the norm of residuals reached the tolerance of 1×10−8. Simulations of the GEJ model were carried out using a single 1.9 GHz processor of an IBM pSeries P595 computer (IBM, United States). Numerical simulations were all carried out using the CMISS2 software package.

2.6 Investigating the contribution of the crura

Both the GEJ and the crura contribute towards the intraluminal pressure of the GEJ measured during manometry. To investigate the contribution of the crura towards the physiological behavior of the GEJ, two simulations were carried out. In the first simulation, the muscle layers of the GEJ were actively contracted. In the second simulation, the GEJ was actively contracted whilst an external passive pressure of 37.5 mmHg (5 kPa) was applied to each of the elements of the LM layer surrounded by the crura. This load was estimated to account for the 44% contribution of the crura towards the final recorded pressure of the GEJ (Shafik et al., 2006). The external pressure was applied using incremental load steps each of 1.5 mmHg (0.2 kPa). Since this is a quasi-static problem, the external pressure and the Caactn parameter were incremented simultaneously.

During manometry recordings, the resting pressure is usually reached at approximately 45% of the time taken to reach the peak pressure. In this study, we assumed that the increase in the Caactn parameter varied linearly with respect to the time taken to reach the peak pressure. Therefore, the resting pressure was obtained when the Caactn parameter reached a value of 0.45. In both cases, with and without crural contribution, the Caactn parameter was increased in increments of 0.05 to ensure Newton convergence for nonlinear finite deformation elasticity mechanics. Intraluminal pressures of the GEJ due to muscle contraction with and without a crural contribution were calculated.

2.7 Examining the role of different muscle layers

Studies have speculated that the contribution of the GEJ to the intraluminal pressure is mainly due to the contraction of the innermost CM layer (Brasseur et al., 2007). In this study, we aimed to investigate the role of the CM layer towards the intraluminal pressure of the GEJ. The 3D model of the GEJ provided the flexibility to examine the respective role of each muscle layer in a way that is not feasible to perform experimentally on human subjects in-vivo. Within the GEJ model, each muscle layer was individually contracted and the effect on the intraluminal pressure was calculated.

3 Results

3.1 Mesh refinement and solution convergence

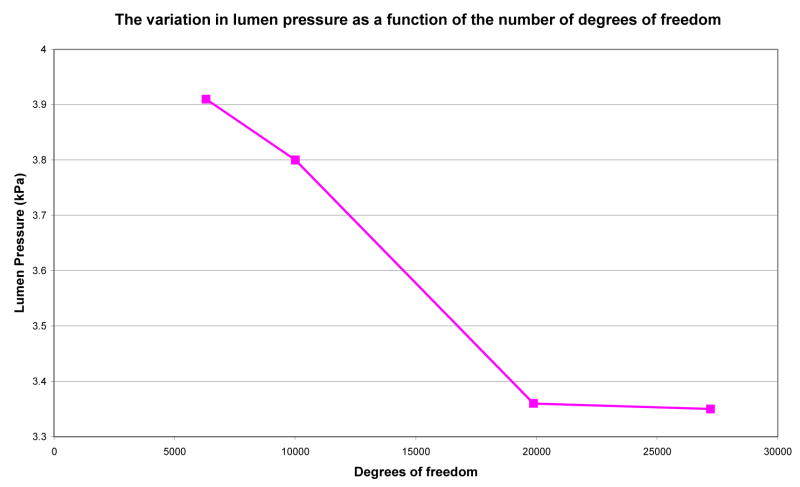
As shown in Figure 3, the change in the intraluminal pressure decreased with an increase in the number of DOF. The mesh with 19877 DOF was chosen in this study to model the physiological behavior of the GEJ as the mesh predicted converged pressure values. The mesh consisted of a total of 672 nodes, 416 tri-cubic Hermite elements. Thirty two elements represented the lower esophagus, 320 elements the GEJ and 64 elements represented the top region of the stomach. The CPU time for each simulation was approximately 2 days.

Figure 3.

Figure 3

Open in a new tab

The variation of intraluminal pressure as a function of the number of degrees of freedom of the GEJ computer model. The figure shows that the pressure value was converged when the mesh had 19877 degrees of freedom or more.

3.2 Contribution of the crura

Intraluminal pressures of the GEJ due to muscle contraction with and without a crural contribution were calculated. Table 1 lists the pressure of the 3D model due to the contraction of the GEJ with and without the contribution of the crura. Results from the 3D model show that approximately 53% of the intraluminal pressure was due to the GEJ.

Table 1.

The intraluminal pressure values predicted by the model during the contraction of the GEJ with and without the contribution of the crura.

With crural contribution GEJ only
Basal pressure mmHg (kPa) 22 (2.95) 12 (1.54)
Experimental basal pressure mmHg (kPa) 10–40 (1.33–5.33)3 6–22 (0.74 – 2.98)4
Peak pressure mmHg (kPa) 52 (6.96) 28 (3.78)
Experimental peak pressure mmHg (kPa) 50–80 (6.67–10.67)5 28–45 (3.74–5.98)
Open in a new tab
4

Values have been calculated by subtracting the 44% contribution of the crura from the values with crural contribution.

5

Values were taken from the following references (Christensen, 1987; Mittal and Balaban, 1997; Sugarbaker et al., 1993; Tytgat, 1991).

3.3 The role of muscle contraction

Results obtained from examining the role of each muscle layer are listed in Table 2 and show that the pressure values obtained from the 3D model are mainly due to the contraction of the CM layer. If the CM layer was quiescent, the contraction of the LM layer resulted in an expansion of the GEJ. This expansion is illustrated by the negative intraluminal pressure during the contraction of only the LM. However, with the presence of both layers, the contraction of the CM layer dominated the effect of the LM layer and resulted in an overall increase in pressure.

Table 2.

The intraluminal pressure values predicted by the model with the contraction of each individual muscle layer, and both layers of the GEJ. CM (circular muscle), LM (longitudinal muscle),.

LM only CM only Both layers
Basal pressure mmHg (kPa) −4 (−0.49) 15 (2.04) 12 (1.54)
Peak pressure mmHg (kPa) −7 (−0.97) 38 (5.11) 28 (3.78)
Open in a new tab

4 Discussion

A mathematical model that provides a realistic representation of a human GEJ would be beneficial to perform numerical studies in order to provide a better understanding of the functionality of the GEJ both in health and disease states. In order to accurately model the behavior of the different layers that contribute to the functionality of the GEJ, a more detailed understanding of the correlation between the physiology and anatomy is required. Such information includes the tissue properties of the different layers of the human GEJ, and a constitutive relation to model the behavior of these tissues, which is presently lacking. With the limited available data in the literature, the focus of our study was to construct a computer model that provides a prediction of the intraluminal pressure and can be validated with pressure recordings from manometry.

The intraluminal pressure results obtained from the 3D model constructed in this study showed a 53% contribution of the GEJ to the overall pressure, which was similar to the predicted value of 56% from experimental data available in the literature (Shafik et al., 2006). Results showed that the 3D model presented in this study, was capable of predicting realistic intraluminal pressure values when modeling the contraction of a normal GEJ.

To examine the role of each muscle layer, the muscle layers were each contracted individually while the other layer was quiescent. Results showed that the intraluminal pressure values predicted by the 3D model are mainly due to the contraction of the CM layer, and are consistent with the predictions of experimental data found in the literature (Edmundowicz and Clouse, 1991; Nicosia et al., 2001; Pouderoux et al., 1997). Results also showed that while the CM was quiescent, the contraction of the LM layer resulted in an expansion of the GEJ. Similar behavior has previously been reported by Nicosia, et al. (2001) during a 2.5 s period where the contraction of the LM layer preceded the contraction of the CM layer. The benefit of using the 3D model was the ability to show the role of the LM layer over a prolonged period of time and during quiescence of the CM layer.

One of the limitations with the model presented in this study was the uniform pressure magnitude in the circumferential and longitudinal directions due to the use of the cavity mesh. However, Stein et al., (1995) and Liu et al., (1997) have shown that the pressure recorded from the GEJ is axially asymmetrical due to the axial asymmetry of the muscles thickness of the GEJ. The ability to allow variation of pressure throughout the cavity mesh may result in a more realistic pressure profile that could be directly compared with experimental measurements.

Furthermore, to obtain a more realistic physiological model of the GEJ, a specific constitutive relation describing the properties of the smooth muscle layers of a human GEJ is needed. With the availability of a smooth muscle constitutive relation, the 3D model could be used to include the asymmetry of the GEJ and predict different intraluminal pressure values around the circumference of the GEJ as is reported in the literature. The dynamics of the peristaltic wave along the lower esophagus and the GEJ could also be incorporated by spatially varying the calcium activation parameter (Caactn). With the developments of the GEJ model, the contribution of surrounding structures that contribute to the functionality of the GEJ could also be included.

Although simulations are time consuming, with the rapid developments of computer hardware, and with the use of parallel processing, the development of the 3D computer model of the GEJ has several potential applications. The anatomical model could be adapted to provide a useful tool for health professional training and patient education. Also, the 3D model could be used to mimic the physiological behavior of a human GEJ. In addition to modeling normal physiological events, it is also possible to use the 3D model to study abnormal physiology, such as gastroesophageal reflux disease. Our long term goal is to construct 3D computer models on an individual-specific basis using CT or MR images from patients. Such patient-specific modeling may allow the ability to custom design aspects of an operation. In addition, results obtained from the model could potentially be used to guide clinical trials on an individual-specific basis.

Supplementary Material

01

Acknowledgments

The authors would like to acknowledge the assistance of Dr Jae-Hoon Chung. The authors would also like to thank Dr Ian Wallace for demonstrating the use of manometry and Prof. Stuart Heap for the barium swallow demonstration. This work has been funded by the Royal Society of NZ Marsden Grant and the NIH grant R01 DK64775

Grant: This work has been funded by the Royal Society of NZ Marsden Grant and the NIH grant R01 DK64775

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

References

  1. Bombeck CT, Dillard DH, Nyhus LM. Muscular Anatomy of the Gastroesophageal Junction and Role of Phrenoesophageal Ligament. Annals of Surgery. 1966;164(4):643–654. doi: 10.1097/00000658-196610000-00011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Bradley CP, Pullan AJ, Hunter PJ. Geometric Modelling of the Human Torso Using Cubic Hermite Elements. Annals of Biomedical Engineering. 1997;76(7):96–111. doi: 10.1007/BF02738542. [DOI] [PubMed] [Google Scholar]
  3. Brasseur JG, Nicosia MA, Pal A, Miller LS. Function of Longitudinal vs Circular Muscle Fibers in Esophageal Peristalsis, Deduced with Mathematical Modeling. World Journal of Gastroenterology. 2007;13(9):1335–1346. doi: 10.3748/wjg.v13.i9.1335. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Castell DO. The Lower Esophageal Sphincter. Annals of Internal Medicine. 1975;83:390–401. doi: 10.7326/0003-4819-83-3-390. [DOI] [PubMed] [Google Scholar]
  5. Castell DO. The Esophagus. 2. United States of America: Little, Brown and Company; 1995. pp. 1–9.pp. 133–144. [Google Scholar]
  6. Castell DO, Richter JE. The Esophagus. 4. Philadelphis: Lippincott Williams and Wilkins; 2004. p. 714. [Google Scholar]
  7. Christensen J. Physiology of Gastrointestinal Tract: motor functions of the pharynx and esophagus. 2. New York: Raven Press; 1987. pp. 595–612. [Google Scholar]
  8. Delattre J-F, Avisse C, Marcus C, Flament J-B. Functional Anatomy of the Gastroesophageal Junction. Surgical Clinics of North America: Surgical Anatomy and Embryology. 2000;80(1):241–260. doi: 10.1016/s0039-6109(05)70404-7. [DOI] [PubMed] [Google Scholar]
  9. Edmundowicz SA, Clouse RE. Shortening of the Esophagus in Response to Swallowing. American Journal of Physiology: Gastrointestinal and Liver Physiology. 1991;260(23):G512–G516. doi: 10.1152/ajpgi.1991.260.3.G512. [DOI] [PubMed] [Google Scholar]
  10. Egorov VI, Schastlivtsev IV, Prut EV, Baranov AO, Turusov RA. Mechanical Properties of the Human Gastrointestinal Tract. Journal of Biomechanics. 2002;35:1417–1425. doi: 10.1016/s0021-9290(02)00084-2. [DOI] [PubMed] [Google Scholar]
  11. Fan Y, Gregersen H, Kassab GS. A Two-layered Mechanical Model of the Rat Esophagus: experiment and theory. BioMedical Engineering OnLine. 2004;3(40):1–9. doi: 10.1186/1475-925X-3-40. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Gray SW, Rowe JS, Skandalakis JE. Surgical Anatomy of the Gastroesophageal Junction. The American Surgeon. 1979;45(9):575–587. [PubMed] [Google Scholar]
  13. Gregersen H. Biomechanics of the Gastrointestinal Tract: new perspectives in motility research and diagnostics. London: Springer; 2003. p. 268. [Google Scholar]
  14. Gregersen H, Kassab GS, Fung YC. The Zero-Stress State of the Gastrointestinal Tract: biomechanical and functional implications. Digestive Diseases and Sciences. 2000;45(12):2271–2281. doi: 10.1023/a:1005649520386. [DOI] [PubMed] [Google Scholar]
  15. Gregersen H, Lee TC, Chien S, Skalak R, Fung YC. Strain Distribution in the Layered Wall of the Esophagus. Journal of Biomechanical Engineering. 1999;121:442–448. doi: 10.1115/1.2835072. [DOI] [PubMed] [Google Scholar]
  16. Guccione JM, McCulloch AD, Waldman LK. Passive Material Properties of Intact Ventricular Myocardium Determined From a Cylindrical Model. Journal of Biomechanical Engineering. 1991;113:42–55. doi: 10.1115/1.2894084. [DOI] [PubMed] [Google Scholar]
  17. Hunter PJ, McCulloch A, ter-Keurs HEDJ. Modelling the Mechanical Properties of Cardiac Muscle. Progress in Biophysics and Molecular Biology. 1998;69(2):289–331. doi: 10.1016/s0079-6107(98)00013-3. [DOI] [PubMed] [Google Scholar]
  18. Hunter PJ, Nash MP, Sands GB. Computational electromechanics of the heart. In: Panfilov AV, Holden AV, editors. Computational Biology of the Heart. West Sussex UK: John Wiley and Sons Ltd; 1997. pp. 345–407. [Google Scholar]
  19. Kahrilas PJ. Anatomy and Physiology of the Gastroesophageal Junction. Gastroenterology Clinics of North America: The Columnar-Lined Esophagus. 1997;26(3):467–486. doi: 10.1016/s0889-8553(05)70307-1. [DOI] [PubMed] [Google Scholar]
  20. Liao D, Fan Y, Zeng Y, Gregersen H. Stress Distribution in the Layered Wall of the Rat Oesophagus. Medical Engineering and Physics. 2003;25:731–738. doi: 10.1016/s1350-4533(03)00122-x. [DOI] [PubMed] [Google Scholar]
  21. Liebermann-Meffert D, Brauer RB. Surgery of the Esophagus, Stomach, and Small Intestine: surgical anatomy of the distal esophagus and cardia. 5. Boston: Little, Brown and Company; 1995. pp. 32–44. [Google Scholar]
  22. Liu J, Parashar VK, Mittal RK. Asymmetry of Lower Esophageal Sphincter Pressure: is it related to the muscle thickness or its shape. American Journal of Physiology: Gastrointestinal and Liver Physiology. 1997;272(35):G1509–G1517. doi: 10.1152/ajpgi.1997.272.6.G1509. [DOI] [PubMed] [Google Scholar]
  23. Lu X, Gregersen H. Regional Distribution of Axial Strain and Circumferential Residual Strain in the Layered Rabbit Oesophagus. Journal of Biomechanics. 2001;34:225–233. doi: 10.1016/s0021-9290(00)00176-7. [DOI] [PubMed] [Google Scholar]
  24. Malvern LE. Introduction to the Mechanics of a Continuous Medium. New Jersey: Prentice-Hall Inc; 1969. [Google Scholar]
  25. Mittal RK, Balaban DH. The Esophagogastric Junction. The New England Journal of Medicine. 1997;336(13):924–932. doi: 10.1056/NEJM199703273361306. [DOI] [PubMed] [Google Scholar]
  26. Mosher HP. The Lower end of the Oesophagus at Birth and in the Adult. The Journal of Laryngology and Otology. 1930;45(3):161–180. [Google Scholar]
  27. Nash MP. PhD Thesis. Auckland: The University of Auckland; 1998. Mechanics and Material Properties of the Heart using an Anatomically Accurate Mathematical Model; p. 246. [Google Scholar]
  28. Nash MP, Hunter PJ. Computational mechanics of the heart: From tissue structure to ventricular function. Journal of Elasticity. 2000;61(1–3):113–141. [Google Scholar]
  29. Nicosia MA, Brasseur JG, Liu J-B, Miller LS. Local Longitudinal Muscle Shortening of the Human Esophagus from High-Frequency Ultrasonography. American Journal of Physiology: Gastrointestinal and Liver Physiology. 2001;281:G1022–G1033. doi: 10.1152/ajpgi.2001.281.4.G1022. [DOI] [PubMed] [Google Scholar]
  30. Patti MG, Gantert W, Way LW. Surgery of the Esophagus: Anatomy and Physiology. Surgical Clinics of North America: Surgery of the Esophagus. 1997;77(5):959–970. doi: 10.1016/s0039-6109(05)70600-9. [DOI] [PubMed] [Google Scholar]
  31. Pouderoux P, Lin S, Kahrilas PJ. Timing, Propagation, Coordination, and Effect of Esophageal Shortening During Peristalsis. Gastroenterology. 1997;112:1147–1154. doi: 10.1016/s0016-5085(97)70125-2. [DOI] [PubMed] [Google Scholar]
  32. Richter JE, Wu WC, Johns DN, Blackwell JN, Nelson JL, Castell JA, Castell DO. Esophageal Manometry in 95 Healthy Adult Volunteers: variability of pressures with age and frequency of “abnormal” contractions. Digestive Diseases and Sciences. 1987;32(6):583–592. doi: 10.1007/BF01296157. [DOI] [PubMed] [Google Scholar]
  33. Shafik A, Shafik I, El-Sibai O, Mostafa RM. The Effect of Esophageal and Gastric Distension on the Crural Diaphragm. World Journal of Surgery. 2006;30:199–204. doi: 10.1007/s00268-005-0282-8. [DOI] [PubMed] [Google Scholar]
  34. Shi G, Ergun GA, Manka M, Kahrilas PJ. Lower Esophageal Sphincter Relaxation Characteristics Using a Sleeve Sensor in Clinical Manometry. The American Journal of Gastroenterology. 1998;93(12):2373–2379. doi: 10.1111/j.1572-0241.1998.00690.x. [DOI] [PubMed] [Google Scholar]
  35. Spitzer V, Ackerman MJ, Scherzinger AL, Whitlock D. The visible human male: a technical report. Journal of the American Medical Informatics Association. 1996;3(2):118–130. doi: 10.1136/jamia.1996.96236280. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Stein HJ, Liebermann-Meffert D, Demeester TR, Siewert JR. Three-dimensional Pressure Image and Muscular Structure of the Human Lower Esophageal Sphincter. Surgery. 1995;117(6):692–698. doi: 10.1016/s0039-6060(95)80014-x. [DOI] [PubMed] [Google Scholar]
  37. Sugarbaker DJ, Kearney DJ, Richards WG. Esophageal Physiology and Pathophysiology. Surgical Clinics of North America: Motility Disorders of the Gastrointestinal Tract. 1993;73(6):1101–1118. doi: 10.1016/s0039-6109(16)46182-7. [DOI] [PubMed] [Google Scholar]
  38. Takeda T, Kassab GS, Liu J, Puckett JL, Mittal RR, Mittal RK. A Novel Ultrasound Technique to Study the Biomechanics of the Human Esophagus in Vivo. American Journal of Physiology: Gastrointestinal and Liver Physiology. 2002;282:785–793. doi: 10.1152/ajpgi.00394.2001. [DOI] [PubMed] [Google Scholar]
  39. Takeda T, Nabae T, Kassab GS, Liu J, Mittal RK. Oesophageal Wall Stretch: the stimulus for distension induced oesophageal sensation. Neurogastroenterol and Motility. 2004;16:721–728. doi: 10.1111/j.1365-2982.2004.00620.x. [DOI] [PubMed] [Google Scholar]
  40. Tytgat GNJ. Gastro-Oesophageal Reflux and Gastric Stasis: pathophysiology, diagnosis and therapy. Auckland: Adis International Ltd; 1991. p. 144. [Google Scholar]
  41. Vanags I, Petersons A, Ose V, Ozolanta I, Kasyanov V, Laizans J, Vjaters E, Gardovskis J, Vanags A. Biomedical Properties of Oesophagus Wall Under Loading. Journal of Biomechanics. 2003;36:1387–1390. doi: 10.1016/s0021-9290(03)00160-x. [DOI] [PubMed] [Google Scholar]
  42. Weinstock LB, Clouse RE. Esophageal Physiology: normal and abnormal motor function. The American Journal of Gastroenterology. 1987;82(5):399–405. [PubMed] [Google Scholar]
  43. Winans CS. Alteration of Lower Esophageal Sphincter Characteristics with Respiration and Proximal Esophageal Balloon Distension. Gastroenterology. 1972;62(3):380–388. [PubMed] [Google Scholar]
  44. Yang J, Liao D, Zhao J, Gregersen H. Shear Modulus of Elasticity of the Esophagus. Annals of Biomedical Engineering. 2004;32(9):1223–1230. doi: 10.1114/b:abme.0000039356.24821.6c. [DOI] [PubMed] [Google Scholar]
  45. Yang J, Zhao J, Liao D, Gregersen H. Biomechanical Properties of the Layered Oesophagus and its Remodelling in Experimental Type-1 Diabetes. Journal of Biomechanics. 2006;39:894–904. doi: 10.1016/j.jbiomech.2005.01.022. [DOI] [PubMed] [Google Scholar]
  46. Zhao J, Chen X, Yang J, Liao D, Gregersen H. Opening Angle and Residual Strain in a Three-layered Model of Pig Oesophagus. Journal of Biomechanics. 2007;40(14):3187–3192. doi: 10.1016/j.jbiomech.2007.04.002. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

01
NIHMS128781-supplement-01.doc (38KB, doc)

RESOURCES