A Survey of the Likelihood Approach to Bioequivalence Trials

SUMMARY

Bioequivalence trials are abbreviated clinical trials whereby a generic drug or new formulation is evaluated to determine if it is “equivalent” to a corresponding previously approved brand-name drug or formulation. In this manuscript, we survey the process of testing bioequivalence and advocate the likelihood paradigm for representing the resulting data as evidence. We emphasize the unique conflicts between hypothesis testing and confidence intervals in this area - which we believe are indicative of the existence of the systemic defects in the frequentist approach - that the likelihood paradigm avoids. We suggest the direct use of profile likelihoods for evaluating bioequivalence. We discuss how the likelihood approach is useful to present the evidence for both average and population bioequivalence within a unified framework. We also examine the main properties of profile likelihoods and estimated likelihoods under simulation. This simulation study shows that profile likelihoods offer a viable alternative to the (unknown) true likelihood for a range of parameters commensurate with bioequivalence research.

1. Introduction

When pharmaceutical companies would like to market a generic drug after the patent of a brand-name drug expires or when they would like to market a new formulation of an approved drug, regulatory authorities do not require the performance of costly full scale clinical trials to demonstrate the efficacy and safety. Instead, pharmaceutical companies conduct bioequivalence (BE) trials to establish that the generic drug or new formulation (“the test”) is bioequivalent to the brand-name drug or originally approved drug (“the reference”).

It might seem strange, for those who are not familiar with BE trials, that a drug formulation containing the same active ingredient can show different effects or toxicities. Two formulations having different excipients, or the same excipients formulated differently, can result in different effects. Stated more succinctly, chemical equivalence of the active agent does not guarantee biological equivalence. Such problems often occur when the drugs have a narrow therapeutic index, as with digoxin (a heart medication), warfarin (a blood thinner), sustained-release theophylline formulations (asthma medications) and phenytoin (an anticonvulsant or antiepileptic drug). For example, digoxin intoxication in 1977 received a great deal of public attention [1] due to inadvertent toxicity attributed to generic drugs that were not bioequivalent to the brand name drug.

Balancing the need to protect patients from the failure of treatment or toxicity via rigorous evaluation methods, is the desire for safe and effective generic drugs, which are typically less expensive. As such, bioequivalence trials are of interest to many groups: pharmaceutical companies, insurance companies, prescribing doctors, pharmacists, patient-consumer groups, regulatory authorities, etcetera. Moreover, because their interests do not always coincide, discussions regarding bioequivalence statistical methodology are complex and even sometimes politically charged (see Metzler [2]). In this manuscript, we propose the use of the likelihood as a useful first step in summarizing the data as evidence, regardless of the researcher’s perspective.

There are several statistical challenges in BE trials. First, unlike most statistical analysis, interest does not lie in estimating the parameter of interest, the difference between the test and the reference. Rather we are interested in whether the parameter of interest lies within an equivalent range. Second, we may want to ensure that both the means and the variances of the test and the reference are equivalent, giving rise to average and population BE respectively. Third, we may also want to evaluate two correlated measures in BE trials together, the area under the curve and the maximum plasma concentration. Such as proposed likelihood approach can address these challenges appropriately. We propose the use of standardized likelihood plots, which display a continuous scale of evidence regarding how much the data support the neighbor values of the maximum likelihood estimate (MLE). We propose to quantify evidence for both average and population BE within a unified framework of the likelihood paradigm. We will show the importance of the consideration of both average and population BE together, especially for highly variable drugs. We will also present how the strength of evidence can be decoupled from the probability of misleading evidence, an analogue of the type I error rate. This fundamental step is missing in the current practice of BE trials, where the P-values have been incorrectly used for both measuring the strength of evidence and the observed type I error rate [3]. Since there are several nuisance parameters, we use the profile likelihood and performed simulation studies to examine its operating characteristics in the BE setting. We believe this is the first manuscript to propose and evaluate the use of these methods in the BE setting.

This manuscript outline is as follows. In Section 2.1–2.3, we review the basic concepts of BE while in Section 2.4 we examine problems in the current statistical practice in BE trials. Section 3 describes the likelihood paradigm while Section 4 illustrates how this paradigm can be applied to BE trials. Moreover, we examine important properties of profile likelihoods using simulation. A summary and discussion follows in Section 5.

2. A Review of Bioequivalence Testing

2.1. Definition and metrics of bioequivalence

The bioequivalence of a test and reference formulation depends on the closeness of characteristics of the extent and rate of absorption, generally referred to as the bioavailability of the drug. To measure bioavailability, pharmacokinetic (PK) studies are carried out. In PK studies, drug concentrations measured from blood samples obtained at pre-specified sampling times for each subject are summarized as AUC, C_max, and the time to reach the maximum concentration (t_max), all of which represent bioavailability. Comparisons between these measures are used to determine bioequivalence. Thus BE relies on the fundamental assumption that two formulations are therapeutically equivalent if their bioavailabilities are the same.

The metric AUC holds a special place amongst these summaries, being the required primary metric of the extent of absorption for most countries. The C_max is also an important metric, being a measure of the rate of absorption, although many researchers criticized its usage arguing that it is confounded by the amount of absorption. A number of alternative metrics have been suggested. For example, C_max/AUC [4] or partial AUC [5], as a better measure of the rate of absorption, but none have been proven satisfactory [6]. Sometimes t_max is employed as a measure of rate of absorption, although its poor temporal resolution, due to the discrete nature of the sampling times, limits its use. Despite this ongoing interest and research in other metrics, AUC and C_max remain the most important summaries for BE trials, and hence remain our primary focus.

2.2. Distributional assumptions for metrics in BE trials

Before performing a statistical analysis in BE trials, AUC and C_max are generally log transformed. The three most commonly cited reasons for using the log transformed AUC are that: i) AUC is non-negative, ii) the distribution of AUC is highly skewed, iii) PK models are multiplicative, both theoretically and conceptually. Further discussion of the third reason is as follows.

As a conceptual rationale for the log-normal model, we note that many biological effects act multiplicatively, as well described in Limpert et al. [7]. If an outcome is the result of many random causes, each of which produces a small proportional effect, then the resulting distribution is often log-normal [8]. Since the drug concentration at each time is a function of many random processes (absorption, distribution, metabolism and elimination) that reasonably would act proportionally to the amount of drug present in the body, this suggests that the resulting distribution is log-normal [9].

More theoretically, the FDA [10] provides a pharmacokinetic rationale based on Westlake [11] which states that PK models are comprised of multiplicative components. Assuming that the elimination of the drug is first-order and only occurs from the central compartment, AUC can be expressed as follows:

$$\mathit{\text{AUC}}=\frac{\mathit{\text{FD}}}{\mathit{\text{CL}}}=\frac{\mathit{\text{FD}}}{{\mathit{\text{Vk}}}_e},$$

where F is the fraction of drug absorbed, D is the administered dose, CL is the clearance, V is the apparent volume of distribution, and k_e is the elimination rate constant. Notice that AUC involves multiplicative terms of the PK parameters (F, V, and k_e). A log transformation of AUC results in the PK parameters entering as additively. Furthermore, if we are willing to assume that the distributions of PK parameters are log-normal, then the distribution of AUC is also log-normal.

Although there has been only a small amount of research on the distribution of PK parameters, all of the available studies support that the data are more consistent with the log-normal distribution than the normal distribution [12, 13, 14]. Based on these results and rationale, our discussion assumes that the metric is log transformed.

2.3. Design and analysis of BE trials

In a typical BE trial, the test (T) and the reference (R) formulations are administered to (12 to 30) healthy volunteers and the drug concentrations are measured over time. Frequently cross-over designs are employed, although parallel group designs are used as well. Cross-over designs are generally preferred, because of their ability to compare the test and reference formulations within a subject. As such, our discussions focus on BE trials using a 2 × 2 cross-over design.

Throughout we assume the critical assumption that there is no carry-over effect, or that the carry-over effect is negligible. Such carry-over effects can be due to left-over active drug in the previous period, due to psychological effects [15] or other pharmacologic effects, such as induction of metabolism or elimination by the previously administered drug. However, the carry-over effect is often negligible in most BE trials [16, 17].

Design issues aside, analyses of BE trials often considers average bioequivalence (ABE) as a primary goal. The purpose of average bioequivalence studies is to show that the population means of the test and the reference are sufficiently close. Establishing ABE has been the only required criteria in BE trials for more than 20 years in many countries.

The current USA FDA guidelines [10] declare the test and the reference as average bioequivalent if the difference in their population means is within the regulatory limit, say θ_A. That is

$$|{\mu }_T-{\mu }_R|\le {\theta }_A,$$

where μ_T and μ_R are the population means of the log-transformed measure for the test and the reference, respectively, and (usually) θ_A = log 1.25 = −log 0.80 = 0.223. This value is originated from the notion that the ratio of the population means in the original scale of 0.80 – 1.25 (the mean of the test is 80 – 125% of that of the reference) is considered as sufficiently close for drugs having an average therapeutic window.

Since Anderson and Hauck [18] raised the issue of “switchability” between the old formulation and the new formulation, individual bioequivalence (IBE) and population bioequivalence (PBE) garnered more attention.

When a physician wants to switch a drug from an old formulation to a new one for her patient who has been titrated for the old formulation, she requires evidence that the new formulation is as safe and effective as the old. This concept is called switchability. Establishing IBE is intended to ensure switchability between two formulations within individuals. Anderson and Hauck [18] defined two formulations as individually bioequivalent if they are sufficiently close for most subjects and proposed a method to evaluate IBE, based on the binomial distribution.

On the other hand, if physicians prescribe the new formulation for new patients, then there is a need to ensure that the two formulations are sufficiently close in the population. This concept is referred to as “prescribability”; PBE is intended to ensure prescribability. The two formulations are declared population bioequivalent if the distributions (usually just the means and variances) of two formulations are sufficiently close. Thus, PBE conceptually includes ABE.

The USA FDA recommended replacing ABE with PBE and IBE. However, PBE and IBE are not required for approval of BE, perhaps because the suggested approach is not completely satisfactory from both practical and statistical viewpoints. Depending on the variability of the drug, they adopted the mixed-scaling approach for both PBE and IBE. A brief description of the current USA FDA [10] for PBE follows.

The test and the reference are population bioequivalent if the squared difference of their population means plus the difference in the total variances of the two formulations relative to a bounded version of the total variance of the reference is within the regulatory limit θ_P. That is:

$$\frac{{({\mu }_T-{\mu }_R)}^2+({\sigma }_{\mathit{\text{TT}}}^2-{\sigma }_{\mathit{\text{RR}}}^2)}{\text{max}({\sigma }_{\mathit{\text{RR}}}^2,{\sigma }_{T0}^2)}\le {\theta }_P,$$

where ${\sigma }_{\mathit{\text{TT}}}^2={\sigma }_{\mathit{\text{WT}}}^2+{\sigma }_{\mathit{\text{BT}}}^2\text{and}{\sigma }_{\mathit{\text{RR}}}^2={\sigma }_{\mathit{\text{WR}}}^2+{\sigma }_{\mathit{\text{BR}}}^2$ are the total variances of the test and the reference. Here the subscripts W and B refer to “within” and “between” subjects. The constants, ${\sigma }_{T0}^2$ and θ_P, are fixed regulatory standards.

As seen above, the USA guidance currently adopts an aggregate approach, using an aggregated test statistic for evaluating both means and variance components at the same time. However, it is difficult to evaluate which component contributes bioinequivalence as well as the statistical properties for the suggested statistics are unknown. In contrast, several disaggregate approaches have been suggested where tests for each component are performed separately. For example, Liu and Chow [26] proposed to use a disaggregate approach for evaluating IBE where three components (intrasubject variability, subject-by-formulation interaction, and average) are separately tested applying multiple times of intersection-union tests. However, as the dimension (p) of tests increases, the power of the (1 − 2α) confidence set based approach, could decrease sharply for p > 1 as shown in Hwang [19]. We adopt a disaggregate approach for evaluating PBE, which can highlight a source of inequivalence more clearly.

2.4. Testing methodology

A review of the main articles in the development of BE tests reveals the (at a first glance) odd fact that 100(1 − 2α)% confidence intervals are often used when the level of type I error for the consumer’s risk is to be controlled at most α%. In fact, there has been much debate among pharmaceutical scientists about which confidence level should be used, 100(1 − 2α)% or 100(1 − α)%. Table I illustrates several examples of BE tests with different operational confidence levels despite a constant desired nominal level of α = 0.05. Currently, the USA FDA guidance adopts the two one-sided tests (TOST) as the standard method of ABE; hence, recommending the 100(1 − 2α)% confidence interval which (discussed below) is an operational equivalent of TOST.

Table I.

The comparison of operational methods and the nominal level of α among several proposed BE tests.

Paper	Operational Method
Metzler [2] and Kirkwood [20]	100(1 − α)% confidence interval
FDA [10]	100(1 − 2α)% confidence interval
Westlake [21]	100(1 − α)% symmetric confidence interval
Anderson and Hauck [22]	P-value (level α)
Locke [23]	100(1 − α)% confidence interval
Schuirmann [24]	two one-sided tests (level α for each test)

Consider the problem where interest lies in estimating the difference in the population means of the two formulations, θ = μ_T − μ_R. If BE holds, one would expect the estimate of θ to be within regulatory boundaries of 0, say between δ_L and δ_U. In this setting, the statement “the two formulations are bioequivalent if the 100(1 − α)% confidence interval is contained within δ_L and δ_U” seems reasonable. On the other hand, consider casting the problem as two one-sided hypothesis tests consisting of the hypotheses H₀₁ : θ ≤ δ_L vs. H_a1 : θ ≥ δ_L and H₀₂ : θ ≤ δ_U vs. H_a2 : θ ≤ δ_U. Then, the statement “the two formulations are bioequivalent if both null hypotheses are rejected at the level α” seems equally reasonable.

With regard this distinction Berger and Hsu [25] commented in Section 2.3

… our conclusion is that the practice of defining bioequivalence tests in terms of 100(1 − 2α)% confidence intervals should be abandoned. If both a confidence interval and a test are required, a 100(1 − α)% confidence intervals that corresponds to the given size-α test should be used.

They proved that the suggested 100(1 − α)% confidence interval has the correct size. However, the suggested interval is exactly same as the classical 100(1 − 2α)% confidence interval when the interval includes zero, which is typical for most BE trials, unless the variances of two formulations are very small or the two formulations are obviously bioinequivalent. Liu and Chow [26] showed that the conclusion for bioequivalence/bioinequivalence would be the same from the two procedures in a variety of scenarios.

These results beg the question of why these mathematically correct results defy experimental intuition. We believe that this conflict between intuition and mathematics, indicates a defect in the logical framework. As discussed by Blume [27], strength of evidence and control of the type I error rate should be distinguished, an impossibility in the frequentist framework. This is one of the motivations of this research. Hence, we present an alternative framework developed by Hacking [28], Edwards [29] and Royall [30], which does not suffer from some of the fundamental flaws in the current statistical practices in this area.

3. The Likelihood Paradigm

The source of the confusion amongst the frequentist approaches in BE trials arises from viewing the data as a decision making tool, rather than representing the data as evidence. Such practice skips the fundamental step of evaluating what the data say.

Given a statistical model for the observed data, the Law of the Likelihood plays the fundamental role in interpreting data as evidence. It was coined by Hacking [28], and restated in Royall [30]:

Law of the Likelihood: If hypothesis A implies that the probability that a random variable X takes the value x is p_A(x), while hypothesis B implies that the probability is p_B(x), then the observation X = x is evidence supporting A over B if and only if p_A(x) > p_B(x), and the likelihood ratio, p_A(x)/p_B(x), measures the strength of that evidence.

When we have a random variable X whose probability model is indexed by a parameter θ, an observation x generates a likelihood function, L(θ; x). As a consequence of the Law of the Likelihood, the Likelihood Principle, formally stated by Birnbaum [31], suggests that experimental results are fully characterized by the likelihood function. Therefore, two experiments resulting identical likelihood functions have the same evidential meaning.

The Likelihood Principle has far-reaching consequences for statistical practice. For example, it implies that the sample space or experimental design has no bearing on its evidential interpretation. Hence, frequency-style interpretations leading to P-values and confidence intervals, which depend on the sample space, experimental design or fictitious repetitions of the experiment, do not lead to evidential interpretations.

Royall and other proponents of this likelihood paradigm, apply the Likelihood Principle and suggest representing the data as evidence using a standardized likelihood plot, which is the plot of the likelihood values divided by MLE as a function of the parameter of interest. The plot succinctly presents the likelihood ratios of all alternatives values versus MLE over the wide range of the parameter values. Reference lines can be drawn to indicate 1/k likelihood intervals which summarize a set of supported values consistent with data. Royall [30] provides an intuitive interpretation of several benchmarks k such as k = 8 or k = 32 as “moderate” or “strong” evidence. Notice, however, that k is on a continuum in measuring the strength of evidence and hence the labeling various values of k as weak or strong is as much arbitrary as using 5% for type I error rates. An excellent tutorial for the likelihood paradigm can be found in Blume [3]. We promote the use of this likelihood paradigm as an important first step which is missing in the current practice of BE trials.

An experiment may not always produce moderate or strong evidence. For example, it may produce “weak evidence” in the form of a likelihood ratio between 1/k and k, or “misleading evidence” [30, 32], where a likelihood of k (or 1/k respectively) is obtained when in fact the denominator (numerator) hypothesis is correct. Strong misleading evidence cannot occur very often. A straightforward application of Markov’s inequality suggests that the probability of misleading evidence cannot exceed 1/k, referred to as the universal bound by Royall [30]. After an experiment is completed, whether the data represent weak evidence or not is known. In contrast, it is impossible to know whether or not the evidence is misleading when the data produced strong evidence. Hence the misleading evidence is more important concept in this context. Later we evaluate the probability of such undesirable results in the presence of nuisance parameters in the context of BE trials.

3.1. Likelihoods in the presence of nuisance parameters

When the likelihood function for a model is indexed by a single parameter, the likelihood provides the evidence for the parameter in the data, as stated in the Law of the Likelihood. However, in the BE setting, the likelihood function typically has several parameters of interest, and nuisance parameters. As such, it is challenging to present the likelihood as a function of the parameter of interest alone.

Although there is no single universally adopted solution for eliminating nuisance parameters, there are several ad-hoc methods to circumvent this difficulty. Some of these methods include orthogonal parameterization, marginal likelihoods, conditional likelihoods, estimated likelihoods, and profile likelihoods (see Royall [30]). The definitions for the estimated and profile likelihoods can be found in Pawitan [33]. Since marginal, conditional, and orthogonal likelihoods are all genuine likelihoods, they share the properties of likelihood, such as general results for the probability of misleading evidence. When these approaches are not available, we contend that the profile likelihood is the most promising alternative. Even though the universal bound on the probability of misleading evidence does not technically apply to profile likelihoods, the maximum of the probability of misleading evidence converges to the maximum possible value of the bump function [32]. In the sequel we demonstrate, that in the BE setting, the profile likelihood is a good alternative and that the probability of misleading evidence does not exceed the maximum possible value of the bump function.

In Appendix, we define our model without covariates and find the analytical solution for the profile likelihoods for the ratio of means and the ratio of variances of two formulations, which will be used in evaluating ABE and PBE in Section 4. In the presence of covariates, the profile likelihoods cannot be solved for analytically, but can be obtained numerically.

4. The Likelihood Paradigm: Application to BE Using Profile Likelihoods

Appropriate null and alternative hypotheses can be specified as follows:

$$\begin{array}{cc}\hfill H_1:\theta \le {\delta }_L\text{or}\theta \ge {\delta }_U\hfill & \hfill \text{versus}\hfill \\ \hfill H_2:{\delta }_L<\theta <{\delta }_U\hfill & \hfill \hfill \end{array}$$ (1)

where θ, is either the ratio of means or the ratio of variances, and the outcomes of interest are log transformed AUC and C_max. We begin by evaluating them separately.

Examples of profile likelihood plots are shown in Figure 1–Figure 3. An accurate portrait of the evidence can be shown by a profile likelihood plot along with 1/k likelihood intervals and the predefined limit. The 1/k likelihood interval can be interpreted as follows: the best-supported value of the parameter θ (which is the MLE) is at least k times better supported than all of the values outside the interval. Hence, the 1/k likelihood interval summarizes a set of values supported by the data, which can be used as a measure of strength of evidence for BE versus bioinequivalence (BIE). If the 1/k likelihood interval lies completely within the limit, the data support BE; the larger the k the greater strength of the evidence. We illustrate how to evaluate ABE and PBE within the likelihood paradigm using data from Chow and Liu [34] and several modified versions of their data where variances and period effects are modified.

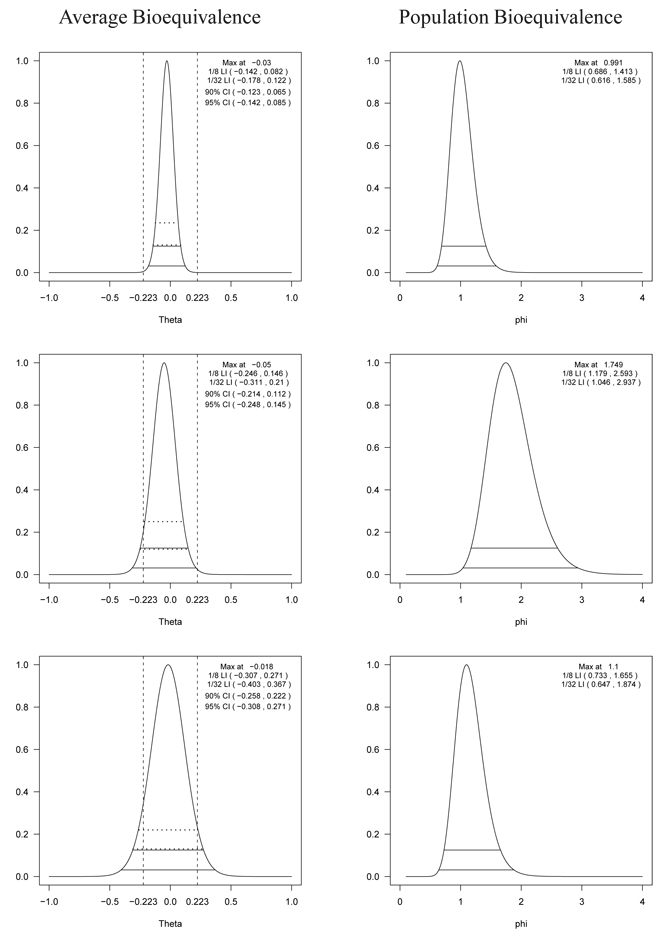
Figure 1.

The profile likelihood, 1/8 (upper solid line) and 1/32 (lower solid line) likelihood intervals for the difference of means (left panel) and the ratio of variances (right) of the test drug and the reference drug for log AUC using the data in Chow and Liu [34] (top panel), the modified version of Chow and Liu’s data [34] where the standard deviation of the test drug is 1.7 times greater than the standard deviation of the reference drug (middle panel), and the modified version of Chow and Liu’s data [34] where the standard deviations of the test drug and the reference drug are both inflated by 50% (bottom panel). In the left panel, the horizontal dotted lines represent the 90% (upper) and 95% (lower) confidence intervals estimated by a random effects model without covariates and the vertical lines represent the regulatory lower (δ_L) and upper (δ_U) limits. Notice that there are no regulatory limits available for the ratio of variances in the right panel.

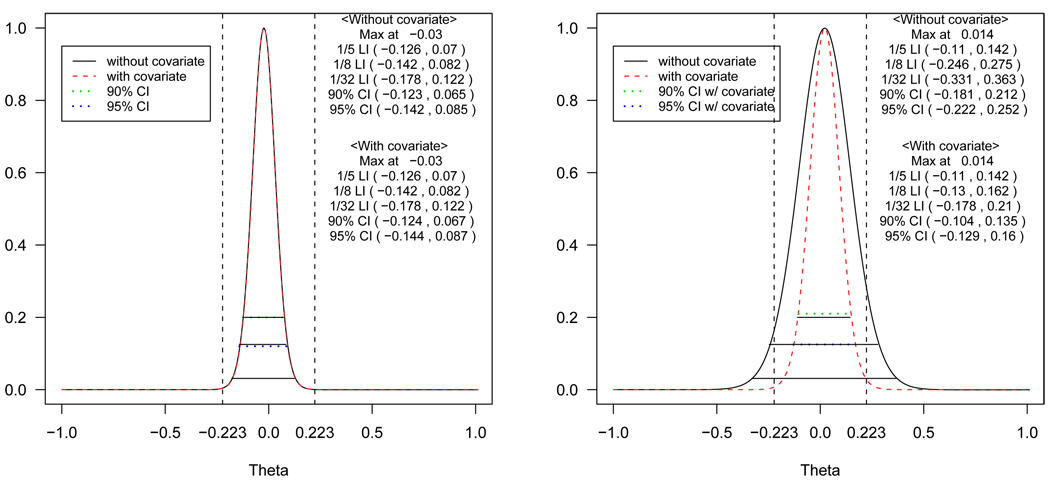
Figure 3.

The profile likelihoods with and without covariates, 1/5 (upper solid line), 1/8 (middle solid line) and 1/32 (lower solid line) likelihood intervals for the difference of means of log AUC using the data in Chow and Liu [34] (left panel) and the modified version of Chow and Liu’s data [34] where the values for the second period are inflated so that period effect exists (right panel). The horizontal dotted lines represent the 90% (upper) and 95% (lower) confidence interval estimated by a random effects models with and without covariates and the vertical lines represent the regulatory lower (δ_L) and upper (δ_U) limits.

4.1. Evidence for equivalence of the ratio of means (ABE) and the ratio of variances (PBE)

To examine the effect of the variance in evaluating ABE, we artificially modified the data from Chow and Liu [34]. First, the empirical standard deviation of the test formulation was increased by 70% compared to the reference. Second, we modified the data so that both the standard deviations of the test and reference formulations are inflated by 50%. In Figure 1, the evidences for ABE (left panel) and PBE (right panel) are presented for the original data (top panel), the first modified data (middle panel) and the second modified data (bottom panel).

For the original data, the top left panel of Figure 1 shows the profile likelihood for the ratio of means where the 1/32 likelihood interval completely lies within the BE limit. Thus, the data provide strong evidence that the two formulations are average bioequivalent. With the 90% and 95% confidence intervals, two formulations are also to be concluded as BE. The 95% confidence intervals in the figure are almost the same as the 1/8 likelihood intervals. There is a straightforward reason for this agreement. Specifically, Royall [30] showed that if the measurements follow a normal distribution, the 1/8 and 1/32 likelihood intervals are approximately the same as the 95% and 99% confidence intervals, respectively. The top right panel of Figure 1 shows that the supported values are concentrated around 1 (no difference between the two variances) suggesting that the data also support the equivalence of the variances. Notice that the profile likelihood for the ratio of variances is much wider than that for the ratio of the means. Therefore, more subjects are required to estimate the ratio of variances precisely.

For the first modified data shown in the middle panel of Figure 1, the 1/8 likelihood interval for ABE (left) does not completely fall within the limit, but the 1/5 one does. Thus, there is only weak evidence in favor of ABE over BIE, even though the TOST (equivalently the 90% confidence interval) concludes ABE. On the other hand, the middle right panel for PBE shows that the supported values of the ratio of variances are concentrated at close to 2, suggesting that there is clear evidence that the variance of the test is almost twice that of the reference. Thus, the two formulations do not appear to be population bioequivalent, even though they do appear to be average bioequivalent and TOST would conclude ABE.

In evaluating ABE for the second modified data (bottom left panel of Figure 1), notice that the interval is wide enough so that neither the 1/k likelihood intervals nor the 90% confidence interval lie within the regulatory limits; the profile likelihood plot suggests that the data does not provide enough evidence to support either ABE or BIE. In contrast, TOST concludes BIE. The width of the profile likelihoods increases as the variability increases. The figures clearly show that the variability is large relative to the scale of interest. However, from the bottom right panel of Figure 1, it appears to support the equivalence of the variances, though the 1/8 interval is wide, ranging from 0.7 – 1.7. This suggests, along with the profile likelihood plot for ABE, that we do not have enough information to clearly see whether the data supports bioequivalence or not. It is worth noting that after a second stage of data collection, it is straightforward to combine the information from the two stages within the likelihood paradigm. Specifically, there is no need for adjusting P-values as is required for frequentist sequential trials. Instead, one simply combines the two data sets and plots the profile likelihood for the parameter of interest. These two modified data sets strongly suggest the importance of jointly evaluating ABE and PBE for highly variable drugs.

4.2. Evaluating AUC and C_max jointly

In the current practice of BE trials in the USA, bioequivalence is determined using both AUC and C_max. Typically, these metrics are evaluated separately. Usually AUC and C_max are highly correlated, as they are calculated based on the drug concentrations measured from the same subject. Thus, it is natural to treat them as a vector of four measurements within each subject: AUC and C_max for the test and reference formulations, respectively. Let $\left(Y_{\mathit{\text{Ri}}}^{(A)},Y_{\mathit{\text{Ti}}}^{(A)},Y_{\mathit{\text{Ri}}}^{(C)},Y_{\mathit{\text{Ti}}}^{(C)}\right)$ be the log-transformed AUC and C_max for the reference and the test on subject i. Assume that the distribution of these measures follows a multivariate normal (MVN) as:

$$\left(\begin{array}{c}{Y}_{Ri}^{(A)}\hfill \\ Y_{Ti}^{(A)}\hfill \\ Y_{Ri}^{(C)}\hfill \\ Y_{Ti}^{(C)}\hfill \end{array}\right)\sim \text{MVN}\left\{\left(\begin{array}{c}{\mu }_R^{(A)}\hfill \\ {\mu }_T^{(A)}\hfill \\ {\mu }_R^{(C)}\hfill \\ {\mu }_T^{(C)}\hfill \end{array}\right),\mathrm{\Omega }\right\},$$ (2)

where Ω is a covariance matrix. We reparametrize such that ${\mu }_T^{(A)}={\mu }_R^{(A)}+{\theta }^{(A)}\text{and}{\mu }_T^{(C)}={\mu }_R^{(C)}+{\theta }^{(C)}$. Hence, θ^(A) and θ^(C) are the mean differences between two formulations for each outcome. Using the joint likelihood, we can find the profile likelihood with respect to θ^(A) and θ^(C) one at a time. That is, we treat one of them as the parameter of interest and consider the other as nuisance parameter along with other nuisance parameters.

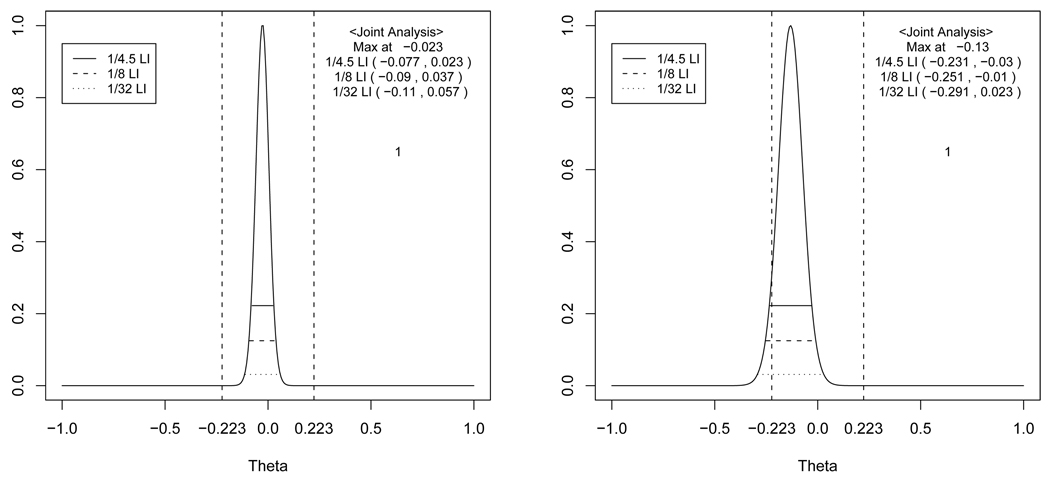
Figure 2 shows the profile likelihood for θ^(A) and θ^(C) using a data set obtained from a recent BE trial performed at a pharmaceutical company. The data were modified prior to analysis, to maintain confidentiality. The profile likelihood for θ^(A) represents very strong evidence supporting BE for AUC, whereas the profile likelihood for θ^(C) presents only moderate evidence supporting BE for C_max. TOST, however will reject BE. The test formulation has a smaller C_max then the reference. Thus, evidence suggests that the test may be absorbed more slowly than the reference although overall amounts of drug absorbed are very similar. This apparent difference in C_max might be due to higher variability of C_max compared to AUC. Indeed, this drug has a unique characteristics such that the blood concentration time profile often shows two peaks resulting in a more variable C_max. Therefore, even in this simple setting, a great deal of complexity arises. We suggest that the presentation of the evidence vis-a-vis the likelihood gives the regulatory authorities substantially more relevant information to make informed decisions than the result of the TOST procedure.

Figure 2.

The profile likelihood, 1/4.5 (upper solid line), 1/8 (middle solid line) and 1/32 (lower solid line) likelihood intervals of θ^(A) (left panel) and θ^(C) (right panel). The horizontal dotted lines represent the 90% (upper) and 95% (lower) confidence intervals estimated by a random effects model without covariates and the vertical lines represent the regulatory lower (δ_L) and upper (δ_U) limits.The joint likelihood for AUC and C_max are profiled one at a time.

4.3. Evaluating potential confounding effects

The profile likelihoods with and without adjusting for covariates (sequence and period) are shown in Figure 3 using the data from Chow and Liu [34] (left panel) and another modified version of their data (right panel), where the values for the second period were about 10% increased from the mean; hence in this modified data set, a period effect is present.

The 1/5, 1/8 and 1/32 likelihood intervals along with 90% and 95% confidence intervals are shown for comparison. When there are no period and sequence effects, the profile likelihoods with and without adjustment are almost same (left panel). In contrast, the likelihood without adjustment is much flatter than the one with adjustment (right panel) when a period effect really exists. This illustrates the point that when period or sequence effects exist, the unadjusted profile likelihood will represent weaker evidence than the adjusted one, because the variation explained by the period effects gets absorbed into the error. As confounding effects, such as carry-over effects, which are indistinguishable from treatment-period interaction or sequence effects, could be present in cross-over designs, it is advisable to always look at the profile likelihoods, with and without adjustment. It is critical to adjust for confounding variables to make correct inference in the presence of confounding variables as discussed by Blume [35] within the likelihood paradigm. A large discrepancy between the two suggests potential carry-over effects, treatment-period interaction or sequence effects.

4.4. Probabilities of undesirable results

Not all scientific experiments generate desirable results. Sometimes they produce undesirable results, such as weak evidence supporting the correct hypothesis or misleading evidence in favor of the wrong hypothesis. Royall [30] defined the probability of weak evidence as W₁ = P₁[1/k < L(θ₁)/L(θ₂) < k] and the probability of misleading evidence as M₁ = P₁[L(θ₂)/L(θ₁) ≥ k] when two point hypotheses H₁ : θ = θ₁ versus H₂ : θ = θ₂ are compared where H₁ is true. We examine the probabilities of undesirable results produced by the profile likelihoods in the context of BE trials. Because interval hypotheses (1) are used in BE trials, we consider how the probability of weak and misleading evidence can be interpreted and calculated in this setting.

The data present evidence in favor of BE if the entire 1/k likelihood interval is contained within the BE limit with the greater strength of evidence with the larger k. As an extension of the probability of misleading evidence, we define the probability of incorrectly presenting (evidence supporting) BE using likelihood intervals obtained from the true, profile and estimated likelihoods. As there is no closed form solution for this probability in the BE setting, a simulation study using Model (3) was performed assuming that the two formulations are marginally BIE with common error variances. We focused on the degree of similarity to the true likelihood under parameter values that are reasonable for BE studies. The probability of incorrectly presenting BE was calculated as the number of times of 1/k likelihood interval being contained within the BE limit divided by the number of simulations, which is an analogue of the type I error rate. Let denote LI(k), LI_P (k) and LI_E(k) be the 1/k likelihood intervals for true, profile and estimated likelihoods, respectively. Accordingly, denote P_BIE{LI(k) ⊂ (θ_L, θ_U)}, P_BIE{LI_P (k) ⊂ (θ_L, θ_U)} and P_BIE{LI_E(k) ⊂ (θ_L, θ_U)} as the corresponding probabilities of incorrectly presenting BE.

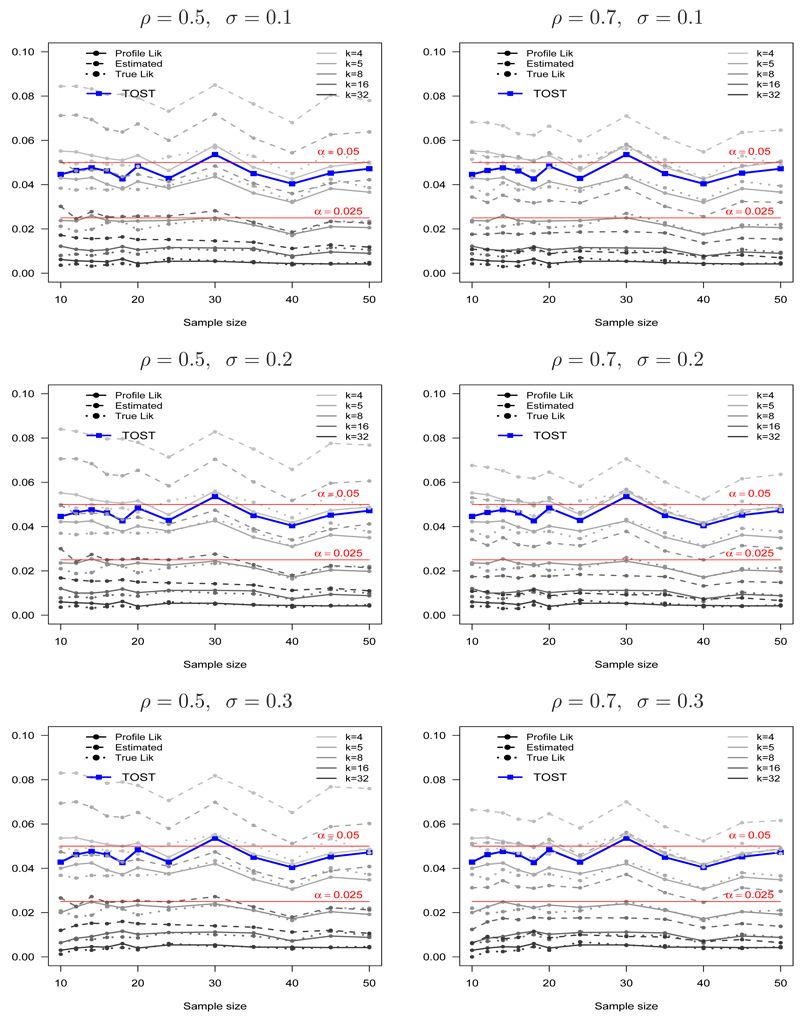
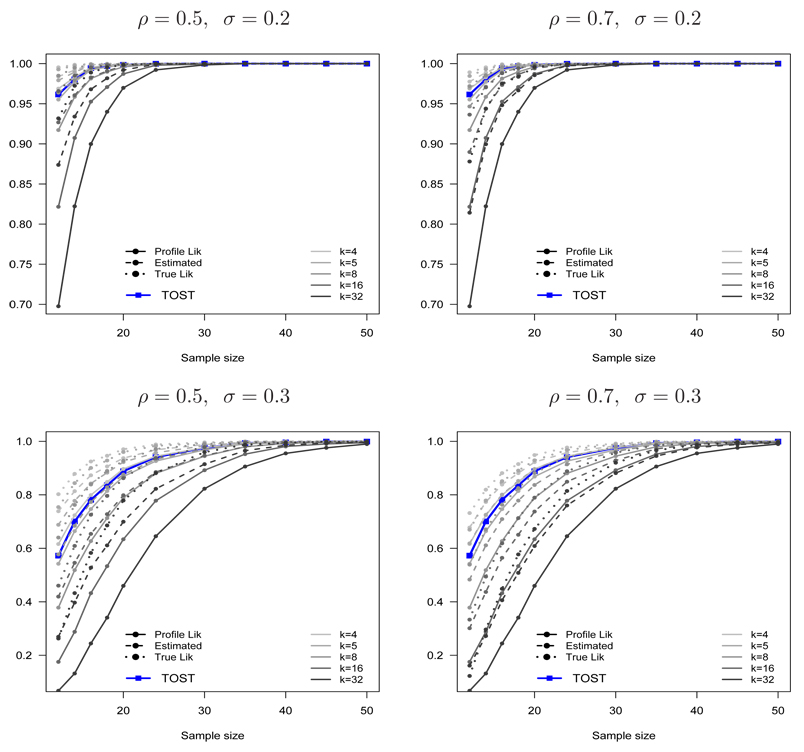
Figure 5 shows the estimated probabilities of incorrectly presenting BE, P_BIE{LI(k) ⊂ (θ_L, θ_U)}, P_BIE{LI_P(k) ⊂ (θ_L, θ_U)} and P_BIE{LI_E(k) ⊂ (θ_L, θ_U)}, as functions of k and the sample size n for ρ = (0.5, 0.7) and σ = (0.1, 0.2, 0.3). The type I error probability for TOST and a reference line 0.05 are shown for comparison. Notice that P_BIE{LI(k) ⊂ (θ_L, θ_U)} and P_BIE{LI_P(k) ⊂ (θ_L, θ_U)} are almost the same, regardless of the sample size, parameter values and choice of k. This small difference diminishes as the sample size increases. In contrast, P_BIE{LI_E(k) ⊂ (θ_L, θ_U)} is much larger than those from P_BIE{LI(k) ⊂ (θ_L, θ_U)} and P_BIE{LI_P(k) ⊂ (θ_L, θ_U)}.

Figure 5.

The probabilities of incorrectly presenting bioequivalence using the true (P_BIE{LI(k) ⊂ (θ_L, θ_U)}), profile (P_BIE{LI_P(k) ⊂ (θ_L, θ_U)}) and estimated (P_BIE{LI_E(k) ⊂ (θ_L, θ_U)}) likelihood intervals when the two formulations are marginally bioinequivalent (θ = θ_L) as a function of k = 4, 5, 8, 16, 32 for ρ = 0.5 (left panel), ρ = 0.7 (right panel), σ = 0.1 (top panel), σ = 0.2 (middle panel) and σ = 0.3 (bottom panel). The type I error for TOST and the line for (α = 0.05) is shown for comparison.

Interestingly, the probabilities of incorrectly presenting BE from the true and profile likelihoods always achieve the maximum possible value for a given k in the bump function, for a wide range of sample sizes and model parameters. It is interesting to contrast this result from the general result from point hypotheses, whose probability of misleading evidence goes to zero with the sample size. A reason for this phenomenon can be explained as follows. For point hypotheses, where Δ (the difference in the two hypothesized means) is fixed, the maximum probability of misleading evidence is reached at n = (2 log k)(σ/Δ)² (see pages 90–93 in Royall [30]). In contrast, for interval hypotheses in this BE setting, Δ is varying and hence there are many sample sizes where the maximum probability of incorrectly presenting BE can be reached. Thus, the probability of incorrectly presenting BE persists for a wide range of sample sizes. Notice, however, that the probabilities of incorrectly presenting BE from the profile likelihood P_BIE{LI_P(k) ⊂ (θ_L, θ_U)} does not go beyond the maximum value in the bump function. Also of note is that it does not appear to be applicable to the estimated likelihood.

Another simulation was performed using the same model, but the two formulations were assumed to be truly BE. We examined the probability of failure to present evidence for BE, an extension of the probability of weak evidence. This is akin to the Type II error probability. However, we present this property in terms of the probability of correctly presenting (evidence supporting) BE when the two formulations are truly bioequivalent (an analogue of power) using the same notations for the probabilities of incorrectly presenting BE except that the truth is BE: denote P_BE{LI(k) ⊂ (θ_L, θ_U)}, P_BE{LI_P(k) ⊂ (θ_L, θ_U)} and P_BE{LI_E(k) ⊂ (θ_L, θ_U)} as the probabilities of correctly presenting BE based on the 1/k likelihood intervals for true, profile and estimated likelihoods, respectively. The simulation results are shown in Figure 6. The profile likelihood represents the data as BE less often than it should, but eventually becomes close to that of the true likelihood as either σ decreases or the sample size increases. Because the discrepancy between the pseudo-likelihoods and the true likelihood tend to zero (with probability one) as n → ∞, eventually the probabilities of correctly presenting BE based on all three likelihoods also tend to one as the sample size increases (regardless of k).

Figure 6.

The probability of correctly presenting bioequivalence using the true(P_BE{LI(k) ⊂ (θ_L, θ_U)}), profile (P_BE{LI_P(k) ⊂ (θ_L, θ_U)}) and estimated (P_BE{LI_E(k) ⊂ (θ_L, θ_U)}) likelihood intervals when the two formulations are truly bioequivalent as a function of k = 4, 5, 8, 16, 32 for ρ = 0.5 (left panel), ρ = 0.7 (right panel), σ = 0.2 (top panel) and σ = 0.3 (bottom panel). The power for TOST is shown for comparison.

We also examined the coverage probabilities based on the 1/k likelihood intervals for the profile and estimated likelihoods using simulations, which is an analogue of the coverage probability of a classical confidence interval. The coverage probabilities were very good (e.g. for k = 8, it converges to 95% as the sample size increases) whereas those of the estimated likelihoods were unsatisfactory. We do not present the full results because the concept of the coverage probabilities is less important in the BE setting. In BE trials, we are not interested in finding the exact location of the true difference, but rather whether the parameter lies within an equivalence range, and hence the coverage probabilities for the parameter are not of interest.

In Section 2.4, we discussed the controversy over 100(1 − α) versus 100(1 − 2α) confidence intervals and the two hypothesis testing methods between TOST and the test of Berger and Hsu [25]. The two different hypothesis testing methods yield the same confidence intervals for most reasonable scenarios. However, the two methods can yield different intervals for pathological cases. Therefore, the coverage probabilities are different as they are based on long-run error rates. This is a dilemma due to coupling evidence and the error rates in frequentist paradigm. This was pointed out in Cox’s well known example [36] regarding a randomized test (and the corresponding confidence interval) which is the most powerful test with no practical usefulness. In the likelihood paradigm, we use the likelihood ratio to measure the strength of evidence; this evidence and the error rates are decoupled as discussed. Hence it does not suffer from this dilemma. The likelihood plot presents evidence. Since it could present undesirable results, we examined the probability of incorrectly presenting BE (analogue of the error rate) using simulations.

5. Summary and Discussion

In this manuscript we explored an alternative method for presenting and interpreting bioequivalence data as evidence, using likelihood methods. Motivated by simulations studies and prior theoretical development, we recommend the use of the profile likelihood as the relevant measure of evidence in the presence of nuisance parameters. Since we are the first to apply the profile likelihood in BE setting, we examined the operational characteristics of the profile likelihood compared with the true likelihood using simulations. In particular, the simulations results suggest that the profile likelihood behaves similarly to the true likelihood, as long as the sample size is moderate. For example, with 14 subjects in each treatment sequence and σ = 0.2 (a moderate error variance in BE trials) the probability of presenting fairly strong evidence (k = 8) using the profile likelihood is more than 0.95, which is similar to that of the true likelihood. In addition, regardless of the parameter values and the sample size, the probability of incorrectly presenting BE is very small, about 0.02, which is very similar to that of the true likelihood, suggesting that the probability of incorrectly presenting BE does not exceed the maximum possible value of the bump function. We assessed the probability of misleading evidence in BE setting to show whether it does not exceed the maximum possible value of the bump function. We found that the proposed method does not present the undesirable results often which is certainly desirable.

We also presented a straightforward extension of likelihood analysis to evaluate population BE as well as average BE in a unified framework, which is missing in the current practice of BE trials. Our results suggested that it would be important to jointly evaluate both average and population BE, especially for highly variable drugs.

The standard method in the current practice of BE trials, TOST, is based on the Neyman-Pearson testing theory. Likelihood theory and Neyman-Pearson testing theory have much in common, in that they both explicitly compare two hypotheses and depend on likelihood ratios. The simulation studies suggested that the overall properties of TOST are similar to those of the profile likelihood with k = 4.5, which only represents weak evidence. However, with TOST, it is difficult to see how much the data support BE or BIE, because of the emphasis on decision making rather than evidential interpretation. On the other hand, the likelihood plot gives the most direct and complete representation of the data as evidence. Of note, however, how strong is strong enough should be viewed within the context of each BE trial, which should depend on characteristics of the drug such as therapeutic index, variability, usage, etcetera.

Finally, we would also note that the decision for declaring BE or BIE is ultimately in the hands of the regulatory authorities and clinical pharmacologists. After examining what the data say, the regulatory authorities can decide BE or BIE depending on the characteristics of drug. For example, if the therapeutic index of a drug is narrow, they might want to use a more strict criteria. In contrast, if the therapeutic index of a drug is wide and the variability of a drug is large, then a less stringent criteria might be applied, evaluation of population BE or additional data required. We showed that within the likelihood paradigm how all of these considerations can be incorporated seamlessly. Although we concede that it would be difficult to sway current practice, we believe that the proposed likelihood methods could be a useful tool for the FDA and drug companies, especially for highly variable drugs. In this manuscript, we clarified the distinction between evidence and decision making in the BE setting and hence proposed a new paradigm to represent bioequivalence data as evidence.

Figure 4.

The legend used for Figure 5 and Figure 6.

APPENDIX

A. Profile likelihood for the ratio of means in evaluating ABE

When there is no sequence or period effects, the measures for the test and the reference formulations from a 2 × 2 cross-over BE trial can be assumed to be bivariate log-normal. We assume that the distribution of log transformed test and reference measures on the ith subject, $Y_{\mathit{\text{Ri}}}=\text{log}{Y}_{\mathit{\text{Ri}}}^{*}\text{and}{Y}_{\mathit{\text{Ti}}}=\text{log}{Y}_{\mathit{\text{Ti}}}^{*}$, follows a bivariate normal as:

$$\left(\begin{array}{c}\hfill Y_{\mathit{\text{Ri}}}\hfill \\ \hfill Y_{\mathit{\text{Ti}}}\hfill \end{array}\right)\sim \text{BVN}\left(\left(\begin{array}{c}\hfill {\mu }_R\hfill \\ \hfill {\mu }_T\hfill \end{array}\right),\left(\begin{array}{cc}\hfill {\sigma }_R^2\hfill & \hfill \rho {\sigma }_R{\sigma }_T\hfill \\ & {\sigma }_T^2\end{array}\right)\right).$$ (3)

Let y_Ri and y_Ti be log transformed observations for the reference and the test formulations on the ith subject, i = 1,…,n, and y_R and y_T be the associated vectors. The likelihood function for μ_R, μ_T, σ_R, σ_T, ρ can be written as:

$$\begin{array}{c}L({\mu }_R,{\mu }_T,{\sigma }_R,{\sigma }_T,\rho |{\mathbf{y}}_{\mathbf{R}},{\mathbf{y}}_{\mathbf{T}})\hfill \\ ={\displaystyle \prod _{i=1}^n\frac{1}{2\pi {\sigma }_R{\sigma }_T\sqrt{1-{\rho }^2}}}\hfill \\ \times \text{exp}\left\{-\frac{1}{2(1-{\rho }^2)}\left[\frac{{(y_{Ri}-{\mu }_R)}^2}{{\sigma }_R^2}-2\rho \frac{(y_{Ri}-{\mu }_R)(y_{Ti}-{\mu }_T)}{{\sigma }_R{\sigma }_T}+\frac{{(y_{Ti}-{\mu }_T)}^2}{{\sigma }_T^2}\right]\right\},\hfill \end{array}$$ (4)

where σ_R > 0, σ_T > 0 and −1 < ρ < 1.

After exponentiating, the difference of means in the log transformed scale is the ratio of the means in the original scale. Note that this equivalence relationship is only true in the instance of equal variances for the two formulations. More precisely, the ratio of medians in the original scale is equivalent to the exponentiated difference of medians in the log transformed scale. Regardless, we focus entirely on the difference of means in the log scale even though we allow non-constant variance across the two arms. This is because we are interested in whether or not the central tendency of the two formulations are sufficiently close.

We reparametrize θ = μ_T − μ_R and γ = μ_R, and reexpress the likelihood function for θ,γ, σ_R, σ_T, ρ as:

$$\begin{array}{c}L(\theta ,\gamma ,{\sigma }_R,{\sigma }_T,\rho |{\mathit{y}}_{\mathit{R}},{\mathit{y}}_{\mathit{T}})\hfill \\ \propto {\left(\frac{1}{{\sigma }_R^2{\sigma }_T^2(1-{\rho }^2)}\right)}^{n/2}\text{exp}\{-\frac{1}{2(1-{\rho }^2)}\hfill \\ \times [\frac{{\displaystyle {\sum }_{i=1}^n{(y_{Ri}-\gamma )}^2}}{{\sigma }_R^2}-2\rho \frac{{\displaystyle {\sum }_{i=1}^n(y_{Ri}-\gamma )(y_{Ti}-\theta -\gamma )}}{{\sigma }_R{\sigma }_T}+\frac{{\displaystyle {\sum }_{i=1}^n{(y_{Ti}-\theta -\gamma )}^2}}{{\sigma }_T^2}]\}.\hfill \end{array}$$ (5)

The profile likelihood of θ and γ for the likelihood function (5) can be written as:

$$\begin{array}{c}{L}_P(\theta ,\gamma |{\mathit{y}}_{\mathit{R}},{\mathit{y}}_{\mathit{T}})=\underset{{\sigma }_R,{\sigma }_T,\rho }{\text{max}}L(\theta ,\gamma ,{\sigma }_R,{\sigma }_T,\rho |{\mathit{y}}_{\mathit{R}},{\mathit{y}}_{\mathit{T}})=L(\theta ,\gamma ,{\tilde{\sigma }}_R,{\tilde{\sigma }}_T,\tilde{\rho }|{\mathit{y}}_{\mathit{R}},{\mathit{y}}_{\mathit{T}})\hfill \\ \propto {\{{\displaystyle \sum _{i=1}^n{(y_{Ri}-\gamma )}^2}{\displaystyle \sum _{i=1}^n{(y_{Ti}-\theta -\gamma )}^2}-[{\displaystyle \sum _{i=1}^n(y_{Ri}-\gamma )}{(y_{Ti}-\theta -\gamma )]}^2\}}^{-n/2},\hfill \end{array}$$ (6)

where

$$\begin{array}{cc}\hfill {\tilde{\sigma }}_R^2& =\frac{{\displaystyle {\sum }_{i=1}^n{(y_{Ri}-\gamma )}^2}}{n},\hfill \\ \hfill {\tilde{\sigma }}_T^2& =\frac{{\displaystyle {\sum }_{i=1}^n{(y_{\mathit{\text{Ti}}}-\theta -\gamma )}^2}}{n}\text{\hspace{1em}and}\hfill \\ \hfill \tilde{\rho }& =\frac{{\displaystyle {\sum }_{i=1}^n(y_{\mathit{\text{Ri}}}-\gamma )(y_{\mathit{\text{Ti}}}-\theta -\gamma )}}{\sqrt{{\displaystyle {\sum }_{i=1}^n{(y_{\mathit{\text{Ri}}}-\gamma )}^2}{\displaystyle {\sum }_{i=1}^n{(y_{\mathit{\text{Ti}}}-\theta -\gamma )}^2}}}.\hfill \end{array}$$

Then the profile likelihood of θ is:

$$\begin{array}{cc}{L}_P(\theta )\hfill & =L_P(\theta |{\mathit{y}}_{\mathit{R}},{\mathit{y}}_{\mathit{T}})=\underset{\gamma }{\text{max}}{L}_P(\theta ,\gamma |{\mathit{y}}_{\mathit{R}},{\mathit{y}}_{\mathit{T}})=L_P(\theta ,\tilde{\gamma }|{\mathit{y}}_{\mathit{R}},{\mathit{y}}_{\mathit{T}})\hfill \\ \hfill & \propto {\left\{{\displaystyle \sum _{i=1}^n{(y_{\mathit{\text{Ri}}}-\tilde{\gamma })}^2}{\displaystyle \sum _{i=1}^n{(y_{\mathit{\text{Ti}}}-\theta -\tilde{\gamma })}^2}-[{\displaystyle \sum _{i=1}^n(y_{\mathit{\text{Ri}}}-\tilde{\gamma })}{(y_{\mathit{\text{Ti}}}-\theta -\tilde{\gamma })]}^2\right\}}^{-n/2},\hfill \end{array}$$

where

$$\tilde{\gamma }=\frac{{\displaystyle \sum y_{\mathit{\text{Ri}}}}\left[{\displaystyle \sum {(y_{\mathit{\text{Ti}}})}^2-{\displaystyle \sum (y_{\mathit{\text{Ri}}}{y}_{\mathit{\text{Ti}}})}}\right]+{\displaystyle \sum y_{\mathit{\text{Ti}}}}\left[{\displaystyle \sum {(y_{\mathit{\text{Ri}}})}^2-{\displaystyle \sum (y_{\mathit{\text{Ri}}}{y}_{\mathit{\text{Ti}}})}}\right]-\theta {\displaystyle \sum y_{\mathit{\text{Ri}}}}\left({\displaystyle \sum y_{\mathit{\text{Ti}}}-y_{\mathit{\text{Ri}}}}\right)-n\theta \left[{\displaystyle \sum {(y_{\mathit{\text{Ri}}})}^2-{\displaystyle \sum (y_{\mathit{\text{Ri}}}{y}_{\mathit{\text{Ti}}})}}\right]}{n{{\displaystyle \sum {(y_{\mathit{\text{Ti}}}-y_{\mathit{\text{Ri}}})}^2-\left({\displaystyle \sum y_{\mathit{\text{Ti}}}}-{\displaystyle \sum y_{\mathit{\text{Ri}}}}\right)}}^2}.$$

B. Profile likelihood for the ratio of variances in evaluating PBE

The parameter of interest is the ratio of variances σ_T/σ_R while the means μ_R and μ_T and ρ are the nuisance parameters. Using the reparameterization θ = σ_T/σ_R and γ = σ_R, the likelihood function (4) for μ_R, μ_T, σ_R, σ_T, ρ can be reexpressed as:

$$\begin{array}{c}L({\mu }_R,{\mu }_T,\theta ,\gamma ,\rho |{\mathit{y}}_{\mathit{R}},{\mathit{y}}_{\mathit{T}})\hfill \\ ={\displaystyle \prod _{i=1}^n\frac{1}{2\pi {\gamma }^2\theta \sqrt{1-{\rho }^2}}\text{exp}\{-\frac{1}{2(1-{\rho }^2)}}\hfill \\ \times [\frac{{(y_{\mathit{\text{Ri}}}-{\mu }_R)}^2}{{\gamma }^2}-2\rho \frac{(y_{\mathit{\text{Ri}}}-{\mu }_R)(y_{\mathit{\text{Ti}}}-{\mu }_T)}{{\gamma }^2\theta }+\frac{{(y_{\mathit{\text{Ti}}}-{\mu }_T)}^2}{{\gamma }^2{\theta }^2}]\},\hfill \end{array}$$ (7)

where −1 < ρ < 1.

The profile likelihood of θ for the likelihood function (7) can be written as:

$$\begin{array}{cc}{L}_P(\theta )\hfill & =L_P(\theta |{\mathit{y}}_{\mathit{R}},{\mathit{y}}_{\mathit{T}})=\underset{{\mu }_R,{\mu }_T,\theta ,\gamma ,\rho }{\text{max}}L({\mu }_R,{\mu }_T,\theta ,\gamma ,\rho |{\mathit{y}}_{\mathit{R}},{\mathit{y}}_{\mathit{T}})\hfill \\ \hfill & =L({\tilde{\mu }}_R,{\tilde{\mu }}_T,\theta ,\tilde{\gamma },\tilde{\rho }|{\mathit{y}}_{\mathit{R}},{\mathit{y}}_{\mathit{T}})\propto {\left(\frac{1}{{\tilde{\gamma }}^2\theta \sqrt{1-{\tilde{\rho }}^2}}\right)}^n\text{exp}\{-\frac{1}{2(1-{\tilde{\rho }}^2)}\hfill \\ \hfill & \times [\frac{{\displaystyle {\sum }_{i=1}^n{(y_{\mathit{\text{Ri}}}-{\tilde{\mu }}_R)}^2}}{{\tilde{\gamma }}^2}-2\tilde{\rho }\frac{{\displaystyle {\sum }_{i=1}^n(y_{\mathit{\text{Ri}}}-{\tilde{\mu }}_R)(y_{\mathit{\text{Ti}}}-{\tilde{\mu }}_T)}}{{\tilde{\gamma }}^2\theta }+\frac{{\displaystyle {\sum }_{i=1}^n{(y_{\mathit{\text{Ti}}}-{\tilde{\mu }}_T)}^2}}{{\tilde{\gamma }}^2{\theta }^2}]\},\hfill \end{array}$$ (8)

where

$$\begin{array}{cc}\hfill {\tilde{\mu }}_R& =\frac{{\displaystyle {\sum }_{i=1}^n{y}_{\mathit{\text{Ri}}}}}{n}={\overline{y}}_R,\hfill \\ \hfill {\tilde{\mu }}_T& =\frac{{\displaystyle {\sum }_{i=1}^n{y}_{\mathit{\text{Ti}}}}}{n}={\overline{y}}_T,\hfill \\ \hfill \tilde{\rho }& =\frac{{\displaystyle {\sum }_{i=1}^n(y_{\mathit{\text{Ri}}}-{\overline{y}}_R)(y_{\mathit{\text{Ti}}}-{\overline{y}}_T)}}{\sqrt{{\displaystyle {\sum }_{i=1}^n{(y_{\mathit{\text{Ri}}}-{\overline{y}}_R)}^2}{\displaystyle {\sum }_{i=1}^n{(y_{\mathit{\text{Ti}}}-{\overline{y}}_T)}^2}}}\text{and}\hfill \\ \hfill {\tilde{\gamma }}^2& =\frac{1}{2n(1-{\tilde{\rho }}^2)}\left[{\displaystyle \sum _{i=1}^n{(y_{\mathit{\text{Ri}}}-{\tilde{\mu }}_R)}^2-2\tilde{\rho }\frac{{\displaystyle {\sum }_{i=1}^n(y_{\mathit{\text{Ri}}}-{\tilde{\mu }}_R)(y_{\mathit{\text{Ti}}}-{\tilde{\mu }}_T)}}{\theta }+\frac{{\displaystyle {\sum }_{i=1}^n{(y_{\mathit{\text{Ti}}}-{\tilde{\mu }}_T)}^2}}{{\theta }^2}}\right].\hfill \end{array}$$

Notice that only γ̃ depends on the parameter of interest.